Advances in Pure Mathematics
Vol.05 No.05(2015), Article ID:55791,9 pages
10.4236/apm.2015.55030
On Simple Completely Reducible Binary-Lie Superalgebras over 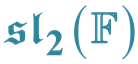
Manuel Arenas
Departamento de Matemática, Facultad de Ciencias, Universidad de Chile, Santiago, Chile
Email: mcarenascl@yahoo.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 9 March 2015; accepted 12 April 2015; published 20 April 2015

ABSTRACT
In this article, we prove that if 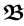 is a simple binary-Lie superalgebra whose even part is isomor- phic to
is a simple binary-Lie superalgebra whose even part is isomor- phic to 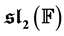 and whose odd part is a completely reducible binary-Lie-module over the even part, then
and whose odd part is a completely reducible binary-Lie-module over the even part, then  is a Lie superalgebra. We introduce also a binary-Lie module over
is a Lie superalgebra. We introduce also a binary-Lie module over  which is not completely reducible.
which is not completely reducible.
Keywords:
Binary-Lie, Super-Algebras

1. Introduction
All algebras mentioned in this article are algebras over a fixed arbitrary field  of characteristic zero.
of characteristic zero.
A superalgebra is a  -graded algebra, i.e., an algebra
-graded algebra, i.e., an algebra 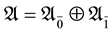 such that
such that 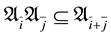 for every
for every
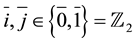 . The elements of
. The elements of  are called homogeneous. Given a homogeneous element x we de-
are called homogeneous. Given a homogeneous element x we de-
fine 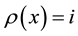 if
if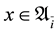 ,
,  If
If 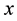 is homogeneous we say that
is homogeneous we say that 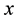 is even if
is even if![]() , and that
, and that ![]() is odd if
is odd if![]() . A superalgebra
. A superalgebra ![]() is said to be anti-commutative if
is said to be anti-commutative if
![]()
Let us remember that for any anti-commutative algebra we define the Jacobian ![]() by the formula
by the formula![]() , and a Lie algebra is an anti-commutative alge- bra whose Jacobian is the null function (see [1] or [2] for properties of Lie algebras). The super-analog of the Jacobian, i.e. the analog of the Jacobian for anti-commutative superalgebras is the function defined by
, and a Lie algebra is an anti-commutative alge- bra whose Jacobian is the null function (see [1] or [2] for properties of Lie algebras). The super-analog of the Jacobian, i.e. the analog of the Jacobian for anti-commutative superalgebras is the function defined by
![]()
Since the Jacobian is an 3-linear alternating function, its super-analog ![]() satisfies the identities
satisfies the identities
![]() (1)
(1)
for every ![]() homogeneous. A superalgebra
homogeneous. A superalgebra ![]() is a Lie superalgebra if and only if
is a Lie superalgebra if and only if ![]() for every
for every![]() , (see [3] for information about Lie superalgebras).
, (see [3] for information about Lie superalgebras).
Lie algebras are a particular case of Malcev algebras (see [4] - [7] for definition and properties of Malcev algebras). Analogously Lie superalgebras are a particular case of Malcev superalgebras, (see [8] - [10] for infor- mation about Malcev superalgebras).
An algebra is called binary-Lie if every pair of elements generates a Lie algebra. This class of algebras con- tains properly the class of Malcev algebras and it was characterized by A. T. Gainov (see Id. (2) in [11] , Section 2, p. 142). Gainov proved that an anti-commutative algebra ![]() was binary Lie if and only if
was binary Lie if and only if
![]() (2)
(2)
or equivalently
![]() (3)
(3)
for every![]() . If we define the function
. If we define the function
![]() (4)
(4)
we have that the identity ![]() is the complete linearization of (3), so it is satisfied in every binary- Lie algebra (see also [12] -[18] for information about binary-Lie algebras).
is the complete linearization of (3), so it is satisfied in every binary- Lie algebra (see also [12] -[18] for information about binary-Lie algebras).
In consequence, we say that an anti-commutative superalgebra ![]() is a binary-Lie superalgebra, if it satisfies
is a binary-Lie superalgebra, if it satisfies ![]() for every
for every ![]() homogeneous in
homogeneous in![]() , where
, where ![]() is the super-analog of the function
is the super-analog of the function![]() , i.e.
, i.e.
![]() (5)
(5)
A subset ![]() of a superalgebra
of a superalgebra ![]() is said to be a super-ideal of
is said to be a super-ideal of![]() , if and only if
, if and only if ![]() is an ideal of
is an ideal of ![]() and
and ![]() where
where ![]() for every
for every![]() . We say that a superalgebra is simple if its unique super- ideals are
. We say that a superalgebra is simple if its unique super- ideals are ![]() and the superalgebra itself. Simple Lie superalgebras have been classified by V. G. Kac in [3] and simple Malcev superalgebras have been classified by I. P. Shestakov in [19] .
and the superalgebra itself. Simple Lie superalgebras have been classified by V. G. Kac in [3] and simple Malcev superalgebras have been classified by I. P. Shestakov in [19] .
For every superalgebra![]() , the space
, the space ![]() is an algebra and
is an algebra and ![]() is a module over
is a module over![]() . If
. If ![]() is a Lie superalgebra then
is a Lie superalgebra then ![]() is a Lie algebra and
is a Lie algebra and ![]() is a Lie module. The same is true for binary-Lie superalgebras, i.e., for any binary-Lie superalgebra
is a Lie module. The same is true for binary-Lie superalgebras, i.e., for any binary-Lie superalgebra ![]() the algebra
the algebra ![]() is a binary-Lie algebra and
is a binary-Lie algebra and ![]() is a binary-Lie mo- dule over
is a binary-Lie mo- dule over![]() .
.
As usual we call ![]() the Lie algebra consisting in all two by two matrices with coficients in
the Lie algebra consisting in all two by two matrices with coficients in ![]() and null trace. This algebra is a simple Lie algebra of dimension three, moreover if
and null trace. This algebra is a simple Lie algebra of dimension three, moreover if ![]() is algebraically closed,
is algebraically closed, ![]() is the unique 3-dimensional simple Lie algebra over
is the unique 3-dimensional simple Lie algebra over![]() . Our aim is to characterize binary-Lie superalgebras whose even part is isomorphic to
. Our aim is to characterize binary-Lie superalgebras whose even part is isomorphic to ![]() and whose odd part is a completely reducible module over the even part. In particular we want to prove the following theorem.
and whose odd part is a completely reducible module over the even part. In particular we want to prove the following theorem.
Main Theorem. Let ![]() be a simple binary-Lie superalgebra, such that
be a simple binary-Lie superalgebra, such that ![]() is isomorphic to
is isomorphic to ![]() and
and ![]() is a completely reducible module over
is a completely reducible module over![]() . Then
. Then ![]() is a Lie superalgebra.
is a Lie superalgebra.
In Section 2, we explain some basics facts about binary-Lie superalgebras and irreducible binary-Lie modules over ![]() We also give an example of a non-completely reducible binary-Lie module over
We also give an example of a non-completely reducible binary-Lie module over![]() . In Section 3, we prove that, under the conditions described in the last parragraph the odd part is a Lie module over the even part. Finally in Section 4, we prove the main theorem.
. In Section 3, we prove that, under the conditions described in the last parragraph the odd part is a Lie module over the even part. Finally in Section 4, we prove the main theorem.
2. Modules and Superalgebras
According to our main purpose, we must pay attention to the theory of modules over![]() . We know that
. We know that ![]() has a basis
has a basis ![]() whose products are given by
whose products are given by![]() ,
, ![]() ,
,![]() . If
. If ![]() is an irreducible Lie module over
is an irreducible Lie module over ![]() of dimension
of dimension![]() , then
, then ![]() has a basis
has a basis ![]() whose products are defined by
whose products are defined by
![]() (6)
(6)
We call this module, the irreducible Lie module of type![]() . Besides those modules, there is a non-Lie, binary- Lie module over
. Besides those modules, there is a non-Lie, binary- Lie module over ![]() (in fact it is Malcev) called the irreducible module of type
(in fact it is Malcev) called the irreducible module of type ![]() (see Id. (5) in [16] , Section 1, p. 245). This module have a basis
(see Id. (5) in [16] , Section 1, p. 245). This module have a basis ![]() with products given by:
with products given by:
![]() (7)
(7)
The following result of A. N. Grishkov (see Lemma 3 in [16] , Section 1, p. 247) implies that there is no other irreducible ![]() -module:
-module:
Let ![]() be a binary-Lie module over
be a binary-Lie module over ![]() Then
Then ![]() has a Lie sub-module
has a Lie sub-module ![]() such that
such that ![]() can be decomposed as the direct sum of
can be decomposed as the direct sum of ![]() -modules of type
-modules of type![]() .
.
We conclude that if an irreducible module over ![]() is not Lie it has to be isomorphic to the irreducible binary-Lie module of type
is not Lie it has to be isomorphic to the irreducible binary-Lie module of type![]() .
.
Remark 1. For every ![]() let
let ![]() be the adjoint operator in
be the adjoint operator in![]() , i.e.,
, i.e.,![]() . Since
. Since ![]() and
and ![]() are nilpotent operators, both have 0 as its only eigenvalue. Therefore, if
are nilpotent operators, both have 0 as its only eigenvalue. Therefore, if ![]() satisfies that
satisfies that ![]() or
or ![]() for some
for some![]() , then
, then![]() . The set of eigenvalues of
. The set of eigenvalues of ![]() is
is![]() . Therefore, if
. Therefore, if ![]() satisfies that
satisfies that ![]() for some
for some![]() , then
, then![]() .
.
Remark 2. For every ![]() we have that
we have that ![]() implies
implies ![]() for some
for some![]() , also
, also ![]() implies
implies ![]() for some
for some![]() , and finally
, and finally ![]() implies
implies ![]() for some
for some![]() .
.
We notice that not every binary Lie module over ![]() is completely reducible as we can see in the following example:
is completely reducible as we can see in the following example:
Example 1. Let ![]() be the
be the ![]() -module where the products are given by
-module where the products are given by
![]() (8)
(8)
We observe that ![]() is an irreducible Lie module of type 0 and the quotient
is an irreducible Lie module of type 0 and the quotient ![]() is an irreducible mo- dule of type
is an irreducible mo- dule of type![]() . Let
. Let ![]() be a non trivial sub-module of
be a non trivial sub-module of![]() , then we have that
, then we have that ![]() for some scalars
for some scalars ![]() and at least one of them is different from zero. We have that
and at least one of them is different from zero. We have that ![]() and
and![]() . Thus, if
. Thus, if ![]() or
or![]() , then
, then![]() . If
. If![]() , then
, then ![]() with
with![]() . We conclude that in any case
. We conclude that in any case ![]() therefore
therefore ![]() is a sub-module of
is a sub-module of![]() , but
, but ![]() is irreducible. This implies that either
is irreducible. This implies that either ![]() or
or![]() . We conclude that
. We conclude that ![]() is the only irreducible sub-module of
is the only irreducible sub-module of ![]() which is not completely reducible.
which is not completely reducible.
Therefore, it only remains to prove that the split null extension ![]() is a binary-Lie algebra. To do that we define
is a binary-Lie algebra. To do that we define ![]() by:
by:
![]()
Note that the vector on the right hand side is written as a column to fit the equation in one line. This function gives the coordinates of the product ![]() in the ordered basis
in the ordered basis![]() , where
, where ![]() and
and ![]() hence the expression
hence the expression
![]() is checked to be identically 0.
is checked to be identically 0.
In what follows ![]() is a binary-Lie superalgebra whose even part
is a binary-Lie superalgebra whose even part ![]() is
is ![]() and whose odd part
and whose odd part ![]() is a completely reducible module over
is a completely reducible module over![]() , Under such conditions we have that
, Under such conditions we have that
![]() (9)
(9)
for some pair![]() , where
, where ![]() is a Lie irreducible module of type
is a Lie irreducible module of type ![]() for every
for every![]() , and
, and ![]() is a module of type
is a module of type ![]() for every
for every![]() .
.
We finish this section with the following lemma.
Lemma 1. Let ![]() be a simple binary-Lie superalgebra with a direct decomposition as in (9).
be a simple binary-Lie superalgebra with a direct decomposition as in (9).
Then ![]() for any
for any![]() .
.
Proof. Assume ![]() for some
for some![]() . Without loss of generality we can suppose that
. Without loss of generality we can suppose that![]() . It follows that
. It follows that![]() , where
, where![]() . We conclude
. We conclude![]() . Define
. Define
![]()
We have that ![]() is a sub-module of
is a sub-module of ![]() over
over![]() . Next define
. Next define ![]() and note that
and note that![]() .
.
We can easily see that![]() , and
, and![]() . It follows that
. It follows that![]() , whence
, whence ![]() is a
is a
super-ideal of ![]() with
with ![]() and
and![]() . It is not zero because
. It is not zero because![]() , and it is not
, and it is not ![]() since
since![]() . We obtain a contradiction with the simplicity of
. We obtain a contradiction with the simplicity of![]() . □
. □
3. Sub-Modules of Type ![]()
The aim of this section is to prove that none element of type ![]() can be found in the decomposition given by (9). This implies that
can be found in the decomposition given by (9). This implies that ![]() is a Lie module over
is a Lie module over![]() . Since
. Since ![]() is a Lie algebra,
is a Lie algebra, ![]() is zero for every
is zero for every![]() . So, if we set
. So, if we set ![]() even and
even and ![]() odd in (5), we get
odd in (5), we get
![]() . (10)
. (10)
On the other hand, if we set![]() , and
, and ![]() in (5) we get
in (5) we get
![]() . (11)
. (11)
Lemma 2. Let ![]() be a binary-Lie superalgebra with a decomposition given by (9). Let
be a binary-Lie superalgebra with a decomposition given by (9). Let ![]() be the basis of
be the basis of ![]() that satisfies (7). Then, there are three functions
that satisfies (7). Then, there are three functions ![]() such that,
such that,
for every![]() , we have
, we have![]() ,
, ![]() and
and
![]() .
.
Remark 3. Observe that, since odd elements commute, the functions ![]() and
and ![]() are always symmetric while
are always symmetric while ![]() might fail to be.
might fail to be.
Proof. Using (10), a straightforward computation gives
![]()
Therefore, Remark 2 implies that ![]() for some
for some![]() . In the same way we obtain
. In the same way we obtain
![]() ,
,
and
![]() .
.
It follows that![]() , for some
, for some![]() , and
, and![]() , for some
, for some![]() . □
. □
Lemma 3. Let ![]() be a binary-Lie superalgebra with a decomposition given by (9). Let
be a binary-Lie superalgebra with a decomposition given by (9). Let ![]() for some
for some![]() , be a sub-module of type
, be a sub-module of type![]() . Then
. Then![]() .
.
Proof. Let ![]() be the basis of
be the basis of ![]() satisfying (7), while we write
satisfying (7), while we write![]() ,
, ![]() and
and ![]() for simplicity. It suffices to prove that
for simplicity. It suffices to prove that![]() . Using (11), straightforward computations give both
. Using (11), straightforward computations give both
![]() ,
,
and
![]() .
.
It follows that![]() . Assuming this result, and using (11) again, we obtain
. Assuming this result, and using (11) again, we obtain
![]() ,
,
we conclude ![]() as claimed. □
as claimed. □
Lemma 4. Let ![]() be a simple binary-Lie superalgebra with decomposition given by (9). Let be
be a simple binary-Lie superalgebra with decomposition given by (9). Let be ![]() and
and ![]() for some pair
for some pair ![]() with
with![]() , and
, and![]() , two sub-modules of type
, two sub-modules of type![]() . Then
. Then![]() .
.
Proof. If ![]() the result follows from lemma 3. Fix a pair
the result follows from lemma 3. Fix a pair ![]() with
with![]() . Denote by
. Denote by ![]() and
and
![]() the basis of
the basis of ![]() and
and ![]() respectively satisfying (7). Because of remark 3, it suffices to prove that
respectively satisfying (7). Because of remark 3, it suffices to prove that
![]() . Using (11) and Lemma 3, straightforward computations give us the following results:
. Using (11) and Lemma 3, straightforward computations give us the following results:
![]()
![]()
It follows that![]() . Using this last result and (11) we get that
. Using this last result and (11) we get that
![]()
and
![]()
We conclude ![]() as claimed. □
as claimed. □
Lemma 5. Let ![]() be a superalgebra with a direct decomposition given by (9). Let
be a superalgebra with a direct decomposition given by (9). Let ![]() for some
for some ![]() be a Lie sub-module of type
be a Lie sub-module of type ![]() and let
and let ![]() for some
for some![]() , be a sub-module of type
, be a sub-module of type![]() . Then
. Then![]() .
.
Proof. Call![]() ,
, ![]() , the elements of the basis of
, the elements of the basis of ![]() satisfying (6) and
satisfying (6) and![]() ,
, ![]() the elements of the basis of
the elements of the basis of ![]() satisfying (7). Let
satisfying (7). Let![]() . Using (10) we obtain
. Using (10) we obtain![]() , whence it follows
, whence it follows
![]() , (12)
, (12)
for every![]() . On the other hand, setting
. On the other hand, setting![]() ,
, ![]() ,
, ![]() ,
, ![]() in (10), we obtain
in (10), we obtain
![]() . So (12) is satisfied by every
. So (12) is satisfied by every![]() . Computing the left hand side of (12), we find that, for every
. Computing the left hand side of (12), we find that, for every![]() , identity
, identity ![]() holds. At this point, a simple in- duction proves that
holds. At this point, a simple in- duction proves that
![]() (13)
(13)
for every ![]() (the case
(the case ![]() is trivial). Now using (10), we obtain
is trivial). Now using (10), we obtain
![]() .
.
Since, ![]() by Lemma 1, we have that
by Lemma 1, we have that![]() . Thus Remark 1 implies that
. Thus Remark 1 implies that![]() , and (13) implies that
, and (13) implies that ![]() for every
for every![]() .
.
Let be![]() . Using (10) again we conclude
. Using (10) again we conclude
![]() and since
and since ![]() it follows that
it follows that
![]() , (14)
, (14)
for every![]() . On the other hand, setting
. On the other hand, setting![]() ,
, ![]() ,
, ![]() ,
, ![]() in (10), we obtain
in (10), we obtain ![]() . So (14) is satisfied by every
. So (14) is satisfied by every![]() . Computing the left side of (14) when
. Computing the left side of (14) when![]() , we have
, we have
![]() (15)
(15)
Form here a simple induction proves
![]() (16)
(16)
for every![]() , where
, where
![]()
Now using (10) we obtain![]() . Since
. Since ![]() we have
we have![]() , whence remark 1 implies that
, whence remark 1 implies that![]() , and therefore (16) implies
, and therefore (16) implies ![]() for every
for every![]() . □
. □
Now we can prove the following:
Theorem 1. Let ![]() be a simple binary-Lie superalgebra, such that
be a simple binary-Lie superalgebra, such that ![]() is
is ![]() and
and ![]() has a decomposition given by (9). Then
has a decomposition given by (9). Then![]() , i.e there is no sub-module of type
, i.e there is no sub-module of type ![]() in the decomposition. In other words
in the decomposition. In other words ![]() is a Lie module over
is a Lie module over![]() .
.
Proof. Let ![]() be a space of type
be a space of type ![]() in the direct decomposition given by (9). Thanks to Lemma 4 we have
in the direct decomposition given by (9). Thanks to Lemma 4 we have ![]() for every
for every![]() . As a consequence of Lemma 5 we get
. As a consequence of Lemma 5 we get ![]() for every
for every![]() . Thus
. Thus![]() , and since
, and since![]() , we conclude that
, we conclude that ![]() is a super-ideal of
is a super-ideal of ![]() with
with ![]() and
and ![]() Since
Since ![]() and
and ![]() is simple, necessarily
is simple, necessarily![]() .
.
We have prove that the decomposition of ![]() given by (9) reduces to
given by (9) reduces to
![]() (17)
(17)
where ![]() is a Lie irreducible sub-module of type
is a Lie irreducible sub-module of type![]() , for every
, for every![]() . Therefore
. Therefore ![]() is a Lie module over
is a Lie module over![]() . □
. □
4. The Main Theorem
In this section we are going to prove that ![]() is a Lie superalgebra. We need two previous lemmas.
is a Lie superalgebra. We need two previous lemmas.
Lemma 6. Let ![]() and
and ![]() be two sub-modules of type
be two sub-modules of type ![]() and m respectively in the decomposition given by (17). Then
and m respectively in the decomposition given by (17). Then![]() , which clearly implies that
, which clearly implies that![]() .
.
Proof. Since ![]() is a Lie module if
is a Lie module if ![]() and
and ![]() we have that
we have that![]() , whence (11) becomes
, whence (11) becomes
![]() (18)
(18)
Without loss of generality, we assume that![]() . Let w be an arbitrary element of
. Let w be an arbitrary element of![]() . Set
. Set![]() ,
, ![]() ,
, ![]() , and
, and ![]() in (18). We have
in (18). We have
![]()
Therefore, if ![]() satisfy
satisfy ![]() then
then![]() . In particular, if
. In particular, if ![]() is odd, then
is odd, then ![]() for every
for every ![]() and
and![]() . Assume that
. Assume that ![]() is an even integer (zero included). If we set
is an even integer (zero included). If we set![]() ,
, ![]() ,
, ![]() , and
, and ![]() in (18) we get
in (18) we get
![]() (19)
(19)
If ![]() are two indices such that
are two indices such that ![]() and
and![]() , then
, then
![]() . Thus Equation (18) implies
. Thus Equation (18) implies
![]() .
.
for every ![]() and every
and every![]() . On the other hand (19) implies
. On the other hand (19) implies
![]()
for every![]() . Observe that
. Observe that ![]() implies
implies![]() . Then
. Then ![]() for every
for every ![]() .
.
Next, set![]() ,
, ![]() ,
, ![]() , and
, and ![]() in (18). It follows that
in (18). It follows that
![]()
Since ![]() by lemma (1), necessarily
by lemma (1), necessarily![]() . We conclude that
. We conclude that ![]() for every
for every![]() . □
. □
Lemma 7. Let![]() ,
, ![]() be two submodules of type
be two submodules of type ![]() and
and ![]() respectively in the decom-
respectively in the decom-
position given by (17). Then![]() , which clearly implies that
, which clearly implies that![]() .
.
Proof. Let be ![]() and
and ![]() the basis of
the basis of ![]() and
and ![]() respectively satisfying (6). It is enough to prove that every pair of indices
respectively satisfying (6). It is enough to prove that every pair of indices ![]() satisfies
satisfies
![]() . For simplicity we use the notation
. For simplicity we use the notation![]() ,
,
![]() and
and![]() . We call
. We call ![]() -matrix to the
-matrix to the ![]() by
by ![]() matrix with entrances in
matrix with entrances in ![]() whose
whose ![]() entrence is
entrence is ![]() (called the
(called the ![]() -coefficients). Similarly we define the
-coefficients). Similarly we define the ![]() -matrix and the
-matrix and the ![]() -matrix. We need to prove that these three matrices are the null matrix. Table 1 shows us some identities obtained using (10) by evaluating
-matrix. We need to prove that these three matrices are the null matrix. Table 1 shows us some identities obtained using (10) by evaluating ![]() in different 4-tuples in
in different 4-tuples in![]() .
.
We claim that the eight identities of Table 1 suffice to prove that the ![]() -coefficient and the
-coefficient and the ![]() -coefficient are zero, with the only possible exception of
-coefficient are zero, with the only possible exception of ![]() when
when![]() .
.
To explain how this implication works we notice that identity (1) of Table 1 implies that the ![]() -matrix is zero if
-matrix is zero if ![]() is odd and has the form in Figure 1 if
is odd and has the form in Figure 1 if ![]() is even. We also see that identities (4), (5), (7) and (8) imply that the
is even. We also see that identities (4), (5), (7) and (8) imply that the ![]() -matrix is as in Figure 2, note that, in every position where neither (4) nor (5) implies that
-matrix is as in Figure 2, note that, in every position where neither (4) nor (5) implies that ![]() -coefficient is zero, either (7) or (8) does.
-coefficient is zero, either (7) or (8) does.
We introduce now a diagram notation to keep track of the information involved by the other identities. First we write down two matrices in the same diagram as follows: If ![]() and
and ![]() are two matrices of the same size we put both in a double matrix diagram as in the left side of Figure 3.
are two matrices of the same size we put both in a double matrix diagram as in the left side of Figure 3.
![]()
Table 1. Some identities involving H-coefficients and X-coefficients implied by (10).
![]()
Figure 2. The X-matrix with m and n arbitrary.
![]()
Figure 3. Left: Example of a 2 × 2 double matrix. Right: Digram of identity (6) in Table 1.
In those diagrams we draw an arrow from a coefficient to another one if the nullity of the second one can be obtained from the nullity of the first one. We use a full triangle on the tip of the arrow if the implication works without any restriction and an empty triangle on the tip of the arrow if the implication depend of some restriction explained in the legend of the figure. With this notation, the information from identities (2) and (3) of Table 1 is encoded in Figure 4, and information from identity (6) of Table 1 is encoded in the right side of Figure 3. If a coefficient of the ![]() -matrix is in the last column or in the last row it is zero as we see in Figure 2. Otherwise we can see in Figure 4 that we can apply identity (2) or (3) in Table 1 and conclude that it is zero except in the following situations.
-matrix is in the last column or in the last row it is zero as we see in Figure 2. Otherwise we can see in Figure 4 that we can apply identity (2) or (3) in Table 1 and conclude that it is zero except in the following situations.
1) Neither identity (2) nor identity (3) can be applied. This occurs only when ![]() and
and![]() .
.
2) Identity (2) cannot be applied and the ![]() -coefficient that is pointed by the empty triangle in the right side of Figure 4 corresponds to a bullet in Figure 1. This occurs only when
-coefficient that is pointed by the empty triangle in the right side of Figure 4 corresponds to a bullet in Figure 1. This occurs only when ![]() and
and![]() .
.
3) Identity (3) cannot be applied and the ![]() -coefficient that is pointed by the empty triangle in the left side of Figure 4 corresponds to a bullet in Figure 1. This occurs only when
-coefficient that is pointed by the empty triangle in the left side of Figure 4 corresponds to a bullet in Figure 1. This occurs only when ![]() and
and![]() .
.
Therefore, the only coefficients that might be different from zero are![]() ,
, ![]() or
or ![]() We
We
call them the exceptional ![]() -coefficients.
-coefficients.
As we see in Figure 2, if any of this three coefficients is in the last row or the last column, then it is zero. Otherwise this ![]() -coefficient can be put in the right side of Figure 3 with a non-exceptional
-coefficient can be put in the right side of Figure 3 with a non-exceptional ![]() -coefficient in
-coefficient in
the other side of the arrow. Therefore, it is zero (notice that ![]() and
and ![]() can be put in the left side of Figure 3 in each tip of the arrow, but if one them is not in the last row or column, then either
can be put in the left side of Figure 3 in each tip of the arrow, but if one them is not in the last row or column, then either ![]() or
or ![]() is available).
is available).
We have proved that the ![]() -matrix is the matrix zero. Now we can see that every
-matrix is the matrix zero. Now we can see that every ![]() -coefficient different than
-coefficient different than ![]() can be put either in the left side or in the right side of Figure 4 with an
can be put either in the left side or in the right side of Figure 4 with an ![]() -coefficient on the other side of the arrow. We conclude that
-coefficient on the other side of the arrow. We conclude that![]() , for every
, for every![]() .
.
Now we have to look at Table 2. Information from identities (1) and (2) is encoded in Figure 5. We can see that the ![]() -coefficients are 0 except in three cases.
-coefficients are 0 except in three cases.
1) Neither identity (1) nor identity (2) can be applied. This occurs only for![]() .
.
2) Identity (1) cannot be applied, and the ![]() -coefficient pointed by the triangle in the right side of Figure 5 is
-coefficient pointed by the triangle in the right side of Figure 5 is![]() . This occurs only for
. This occurs only for ![]() when
when![]() .
.
![]()
Figure 4. Diagram of identities (2) and (3) in Table 1 with their restrictions.
![]()
Figure 5. Diagram of identities (1) and (2) in Table 2.
![]()
Table 2. Identities involving the H-coefficients and A-coefficients implied by (10) and the nullity of the X-matrix.
3) Identity (2) cannot be applied, and the ![]() -coefficient pointed by the triangle in the left side of Figure 5 is
-coefficient pointed by the triangle in the left side of Figure 5 is![]() . This occurs only for
. This occurs only for ![]() when
when![]() .
.
To prove that ![]() we set
we set ![]() in identity (3) of Table 2. This always can be done since
in identity (3) of Table 2. This always can be done since![]() . The second and the third cases occur only if
. The second and the third cases occur only if![]() , and in this case, it is enough to prove that just one among
, and in this case, it is enough to prove that just one among![]() ,
, ![]() ,
, ![]() is zero. In this case the desired result can be proved using identity (3) of Table 2 with
is zero. In this case the desired result can be proved using identity (3) of Table 2 with![]() , but we are able do that provided
, but we are able do that provided![]() . Thus, the only coefficients we have not proved yet to be zero, are
. Thus, the only coefficients we have not proved yet to be zero, are ![]() when
when![]() . This is the reason why we included identity (4) in Table 2. At this point we have proved that every
. This is the reason why we included identity (4) in Table 2. At this point we have proved that every ![]() -coefficient is zero, every
-coefficient is zero, every ![]() -coefficient is zero and every
-coefficient is zero and every ![]() -coefficient is zero. This means that
-coefficient is zero. This means that
![]()
for every pair ![]() finishing thus the proof of the lemma. □
finishing thus the proof of the lemma. □
Proof of the main theorem: We need to prove that ![]() for every w, u, v homogeneous. Since
for every w, u, v homogeneous. Since ![]() is a Lie algebra
is a Lie algebra ![]() whenever these three elements are even. Theorem 1 implies that the identity holds whenever two of these elements are even and the other one is odd. So we only have to prove that
whenever these three elements are even. Theorem 1 implies that the identity holds whenever two of these elements are even and the other one is odd. So we only have to prove that ![]() when at least two of this three elements are odd. Thanks to the simmetries described in identity (1) it suffices to prove that
when at least two of this three elements are odd. Thanks to the simmetries described in identity (1) it suffices to prove that ![]() when u and v are odd. Because of the decomposition given by (17) we only have to prove that the identity holds when
when u and v are odd. Because of the decomposition given by (17) we only have to prove that the identity holds when ![]() for some
for some ![]() and
and ![]() for some
for some![]() , but this follows from Lemma 7 if w is even, and from Lemma 6 if w is odd. This proves that
, but this follows from Lemma 7 if w is even, and from Lemma 6 if w is odd. This proves that ![]() is a Lie superalgebra. □
is a Lie superalgebra. □
Funding
Supported by FONDECYT process 2010/11100092.
References
- Humphreys, J.E. (1972) Introduction to Lie Algebras and Representation Theory. Springer Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-6398-2
- Jacobson, N. (1979) Lie Algebras. Dover, New York.
- Kac, V.G. (1977) Lie Superalgebras. Advances in Mathematics, 26, 8-96. http://dx.doi.org/10.1016/0001-8708(77)90017-2
- Malcev, A.I. (1955) Analytic Loops. Mat. Sb. N.S, 36, 569-576.
- Sagle, A.A. (1961) Malcev Algebras. Transactions of the American Mathematical Society, 101, 426-458. http://dx.doi.org/10.1090/S0002-9947-1961-0143791-X
- Perez-Izquierdo, J.M. and Shestakov, I.P. (2004) An Envelope for Malcev Algebras. Journal of Algebra, 272, 379-393. http://dx.doi.org/10.1016/S0021-8693(03)00389-2
- Shestakov, I.P. (1998) Speciality Problem for Malcev Algebras and Poisson Malcev Algebras. Nonassociative Algebra and Its Applications. São Paulo, 365-371.
- Shestakov, I.P. and Zhukavets, N. (2007) The Free Malcev Superalgebras on One Odd Generator and Related Superalgebras. Journal of Mathematical Sciences, 140, 243-249. http://dx.doi.org/10.1007/s10958-007-0421-x
- Shestakov, I.P. and Zhukavets, N. (2006) The Universal Multiplicative Envelope of the Free Malcev Superalgebra on One Odd Generator. Communications in Algebra, 34, 1319-1344. http://dx.doi.org/10.1080/00927870500454570
- Shestakov, I.P. and Zhukavets, N. (2006) The Malcev Poisson Supelalgebra of the Free Malcev Superalgebra on One Odd Generator. Journal of Algebra and Its Applications, 5, 521-535. http://dx.doi.org/10.1142/S0219498806001867
- Gainov, A.T. (1957) Identical Relations for Binary-Lie Rings. Uspehi Mat. Nauk (N.S.), 12, 141-146.
- Arenas, M. and Shestakov, I.P. (2011) On Speciality of Binary-Lie Algebras. Journal of Algebra and Its Applications, 10, 257-268. http://dx.doi.org/10.1142/S0219498811004550
- Filipov, V.T. (2008) Binary-Lie Algebras Satisfying the Third Engel Condition. Sibirskii Matematicheskii Zhurnal, 49, 928-933. http://dx.doi.org/10.1007/s11202-008-0071-3
- Gainov, A.T. (1963) Binary Lie Algebras of Lower Ranks. Algebra i Logika, 2, 21-40.
- Grishkov, A.N. (1977) On the Theory of Finite Dimensional Binary Lie Algebras. Algebra i Logika, 16, 549-556. http://dx.doi.org/10.1007/BF01669476
- Grishkov, A.N. (1980) Structure and Representaion of Binary Lie Algebras. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya, 44, 999-1030.
- Grishkov, A.N. (1988) Finite-Dimensional Solvable Binary Lie Algebras. Sibirskii Matematicheskii Zhurnal, 29, 48- 52.
- Kuzmin, E.N. (1998) Binary Lie Algebras of Small Dimentions. Algebra and Logic, 37, 181-186. http://dx.doi.org/10.1007/BF02671589
- Shestakov, I.P. (1993) Prime Malcev Superalgebras. Mathematics, 182, 1357-1366. http://dx.doi.org/10.1070/SM1993v074n01ABEH003337
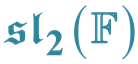



 is a simple binary-Lie superalgebra whose even part is isomor- phic to
is a simple binary-Lie superalgebra whose even part is isomor- phic to 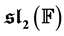 and whose odd part is a completely reducible binary-Lie-module over the even part, then
and whose odd part is a completely reducible binary-Lie-module over the even part, then  is a Lie superalgebra. We introduce also a binary-Lie module over
is a Lie superalgebra. We introduce also a binary-Lie module over  which is not completely reducible.
which is not completely reducible.
 of characteristic zero.
of characteristic zero. -graded algebra, i.e., an algebra
-graded algebra, i.e., an algebra 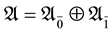 such that
such that 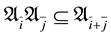 for every
for every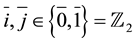 . The elements of
. The elements of  are called homogeneous. Given a homogeneous element x we de-
are called homogeneous. Given a homogeneous element x we de-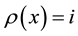 if
if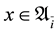 ,
,  If
If 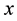 is homogeneous we say that
is homogeneous we say that 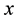 is even if
is even if
























































































































































































































































































































































































































































































































