Advances in Pure Mathematics
Vol.3 No.1(2013), Article ID:27001,7 pages DOI:10.4236/apm.2013.31007
Bc-Open Sets in Topological Spaces
Department of Mathematics, Faculty of Science, University of Zakho, Zakho, Iraq
Email: hariwan_math@yahoo.com
Received August 1, 2012; revised September 24, 2012; accepted October 3, 2012
Keywords: Closed; b-Open; Bc-Open
ABSTRACT
In this paper, we introduce a new class of b-open sets called Bc-open, this class of sets lies strictly between the classes of θ-semi open and b-open sets. We also study its fundamental properties and compare it with some other types of sets and we investigate further topological properties of sets and we introduce and investigate new class of space named Bccompact.
1. Introduction
In 1937, regular open sets were introduced and used to define the semi-regularization space of a topological space. Throughout this paper,  and
and 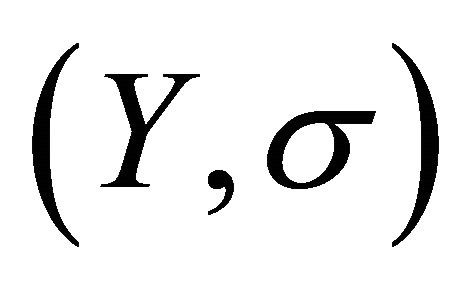 stand for topological spaces with no separation axioms assumed unless otherwise stated. For a subset A of X, the closure of A and the interior of A will be denoted by
stand for topological spaces with no separation axioms assumed unless otherwise stated. For a subset A of X, the closure of A and the interior of A will be denoted by  and
and  respectively. Stone [1] defined a subset A of a space X to be a regular open if
respectively. Stone [1] defined a subset A of a space X to be a regular open if  . Norman Levine [2] defined a subset A of a space X to be a semi-open if
. Norman Levine [2] defined a subset A of a space X to be a semi-open if , or equivalently, a set A of a space X will be termed semiopen if and only if there exists an open set
, or equivalently, a set A of a space X will be termed semiopen if and only if there exists an open set  such that
such that . Mashhour et al. [3] defined a subset A of a space X to be a preopen if
. Mashhour et al. [3] defined a subset A of a space X to be a preopen if . Njastad [4] defined a subset A of a space X to be an
. Njastad [4] defined a subset A of a space X to be an  -open if
-open if . The complement of a semi-open (resp., regular open) set is said to be semi-closed [5] (resp., regular closed). The intersection of all semi-closed sets of X containing A is called the semi-closure [6] of A. The union of semi-open sets of X contained in A is called the semi-interior of A. Joseph and Kwack [7] introduced the concept of
. The complement of a semi-open (resp., regular open) set is said to be semi-closed [5] (resp., regular closed). The intersection of all semi-closed sets of X containing A is called the semi-closure [6] of A. The union of semi-open sets of X contained in A is called the semi-interior of A. Joseph and Kwack [7] introduced the concept of  -semi open sets using semi-open sets to improve the notion of
-semi open sets using semi-open sets to improve the notion of  -closed spaces. Also Joseph and Kwack [7] introduced that a subset A of a space X is called
-closed spaces. Also Joseph and Kwack [7] introduced that a subset A of a space X is called  -semi-open if for each
-semi-open if for each , there exists a semi-open set
, there exists a semi-open set 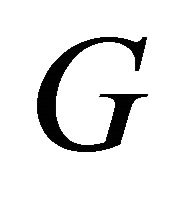 such that
such that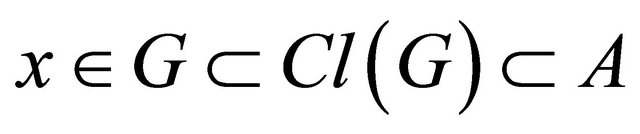 . It is well-known that, a space X is called
. It is well-known that, a space X is called  if to each pair of distinct points x, y of X, there exists a pair of open sets, one containing x but not y and the other containing y but not x, as well as is
if to each pair of distinct points x, y of X, there exists a pair of open sets, one containing x but not y and the other containing y but not x, as well as is  if and only if for any point
if and only if for any point , the singleton set
, the singleton set  is closed. A space X is regular if for each
is closed. A space X is regular if for each  and each open set G containing x, there exists an open set H such that
and each open set G containing x, there exists an open set H such that
 . Ahmed [8] defined a topological space
. Ahmed [8] defined a topological space  to be s**-normal if and only if for every semi-closed set F and every semi-open set G containing F, there exists an open set H such that
to be s**-normal if and only if for every semi-closed set F and every semi-open set G containing F, there exists an open set H such that  . In 1968, Velicko [9], defined the concepts of
. In 1968, Velicko [9], defined the concepts of  -open and
-open and  -open as, a subset A of a space X is called
-open as, a subset A of a space X is called  -open (resp.,
-open (resp.,  -open) if for each
-open) if for each , there exists an open set
, there exists an open set  such that
such that  (resp.,
(resp., ). Di Maio and Noiri [10] introduced that a subset A of a space X is called semi-
). Di Maio and Noiri [10] introduced that a subset A of a space X is called semi- -open if for each
-open if for each , there exists a semi-open set G such that
, there exists a semi-open set G such that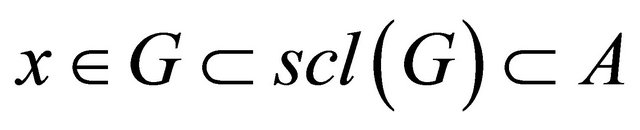 . The family of all open (resp., semi-open,
. The family of all open (resp., semi-open,  -open, preopen, θ-semi-open, semi-θ-open, θ-open, δ-open, regular open, semi-closed and regular closed) subsets of a topological space
-open, preopen, θ-semi-open, semi-θ-open, θ-open, δ-open, regular open, semi-closed and regular closed) subsets of a topological space  are denoted by
are denoted by  (resp.,
(resp.,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 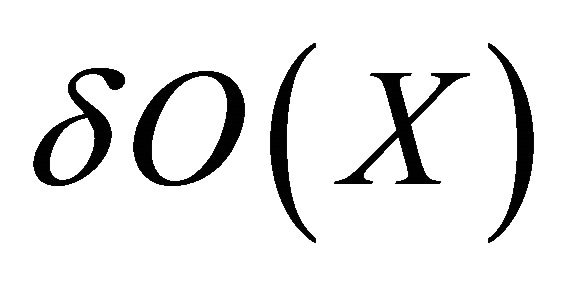 ,
,  ,
,  and
and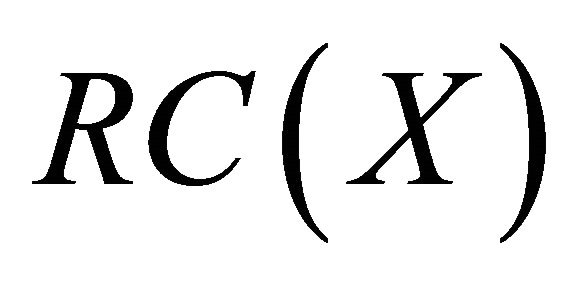 ).
).
Definition 1.1. [11] A subset A of a space X is called b-open if . The family of all b-open subsets of a topological space
. The family of all b-open subsets of a topological space  is denoted by
is denoted by 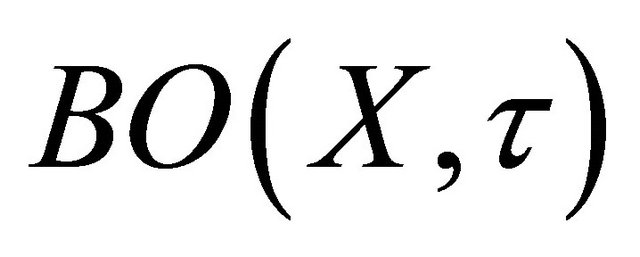 or (Briefly.
or (Briefly. ).
).
In 1999, J. Dontchev and T. Noiri [12] have shown the following lemma:
Lemma 1.2. For a subset A of a space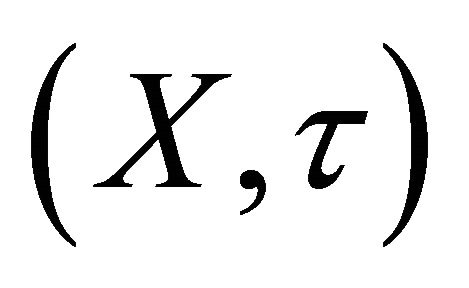 , the following conditions are equivalent:
, the following conditions are equivalent:
1) 
2) 
3) 
4) 
Theorem 1.3. [13] If  is s**-normal, then
is s**-normal, then
 .
.
We recall that a topological space X is said to be extremally disconnected [14] if 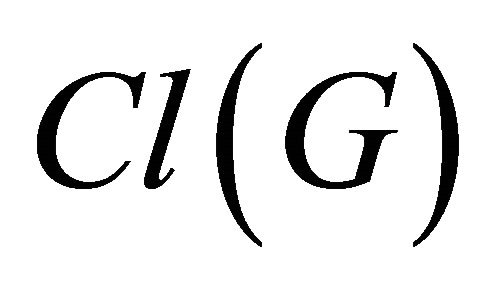 is open for every open set G of X.
is open for every open set G of X.
Definition 1.4. [15] A space X is called locally indiscrete if every open subset of X is closed.
Theorem 1.5. [13] A space X is extremally disconnected if and only if .
.
Theorem 1.6. [15] A space  is extremally disconnected if and only if
is extremally disconnected if and only if .
.
2. Bc-Open Sets
In this section, we introduce a new class of b-open sets called Bc-open sets in topological spaces.
Definition 2.1. A subset A of a space X is called Bcopen if for each , there exists a closed set F such that
, there exists a closed set F such that . The family of all Bc-open subsets of a topological space
. The family of all Bc-open subsets of a topological space  is denoted by
is denoted by  or (Briefly.
or (Briefly. ).
).
Proposition 2.2. A subset A of a space X is Bc-open if and only if A is b-open and it is a union of closed sets. That is 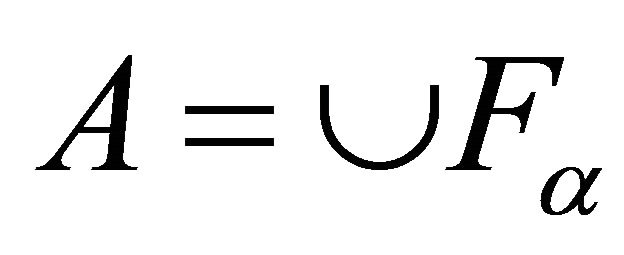 where A is b-open set and
where A is b-open set and  is closed sets for each
is closed sets for each .
.
Proof. Obvious.
It is clear from the definition that every Bc-open subset of a space X is b-open, but the converse is not true in general as shown by the following example.
Example 2.3. Consider  with the topology
with the topology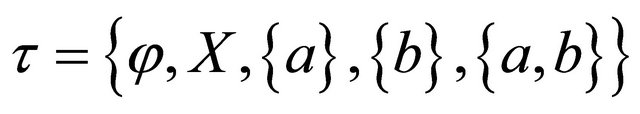 . Then the family of closed sets are:
. Then the family of closed sets are: . We can find easily the following families:
. We can find easily the following families:
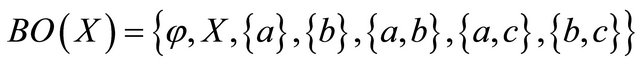
and
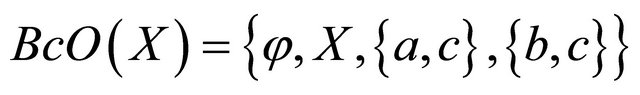 .
.
Then 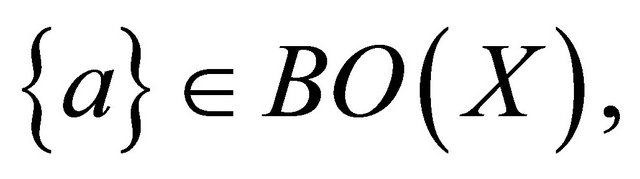 but
but 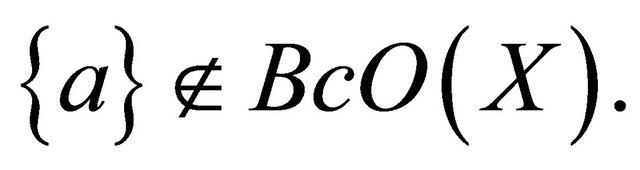
The next example notices that a Bc-open set need not be a closed set.
Example 2.4. Consider the space R with usual topology, if  such that
such that , then
, then  is Bc-open set, but it is not closed.
is Bc-open set, but it is not closed.
The following result shows that the arbitrary union of Bc-open sets in a topological space  is Bc-open.
is Bc-open.
Proposition 2.5. Let  be a collection of Bc-open sets in a topological space X. Then
be a collection of Bc-open sets in a topological space X. Then
 is Bc-open.
is Bc-open.
Proof. Let  be a Bc-open set for each
be a Bc-open set for each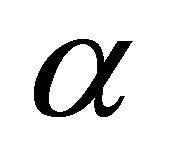 , then
, then 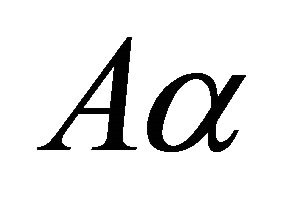 is
is  -open and hence
-open and hence  is b-open. Let
is b-open. Let , there exist
, there exist  such that
such that . Since
. Since 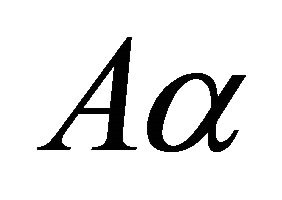 is b-open for each
is b-open for each , there exists a closed set
, there exists a closed set  such that
such that
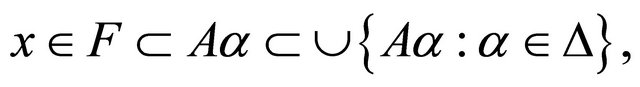
so  Therefore,
Therefore,  is Bc-open set.
is Bc-open set.
The following example shows that the intersection of two Bc-open sets need not be Bc-open set.
Example 2.6. Consider the space 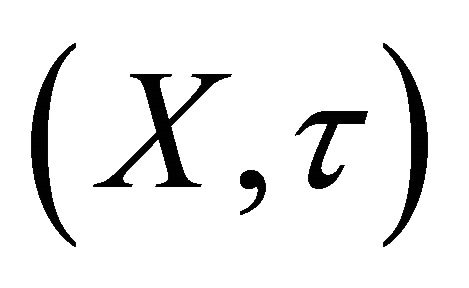 as in example 2.3, There
as in example 2.3, There  and
and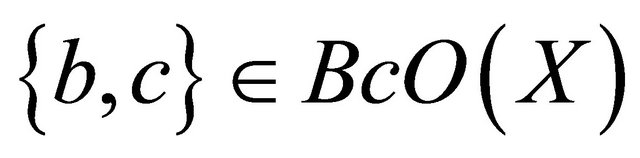 , but
, but 
From the above example we notice that the family of all Bc-open subsets of a space X is a supratopology and need not be a topology in general.
The following result shows that the family of all Bcopen sets will be a topology on X.
Proposition 2.7. If the family of all b-open sets of a space X is a topology on X, then the family of Bc-open is also a topology on X.
Proof. Clearly 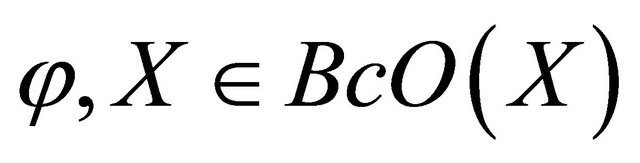 and by Proposition 2.5 the union of any family of Bc-open sets is Bc-open. To complete the proof it is enough to show that the finite intersection of Bc-open sets is Bc-open set. Let A and B be two Bc-open sets then A and B are
and by Proposition 2.5 the union of any family of Bc-open sets is Bc-open. To complete the proof it is enough to show that the finite intersection of Bc-open sets is Bc-open set. Let A and B be two Bc-open sets then A and B are  -open sets. Since
-open sets. Since 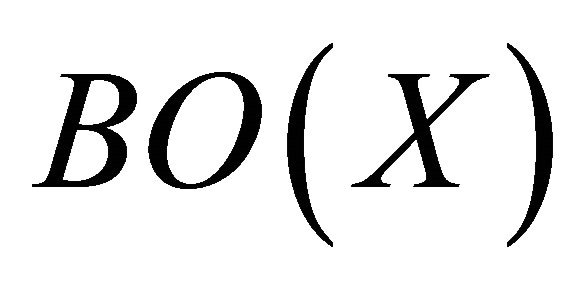 is a topology on X, so
is a topology on X, so  is b-open. Let
is b-open. Let , then
, then  and
and , so there exists F and E such that
, so there exists F and E such that 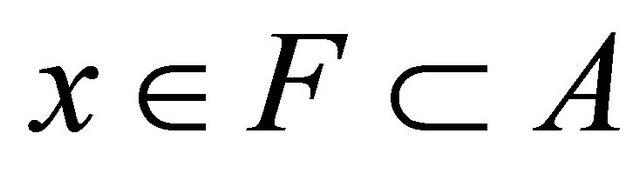 and
and  this implies that
this implies that . Since any intersection of closed sets is closed,
. Since any intersection of closed sets is closed,  is closed set. Thus
is closed set. Thus  is Bc-open set. This completes the proof.
is Bc-open set. This completes the proof.
Proposition 2.8. The set A is Bc-open in the space  if and only if for each
if and only if for each , there exists a Bcopen set B such that
, there exists a Bcopen set B such that .
.
Proof. Assume that A is Bc-open set in the , then for each
, then for each , put
, put  is Bc-open set containing x such that
is Bc-open set containing x such that .
.
Conversely, suppose that for each , there exists a Bc-open set B such that
, there exists a Bc-open set B such that , thus
, thus  where
where  for each x, therefore A is Bc-open set.
for each x, therefore A is Bc-open set.
In the following proposition, the family of b-open sets is identical to the family of Bc-open sets.
Proposition 2.9. If a space X is  -space, then the families
-space, then the families 
Proof. Let A be any subset of a space X and 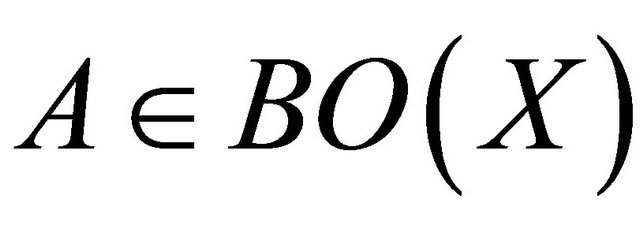 , if
, if , then
, then 
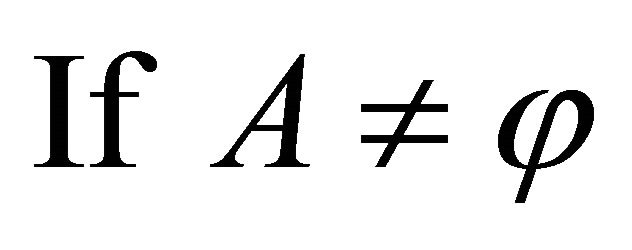 , then for each
, then for each . Since a space X is
. Since a space X is , then every singleton is closed set and hence
, then every singleton is closed set and hence . Therefore
. Therefore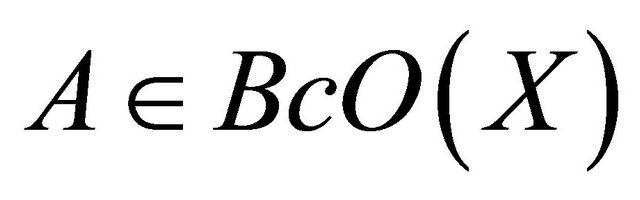 . Hence
. Hence , but
, but
 generally, therefore
generally, therefore
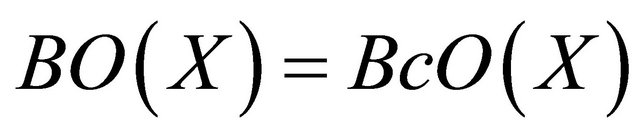 .
.
Proposition 2.10. Every  -semi open set of a space X is Bc-open set.
-semi open set of a space X is Bc-open set.
Proof. Let A be a  -semi open set in X, then for each
-semi open set in X, then for each , there exists a semi-open set G such that
, there exists a semi-open set G such that
 , so
, so  for each
for each 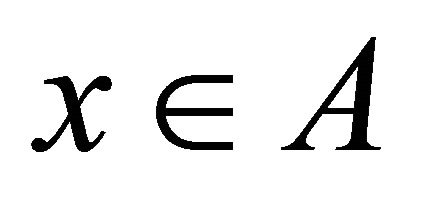 implies that
implies that 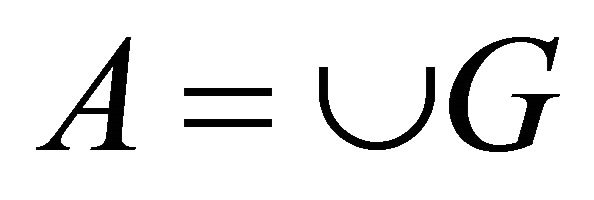 which is semi-open set and
which is semi-open set and 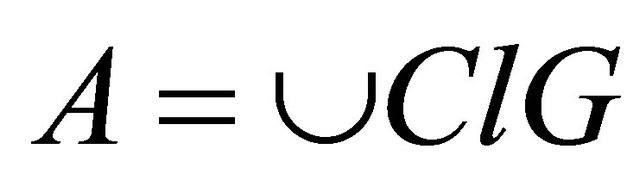 is a union of closed sets, by Proposition 2.2, A is Bc-open set.
is a union of closed sets, by Proposition 2.2, A is Bc-open set.
The following example shows that the converse of the above Proposition may not be true in general.
Example 2.11. Since a space X with cofinite topology is T1, and then the family of b-open and Bc-open sets are identical. Hence any open set G is Bc-open but not  - semi open.
- semi open.
The proof of the following corollaries is clear from their definitions.
Corollary 2.12. Every  -open set is Bc-open.
-open set is Bc-open.
Corollary 2.13. Every regular-closed is Bc-open set.
Proposition 2.14. If a topological space 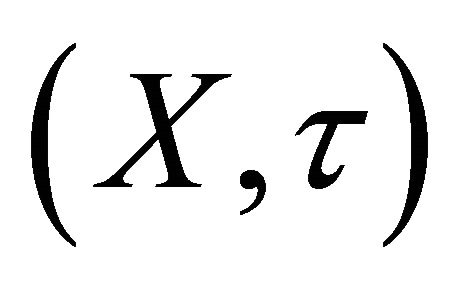 is locally indiscrete, then
is locally indiscrete, then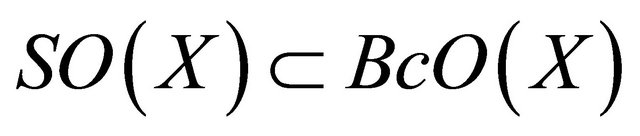 .
.
Proof. Let A be any subset of a space X and  , if
, if , then
, then . If
. If , then
, then . Since X is locally indiscrete, then
. Since X is locally indiscrete, then 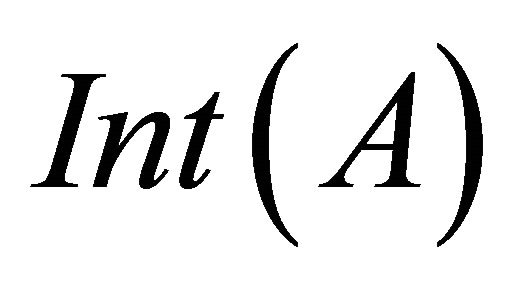 is closed and hence
is closed and hence , this implies that for each
, this implies that for each ,
, . Therefore, A is Bc-open set. Hence
. Therefore, A is Bc-open set. Hence .
.
Remark 2.15. Since every open set is semi-open, it follows that if a topological space  is
is  or locally indiscrete, then
or locally indiscrete, then 
Proposition 2.16. Let  be a topological space, if X is regular, then
be a topological space, if X is regular, then 
Proof. Let A be any subset of a space X, and A is open, if , then
, then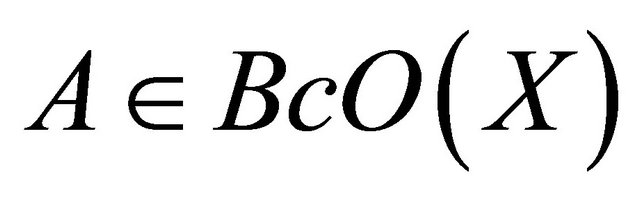 . If
. If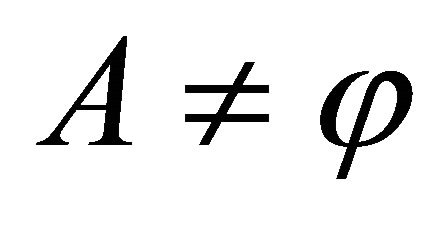 , since X is regular, so for each
, since X is regular, so for each , there exists an open set G such that
, there exists an open set G such that . Thus we have
. Thus we have  . Since
. Since  and hence
and hence , therefore
, therefore .
.
Proposition 2.17. Let  be an extremally disconnected space. If
be an extremally disconnected space. If , then
, then .
.
Proof. Let . If
. If , then
, then  . If
. If . Since a space X is extremally disconnected, then by Theorem 1.5,
. Since a space X is extremally disconnected, then by Theorem 1.5, . Hence
. Hence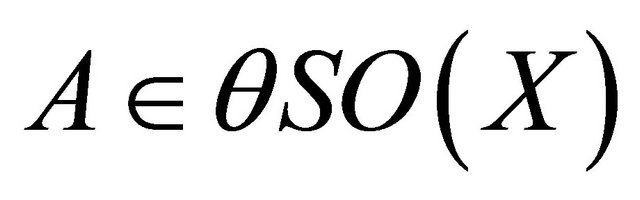 . But
. But  in general. Therefore,
in general. Therefore, .
.
Corollary 2.18. Let be an extremally disconnected space. If
be an extremally disconnected space. If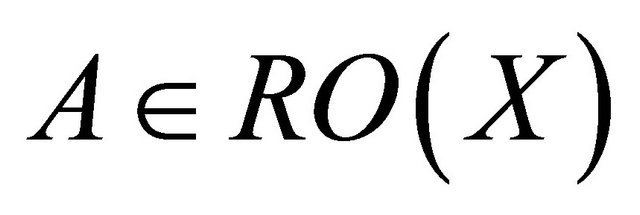 , then
, then .
.
Proof. The proof is directly from Proposition 2.28 and the fact that 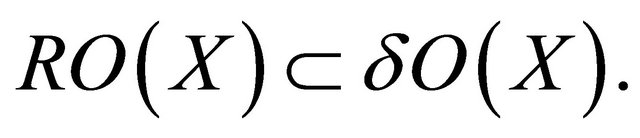
Proposition 2.19. Let be an s**-normal space. If
be an s**-normal space. If , then
, then .
.
Proof. Let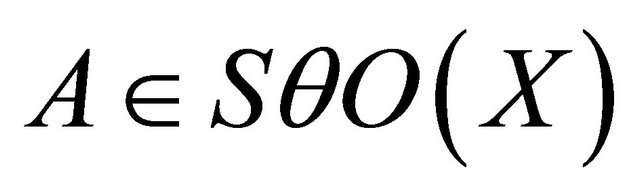 . If
. If , then
, then  . If
. If , since a space X is s**-normal, then by Theorem 1.3,
, since a space X is s**-normal, then by Theorem 1.3,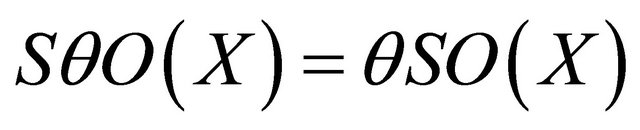 . Hence
. Hence  . But
. But  in general. Therefore,
in general. Therefore, .
.
Proposition 2.20. For any subset A of a space  and
and . The following conditions are equivalent:
. The following conditions are equivalent:
1) A is regular closed.
2) A is closed and Bc-open.
3) A is closed and b-open.
4) A is α-closed and b-open.
5) A is pre-closed and b-open.
Proof. Follows from Lemma 1.2.
Definition 2.21. A subset B of a space X is called Bcclosed if  is Bc-open. The family of all Bc-closed subsets of a topological space
is Bc-open. The family of all Bc-closed subsets of a topological space is denoted by
is denoted by  or (Briefly,
or (Briefly,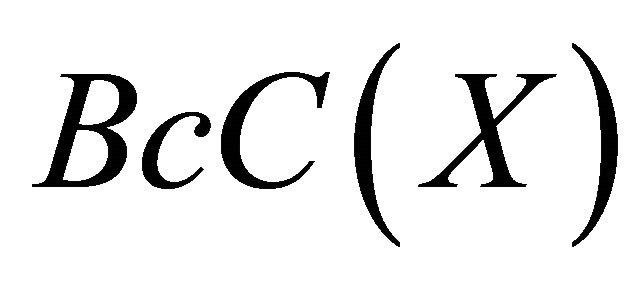 ).
).
Proposition 2.22. A subset B of a space X is Bc-closed if and only if B is a b-closed set and it is an intersection of open sets.
Proof. Clear.
Proposition 2.23. Let  be a collection of Bc-closed sets in a topological space X. Then
be a collection of Bc-closed sets in a topological space X. Then 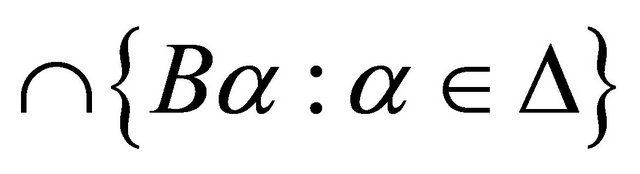 is Bc-closed.
is Bc-closed.
Proof. Follows from Proposition 2.5.
The union of two Bc-closed sets need not be Bc-closed as is shown by the following counterexample.
Example 2.24. In Example 2.3, the family of Bcclosed subset of X is: . Here
. Here  and
and , but
, but
 .
.
All of the following results are true by using complement.
Proposition 2.25. If a space X is , then
, then

Proposition 2.26. For any subset B of a space X. If , then
, then .
.
Corollary 2.27. Each  -closed set is Bc-closed.
-closed set is Bc-closed.
Corollary 2.28. Each regular open set is Bc-closed.
Proposition 2.29. If a topological space  is locally indiscrete, then
is locally indiscrete, then .
.
Proposition 2.30. Let  be a topological space, if X is regular or locally indiscrete, then the family of closed sets is a subset of the family of Bc-closed sets.
be a topological space, if X is regular or locally indiscrete, then the family of closed sets is a subset of the family of Bc-closed sets.
Proposition 2.31. Let  be any extremally disconnected space. If
be any extremally disconnected space. If , then
, then .
.
Corollary 2.32. Let  be an extremally disconnected space. If
be an extremally disconnected space. If , then
, then .
.
Proposition 2.33. Let  be a s**-normal space. If
be a s**-normal space. If , then
, then .
.
Proposition 2.34. For any subset B of a space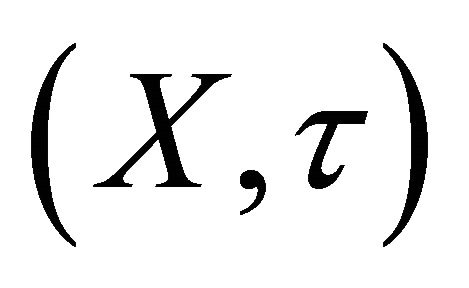 and
and . The following conditions are equivalent:
. The following conditions are equivalent:
1) B is regular open.
2) B is open and Bc-closed.
3) B is open and b-closed.
4) B is α-open and b-closed.
5) B is preopen and b-closed.
Diagram 1 shows the relations among ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 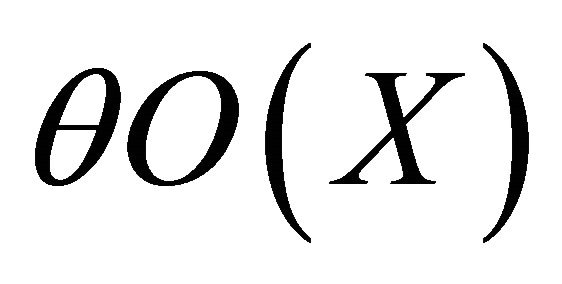 and
and .
.

Diagram 1.
3. Some Properties of Bc-Open Sets
In this section, we define and study topological properties of Bc-neighborhood, Bc-interior, Bc-closure and Bcderived of a set using the concept of Bc-open sets.
Definition 3.1. Let  be a topological space and
be a topological space and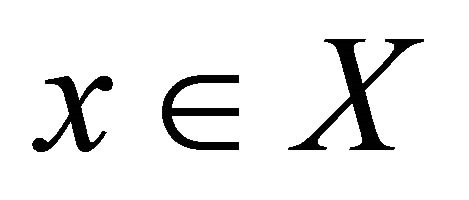 , then a subset N of X is said to be Bc-neighborhood of
, then a subset N of X is said to be Bc-neighborhood of , if there exists a
, if there exists a  -open set U in X such that
-open set U in X such that .
.
Proposition 3.2. In a topological space , a subset A of X is Bc-open if and only if it is a Bcneighbourhood of each of its points.
, a subset A of X is Bc-open if and only if it is a Bcneighbourhood of each of its points.
Proof. Let  be a Bc-open set, since for every
be a Bc-open set, since for every  and A is Bc-open. this shows A is a Bc-neighborhood of each of its points.
and A is Bc-open. this shows A is a Bc-neighborhood of each of its points.
Conversely, suppose that A is a Bc-neighborhood of each of its points. Then for each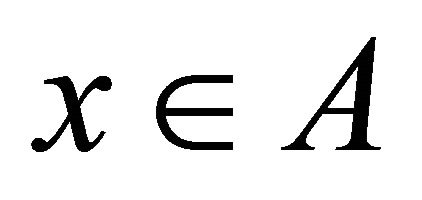 , there exists
, there exists  such that
such that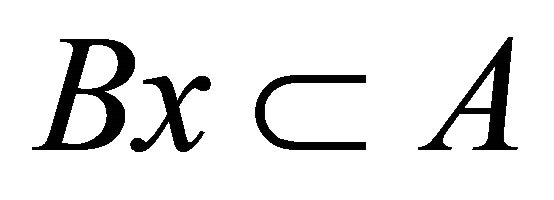 . Then
. Then
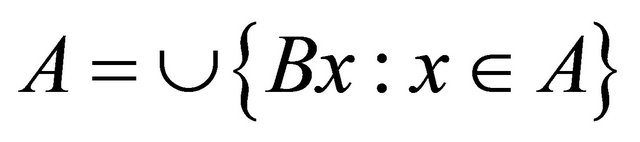 . Since each Bx is Bc-open. It follows that A is Bc-open set.
. Since each Bx is Bc-open. It follows that A is Bc-open set.
Proposition 3.3. For any two subsets A, B of a topological space  and
and , if A is a Bc-neighborhood of a point
, if A is a Bc-neighborhood of a point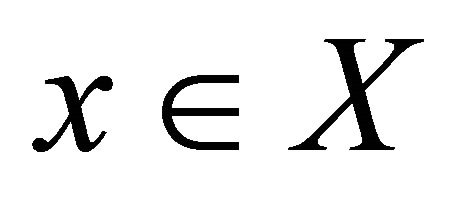 , then B is also Bc-neighborhood of the same point
, then B is also Bc-neighborhood of the same point .
.
Proof. let A be a Bc-neighborhood of , and
, and , then by Definition 2.1, there exists a Bc-open set U such that
, then by Definition 2.1, there exists a Bc-open set U such that , this implies that B is also a Bc-neighborhood of x.
, this implies that B is also a Bc-neighborhood of x.
Remark 3.4. Every Bc-neighborhood of a point is bneighborhood, it follows from every Bc-open set is bopen.
Definition 3.5. Let A be a subset of a topological space , a point
, a point 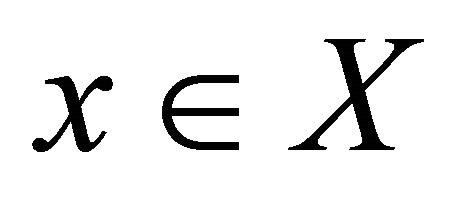 is said to be Bc-interior point of
is said to be Bc-interior point of , if there exist a Bc-open set
, if there exist a Bc-open set  such that
such that . The set of all Bc-interior points of A is called Bc-interior of A and is denoted by
. The set of all Bc-interior points of A is called Bc-interior of A and is denoted by .
.
Some properties of the Bc-interior of a set are investigated in the following theorem.
Theorem 3.6. For subsets A, B of a space X, the following statements hold.
1)  is the union of all Bc-open sets which are contained in A.
is the union of all Bc-open sets which are contained in A.
2)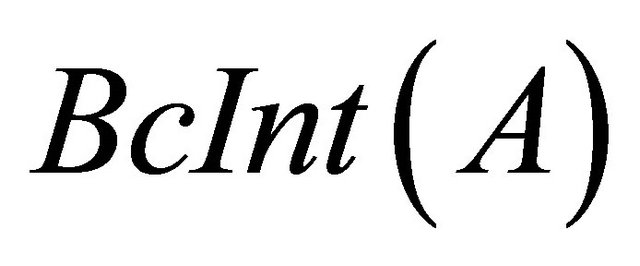 is
is  -open set in X.
-open set in X.
3) is
is  -open if and only if
-open if and only if .
.
4) .
.
5) and
and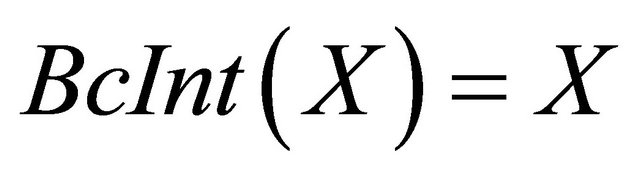 .
.
6) .
.
7) If , then
, then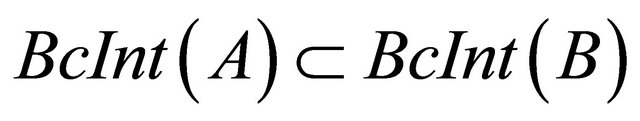 .
.
8) If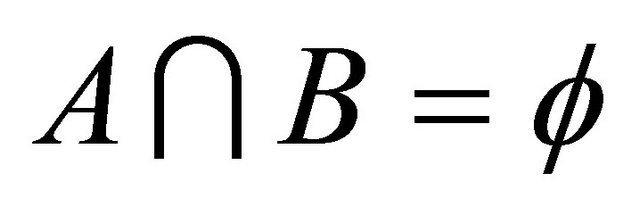 , then
, then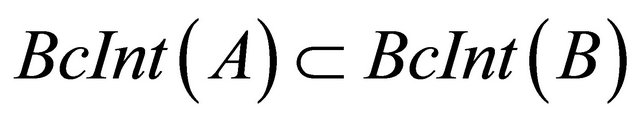 .
.
9)
10) .
.
Proof. 7) Let  and
and , then by Definition 3.5, there exists a Bc-open set
, then by Definition 3.5, there exists a Bc-open set  such that
such that  implies that
implies that . thus
. thus  .
.
The other parts of the theorem can be proved easily.
Proposition 3.7. For a subset A of a topological space , then
, then .
.
Proof. This follows immediately since all  -open set is b-open.
-open set is b-open.
Definition 3.8. Let A be a subset of a space X. A point  is said to be Bc-limit point of A if for each Bcopen set U containing
is said to be Bc-limit point of A if for each Bcopen set U containing . The set of all Bc-limit points of A is called a Bc-derived set of A and is denoted by
. The set of all Bc-limit points of A is called a Bc-derived set of A and is denoted by .
.
Proposition 3.9. Let A be a subset of X, if for each closed set F of X containing x such that 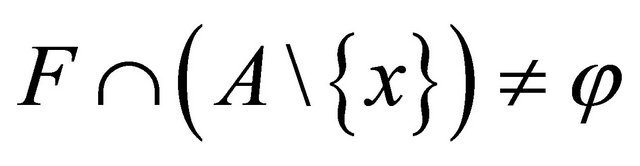 , then a point
, then a point  is Bc-limit point of A.
is Bc-limit point of A.
Proof. Let U be any Bc-open set containing x, then for each , there exists a closed set F such that
, there exists a closed set F such that . By hypothesis, we have
. By hypothesis, we have 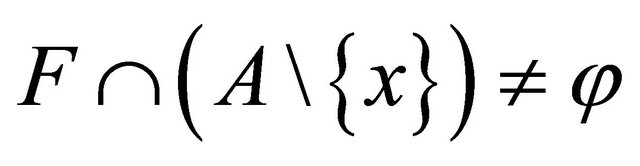 . Hence
. Hence . Therefore, a point
. Therefore, a point 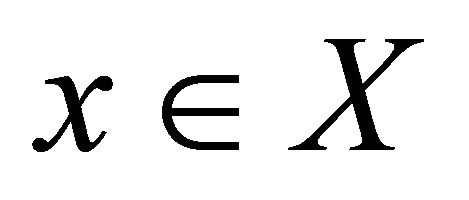 is Bc-limit point of A.
is Bc-limit point of A.
Some properties of Bc-derived set are stated in the following theorem.
Theorem 3.10. Let A and B be subsets of a space X. Then we have the following properties:
1) .
.
2) If , then
, then .
.
3) If , then
, then .
.
4) .
.
5)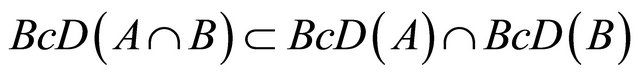 .
.
6) .
.
7) .
.
Proof. We only prove 6), 7), and the other parts can be proved obviously.
6) If  and
and  is a Bc-open set containing x, then
is a Bc-open set containing x, then . Let
. Let  . Then, since
. Then, since  and
and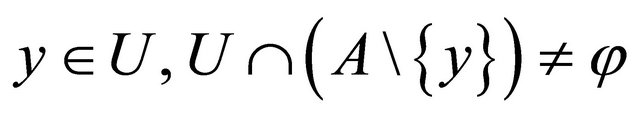 . Let
. Let . Then,
. Then,  for
for  and
and . Hence,
. Hence,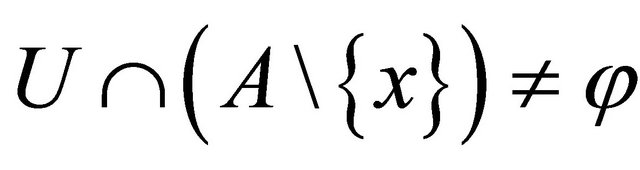 . Therefore,
. Therefore, 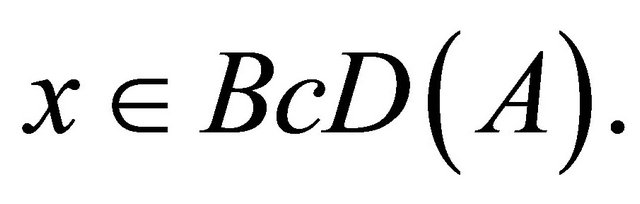
7) Let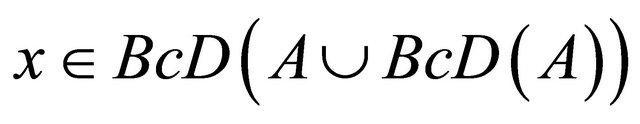 . If
. If , the result is obvious. So, let
, the result is obvious. So, let , then, for Bcopen set
, then, for Bcopen set  containing
containing . Thus,
. Thus,  or
or . Now, it follows similarly from 1) that
. Now, it follows similarly from 1) that  . Hence,
. Hence, . Therefore, in any case,
. Therefore, in any case,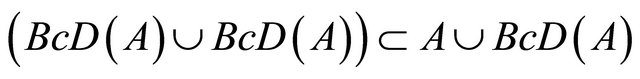 .
.
Corollary 3.11. For a subset A of a space X, then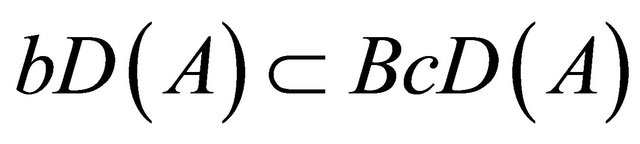 .
.
Proof. It is sufficient to recall that every Bc-open set is b-open.
Definition 3.12. For any subset A in the space X, the Bc-closure of A, denoted by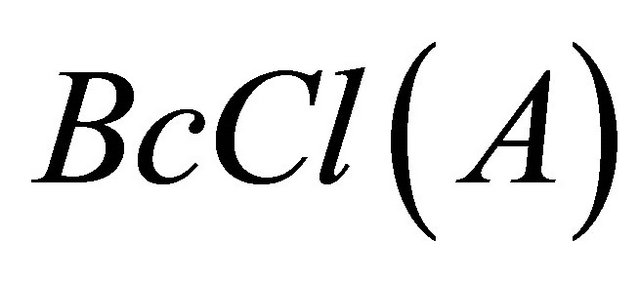 , is defined by the intersection of all Bc-closed sets containing A.
, is defined by the intersection of all Bc-closed sets containing A.
Proposition 3.13. A subset A of a topological space X is Bc-closed if and only if it contains the set of its Bclimit points.
Proof. Assume that A is Bc-closed and if possible that x is a Bc-limit point of A which belongs to , then
, then  is Bc-open set containing the Bc-limit point of A, therefore
is Bc-open set containing the Bc-limit point of A, therefore , which is a contradiction.
, which is a contradiction.
Conversely, assume that A contains the set of its Bclimit points. For each , there exists a Bc-open set U containing x such that
, there exists a Bc-open set U containing x such that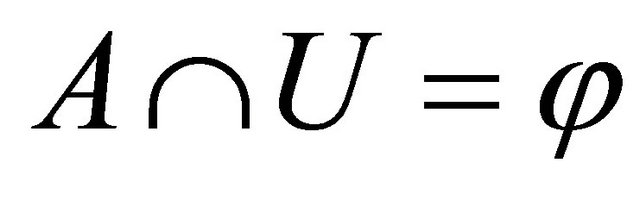 , that is
, that is 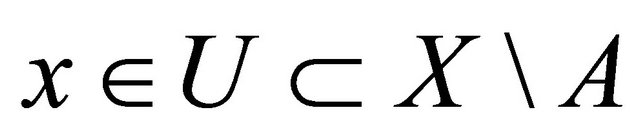 by Proposition 2.8,
by Proposition 2.8, 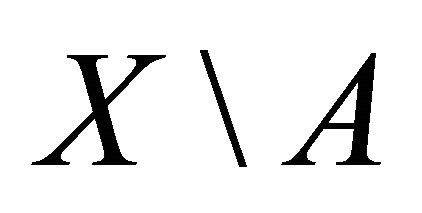 is Bc-open set and hence A is Bc-closed set.
is Bc-open set and hence A is Bc-closed set.
Proposition 3.14. Let A be a subset of a space X, then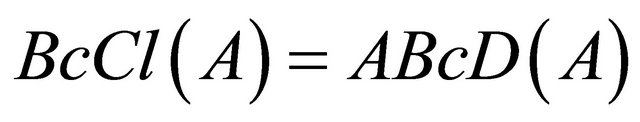 .
.
Proof. Since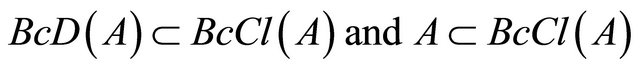 , then
, then .
.
On the other hand. To show that  , since
, since 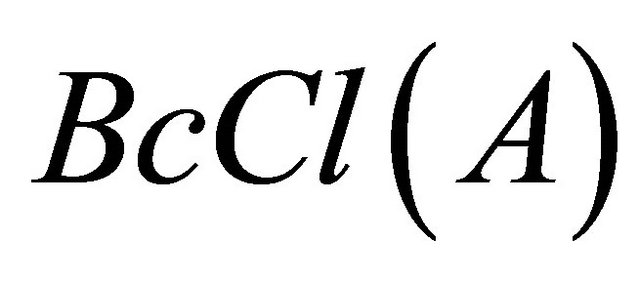 is the smallest Bc-closed set containing A, so it is enough to prove that
is the smallest Bc-closed set containing A, so it is enough to prove that  is Bc-closed. Let
is Bc-closed. Let . This implies that
. This implies that and
and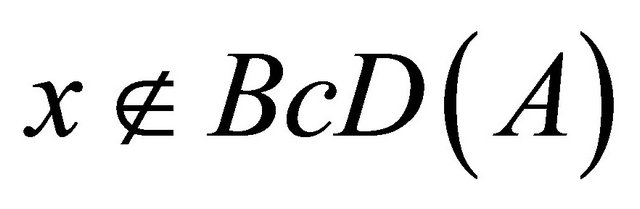 . Since
. Since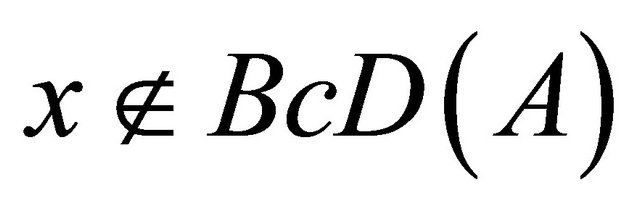 , there exists a Bc-open set
, there exists a Bc-open set  of
of  which contains no point of A other than x but
which contains no point of A other than x but . So Gx contains no point of A, which implies
. So Gx contains no point of A, which implies . Again, Gx is a Bc-open set of each of its points. But as Gx does not contain any point of A, nopoint of Gx can be a Bc-limit point of A. Therefore, nopoint of Gx can belong to
. Again, Gx is a Bc-open set of each of its points. But as Gx does not contain any point of A, nopoint of Gx can be a Bc-limit point of A. Therefore, nopoint of Gx can belong to . This implies that
. This implies that . Hence, it follows that
. Hence, it follows that

Therefore,  is Bc-closed. Hence
is Bc-closed. Hence
 . Thus
. Thus
 .
.
Corollary 3.15. Let A be a set in a space X. A point  is in the Bc-closure of A if and only if
is in the Bc-closure of A if and only if 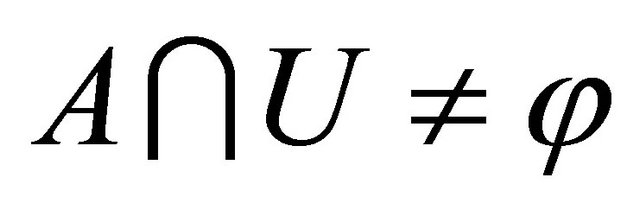 for every Bc-open set U containing x.
for every Bc-open set U containing x.
Proof. Let . Then
. Then , where F is Bc-closed with
, where F is Bc-closed with . So
. So  and
and 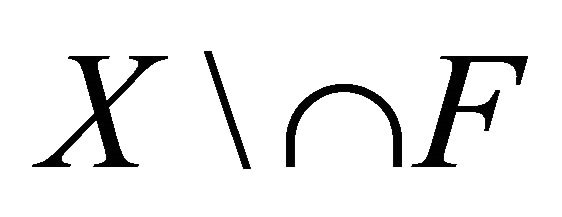 is a Bc-open set containing x and hence
is a Bc-open set containing x and hence

Conversely, suppose that there exists a Bc-open set containing x with . Then
. Then  and
and  is a Bc-closed. Hence
is a Bc-closed. Hence .
.
Proposition 3.16. Let A be any subset of a space X. If  for every closed set F of X containing x, then the point x is in the Bc-closure of A.
for every closed set F of X containing x, then the point x is in the Bc-closure of A.
Proof. Suppose that U be any Bc-open set containing x, then by Definition 2.1, there exists a closed set F such that . So by hypothesis
. So by hypothesis 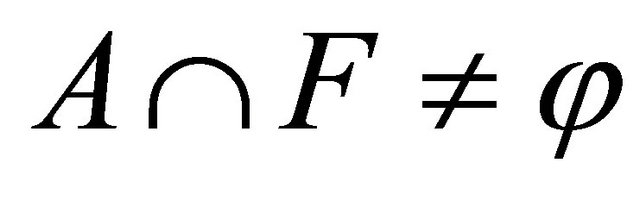 implies
implies  for every Bc-open set U containing x. Therefore
for every Bc-open set U containing x. Therefore .
.
Here we introduce some properties of Bc-closure of the sets.
Theorem 3.17. For subsets A, B of a space X, the following statements are true.
1) The Bc-closure of A is the intersection of all Bcclosed sets containing A.
2)
3)
 -closed set in X 4)
-closed set in X 4) is Bc-closed set if and only if
is Bc-closed set if and only if 
5)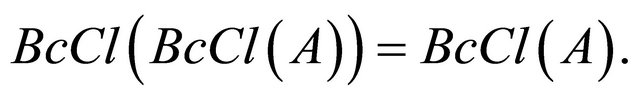
6)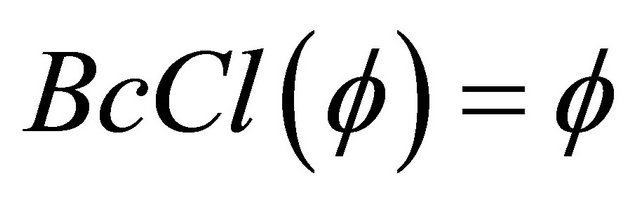 and
and .
.
7) If , then
, then 
8) If 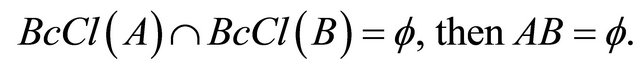
9)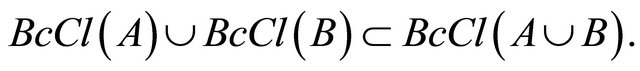
10) .
.
Proof. Obvious.
Proposition 3.18. For any subset A of a topological space X. The following statements are true.
1)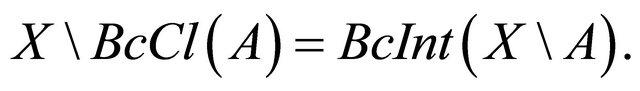
2)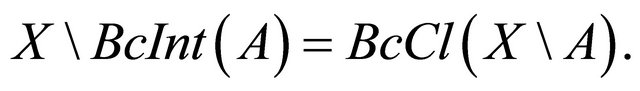
3)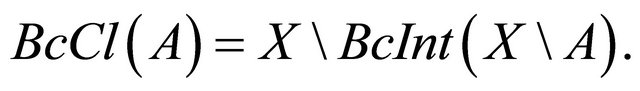
4)
Proof. We only prove 1), the other parts can be proved similarly. For any point ,
,  implies that
implies that , then for each
, then for each  containing
containing , then
, then . Thus
. Thus .
.
Conversely, by reverse the above steps, we can prove this part.
Remark 3.19. If  is a subset of a topological space X. Then
is a subset of a topological space X. Then

Proof. Obvious.
4. Bc-Compactness
In this section, we introduce and investigate new class of space named Bc-compact.
Definition 4.1. A filter base  in a topological space
in a topological space  Bc-converges to a point
Bc-converges to a point  if for every Bcopen set V containing x, there exists an
if for every Bcopen set V containing x, there exists an 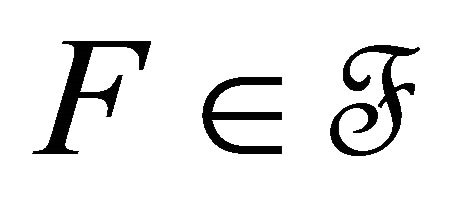 such that
such that .
.
Definition 4.2. A filter base  in a topological space
in a topological space 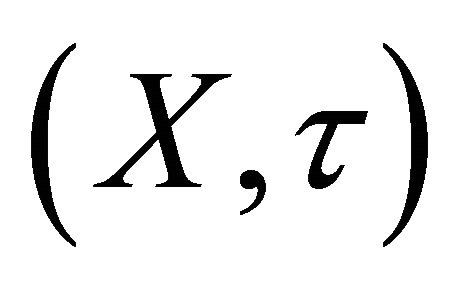 Bc-accumulates to a point
Bc-accumulates to a point 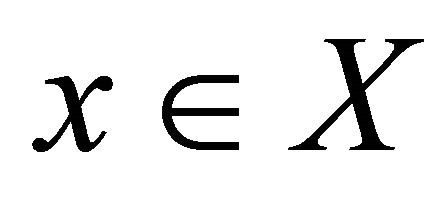 if
if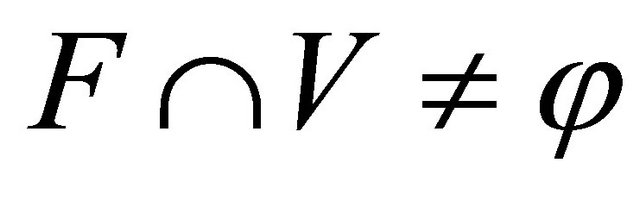 , for every
, for every  -open set V containing
-open set V containing  and every
and every .
.
Proposition 4.3. Let  be a filter base in a topological space
be a filter base in a topological space . If
. If  Bc-converges to a point
Bc-converges to a point , then
, then  rc-converges to a point x.
rc-converges to a point x.
Proof. Suppose that  Bc-converges to a point
Bc-converges to a point . Let V be any regular closed set containing x, then
. Let V be any regular closed set containing x, then . Since
. Since  Bc-converges to a point
Bc-converges to a point , there exists an
, there exists an 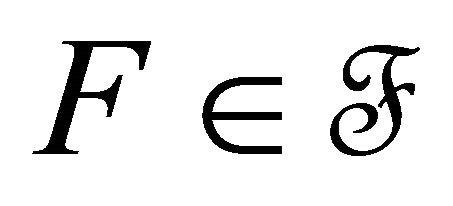 such that
such that . This shows that
. This shows that  rc-converges to a point x.
rc-converges to a point x.
In general the converse of the above proposition is not necessarily true, as the following example shows.
Example 4.4. Consider the space . Let
. Let 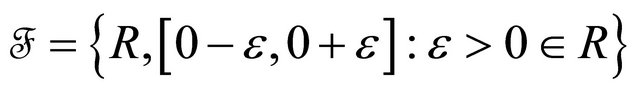 . Then
. Then  rc-converges to 0, but
rc-converges to 0, but  does not Bc-converges to 0, because the set
does not Bc-converges to 0, because the set 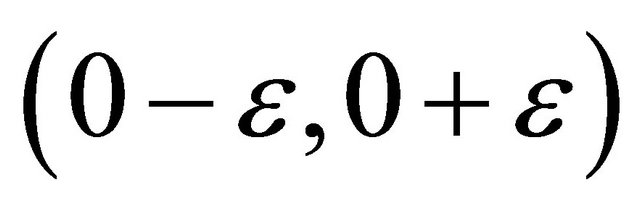 is Bc-open containing 0, there exist no
is Bc-open containing 0, there exist no  such that
such that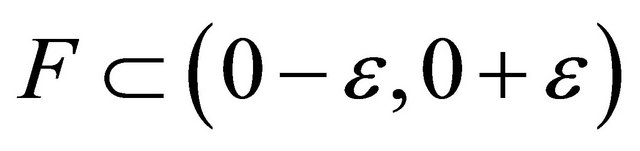 .
.
Corollary 4.5. Let  be a filter base in a topological space
be a filter base in a topological space . If
. If  Bc-accumulates to a point
Bc-accumulates to a point , then
, then  rc-accumulates to a point x.
rc-accumulates to a point x.
Proof. Similar to Proposition 4.3.
Proposition 4.6. Let  be a filter base in a topological space
be a filter base in a topological space  and E is any closed set containing
and E is any closed set containing . If there exists an
. If there exists an  such that
such that , then
, then  Bcconverges to a point
Bcconverges to a point .
.
Proof. Let  be any Bc-open set containing
be any Bc-open set containing , then for each
, then for each , there exists a closed set E such that
, there exists a closed set E such that . By hypothesis, there exists an
. By hypothesis, there exists an  such that
such that  which implies that
which implies that . Hence
. Hence  Bc-converges to a point
Bc-converges to a point .
.
Proposition 4.7. Let  be a filter base in a topological space
be a filter base in a topological space  and E is any closed set containing
and E is any closed set containing , such that
, such that  for each
for each , then
, then  is Bcaccumulation to a point
is Bcaccumulation to a point .
.
Proof. The proof is similar to Proposition 4.6.
Definition 4.8. We say that a topological space  is Bc-compact if for every Bc-open cover
is Bc-compact if for every Bc-open cover  of X, there exists a finite subset
of X, there exists a finite subset  of
of  such that
such that .
.
Theorem 4.9. If every closed cover of a space X has a finite subcover, then X is Bc-compact.
Proof. Let  be any Bc-open cover of X, and
be any Bc-open cover of X, and , then for each
, then for each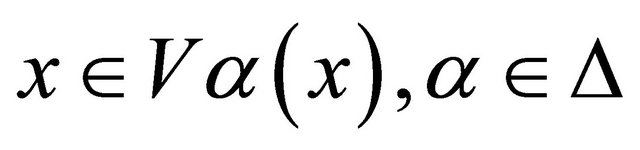 , there exists a closed set
, there exists a closed set 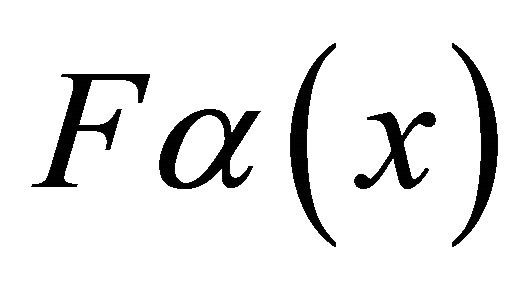 such that
such that . So the family
. So the family  is a cover of X by closed set, then by hypothesis, this family has a finite subcover such that
is a cover of X by closed set, then by hypothesis, this family has a finite subcover such that
 .
.
Therefore, . Hence X is Bccompact.
. Hence X is Bccompact.
Proposition 4.10. If a topological space 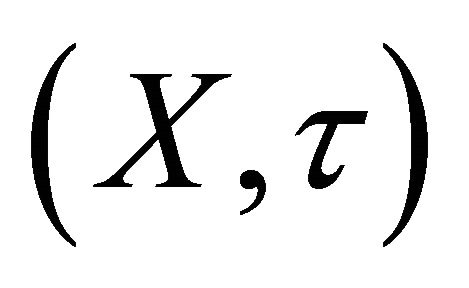 is bcompact, then it is Bc-compact.
is bcompact, then it is Bc-compact.
Proof. Let  be any Bc-open cover of X. Then
be any Bc-open cover of X. Then  is b-open cover of X. Since X is bcompact, there exists a finite subset
is b-open cover of X. Since X is bcompact, there exists a finite subset  of
of  such that
such that . Hence X is Bc-compact.
. Hence X is Bc-compact.
Proposition 4.11. Every Bc-compact  -space is bcompact.
-space is bcompact.
Proof. Suppose that X is  and Bc-compact space. Let
and Bc-compact space. Let 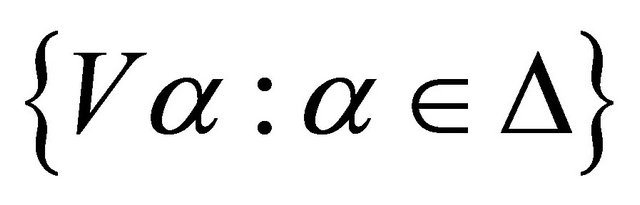 be any b-open cover of X. Then for every
be any b-open cover of X. Then for every , there exists
, there exists  such that
such that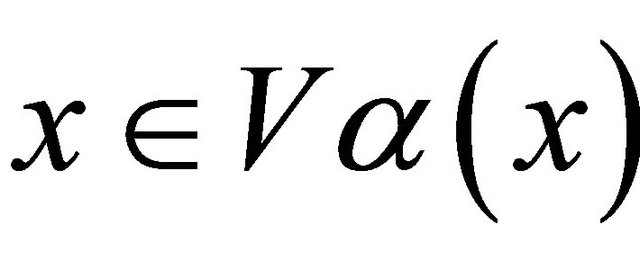 . Since X is
. Since X is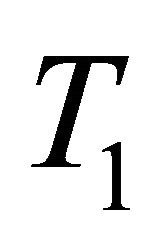 , by Since X is Bc-compact, so there exists a finite subset
, by Since X is Bc-compact, so there exists a finite subset  of
of  in X such that
in X such that 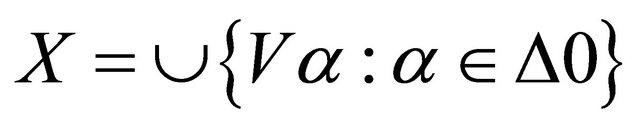 . Hence X is b-compact.
. Hence X is b-compact.
The next corollary is an immediate consequence of Proposition 4.10 and 4.11.
Corollary 4.12. Let X be a  -space. Then X is Bccompact if and only if X is b-compact.
-space. Then X is Bccompact if and only if X is b-compact.
Proposition 4.13. Let a topological space  be locally indiscrete. If X is Bc-compact then X is s-compact.
be locally indiscrete. If X is Bc-compact then X is s-compact.
Proof. Follows from Proposition 2.14.
Proposition 4.14. If a topological space  is Bccompact, then it is rc-compact.
is Bccompact, then it is rc-compact.
Proof. Let  be any regular closed cover of X. Then
be any regular closed cover of X. Then  is a Bc-open cover of X. Since X is
is a Bc-open cover of X. Since X is  -compact, there exists a finite subset
-compact, there exists a finite subset  of
of  such that
such that . Hence X is rc-compact.
. Hence X is rc-compact.
Proposition 4.15. Let a topological space 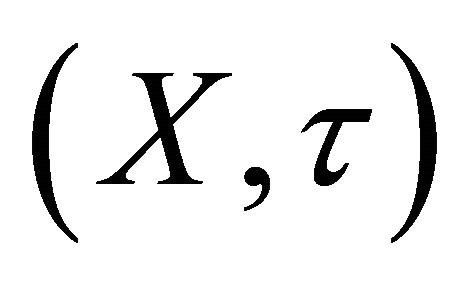 be regular. If X is Bc-compact, then it is compact.
be regular. If X is Bc-compact, then it is compact.
Proof. Let 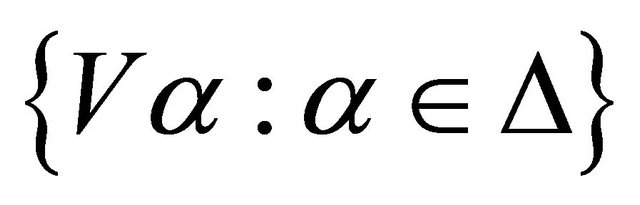 be any open cover of X. By Proposition 2.16,
be any open cover of X. By Proposition 2.16,  forms a Bc-open cover of X. Since X is Bc-compact, there exists a finite subset
forms a Bc-open cover of X. Since X is Bc-compact, there exists a finite subset  of
of  such that
such that . Hence X is compact.
. Hence X is compact.
Proposition 4.16. Let X be an almost regular space. If X is Bc-compact, then it is nearly compact.
Proof. Let 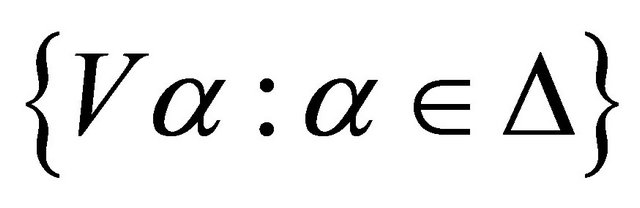 be any regular open cover of X. Since X is almost regular space, then, for each
be any regular open cover of X. Since X is almost regular space, then, for each  and regular open
and regular open  there exists an open set Gx such that
there exists an open set Gx such that  But
But 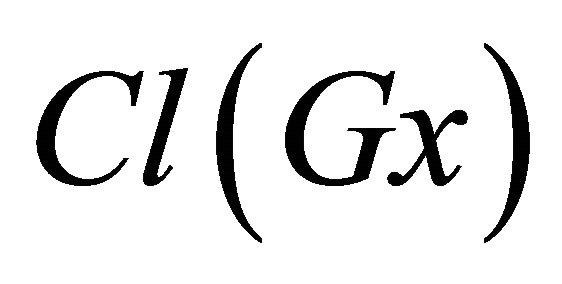 is regulaclosed for each
is regulaclosed for each , this implies that the family
, this implies that the family  is Bc-open cover of X, since X is Bc - compact, then there exists a subfamily
is Bc-open cover of X, since X is Bc - compact, then there exists a subfamily
 such that
such that
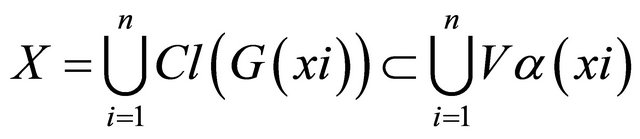 . Thus X is nearly compact.
. Thus X is nearly compact.
REFERENCES
- M. H. Stone, “Applications of the Theory of Boolean Rings to Topology,” Transactions of the American Mathematical Society, Vol. 41, No. 3, 1937, pp. 375-481. doi:10.1090/S0002-9947-1937-1501905-7
- N. Levine, “Semi-Open Sets and Semi-Continuity in Topological Spaces,” American Mathematical Monthly, Vol. 70, No. 1, 1963, pp. 36-41. doi:10.2307/2312781
- A. S. Mashhour, M. E. Abd El-Monsef and S. N. El-Deeb, “On Precontinuous and Week Precontinuous Mappings,” Proceedings of Mathematical and Physical Society of Egypt, Vol. 53, 1982, pp. 47-53.
- O. Njastad, “On Some Classes of Nearly Open Sets,” Pacific Journal of Mathematics, Vol. 15, No. 3, 1965, pp. 961-970. doi:10.2140/pjm.1965.15.961
- S. N. El-Deeb, I. A. Hasanein, A. S. Mashhour and T. Noiri, “On p-Regular Spaces,” Bulletin Mathématique de la Société des Sciences Mathématiques de Roumanie, Vol. 27, No. 4, 1983, pp. 311-315.
- S. G. Crossley and S. K. Hildebrand, “Semi-Closure,” Texas Journal of Science, Vol. 22, No. 2-3, 1971, pp. 99-112.
- J. E. Joseph and M. H. Kwack, “On S-Closed Spaces,” Bulletin of the American Mathematical Society, Vol. 80, No. 2, 1980, pp. 341-348.
- N. K. Ahmed, “On Some Types of Separation Axioms,” M.Bc. Thesis, Salahaddin University, Arbil, 1990.
- N. V. Velicko, “H-Closed Topological Spaces,” American Mathematical Society, Vol. 78, No. 2, 1968, pp. 103-118.
- G. Di Maio and T. Noiri, “On s-Closed Spaces,” Indian Journal of Pure and Applied Mathematics, Vol. 18, No. 3, 1987, pp. 226-233.
- D. Andrijevic, “On b-Open Sets,” Matematički Vesnik, Vol. 48, No. 3, 1996, pp. 59-64.
- J. Dontchev and T. Noiri, “Contra-Semicontinuous Functions,” Mathematica Pannonica, Vol. 10, No. 2, 1999, pp. 159-168.
- R. H. Yunis, “Properties of θ-Semi-Open Sets,” Zanco Journal of Pure and Applied Sciences, Vol. 19, No. 1, 2007, pp. 116-122.
- M. H. Stone, “Algebraic Characterizations of Special Boolean Rings,” Fundamenta Mathematicae, Vol. 29, No. 1, 1937, pp. 223-302.
- J. Dontchev, “Survey on Preopen Sets,” The Proceedings of the Yatsushiro Topological Conference, 22-23 August 1998, pp. 1-18.

