Advances in Pure Mathematics
Vol.3 No.3(2013), Article ID:31397,6 pages DOI:10.4236/apm.2013.33050
Trigonometric Approximation of Signals (Functions) Belonging to the 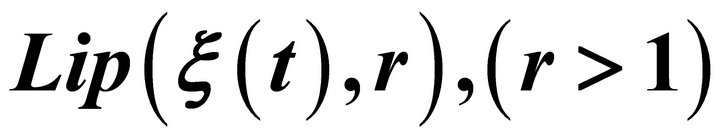 -Class by
-Class by 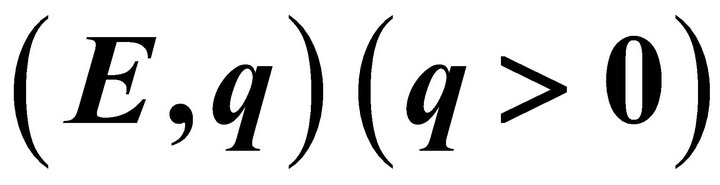 -Means of the Conjugate Series of Its Fourier Series*
-Means of the Conjugate Series of Its Fourier Series*
1Department of Applied Mathematics & Humanities, Sardar Vallabhbhai National Institute of Technology, Surat, India
2Department of Mathematics, Aligarh Muslim University, Aligarh, India
3Dr. Ram Manohar Lohia Avadh University, Faizabad, India
Email: vishnu_narayanmishra@yahoo.co.in, kejal0909@gmail.com, huzoorkhan@yahoo.com, idrees_maths@yahoo.com, lakshminarayanmishra04@gmail.com
Copyright © 2013 Vishnu Narayan Mishra et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 13, 2012; revised January 14, 2013; accepted February 9, 2013
Keywords: Signals; Conjugate Fourier Series; Trigonometric Fourier Approximation; Degree of Approximation; 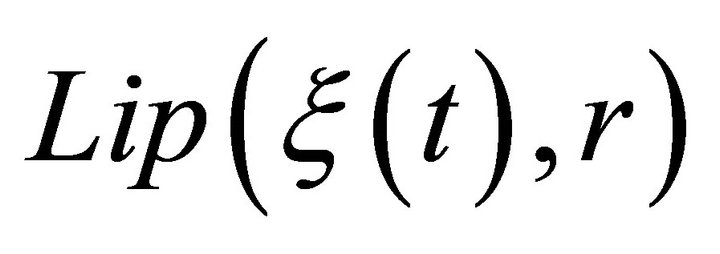 -Class;
-Class;  Summability
Summability
ABSTRACT
Various investigators such as Khan ([1-4]), Khan and Ram [5], Chandra [6,7], Leindler [8], Mishra et al. [9], Mishra [10], Mittal et al. [11], Mittal, Rhoades and Mishra [12], Mittal and Mishra [13], Rhoades et al. [14] have determined the degree of approximation of 2π-periodic signals (functions) belonging to various classes 
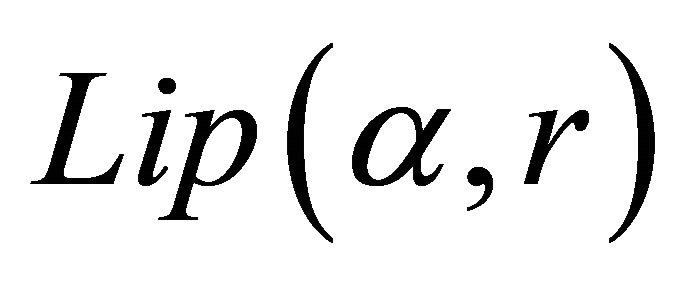 ,
,  and
and 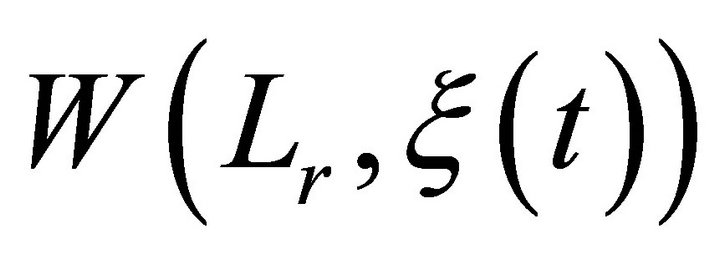 of functions through trigonometric Fourier approximation (TFA) using different summability matrices with monotone rows. Recently, Mittal et al. [15], Mishra and Mishra [16], Mishra [17] have obtained the degree of approximation of signals belonging to
of functions through trigonometric Fourier approximation (TFA) using different summability matrices with monotone rows. Recently, Mittal et al. [15], Mishra and Mishra [16], Mishra [17] have obtained the degree of approximation of signals belonging to 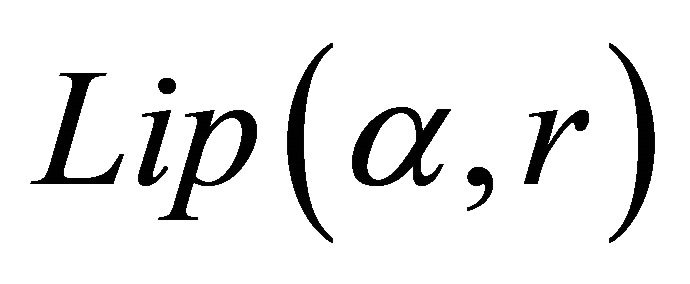 -class by general summability matrix, which generalizes the results of Leindler [8] and some of the results of Chandra [7] by dropping monotonicity on the elements of the matrix rows (that is, weakening the conditions on the filter, we improve the quality of digital filter). In this paper, a theorem concerning the degree of approximation of the conjugate of a signal (function) f belonging to
-class by general summability matrix, which generalizes the results of Leindler [8] and some of the results of Chandra [7] by dropping monotonicity on the elements of the matrix rows (that is, weakening the conditions on the filter, we improve the quality of digital filter). In this paper, a theorem concerning the degree of approximation of the conjugate of a signal (function) f belonging to  class by
class by  summability of conjugate series of its Fourier series has been established which in turn generalizes the results of Chandra [7] and Shukla [18].
summability of conjugate series of its Fourier series has been established which in turn generalizes the results of Chandra [7] and Shukla [18].
1. Introduction
The theory of approximation is a very extensive field and the study of the theory of trigonometric approximation is of great mathematical interest and of great practical importance. Broadly speaking, Signals are treated as functions of one variable and images are represented by functions of two variables. The study of these concepts is directly related to the emerging area of information technology. Khan [1-4] and Mittal, Rhoades and Mishra [12] have initiated the studies of error estimates En(f) through trigonometric Fourier approximation (TFA) using different summability matrices. Chandra [7] has studied the degree of approximation of a signal (function) belonging to Lip α-class by (E,q) means, q > 0.
Generalizing the result of Chandra [7], very interesting result has been proved by Shukla [18] for the signals (functions) of 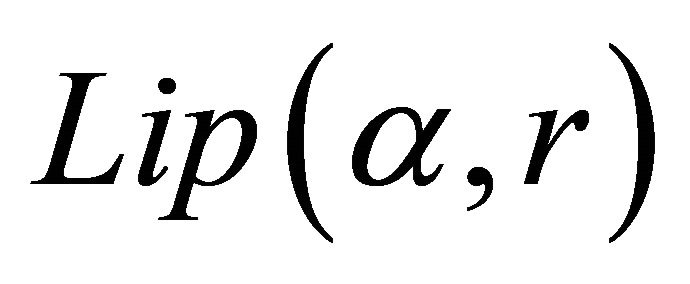 -class through trigonometric Fourier approximation by applying (E,q) (q > 0) summability matrix.
-class through trigonometric Fourier approximation by applying (E,q) (q > 0) summability matrix.
Let 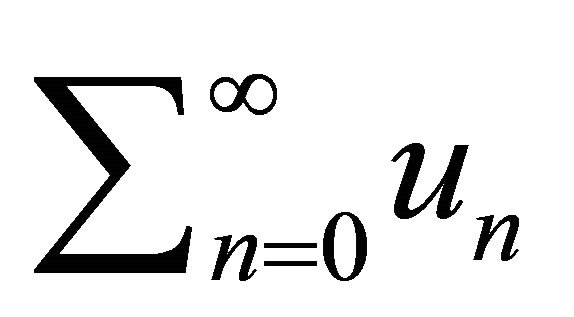 be a given infinite series with sequence of its partial sums
be a given infinite series with sequence of its partial sums .
.
The  transform is defined as the
transform is defined as the 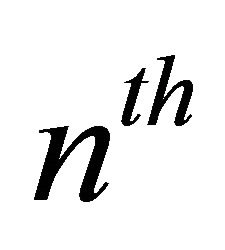 partial sum of
partial sum of 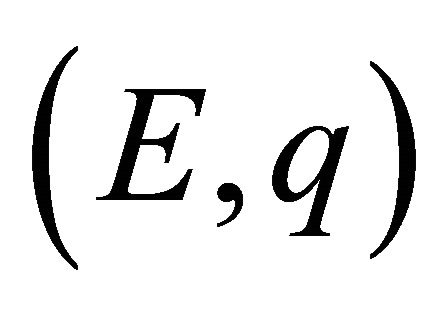 summability and we denote it by
summability and we denote it by 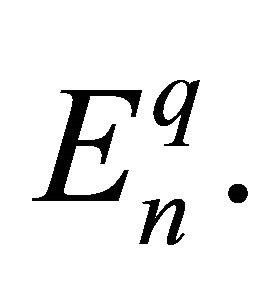
If
 as
as , (1.1)
, (1.1)
then the series  is said to be
is said to be  summable to a definite number “s” [19].
summable to a definite number “s” [19].
A signal (function) 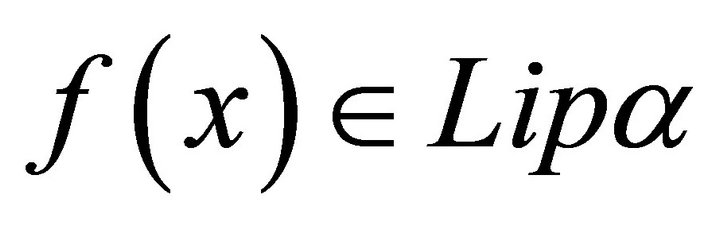 if
if
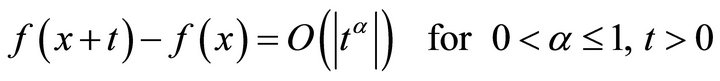 (1.2)
(1.2)
and  [1], if
[1], if
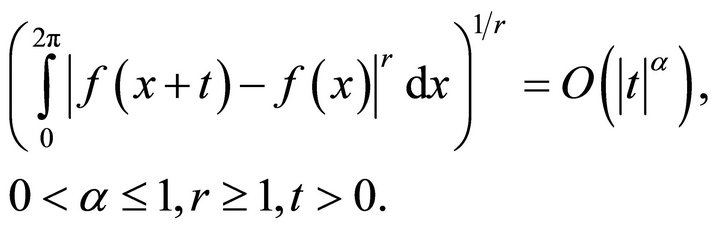 (1.3)
(1.3)
Given a positive increasing function 
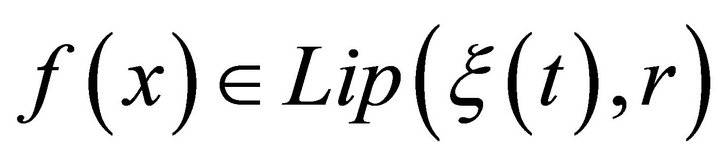 , if
, if
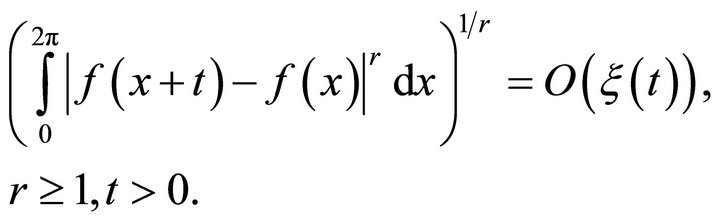 (1.4)
(1.4)
We observe that
 (1.5)
(1.5)
The  -norm of a signal
-norm of a signal 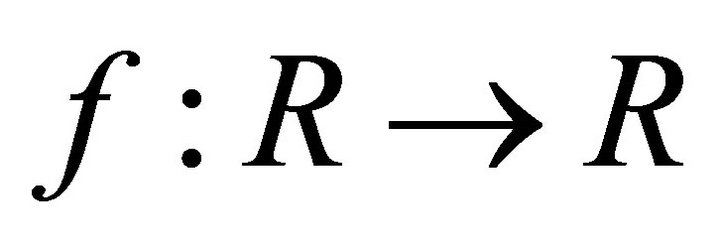 is defined by
is defined by

The 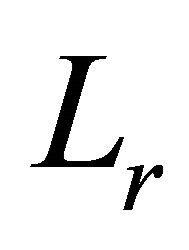 -norm of a signal is defined by
-norm of a signal is defined by
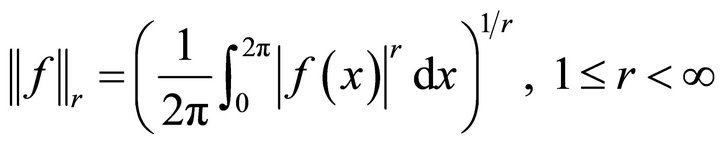 . (1.6)
. (1.6)
The degree of approximation of a function  by trigonometric polynomial
by trigonometric polynomial 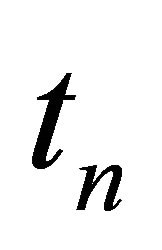 of order “
of order “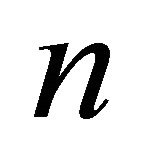 ” under sup norm
” under sup norm  is defined by Zygmund [20].
is defined by Zygmund [20].
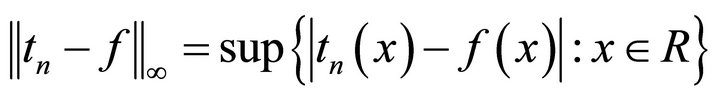
and  of a function
of a function is given by
is given by
 (1.7)
(1.7)
in terms of n, where 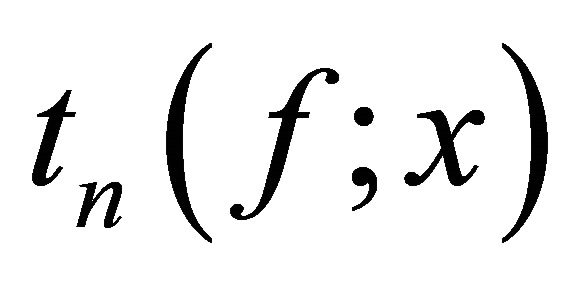 is a trigonometric polynomials of order “n”.
is a trigonometric polynomials of order “n”.
This method of approximation is called Trigonometric Fourier Approximation (TFA) [12].
Let  be a
be a  -periodic signal (function) and Lebesgue integrable. The Fourier series of
-periodic signal (function) and Lebesgue integrable. The Fourier series of 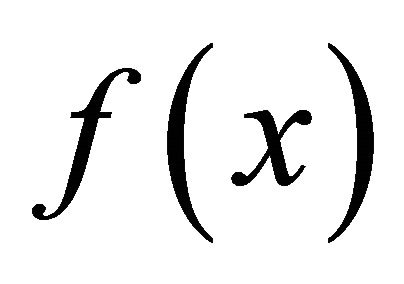 is given by
is given by
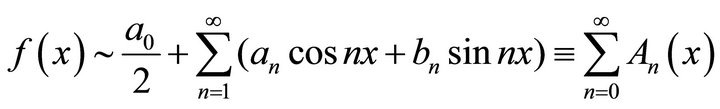 (1.8)
(1.8)
with 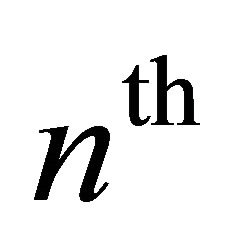 partial sum
partial sum  called trigonometric polynomial of degree (order) n of the first (n + 1) terms of the Fourier series of f.
called trigonometric polynomial of degree (order) n of the first (n + 1) terms of the Fourier series of f.
The conjugate series of Fourier series (1.8) is given by
 . (1.9)
. (1.9)
We note that 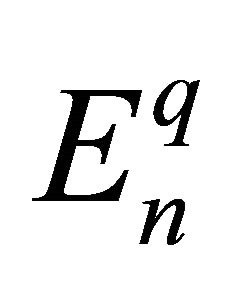 is also trigonometric polynomial of degree (or order) “n”.
is also trigonometric polynomial of degree (or order) “n”.
We use the following notations throughout this paper

 .
.
2. Known Results
Chandra [7] has studied the degree of approximation to a function 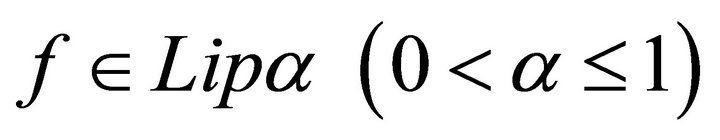 by
by 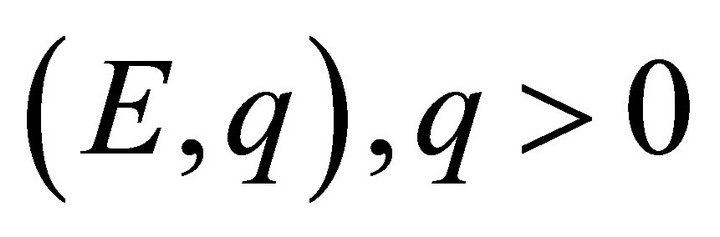 of Fourier series (1.8) by proving the following theorem. He proved:
of Fourier series (1.8) by proving the following theorem. He proved:
Theorem 2.1 The degree of approximation of a periodic function f(x) with period  and belonging to the class
and belonging to the class  by Euler’s mean of its Fourier series is given by
by Euler’s mean of its Fourier series is given by
 (2.1)
(2.1)
where 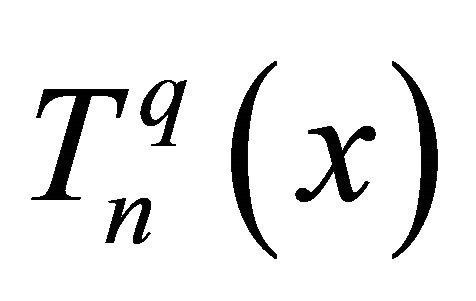 is the
is the 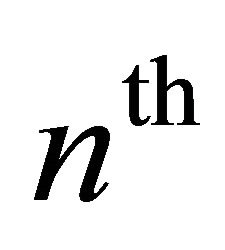 Euler mean of order q > 0 of the sequence
Euler mean of order q > 0 of the sequence 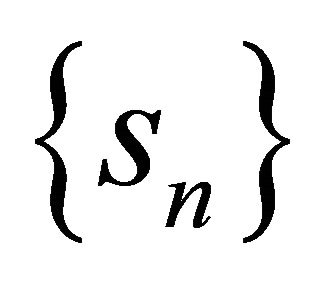 of partial sums of the Fourier series (1.8) of the function f at a point x in
of partial sums of the Fourier series (1.8) of the function f at a point x in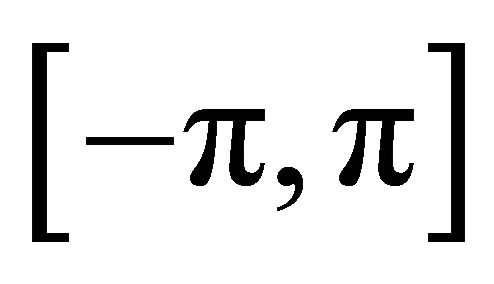 .
.
Shukla [18] improved Theorem 2.1 by extending to a function 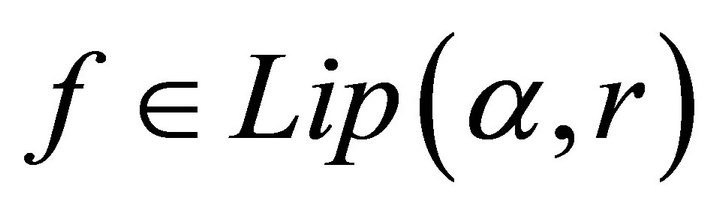 by
by  matrix means of the conjugate series (1.9) of its Fourier series (1.8). He proved:
matrix means of the conjugate series (1.9) of its Fourier series (1.8). He proved:
Theorem 2.2 Let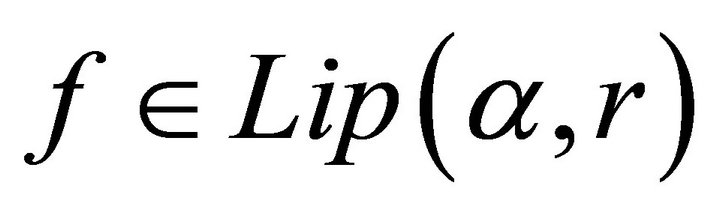 ,
, ,
,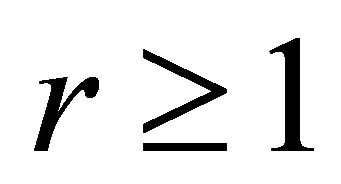 be a
be a  -periodic and Lebesgue integrable function of “t” in the interval
-periodic and Lebesgue integrable function of “t” in the interval . If
. If
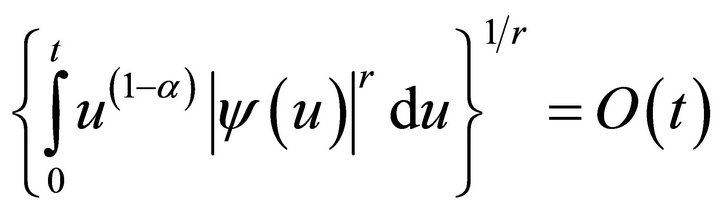 (2.2)
(2.2)
and
 (2.3)
(2.3)
where  is an arbitrary number such that
is an arbitrary number such that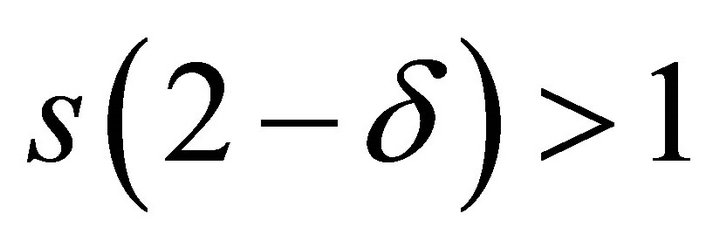 , s being conjugate to
, s being conjugate to  with
with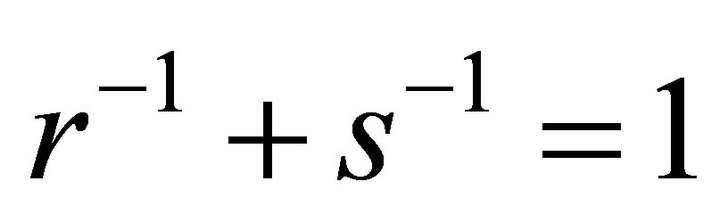 , then the degree of approximation of the conjugate to a function
, then the degree of approximation of the conjugate to a function , by
, by 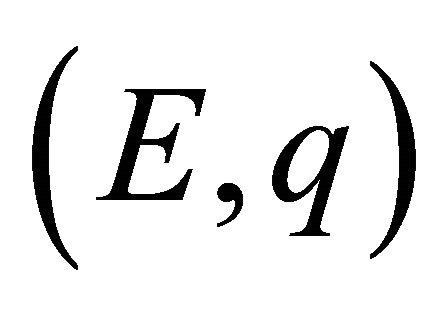 means,
means,  , of the conjugate series (1.9) of its Fourier series (1.8) will be given by
, of the conjugate series (1.9) of its Fourier series (1.8) will be given by
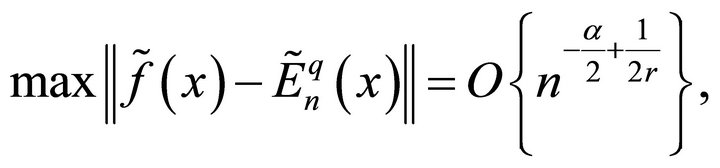 (2.4)
(2.4)
where  is nth
is nth 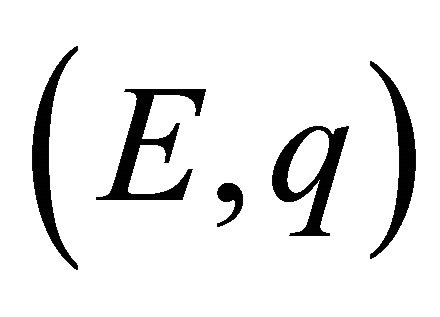 mean of the sequence
mean of the sequence  of partial sums of the conjugate series (1.9) of the Fourier series (1.8) of the function f at every point x in
of partial sums of the conjugate series (1.9) of the Fourier series (1.8) of the function f at every point x in 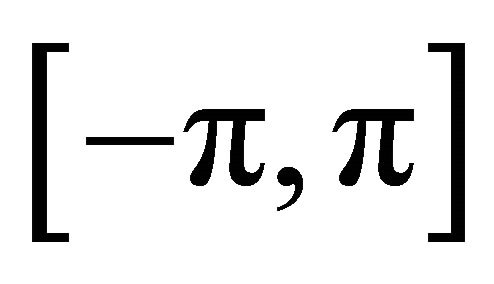 at which
at which
 (2.5)
(2.5)
exists.
3. Main Result
The purpose of the present paper is to extend Theorems 2.1 and 2.2 on the degree of approximation of signal  conjugate to a 2π-periodic signal
conjugate to a 2π-periodic signal
 class by
class by  summability means with a proper set of conditions. More precisely, we prove:
summability means with a proper set of conditions. More precisely, we prove:
Theorem 3.1
If 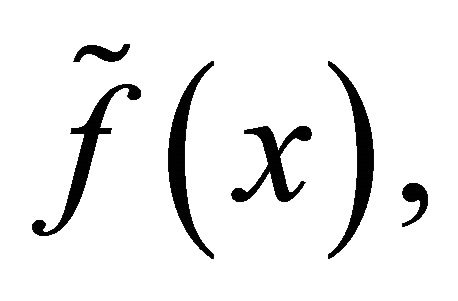 conjugate to a 2π-periodic signal (function) f belonging to
conjugate to a 2π-periodic signal (function) f belonging to 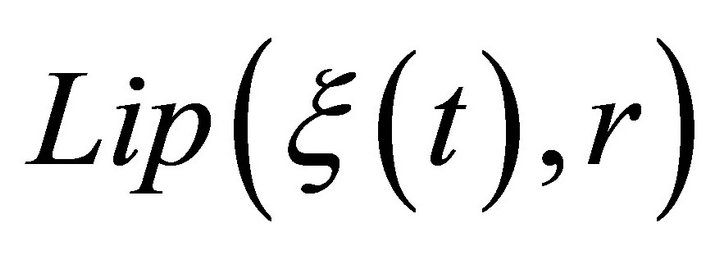 -class, then its degree of approximation by
-class, then its degree of approximation by  means of conjugate series of Fourier series (1.9) is given by
means of conjugate series of Fourier series (1.9) is given by
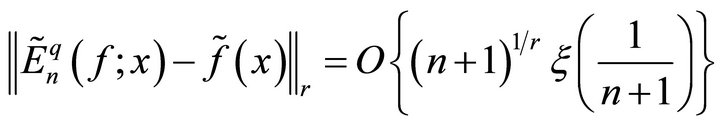 (3.1)
(3.1)
provided positive increasing ξ(t) satisfies the following conditions
 (3.2)
(3.2)
 (3.3)
(3.3)
and
 is non-increasing in “t”, (3.4)
is non-increasing in “t”, (3.4)
where  is an arbitrary number such that
is an arbitrary number such that
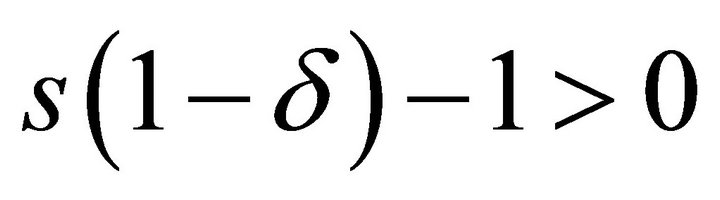 ,
,  ,
,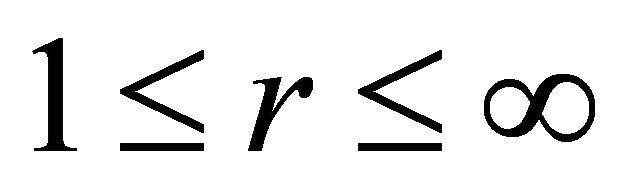 , condition (3.2) and (3.3) hold uniformly in x and
, condition (3.2) and (3.3) hold uniformly in x and 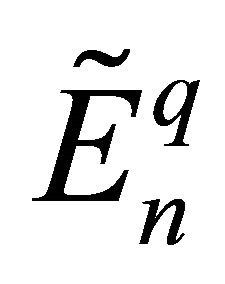 is the nth
is the nth  means of the series (1.9) and the conjugate function
means of the series (1.9) and the conjugate function  is defined for almost every x by
is defined for almost every x by
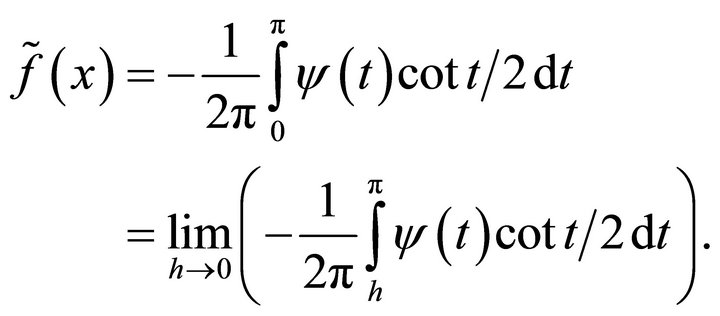 (3.5)
(3.5)
Note 3.2 Using condition (3.4), we get

Note 3.3 Also, if , then our main Theorem (3.1) reduces to Theorem 2.2, and thus generalizes the theorem of Shukla [18].
, then our main Theorem (3.1) reduces to Theorem 2.2, and thus generalizes the theorem of Shukla [18].
Note 3.4 The transform (E, q) plays an important role in signal theory and the theory of Machines in Mechanical Engineering.
4. Lemma
For the proof of our theorem, we need the following lemma.
Lemma 4.1 [18]: For 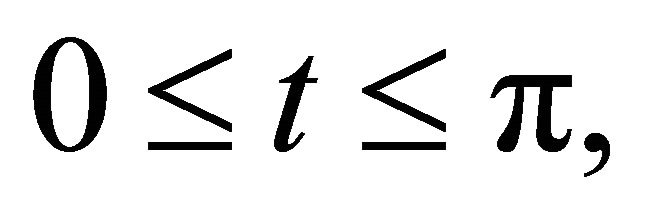 we have
we have
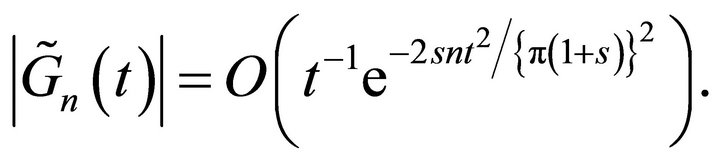
5. Proof of Theorem 3.1
Let  denote the partial sum of series (1.9), then we have
denote the partial sum of series (1.9), then we have

Therefore the 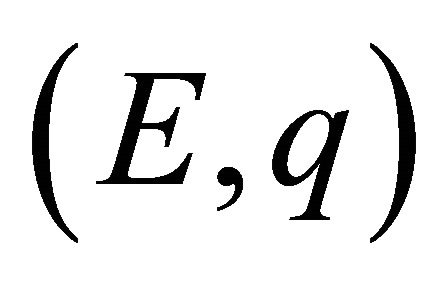 transform
transform 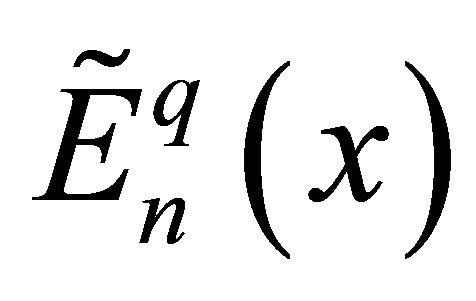 of
of  is given by
is given by

(5.1)
Now, we consider

Applying Hölder’s inequality, using the fact that
 due to
due to 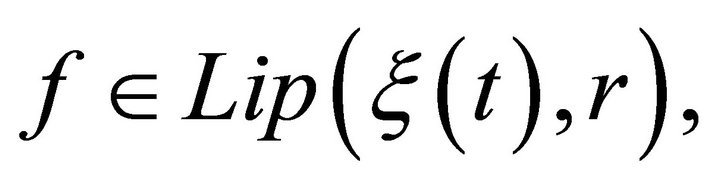 condition (3.2) and Lemma 4.1, we have
condition (3.2) and Lemma 4.1, we have
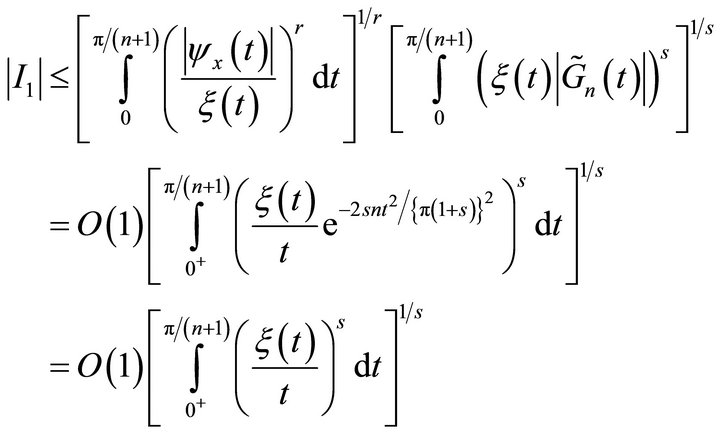
Since 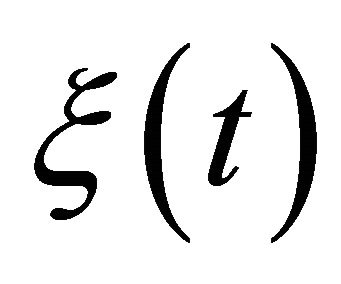 is positive increasing function so using condition (3.4), we have
is positive increasing function so using condition (3.4), we have
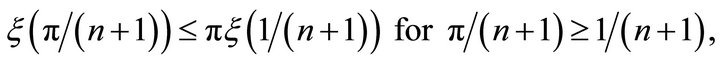
 and Second Mean Value Theorem for integrals, we get
and Second Mean Value Theorem for integrals, we get
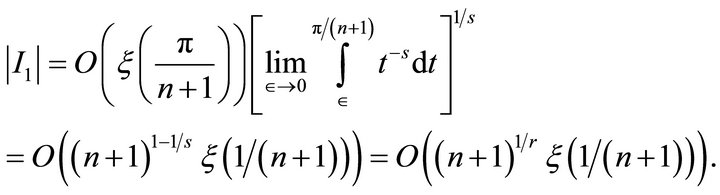
(5.2)
Now, we consider
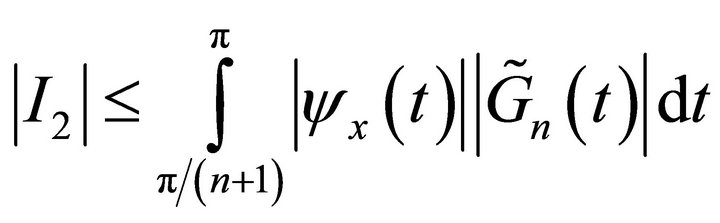 .
.
Again applying Hölder’s inequality, using the fact that
 due to
due to 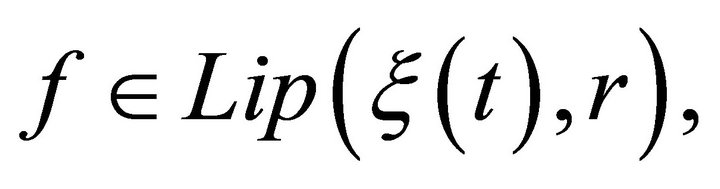 condition (3.3) and Lemma 4.1, we obtain
condition (3.3) and Lemma 4.1, we obtain

(5.3)
in view of increasing nature of ,
, 
where  lie in
lie in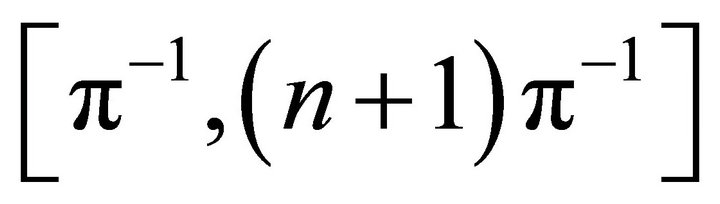 , Second Mean Value Theorem for integrals and Note 3.2.
, Second Mean Value Theorem for integrals and Note 3.2.
Collecting (5.1) - (5.3), we get
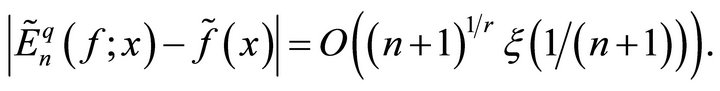
Now, using the 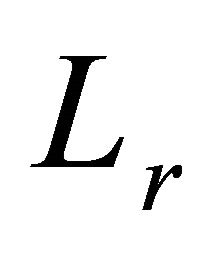 -norm of a function, we get
-norm of a function, we get
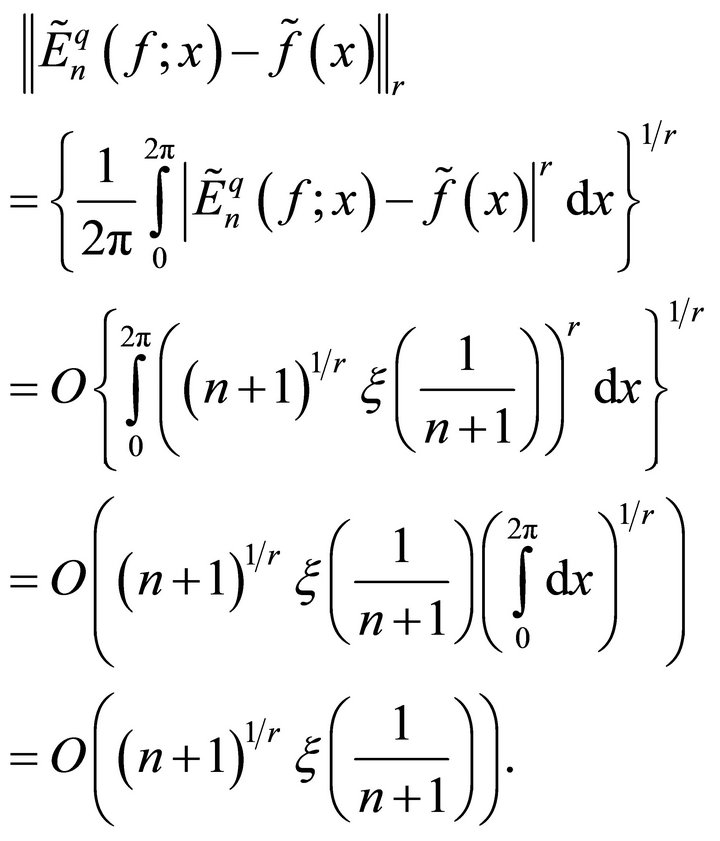
This completes the proof of Theorem 3.1.
6. Corollaries
The following corollaries can be derived form Theorem 3.1.
Corollary 6.1: If 
 then the class
then the class
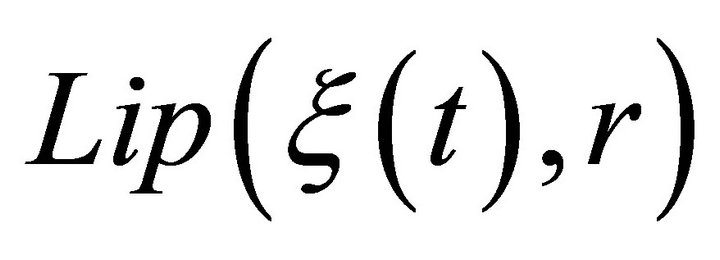 ,
,  reduces to the class
reduces to the class ,
,
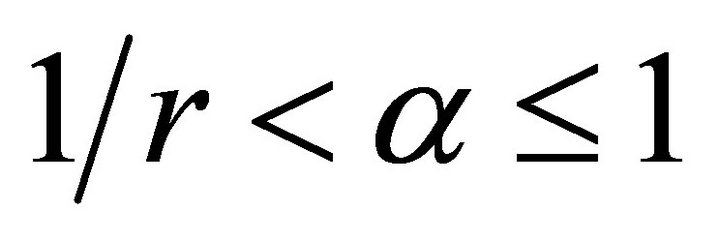 and the degree of approximation of a function
and the degree of approximation of a function , conjugate to a
, conjugate to a  -periodic function f belonging to the
-periodic function f belonging to the  class is given by
class is given by
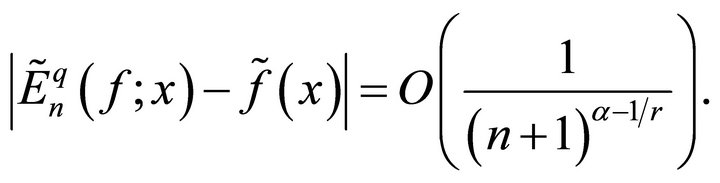 (6.1)
(6.1)
Proof. Putting  in Theorem 3.1, we have
in Theorem 3.1, we have
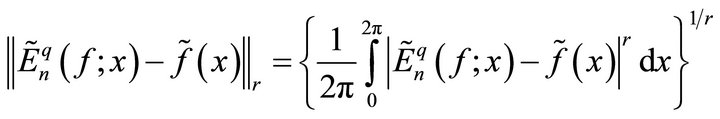
or,

or,
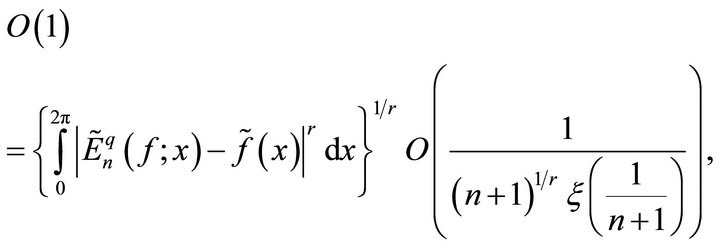
For if not the right hand side of the above equation will be O(1), therefore, we have

This completes the proof of Corollary 6.1.
Corollary 6.2 If 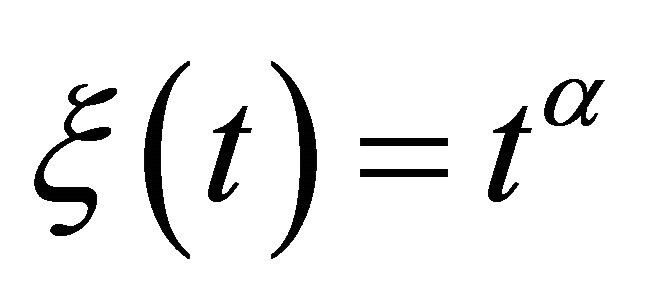 for
for  and
and  in Theorem 3.1, then
in Theorem 3.1, then 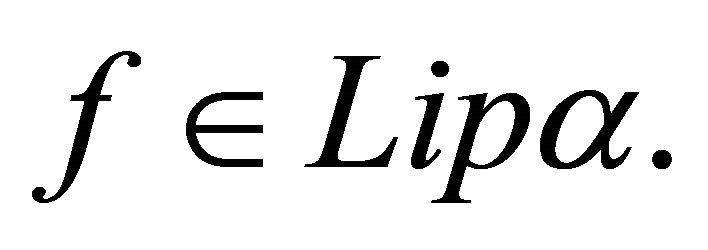 In this case, the degree of approximation of a function
In this case, the degree of approximation of a function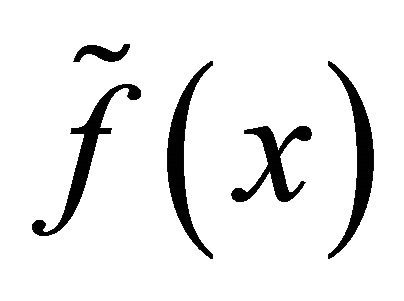 , conjugate to a
, conjugate to a  -periodic function f belonging to the class
-periodic function f belonging to the class  is given by
is given by
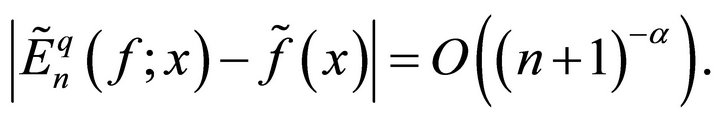
Proof. For  in Corollary 6.1, we get
in Corollary 6.1, we get

Thus, we have

This completes the proof of Corollary 6.2.
7. An Example
Consider an infinite series
 (7.1)
(7.1)
The nth partial sums 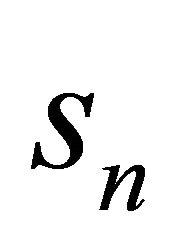 of series (7.1) at
of series (7.1) at  is given by
is given by
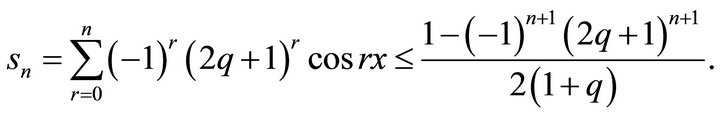
Since  does not exist. Therefore the series (7.1)
does not exist. Therefore the series (7.1)
is non-convergent.
Now, we have the (E,q) transform of (7.1) is given by
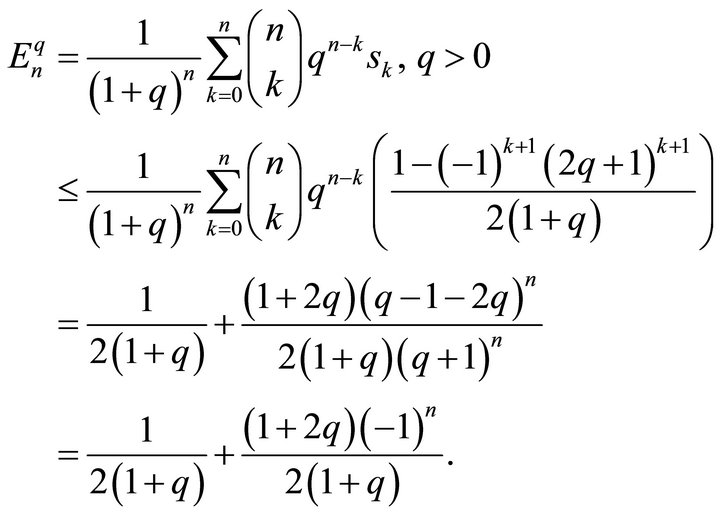
Here, 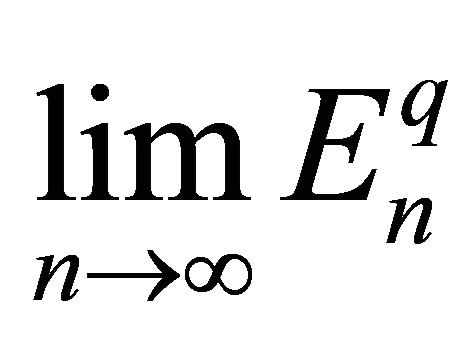 does not exist. Hence the series (7.1) is not summable, while the series (7.1) is product summable.
does not exist. Hence the series (7.1) is not summable, while the series (7.1) is product summable.
8. Conclusion
Several results concerning to the degree of approximation of periodic signals (functions) belonging to the Lipschitz class by matrix (E,q) operator have been reviewed. Further, a proper set of conditions have been discussed to rectify the errors. Some interesting application of the operator (E,q) used in this paper pointed out in Note 3.4. An example has been discussed also.
9. Acknowledgements
The authors are very grateful to the anonymous referees for many valuable comments and suggestions which helped to improve the presentation of the paper considerably. The authors are also thankful to all the members of editorial board of Advances in Pure Mathematics (APM) and Dr. Melody Liu, APM Editorial Board Assistant for their kind cooperation and smooth behavior during communication.
REFERENCES
- H. H. Khan, “On Degree of Approximation to a Functions Belonging to the Class
 ,” Indian Journal of Pure and Applied Mathematics, Vol. 5, No. 2, 1974, pp. 132-136.
,” Indian Journal of Pure and Applied Mathematics, Vol. 5, No. 2, 1974, pp. 132-136. - H. H. Khan, “On the Degree of Approximation to a Function by Triangular Matrix of Its Fourier Series I,” Indian Journal of Pure and Applied Mathematics, Vol. 6, No. 8, 1975, pp. 849-855.
- H. H. Khan, “On the Degree of Approximation to a Function by Triangular Matrix of Its Conjugate Fourier Series II,” Indian Journal of Pure and Applied Mathematics, Vol. 6, No. 12, 1975, pp. 1473-1478.
- H. H. Khan, “A Note on a Theorem Izumi,” Communications De La Faculté Des Sciences Mathématiques Ankara (TURKEY), Vol. 31, 1982, pp. 123-127.
- H. H. Khan and G. Ram, “On the Degree of Approximation,” Facta Universitatis Series Mathematics and Informatics (TURKEY), Vol. 18, 2003, pp. 47-57.
- P. Chandra, “A Note on the Degree of Approximation of Continuous Functions,” Acta Mathematica Hungarica, Vol. 62, No. 1-2, 1993, pp. 21-23.
- P. Chandra, “Trigonometric Approximation of Functions in
 -Norm,” Journal of Mathematical Analysis and Applications, Vol. 275, No. 1, 2002, pp. 13-26. doi:10.1016/S0022-247X(02)00211-1
-Norm,” Journal of Mathematical Analysis and Applications, Vol. 275, No. 1, 2002, pp. 13-26. doi:10.1016/S0022-247X(02)00211-1 - L. Leindler, “Trigonometric Approximation in
 -Norm,” Journal of Mathematical Analysis and Applications, Vol. 302, No. 1, 2005, pp. 129-136. doi:10.1016/j.jmaa.2004.07.049
-Norm,” Journal of Mathematical Analysis and Applications, Vol. 302, No. 1, 2005, pp. 129-136. doi:10.1016/j.jmaa.2004.07.049 - V. N. Mishra, H. H. Khan and K. Khatri, “Degree of Approximation of Conjugate of Signals (Functions) by Lower Triangular Matrix Operator,” Applied Mathematics, Vol. 2, No. 12, 2011, pp. 1448-1452. doi:10.4236/am.2011.212206
- V. N. Mishra, “On the Degree of Approximation of Signals (Functions) Belonging to the Weighted

 -Class by Almost Matrix Summability Method of Its Conjugate Fourier Series,” International Journal of Applied Mathematics and Mechanics, Vol. 5, No. 7, 2009, pp. 16-27.
-Class by Almost Matrix Summability Method of Its Conjugate Fourier Series,” International Journal of Applied Mathematics and Mechanics, Vol. 5, No. 7, 2009, pp. 16-27. - M. L. Mittal, U. Singh, V. N. Mishra, S. Priti and S. S. Mittal, “Approximation of functions belonging to
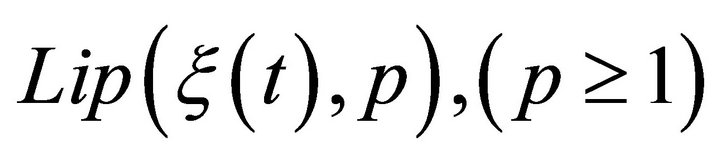 -Class by means of conjugate Fourier series using linear operators,” Indian Journal of Mathematics, Vol. 47, No. 2-3, 2005, pp. 217-229.
-Class by means of conjugate Fourier series using linear operators,” Indian Journal of Mathematics, Vol. 47, No. 2-3, 2005, pp. 217-229. - M. L. Mittal, B. E. Rhoades and V. N. Mishra, “Approximation of Signals (Functions) Belonging to the Weighted
 -Class by linear operators,” International Journal of Mathematics and Mathematical Sciences, Vol. 2006, 2006, Article ID: 53538. doi:10.1155/IJMMS/2006/53538
-Class by linear operators,” International Journal of Mathematics and Mathematical Sciences, Vol. 2006, 2006, Article ID: 53538. doi:10.1155/IJMMS/2006/53538 - M. L. Mittal and V. N. Mishra, “Approximation of Signals (Functions) Belonging to the Weighted
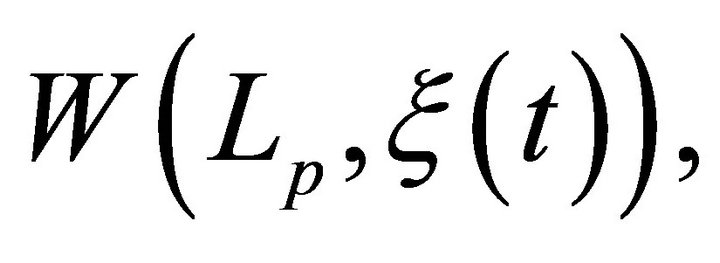
 -Class by Almost Matrix Summability Method of Its Fourier Series,” International Journal of Mathematical Sciences and Engineering Applications, Vol. 2, No. 4, 2008, pp. 285-294.
-Class by Almost Matrix Summability Method of Its Fourier Series,” International Journal of Mathematical Sciences and Engineering Applications, Vol. 2, No. 4, 2008, pp. 285-294. - B. E. Rhoades, K. Ozkoklu and I. Albayrak, “On Degree of Approximation to a Functions Belonging to the Class Lipschitz Class by Hausdroff Means of Its Fourier Series,” Applied Mathematics and Computation, Vol. 217, No. 16, 2011, pp. 6868-6871. doi:10.1016/j.amc.2011.01.034
- M. L. Mittal, B. E. Rhoades, V. N. Mishra and U. Singh, “Using Infinite Matrices to Approximate Functions of Class
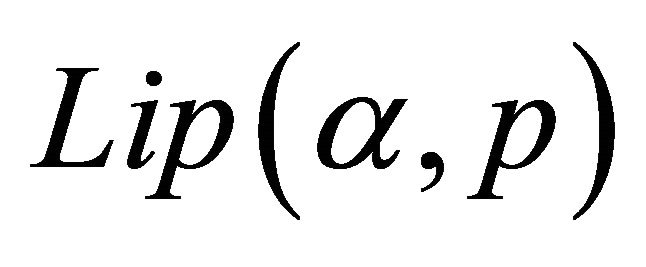 Using Trigonometric Polynomials,” Journal of Mathematical Analysis and Applications, Vol. 326, No. 1, 2007, pp. 667-676. doi:10.1016/j.jmaa.2006.03.053
Using Trigonometric Polynomials,” Journal of Mathematical Analysis and Applications, Vol. 326, No. 1, 2007, pp. 667-676. doi:10.1016/j.jmaa.2006.03.053 - V. N. Mishra and L. N. Mishra, “Trigonometric Approximation of Signals (Functions) in
 -Norm,” International Journal of Contemporary Mathematical Sciences, Vol. 7, No. 19, 2012, pp. 909-918.
-Norm,” International Journal of Contemporary Mathematical Sciences, Vol. 7, No. 19, 2012, pp. 909-918. - V. N. Mishra, “Some Problems on Approximations of Functions in Banach Spaces,” Ph.D. Thesis, Indian Institute of Technology, Roorkee, 2007.
- R. K. Shukla, “Certain Investigations in the theory of Summability and that of Approximation,” Ph.D. Thesis, V.B.S. Purvanchal University, Jaunpur, 2010.
- G. H. Hardy, “Divergent Series,” Oxford University Press, Oxford, 1949.
- A. Zygmund, “Trigonometric Series, Vol. I,” 2nd Edition, Cambridge University Press, Cambridge, 1959.
NOTES
*The authors declare that they have no competing interests. All the authors contributed equally to this work and they read and approved the final manuscript.

