World Journal of Mechanics
Vol. 1 No. 2 (2011) , Article ID: 4674 , 6 pages DOI:10.4236/wjm.2011.12009
Radiative Heat Transfer of an Optically Thick Gray Gas in the Presence of Indirect Natural Convection
1Department of Applied Mathematics, Vidyasagar University, Midnapore, India
2Department of Mathematics, Narajole Raj College, Narajole, India
E-mail: jana261171@yahoo.co.in, g_swapan2002@yahoo.com
Received March 7, 2011; revised March 30, 2011; accepted April 10, 2011
Keywords: Thermal Radiation, Indirect Natural Convection, Reynold Number, Stefan-Boltzman Radiation Parameter
ABSTRACT
We study the effects of thermal radiation of a viscous incompressible fluid occupying a semi-infinite region of space bounded by an infinite horizontal moving hot flat plate in the presence of indirect natural convection by way of an induced pressure gradient. The fluid is a gray, absorbing emitting radiation but a non scattering medium. An exact solution is obtained by employing Laplace transform technique. Since temperature field depends on Reynold number the flow is considered to be non-isothermal case (the temperature of the plate Tw ≠ constant) and for an isothermal case (Tw = constant) the flow is determined by the Reynold number which is equal to 1.
1. Introduction
Thermal radiation of an optically thick gray gas is of great importance to the study of high temperature physics and space technology. Mentioning the study of this type of problem with a view to analyse the transient approach of a radiative heat-transfer aspects of an optically thick fluid it seems to be appeared in the literature as studied by many authors. England and Emery [1] have investigated the thermal radiation effects of an optically thin gray gas bounded by a stationary plate. The hydromagnetic free convection flow with radiative heat transfer in a rotating and optically thin fluid has been investigated by Bestman and Adiepong [2] and Naroua et al. [3]. Soundalgakar and Takhar [4] considered the radiative free convictive flow of an optically thin gray gas past a semi-infinite vertical plate.Takher et al. [5] have studied the radiation effects on MED free convection flow of a radiating gas past a semi-infinite vertical plate. Radiation effects on mixed convection along an isothermal vertical plate were studied by Hossain and Takhar [6]. Raptis and Perdikis [7] studied the effects of thermal radiation and free convection flow past a moving vertical plate. Thermal radiation effects of an optically thin gray gas were studied by Raptis and Perdikis [8]. Muthukumarswamy and Ganeshan [9] have considered radiation effects on flow past an impulsively started infinite vertical plate with variable temperature. Ghosh and Pop [10] have studied thermal radiation of an optically thick gray gas in the presence of indirect natural convection. Recently, several studies on radiative heat transfer have been reported by Raptis et al. [11], Duwairi and duwairi [12], Vasil’ev and Nesterov [13], Duwairi [14], Quaf MEM [15], Ghosh [16,17], Zueco [18], Samad and Rahman [19] and Beg and Ghosh [20]. In the light of Ghosh and Pop [10] work it is stated that the effect of pressure on velocity remains present at  for
for  so that the pressure rise region near the leading edge of the hot plate leads to increase the velocity .Thus it comes to a justification of this problem leading to a fact that the pressure becomes absent due to a stagnation point flow. Since a thin radiation boundary layer is formed due to an optically thick fluid it is considered that the temperature varies linearly along the hot plate so that the temperature field is depend on the thickness of the radiation boundary layer
so that the pressure rise region near the leading edge of the hot plate leads to increase the velocity .Thus it comes to a justification of this problem leading to a fact that the pressure becomes absent due to a stagnation point flow. Since a thin radiation boundary layer is formed due to an optically thick fluid it is considered that the temperature varies linearly along the hot plate so that the temperature field is depend on the thickness of the radiation boundary layer 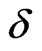 where
where  and the thickness of the radiation layer is considered to be unity.
and the thickness of the radiation layer is considered to be unity.
Although the radiation boundary layer thickness depends on Reynolds number the aim of the present investigation of the problem is to a study of thermal radiation of an optically thick gray gas in taking into account of an unsteady flow of an incompressible viscous fluid occupying a semi-infinite region of space bounded by an infinite horizontal moving hot flat plate in the presence of indirect natural convection by way of induced pressure gradient. Since the temperature field depends on Reynolds number the wall temperature does not constant (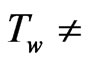 constant) as the temperature varies along the plate and the recovery factor is determined by the Reynolds number. An uniform wall temperature (
constant) as the temperature varies along the plate and the recovery factor is determined by the Reynolds number. An uniform wall temperature (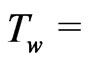 constant) for an isothermal flat plate is fully understood if the value of Reynolds number is equal to 1. Thus it comes to a conclusion that since the temperature field depends on radiation layer thickness
constant) for an isothermal flat plate is fully understood if the value of Reynolds number is equal to 1. Thus it comes to a conclusion that since the temperature field depends on radiation layer thickness  it is a decisive importance to an isothermal flat plate (
it is a decisive importance to an isothermal flat plate (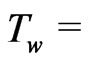 constant) with regard to a finite thickness (
constant) with regard to a finite thickness (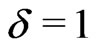 ) [see Ghosh and Pop [10]. In our present problem, the temperature field depends on Reynolds number so that the problem is to be considered non-isothermal case (
) [see Ghosh and Pop [10]. In our present problem, the temperature field depends on Reynolds number so that the problem is to be considered non-isothermal case ( constant) and the problem turns into isothermal case (
constant) and the problem turns into isothermal case ( constant) when the value of Reynolds number is equal to 1. An interesting feature of this problem is to be determined an indirect natural convection flow where the induced pressure gradient is considered to be zero at infinity.
constant) when the value of Reynolds number is equal to 1. An interesting feature of this problem is to be determined an indirect natural convection flow where the induced pressure gradient is considered to be zero at infinity.
2. Formulation of the Problem and Its Solution
Consider the unsteady flow of a viscous incompressible fluid occupying a semi-infinite region of space bounded by an infinite horizontal plates moving with constant velocity  with reference to indirect natural convection by way of induced pressure gradient. The flow is considered optically thick gray gas with indirect natural convection and radiation. We choose the cartesian coordinate system is such a way that x-axis is taken along the plate in the direction of the flow and y-axis is normal to it [see Figure 1]. The induced pressure gradient lies in x-direction to the origin of the flow parallel to the plate. All the fluid properties are considered constant expect the influence of density variation in the body force term. The radiation heat flux in the x-direction is considered negligible in comparison to the y-axis.
with reference to indirect natural convection by way of induced pressure gradient. The flow is considered optically thick gray gas with indirect natural convection and radiation. We choose the cartesian coordinate system is such a way that x-axis is taken along the plate in the direction of the flow and y-axis is normal to it [see Figure 1]. The induced pressure gradient lies in x-direction to the origin of the flow parallel to the plate. All the fluid properties are considered constant expect the influence of density variation in the body force term. The radiation heat flux in the x-direction is considered negligible in comparison to the y-axis.
The momentum equations in component form can take the form
 (1)
(1)
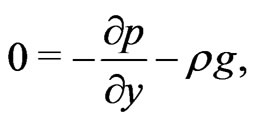 (2)
(2)
where 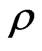 is the fluids density, p the pressure,
is the fluids density, p the pressure,  the co-
the co-
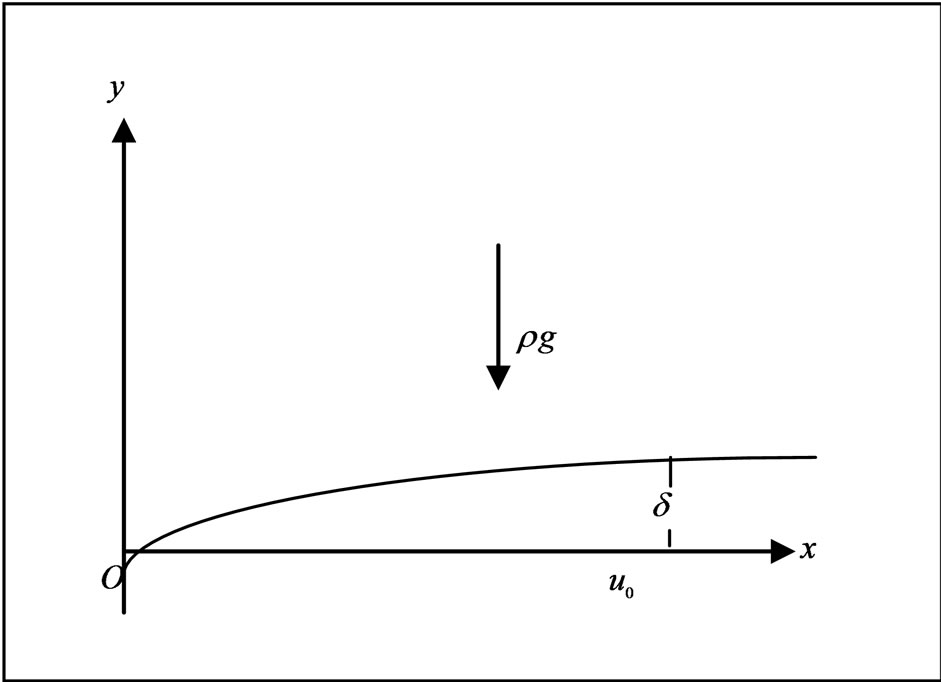
Figure 1. Geometry of the problem.
efficient of viscosity and g the acceleration due to gravity.
The equation of energy is
 (3)
(3)
where  is the specific heat and k the thermal conductivity.
is the specific heat and k the thermal conductivity.
It is assumed that there is a temperature variation along the x-direction of the horizontal plate. The temperature of the flow can be written as
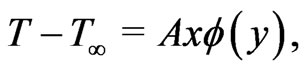 (4)
(4)
where T is the temperature of the fluid, 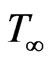 the temperature of the fluid far away the plate and
the temperature of the fluid far away the plate and 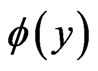 the dimensionless temperature and
the dimensionless temperature and .
.
The equation of state becomes
 (5)
(5)
where 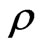 is the density of the fluid,
is the density of the fluid, 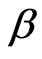 the coefficient of thermal expansion and the other symbols have their usual meanings.
the coefficient of thermal expansion and the other symbols have their usual meanings.
From (2) and (5) we have
 (6)
(6)
Sine the temperature is uniform at infinity, it is reasonably assumed to be 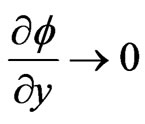 as
as . Thus
. Thus 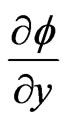
is zero everywhere in the flow. Hence (6) becomes
 (7)
(7)
On the use of (7), the Equation (1) becomes
 (8)
(8)
Using infinity conditions in (8), one find

Hence the Equation (8) reduced to
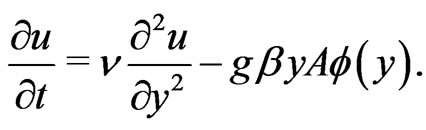 (9)
(9)
The initial and boundary conditions are
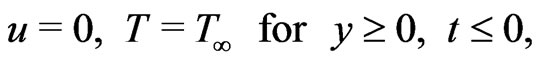 (10)
(10)
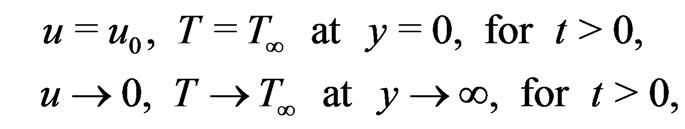 (11)
(11)
From (4), it is stated that the temperature of the flow is dependent on Reynolds number.
The dimensionless temperature with the help of (4), we get
 (12)
(12)
where 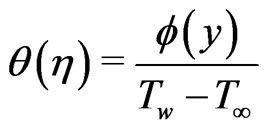 and
and  the Reynolds number.
the Reynolds number.
In comparison to the study of Ghosh and Pop [10] with reference to the dimensionless temperature
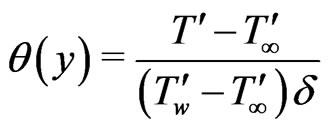 , where δ the radiation layer thickness and the other symbols have their usual meanings with
, where δ the radiation layer thickness and the other symbols have their usual meanings with
 (L is the characteristic length), it is rigorously stated that the radiation layer thickness depends on Reynolds number and the plate temperatures does not constant (
(L is the characteristic length), it is rigorously stated that the radiation layer thickness depends on Reynolds number and the plate temperatures does not constant (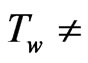 constant). For an isothermal plate (
constant). For an isothermal plate (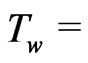 constant), the thickness of the radiation layer should be taken finite value i.e.
constant), the thickness of the radiation layer should be taken finite value i.e.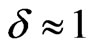 . In this situation, Ghosh and Pop [10] have considered finite thickness of radiation layer with isothermal flat plate (
. In this situation, Ghosh and Pop [10] have considered finite thickness of radiation layer with isothermal flat plate ( constant). The present investigation deals with non-isothermal, flat plate (
constant). The present investigation deals with non-isothermal, flat plate (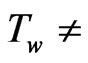 constant) as the temperature varies along the plate and the recovery factor is determined by the Reynolds number. It seems to be understood that this problem turns into isothermal case (
constant) as the temperature varies along the plate and the recovery factor is determined by the Reynolds number. It seems to be understood that this problem turns into isothermal case (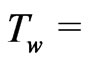 constant) if the Reynolds number
constant) if the Reynolds number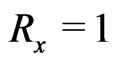 .
.
Introduce the dimensionless quantities


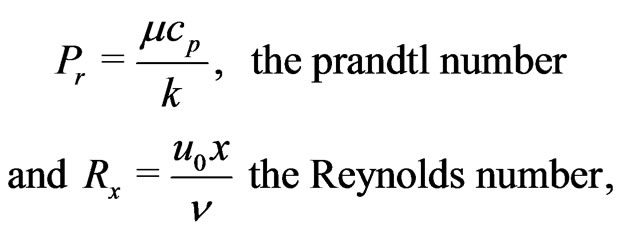 (13)
(13)
where ,
, 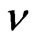 ,
,  , k, g and
, k, g and 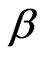 are, respectively, the coefficient of viscosity, kinemetic coefficient of viscosity, specific heat at constant pressure, thermal conductivity, gravitational acceleration and the coefficient of thermal expansion and the other symbols have their usual meanings.
are, respectively, the coefficient of viscosity, kinemetic coefficient of viscosity, specific heat at constant pressure, thermal conductivity, gravitational acceleration and the coefficient of thermal expansion and the other symbols have their usual meanings.
On the use of (13), the Equation (9) becomes
 (14)
(14)
The radiation flux vector can be found from Isachenko et al. [21], Equations (16)-(38), page 382 and its formula is derived on the basis of the diffusion concept of radiation heat transfer in the following way:
 (15)
(15)
where  and
and 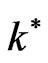 are, respectively, the Stefan-Boltzman constant and the spectral mean absorption coefficient of the medium.
are, respectively, the Stefan-Boltzman constant and the spectral mean absorption coefficient of the medium.
It is assumed that the temperature differences within the flow are sufficiently small such that  may be regarded as a linear function of the temperature. It can be established by expanding
may be regarded as a linear function of the temperature. It can be established by expanding  i.e. a Taylor series about
i.e. a Taylor series about 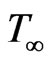 and neglecting higher order term. Therefore,
and neglecting higher order term. Therefore,  can be expressed in the following form
can be expressed in the following form
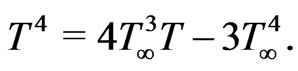 (16)
(16)
Using Equations (15) and (16), the energy Equation (3) can be written in a dimensionless form subject to (13) such as
 (17)
(17)
where 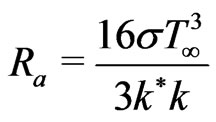 is the radiation paeameter.
is the radiation paeameter.
The corresponding boundary conditions are
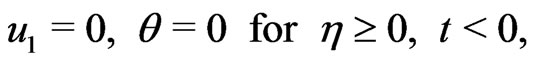 (18)
(18)
 (19)
(19)
The solutions for the velocity and temperature distributions can be obtained by applying Laplace transform technique subject to the boundary conditions (18) and (19) together with the Equations (14) and (17) become
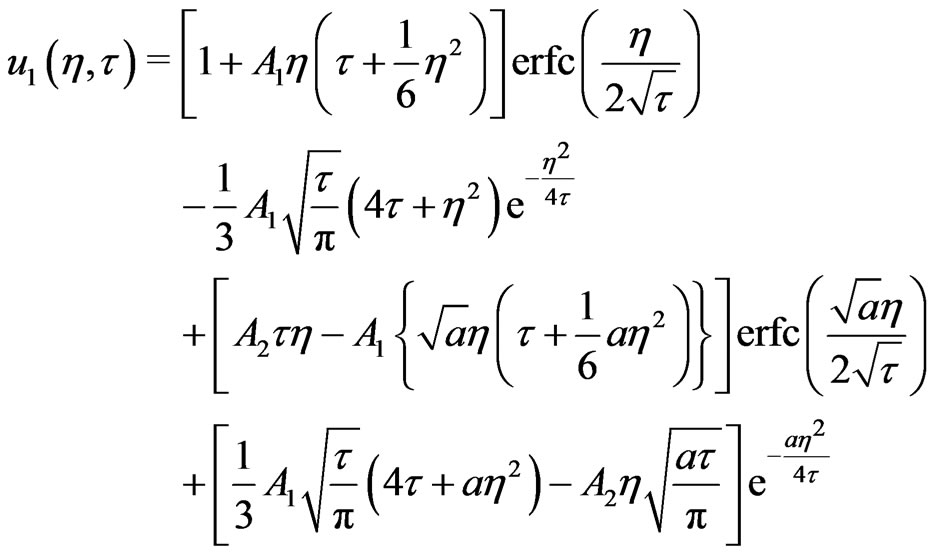 (20)
(20)
and
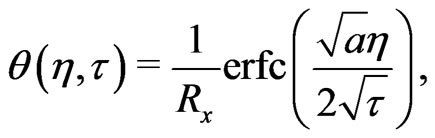 (21)
(21)
where
 (21a)
(21a)
We shall now discuss some particular cases of interest Case I: In the absence of radiation parameter 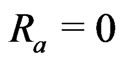 and the prandtl number
and the prandtl number , the solutions (20) and (21) reduce to
, the solutions (20) and (21) reduce to
 (22)
(22)
and
 (23)
(23)
Case II: In the absence of radiation temperature
(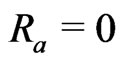 ) and the pressure gradient
) and the pressure gradient  the Equations (1)-(3) transform into a flat plate at zero incidence so that the velocity and the temperature fields are identical when the prandtl number
the Equations (1)-(3) transform into a flat plate at zero incidence so that the velocity and the temperature fields are identical when the prandtl number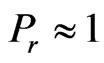 .
.
3. Discussion and Results
The graphical representations of numerical results with different parameters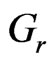 ,
, 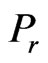 ,
,  ,
, 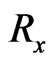 and
and 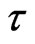 for the velocity and temperature distributions are plotted against
for the velocity and temperature distributions are plotted against  in Figures 2-8. There is steep decline from the wall for all profiles in Figures 2-8 and no velocity and temperature overshoot. The profiles of spatial dimensionless velocity
in Figures 2-8. There is steep decline from the wall for all profiles in Figures 2-8 and no velocity and temperature overshoot. The profiles of spatial dimensionless velocity  with distance from the wall, at various time
with distance from the wall, at various time 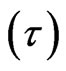 are shown in Figure 2. As time,
are shown in Figure 2. As time, 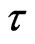 , increases from 0.02, 0.04 to 0.08. we observed that the velocity
, increases from 0.02, 0.04 to 0.08. we observed that the velocity 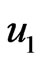 is increased markedly. With time in Figure 2 the flow is therefore, accelerate in the downward direction. Figure 3 reveals that the velocity
is increased markedly. With time in Figure 2 the flow is therefore, accelerate in the downward direction. Figure 3 reveals that the velocity  slightly increases with increase in radiation parameter
slightly increases with increase in radiation parameter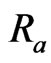 . The radiation conduction parameter
. The radiation conduction parameter 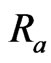 defines the relative contribution of radiation heat transfer to thermal conduction transfer. By applying Stefan-Boltzman constant for an optically dense medium it is stated from Figure 3 that an increase in radiation parameter
defines the relative contribution of radiation heat transfer to thermal conduction transfer. By applying Stefan-Boltzman constant for an optically dense medium it is stated from Figure 3 that an increase in radiation parameter 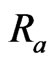 leads to a slightly rise in velocity
leads to a slightly rise in velocity 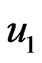 for any value of
for any value of . It is interesting to note that in a pressure rise region a slightly increase in velocity
. It is interesting to note that in a pressure rise region a slightly increase in velocity  is a remarkable feature of an optically thick (dense) medium. It is shown from Figure 4 that an increase in Prandtl number
is a remarkable feature of an optically thick (dense) medium. It is shown from Figure 4 that an increase in Prandtl number 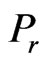 leads to decrease the velocity
leads to decrease the velocity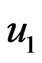 . Usually the value of Prandtl number
. Usually the value of Prandtl number 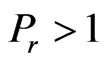 determines the highly ionized gas. In Figure 4 it reveals that the velocity
determines the highly ionized gas. In Figure 4 it reveals that the velocity  always decreases with increase in prandtl number
always decreases with increase in prandtl number  for tri-atomic gas of its optical measurement. It is noticed from Figure 5 that the velocity
for tri-atomic gas of its optical measurement. It is noticed from Figure 5 that the velocity  increases with increase in Grashof number
increases with increase in Grashof number . This situation reveals that the buoyancy force accelerates the velocity field and no flow reversal occurs to prevent separation. Figures 6 and 7 demonstrate that the temperature
. This situation reveals that the buoyancy force accelerates the velocity field and no flow reversal occurs to prevent separation. Figures 6 and 7 demonstrate that the temperature  increases with increase in either time
increases with increase in either time  or radiation parameter
or radiation parameter . Figure 8 shows that an increase in Prandtl number
. Figure 8 shows that an increase in Prandtl number 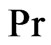 leads to fall the temperature. In relevance to the physical situation of interest it reveals that the temperature decreases with an increase in Prandtl number
leads to fall the temperature. In relevance to the physical situation of interest it reveals that the temperature decreases with an increase in Prandtl number 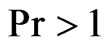 for highly ionized gas.
for highly ionized gas.

Figure 2. Velocity distributions u1 with Gr = 2.0, Pr = 4.4, Ra = 0.2, Rx = 1.0.

Figure 3. Velocity distributions u1 with Gr = 2.0, Pr = 4.4, τ = 0.02, Rx = 1.0.

Figure 4. Velocity distributions u1 with Gr = 2.0, Ra = 0.2, τ = 0.02, Rx = 1.0.

Figure 5. Velocity distributions u1 with Ra = 0.2, Pr = 4.4, τ = 0.02, Rx = 1.0.

Figure 6. Temperature distributions θ with Pr = 4.4, Ra = 0.2, Rx = 1.0.
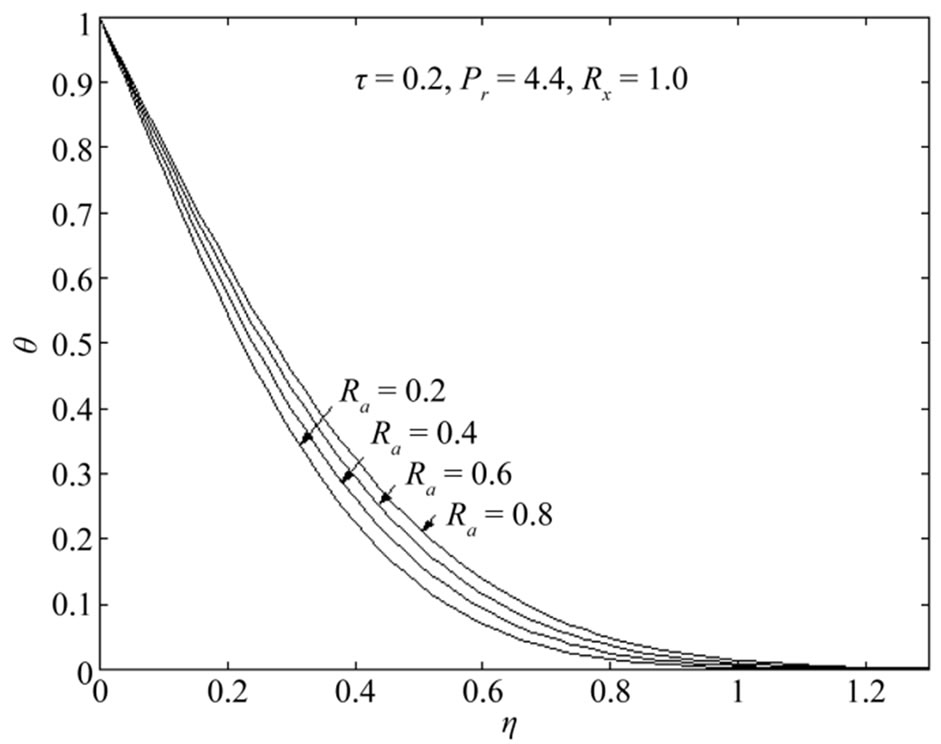
Figure 7. Temperature distributions θ with Pr = 4.4, τ = 0.2, Rx = 1.0.
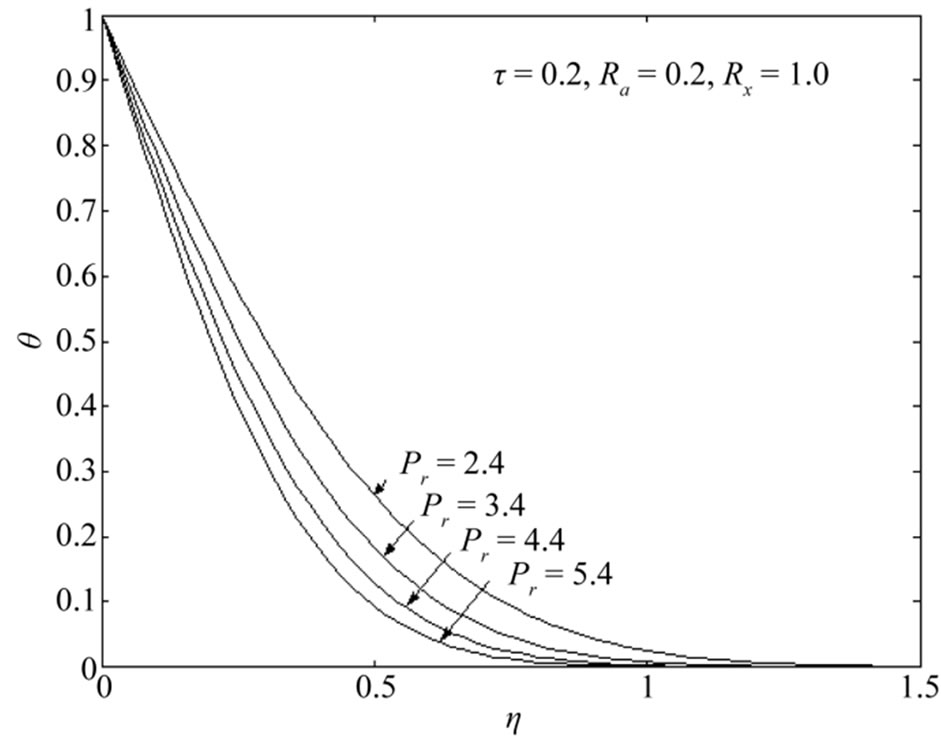
Figure 8. Temperature distributions θ with Ra = 0.2, τ = 0.2, Rx = 1.0.
REFERENCES
- W. G. England and A. F. Emery, “Thermal Radiation Effects on the Laminear Free Convection Boundary Layer of an Absorbing Gas,” Journal of Heat Transfer, Vol. 91, 1969, pp. 37-44.
- A. R. Bestman and S. K. Adiepong, “Unsteady Hydromagnetic Free-Convection Flow with Radiation Heat Transfer in a Rotating Fluid,” Astrophysics and Space Science, Vol. 143, No. 1, 1988, pp. 73-80.
- doi:10.1007/BF00636756
- H. Naroua, P. C. Ram, A. S. Sambo and H. S. Takhar, “Finite Element Analysis of Natural Convection Flow in a Rotating Fluid with Radiative Heat Transfer,” Journal of Magnetohydrodynamics and Plasma Research, Vol. 7, No. 4, 1998, pp. 257-274.
- V. M. Soundalgekar and H. S. Takhar, “Radiation Effects on Free Convection Flow past a Semi-Infinite Vertical Plate,” Modelling, Measurement and Control, Vol. B51, 1993, pp. 31-40.
- H. S. Takhar, R. S. S. Gorla and V. M. Soundalgekar, “Radiation Effects on MED Free Convection Flow of a Radiating Gas Past a Semi-Infinite Vertical Plate,” International Journal of Numerical Methods for Heat & Fluid Flow, Vol. 6, 1996, pp. 77-83.
- M. A. Hossain and H. S. Takhar, “Radiation Efeects on Mixed Convection along a Vertical Plate with Uniform Surface Temperature,” Heat and Mass Transfer, Vol. 31, No. 4, 1996, pp. 243-248. doi:10.1007/BF02328616
- A. Raptis and C. Perdikis, “Radiation and Free Convection Flow past a Moving Plate,” Applied Mechanics and Engineering, Vol. 4, No. 4, 1990, pp. 817-821.
- A. Raptis and C. Perdikis, “Thermal Radiation of an Optically Thin Gray Gas,” International Journal of Applied Mechanics and Engineering, Vol. 8, No. 1, 2003, pp. 131-134.
- R. Madhucumaraswamy and P. Ganesan, “Radiation Effects on Flow past an Impulsively Started Infinite Vertical Plate with Variable Temperature,” International Journal of Applied Mechanics and Engineering, Vol. 8, No. 1, 2003, pp. 125-129.
- S. K. Ghosh and I. Pop, “Thermal Radiation of an Optically Thick Gray Gas in the Presence of Indirect Natural Convection,” International Journal of Fluid Mechanics Research, Vol. 34, No. 6, 2007, pp. 515-520.
- A. Raptis, C. Perdikis and H. S. Takhar, “Effect of Thermal Radiation on MHD Flow,” Applied Mathematics and Computation, Vol. 153, No. 3, 2004, pp. 645-649.
- doi:10.1016/S0096-3003(03)00657-X
- H. M. Duwairi and R. M. Duwairi, “Thermal Radiation Effect on Mhd Rayleigh Flow with Constant Surface Heat Flux,” Heat and Mass Transfer, Vol. 41, No. 1, 2005, pp. 51-57.
- E. N. Vasil’ev and D. A. Nesterov, “The Effect of Radiative — Convective Heat Transfer on the Formation of Current Layer,” High Temperature, Vol. 43, No. 3, 2005, pp. 396-403.
- H. M. Duwairi, “Viscous and Joule Heating Effects on Forced Convection Flow From Radiate Isothermal Porous Surface,” International Journal of Numerical methods Heat Fluid Flow, Vol. 15, No. 5, 2005, pp. 429-440.
- doi:10.1108/09615530510593620
- M. E. M. Quaf, “Exact Solution of Thermal Radiation on Mhd Flow over a Stretching Porous Sheet,” Applied Mathematics and Computation, Vol. 170, No. 2, 2005, pp. 1117-1125.
- S. K. Ghosh, “Radiative Heat Transfer Aspect of an Optically Thick Gray Gas in the Presence of a Magnetic Field,” International Journal of Applied Mechanics and Engineering, Vol. 12, No. 3, 2007, pp. 849-855.
- S. K. Ghosh, “Radiative Heat Transfer Aspect of an Optically Thick Gray Gas in the Presence of a Magnetic Field,” International Journal of Applied Mechanics and Engineering, Vol. 12, No. 4, 2007, pp. 1181.
- J. Zueco, “Network Simulation Method Applied to Radiation and Viscous Dissipation Effects on MHD Unsteady Free Convection Over a Vertical Porous Plate,” Applied Mathematical Modelling, Vol. 31, No. 9, 2007, pp. 2019-2033.
- M. A. Samad and M. M. Rahman, “Thermal Radiation Interaction with Unsteady MHD Flow past a Vertical Porous Plate Immersed in a Porous Medium,” Journal of Naval Architecture and Marine Engineering, Vol. 3, No. 1, 2006, pp. 7-14.
- O. A. Beg and S. K. Ghosh, “Analytical Study of Magnetohydrodynamic Radiation — Convection with Surface Temperature Oscillation and Secondary Flow Effects,” International Journal of Applied Mathematics and Mechanics, Vol. 6, No. 6, 2010, pp. 1-22.
- V. P. Isachenko, V. A. Osipova and A. S. Sukomel, “Heat Transfer,” Mir Publishers, Moscow, 1969, pp. 341-451.

