World Journal of Condensed Matter Physics
Vol.06 No.02(2016), Article ID:66966,14 pages
10.4236/wjcmp.2016.62015
Phase Diagrams of the Semi-Infinite Blume-Capel Model with Mixed Spins (SA = 1 and SB = 3/2) by Migdal Kadanoff Renormalization Group
Mohamed El Bouziani1*, Mohamed Madani1,2, Abou Gaye1, Abdelhameed Alrajhi1
1Laboratoire L.P.M.C., Equipe de Physique théorique, Faculté des Sciences, Université Chouaib Doukkali, El Jadida, Maroc
2Département de Physique-Chimie, CRMEF El Jadida-Safi, Safi, Maroc

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 January 2016; accepted 28 May 2016; published 31 May 2016
ABSTRACT
We study the mixed spin-1 and spin-3/2 Blume-Capel model under crystal field in the tridimensional semi-infinite case. This has been done by using the real-space renormalization group approximation and specifically the Migdal-Kadanoff technique. As a function of the ratio R of bulk and surface interactions and the ratios R1 and R2 of bulk and surface crystals fields on the spin-1 and spin-3/2 respectively, we have determined various types of phase diagrams. Besides second- order transition lines, first-order phase transition lines terminating at tricritical points are obtained. We found that there existed nine main types of phase diagram showing a variety of phase transitions associated with the surface, including ordinary, extraordinary, surface and special phase transitions.
Keywords:
Semi-Infinite, Mixed Spins, Blume-Capel Model, Renormalization Group, Surface Transitions

1. Introduction
The problems of surface magnetism have been investigated for many years. Among them the effects of surface on phase transitions in semi-infinite systems have received increasing interest. Real systems have surfaces, interfaces or boundaries and the translational symmetry is not preserved. This gives a set of surface phase diagrams richer than the infinite bulk one [1] - [4] . The simplest model is to assume that the surface is single planar, which defines the semi-infinite model.
Several experimental studies show a critical behaviour of the surface different than the bulk. As example, we mention the work done on mixed compounds NbSe2 [5] , NiO (111) [6] and Co/Ni (111) overlayers [7] , on which are observed surface and extraordinary phase transitions. In those cases, the surface has a critical temperature greater than the bulk. In other pure samples of Gd [8] , the surface and the bulk are at the same critical temperature, the transition is ordinary. The practice researches in magneto-electronic and materials using carriers based on spin properties instead of electrons and holes in traditional semiconductors are motivated by the development and application for information storage [9] and other applications in thermo-magnetic recording [10] . In the other hand, the theoretical studies of the critical surface effects have been developed during the last years, using a variety of approximations and mathematical techniques. An interesting literature review of the subject is in the work of K. Binder and Diehl [1] - [3] . The existence and critical behaviour of surface, extraordinary, special [11] [12] and extraordinary phase transitions have been illustrated using different approaches [2] [3] [13] - [16] , and various situations as pure, quenched and random systems at bulk or surface [17] - [20] have been studied. Also, the exact solution of the 2D semi-infinite Ising model has been proved [21] - [24] . The semi- infinite Blume-Capel model was also used to describe the wetting phenomenon. In reference [25] , the authors show that critical wetting in d = 2 is equivalent to a “bulk” critical phenomenon. A detailed study with a rich bibliography is found in reference [26] .
The three-dimensional semi-infinite spin-1 Ising model with a crystal field has been studied [27] . The spin-1 ferromagnetic Ising model with a crystal field has been introduced independently by Blume [28] and Capel [29] and is often called the Blume-Capel (BC) model. An extension of the BC model is the possibility of inclusion of higher spin values. Various types of phase diagram of a three-dimensional semi-infinite ferromagnetic spin-3/2 BC model were obtained within the framework both of the mean field theory and renormalization-group techniques [30] .
In the last years, a great attention has been devoted to systems of mixed spins and this is related to their importance in the study of magnetic materials with ferrimagnetic properties [31] . The system of mixed spins S = 1/2 and S = 1 has been one of the simplest to be studied early and largely, namely by the techniques of renormalization group [32] [33] , the Bethe-Peierls approximation [34] , the effective field theory [35] [36] , the Monte- Carlo simulation [37] [38] and the finite cluster approximation [39] .
Recently, this attention has been expanded on systems of mixed spins higher than 1/2, like the case S = 1 and S = 3/2, which has been also studied by several methods, as the mean field approximation (MF) [40] , the Bethe lattice recursion relations [41] [42] , the effective field theory [43] [44] , the Monte-Carlo simulation [45] , the Green’s function [46] , the recursion relations on Cayley tree [47] and the real space renormalization group theory [48] .
Our aim in this present paper is to determine the various types of phase diagram in the semi-infinite system of mixed spins S = 1 and S = 3/2 on the Blume-Capel model [28] [29] , which we study by using a renormalization group (RG) method, namely the Migdal-Kadanoff one [49] [50] , combining the decimation as well as the bond shifting. Our study focuses on the effect of two different single-ion anisotropies in the phase diagram of the mixed spin-1 and spin-3/2 Ising ferrimagnetic system. We organize our paper as follows. In Section 2, we treat the formalism of our method and we establish the Migdal-Kadanoff recursion equations. In Section 3, we present our results and discuss important points. Finally, we give our conclusion in Section 4.
2. Model and Method
2.1. Infinite Blume-Capel Model
We consider a two sublattice mixed spin-1 and spin-3/2 Blume-Capel model with different single-ion anisotropies ΔA and ΔB acting on the spin-1 and spin-3/2, respectively. The Hamiltonian of the system is given by
 (1)
(1)
where the sites of sublattice A are occupied by spins , which take the values of
, which take the values of 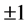 and 0, while those of the sublattice B are occupied by spins
and 0, while those of the sublattice B are occupied by spins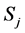 , which take the values of
, which take the values of 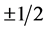 and
and . J is the reduced bilinear exchange interaction and
. J is the reduced bilinear exchange interaction and  (with
(with  the Boltzmann constant and T the absolute temperature). The first summation is over all nearest neighbor pairs of spins, the second and the third summations one over all sites.
the Boltzmann constant and T the absolute temperature). The first summation is over all nearest neighbor pairs of spins, the second and the third summations one over all sites.
In the Blume-Capel model, the reduced biquadratic interaction K is equal to zero, but we will take it into account due to the renormalization group technique we are using. We also introduce one additional interaction C to obtain self-consistent recursion relations. Thus, the Hamiltonian we will effectively use in the remainder of our work is as follows:
 . (2)
. (2)
The renormalization does not keep in general the parameters space of the Hamiltonian. The terms added to the original Blume-Capel Hamiltonian model, in addition to their role in the conservation of the parameter space, can be used in the improvement of critical exponents and precision Monte Carlo simulation: scaling correction [51] .
For example, in the Blume-Emery-Griffiths model, the three parameters 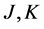 and
and  are insufficient to stabilize the ferromagnetic phase which has been obtained by all the methods of effective fields.
are insufficient to stabilize the ferromagnetic phase which has been obtained by all the methods of effective fields.
To have a more reliable qualitative appreciation of the phase transitions characteristics, we use an approximation of the real space renormalization group, namely the Migdal-Kadanoff one, which combines decimation and bond shifting and is tractable in all space dimensionalities. In order to implement the renormalization machinery, we consider a one-dimensional chain (Figure 1) of four spins  and
and  (
(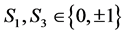 and
and  ), coupled by the interactions
), coupled by the interactions 
The spatial factor rescaling, denoted by b, is chosen as an odd integer to keep the possible sublattice symmetry breaking character of the system. In our present study, we take

After performing the decimation on the two middle spins 



with 



Figure 1. Chain of four spins, S1, S2, S3 and S4. J and K denote, respectively, the reduced bilinear and biquadratic interactions, while ∆i (i = A, B) is the crystal field at site i. Decimation will be performed on the two middle spins, S2 and S3.
Figure 2. Chain after decimation.
By using the renormalization group equation, we can make the link between (3) and (4) to obtain

with 

Replacing the expressions of the Equations (3) and (4) in Equation (5), and knowing that 


Since 




For

For

For

For

For

For

The Equations (7) to (12) and the bond-shifting process yield the final renormalized couplings 


Numerical analysis of these equations gives the flow in the parameter space of the Hamiltonian. We have already obtained [48] phase diagrams of the infinite Blume-Capel model (2D and 3D) and the table of fixed points that govern the phases and phase transitions. In the reference [48] , the second-order phase transitions are described by the fixed point C, the first order by the fixed point A and the tricritical point by the fixed point T. The various phase diagrams of the infinite model were also obtained according to the ratios of the interactions of the model.
Our results in the infinite model can be compared with those obtained by other methods: concerning the existence of tricritical point and its domain according to the values of the ratios of the interactions, we are in agreement with mean field theory result [52] , cluster variational theory [53] and Monte Carlo study [54] . At low temperatures, those approaches predict the possibility of first order transition between two ordered phases terminating at an end point. In our Migdal-Kadanoff approximation, we find only first order transition between ordered and disordered phases. Another common point is that there is no universality violation in the phase diagrams obtained. There is no marginality in all the fixed points obtained by Migdal-Kadanoff approach. Note that in general theory, the universality in phase transitions and critical phenomena is expressed explicitly by the existence of the non marginal fixed point describing a line or surface phase transitions. Each line or surface is consequently described by the same critical exponent evaluated at the fixed point by linearizing the renormalization group transformation.
Another comparison is possible, with the pure BC model S = 1 or S = 3/2. In this case all those approximations are in agreement with the existence of the tricritical point in the integer spin case, but for the half integer spin, there exist a first order transition between two ordered phases at low temperature and the non existence of disorder in this domain. In reference [53] , we are agreeing with the fact that the phase diagrams obtained in the mixed BC model are reminiscent of that in pure model.
2.2. Semi-Infinite Blume-Capel Model
We consider a system consisting of two mixed spin-1 and spin-3/2 sublattices, limited by a surface where the single-ion anisotropies acting on the spin-1 and spin-3/2 are denoted, respectively, 

In the bulk, we keep the same notations of Section 2.1. On the surface, the reduced bilinear exchange interaction J, the reduced biquadratic interaction K and the interaction C mentioned in the Hamiltonian (2), are denoted by



Each spin at the surface can interact with a spin located in the bulk and increasingly with its first neighbors at the surface. With this new environment, some new critical properties will appear at the surface which will have recursion equations coupled to the bulk. This latter keeps the same equations as in the infinite model, forming an invariant subspace.
Concerning the surface, we can write the recursion equations in the following compact form [55] [56] :

with

model
We introduce the ratios


phase diagrams are constructed in the plane 



In the renormalization procedure, the critical behaviors are derived from fixed points, by evaluating the eingenvalues of the transformation as
In our case, the additive terms of the infinite and semi infinite (bulk terms) model can be considered useful for finding a point of the second order transition line for which the irrelevant field vanishes.
3. Results and Discussions
The calculation of the critical temperature of infinite Blume-Capel model with mixed spins SA = 1 and SB = 3 /2 (Section 2.1), in the three-dimensional case d = 3, shows three main types of diagram, labelled I, II and III. These types of diagrams can be classified as follows:
Type I: appears in the diagrams 

Type II: appears in the diagrams 

Type III: appears in the diagrams 


The phase diagrams in the 


The second and third types of phase diagrams (Figure 4 and Figure 5) are characterized by the presence of only second-order transitions and they have different shapes.
Using renormalization-group calculations in the semi-infinite case (Section 2.2), we have obtained five generic types of phase diagram, illustrated in the 


1) For 

Figure 3. (Diagram of type I): The transition temperature of the mixed spin-1 and spin-3/2 Ising system as a function of 


Figure 4. (Diagram of type II): The transition temperature of the mixed spin-1 and spin-3/2 Ising system as a function of 

Figure 5. (Diagram of type III): The transition temperature of the mixed spin-1 and spin-3/2 Ising system as a function of 

2) For 


3) For 

Figure 6. Typical phase diagrams in the plane 

This ordinary phase transition can be first-order, second-order or tricritical. Figure 6(c) represents a typical phase diagram.
4) For 


5) For 



Thereafter, we present the phase diagrams in the 





a) For 

b) For 

Figure 7. Typical phase diagrams in the plane 



c) For 




d) For 



Let us comment the types of phase diagrams obtained by Migdal-Kadanoff renormalization:
1) The presence of a semi infinite surface gives rise to a variety of new phase diagrams. Are highlighted, ordinary transitions (e.g. Figure 6(a)), extraordinary transitions (Figure 6(b)), surface transitions (Figure 7(b)) and special transitions (Figure 7(d)).
2) Each of these phase transitions is represented by a different fixed point, and that they belongs to a new universality class different from that of the bulk. For example, the surface performs two different types of second order phase transitions. The first has a temperature higher than that of the bulk; this surface transition is described by the fixed point (OB, CS), where OB is the fixed point (disorder) of the bulk [48] , and CS is that of the surface: CS (JS = 1.55, KS = 0, ΔA(S) = ¥. ΔB(S) = −¥, CS = −0.47). The second possible transition occurs at the same temperature as that of the bulk; it is the special transition, represented by another different fixed point (CB, CSp). CB is the second order fixed point of the bulk [48] , and CSp the surface one with coordinates CSp (JS = 1.29, KS = 0, ΔA(S) = ¥, ΔB(S) = −¥, CS = −0.074).
3) The topology of the phase diagrams obtained is compared with that already established in the references [57] [58] for pure semi infinite BC models with S = 1 and S = 3/2. As in the infinite case [53] , this similarity is the result of the competition effects of the two different anisotropies in the system. For example, Figures 6(c)-(e) remind types obtained in reference [58] by the same approximation for the spin model S = 1. Whereas Figures 7(a)-(d) are to be compared with the results [30] of the pure semi infinite BC model with S = 3/2. The remaining two diagrams, Figure 6(a) & Figure 6(b), are non existing types for the same model with spin S = 1 or S = 3/2 by the Migdal-Kadanoff renormalization approach.
4) In these types of phase diagrams obtained by using the Migdal-Kadanoff approximation, we note the absence of successive (surface/bulk) first order phase transitions and only the successive (surface/bulk) second-order phase transitions can occur. Also, simultaneous phase transitions of different orders are not observed. This was already met in the study of pure semi infinite models, see references [32] [57] [58] . But, the mean field theory finds such situations [30] [59] .
Lipowski had already mentioned the expected difference between the two approaches (MF and RG), in the study of semi infinite Potts model [60] . In fact the mean field treats the bulk as field acting on the surface and the surface order parameter can cause a non ordinary first order phase transition. In the Migdal-Kadanoff renormalization procedure, the fixed point surface obeys the bond-moving relation (15). When the bulk fixed point is at a finite temperature, the surface may converge to a finite fixed point and have a surface transition. While, if the bulk fixed point is at T = 0 K (JB infinite), the surface one is also at 0 K. In particular, the fixed point of the bulk first order phase transition is precisely at 0 K, which causes ordinary first order transitions at surface.
The experimental results confirm the existence of a continuous transition at surface, while the bulk exhibit simultaneously a first order transition, what is called in the literature “surface induced disordering” (SID). This type of transition was highlighted in the Cu3Au alloy, see reference [61] . It has been observed that when the bulk exhibits a first order transition, the order parameter of the surface vanishes continuously and in reference [62] , a theoretical study has been made using landau free energy. For a complete comparison, it is interesting to treat this model by the mean field approximation and to compare the types of phase diagrams with those obtained by renormalization.
4. Conclusions
During this work, we have studied the pure Blume-Capel model in the semi-infinite case. To achieve our goal, we have determined the global phase diagrams of the mixed spin-1 and spin-3/2 in the semi-infinite system with different single-ion anisotropies acting on the spin-1 and spin-3/2 (on the surface and in the bulk) by using the Migdal-Kadanoff renormalization group technique, which combines decimation (with a space scale ration b = 3) and bond shifting. In the phase diagrams, the critical temperature lines versus single-ion anisotropies are shown. We have classified the various phase diagrams at fixed 

A comparison with the types of phase diagrams in the pure semi-infinite model with S = 1 and S = 3/2 obtained by the renormalization and the mean field approaches was performed.
In perspective, we hope that this work could stimulate further theoretical and experimental works on ferrimagnetic systems such as mixed spins with random fields in finite, infinite and semi-infinite systems.
Cite this paper
Mohamed El Bouziani,Mohamed Madani,Abou Gaye,Abdelhameed Alrajhi,1 1, (2016) Phase Diagrams of the Semi-Infinite Blume-Capel Model with Mixed Spins (SA = 1 and SB = 3/2) by Migdal Kadanoff Renormalization Group. World Journal of Condensed Matter Physics,06,109-122. doi: 10.4236/wjcmp.2016.62015
References
- 1. Binder, K. (1983) Critical Behavior at Surfaces. In: Domb, C. and Lebowitz, J., Eds., Phase Transitions and Critical Phenomena, Vol. 8, Academic Press, New York, 1-444.
- 2. Diehl, H.W. (1986) Field-Theoretical Approach to Critical Behaviour at Surfaces. In: Domb, C. and Lebowitz, J.L., Eds., Phase Transition and Critical Phenomena, Vol. 10, Academic Press, London, 75-267.
- 3. Diehl, H.W. (1997) The Theory of Boundary Critical Phenomena. International Journal of Modern Physics B, 11, 3503.
http://dx.doi.org/10.1142/S0217979297001751 - 4. Binder, K. and Hohenberg, P.C. (1974) Surface Effects on Magnetic Phase Transitions. Physical Review B, 9, 2194.
- 5. Rau, C. and Robert, M. (1987) Surface Magnetization of Gd at the Bulk Curie Temperature. Physical Review Letters, 58, 2714.
- 6. Tang, H., Weller, D., Walker, T.G., Scott, J.C., Chappert, C., Hopster, H., Pang, A.W., Dessau, D.S. and Pappas, D.P. (1993) Magnetic Reconstruction of the Gd(0001) Surface. Physical Review Letters, 71, 444.
- 7. Gimbert, F., Calmels, L. and Andrieu, S. (2011) Localized Electron States and Spin Polarization in Co/Ni (111) Overlayers Physical Review, 84, Article ID: 094432.
- 8. Arnold, C.S. and Pappas, D.P. (2000) Gd(0001): A Semi-Infinite Three-Dimensional Heisenberg Ferromagnet with Ordinary Surface Transition. Physical Review Letters, 85, 5202.
- 9. Prinz, G.A. (1998) Magnetoelectronics. Science, 282, 1660.
http://dx.doi.org/10.1126/science.282.5394.1660 - 10. Monsuripur, M. (1987) Magnetization Reversal, Coercivity, and the Process of Thermomagnetic Recording in Thin Films of Amorphous Rare Earth-Transition Metal Alloys. Journal of Applied Physics, 61, 1580.
http://dx.doi.org/10.1063/1.338094 - 11. Hasenbusch, M. (2011) A Monte Carlo Study of Surface Critical Phenomena: The Special Point. Physical Review B, 84, Article ID: 134405.
- 12. Eisenriegler, E. and Diehl, H.W. (1988) Surface Critical Behavior of Tricritical Systems. Physical Review B, 37, 5257-5273.
- 13. Bray, A.J. and Moore, M.A. (1977) Critical Behaviour of Semi-Infinite Systems. Journal of Physics A: Mathematical and General, 10, No. 11.
http://dx.doi.org/10.1088/0305-4470/10/11/021 - 14. Lubensky, T.C. and Rubin, M.H. (1975) Critical Phenomena in Semi-Infinite Systems: I. ε Expansion for Positive Extrapolation Length. Physical Review B, 11, 4533.
- 15. Lubensky, T.C. and Rubin, M.H. (1975) Critical Phenomena in Semi-Infinite Systems: II. Mean-Field Theory. Physical Review B, 12, 3885.
- 16. Diehl, H.W. and Dietrich, S. (1981) Field-Theoretical Approach to Static Critical Phenomena in Semi-Infinite Systems. Zeitschrift für Physik B Condensed Matter, 42, 65-86.
http://dx.doi.org/10.1007/BF01298293 - 17. Diehl, H.W., Dietrich, S. and Eisenriegler, E. (1983) Universality, Irrelevant Surface Operators and Corrections to Scaling in Systems with Free Surfaces and Defect Planes. Physical Review B, 27, 2937.
- 18. Diehl, H.W. and Shpot, M. (1998) Massive Field-Theory Approach to Surface Critical Behavior in Three-Dimensional Systems. Nuclear Physics B, 528, 595-647.
http://dx.doi.org/10.1016/S0550-3213(98)00489-1 - 19. Diehl, H.W. and Nusser, A. (1990) Critical Behavior at Dirty Surfaces. Zeitschrift für Physik B Condensed Matter, 79, 79-90.
http://dx.doi.org/10.1007/BF01387828 - 20. Usatenko, Z.E., Shpot, M.A. and Hu, C.-K. (2001) Surface Critical Behavior of Random Systems: Ordinary Transition. Physical Review E, 63, Article ID: 056102.
- 21. Au-Yang, H. (1973) Thermodynamics of an Anisotropic Boundary of a Two-Dimensional Ising Model. Journal of Mathematical Physics, 14, 937.
http://dx.doi.org/10.1063/1.1666420 - 22. Fisher, M.E. and Caginalp, G. (1977) Wall and Boundary Free Energies. Communications in Mathematical Physics, 56, 11-56.
http://dx.doi.org/10.1007/BF01611116 - 23. Reedm P. (1978) Correlation near the Free Surface of an Ising Ferromagnet. Journal of Physics A: Mathematical and General, 11, 137.
http://dx.doi.org/10.1088/0305-4470/11/1/015 - 24. Au-Yang, H. and Fisherm M.E. (1980) Wall Effects in Critical Systems: Scaling in Ising Model Strips. Physical Review B, 21, 3956.
http://dx.doi.org/10.1103/PhysRevB.21.3956 - 25. Albano, E.V. and Binder, K. (2012) Wetting Transition in the Two-Dimensional Blume-Capel Model: A Monte Carlo Study. Physical Review E, 85, Article ID: 061601.
http://dx.doi.org/10.1103/PhysRevE.85.061601 - 26. Dietrich, S. (1988) Wetting Phenomena in Phase Transitions and Critical Phenomena. In: Domb, C. and Lebowitz, J.L., Eds., Phase Transitions and Critical Phenomena, Vol. 12, Academic, London, 1-218.
- 27. Benyoussef, A., Boccara, N. and Saber, M. (1986) Three-Dimensional Semi-Infinite Spin-1 Ising Model Interaction with Crystal Field. Journal of Physics C: Solid State Physics, 19, 1983.
http://dx.doi.org/10.1088/0022-3719/19/12/012 - 28. Blume, M. (1966) Theory of the First-Order Magnetic Phase Change in U O 2. Physical Review, 141, 517-524.
http://dx.doi.org/10.1103/PhysRev.141.517 - 29. Capel, H.W. (1966) On the Possibility of First-Order Phase Transitions in Ising Systems of Triplet Ions with Zero-Field Splitting. Physica, 32, 966-988.
http://dx.doi.org/10.1016/0031-8914(66)90027-9 - 30. Bakchich, A. and El Bouziani, M. (1999) The Semi-Infinite Spin-3/2 Blume-Capel Model. Journal of Physics: Condensed Matter, 11, 6147.
http://dx.doi.org/10.1088/0953-8984/11/32/306 - 31. Khan, O. (1993) Molecular Magnetism, VCH, New York.
- 32. Benayad, N. and Zittartz, J. (1990) Real-Space Renormalization Group Investigation of the Three-Dimensional Semi-Infinite Mixed Spin Ising Model. Zeitschrift für Physik B Condensed Matter, 81, 107-112.
http://dx.doi.org/10.1007/BF01454221 - 33. Schofield, S.L. and Bowers, R.G. (1980) Renormalisation Group Calculations on a Mixed-Spin System in Two Dimensions. Journal of Physics A: Mathematical and General, 13, 3697.
http://dx.doi.org/10.1088/0305-4470/13/12/019 - 34. Iwashia, T. and Uryu, N. (1983) The Effect of the Biquadratic Exchange Interaction on the Curie Temperature of the Mixed Ising Ferromagnet. Physics Letters A, 96, 311-313.
http://dx.doi.org/10.1016/0375-9601(83)90187-1 - 35. Kaneyoshi, T. (1986) Role of Single-Ion Anisotropy in Amorphous Ferrimagnetic Alloys. Physical Review B, 34, 7866-7872.
http://dx.doi.org/10.1103/PhysRevB.34.7866 - 36. Kaneyoshi, T. (1987) Curie Temperatures and Tricritical Points in Mixed Ising Ferromagnetic Systems. Journal of the Physical Society of Japan, 56, 2675-2680.
http://dx.doi.org/10.1143/JPSJ.56.2675 - 37. Zhang, G.M. and Yang, C.Z. (1993) Monte Carlo Study of the Two-Dimensional Quadratic Ising Ferromagnet with Spins S = 1/2 and S = 1 and with Crystal-Field Interactions. Physical Review B, 48, 9452-9455.
http://dx.doi.org/10.1103/PhysRevB.48.9452 - 38. Buendia, G.M. and Novotny, M.A. (1997) Numerical Study of a Mixed Ising Ferrimagnetic System. Journal of Physics: Condensed Matter, 9, 5951.
http://dx.doi.org/10.1088/0953-8984/9/27/021 - 39. Benayad, N., Klumper, A., Zittartz, J. and Benyoussef, A. (1989) Re-Entrant Ferromagnetism in a Two-Dimensional Mixed Spin Ising Model with Random Nearest-Neighbour Interactions. Zeitschrift für Physik B Condensed Matter, 77, 333-338.
http://dx.doi.org/10.1007/BF01313678 - 40. Bobák, A., Abubrig, O.F., Horváth, D. and Jascur, M. (2001) Mean-Field Solution of the Mixed Spin-1 and Spin- Full-Size Image (<1 K) Ising System with Different Single-Ion Anisotropies. Physica A: Statistical Mechanics and Its Applications, 296, 437-450.
http://dx.doi.org/10.1016/S0378-4371(01)00176-5 - 41. Albayrak, E. (2003) Mixed Spin-1 and Spin-3/2 Blume-Capel Ising Ferrimagnetic System on the Bethe Lattice. International Journal of Modern Physics B, 17, 1087.
http://dx.doi.org/10.1142/S0217979203015978 - 42. Ekiz, C. (2006) The Possibility of Two Compensation Points in a Ferrimagnetic Mixed Spin-1 and Spin-3/2 Ising System Using Bethe Lattice Approach. Journal of Magnetism and Magnetic Materials, 307, 139-147.
http://dx.doi.org/10.1016/j.jmmm.2006.03.059 - 43. Bobák, A. (1998) The Effect of Anisotropies on the Magnetic Properties of a Mixed Spin-1 and Spin-3/2 Ising Ferrimagnetic System. Physica A: Statistical Mechanics and Its Applications, 258, 140-156.
http://dx.doi.org/10.1016/S0378-4371(98)00233-7 - 44. Bobák, A. (2000) Multicritical Points in the Mixed Spin-1 and Spin-3/2 Ising System on a Square Lattice with Different Single-Ion Anisotropies. Physica A: Statistical Mechanics and Its Applications, 286, 531-540.
http://dx.doi.org/10.1016/S0378-4371(00)00404-0 - 45. Nakamura, Y. and Tucker, J.W. (2002) Monte Carlo Study of a Mixed Spin-1 and Spin-3/2 Ising Ferromagnet. IEEE Transactions on Magnetics, 38, 2406-2408.
http://dx.doi.org/10.1109/TMAG.2002.803598 - 46. Mert, G. (2012) Green’s Function Study of a Mixed Spin-1 and Spin-3/2 Heisenberg Ferrimagnetic System. Journal of Magnetism and Magnetic Materials, 324, 2706-2710.
http://dx.doi.org/10.1016/j.jmmm.2012.03.033 - 47. Yessoufou, R.A., Amoussa, S.H. and Hontinfinde, F. (2009) Magnetic Properties of the Mixed Spin-5/2 and Spin-3/2 Blume-Capel Ising System on the Two-Fold Cayley Tree. Central European Journal of Physics, 7, 555-567.
- 48. Madani, M., Gaye, A., El Bouziani, M. and Alrajhi, M. (2015) Migdal-Kadanoff Solution of the Mixed Spin-1 and Spin-3/2 Blume-Capel Model with Different Single-Ion Anisotropies. Physica A: Statistical Mechanics and Its Applications, 437, 396-404.
http://dx.doi.org/10.1016/j.physa.2015.06.003 - 49. Migdal, A.A. (1975) Recursion Equations in Gauge Field Theories. Zh. Eksp. Teor. Fiz, 69, 810-822 [Soviet Physics—JETP, 42, (1975) 413-418].
- 50. Kadanoff, L.P. (2010) Notes on Migdal’s Recursion Formulas. Annals of Physics, 100, 359-394.
http://dx.doi.org/10.1016/0003-4916(76)90066-X - 51. Hasenbusch, M. (2010) Finite Size Scaling Study of Lattice Models in the Three-Dimensional Ising Universality Class. Physical Review B, 82, Article ID: 174433.
http://dx.doi.org/10.1103/PhysRevB.82.174433 - 52. Abubrig, O.F., Horv1ath, D., Bobák, A. and Jascur, M. (2001) Mean-Field Solution of the Mixed Spin-1 and spin-3/2 Ising System with Different Single-Ion Anisotropies. Physica A: Statistical Mechanics and Its Applications, 296, 437-450.
http://dx.doi.org/10.1016/S0378-4371(01)00176-5 - 53. Tucker, J.W. (2001) Mixed Spin 1-Spin 3/2 Blume-Capel Ising Ferromagnet. Journal of Magnetism and Magnetic Materials, 237, 215-224.
http://dx.doi.org/10.1016/S0304-8853(01)00691-6 - 54. Niemeijer, Th. and van Leeuwen, J.M.J. (1976) Renormalization Theory for Ising-Like Spin Systems. In: Dom, C. and Green, M.S., Eds., Phase Transitions and Critical Phenomena, Vol. 6, Academic Press, New York, 425-505.
- 55. Lipowsky, R. and Wagner, H. (1981) The Migdal-Kadanoff Renormalization Group Scheme for the Ising Model with a Free Surface. Zeitschrift für Physik B Condensed Matter, 42, 355-365.
http://dx.doi.org/10.1007/BF01293202 - 56. Nagai, O. and Toyonaga, M. (1981) Critical Behaviour of Ising Magnets: Infinitesimal Migdal-Kadanoff Approximation. Journal of Physics C: Solid State Physics, 14, L545.
- 57. Bakchich, A. and El Bouziani, M. (1997) Phase Diagrams of the Three-Dimensional Semi-Infinite Blume-Emery- Griffiths Model. Physical Review B, 56, 11155-11160.
http://dx.doi.org/10.1103/PhysRevB.56.11155 - 58. Benyoussef, A., Boccara, N. and El Bouziani, M. (1986) Real-Space Renormalization-Group Investigation of the Three-Dimensional Semi-Infinite Blume-Emery-Griffiths Model. Physical Review B, 34, 7775-7783.
http://dx.doi.org/10.1103/PhysRevB.34.7775 - 59. Bakchich, A. and El Bouziani, M. (1997) Surface Critical Behavior of the Semi-Infinite Blume-Emery-Griffiths Model. Physical Review B, 56, 11161-11168.
http://dx.doi.org/10.1103/PhysRevB.56.11161 - 60. Lipowsky, R. (1982) The Semi-Infinite Potts Model: A New Low Temperature Phase. Zeitschrift für Physik B Condensed Matter, 45, 229-235.
- 61. Sundaram, V.S., Farrell, B., Alben, R.S. and Robertson, W.D. (1973) Order-Disorder Transformation at the {100} Surface of Cu 3 Au. Physical Review Letters, 31, 1136-1139.
http://dx.doi.org/10.1103/PhysRevLett.31.1136 - 62. Lipowsky, R. (1983) Surface Induced Disordering at First-Order Bulk Transitions. Zeitschrift für Physik B Condensed Matter, 51, 165-172.
http://dx.doi.org/10.1007/BF01308770
NOTES
*Corresponding author.















