ABSTRACT

We compute the shear viscosity of superfluid Bose and Fermi gases on the base of Boltzmann equation and rela- xation times. We show that, in the low temperature limit, the shear viscosities of Bose and Fermi gases are pro- portional to and T-4, respectively. For the superfluid Bose gas at low temperature limit, only splitting processes contribute to the shear viscosity.

1. Introduction

A Bose-Einestein Condensation (BEC) whose particles interact via dipole-dipole forces constitutes an example of a superfluid with anisotropic inter-particle interactions. The action has been predicted to lead to BECs with unusual stability properties [1]. Advances in the cooling of polar molecules [2] and molecular BECs [3] suggest that molecules can have very large dipole moments. In this respect, transport properties of dipolar gas, such as the shear viscosity, are of particular interest. Eckern, on the basis of the self-consistent mean-field approximation and the kinetic theory for a dilute Bose gas, obtained the collision operator in the Boltzmann equation by golden rule arguments [4]. The shear viscosity of a superfluid Fermi gas in the unitary limit was computed by Rupak and Schafer [5]. They showed that in the low temperature limit the shear viscosity scale was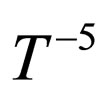. Previous works on transport properties have studied the bulk viscosity [6, 7], specific heat [8], thermal conductivity [9,10] of neutron stars, the shear viscosity of dilute Fermi gas at unitarity [11], transport properties of strongly interacting dilute Fermi gases [12], and transport theory for a weakly interacting condensed Bose gas [13]. Then, we investigate the shear viscosity of a superfluid gas with dipoledipole interaction.

In this article, we explore the shear viscosity of a superfluid dipolar gas. Recent experimental development in trapping and cooling of polar molecules [14,15] has shown that the dominant interactions are dipole-dipole interactions. We calculate the shear viscosity by using the Boltzmann equation. It should be noted that the Boltzmann equation is not appropriate for long-range potential like coulomb potential, 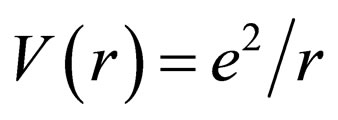, whereas it is suitable for weak, short-ranged potentials like contact and probably dipole-dipole potentials [16].

The rest of the article is laid out as follows: Section 2 will discuss the basic equations relating the shear viscosity to the phonon collision operator. The transition probability is derived in Section 3, and then g(p) is obtained for the calculation of the viscosity. The discussion of the result is presented in Section 4.

2. Shear Viscosity

Shear viscosity can be defined simply as below,

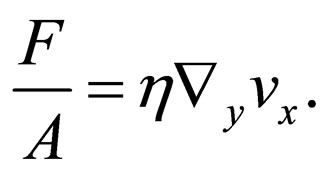(1)

Viscosity is related to stress tensor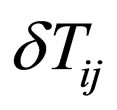, which is the deviation from equilibrium of the stress-energy tensor 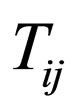for a fluid with pressure 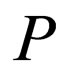and energy density

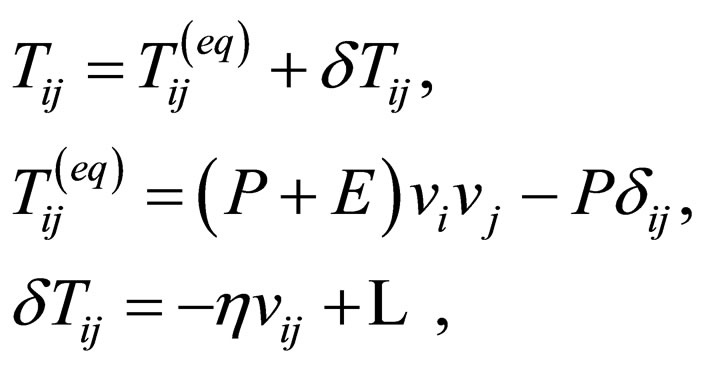(2)

where

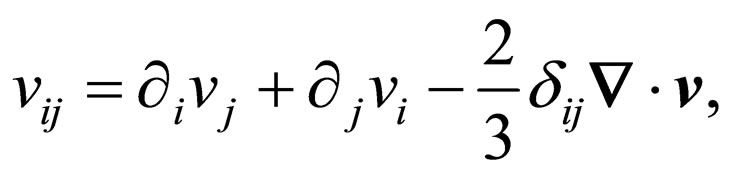(3)

the ellipsis part of 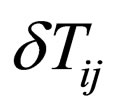is related to bulk viscosity and thermal conductivity. 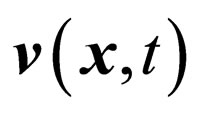is the fluid velocity at a given position and time. At low temperature, a linear dispersion relation for dipolar Bose gas is the phonons:

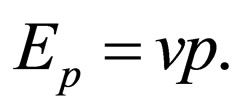(4)

The stress-energy tensor and the viscosity can be calculated by using kinetic theory [17]. For a system of identical dipolar particles with dispersion relation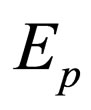, one may write 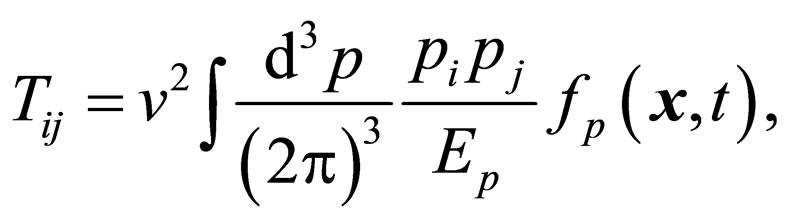[5]

(5)

where is the distribution function of the phonons with speed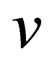, momenta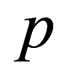, and energy We work in units where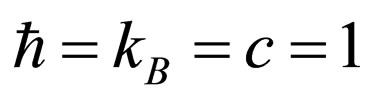. The full distribution function is given by

(6)

where 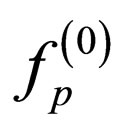is the Bose-Einstein distribution and 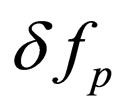is a small departure from equilibrium. We write the deviation from equilibrium as

(7)

where

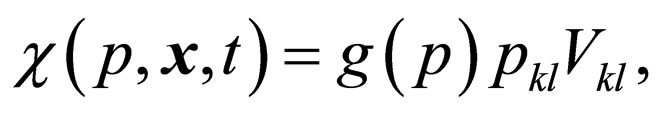
and

(8)

By substituting Equation (7) in to Equation (5) and Equation (2), we find

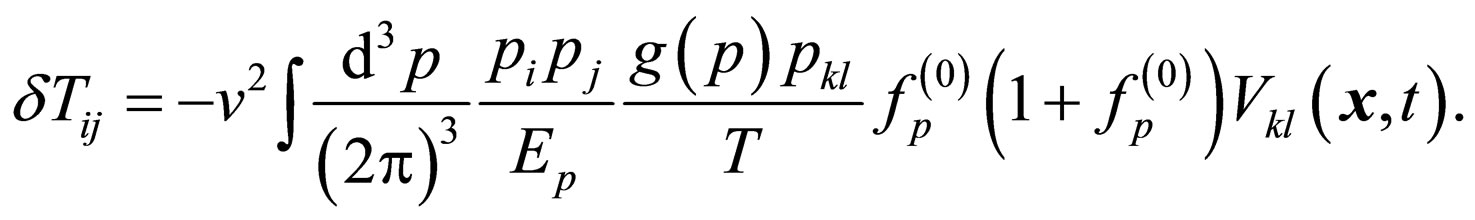(9)

On the basis of symmetry consideration and by using the definition of [see Equation (3)], we can write 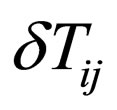[Equation (2)] in the following form

(10)

Then, by contracting the tensor on the left-hand side with respect to the pairs of indices (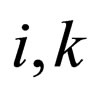and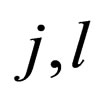) we can determine the shear viscosity in terms of the function g(p),

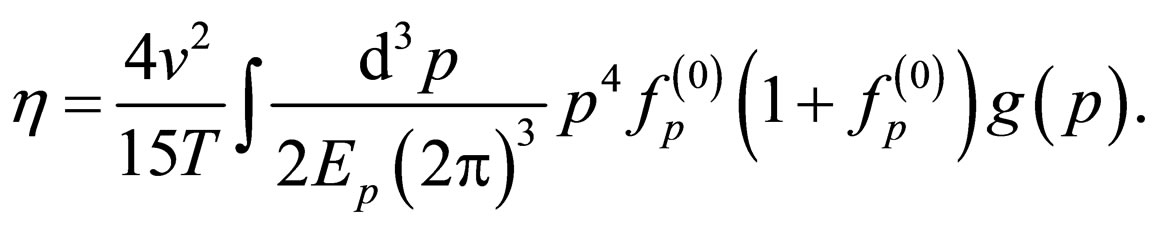(11)

3. Solutions of g(p)

The process now is to evaluate 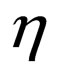from Equation (11), we need to find a form for g(p) in two cases: dipolar Bose and Fermi dilute gas at low temperature limit. For the former case, we follow the approach of Eckern [4] in obtaining the collision operators and scattering rates for a dipolar Bose dilute gas at low temperature limit. In the case of the phonon interaction for the unitarity gas in the superfluid Fermi phase, the phonon cross section has been obtained from Galilean and gauge invariance of the lagrangian by Rupak and Schafer [5].

To calculate the first case, we can use the Boltzmann equation given in the absence of external forces by

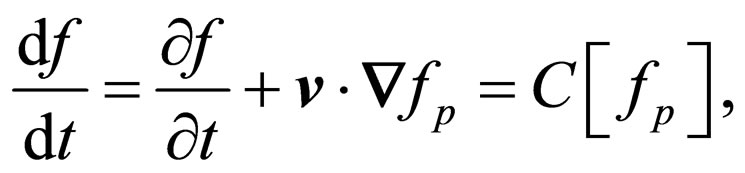(12)

the left-hand side can be written as [17]

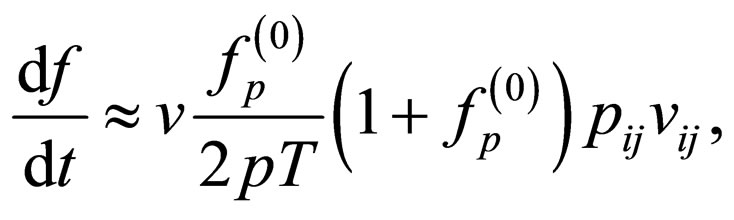(13)

where only the contribution relevant for shear viscosity was retained in the linear response approximation, leading order in the small deviation from equilibrium. Thermal gradients and bulk flows would give an additional term on the right-hand side of Equation (13).

The collision operator 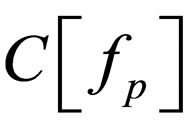should contain any possible collision terms that are typically considered: 1) binary collisions (2↔2) in which the number of particles is conserved, and 2) splitting processes (1↔2) in which the number of particles is not conserved.

Eckern [4], by introducing the Bogoliubov approximation, has shown that the scattering amplitude for splitting processes if all momenta are small, , are proportional to where  is the characteristic momentum for the crossover between the linear and the quadratic part of the spectrum. On the other hand the scattering amplitude for four-excitation processes as four-phonon processes are proportional to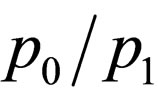, which is contrary to the opinion of many authors that four-phonon processes can be neglected compared to three-phonon regime [4,16,17].

We show in the following that even with this scattering amplitude, the binary collisions do not contribute to the collision operator and the dominated ones are the splitting processes at low temperature limit.

The collision integral is written as [4]

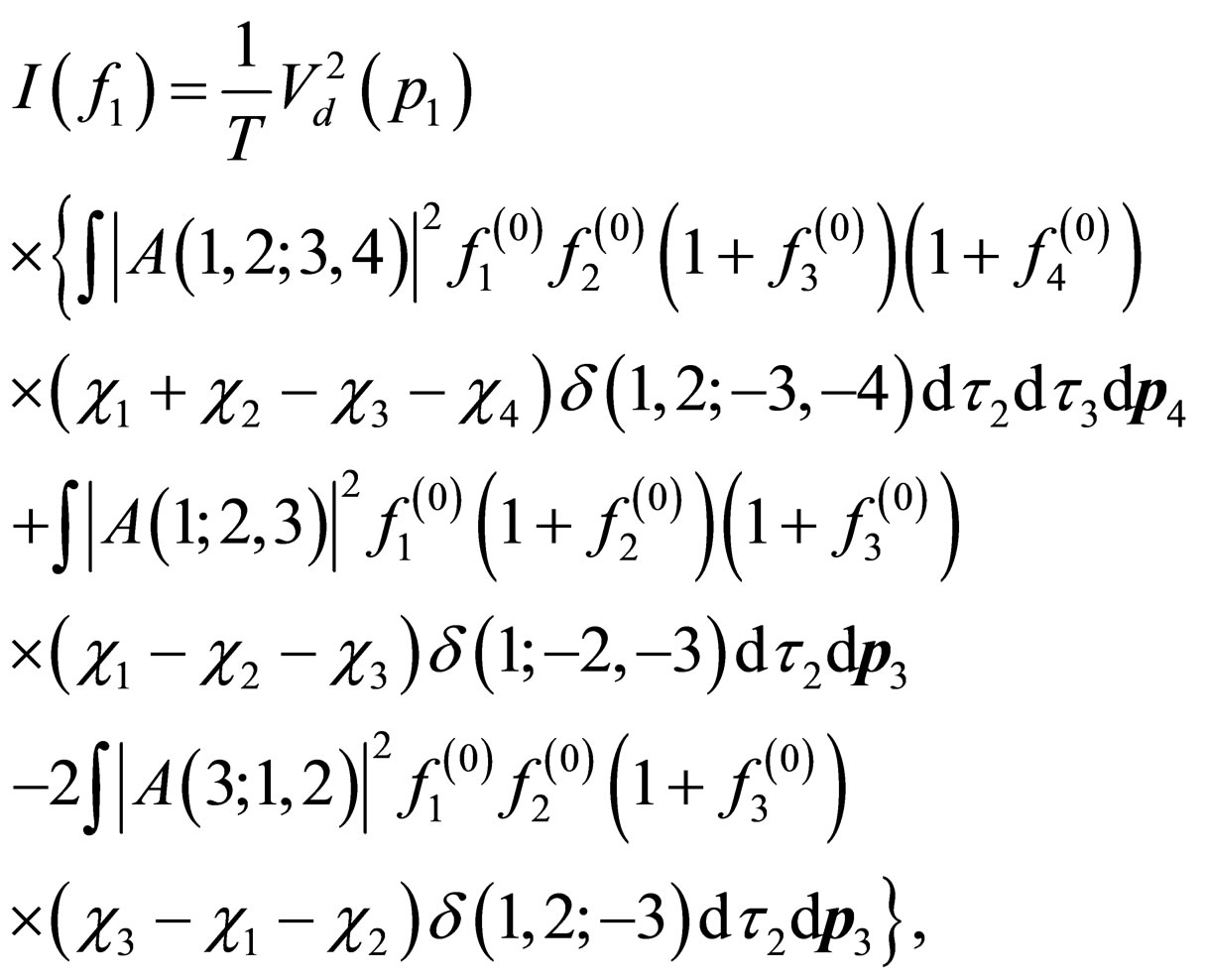(14)

where the scattering amplitudes are [4]

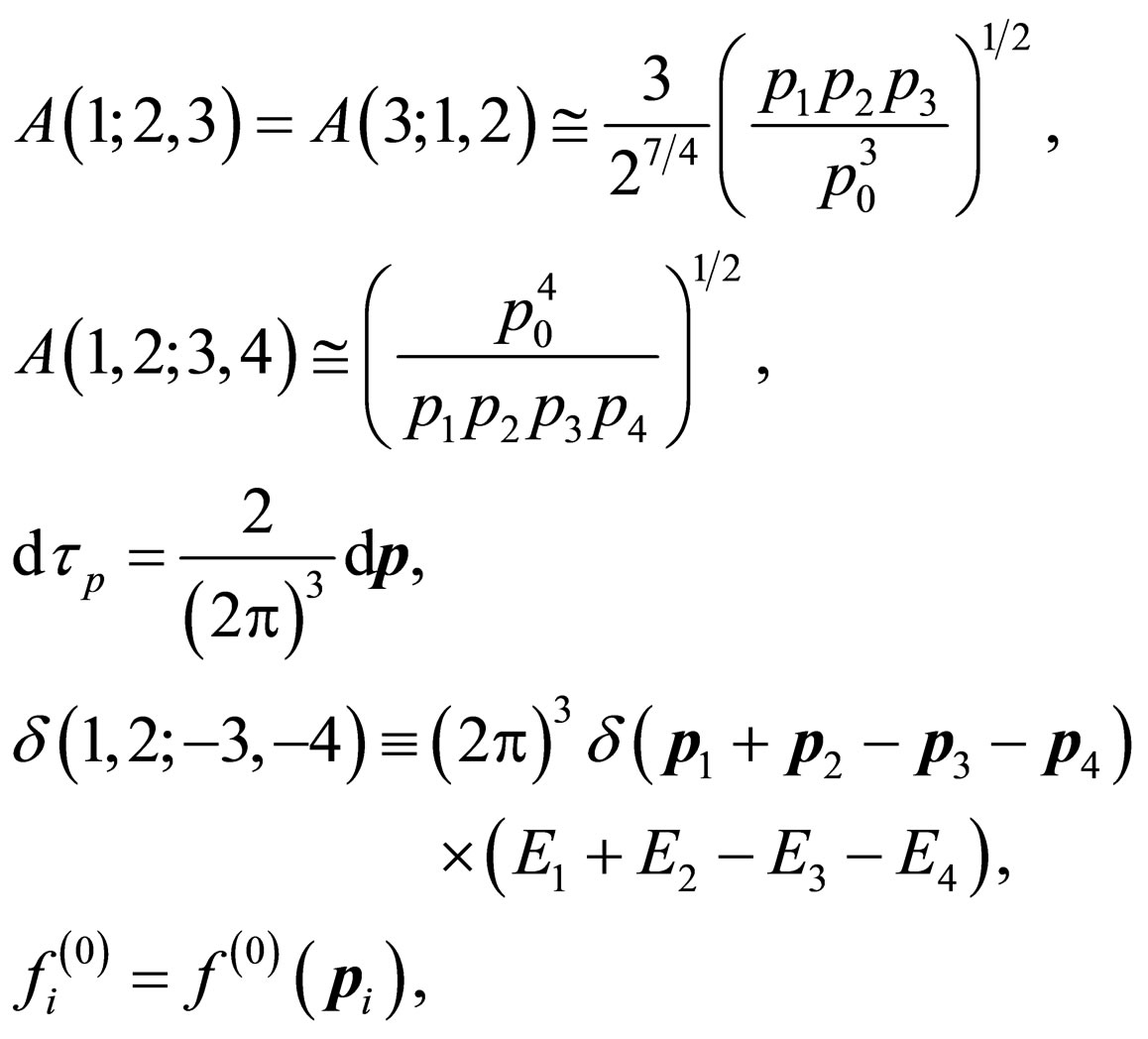(15)

and the Fourier transform of the dipole-dipole interaction:

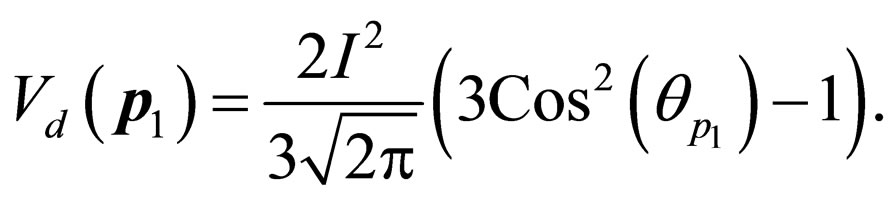
Manuel et al. [18] have found that small-angle processes have a shorter mean free path than large-angle ones. Shear viscosity describes the relaxation of the momentum components perpendicular to the direction of transport, and it is usually dominated by large-angle collisions, but this suggests that large-angle collisions can always be achieved by the addition of many small-angle ones. To solve the integrals of the collision integral in Equation (14), we use the small-angle processes. In this case, by doing the integrals we find that the binary collisions 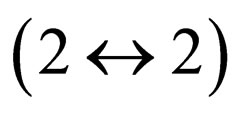do not contributed to the collision integrals.

By using the definition of collision integral in Equation (13) and Equation (14) and using the ansatz in Equation (7) for 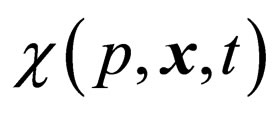and the linear dispersion relation, we get

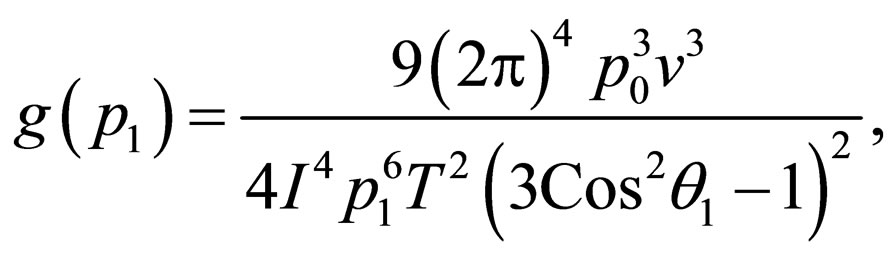(16)

by inserting Equation (16) in Equation (11), we get finally

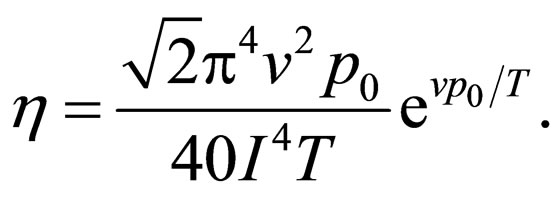(17)

The explicit expression for the shear viscosity of a superfluid dipolar Bose gases is given by Equation (17). The temperature dependence of the shear viscosity coefficient in normal dipolar Bose gas is proportional to 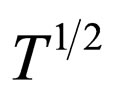[19]. When we compare the result in superfluid state with normal state, it is suggested that the viscosity should has a minimum near critical temperature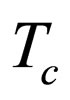, which is consistent with experimental results that near the critical temperature 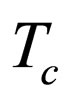the viscosity have a minimum [20].

In the case of the phonon interaction for the unitarity gas in the superfluid Fermi gas, the phonon cross section has been calculated by Rupak and Schafer [5]. For brevity here we only use the results of the imaginary part of the phonon self-energy. Contrary to the case of dipolar Bose gas that only splitting processes are dominating at low temperatures in the collision integrals, here the binary processes are dominating [5]. The damping rate is defined in terms of the on shell imaginary part of the self-energy as [21]

(18)

(19)

with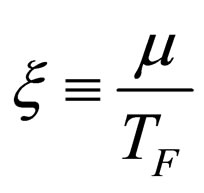. Equations (18), (19) and (11) finally gives

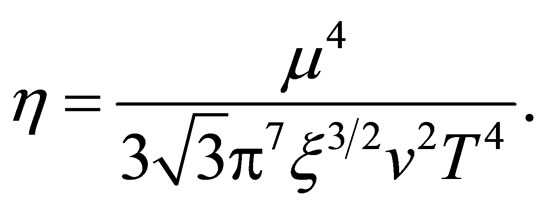(20)

4. Conclusion

We have calculated the shear viscosity arising from dipolar interaction in a dipolar Bose and Fermi gas system. At low temperatures, the linear dispersion relation for dipolar gas is phonon, and the viscosity is dominated by phonons in superfluid dipolar gas. For dipolar Bose gas, the basis of the calculation is the linearized Boltzmann equation. By using small-angle processes, we obtain that at low temperatures, only splitting processes are dominating in the collision integrals. However, this result is contrary to the case of dilute Fermi gases. Rupak and Schafer [5], by using the argument, have found that the splitting processes are collinear and cannot contribute to the shear viscosity.

We obtain for dipolar Bose gas and the temperature dependence of the shear viscosity as 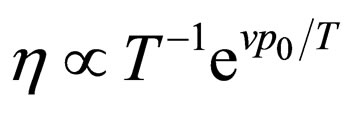(see Equation (17)).

Experimental results [20] show that has a minimum near and slowly grows with temperature for. We see that there are no experimental data at low temperatures 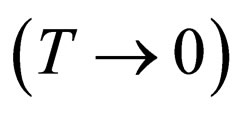which are related to the fact that the phonon mean free path becomes so large that it is comparable to the size of the experimental sample, but due to the minimum near the transition temperature, this ratio should increase. This is also consistent with our calculation.

At the leading order in the polynomial expansion and variational calculation, the temperature dependence of shear viscosity in superfluid Fermi gas in the unitarity limit is observed as T⁻⁵ by Rupak and Schafer [5]. We obtain this dependence as T⁻⁴ on the basis of damping relaxation time.

REFERENCES