World Journal of Condensed Matter Physics
Vol.1 No.4(2011), Article ID:8775,6 pages DOI:10.4236/wjcmp.2011.14024
Radiative Recombination Mechanisms of Large InAs/GaAs Quantum Dots
![]()
1Research Group of Micoreletronic and Optoelectronic Devices, São Judas Tadeu University, São Paulo, Brazil; 2Group of Semiconductor Materials and Nanotechnology, Technological Institute of Aeronautics, São José dos Campos, São Paulo, Brazil; 3New Semiconductor Materials Laboratory, Phycics Institute, University São Paulo, São Paulo, Brazil.
Email: *prof.martini@gmail.com
Received July 27th, 2011; revised September 26th, 2011; accepted October 8th, 2011.
Keywords: Quantum dots, Photoluminescence, Carrier Dynamics
ABSTRACT
The optical properties of large InAs/GaAs quantum dots were investigated by low-temperature photoluminescence as a function of the excitation-power density. The presence of excited states was clearly detected below the saturation regime of the ground state. We analyzed the dependence of the integrated-photoluminescence intensity on the excitation-power density and the type of radiative recombination involving the electronic ground state and the excited states inside the quantum dots. We concluded that the probability to have more than one exciton by dots must be considered, and the usual equation , must be revised to correctly describe the origin of the recombination and must include other factors as scattering, relaxation time, radiative recombination rate, and others.
, must be revised to correctly describe the origin of the recombination and must include other factors as scattering, relaxation time, radiative recombination rate, and others.
1. Introduction
During the past few years, remarkable progress has been made in the development of nano-optoelectronic devices based on quantum dots (QDs). Important examples are the application of QDs as active media in light emitters, as light-emitting diodes (LEDs) and lasers for telecommunication purposes, and optical amplifiers [1-4]. Although, more recently, the research in the field of QD materials is also committed to the exploration of the peculiar electronic properties of these systems as, e.g., the use of quantum dots in high-performance photodetectors or DNA nanosensors for medical diagnosis and biomolecular investigations [5,6], as well as, in the field of quantum cryptography and quantum computing using single-QD devices [7-10].
However, an important issue still remains: the achievement of a reliable and cheap semiconductor laser operating in the telecommunication windows at 1.3 or 1.55 µm corresponding, respectively, to the minimum dispersion and attenuation of the optical signal in silicate optical fibers [11,12]. Systems based on large-size InAs/GaAs QDs, obtained by low growth rates, have been shown to be optically active in the vicinity of 1.3 and 1.5 µm [11,13]. Although this technique usually leads to lower QD densities (1010 cm–2), its advantage is that the confinement energy in the nanostructures is larger than in usual QDs (obtained with higher growth rates) and yields a better temperature stability of the devices.
In order to obtain optical devices with high performance, it is crucial to understand the optical processes involved in these complex nanostructures. In this sense, the optical properties of InAs/GaAs QDs have been widely investigated by photoluminescence (PL) [14-19], photoluminescence excitation spectroscopy (PLE) [15, 17], and time-resolved photoluminescence (TRPL) [15, 17,20]. However, in spite of the large number of experimental works dealing with the investigation of the fundamental properties of InAs/GaAs QDs, little attention has been paid to the excited states in order to study the dependence of the integrated photoluminescence (IPL) on the excitation-power density (Pexc), which is of great importance to understand the carrier dynamics inside the QDs. The difficult to study the excited states, is due to the fact that, under usual growth conditions, the QDs ensemble has a non homogeneous size-distribution of 10% - 20% which yields broad PL spectra (60 - 90 meV) that mask any presence of the excited states at high excita-tion-power density. By using low growth rates, sharp PL spectra with well resolved emissions corresponding to the excited states can be obtained. With these conditions, the study of the dependence of IPL on Pexc is possible and can shed light on the type of recombination processes that actually take place inside the QDs.
In this paper, we report a set of PL measurements performed on large-size QDs obtained by the low growthrate method that were optically active at 1.3 µm and provided PL spectra with sharp features. We present a study of the excited states behavior based on the measurement of the integrated PL intensity IPL as a function of the excitation power density Pexc. Excited states were clearly observed below the saturation regime of the ground state (GS). The article is organized as follows. In section 2 the experimental details are described. In section 3 we present the PL measurements and discuss the results. Section 4 is devoted to the conclusions.
2. Experimental Details
The two samples analyzed here were grown in a Gen II MBE system on a semi-insulating GaAs (001) substrate. The first of them consists of 300 nm of GaAs buffer layer deposited at 580˚C followed by 2.4 monolayers (MLs) of InAs material (to form the QDs), and a 30 nm-thick GaAs cap layer. The InAs growth rate was kept very low (0.005 ML/s) in order to lead to atypically large QDs, optimized for 1.3 µm emission [12]. The QDs and cap layer were deposited at 490˚C in order to limit In reevaporation from the QDs that is no longer negligible at such a low growth rate. A second sample was grown under the same conditions but without GaAs cap layer to provide the structural characterization of the QDs by ex situ atomic-force microscopy (AFM) using a Nanoscope IIIa system operating in tapping mode. The optical emission of the capped sample was investigated by photoluminescence using conventional lock-in techniques, the 514.5-nm line of an Ar laser and a Ge detector cooled with liquid nitrogen.
3. Results and Discussions
Figure 1 shows a 1 × 1 µm2 AFM image of the uncapped sample where the QDs formation is clearly verified. The QDs are homogeneously sized, with an average height and density of respectively 10.7 nm and ~1010 cm–2.
Figure 2 shows the PL spectra of the capped sample measured at room temperature with an excitation-power density of 0.9 kW/cm2. As expected, the large QDs observed in Figure 1 provided a major PL emission at 1.3 µm, labeled 0 (peak at 0.953 eV in Figure 2). Two other minor emissions can also be clearly distinguished around 1.023 eV (labeled 1) and 1.093 eV (2). It is a well known fact that the presence of several peaks in a PL spectrum can be related to different physical processes as state filling, phonon bottleneck, or even the presence of several families of QDs, with different shape, size or composition, emitting at different wavelengths [21]. The statefilling process typically appears at high excitation and leads to the saturation of the QDs ground state (due to the large number of photogenerated carriers), thus increasing the probability of radiative recombination from the excited states. In contrast, the phonon bottleneck allows interband transitions from the excited-states even at low excitation-power density, which distinguishes it from the state filling effect. On the other hand, in the presence of several families of QDs, the relative intensity of the peaks should reveal the abundance of QDs in each respective ensemble.
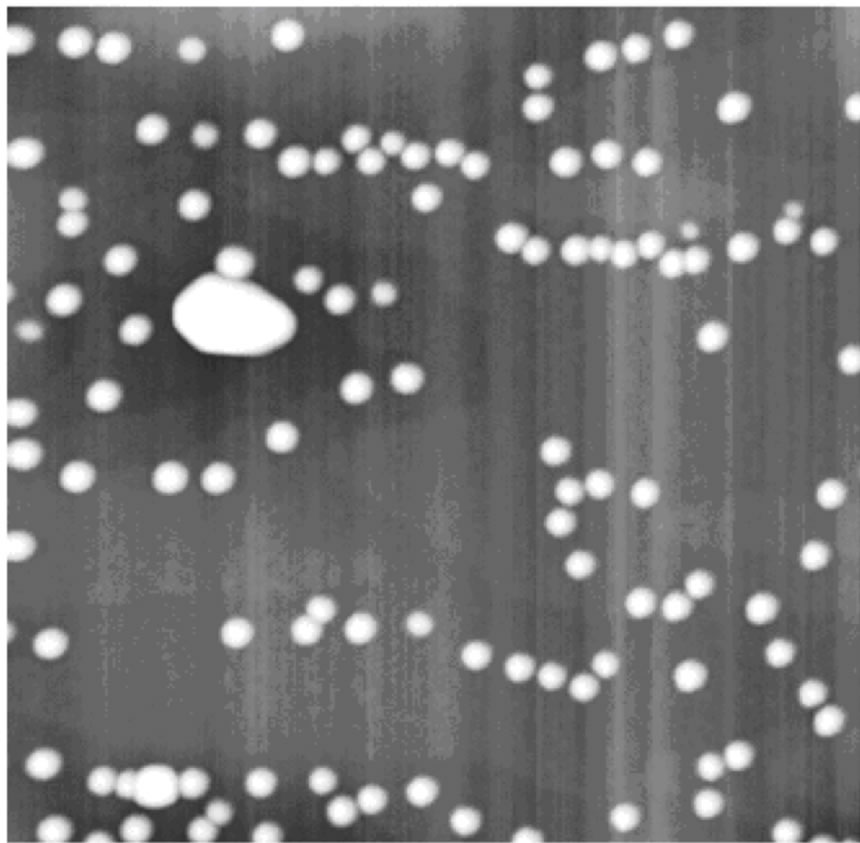
Figure 1. 1 × 1 µm2 AFM image of the uncapped sample showing an homogeneous ensemble of large-size QDs obtained by the low growth rate method. The average diameter and height of the nanostructures are respectively 49 nm and 10.7 nm.
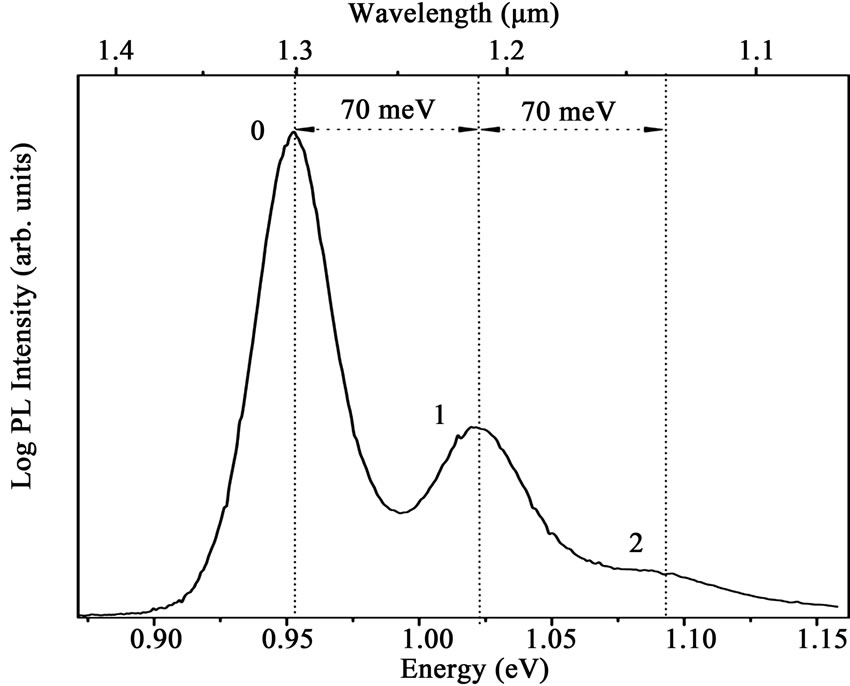
Figure 2. PL spectra of the capped sample measured at 300 K with an excitation-power density of 0.9 kW/cm2. Three different regions of emission can be observed. Regions 0, 1, and 2 are peaked around 0.953 eV, 1.023 eV and 1.093 eV, respectively.
In order to be able to distinguish which of these 3 effects is responsible (or at least dominant) for the typical PL spectum of our capped sample presented in Figure 2, we carried out PL measurements at low temperature (1.4 K) as a function of the excitation-power density. The results are presented in Figure 3. It can be seen that, at low excitation-power density (0.01% of 1.4 kW/cm2), only one narrow emission is visible at 1.043 eV, with a full width at half maximum (FWHM) of 26 meV. Its peak position and FWHM remain approximately constant at higher excitation power. However, as the excitationpower density increases by a factor 10, 100 or even 1000, other emissions become visible in the PL spectrum. These new emissions are labeled 1, 2, and 3 and are separated from each other by ~70 meV, a behavior that is typical of an harmonic-oscillator-like potential.
It is very clear, when looking at Figures 1 and 3, that the emissions 0, 1, 2, and 3 can only come from the same ensemble of QDs, as confirmed by the AFM measurements, and are thus due to state-filling. These peaks are related, respectively, to the optical transition from the GS (0), first (1), second (2) and third (3) excited states of the QDs.
Now we focus our attention on the influence of the excitation-power density on the emissions. In Figure 4 we show the integrated PL intensity of the GS, first, second, and third excited states as a function of the excitationpower density at 1.4 K and 100 K. All states were well fitted by a Voigt-profile. We can observe that, in a double logarithmic scale, the integrated PL intensity increases linearly with raising excitation-power density and is usually described by the relation [14,15,22],
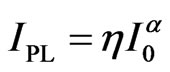 (1)
(1)

Figure 3. PL spectra of the capped sample at 1.4 K as a function of the excitation-power density. At low density (bottom, 0.01% of 1.4 kW/cm2, only one peak (26 meV wide) is observed around 1.043 eV. As the excitation power increases, more states are populated, and at 1.4 kW/cm2 (100%) four states are clearly populated.

Figure 4. Integrated PL intensity of each optical emission coming from the QDs as a function of the excitation-power density at (a) 1.4 and (b) 100 K. The solid lines represent the best fit to the experimental data using Equation (1) and α and h as fitting parameters.
where IPL is the integrated PL intensity and I0 is the excitation-power density [22]. The exponent α depends on the radiative recombination mechanisms and is expected to be close to unity for excitonic recombination and around two in the case a bimolecular recombination of uncorrelated electron-hole pairs. The coefficient h is related to the PL efficiency of the QDs and includes several effects as absorption, capture, ionization and recombination of excitons, as well as sample geometry. From Figure 4, it is interesting to observe that:
1) At low excitation power density only the ground state is observed, in agreement with the state filling process and in contrast to the standard phonon bottleneck, as mentioned before.
2) The first excited state becomes visible at an excitation-power density of 14 W/cm2 (although, as we can observed in Figure 3, it seems to appear at even lower power density ~1.4 W/cm2, however we could not perform the fitting of the peak accurately). The emergence of the first excited state occurs while the integrated-PL intensity of the GS still grows linearly. The second excited state appears at a power density of 137 W/cm2, when neither of the GS and first excited states are saturated.
3) The saturation of the GS and first excited states occurs practically at the same power density (above 350 W/cm2). From the observation that the GS saturation is not achieved before the emission of the excited states, we can infer that the intersublevel relaxation time is considerable in comparison with the interband radiative time. If we did not take measurements at very low excitation power density (0.14 W/cm2), this late GS saturation together with the emergence of the first excited state at low excitation-power density of 1 - 14 W/cm2 could lead to a misinterpretation of a phonon bottleneck effect, which is not the case as explained in item 1).
4) At low temperature (1.4 K), α is less than unity only for the GS (0.82), and is larger than unity for all the excited states (1.37, 2.13 and 2.71 for the first to third excited state, respectively). The same behavior occurs at 100 K (0.80, 1.30, 2.03, and 2.36, respectively). Thus, the PL peak labeled clearly reflects the recombination of excitons from the ground state of the QDs and confirms the strong confinement of the carriers even at 100K. On the other hand, since α is larger than 1 for all the excited states at any temperature. This could suggest that the optical recombinations from those states even at low temperatures, would not be of excitonic nature.
Although the superlinear behavior of the excited states emission in InAs/GaAs QDs has been observed and discussed before [23], the carrier dynamics in QDs are not fully understood yet. R. Heitz et al. [18] observed a sublinear dependence (α < 1) of the integrated PL of both the ground and excited states as a function of the excitation-power density at 10 K for values larger than 100 W/cm2, and suggested that an increase of non-radiative loss in the barrier could be at the origin of their experimental results. On the other hand, Le Ru et al. [14] obtained a superlinear dependence of the QDs’ integrated PL intensity on the excitation-power density even at low optical density but only at high temperatures. Their explanation was that the electrons and holes could be captured and could escape independently from the QDs. The conclusion that the carrier dynamics in QDs is governed by uncorrelated electron-hole pairs was also supported by P. Dawson et al. [24] who based their analysis on the fact that the existing models that describe carrier dynamics in QDs based on correlated electron-hole pairs were inadequate to describe their experimental data. More recently, Sanguinetti et al. [15], in contrast to Le Ru et al. [14] and Dawson et al. [24], concluded that electron and hole populations were strongly correlated, based on resonant and non-resonant-PL measurements. It is worth pointing out that Le Ru et al. [14] and Sanguinetti et al. [15] reported superlinearity at temperatures above 100 K. Moreover, they performed their measurements at low excitationpower density in order to have less than one electron per QD. In that experimental case, state-filling is not observed and only the GS could be investigated. As we can observe there is still no consensus about the behavior of the integrated PL intensity with the excitation-power density. Moreover, in order to have an overall comprehension of the carrier dynamics in QDs, also due to excited states, a wider range of excitation-power density allowing state filling is highly desirable.
As mentioned before, the linearity (α » 1) is usually related to excitonic recombination and the quadratic behavior to uncorrelated electron-hole pairs. In this sense, to our judgement the Equation (1) fails to predict the correct behavior for QDs, for which only the GS appeared as an excitonic recombination. However, at low temperature there is no loss by thermal scape, and the pairs electron-hole are necessarily strongly correlated, they are excitons, even for the excited states. Thus, though the data was well fitted by the equation, the α is not a single value, but must be related to the relaxation time, radiative recombination rate, and other factors. This means that the equation that correctly describe the behavior of the IPL with Pexc is more complex than Equation (1), and one must pay attention to the fact that even a quadratic behavior can be related to excitonic recombination. Our conclusion that we have excitonic recombination even for the excited states is corroborated by the work of Zhang et al. [25],in which they show some QDs are randomly occupied by multiple excitons. In their work, they show that in these dots, one electron-hole pair will rapidly relax into a ground state exciton, and Pauli blocking in the ground state will force (for appropriate spin) the second exciton into the excited state, increasing the excited-state transition probability. This behavior explains why in our case the first excited state emission is observed even before the state filling of the ground state. At the same time, it is well known that the recombination can be different for each state and, as occurs in a state filling process, it is lower for higher excited states. Moreover, under high excitation power density conditions, in the exciton-exciton scattering process, the excitation power dependence of the excitated states is expected to be close to quadratic because a collision of two excitons is essential [26]. Therefore, it is reasonable that α increases, as we go from 0 to 1, 2, 3 even for excitonic recombination, which means again that the assumption of α » 2 is due to uncorrelated electron-hole pair recombination does not match for QD and one needs a more complex equation instead of Equation (1).
4. Conclusions
Summarizing, our experimental findings suggest that the due to the fact that our dots are large, presenting a high confinement, together to the fact that we have a small density of dots, the probability to have more than one exciton by dots must be considered. Moreover, the fact that in our case the intersublevel relaxation time is considerable with respect to the interband transition due to both Pauling blocking and the reduced number of available final states already caused by the state filling effect leads to the fact that the GS saturation is not achieved before the appearing of the first-excited state, and one needs a more complete equation to correctly describe the origin of the recombinations.
5. Acknowledgements
This work was supported by the Brazilian funding age cies CNPq and FAPESP (06/04485-5 and 06/05858-0) and the research center of Universidade São Judas Tadeu.
REFERENCES
- N. Yasuoka, K. Kawaguchi, H. Ebe and T. Akiyama, M. Ekawa, S. Tanaka, K. Morito, A. Uetake, M. Sugawara and Y. Arakawa, “Demonstration of Transverse-Magnetic Dominant Gain in Quantum Dot Semiconductor Optical Amplifiers,” Applied Physics Letters, Vol. 92, No. 10, 2001, pp. 101108-101110. doi:10.1063/1.2883978
- I. L. Krestnikov, N. A. Maleev, A. V. Sakharov, A. R. Kovsh, A. E. Zhukov, A. F. Tsatsulnikov, V. M. Ustinov, Zh. I. Alferov, N. N. Ledentsov, D. Bimberg and J. A. Lott, “1.3 µm Resonant-Cavity InGaAs/GaAs Quantum Dot Light-Emitting Devices,” Semiconductor Science Technolology, Vol. 16, No. 10, 2001, p. 844. doi:10.1088/0268-1242/16/10/306
- Q. Sun, Y. A. Wang, L. S. Li, D. Wang, T. Zhu, J. Xu, C. Yang and Y. Li, “Bright, Multicoloured Light-Emitting Diodes Based on Quantum Dots,” Nature Photonics, Vol. 1, No. 12, 2007, pp. 717-722. doi:10.1038/nphoton.2007.226
- C. Y. Liu, S. F. Yoon, Q. Cao, C. Z. Tong and H. F. Li, “Low Transparency Current Density and High Temperature Operation from Ten-Layer P-Doped 1.3 μm InAs/InGaAs/ GaAs Quantum Dot Lasers,” Applied Physics Letters, Vol. 90, No. 4, 2007, pp. 041103-041105. doi:10.1063/1.2434156
- C.-Y. Zhang, H.-C. Yeh, M. T. Kuroki and T.-H. Wang, “Single-Quantum-Dot-Based DNA Nanosensor,” Nature Materials, Vol. 4, No. 11, 2005, pp. 826-831. doi:10.1038/nmat1508
- B. Dubertret, “Quantum Dots: DNA Detectives,” Nature Materials, Vol. 4, No. 11, 2005, pp. 797-798. doi:10.1038/nmat1520
- D. Loss and D. P. DiVincenzo, “Quantum Computation with Quantum Dots,” Physical Review A, Vol. 57, No. 1, 1998, pp. 120-126. doi:10.1103/PhysRevA.57.120
- Q. A. Turchette, C. J. Hood, W. Lange, H. Mabuchi and H. J. Kimble, “Measurement of Conditional Phase Shifts for Quantum Logic,” Physical Review Letters, Vol. 75, No. 25, 1995, pp. 4710-4713. doi:10.1103/PhysRevLett.75.4710
- C. Monroe, D. M. Meekhof, B. E. King, W. M. Itano and D. J. Wineland, “Demonstration of a Fundamental Quantum Logic Gate,” Physical Review Letters, Vol. 75, No. 25, 1995, pp. 4714-4717. doi: 10.1103/PhysRevLett.75.4714
- M. H. Baier, E. Pelucchi, E. Kapon, S. Varoutsis, M. Gallart, I. Robert-Philip and I. Abram, “Single Photon Emission from Site-Controlled Pyramidal Quantum Dots,” Applied Physics Letters, Vol. 84, No. 5, 2001, pp. 1643533- 1643535. doi:10.1063/1.1643533
- M. J. da Silva, A. A. Quivy, S. Martini, T. E. Lamas, E. C. F. da Silva and J. R. Leite, “InAs/GaAs Quantum Dots Optically Active at 1.5 μm,” Applied Physics Letters, Vol. 82, No. 16, 2003, pp. 2646-2648. doi:10.1063/1.1569053
- M. J. da Silva, A. A. Quivy, S. Martini, T. E. Lamas, E. C. F. da Silva and J. R. Leite, “Optical Response at 1.3 μm and 1.5 μm with InAs Quantum Dots Embedded in a Pure GaAs Matrix, ” Journal of Crystal Growth, Vol. 251, No. 1-4, pp. 181-185. doi:10.1016/S0022-0248(02)02405-3
- W. Rudno-Rudziński, G. Sęk, J. Misiewicz, T. E. Lamas, and A. A. Quivy, “The Formation of Self-Assembled InAs/ GaAs Quantum Dots Emitting at 1.3 μm Followed by Photoreflectance Spectroscopy,” Journal of Applied Physics, Vol. 101, No. 7. 2007, pp. 073518-073521. doi:10.1063/1.2714686
- E. C. Le Ru, J. Fack and R. Murray, “Temperature and Excitation Density Dependence of the Photoluminescence from Annealed InAs/GaAs Quantum Dots,” Physical Review B, Vol. 67, No. 24, 2003, pp. 245318-245329. doi:10.1103/PhysRevB.67.245318
- S. Sanguinetti, D. Colombo, M. Guzzi, E. Grilli, M. Gurioli, L. Seravalli, P. Frigeri, and S. Franchi, “Carrier Thermodynamics in InAs/InxGa1−xAs Quantum Dots,” Physical Review B, Vol. 74, No. 20, 2006, pp. 205302-205307. doi: 10.1103/PhysRevB.74.205302
- K. Mukai, N. Ohtsuka, H. Shoji and M. Sugawara, “Emission from Discrete Levels in Self-Formed InGaAs/GaAs Quantum Dots by Electric Carrier Injection: Influence of Phonon Bottleneck,” Applied Physics Letters, Vol. 68, No. 21, 1996, pp. 3013-3015. doi:10.1063/1.116681
- R. Heitz, M. Veit, N. N. Ledentsov, A. Hoffmann, D. Bimberg, V. M. Ustinov, P. S. Kop’ev and Zh. I. Alferov, “Energy Relaxation by Multiphonon Processes in InAs/ GaAs Quantum Dots,” Physical Review B, Vol. 56, No. 16, 1997, pp. 10435-10445. doi:10.1103/PhysRevB.56.10435
- R. Heitz, F. Guffarth, I. Mukhametzhanov, M. Grundmann, A. Madhukar and D. Bimberg, “Many-Body Effects on the Optical Spectra of InAs/GaAs Quantum Dots” Physical Review B, Vol. 62, No. 24, 2000, pp. 16881-16885. doi: 10.1103/PhysRevB.62.16881
- M. Grundmann, N. N. Ledentsov, O. Stier, J. Böhrer, D. Bimberg, V. M. Ustinov, P. S. Kop’ev and Zh. I. Alferov, “Nature of Optical Transitions in Self-Prganized InAs/GaAs Quantum Dots,” Physical Review B, Vol. 53, No. 16, 1996, pp. R10509-R10511. doi: 10.1103/PhysRevB.53.R10509
- D. Morris, N. Perret and S. Fafard, “Carrier Energy Relaxation by Means of Auger Processes in InAs/GaAs SelfAssembled Quantum Dots,” Applied Physics Letters, Vol. 75, No. 23, 1999, pp. 3593-3595. doi:10.1063/1.125398
- S. Raymond, S. Fafard, P. J. Poole, A. Wojs, P. Hawrylak, S. Charbonneau, D. Leonard, R. Leon, P. M. Petroff and J. L. Merz, “State Filling and Time-Resolved Photoluminescence of Excited States in InxGa1-xAs/GaAs SelfAssembled Quantum Dots,” Physical Review B, Vol. 54, No. 16, 1996, pp. 11548-11554. doi: 10.1103/PhysRevB.54.11548
- S. R. Jin, Y. L. Zheng and A. Z. Li, “Characterization of Photoluminescence Intensity and Efficiency of Free Excitons in Semiconductor Quantum Well Structures,” Journal of Applied Physics, Vol. 82, No. 8, 1997, pp. 3870- 3973. doi: 10.1063/1.365689
- M. Abbarchi, C. Mastrandrea, T. Kuroda1, T. Mano, A. Vinattieri, K. Sakoda and M. Gurioli, “Poissonian Statistics of Excitonic Complexes in Quantum Dots,” Journal of Applied Physics, Vol. 106, No. 5, 2009, pp. 053504- 053509. doi:10.1063/1.3197848
- P. Dawson1, O. Rubel, S. D. Baranovskii, K. Pierz, P. Thomas and E. O. Göbel, “Temperature-Dependent Optical Properties of InAs/GaAs Quantum Dots: Independent Carrier versus Exciton Relaxation,” Physical Review B, Vol. 72, No. 23, 2005, pp. 235301-235310. doi: 10.1103/PhysRevB.72.235301
- L. Zhang, Thomas F. Boggess, K. Gundogdu, Michael E. Flatté, D. G. Deppe, C. Cao and O. B. Shchekin, “Excited-State Dynamics and Carrier Capture in InGaAs/GaAs Quantum Dots,” Applied Physics Letters, Vol. 79, No. 20, 2001, pp. 3320-3322. doi:10.1063/1.1418035
- J. Hashimoto, Y. Maeda and M. Nakayama, “Photoluminescence from Exciton-Exciton Scattering in a GaAs1−xNx Thin Film,” Applied Physics Letters, Vol. 96, No. 8, 2010, pp. 081910-081912. doi: 10.1063/1.3309695

