Atmospheric and Climate Sciences
Vol.05 No.03(2015), Article ID:57697,11 pages
10.4236/acs.2015.53018
The Introduction of Specific Water and Maximum Airborne Specific Water & the Improvement of Dynamic Equations on Non-Uniform Saturated Moist Atmosphere
Xingrong Wang*, Yan Feng
Anhui Key Lab of Atmospheric Science and Satellite Remote Sensing, Anhui Meteorology Institute, Hefei, China
Email: *wxr_ahqks@sohu.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 April 2015; accepted 28 June 2015; published 1 July 2015
ABSTRACT
To eliminate the irrational supposition that condensed liquid water always falls immediately, specific water m and maximum airborne specific water 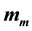 are introduced into the dynamic framework on non-uniform saturated moist atmosphere (m is the ratio of the airborne liquid water mass to the moist air mass in unit cubage moist air,
are introduced into the dynamic framework on non-uniform saturated moist atmosphere (m is the ratio of the airborne liquid water mass to the moist air mass in unit cubage moist air, 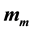 is its maximum value with
is its maximum value with ,
, 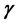 , w and
, w and 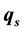 are airborne coefficient, vertical velocity and saturated specific humidity respectively). The balance equation between water vapor and airborne liquid water is derived. From the balance equation, a new formula of precipitate rate is got. The analysis shows that in the air stream with some upward vertical velocity (
are airborne coefficient, vertical velocity and saturated specific humidity respectively). The balance equation between water vapor and airborne liquid water is derived. From the balance equation, a new formula of precipitate rate is got. The analysis shows that in the air stream with some upward vertical velocity (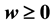 ), the condensed liquid water can precipitate under the condition with
), the condensed liquid water can precipitate under the condition with 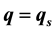 (q is specific humidity) and
(q is specific humidity) and 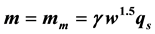 only, otherwise it is detained in the air and becomes airborne liquid water. Not only does precipitating liquid water contain condensed liquid water, but also contains converged and existing airborne liquid water. Following above discussion, improved dynamic equations on non-uniform saturated moist atmosphere are provided.
only, otherwise it is detained in the air and becomes airborne liquid water. Not only does precipitating liquid water contain condensed liquid water, but also contains converged and existing airborne liquid water. Following above discussion, improved dynamic equations on non-uniform saturated moist atmosphere are provided.
Keywords:
Airborne Liquid Water, Specific Water, Maximum Airborne Specific Water, Airborne Coefficient, Dynamic on Non-Uniform Saturated Moist Atmosphere

1. Introduction
Due to the important roles of water vapor in the genesis and development of weather systems, many studies have contributed to the dynamical discussion on moist atmosphere, e.g., Betts A. K., (1973) [1] ; Xie Y. B., (1978) [2] ; Wang L. M., (1980) [3] [4] ; Tripoli G. J., W. R. Cotton, (1981) [5] ; Pointin Y., (1984) [6] ; Hauf T., H. Holler, (1987) [7] ; Ooyama K. V., (1990) [8] ; (2000) [9] ; Persson O., (1995) [10] ; Wu G. X., Y. P. Cai and X. J. Tang, (1995) [11] ; Soriano L. J., E. L. Diez, (1997) [12] ; Schubert W. H., S. A. Hausman, and M. Garcia et al., (2001) [13] ; Bannon P. R., (2002) [14] .
To consider the transitional area between the unsaturated and saturated atmosphere, the discontinuity could occur in the latent heat term of the thermodynamic equation when the latent heat is released in the saturated atmosphere whereas latent heat is not released in the unsaturated atmosphere. Traditionally, the discontinuity in the latent heat term of the thermodynamic equation can be summarized by the Dirac delta function. The discontinuity makes the theoretical analysis very difficult for near saturated atmosphere, where the relative humidity is usually large enough to condensate but not saturated (just like rain regions), so these discussions are limit to the condition of saturated atmosphere e.g., Wang L. M., (1980) [3] [4] ; Wu G. X., Y. P. Cai and X. J. Tang, (1995) [11] , (realistic atmosphere is non-uniform saturated), or limit to the condition of equilibrium airflow, e.g., Ooyama K.V., (1990) [8] ; (2000) [9] ; Schubert W.H., S.A. Hausman, and M. Garcia et al., (2001) [13] , (realistic airflow is not always equilibrium).
However, the condensation process does not occur so abruptly in realistic atmosphere. According to the observational evidences pointed by Mason, (1971) [15] , the condensation process might occur at 78% of relative humidity under the condition of the appropriate condensation nuclear in real atmosphere. Therefore, a condensation probability function  is introduced by Wang X. R. and K. J. Wu, (1995) [16] , Wang X. R., C. E. Chi and Z. X. Wang, (1997) [17] and Wang X. R., Z. X. Wang, and C. N. Shi, (1999) [18] , which is expected to represent the continuity of this kind of variation, here
is introduced by Wang X. R. and K. J. Wu, (1995) [16] , Wang X. R., C. E. Chi and Z. X. Wang, (1997) [17] and Wang X. R., Z. X. Wang, and C. N. Shi, (1999) [18] , which is expected to represent the continuity of this kind of variation, here 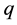 and
and 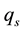 are the specific humidity and saturated specific humidity respectively,
are the specific humidity and saturated specific humidity respectively,  is a function of pressure, temperature, specific humidity and the density of condensation cores. When
is a function of pressure, temperature, specific humidity and the density of condensation cores. When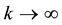 , the function is degraded to the Heaviside step function. Thus, the condensation probability function is a generalized Heaviside step function, which leads to the continuity of the latent heat term of the thermodynamic equation in the transition area between the unsaturated and saturated air. They constituted a more approximate thermodynamic equation for the saturated and/or near saturated atmosphere, where the relative humidity is usually large enough to condensate but not saturated (just like rain regions). Based on the fact that condensation occurs when
, the function is degraded to the Heaviside step function. Thus, the condensation probability function is a generalized Heaviside step function, which leads to the continuity of the latent heat term of the thermodynamic equation in the transition area between the unsaturated and saturated air. They constituted a more approximate thermodynamic equation for the saturated and/or near saturated atmosphere, where the relative humidity is usually large enough to condensate but not saturated (just like rain regions). Based on the fact that condensation occurs when 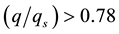 in the real atmosphere due to the existence of condensation cores, and by theoretical analysis and numerical simulation, Wang X. R., Z. X. Wang, and C. N. Shi, (1999) [18] , found when k is about 9, the condensation in the atmosphere is represented well. And hence, we specify
in the real atmosphere due to the existence of condensation cores, and by theoretical analysis and numerical simulation, Wang X. R., Z. X. Wang, and C. N. Shi, (1999) [18] , found when k is about 9, the condensation in the atmosphere is represented well. And hence, we specify 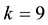 in our study. Following this discussion, the dynamic equations on non-uniform saturated moist atmosphere (EQSNUSMA) are provided.
in our study. Following this discussion, the dynamic equations on non-uniform saturated moist atmosphere (EQSNUSMA) are provided.
On the basis of EQSNUSMA, a battery of results is got:
Wang X. R. and K. J. Wu, (1995) [16] , found that the direction of geo-strophic equilibrium wind of moist air is parallel to equipotential line, its wind speed is equal to the product of dry air geo-strophic equilibrium wind
speed and static non-equilibrium parameter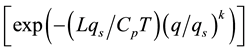 . The wind speed of geo-strophic
. The wind speed of geo-strophic
equilibrium wind of moist air is less than that of dry air, because static non-equilibrium parameter is less than 1. It was pointed out that the super-geo-strophic behavior of low level jet streams is caused by non-equilibrium relating to jet strengthening, it is not equilibrium airflow.
The non-uniform saturated moist potential vorticity (NUSMPV), or the generalized moist potential vorticity (GMPV), is thus defined and its tendency equation is derived by Wang X. R., Z. X. Wang and C. N. Shi, (1998) [19] ; Gao S. T., X. R. Wang and Y. S. Zhou, (2004) [20] ; Wang X. R. and M Wei, (2007) [21] . The analysis shows that in a frictionless and moist adiabatic flow, the NUSMPV, (or GMPV), can be generated in the unsaturated air only and its generation rate is determined by the environmental moisture and its gradient. It is further shown that in the sub-saturated regions
Based on the works by Wang X. R., Z. X. Wang and C. N. Shi, (1998) [19] ; Wang X. R., X. P. Chen and S. P. Xun, (1998) [22] ; Wang X. R., K. J. Wu and X. P. Chen et al., (1999) [23] and Wang X. R., Z. X. Wang, and C. N. Shi, (1999) [18] , the transformation mechanism between weather systems of different scale is discussed by Wang X. R., M. Wei, (2007) [21] . According to the relativity principle of conservation, by discussing the non-dimensional form of the NUSMPV equation, the atmospheric motion is classified into three types: motions with conserved, quasi-conserved, and non-conserved NUSMPV. It is pointed out as follows. When the dynamic non-equilibrium degree 


Furthermore, in recent years, some new variables from EQSNUSMA, such as generalized potential temperature, GMPV, generalized convective vorticity vector et al., are applied more to the dynamical analysis of hot and humid weather systems and torrential rain systems, e.g., Gao S. T., Y. S. Zhou, T. Lei et al. (2005) [25] ; Sheng S. Q. and Y. S. Zhou, (2007) [26] ; Yang S., S. T. Gao, D. H. Wang, (2007) [27] ; Zhou Y. S., J. Cao and D. H. Wang. (2007) [28] ; Duan T. Y., G. Deng. and D. H. Wang, (2007) [29] ; Gao S. T. and C. G. Cui, (2007) [30] ; Cao J. and S. T. Gao, (2008) [31] ; Zhou Y. S., (2009) [32] ; Zhaoming Liang, Chungu Lu and Edward I. Tollerud, (2010) [33] ; Zhou Y. S. and K. F. Zhu. (2010) [34] .
Such great progress for dynamic on non-uniform saturated moist atmosphere has been made in theory and application aspects, but, in all studies, almost no one is involved in the discussion on condensed liquid water. Traditionally, it is supposed that condensed liquid water always precipitates immediately. However, it is not true, in realistic atmosphere, the condensed liquid water either falls down in the form of precipitate or is detained in the air in the form of airborne liquid water (fog or cloud). By the analysis of some failure model experiments on dynamic equations on non-uniform saturated moist atmosphere, it is found that the reason of failure is exactly the irrational supposition that condensed liquid water always falls down immediately. So, in the dynamic equations on non-uniform saturated moist atmosphere, it becomes a question how to consider the condensed liquid water in air. By the discussion of airborne liquid water content and the balance equation between water vapor and liquid water, the new idea (not only precipitate contains condensed liquid water also includes airborne liquid water) is firstly raised and an advanced precipitable formula is set up by Wang, X.R., Gao, S.T. (2007) [35] . But the paper is not involved in the discussion on the condition, under which condensed liquid water can precipitate only, otherwise it is detained in the air and becomes airborne liquid water. And that, in the paper, the deduction in p coordinate is not correct, so the airborne coefficient estimated is also an inaccuracy.
To eliminate the irrational supposition that condensed liquid water always falls down immediately, specific water m and maximum airborne specific water 
2. The Balance Equation between Water Vapor and Airborne Liquid Water
2.1. The Discussion in the Condition of w ³ 0
In the condition of 
Following Wang X. R., Z. X. Wang and C. N. Shi (1999) [18] , by introducing the condensation probability function 


where



Following Mason, (1971) [15] , 

where 




where N is the all number of liquid water droplets, 


According to the observational evidences pointed by Mason, (1971) [15] , Squires P. (1958) [37] , Warner J. (1955) [38] , Warner J. and T. D. Newnham, (1952) [39] and Weickmann H. K. and H. J. Aufm Kampe, (1953) [40] , The distribution of airborne liquid water mass in cloud is related to the distribution of vertical velocity. According to force equilibrium principle, in the condition of



where 


With Equation (5), (6) and (7), Equation (3) becomes


From the physical properties in cumuliform clouds versus height above cloud base (Figure 1) by Weickmann H. K. and H. J. Aufm Kampe, (1953) [40] , it may be found that, if the relation curve 




here a is the coefficient independent of p and T. Because 


here 





When liquid water precipitates, with Equation (13), a new formula of precipitate rate is got as

From Equation (14), not only does precipitating liquid water contains condensed liquid water, but also contains converged and existing airborne liquid water.
In addition, Equation (14) can be rewritten as
Figure 1. The physical properties in cumuliform clouds versus height above cloud base.

The generalized temperature 

in saturated moist air (

In moist adiabatic condition, using thermodynamic equation, state equation and continuity,



Equation (17) can be rewritten as

In real atmosphere,



From Equation (22), (23) and (24), we have

In other words, 
be rewritten as



2.2. The Discussion in the Condition of w < 0
In the condition of


With Equation (30), Equation (2) becomes

From Equation (31), because

In addition, because of down-current, the rising temperature cased by adiabatic expansion restrains condensation process, so

From Equation (32) and (33), we have

3. The Improved Dynamic Equations on Non-Uniform Saturated Moist Atmosphere
Following Wang X. R., Z. X. Wang and C. N. Shi (1999) [18] and above discussion, by introducing the con- densation probability function








In moist adiabatic condition, from Equations (35)-(41) and the definition of generalized temperature 


and the vertical coordinate transform formula based on the non-static equilibrium by Wang X. R., C. E. Chi and Z. X. Wang (1997) [17] , the improved dynamic equations on non-uniform saturated moist frictionless and adiabatic atmosphere in p coordinate may be provided as







From Equation (35)-(41) and (43)-(49), the dynamic equations on non-uniform saturated moist atmosphere are improved, because of introducing specific water m and maximum airborne specific water





4. The Rough Estimation of Airborne Coefficient
Because the character of 


With the new formula of precipitate rate in p coordinate (49), the new formula of rainfall intensity can be written roughly as

where 


When estimating rainfall intensity, it is usually assumed that the local change of meteorological equal to 0, so

If assuming 


where 

here

where Fc is the confluent function of airborne liquid water, it may be expressed as




On the theoretical plane, using the synchronous analysis data with rainfall provided by RAFS (regional analysis and forecasting system), let the actual rainfall intensity







Here, in the supposition that 


The gross-precipitation of this super-heavy rain is 1631.1mm, the maximum rainfall intensity is 189.5 mm/h (in the neighborhood of Banqiao reservoir in August 7, 22:00 Beijing time), in August 7, 20:00 Beijing time (the observation time on schedule), the center rainfall intensity on large scale surface weather chart is 12.5 mm/h, the actual extremes of rainfall intensity is 99.7 mm/h (in the neighborhood of Banqiao reservoir). Although the horizontal distribution graph of 

With the new formula of precipitate rate in p coordinate (49), using mean value theorem, the new formula of rainfall intensity can be written roughly as

where 






From the analysis report provided by LGSHR1975 (1977) [42] , let the center value of 





Based on 8m/s (the surface wind velocity (SWV) recorded at Suiping weather station, which is the nearest from Banqiao reservoir) and 12m/s (the SWV estimated from the physical phenomena at Banqiao reservoir), with an eye on the small scale orographic influence of Banqiao reservoir (climbing and bell-mouthed effects in the condition of NE wind), the




From Table 1, although the traditional estimated values of rainfall intensity at Banqiao reservoir, 


5. Conclusions
In this study, by introducing specific water and maximum airborne specific water into the dynamic framework on non-uniform saturated moist atmosphere, the irrational supposition, that condensed liquid water always falls immediately, is eliminated. The balance equation between water vapor and airborne liquid water is derived. From the balance equation, a new formula of precipitate rate is derived. Following the above discussion, improved dynamic equations on non-uniform saturated moist atmosphere are provided. Finally, in the supposition that 


Table 1. The



It is necessary to point out that the character of 

Acknowledgements
This study was supported by Anhui Provincial Natural Science Foundation under Grant No. 1508085MD64, 1408085MKL60 and China Meteorology Administration Foundation under Grant No. CMAGJ2015M28.
References
- Betts, A.K. (1973) Non Precipitating Cumulus Convection and Its Parameterization. Quarterly Journal of the Royal Meteorological Society, 99, 178-196. http://dx.doi.org/10.1002/qj.49709941915
- Xie, Y.B. (1978) Synoptic Problems in Moist Baroclinic Atmosphere. In: Thesis Collection on Torrential Rain, Jilin Press, Changchun, 1-15. (In Chinese)
- Wang, L.M. (1980) The Basic Equations and Main Characteristics of Saturated Moist Dynamics. Acta Mechanica Sinica, 38, 44-50. (In Chinese)
- Wang, L.M. (1980) The Basic Characteristics of Saturated Moist Thermodynamic. Acta Mechanica Sinica, 38, 106- 109. (In Chinese)
- Tripoli, G.J. and Cotton, W.R. (1981) The Use of Liquid Water Potential Temperature as a Thermodynamic Variable in Deep Atmospheric Models. Monthly Weather Review, 109, 1094-1102. http://dx.doi.org/10.1175/1520-0493(1981)109<1094:TUOLLW>2.0.CO;2
- Pointin, Y. (1984) Wet Equivalent Potential Temperature and Enthalpy as Prognostic Variables in Cloud Modeling. Journal of the Atmospheric Sciences, 41, 651-660. http://dx.doi.org/10.1175/1520-0469(1984)041<0651:WEPTAE>2.0.CO;2
- Hauf, T. and Holler, H. (1987) Entropy and Potential Temperature. Journal of the Atmospheric Sciences, 44, 2887- 2901. http://dx.doi.org/10.1175/1520-0469(1987)044<2887:EAPT>2.0.CO;2
- Ooyama, K.V. (1990) A Thermodynamic Foundation for Modeling the Moist Atmosphere. Journal of the Atmospheric Sciences, 47, 2580-2593. http://dx.doi.org/10.1175/1520-0469(1990)047<2580:ATFFMT>2.0.CO;2
- Ooyama, K.V. (2000) A Dynamic and Thermodynamic Foundation for Modeling the Moist Atmosphere with Parameterized Microphysics. Journal of the Atmospheric Sciences, 58, 2073-2102. http://dx.doi.org/10.1175/1520-0469(2001)058<2073:ADATFF>2.0.CO;2
- Persson, O. (1995) Simulations of the Potential Vorticity Structure and Budget of FRONTS 87 IOP8. Quarterly Journal of the Royal Meteorological Society, 121, 1041-1081. http://dx.doi.org/10.1002/qj.49712152506
- Wu, G.X., Cai, Y.P. and Tang, X.J. (1995) Moist Potential Vorticity and Slantwise Vorticity Development. Acta Meteor Simica, 53, 387-405. (In Chinese)
- Soriano, L.J. and Garcia Diez, E.L. (1997) Effect of Ice on the Generation of a Generalized Potential Vorticity. Journal of the Atmospheric Sciences, 54, 1385-1387. http://dx.doi.org/10.1175/1520-0469(1997)054<1385:EOIOTG>2.0.CO;2
- Schubert, W.H., Hausman, S.A., Garcia, M., Ooyama, K.V. and Kuo, H.-C. (2001) Potential Vorticity in a Moist Atmosphere. Journal of the Atmospheric Sciences, 58, 3148-3157. http://dx.doi.org/10.1175/1520-0469(2001)058<3148:PVIAMA>2.0.CO;2
- Bannon, P.R. (2002) Theoretical Foundations for Models of Moist Convection. Journal of the Atmospheric Sciences, 59, 1967-1982. http://dx.doi.org/10.1175/1520-0469(2002)059<1967:TFFMOM>2.0.CO;2
- Mason, N.B. (1971) The Physics of Clouds. Oxford University Press, Oxford, 671.
- Wang, X.R. and Wu, K.J. (1995) An Approach to the Dynamics of Moist Air. Scientia Meteorologica Sinica, 15, 9-17. (In Chinese)
- Wang, X.R., Chi, C.E. and Wang, Z.X. (1997) The Vertical Coordinate Transformation and the Dynamics Equations of Moist Air Based on the Non-Static Equilibrium. Scientia Meteorologica Sinica, 21, 557-563. (In Chinese)
- Wang, X.R., Wang, Z.X. and Shi, C.N. (1999) The Introduction of Condensation Probability Function and the Dynamic Equations on Non-Uniform Saturated Moist Air. Journal of Tropical Meteorology, 15, 64-70. (In Chinese)
- Wang, X.R., Wang, Z.X. and Shi, C.N. (1998) On the Non-Conservativeness of Wet Potential Vorticity of Air Motion. Scientia Meteorologica Sinica, 13, 136-141. (In Chinese)
- Gao, S.T., Wang, X.R. and Zhou, Y.S. (2004) Generation of Generalized Moist Potential Vorticity in a Frictionless and Moist Adiabatic Flow. Geophysical Research Letters, 31, Article ID: L12113. http://dx.doi.org/10.1029/2003gl019152
- Wang, X.R. and Wei, M. (2007) Theoretical Analysis of Non-Uniform Saturated Moist Potential Vorticity (NUSMPV) Associated with the Occurrence and Development of Weather Systems. Journal of Tropical Meteorology, 23, 459-566. (In Chinese)
- Wang, X.R., Chen, X.P. and Xun, S.P. (1998) Study on Sudden Disaster Based on Trigger Mechanism of Unstable Energy. Journal of Natural Disasters, 7, 11-15. (In Chinese)
- Wang, X.R., Wu, K.J., Chen, X.P. and Shi, C.E. (1999) Dynamic Mechanism of the Happening of the Sudden Calamitous Weather. Journal of Nanjing Institute of Meteorology, 22, 711-715. (In Chinese)
- Wang, X.R., Zheng, Y.Y., Gao, S.T. and Zhou, K. (2006) Possible Premonitory Characters of Doppler Radar Product and Cloud Chart for the Mid-Latitude Sudden Heavy Rain. Journal of Tropical Meteorology, 22, 612-617. (In Chinese)
- Gao, S.T., Zhou, Y.S., Lei, T., et al. (2005) Analyses of Hot and Humid Weather in Beijing City in Summer and Its Dynamical Identification. Science in China, Ser. D, Earth Sciences, 48, 128-137.
- Sheng, S.Q. and Zhou, Y.S. (2007) Advances in Meso-Scale Dynamical Analysis of Torrential Rain Systems in Recent Years in China. Chinese Journal of Atmospheric Sciences, 31, 1171-1188. (In Chinese)
- Yang, S., Gao, S.T. and Wang, D.H. (2007) Diagnostic Analysis of the Ageostrophic Q Vector in the Non-Uniformly Saturated, Frictionless and Moist Adiabatic Flow. Journal of Geophysical Research, 112, Article ID: D09114. http://dx.doi.org/10.1029/2006JD008142
- Zhou, Y.S., Cao, S.J. and Wang, D.H. (2007) Application of Generalized Moist Potential Vorticity in Non-Uniformly Saturated Atmosphere to Torrential Rain Forecast. Journal of Applied Meteorological Science, 18, 754-759. (In Chinese)
- Duan, T.Y., Deng, G. and Wang, D.H. (2007) Diagnostic Analysis of Generalized Moist Potential Vorticity and Forecast of Torrential Rain Region. Chinese Journal of Atmospheric Sciences, 31, 1301-1307. (In Chinese)
- Gao, S.T. and Cui, C.G. (2007) The Theory of Generalized Moist Potential Vorticity and Its Applicative Study. Torrential Rain and Disasters, 26, 5-10. (In Chinese)
- Cao, J. and Gao, S.T. (2008) Generalized Potential Temperature in Non-Uniformly Saturated Atmosphere. Chinese Journal of Geophysics, 51, 1651-1656. (In Chinese)
- Zhou, Y.S. (2009) Application of Generalized Moist Potential Vorticity to Analysis and Forecast of Torrential Rain over the Chang Jiang-Huai He River Basin. Chinese Journal of Atmospheric Sciences, 33, 1101-1110. (In Chinese)
- Liang, Z.M., Lu, C.G. and Tollerud, E.I. (2010) Diagnostic Study of Generalized Moist Potential Vorticity in a Non-Uniformly Saturated Atmosphere with Heavy Precipitation. Quarterly Journal of the Royal Meteorological Society, 136, 1275-1288. http://dx.doi.org/10.1002/qj.636
- Zhou, Y.S. and Zhu, K.F. (2010) Comparisons between the Generalized Potential Temperature in the Moist Atmosphere and the Potential Temperature in the Dry Atmosphere and the Equivalent Potential Temperature in the Saturated Moist Atmosphere. Acta Meteor Simica, 68, 612-616. (In Chinese)
- Wang, X.R. and Gao, S.T. (2007) The Reestimate of Rain Intensity Extremes of the Super-Heavy Rain in Henan in China in Aug.1975. Journal of Tropical Meteorology, 23, 196-200. (In Chinese)
- Levin, L.M. (1954) Distribution Function of Cloud and Raindrops by Sizes. Doklady Akademii Nauk SSSR, 94, 1045.
- Squires, P. (1958) The Spatial Variation of Liquid Water Content and Droplet Concentration in Cumuli. Tellus, 10, 372-380. http://dx.doi.org/10.1111/j.2153-3490.1958.tb02024.x
- Warner, J. (1955) The Water Content of Cumuliform Cloud. Tellus, 7, 449-457. http://dx.doi.org/10.1111/j.2153-3490.1955.tb01183.x
- Warner, J. and Newnham, T.D. (1952) A New Method of Measurement of Cloud Water Content. Quarterly Journal of the Royal Meteorological Society, 78, 46-52. http://dx.doi.org/10.1002/qj.49707833506
- Weickmann, H.K. and Aufm Kampe, H.J. (1953) Physical Properties of Cumulus Clouds. Journal of the Meteorology, 10, 204-211. http://dx.doi.org/10.1175/1520-0469(1953)010<0204:ppocc>2.0.co;2
- Zhang, Y., et al. (1990) The Forecast of Heavy Rain. Meteorological Press, Beijing, 424. (In Chinese)
- The Leading Group for Studying the Super-Heavy Rain in Henan in China in August 4-8 1975 (LGSHR1975) (1977) The Analysis Report on the Super-Heavy Rain in Henan in China in August 4-8 1975. (In Chinese)
NOTES
*Corresponding author.




