Soft Nanoscience Letters
Vol.1 No.3(2011), Article ID:6165,10 pages DOI:10.4236/snl.2011.13016
Universal 2D Soft Nano-Scale Mosaic Structure Theory for Polymers and Colloids
![]()
College of Material Science and Engineering, Donghua University, Shanghai, China.
Email: jlwu@dhu.edu.cn
Received April 4th, 2011; revised May 10th, 2011; accepted May 17th, 2011.
Keywords: Glass Transition Theory, Soft Matrix, Mosaic Structure, Macromolecular Motion
ABSTRACT
A basic concept in chain-particle cluster-motion, from frozen glassy state to melt state, is the 2D soft nano-scale mosaic structure formed by 8 orders of 2D interface excitation (IE) loop-flows, from small to large in inverse cascade and rearrangement structure in cascade along local one direction. IE has additional repulsive energy and extra vacancy volume. IE results from that the instantaneous synchronal polarized electron charge coupling pair is able to parallel transport on the interface between two neighboring chain-particles with antiparallel delocalization. This structure accords with de Gennes’ mosaic structure picture, from which we can directly deduce glass transition temperature, melt temperature, free volume fraction, critical entangled chain length, and activation energy to break solid lattice. This is also the inherency maximum order-potential structure in random systems.
1. Introduction
This letter is an introduction of the motion principle in polymer physics theory. The confluence of both the thermodynamic and the kinetic dimensions of the solid ↔ liquid glass transition (GT) presents one of the most formidable problems in condensed matter physics [1]. Many theories [2], containing current Mode-Coupling Theories, have been proposed to explain glasses and GT; however, GT theory is still an open problem [2]. An acceptable GT theory should be in accordance with de Gennes’ simple mosaic structure picture [3]. a) The size of the clusters at GT corresponds to the boson peak wavelength, clusters slightly more compact than the matrix: they cannot grow in size because of frustration effects. Mode-Coupling Theories cannot describe this, because they do not incorporate frustration. b) Clusters move rather than molecules, the required cavity space (“vacancy”) for cluster motion is not empty, but filled with the low density matrix. c) The soft matrix is surrounding the clusters. d) An unsolved problem is what mechanism to balance kinetic and potential at the GT. In polymer engineering, GT may be thought of as an inverse cascade—cascade mode along external stress direction. This idea comes from the insight for cooperative orientation activation energy, 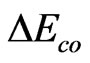 , on polyester melt high-speed spinning-line [4]. When the work of the stress on over 5000 M/min spinning-line reaches
, on polyester melt high-speed spinning-line [4]. When the work of the stress on over 5000 M/min spinning-line reaches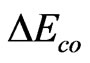 , the structure of the yarn is stable and reaches full orientation, called as FOY (Full Orientation Yarn) in current polyester fiber industry. This phenomenon is called stress-induced GT. The rate of change of the stress-induced liquid-to-solid GT is 107 times of that in general quencher from melt state to frozen glass state. A logical explanation is that the macromolecules can complete liquid-to-solid GT with full orientation within the millisecond of time in z-space. Their motion mode, within the entire range from melt transition temperature
, the structure of the yarn is stable and reaches full orientation, called as FOY (Full Orientation Yarn) in current polyester fiber industry. This phenomenon is called stress-induced GT. The rate of change of the stress-induced liquid-to-solid GT is 107 times of that in general quencher from melt state to frozen glass state. A logical explanation is that the macromolecules can complete liquid-to-solid GT with full orientation within the millisecond of time in z-space. Their motion mode, within the entire range from melt transition temperature  to GT temperature
to GT temperature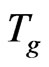 , allows the direction of inverse cascade-cascade in every “excited domain” is in arbitrary in melt state and all apt to z-axial on melt spinning-line; and finally the mode is frozen in glasses as the soft matrix.
, allows the direction of inverse cascade-cascade in every “excited domain” is in arbitrary in melt state and all apt to z-axial on melt spinning-line; and finally the mode is frozen in glasses as the soft matrix.
On the other hand, in physical theory, many complicated phenomena originate from the global properties of parallel transport of simple quantum systems (Berry’s Phase) [5]. In addition, crucial to the endeavor of GT theory is a deeper understanding of the systematics of bonding in condensed matter within a framework going considerable beyond the current GT picture [6]. Thus, the GT theoretical approach may come down to the parallel transport of “bonding” on intermolecular interfaces. This “bonding” here is called as the interface excitation (IE) the new and crucial concept introduced in this letter. Nine physical ingredients, random, self-similar, twobody interaction, fluctuation, frustration, and percolation, delocalization, Berry’s phase and Brownian regression potential, have been incorporated at the GT and in macromolecular motion. The incorporation of physical ingredients results in the 2D soft nano-scale mosaic structure in “excited domain”.
2. Theoretical Model
2.1. Intermolecular Interface Excitation
Van der Waals interaction includes the contribution of instantaneous induced dipole—induced dipole. Generally, instantaneous polarized dipole electron charges randomly distribute on an interface 1 - 2 forming electron cloud (blue zone) on x-y projection plane in Figure 1(a).
At GT, an interesting and unexplored corner of Van der Waals interaction theories is that the instantaneous synchronal polarized electron charge coupling pair (two small blue dots) may parallel transport on an interface, e.g., the interface 1-2 between particles 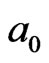 and
and 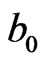 in Figure 1(b) during the local time of (
in Figure 1(b) during the local time of (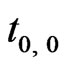 ,
,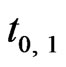 ), and the
), and the
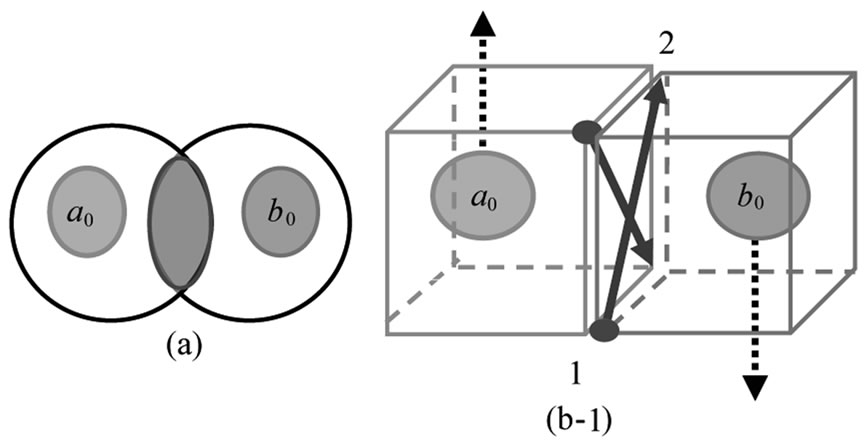
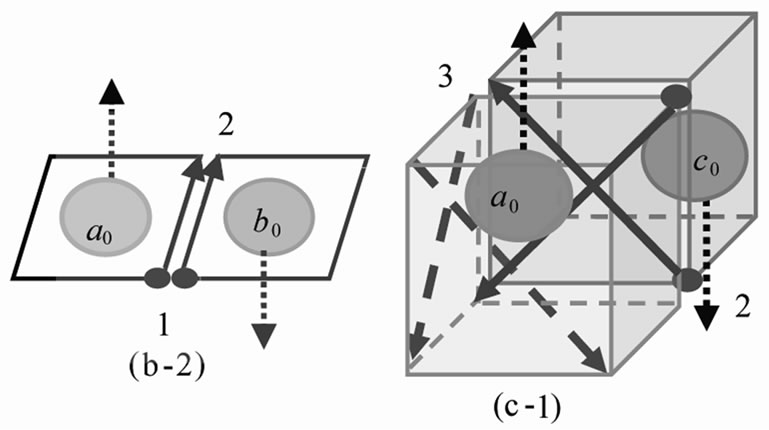
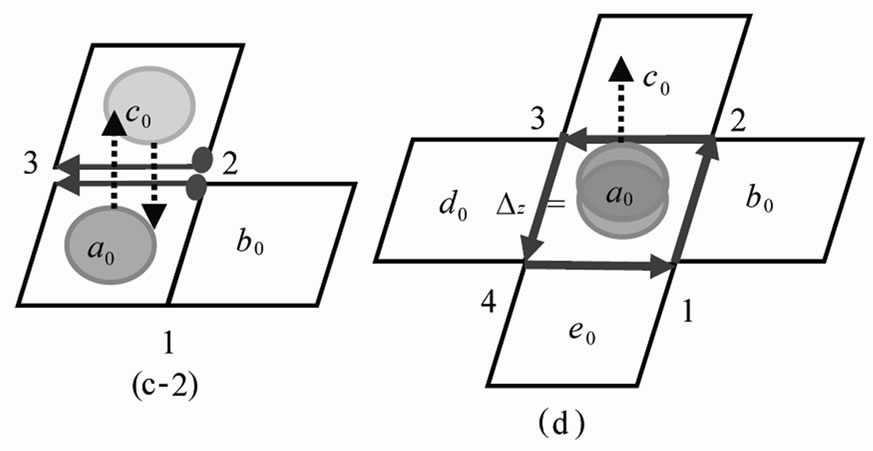
Figure 1. The physical origin of interface excitation. (a) A legitimate state; (b), (c) An absent of attraction state in certain 2D lattices; (d) Instantaneous delocalizing state of ion.
interface 2 - 3 between 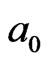 and
and 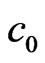 in Figure 1(c) during the local time of (
in Figure 1(c) during the local time of ( ,
,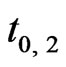 ). The state of parallel transport of coupling pair is defined as interface excitation on 2D projection plane. Black-broken line arrow on an ion denotes its delocalizing direction in Figure 1.
). The state of parallel transport of coupling pair is defined as interface excitation on 2D projection plane. Black-broken line arrow on an ion denotes its delocalizing direction in Figure 1.
Thus, the site-phase difference between two z-component molecules, or chain-particles, is p: the state of all polarized electron charges in each instantaneous dipole in the two z-component chain-particles, in Figure 1(b-1) or 1(c-1), must be in the same state and in the z-axial minimum energy state of single chain-particle instantaneous dipole. In Figures 1 (b-2) and 1(c-2) is respectively the projection of (b-1) and (c-1) on x-y plane. This means IE has an additional repulsive energy 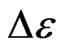 and an extra vacancy volume
and an extra vacancy volume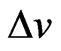 . Two instantaneous synchrony z-axial polarized electron charges parallel transport from one end to other end on an interface, as in Figure 1(b-2), that is simply denoted by an arrowhead, as (1®2) in Figure 1(d). The two IE states of (b-1) and (c-1) occur at different local times. The directions of the next two parallel transports of instantaneous polarized electron charges of the reference
. Two instantaneous synchrony z-axial polarized electron charges parallel transport from one end to other end on an interface, as in Figure 1(b-2), that is simply denoted by an arrowhead, as (1®2) in Figure 1(d). The two IE states of (b-1) and (c-1) occur at different local times. The directions of the next two parallel transports of instantaneous polarized electron charges of the reference 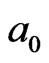 particle denote as two red-broken line arrowheads in Figure 1(c-1). Thus, an IE loop-flow 1 ® 2 ® 3 ® 4 ® 1, occurs during the local time of (
particle denote as two red-broken line arrowheads in Figure 1(c-1). Thus, an IE loop-flow 1 ® 2 ® 3 ® 4 ® 1, occurs during the local time of ( ,
,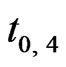 ) denoted as loop-
) denoted as loop- , in Figure 1(d). It is able to offer a non-integrable Berry’s Phase potential
, in Figure 1(d). It is able to offer a non-integrable Berry’s Phase potential  to induce ion
to induce ion 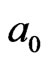 (the center of mass of
(the center of mass of 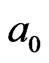 particle) z-direction a conceivable displacement
particle) z-direction a conceivable displacement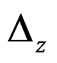 .
.
2.2. 5-Particle Cooperative Excited Field
The IE loop-flow in Figure 1(d) also defined a 2D action particle 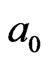 to GT, also denoted as
to GT, also denoted as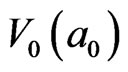 . The needful time (
. The needful time (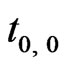 ,
,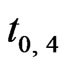 ) to form loop-
) to form loop-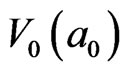 defined as the zero order of relaxation time
defined as the zero order of relaxation time . Thus each IE in Figure 1 has also the relaxation time of
. Thus each IE in Figure 1 has also the relaxation time of 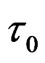 scale. At the GT, because only 2D closed cycle-flow (that will generate a non-integrable phase p and an additional z-axial induced energy) corresponds to the abnormal heat capacity and boson peak [3,7-9], we need only discuss all the IE loopflows on reference
scale. At the GT, because only 2D closed cycle-flow (that will generate a non-integrable phase p and an additional z-axial induced energy) corresponds to the abnormal heat capacity and boson peak [3,7-9], we need only discuss all the IE loopflows on reference 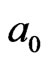 (particle local) filed. The discussion further simplify to only consider the loop-flows formed by several consecutive arrows on a 2D projection plane, see Figures 2-5, and each arrow denotes an IE that has the same IE energy
(particle local) filed. The discussion further simplify to only consider the loop-flows formed by several consecutive arrows on a 2D projection plane, see Figures 2-5, and each arrow denotes an IE that has the same IE energy 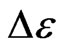 for flexible chain system. The advantage of the model is that it is also able to describe complex system. Some arrows with different markers denote the different IE energies correspond to the non-flexible chain system.
for flexible chain system. The advantage of the model is that it is also able to describe complex system. Some arrows with different markers denote the different IE energies correspond to the non-flexible chain system.
The formation of a central excited particle 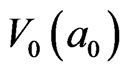 can be also regarded as the cooperative contribution from its 4 neighboring particle fields,
can be also regarded as the cooperative contribution from its 4 neighboring particle fields,  ,
, 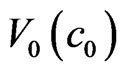 ,
, 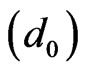
 , and
, and 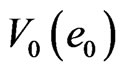 based on Brownian motion theory Figure 2.
based on Brownian motion theory Figure 2.
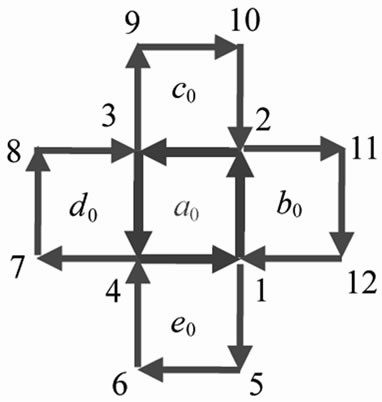
Figure 2. First order of transient 2D IE loop-flow .
.
At the instant (local) time 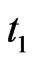 in
in 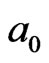 field, once 4th loop-flow
field, once 4th loop-flow  is finished, a new loop-flow of a0 surrounded by the 12 IEs, 1 ® 5 ® 6 ® 4 ® 7 ® 8 ® 3 ® 9 ® 10 ® 2 ® 11 ® 12 ® 1, with
is finished, a new loop-flow of a0 surrounded by the 12 IEs, 1 ® 5 ® 6 ® 4 ® 7 ® 8 ® 3 ® 9 ® 10 ® 2 ® 11 ® 12 ® 1, with ![]() timescale will occur as in Figure 2. The new symmetric loop-flow defined as the first order of transient 2D IE loop-flow and first order of 2D cluster in a0 field, which are all denoted as
timescale will occur as in Figure 2. The new symmetric loop-flow defined as the first order of transient 2D IE loop-flow and first order of 2D cluster in a0 field, which are all denoted as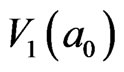 . Whose cycle direction is negative, contrary to that of
. Whose cycle direction is negative, contrary to that of . The energy of IE with
. The energy of IE with ![]() on the loop denoted as
on the loop denoted as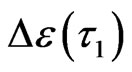 . The 4 excited particles are 4 concomitant mosaic cells with
. The 4 excited particles are 4 concomitant mosaic cells with . Loop
. Loop  has 12 IEs and is of the loop potential energy of 12
has 12 IEs and is of the loop potential energy of 12 . This means that the evolution energy from
. This means that the evolution energy from 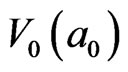 to
to  is 8
is 8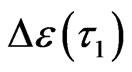 . The number of cooperative excitation particles in
. The number of cooperative excitation particles in 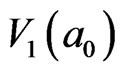 is 5.
is 5.
Similarly, the 2nd order of transient 2D IE loop-flow and 2D cluster with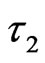 , denoted as
, denoted as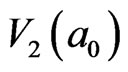 , is formed at the instant local time
, is formed at the instant local time ![]() when its 4 neighboring particle fields:
when its 4 neighboring particle fields: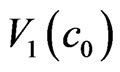 ,
, 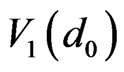 ,
, 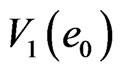 , and
, and 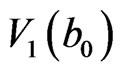 finished in
finished in 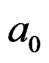 field. Whose cycle direction is positive, contrary to that of
field. Whose cycle direction is positive, contrary to that of , in Figure 3(e). The yellow area in Figure 3(e) represents
, in Figure 3(e). The yellow area in Figure 3(e) represents  loop in
loop in 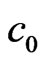 field, which is a first order of mosaic structure in
field, which is a first order of mosaic structure in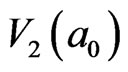 . The streamline diagram of parallel transport between two clusters
. The streamline diagram of parallel transport between two clusters 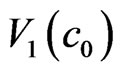 and
and  is Figure 3(a). 4 such mosaic structures,
is Figure 3(a). 4 such mosaic structures, 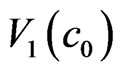 ,
, 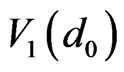 ,
, 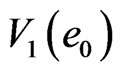 , and
, and 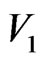
![]() cooperatively generate
cooperatively generate 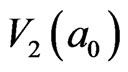 in
in 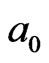 field.
field.
The energy of IE on loop 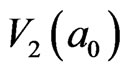 is denoted as
is denoted as 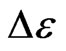
![]() . The number of IEs of loop
. The number of IEs of loop  is 20. The number of IEs inside loop
is 20. The number of IEs inside loop 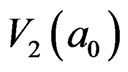 is 12, and equals to the number of the IEs of
is 12, and equals to the number of the IEs of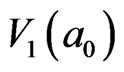 . This means that the evolution energy from
. This means that the evolution energy from 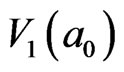 to
to 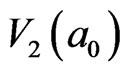 is 8
is 8 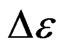
![]() . The number of cooperative excitation particles in
. The number of cooperative excitation particles in 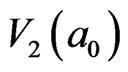 is 13 surrounded by 20 IEs. Thus, 20 IEs can excite 13 particles to hop randomly along local +z-axial direction.
is 13 surrounded by 20 IEs. Thus, 20 IEs can excite 13 particles to hop randomly along local +z-axial direction.
In the same way, the third order of 2D IE loop-flow and cluster at the instant time 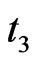 in a0 field,
in a0 field, 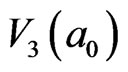 , can be obtained as in Figure 4, which formed by the contribution of its 4 neighboring second order loop-flows,
, can be obtained as in Figure 4, which formed by the contribution of its 4 neighboring second order loop-flows, 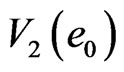 ,
, 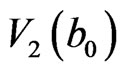 ,
, 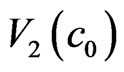 , and
, and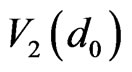 , respectively
, respectively
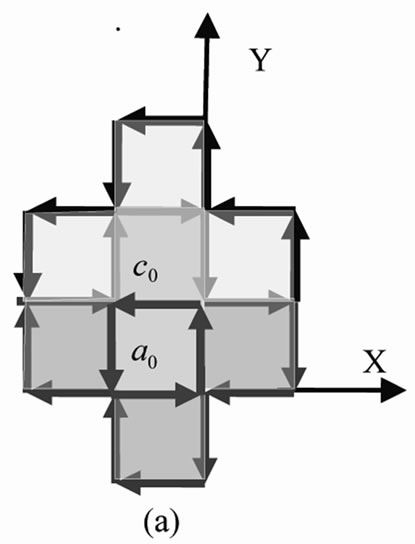
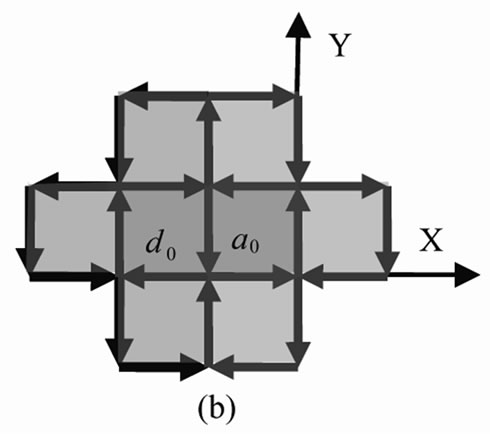
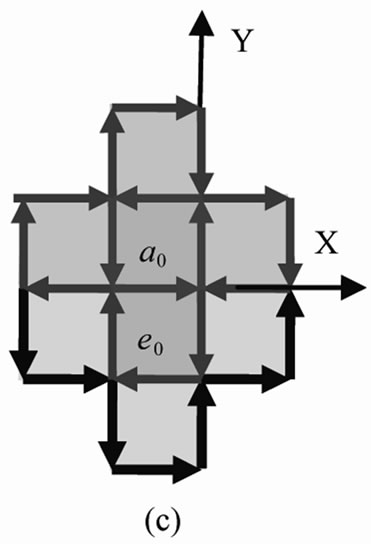

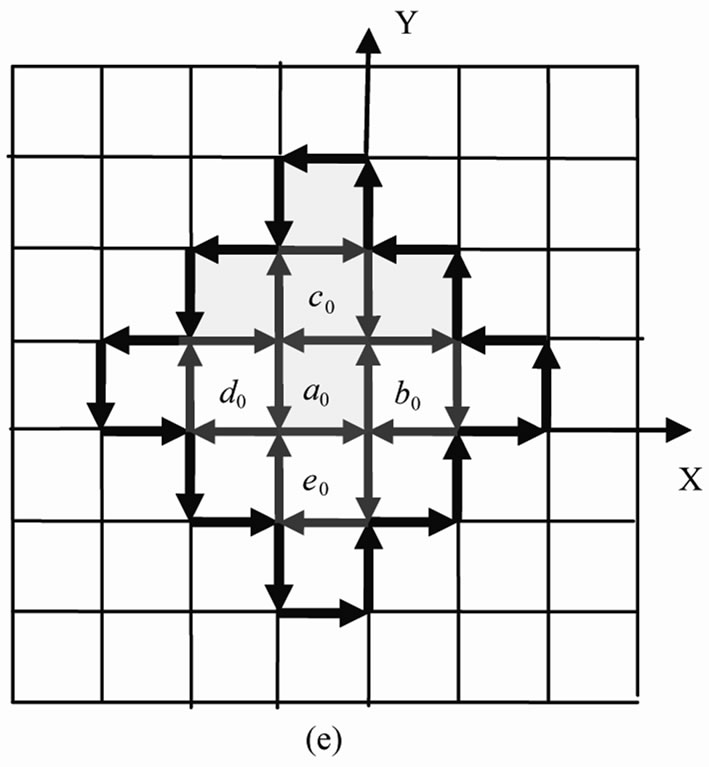
Figure 3. 4 neighboring clusters,  ,
, 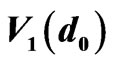 ,
, 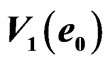 and
and 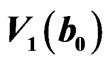 respectively and widdershins interact with
respectively and widdershins interact with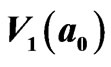 : (a), (b), (c), and (d) cooperatively generate
: (a), (b), (c), and (d) cooperatively generate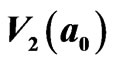 , (e). The 20 thick arrows denote 2nd order of 2D loop-flow and cluster
, (e). The 20 thick arrows denote 2nd order of 2D loop-flow and cluster 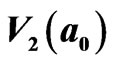 in
in 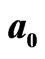 field.
field.
and deasil interacted with  in
in 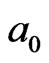 field. In Figure 4, the yellow area represents loop
field. In Figure 4, the yellow area represents loop 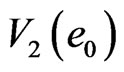 in
in 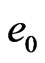 field (whose symmetric center is
field (whose symmetric center is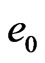 ) which is a second order of mosaic structure in a0 field. The number of IEs of loop
) which is a second order of mosaic structure in a0 field. The number of IEs of loop 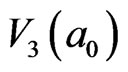 is 28. The number of IEs inside loop
is 28. The number of IEs inside loop 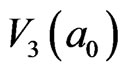 is 20, which equals to the number of the IEs on loop
is 20, which equals to the number of the IEs on loop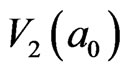 . This means the evolution energy from
. This means the evolution energy from 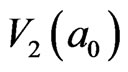 to
to 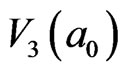 is 8
is 8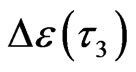 . The number of cooperative excitation particles in third order cluster is 25.
. The number of cooperative excitation particles in third order cluster is 25.

Figure 4. Third order of transient 2D IE loop-flow and cluster 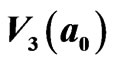 in
in 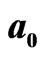 field.
field.
Thus, 28 IEs can excite 25 particles to hop randomly along local z-axial direction.
From the results of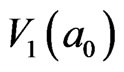 ,
, 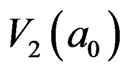 and
and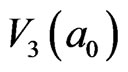 , it is clear that the more the number of cooperatively delocalization particles is, the less the average needful IE energy for each particle is. The key point is what the minimum excited energy is and what the number of cooperatively delocalization particles excited by the energy at the GT is.
, it is clear that the more the number of cooperatively delocalization particles is, the less the average needful IE energy for each particle is. The key point is what the minimum excited energy is and what the number of cooperatively delocalization particles excited by the energy at the GT is.
There are 4 neighboring concomitant excitation centers surrounding the referenced particle center. Thus, the excited field in Figure 2 is defined as 5-particle cooperative excited field to break solid-lattice.
The forming of i-th order cluster 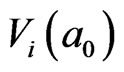 always results from the cooperative contributions of its 4 neighboring (i-1)-th order of clusters around the central particle. This property origins from Brownian motion and is called as the priority of central particle, which is probably the primary reason to generate dynamic heterogeneity [2] and non-ergodic [9] at GT. That means the spatial directions and localities of all the succedent IEs will be completely confirmed, Figures 2-5, once the first IE with the direction 1 ® 2 showed in Figure 1(d) appears at the local time
always results from the cooperative contributions of its 4 neighboring (i-1)-th order of clusters around the central particle. This property origins from Brownian motion and is called as the priority of central particle, which is probably the primary reason to generate dynamic heterogeneity [2] and non-ergodic [9] at GT. That means the spatial directions and localities of all the succedent IEs will be completely confirmed, Figures 2-5, once the first IE with the direction 1 ® 2 showed in Figure 1(d) appears at the local time 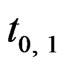 in
in 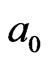 field, otherwise, the total excitation energies will increase. That is the reason and advantage to bring the signature of arrowhead into the standout mode of IE to get the minimum energy required to excite GT. Here the IE represented by arrow is scaled by the IE energy
field, otherwise, the total excitation energies will increase. That is the reason and advantage to bring the signature of arrowhead into the standout mode of IE to get the minimum energy required to excite GT. Here the IE represented by arrow is scaled by the IE energy 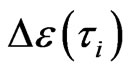 and thus the arrow is of a unit length for different wave lengths of harmonic and anharmonic frequencies on the (energy) lattice model. IE energy
and thus the arrow is of a unit length for different wave lengths of harmonic and anharmonic frequencies on the (energy) lattice model. IE energy 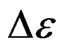 does not depend on temperature in flexible polymer system.
does not depend on temperature in flexible polymer system.
2.3. Eighth Order of 2D Cluster and Percolation
a) The number of IEs of i-th order of 2D cluster can be calculated as 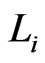 = 4 (2i + 1) = 12, 20, 28, 36, 44, 52, 60, and (68) for i = 1, 2… 8 and
= 4 (2i + 1) = 12, 20, 28, 36, 44, 52, 60, and (68) for i = 1, 2… 8 and 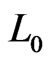 = 4. Note that
= 4. Note that  will be corrected as 60 by geometric frustration-percolation transition.
will be corrected as 60 by geometric frustration-percolation transition.
b) The number of excitation particles in i-th order of cluster is respectively: 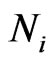 =
= 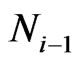 + 4i = 5, 13, 25, 41, 61, 85, 113, and (145) for i = 1, 2… 8 and
+ 4i = 5, 13, 25, 41, 61, 85, 113, and (145) for i = 1, 2… 8 and 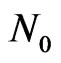 = 1. Note that
= 1. Note that 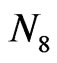 also will be corrected as 136 by geometric frustration-percolation transition.
also will be corrected as 136 by geometric frustration-percolation transition.
c) For z-axial i-th order 2D cluster, the evolution energy from 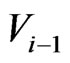 to
to  is 8
is 8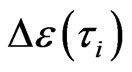 , we emphasize, this evolution is orienting. The energy to excite i-th order cluster orientable evolution thus is the energy of one external degree of freedom (DoF) to i-th order of cluster (loop-flow) orienting, denoted as
, we emphasize, this evolution is orienting. The energy to excite i-th order cluster orientable evolution thus is the energy of one external degree of freedom (DoF) to i-th order of cluster (loop-flow) orienting, denoted as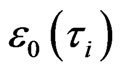 . So we directly deduce from a)
. So we directly deduce from a)
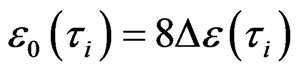 (1)
(1)
d) During the time of (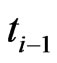 ,
,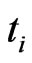 ) in the referenced
) in the referenced 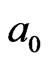 field, each of its 4 neighboring (
field, each of its 4 neighboring (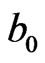 ,
, 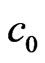 ,
, 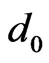 , and
, and ) local coordinates can take any direction (fragmentized and atactic lattices) because of fluctuation. However, from c), at the instant time
) local coordinates can take any direction (fragmentized and atactic lattices) because of fluctuation. However, from c), at the instant time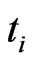 , the direction of i-th order cluster always starts sticking to the direction of the referenced first order cluster. This characteristic in random systems comes from the Brownian regression motion, or the characteristic of Graph of Brownian Motion. This means that each neighboring i-th order of cluster also has one external DoF of energy as
, the direction of i-th order cluster always starts sticking to the direction of the referenced first order cluster. This characteristic in random systems comes from the Brownian regression motion, or the characteristic of Graph of Brownian Motion. This means that each neighboring i-th order of cluster also has one external DoF of energy as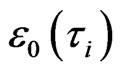 . So the i-th order
. So the i-th order
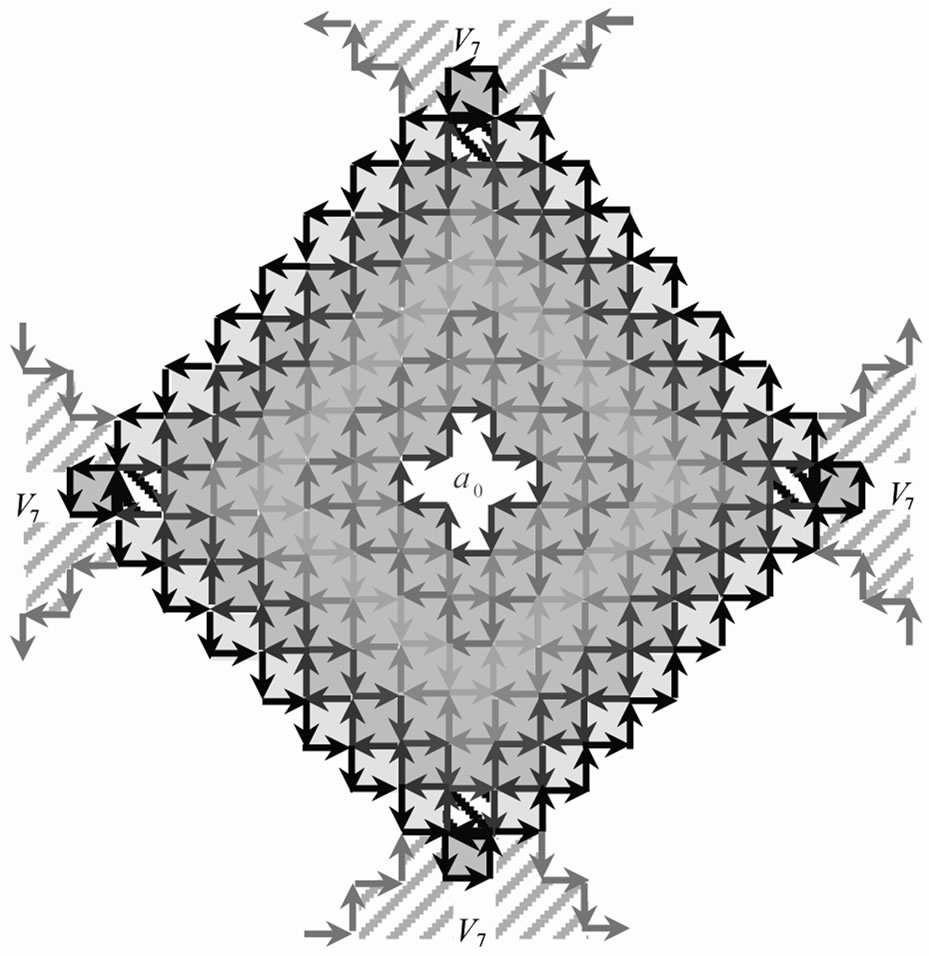
Figure 5. The 2D soft nano-scale mosaic structure occurs in the geometric frustration-percolation transition and is the maximum order potential structure in random systems.
of cluster in the (i + 1)-th order is of 5 inner DoF and taking any directions during the time of (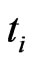 ,
,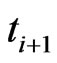 ) in
) in  field.
field.
In the same way, the 8th order of transient 2D cluster, 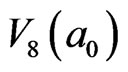 , can be obtained in
, can be obtained in 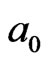 field, as in Figure 5. As there is no 9th cluster in system, (the result of limited domain-wall vibration frequencies based on Random First-Order Transition Theory proposed by Wolynes et al [2,7]) percolation should be adopted at the instant time
field, as in Figure 5. As there is no 9th cluster in system, (the result of limited domain-wall vibration frequencies based on Random First-Order Transition Theory proposed by Wolynes et al [2,7]) percolation should be adopted at the instant time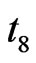 , and the 8th order of cluster must be corrected by percolation.
, and the 8th order of cluster must be corrected by percolation.
The uncorrected number of IEs of 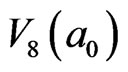 is 68, denoted by blue-black arrows in Figure 5. When percolation appears in system, the 4 excited cells, by thick upward diagonal lines, with τ8 in
is 68, denoted by blue-black arrows in Figure 5. When percolation appears in system, the 4 excited cells, by thick upward diagonal lines, with τ8 in  are also the mosaic cells of in the 4 neighboring
are also the mosaic cells of in the 4 neighboring  -clusters (Note: here the 4
-clusters (Note: here the 4  -clusters are respectively in the 4 neighboring 5-particle cooperative excited fields) with
-clusters are respectively in the 4 neighboring 5-particle cooperative excited fields) with 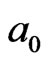 field. And 4 cells with
field. And 4 cells with 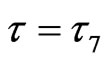 in the 4 neighboring
in the 4 neighboring  -clusters, by the color of blue green, are also the mosaic cells in
-clusters, by the color of blue green, are also the mosaic cells in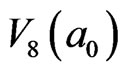 . (A region of space that can be identified by a single mean field solution is called a mosaic cell [10]. Mosaic cell is identified by the different action time in our work.) The 4 thick-black inverted arrows in Figure 5 are the mutual interfaces of
. (A region of space that can be identified by a single mean field solution is called a mosaic cell [10]. Mosaic cell is identified by the different action time in our work.) The 4 thick-black inverted arrows in Figure 5 are the mutual interfaces of 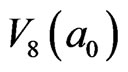 and its 4
and its 4 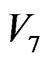 -clusters in neighboring 4 5-particle cooperative excited fields. Thus the number of interfaces of
-clusters in neighboring 4 5-particle cooperative excited fields. Thus the number of interfaces of 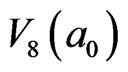 should be corrected as 60, that is,
should be corrected as 60, that is, 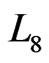 (corrected by percolation) = 60.
(corrected by percolation) = 60.
Note that there are 4 inverted thick-black arrows in the corrected 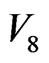 loop-flow in Figure 5. Thus, the number of excited particles in
loop-flow in Figure 5. Thus, the number of excited particles in 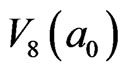 should be firstly corrected as 141 because the 4 mosaic cells of
should be firstly corrected as 141 because the 4 mosaic cells of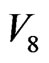 , marked by the color of blue green, belong to that of the
, marked by the color of blue green, belong to that of the 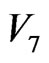 -clusters neighboring 5-particle cooperative excited fields. In addition, the central 5 empty cells, according with de Gennes’ simple picture of a localized “vacancy” among clusters [3], representing the 5 particles in
-clusters neighboring 5-particle cooperative excited fields. In addition, the central 5 empty cells, according with de Gennes’ simple picture of a localized “vacancy” among clusters [3], representing the 5 particles in 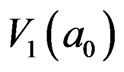 have first delocalized (indicates
have first delocalized (indicates 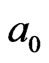 local coordinates invalidation partly!). Therefore, the number of cooperative excited particles in 8th order of cluster should finally be corrected as 136.
local coordinates invalidation partly!). Therefore, the number of cooperative excited particles in 8th order of cluster should finally be corrected as 136.
3. Results and Discussions
3.1. Average Energy of Cooperative Migration
In Figure 5, each (small square) chain-particle has a zaxial hopping energy 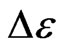 that comes from the non-integrable phase of parallel transport of its 4 IEs surround its z-axis. From (1), the energy of cooperative migration along z-direction in a domain is
that comes from the non-integrable phase of parallel transport of its 4 IEs surround its z-axis. From (1), the energy of cooperative migration along z-direction in a domain is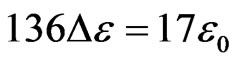 . As the migrating direction in different domain can be statistically selected as x-, y-, z-axial, and the appearing of all thawing domains is one by one and forming flow-percolation, the average energy of cooperative migration,
. As the migrating direction in different domain can be statistically selected as x-, y-, z-axial, and the appearing of all thawing domains is one by one and forming flow-percolation, the average energy of cooperative migration, ![]() , along one local space direction can be denoted by
, along one local space direction can be denoted by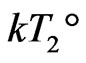 , the non-integrable random Brownian directional regression energy for excited particles inside 8th order of loop-flow.
, the non-integrable random Brownian directional regression energy for excited particles inside 8th order of loop-flow. 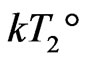 can be also balanced by the random thermal motion energy of
can be also balanced by the random thermal motion energy of 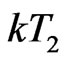 for general unexcited particles.
for general unexcited particles.
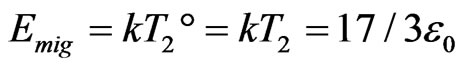 (2)
(2)
Here 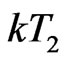 is similar to the energy of Curie temperature in magnetism, also the energy of a ‘critical temperature’ existing in the GT presumed by Gibbs based on thermodynamics years ago [11]. The denotation of
is similar to the energy of Curie temperature in magnetism, also the energy of a ‘critical temperature’ existing in the GT presumed by Gibbs based on thermodynamics years ago [11]. The denotation of  is the same as that of Gibbs. Emig along one direction, e.g., along the direction of external stress at GT, is an intrinsic attractive potential energy, independent of temperature and external stress and response time. This will be one of the key concepts directly prove the WLF equation. It stands to reason that the attractive potential comes of the IE loop-flows in Brownian motion existing in any random system at any temperature.
is the same as that of Gibbs. Emig along one direction, e.g., along the direction of external stress at GT, is an intrinsic attractive potential energy, independent of temperature and external stress and response time. This will be one of the key concepts directly prove the WLF equation. It stands to reason that the attractive potential comes of the IE loop-flows in Brownian motion existing in any random system at any temperature.
3.2. Fractal Dimension
The 8 orders of loop-flows in Figure 5 are the track records of selected IEs, from many dipole charge-electron pairs in fluctuation in 3D local space, respectively at the instant of![]() ,
,  ,
,![]() …
… discrete time on a reference
discrete time on a reference 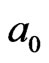 particle 2D projection plane. In other words, in 3D
particle 2D projection plane. In other words, in 3D 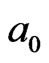 local space, the cyclic direction, selected from many random oriented IE loops, returns to the direction of ± z-axial at the instant of
local space, the cyclic direction, selected from many random oriented IE loops, returns to the direction of ± z-axial at the instant of 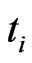 (i = 0, 1, 2, …8) time, which indicates that the distribution of IE loop in 3D local space obeys the distribution of the Graph of Brownian Motion [12]. Therefore, it can be directly obtain the Hausdorff fractal dimension
(i = 0, 1, 2, …8) time, which indicates that the distribution of IE loop in 3D local space obeys the distribution of the Graph of Brownian Motion [12]. Therefore, it can be directly obtain the Hausdorff fractal dimension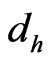 , or the Box fractal dimension dc of dipole charge electron coupling pairs at the GT is the fractal dimension df of Graph of Brownian Motion [12],
, or the Box fractal dimension dc of dipole charge electron coupling pairs at the GT is the fractal dimension df of Graph of Brownian Motion [12],
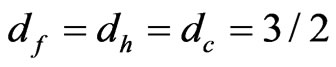 (3)
(3)
3.3. Eight-Order of Hard-Spheres and Chain Segments
We introduce the concept of i-th order of directional 3D hard-sphere (hard-cluster) for directional i-th order of 2D cluster in order to reflect the number of particles in an orienting and compacted cluster in density fluctuation when the maximum loop- occurs.
occurs.
a) Compacting cluster and density fluctuation. The first order of hard-sphere  contains 5 (the number of particles in
contains 5 (the number of particles in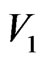 ) + 12 (the number of interfaces of
) + 12 (the number of interfaces of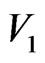 , each interface corresponds to an excited particle taking in any direction in 3D local space) = 17 chain-particles that are compacted to form a hard-sphere. Which has an internal density larger than average, because the IEs with extra volumes on
, each interface corresponds to an excited particle taking in any direction in 3D local space) = 17 chain-particles that are compacted to form a hard-sphere. Which has an internal density larger than average, because the IEs with extra volumes on  inside
inside  have been compacted and transferred to that on
have been compacted and transferred to that on 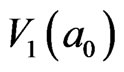 (static electricity screen effect of IE loop-flow).
(static electricity screen effect of IE loop-flow).
b) Hard-sphere with finite acting facets. Note that  is a vector. The direction of
is a vector. The direction of  is negative, as same as the direction of
is negative, as same as the direction of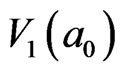 , if the direction of
, if the direction of 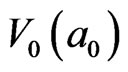 is positive. Finite acting facets surround this orienting 3D hard-sphere. The complexity of dynamical hard-sphere here comes down to the finite acting facets in mosaic structures.
is positive. Finite acting facets surround this orienting 3D hard-sphere. The complexity of dynamical hard-sphere here comes down to the finite acting facets in mosaic structures.
c) 8 orders of self-similar z-axial 3D hard-spheres. In the same way, the second order of hard-sphere  contains 13 (the number of particles in
contains 13 (the number of particles in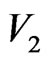 ) + 20 (the number of interfaces of
) + 20 (the number of interfaces of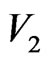 , the number of side-excited particles) = 33 excited particles. The direction of
, the number of side-excited particles) = 33 excited particles. The direction of  is positive. Therefore, the number,
is positive. Therefore, the number, 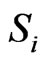 , of particles in i-th order of hard-sphere
, of particles in i-th order of hard-sphere 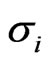 can be obtained as
can be obtained as
 (4)
(4)
In (4), the sign denotes the moving direction along z-axial of i-th order hard-sphere. By i-th order of hardsphere is meant that the interaction-interface energy of its two-body is the IE energy or transferred energy, 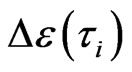 , independent of the distance of two excited cents of two-body in z-space.
, independent of the distance of two excited cents of two-body in z-space.
d) 8 orders of self-similar chain-segments. In Figure 5, each of 200 acting (excited) particles connects with a z-component chain-particle in a chain. Accordingly, in macromolecular system, the lengths of the 8 orders of zcomponent statistical chain-segments  (if chain-long N ³ 200) are also categorize as 8 orders
(if chain-long N ³ 200) are also categorize as 8 orders
 (5)
(5)
e) Number of structure rearrangements. The number of particles in the 8th order of hard-sphere, 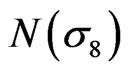 , or the 8th order of chain-segment sizes, l8, also is the number of particles
, or the 8th order of chain-segment sizes, l8, also is the number of particles  in structure rearrangement in
in structure rearrangement in 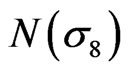 and
and , can be easily found out from Figure 5. The number of excited particles in corrected
, can be easily found out from Figure 5. The number of excited particles in corrected 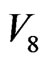 is 136. The number of interfaces of
is 136. The number of interfaces of  before percolation is 68, from which subtracts 4 mutual interfaces (that belong to 4 neighboring local fields) of
before percolation is 68, from which subtracts 4 mutual interfaces (that belong to 4 neighboring local fields) of 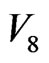 and its 4 neighboring
and its 4 neighboring 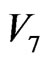 -clusters when percolation appears, and each of the 64 (= 68 - 4) interfaces respectively relates to a side-excited particle taking any direction. Thus, the number of acting particles in
-clusters when percolation appears, and each of the 64 (= 68 - 4) interfaces respectively relates to a side-excited particle taking any direction. Thus, the number of acting particles in 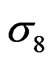 is 136 + 64 = 200, a magic number in mosaic nano-structure,
is 136 + 64 = 200, a magic number in mosaic nano-structure,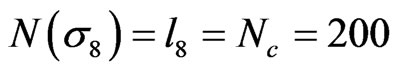 .
.
The numerical value is consistent with the conjectural results of encompassing rearrangements [13].  is also the critical entangled macromolecule length. The numerical value is in accordance with the experimentally determined critical entanglement chain length of ~ 200 [14].
is also the critical entangled macromolecule length. The numerical value is in accordance with the experimentally determined critical entanglement chain length of ~ 200 [14].
f) Evolution direction of cluster growth transition. From 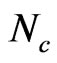 = 200,
= 200, 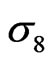 » 5.8 (chain-particle units), which is the size of ‘cage’ at GT. According to the definitions of 2D clusters and 3D hard-sphere, an interaction of two z-space i-th order of 3D hard-spheres is always equal to the IE interaction with
» 5.8 (chain-particle units), which is the size of ‘cage’ at GT. According to the definitions of 2D clusters and 3D hard-sphere, an interaction of two z-space i-th order of 3D hard-spheres is always equal to the IE interaction with![]() . This means that the cluster in [3] turns out to be i-th order of hard-sphere. During the time of (
. This means that the cluster in [3] turns out to be i-th order of hard-sphere. During the time of (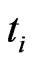 ,
,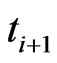 ), i-th order of 2D clusters cannot be welded together, as same as [3], however, at the instant time
), i-th order of 2D clusters cannot be welded together, as same as [3], however, at the instant time , all i-th order of 2D clusters in local field will be compacted together to form a compacted (i + 1)-th order of 2D cluster with the evolution direction of
, all i-th order of 2D clusters in local field will be compacted together to form a compacted (i + 1)-th order of 2D cluster with the evolution direction of 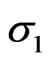 in inverse cascade.
in inverse cascade.
3.4. Localization-Delocalization (Percolation) Transition Energy, 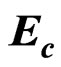
The steady excited energy is exactly the flow-percolation energy in percolation on a continuum of classical model in condensed matter physics. The energy of steadily ‘excited state energy flow’ in the process of 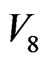 vanishing and reoccurring is defined as the localization-delocalizetion (percolation) transition energy, named as
vanishing and reoccurring is defined as the localization-delocalizetion (percolation) transition energy, named as 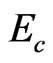 (the same denotation of
(the same denotation of 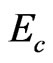 as Zallen [1] did) at GT. The 8 orders of mosaic structures directly manifest that the external DoF of an (inverse cascade) excited state energy flow is 1 and the (i - 1) order inner DoF of a (cascade) ith order cluster in renewed cluster state (rearrangement structures) is 5 at GT.
as Zallen [1] did) at GT. The 8 orders of mosaic structures directly manifest that the external DoF of an (inverse cascade) excited state energy flow is 1 and the (i - 1) order inner DoF of a (cascade) ith order cluster in renewed cluster state (rearrangement structures) is 5 at GT.
a) Macroscopic melt temperature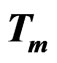 . It is a very important consequence that the external DoF of an energy flow is 5 in the melting state phase transition; and the renewed energy of a microscopic i-th order cluster (i < 8),
. It is a very important consequence that the external DoF of an energy flow is 5 in the melting state phase transition; and the renewed energy of a microscopic i-th order cluster (i < 8),  , being in renewed cluster within (i + 1)- th order cluster zone, is numerically equal to the energy of the macroscopic melting state of
, being in renewed cluster within (i + 1)- th order cluster zone, is numerically equal to the energy of the macroscopic melting state of . Namely,
. Namely, 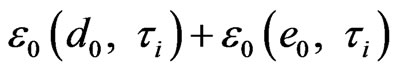
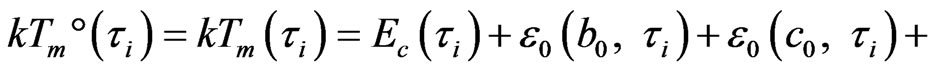 , i < 8, corresponds to 5 inner DoF, in which
, i < 8, corresponds to 5 inner DoF, in which , (10);
, (10); 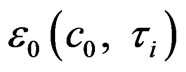 denotes the energy of one external DoF of i-th order loop-flow in
denotes the energy of one external DoF of i-th order loop-flow in 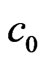 field. The energy of macroscopic melting state can be denoted as
field. The energy of macroscopic melting state can be denoted as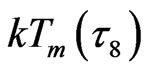 ,
,
 (for flexible system)
(for flexible system)
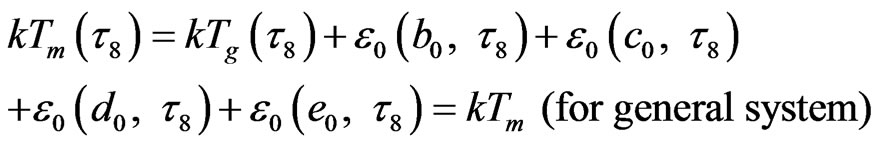 (6)
(6)
b) Percolation transition energy . The step (interface) number of
. The step (interface) number of  -loop is
-loop is  = 60.
= 60. , is less than 60
, is less than 60 because of the regression state energy effect of IE and the dynamical mosaic structures of IE loop-flows. The IE energies on
because of the regression state energy effect of IE and the dynamical mosaic structures of IE loop-flows. The IE energies on 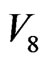 -loop in Figure 5 are shared by
-loop in Figure 5 are shared by 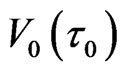 –
–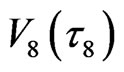 interfaces and
interfaces and  –
–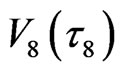 interfaces.
interfaces.
The key concepts are that a few of interfaces, named as Linver, on the 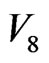 -loop will be excited by the interfaces with relaxation time of
-loop will be excited by the interfaces with relaxation time of 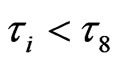 in new local fields after
in new local fields after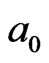 . This is the effect of mosaic structures, or, Linver is the step number of mosaic in slow inverse cascade. The others, named as Lcas, on the
. This is the effect of mosaic structures, or, Linver is the step number of mosaic in slow inverse cascade. The others, named as Lcas, on the 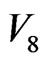 -loop will one by one vanish and their excited energy will rebuild many new
-loop will one by one vanish and their excited energy will rebuild many new  -interfaces in the new local fields in fast cascade.
-interfaces in the new local fields in fast cascade.
Thus, in the flow-percolation on a continuum, the 60 interfaces of a reference 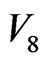 -loop in Figure 5 are dynamically divided into two parts: the Lcas interfaces that occur at the local time of
-loop in Figure 5 are dynamically divided into two parts: the Lcas interfaces that occur at the local time of  in
in  field and the Linver interfaces that are the mosaic structures of energy flow and occur at a time after
field and the Linver interfaces that are the mosaic structures of energy flow and occur at a time after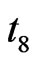 . Formula (7) is obtained
. Formula (7) is obtained
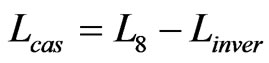 (7)
(7)
The energy of 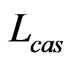 is also the fast-process cascade energy of rebuilding new
is also the fast-process cascade energy of rebuilding new 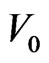 loop-flows when the Lcas interfaces vanish. The energy of Linver is the slow-process inverse cascade energy of all
loop-flows when the Lcas interfaces vanish. The energy of Linver is the slow-process inverse cascade energy of all 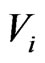 loop-flows from
loop-flows from  to
to 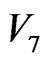 in new local fields.
in new local fields.
The balance excited energy of inverse cascade and cascade in flow-percolation (contained many local fields) is exactly the localized energy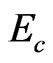 . Therefore, in fastprocess cascade,
. Therefore, in fastprocess cascade, 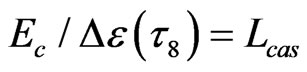 , in which
, in which 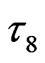 is used as timescale of
is used as timescale of 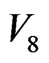 vanishing,
vanishing, 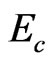 here is the cascade potential energy in flow-percolation.
here is the cascade potential energy in flow-percolation.
Since the excited energy in inverse cascade is not dissipated, the evolution energy of each order closed loop is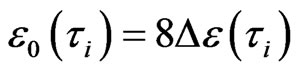 , (1), namely, the ‘singular point energy’ of any i-th order IE closed cycle (Gauss theorem).
, (1), namely, the ‘singular point energy’ of any i-th order IE closed cycle (Gauss theorem).
Each mosaic step (either the inverted arrow, or the shared interface by 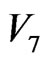 –
–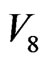 ) in Figure 5 connects a mosaic closed cycle
) in Figure 5 connects a mosaic closed cycle 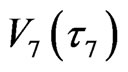 that does not belong to the reference a0 local field. Thus, in the slow-process inverse cascade from
that does not belong to the reference a0 local field. Thus, in the slow-process inverse cascade from 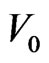 to
to  in flow-percolation, the number of the inverse cascade energy
in flow-percolation, the number of the inverse cascade energy  forming mosaic step is
forming mosaic step is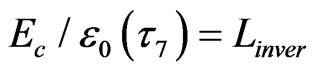 . For flexible polymer,
. For flexible polymer,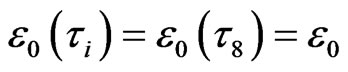 . Therefore, formula (8) is obtained
. Therefore, formula (8) is obtained
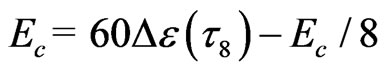 (8)
(8)
Or 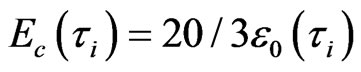 (9)
(9)
Equation 8 is a representative mean field formula. It can be seen that the physics meaning of the right term containing left term on equation is the contribution of mosaic structure. Equation 9 denotes that the delocalized energy 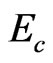 (the localized energy, the percolation transfer energy, the transfer energy from inverse cascade to cascade) at the GT has 8 components,
(the localized energy, the percolation transfer energy, the transfer energy from inverse cascade to cascade) at the GT has 8 components, 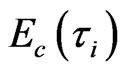 , i = 1, 2…8 and the numerical value of each component energy is the same, namely, 20/3
, i = 1, 2…8 and the numerical value of each component energy is the same, namely, 20/3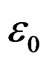 . This is also one of the singularities at GT.
. This is also one of the singularities at GT. 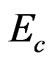 is a characteristic invariable with 8 order of relaxation times at the GT, independent of GT temperature
is a characteristic invariable with 8 order of relaxation times at the GT, independent of GT temperature .
.
c) Glass transition temperature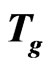 . We see
. We see  also comes from the directional non-integrable additional energy at GT, instead of general thermo-random motion energy of molecules. Similar to (2), z-axial non-integrable random regression vibration energy,
also comes from the directional non-integrable additional energy at GT, instead of general thermo-random motion energy of molecules. Similar to (2), z-axial non-integrable random regression vibration energy, 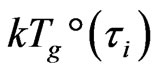 , of i-th order clusters with
, of i-th order clusters with ![]() can be used to denote the energy of
can be used to denote the energy of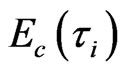 , and it can be also balanced by random thermal vibration (
, and it can be also balanced by random thermal vibration (![]() -scale) energy of
-scale) energy of 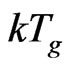 for general unexcited particles. That is
for general unexcited particles. That is
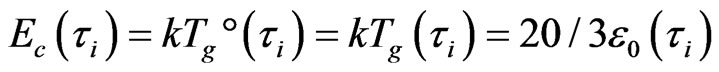 (10)
(10)
The numerical value of  that can be called the fixed point of clusters from small (
that can be called the fixed point of clusters from small (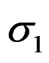 ,
,![]() scale) to large (
scale) to large ( ,
,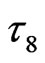 scale) in inverse cascade at GT, it is independent of GT temperature
scale) in inverse cascade at GT, it is independent of GT temperature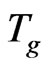 .
. 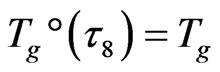 is traditionally accepted as GT temperature, which is obtained by slow heating rate. Therefore,
is traditionally accepted as GT temperature, which is obtained by slow heating rate. Therefore, 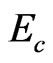 is a measurable by experiments. From (2), numerical relationship is:
is a measurable by experiments. From (2), numerical relationship is:
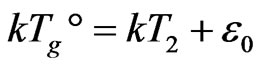 (11)
(11)
d) Geometric frustration and high-density percolation. It can be seen that Equation 9 is based on the result of corrected 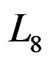 value and this correction from
value and this correction from  to
to  in Figure 5 also can be regard as the geometric frustration effect, which appearance corresponds to the GT [2,3,8] This also indicates that the percolation at GT belongs to the high-density percolation [1]. The filling factor of instantaneous polarized dipole
in Figure 5 also can be regard as the geometric frustration effect, which appearance corresponds to the GT [2,3,8] This also indicates that the percolation at GT belongs to the high-density percolation [1]. The filling factor of instantaneous polarized dipole 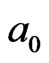 in Figure 1(d) is also 1.
in Figure 1(d) is also 1.
3.5. Activation Energy to Break Solid Lattice
Figure 5 has given out the number of all IE states at GT: the 320 different IE states. The numerical value is from
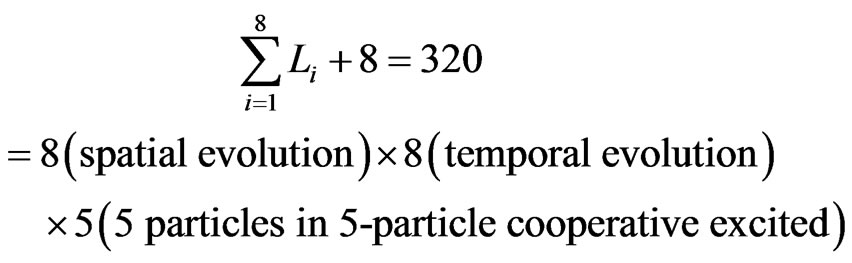 (12)
(12)
The 8 evolution IE states together with the 4 IEs on a reference particle a0 will evolve a new first order of IE loop-flow being of 12 IEs when 8th order cluster appears.
The energy summation of the 320 different IE states is named the cooperative orientation activation energy to break solid lattice, denoted as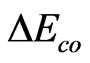 . The reason to call it activation energy is that although in microscopical, the energy to break solid lattice is seemly only
. The reason to call it activation energy is that although in microscopical, the energy to break solid lattice is seemly only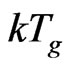 , <
, <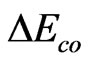 , in microcosmic, the energy of 320 IE space-time states in every solid domain is needed. Thus,
, in microcosmic, the energy of 320 IE space-time states in every solid domain is needed. Thus,
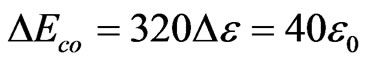 (13)
(13)
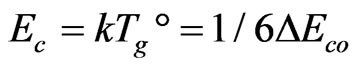 (14)
(14)
Using  , thus,
, thus,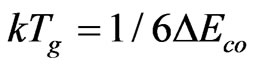 (15)
(15)
 can be measured on melt high-speed spinningline. In fact, the author [4] had obtained the experimental data of
can be measured on melt high-speed spinningline. In fact, the author [4] had obtained the experimental data of 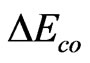 for polyethylene terephthalate (PET) by using the on-line measuring on the stretch orientation zone during melt high-speed spinning. The experimental result shows
for polyethylene terephthalate (PET) by using the on-line measuring on the stretch orientation zone during melt high-speed spinning. The experimental result shows 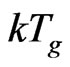 (for PET) » 1/6
(for PET) » 1/6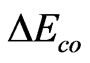 (for PET), and
(for PET), and . Thus, for PET, the extra IE energy
. Thus, for PET, the extra IE energy 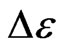
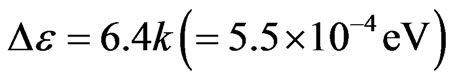 (16)
(16)
Moreover,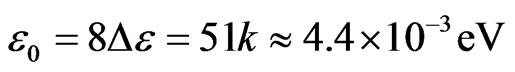 .
.
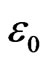 is the energy of one DoF of
is the energy of one DoF of  -loop. This value is consistent with the experimental results (4 ~ 12 x 10-3 eV) for Boson peak measured by high-resolution inelastic neutron scattering [12].
-loop. This value is consistent with the experimental results (4 ~ 12 x 10-3 eV) for Boson peak measured by high-resolution inelastic neutron scattering [12].
3.6. Free Volume
The classical free volume ideas have been questioned because of the misfits with pressure effects, but here the pressure effects should be indeed minor [2]. It is interesting in our model that there is no so-called classical free volume with an atom (molecule) migrating in system. Except the 8th order of 2D clusters, in the i-th order of clusters, all (i - 1)-th order of 2D clusters are compacted to form i-th order clusters, and the extra volumes of the IEs of all (i - 1)-th order clusters vanish and reappear on the interfaces of i-th order. Thus, when the central 8th order loop appears and vanish in cascade, the extra vacancy volumes of the IEs on the loop suddenly form vacancy volumes of 5 cavity sites in the center of the loop, in Figure 5, in order to induce the first order of cluster delocalization. The definition of free volume is modified by the cooperatively appearing 5 cavities, i.e., using clusters rather than atoms, same as that proposed by de Gennes [2]. The modified free volume idea is still true, because the action of pressure should be only through the same percolation field generating cavity volume; and the extra volume energy in the 8 orders of loop-flows in Figure 5 should be balanced with the external pressure or tension. Each cavity is also an orientation vector as same as the direction of excited domain. Since all excited domains are in random orienting at GT, 5 statistically isotropic 3D cavities (so-called classical free volume) thus are obtained by per 200 statistically isotropic 3D particles. In other words, the free volume fraction: 5/200 = 0.025 can be directly and explicitly obtained, which is in accordance with the experimental results for flexible polymer.
 (a)
(a)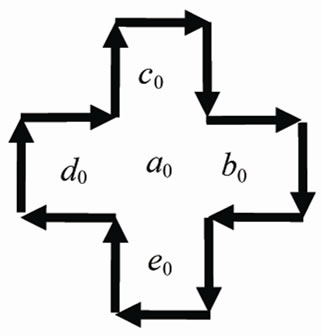 (b)
(b)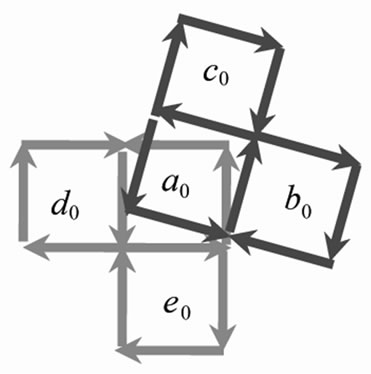 (c)
(c)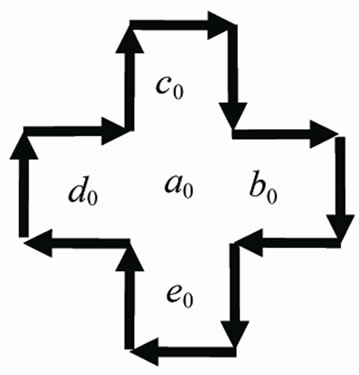 (d)
(d)
Figure 6. The soft matrix of self-similar 2body-3body cluster coupling.
3.7. Mode-Coupling and Icosahedral Directional Ordering
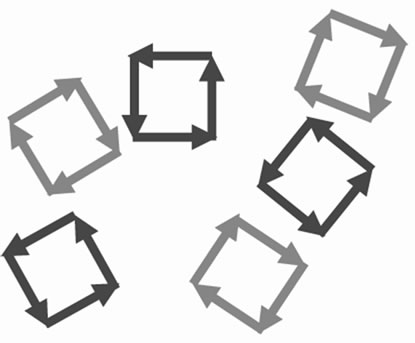
In the inverse cascade at GT, if each IE appears in the way of one arrow after another according to the appearance probability as mentioned in Figures 2-5, the probability is rather low. In fact, the more probable situation is the evolutive mode of self-similar 2body-3body cluster coupling in the soft matrix of IE loop-flows in Figure 6.
In Figure 6, the i-th order of IE loop-flows can be simply denoted as some squares with IE 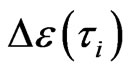 in (a), each of which is self-similar with Figure 1(d). Figure 6(a) first evolves into three 2-body interaction in (b), then into two three-body interactions in (c), named as i-th order of 2body-3body cluster coupling in 5-particle cooperative excited field. Finally into (i + 1)-th order of IE loop-flow in (d) and cooperatively eliminate IEs inside the loop-flow (static screen effect) in order to form 8 order 2D IE loop-flows and clusters slightly more compact than the matrix.
in (a), each of which is self-similar with Figure 1(d). Figure 6(a) first evolves into three 2-body interaction in (b), then into two three-body interactions in (c), named as i-th order of 2body-3body cluster coupling in 5-particle cooperative excited field. Finally into (i + 1)-th order of IE loop-flow in (d) and cooperatively eliminate IEs inside the loop-flow (static screen effect) in order to form 8 order 2D IE loop-flows and clusters slightly more compact than the matrix.
The mode of 2body-3body cluster coupling is in statistically advantage (soft matter concept): e.g., per 4 IEs needs 5 instantaneous polarized ions in Figures 1(d) and 6(a). The parameter of polarized ion numberdensity of per IE (the density of particles occupy additional vacancy volume in IEs) in soft matrix, 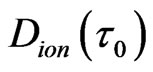 = 5/4 = 1.25. However, 21 IEs needs 24 polarized ions, the ion number-density
= 5/4 = 1.25. However, 21 IEs needs 24 polarized ions, the ion number-density 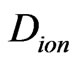 = 24/21 » 1.14 in Figure 6(b), large than
= 24/21 » 1.14 in Figure 6(b), large than 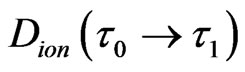 = 22/20 = 1.1 in Figure 6(c), each evolutive 3body cluster only needs the excitation energy of 10 IEs. In Figure 6(c), the two clusters (two 3body clusters excited at different times need 20 IEs) move randomly and they are not in superposition. Once they are in superposition, Figure 6(c) immediately mutates into Figure 6(d) to form first order of uncompacted cluster,
= 22/20 = 1.1 in Figure 6(c), each evolutive 3body cluster only needs the excitation energy of 10 IEs. In Figure 6(c), the two clusters (two 3body clusters excited at different times need 20 IEs) move randomly and they are not in superposition. Once they are in superposition, Figure 6(c) immediately mutates into Figure 6(d) to form first order of uncompacted cluster, 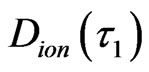 = 17/16 » 1.06 in Figure 6(d). Finally, the IEs inside the loop-flow disappear to form hard-cluster. The parameter
= 17/16 » 1.06 in Figure 6(d). Finally, the IEs inside the loop-flow disappear to form hard-cluster. The parameter 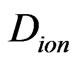 will be less and less in inverse cascade with cluster augment.
will be less and less in inverse cascade with cluster augment.
The minimum value of the polarized ion number density 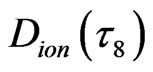 = 200/320 = 5/8, in 8th order 2D cluster in Figure 5, which indicates the single-ion polarization is slow process formed IE closed loop, Figure 1(d), corresponding the maximum static electricity repulsive state in polarized field. In addition, there are 60 + z-axial hopping ions and 60 - z-axial hopping ions in 136 z-axial excited particles in Figure 5. The 120 ions form 60 pairs of antiparallel ion-pairs. So, the polarized ion pair number density in IE soft matrix,
= 200/320 = 5/8, in 8th order 2D cluster in Figure 5, which indicates the single-ion polarization is slow process formed IE closed loop, Figure 1(d), corresponding the maximum static electricity repulsive state in polarized field. In addition, there are 60 + z-axial hopping ions and 60 - z-axial hopping ions in 136 z-axial excited particles in Figure 5. The 120 ions form 60 pairs of antiparallel ion-pairs. So, the polarized ion pair number density in IE soft matrix, 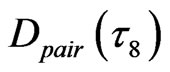 = 120/320 = 3/8, which indicates the polarization of a pair of ion is fast process, Figure 1(b) in IE. It is an important relation equation has been fined that
= 120/320 = 3/8, which indicates the polarization of a pair of ion is fast process, Figure 1(b) in IE. It is an important relation equation has been fined that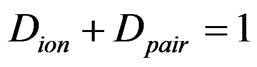 . This implicates the polarized structure of classical boson peak in local polarized filed. Especially, the number of 60 pairs of antiparallel ions inside 8th order loop-flow equals the number of the 60 pairs of synchronal polarized electron charges on the loop-flow. Therefore, z-axial slower randomly non-integrable kinetic energy of antiparallel ionpairs inside 8-th order loop-flow also balances the faster induced potential energy on the IE loop-flow, which is a kind of mode-coupling scheme between the fast-motion induced charge-electron coupling pairs and the slow-motion delocalized ion pairs.
. This implicates the polarized structure of classical boson peak in local polarized filed. Especially, the number of 60 pairs of antiparallel ions inside 8th order loop-flow equals the number of the 60 pairs of synchronal polarized electron charges on the loop-flow. Therefore, z-axial slower randomly non-integrable kinetic energy of antiparallel ionpairs inside 8-th order loop-flow also balances the faster induced potential energy on the IE loop-flow, which is a kind of mode-coupling scheme between the fast-motion induced charge-electron coupling pairs and the slow-motion delocalized ion pairs.
Moreover, there is still 16 (= 136 - 120) + z-axial remainder ions inside the 8-th order of loop-flow, which can offer a static charge repulsive force to facilitate the first excited + z-axial ion a0 delocalization in Figure 5. Since the 16 + z-axial ions to drive ion a0 to leave its coordinates needs 320 IEs, 16/320 = 1/20, this leads to each directional delocalization uncompacted particle needs 20 z-directional excited interfaces with  in its 8-th order of loop-flow. On the other hand, disappearing the 8-th order of loop-flow of reference a0 particle also needs its 4 concomitant excited particle,
in its 8-th order of loop-flow. On the other hand, disappearing the 8-th order of loop-flow of reference a0 particle also needs its 4 concomitant excited particle, 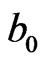 ,
, 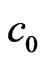 ,
, 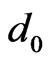 , and
, and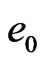 , one by one finish respective 8th order of loopflows in inverse cascade and delocalize along z-axial. This leads to 5 compacted conformational rearrangement particles in cascade precisely need 20 z-directional excited interfaces disappearing with
, one by one finish respective 8th order of loopflows in inverse cascade and delocalize along z-axial. This leads to 5 compacted conformational rearrangement particles in cascade precisely need 20 z-directional excited interfaces disappearing with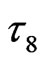 . That is another explanation for icosahedral directional ordering at the GT.
. That is another explanation for icosahedral directional ordering at the GT.
Distinctly, the mode-coupling scheme based on mosaic geometric structure adopted in this paper is different from the mathematical expressions in the current modecoupling theory of GT. However, the spirit in both modecoupling schemes is the same that deals with the coupling of fast-slow relaxation modes and two density modes in structure rearrangements at the GT. In our scheme, we focus on finding out the three direction nonintegrable energies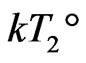 ,
, 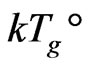 and
and 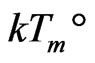 existing in the coordinate invalidation from i-th order clusters to (i + 1)-th order in solid-to-liquid transition, whatever the time complications of anharmonic frequencies may be. The mode-coupling trick is that the relaxation time complications have been beforehand reduced and replaced by the long time Brownian directional regressions with the 2p closed loop-flows of IEs in Figure 5.
existing in the coordinate invalidation from i-th order clusters to (i + 1)-th order in solid-to-liquid transition, whatever the time complications of anharmonic frequencies may be. The mode-coupling trick is that the relaxation time complications have been beforehand reduced and replaced by the long time Brownian directional regressions with the 2p closed loop-flows of IEs in Figure 5.
4. Conclusions
It is proposed that the soft matrix surrounding clusters is 2D soft nano-scale 8 orders of IE loop-flows; the filling factor of 2D lattices is 1. The key of the theory is that the random thermo-motion kinetic energy, from glass transition to melt transition, should be balanced by the nonintegrable random regression vibration energy in random systems. That is, entire molecule-cluster delocalization energy (also the GT energy) origins form the maximum order potential energy in random systems. This 2D structure corresponds to the appearance of boson peak and geometric frustration at the GT, and can directly deduce three non-integrable directional energies: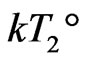 ,
, 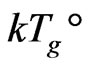 , and
, and 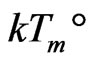 along one local space direction, respectively corresponding to Gibbs temperature
along one local space direction, respectively corresponding to Gibbs temperature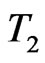 , glass transition temperature
, glass transition temperature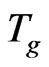 , and melt transition temperature
, and melt transition temperature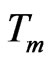 .
.
5. Acknowledgements
The author is grateful to all colleagues he had the pleasure to collaborate and interact, especially when he found the fundamental physics origin for the orientation activation energy obtained experimentally on melt high-speed spinning-line. In particular, the author would like to thank, in random order, Yuan Tseh Lee and Sheng Hsien Lin of Academia Sinica (Taiwan), Yun Huang of Beijing University, Da-Cheng Wu of Sichuan University for useful discussions.
REFERENCES
- R. Zallen, “The Physics of Amorphous Solids,” Wiley Interscience, New York, 1983. doi:10.1002/3527602798
- C. Alba-Simionesco, J.-L., Barrat, L. Berthier, G. Biroli, J.-P. Bouchaud, L. Cipelletti, F. Corberi, L. Cugloandolo, et al., “Dynamical Heterogeneities in Glasses, Colloids and Granular Materials,” In: L. Berthier, G. Biroli, J.-P. Bouchaud, L. Cipelletti and W. van Saarloos, Eds., Oxford University Press, Oxford, 2011, Chapter 1-12. http://www.physics.emory.edu/~weeks/ lab/pubs.html
- P. G. de Genne, “A Simple Picture for Structural Glasses,” Comptes Rendus Physique, Vol. 3, No. 9, 2002, pp. 1263- 1268. doi:10.1016/S1631-0705(02)01387-7
- J.-l. WU, D. Guan and B. Quian, “The Characteristic Behaviour of the Stretch-Orientation Zone during HighSpeed PET Spinning,” International Polymer Processing, Vol. 1, No. 1, 1986, pp. 25-31.
- M. V. Berry, “Foreword to ‘Global Properties of Simple Quantum Systems—Berry’s Phase and Others’,” In: H. Z. Li, Ed., Shanghai Scientific and Technical, Shanghai, 1998. http://www.phy.bris.ac.uk/peple/berry_mv/the_papers/berry 347.pdf
- Physics Survey Committal, “Physics through the 1990s, Condensed-Matter Physics,” National Academy, Washington, 1986, p. 56.
- V. Lubchenko and P. G. Wolynes, “Origin of the Boson Peak and Thermal Conductivity Plateau in Low Temperature Glasses,” P N AN (USA), Vol. 100, No. 4, 2003, pp. 1515-1518. doi:10.1016/S1631-0705(02)01387-7
- G. N. Greaves, F. Meneau, O. Majérus, D. G. Jones and J. Taylor, “Identifying Vibrations That Destabilize Crystals and Characterize the Glassy State,” Science, Vol. 308, No. 5726, 2005, pp. 1299-1302. doi:10.1126/science.1109411
- G. Tarjus, “An Overview of the Theories of the Glass Transition,” Oxford University Press, Oxford, 2010.
- V. Lubchenko and P. G. Wolynes, “Barrier Softening Near the Onset of Nonactivated Transport in Supercooled Liquids: Implications for Establishing Detailed Connection between Thermodynamic and Kinetic Anomalies in Supercooled Liquids,” Journal of Chemical Physics, Vol. 119, No. 17, 2003, pp. 9088-9105. doi:10.1063/1.1614180
- J. Jackle, “Models of the Glass Transition,” Reports on Progress in Physics, Vol. 49, No. 2, 1986, pp. 171-231. doi:10.1088/0034-4885/49/2/002
- K. J. Falconer, “Fractal Geometry-Mathematical Foundations and Applications,” 2nd Edition, John Wiley and Sons, New York, 2003. doi:10.1002/0470013850
- V. Lubchenko and P. G. Wolynes, “The Intrinsic Quantum Excitations of Low Temperature Glasses,” Physical Review Letters, Vol. 87, No. 19, 2001. doi:10.1103/PhysRevLett.87.195901
- S. Pahl, G. Fleischer, F. Fujara and B. Geil, “Anomalous Segment Diffusion in Polydimethylsiloxane Melts,” Macromolecules, Vol. 30, No. 5, 1997, pp. 1414-1418.

