International Journal of Astronomy and Astrophysics
Vol.06 No.01(2016), Article ID:65115,6 pages
10.4236/ijaa.2016.61007
Einstein Rosen Mesonic Perfect Fluid Cosmological Model with Time Dependent Λ-Term
Vijay G. Mete, Vijay D. Elkar
Department of Mathematics, R. D. I. K. & K. D. College, Badnera-Amravati, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 October 2015; accepted 25 March 2016; published 29 March 2016
ABSTRACT
Mesonic perfect fluid solutions are found in general relativity with the aid of Einstein’s Rosen cylindrically symmetric space time. A static vacuum model and a non-static cosmological model corresponding to perfect fluid are investigated. The cosmological term Λ is found to be a decreasing function of time which is supported by the result found from recent type Ia Supernovae observations. The various physical and geometrical features of the model are discussed.
Keywords:
General Relativity, Perfect Fluid, Time-Dependent Term Λ

1. Introduction
Theory of general relativity (Einstein 1916) has served as basis for the study of cosmological models of universe. The cosmological term Λ has been introduced in 1917 by Einstein to modify his own equation of general relativity. Now this Λ-term remains a focal point of interest in modern theories. In 1930s distinguished cosmologists, A. S. Eddington and Abbey Georges Lemaitre felt that introduction of Λ-term has attractive features in cosmology and models, so it should be discussed deeply. Moreover models with cosmological time-dependent term-Λ are becoming popular as they help to solve the cosmological constant problem in natural way. The generalized Einstein’s theory of gravitation with time-dependent G and Λ has been proposed by Lau [1] . The possibility of variable G and Λ in Einstein’s theory has also been studied by Dersarkissian [2] .
To study the nature of scalar field without mass parameters interacting with perfect fluid in Einstein’s Rosen space time is a subject of interest due to its significant role in the description of the universe at the early stages of evolution. Patel [3] obtained the static and nonstatic plane symmetric solutions of the field equations in presence of zero mass scalar field. Singh and Deo [4] considered Robertson-Walker metric and investigated the problem of zero mass scalar field.
Recently many authors like Tsagas and Maartens [5] , Sahni and Starboinsky [6] , Peeble [7] , Padmanabhan [8] , Vishwakarma [9] - [14] , Pradhan et al. [15] [16] , Sahu and Panigrahi [17] , Sahu and Mohapatra [18] motivate us to study the cosmological models involved with Λ-term. Mohanty et al. [19] obtained a class of exact solutions of Einstein’s field equations with attractive massive scalar field in LRS Bianchi type-I space time. Mohanty and Mishra [20] have studied the feasibility of Bianchi type-VIII and IX space time with a time-dependent gauge function and a matter field in the term of perfect fluid. Mishra [21] has constructed the non-static plane symmetric Zeldovich fluid model with a time-dependent gauge function.
Very recently Adhav et al. [22] have studied cylindrically symmetric Einstein Rosen cosmological model with wet dark fluid (WDF) in general relativity. Katore et al. [23] have investigated cylindrically symmetric Einstein Rosen space time with bulk viscosity and zero mass scalar field in Lyra geometry. Bivudutta Mishra et al. [24] have studied the perfect fluid distribution in the scale invariant theory of gravitation. Katore et al. [25] have investigated Einstein Rosen inflationary universe in presence of massless scalar field with flat potential.
In this paper we consider the cylindrically symmetric space time in mesonic perfect fluid with time-dependent Λ-term in general theory of relativity. A static vacuum model and a non-static cosmological model are presented and studied in detail.
2. The Metric and Field Equation
We consider the nonstatic cylindrically symmetric Einstein Rosen metric
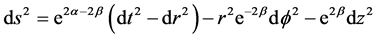 (1)
(1)
where 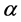 and
and 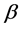 are both the functions of r and t only.
are both the functions of r and t only.
We denote the coordinates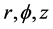 , and t as
, and t as 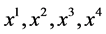 respectively.
respectively.
The Einstein’s field equations with the cosmological term 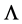 are given by
are given by
 (2)
(2)
where
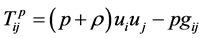 (3)
(3)
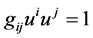 (4)
(4)
and
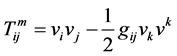 (5)
(5)
are respectively the energy momentum tensors for the perfect fluid and massless scalar field. The massless scalar field satisfies the Klein-Gordan wave equation
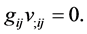 (6)
(6)
Here 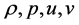 and Λ are respectively the energy density, pressure, four velocity vector of the fluid, scalar
and Λ are respectively the energy density, pressure, four velocity vector of the fluid, scalar
mesonic field and cosmological constant. Hereafter the semicolon (;) denotes covariant differentiation.
Using commoving coordinate system, the set of field Equation (2) for the metric (1) reduces to the following forms
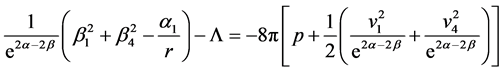 (7)
(7)
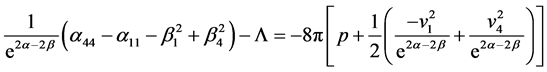 (8)
(8)
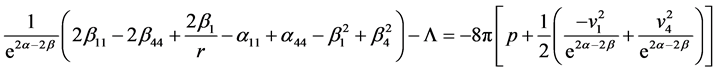 (9)
(9)

and

The Klein-Gordon Equation (6) for the metric (1) yields

Equations (7)-(12) are highly nonlinear partial differential equations and hence it is very difficult to solve them, as there exists no standard method to derive their solution.
Here we consider two particular physical important cases:
1) static vacuum model and 2) non-static cosmological model.
Further to avoid the mathematical complexities, we consider scalar field 
2.1. Static Vacuum Model
In this case we consider 

Therefore, in this case the field Equations (7)-(12) reduces the following set of equations




The solutions of the field equations are given by

where 
After a suitable choice of coordinates, Einstein-Rosen cylindrically symmetric metric (1) can be written as

2.2. Non-Static Cosmological Model
Here we consider 





and

The exact solution of this equation is given by

where 
Now using the equation of state

we obtain the physical quantities

and

where 
After a suitable choice of coordinates and constants, Einstein-Rosen cylindrically symmetric metric (1) becomes

2.3. Physical Model
Here we discuss three models corresponding to
Case-I: When 
From Equation (26), we obtain

Therefore in this case the energy density and cosmological constant takes the form


Case-II: When
In this case the energy density and cosmological constant are equal i.e. 
From Equation (26), we obtain


Case-III: When
In this case from Equation (26), we obtain the energy density and cosmological constant in the form


From Equations (32) and (36) we observe that the cosmological constant term Λ is a decreasing function of time whereas 
3. Some Physical and Kinematical Properties
Here we study Physical and Kinematical properties of the cosmological model given by Equation (29). For the model (29) the expressions for the spatial volume V, scalar expansion





The spatial volume v tend to zero as T tends to


4. Conclusion
We have studied Einstein Rosen cylindrically symmetric static vacuum model and non-static cosmological model with mesonic perfect fluid with time-dependent cosmological constant term Λ in general relativity. We
have discussed three physical models corresponding to values of γ, i.e.
cosmological model is nonsingular; contracting and deceleration parameter indicates inflation. The time-de- pendent cosmological term Λ is decreasing function of time and it approaches to small positive value at late time.
Acknowledgements
V. D. Elkar is thankful to the University Grants Commission, New Delhi, India for providing fellowship under F.I.P.
Cite this paper
Vijay G. Mete,Vijay D. Elkar, (2016) Einstein Rosen Mesonic Perfect Fluid Cosmological Model with Time Dependent Λ-Term. International Journal of Astronomy and Astrophysics,06,99-104. doi: 10.4236/ijaa.2016.61007
References
- 1. Lau, Y.K. (1985) The Large Number Hypothesis and Einstein’s Theory of Gravitation. Australian Journal of Physics, 38, 547-553.
http://dx.doi.org/10.1071/PH850547 - 2. Dersarkissian, M. (1985) The Cosmological Constant (Λ) as a Possible Primordial Link to Einstein’s Theory of Gravity, the Properties of Hadronic Matter and the Problem of Creation. II Nuovo Cimento B (1971-1996), 88, 29-42.
http://dx.doi.org/10.1007/BF02729027 - 3. Patel, L.K. (1975) Plane-Symmetric Solution of Einstein’s Field Equations. Tensor, 29, 237.
- 4. Singh, R.T. and Deo, S. (1986) Zero Mass Scalar Field Interactions in the Robertson-Walker Universe. Acta Physica Hungarica, 59, 321-325.
- 5. Tsagas, C.G. and Maartens, R. (2000) Cosmological Perturbations on a Magnetized Bianchi I Background. Classical and Quantum Gravity, 17, 2215-2242
http://dx.doi.org/10.1088/0264-9381/17/11/305 - 6. Sahni, V. and Starobinsky, A. (2000) The Case for a Positive Cosmological Λ-Term. International Journal of Modern Physics D, 9, 373-443.
http://dx.doi.org/10.1142/S0218271800000542 - 7. Ratra, B. and Peebles, P.J.E. (2003) The Cosmological Constant and Dark Energy. Reviews of Modern Physics, 75, 559-606.
http://dx.doi.org/10.1103/RevModPhys.75.559 - 8. Padmanabhan, T. (2003) Cosmological Constant—The Weight of the Vacuum. Physics Reports, 380, 235-320.
http://dx.doi.org/10.1016/S0370-1573(03)00120-0 - 9. Vishwakarma, R.G., Abdussattar and Beesham, A. (1999) LRS Bianchi Type-I Models with a Time-Dependent Cosmological “Constant”. Physical Review D, 60, Article ID: 063507.
http://dx.doi.org/10.1103/PhysRevD.60.063507 - 10. Vishwakarma, R.G. (2000) A Study of Angular Size Redshift Relation for Models in Which Lambda Decays as the Energy Density. Classical and Quantum Gravity, 17, 3833-3842.
- 11. Vishwakarma, R.G. (2001) Consequences on Variable Lambda Models from Distant Type Ia Supernovae and Compact Radio Sources. Classical and Quantum Gravity, 18, 1159-1172.
http://dx.doi.org/10.1088/0264-9381/18/7/301 - 12. Vishwakarma, R.G. (2001) Study of the Magnitude Redshift-Relation for Type Ia Supernovae in a Model Resulting from a Ricci-Symmetry. General Relativity and Gravitation, 33, 1973-1984.
http://dx.doi.org/10.1023/A:1013051026760 - 13. Vishwakarma, R.G. (2002) Consequences on Some Dark Energy Candidates from SN 1997ff. Monthly Notices of the Royal Astronomical Society, 331, 776-784.
http://dx.doi.org/10.1046/j.1365-8711.2002.05253.x - 14. Vishwakarma, R.G. (2002) A Machian Model of Dark Energy. Classical and Quantum Gravity, 19, 4747-4752.
http://dx.doi.org/10.1088/0264-9381/19/18/309 - 15. Pradhan, A. and Pandey, P. (2005) Plane-Symmetric Inhomogeneous Magnetized Viscous Fluid Universe with a Variable Lambda. Czechoslovak Journal of Physics, 55, 749-764.
http://dx.doi.org/10.1007/s10582-005-0077-z - 16. Pradhan, A., Khadekar, G.S. and Molaei, M.R. (2006) Higher Dimensional Dust Cosmological Implications of a Decay Law for a Lamda Term: Expression for Some Observable Quantities. International Journal of Modern Physics D, 15, 95-105.
http://dx.doi.org/10.1142/S0218271806007638 - 17. Sahu, R.C. and Panigrahi, U.K. (2003) Bianchi Type-I Vacuum Models in Modified Theory of General Relativity. Astrophysics and Space Science, 288, 499-508.
http://dx.doi.org/10.1023/b:astr.0000005123.68634.b8 - 18. Sahu, R.C. and Mohapatra, L.K. (2009) Plane Symmetric Inhomogeneous Cosmological Perfect Fluid Models Boundary. Bulletin of Calcutta Mathematical Society, 101, 497-502.
- 19. Mohanty, G., Sahu, S.K. and Sahoo, P.K. (2004) Mesonic Stiff Fluid Distribution in Bianchi Type Space-Times. Communications in Physics, 14, 84-89.
- 20. Mohanty, G. and Mishra, B. (2003) Scale Invariant Theory for Bianchi Type VIII and IX Space-Times with Perfect Fluid. Astrophysics and Space Science, 283, 67-74.
http://dx.doi.org/10.1023/A:1021272819809 - 21. Mishra, B. (2004) Non-Static Plane Symmetric Zeldovich Fluid Model in Scale Invariant Theory. Chinese Physics Letters, 21, 2359-2361.
http://dx.doi.org/10.1088/0256-307X/21/12/011 - 22. Adhav, K.S., Mete, V.G., Thakare, R.S. and Pund, A.M. (2011) Einstein-Rosen Universe with Wet Dark Fluid in General Relativity. International Journal of Theoretical Physics, 50, 164-170.
http://dx.doi.org/10.1007/s10773-010-0504-1 - 23. Katore, S.D., Shaik, A.Y., Sancheti, M.M. and Pawade, I.D. (2012) Einstein-Rosen Bulk Viscous Cosmological Solution with Zero Mass Scalar Field in Lyra Geometry. Prespacetime Journal, 3, 83-89.
- 24. Mishra, B., Sahu, P.K. and Ramu, A. (2010) Scale Invariant Theory of Gravitation in Einstein-Rosen Space-Time. Journal of Modern Physics, 1, 185-189.
http://dx.doi.org/10.4236/jmp.2010.13027 - 25. Katore, S.D., Rane, R.S., Wannkhade, K.S. and Sarkate, N.K. (2010) Einstein-Rosen Inflationary Universe in General Relativity. Pramana, 74, 669-673.
http://dx.doi.org/10.1007/s12043-010-0059-y




