Received 31 July 2015; accepted 25 December 2015; published 30 December 2015

ABSTRACT

Bianchi type-IX cosmological models with variable equation of state (EoS) parameter have been investigated in general relativity when universe is filled with dark energy. The field equations have been solved by considering (i) 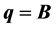(variable); (ii)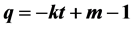, where k and m are constants; (iii)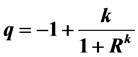, where k is constant and R is average scale factor; (iv) 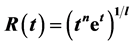which gives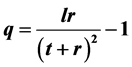. This renders early decelerating and late time accelerating cosmological models. The physical and geometrical properties of the models are also discussed.

Keywords:

Dark Energy, Deceleration Parameter, Bianchi Type-IX Space Time

1. Introduction

Most remarkable observational discoveries in cosmology prevail that the universe is undergoing an accelerated expansion. Analysis of type-Ia supernovae (SN Iae) [1] -[5] observations of anisotropies in the Cosmic Microwave Background Radiations (CMBR) [6] [7] and large scale structure (LSS) [8] has confirmed the accelerated expansion of the universe which is driven by an exotic energy with large negative pressure known as dark energy (DE). It is believed that the universe consists of 76% DE, 20% dark matter and 4% baryon matter. Usually

DE is characterized by the equation of state (EoS) parameter defined by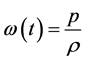, where p is the fluid pressure and is the energy density. The simplest DE candidate is the vacuum energy 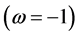which is mathematically equivalent to the cosmological constant. When EoS, it is called quintessence [9] and when, it is phantom [10] . There are some other DE models which can cross the phantom divide both sides are called quintom. Some other limits obtained from observational results coming from SN-Ia data [11] , CMBR anisotropy collaborated with SN-Ia data and galaxy clustering statistics [12] are 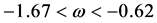and respectively. However, it is not at all obligatory to use a constant value of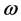. Due to lack of observational evidence in making a distinction between constant and variable, usually the EoS parameter is considered as a constant [13] [14] with phase wise values −1, 0, 1/3 and +1 for vacuum fluid, dust fluid, radiation and stiff fluid dominated universe respectively. But in general is a function of time or redshift [15] - [17] . Chaplygin gas as well as generalized Chaplygin gas also has been considered as possible DE sources due to negative pressure [18] - [22] . Many relativists [23] - [28] have studied anisotropic DE cosmological models with different contexts.

The studies of Bianchi type models are important in achieving better understanding of anisotropy in the universe. Moreover, the anisotropic universes have greater generality than FRW isotropic models. The simplicity of the field equations made Bianchi type space-times useful. Bianchi type I-IX cosmological models are homogeneous and anisotropic. Bianchi type-IX universe is studied by a number of cosmologists because of familiar solutions like Robertson-Walker Universes, the de-sitter universe, the Taub-Nut solutions, etc. Reddy and Naidu [29] have obtained Bianchi type-IX string cosmological model in scalar tensor theory of gravitation. Adhav et al. [30] have studied axially symmetric Bianchi type-IX inflationary universe in general relativity. Bagora, Purohit and Bagora [31] [32] have investigated Bianchi type-IX dust fluid and magnetized stiff fluid cosmological models in general relativity. Many relativists [33] - [43] have investigated certain properties of Bianchi type-IX space- times. Recently Ghate and Sontakke [44] [45] have studied Bianchi type-IX cosmological models with different contexts.

To study cosmological models one of the important observational quantities is the deceleration parameter q. In any cosmological model, the Hubble constant and deceleration parameter q play an important role in describing the nature of evolution of the universe. The former one tells us the expansion rate of the universe today while the latter one characterizes the accelerating or decelerating nature of the universe. A number of relativists assume various physical or mathematical conditions to obtain exact solution of the Einstein’s field equations. Berman [46] proposed a special law of variation for Hubble’s parameter to obtain the

cosmological solutions called the models with Constant Deceleration Parameter (CDP) by assuming. This law is used by number of authors to study the cosmological models. Many relativists

(Berman and Gomide [47] , Maharaj and Naidoo [48] , Johri and Desikan [49] [50] , Singh and Desikan [51] , Pradhan et al. [52] , Pradhan and Vishwakarma [53] , Pradhan and Aotemshi [54] , Saha and Rikhvitsky [55] , Saha [56] , Singh and Kumar [57] - [59] , Singh and Chaubey [60] [61] , Reddy et al. [62] [63] , Zeyauddin and Ram [64] , Singh and Baghel [65] , Pradhan and Jotania [66] ) have obtained cosmological models by using Berman’s law of deceleration parameter. Akarsu and Kilinc [67] have obtained LRS Bianchi type-I model with anisotropic dark energy and constant deceleration parameter. Pradhan et al. [68] [69] have investigated Bianchi type-I Anisotropic dark energy with constant deceleration parameter in general relativity as well as in Lyra manifold. Recently, Ghate and Sontakke [70] [71] have studied anisotropic dark energy model with negative constant deceleration parameter in Bianchi type-IX space-time in general relativity and Brans-Dicke theory of gravitation.

During 1960s and 1970s, Redshift magnitude test claimed that, the DP lied between 0 and 1 and thus the universe was decelerating. But the observations of CMBR and SNe-Ia experiments concluded that the expansion of the universe was accelerating. Riess et al. [72] , Amendola [73] , Padmanabhan and Chowdhary [74] investigated that, for a universe which was decelerating in the past and accelerating at present time, DP parameter must show signature flipping. From the observations of SNe type Ia, Lima et al. [75] agree with the results of Riess and Amendola.

In 2006, Pradhan et al. [76] proposed the deceleration parameter to be variable parameter as:

(variable)

where R is the average scale factor. Yadav [77] , Tripathi et al. [78] and Chawla et al. [79] have studied cosmological models with variable deceleration parameter.

In 2011, Akarsu and Dereli [80] have modified Berman’s special law of variation for Hubble’s parameter by setting, where k and m are constants which yield Linearly Varying Deceleration Parameter (LVDP) models of universe. They have investigated accelerating cosmological solutions for Robertson-Walker space-time by considering LVDP. These models may have Big Rip type of future singularity. Adhav et al. [81] [82] have investigated cosmological model with LVDP. Singh et al. [83] have obtained LVDP in viscous Bianchi type-I universe. Recently, Akarsu et al. [84] investigated probing kinematics and fate of the universe with linearly time varying decelerating parameter.

In 2009, Singha and Debnath [85] have investigated the quintessence model with a minimally coupled scalar field by taking a special form of deceleration parameter q in such a way that the model behaves early decelerating and late time accelerating for barotropic fluid and Chaplygin gas dominated models. The special form of DP

q is defined as, where k is a constant and R is average scale factor. Adhav et al. [86] - [88] have

investigated Bianchi cosmological models by using special form of DP. Recently, Chirde and Shekh [89] have studied cosmological models with anisotropic dark energy in Lyra geometry.

In 2012, Saha et al. [90] have obtained cosmological solutions for FRW universe filled with two fluids consisting of dark energy and barotropic fluid by selecting the average scale factor which generates a

time dependent deceleration parameter such that the model generates a transition of the universe from early decelerating phase to the recent accelerating phase. Pradhan and Amirshachi [91] have also investigated accelerating dark energy models in Bianchi type-V space-time by selecting the scale factor as in Saha. However, Yadav

[92] [93] , Pradhan [94] , Rahman and Ansari [95] have generalized the average scale factor a given by , where n, m are positive constants and obtained the cosmological solutions.

Motivated by this study about the deceleration parameter from constant to time dependent, an attempt is made to study Bianchi type-IX space-time when universe is filled with DE with time dependent DP in general relativity. This work is organized as follows: In Section 2, the model and field equations have been presented. The field equations have been solved in Section 3 by choosing four different time depending deceleration parameters. The physical and geometrical behaviors of the models have been discussed in Sections 3.1-3.4. In the last Section 4, concluding remarks have been expressed.

2. Metric and Field Equations

Bianchi type-IX metric is considered in the form,

(1)

where a, b are scale factors and are functions of cosmic time t.

The energy-momentum tensor for the anisotropic dark energy fluid is

(2)

Here is the energy density of the fluid, is the deviation free EoS parameter, and are the skewness parameters which are deviations from on y and z axes respectively. and are not necessarily constants and can be functions of the cosmic time t.

The Einstein field equations in gravitational units () are

(3)

Here is the Ricci tensor, R is the Ricci scalar, is the energy momentum tensor.

In the co-moving coordinate system the field Equations (3) for the metric (1) and with the help of energy- momentum tensor (2) can be written as

(4)

(5)

(6)

(7)

where the overdot (^×) denotes the differentiation with respect to t.

From Equations (6) and (7) we see that, the deviations from along y and z axes are same i.e..

3. Solution of Field Equations

The field Equations (4) to (6) are a system of three highly non-linear differential equations with five unknown parameters. The system is thus initially undetermined. To obtain a deterministic solution the following physical conditions are used.

(i) The expansion scalar () is proportional to the shear scalar () which leads to

, (8)

where m is proportionality constant.

The motive behind assuming condition is explained with reference to Thorne [96] , the observations of the velocity red-shift relation for extragalactic sources suggest that Hubble expansion of the universe is isotropy today within » 30 percent (Kantowski and Sachs [97] ; Kristian and Sachs [98] ). To put more precisely, red-shift stu-

dies place the limit on the ratio of shear to Hubble constant H in the neighborhood of our galaxy today. Collin et al. [99] have pointed out that for spatially homogeneous metric, the normal congruence to the homogeneous expansion satisfies that the condition is constant.

(ii) Now one extra condition is needed to solve the system completely. Hence different models of deceleration parameters are considered as

3.1. Models with Time Dependent Deceleration Parameter

The average scale factor as an integrating function of time is (Saha et al. [90] ) given by

(9)

where r and l are positive constants.

Using Equation (9), the value of DP becomes

(10)

The proposed law yields a time-dependent DP which describes the transition of the universe from the early decelerating phase to current accelerating phase.

The metric (1) is completely characterized by average scale factor R is given by

(11)

Solving Equations (8) and (11), Equation (9) reduces to

(12)

With the help of Equation (8), Equation (12) leads to

(13)

Using Equations (12) and (13), the metric (1) takes the form

(14)

Equation (14) represents Bianchi type-IX DE cosmological model in general relativity with time-dependent deceleration parameter.

Some Physical Properties of the Model

For the cosmological model (14), the physical quantities such as spatial volume V, Hubble parameter H, expansion scalar, mean anisotropy parameter, shear scalar, energy density, equation of state (EoS) parameter and skewness parameter are obtained as follows:

The spatial volume is in the form

(15)

The Hubble parameter is given by

(16)

The expansion scalar is

(17)

The mean anisotropy parameter is

(18)

The shear scalar is given by

(19)

Here

(20)

The energy density is obtained as

(21)

The EoS parameter is

(22)

The skewness parameter is given by

(23)

For illustrative purposes, evolutionary behaviors of some cosmological parameters are shown graphically (Figures 1-3).

Physical Behavior of the Model

From Equations (15) and (19), we observed that, the spatial volume is zero at and the expansion scalar is infinite showing that, the universe starts evolving with zero volume at and expands with cosmic time t which is big bang scenario. Also from Equations (12) and (13), the spatial scale factors are zero at the initial epoch hence the model has a point type singularity (MacCallum [100] ). At, we have

and indicating that the Hubble’s parameter is maximum and the model has fastest rate of expansion for. From Equations (18) and (20), the mean anisotropy parameter is constant and is

also constant, hence the model is anisotropic throughout the evolution of the universe except at i.e. the model does not approach isotropy. In Figure 2, the plot of energy density verses time is given which indicates that the model starts with infinite density and as time increases the energy density tends to a finite value. Hence, after some finite time, the model approaches steady state. In Figure 3, the plot of deceleration parameter verses time is given from which we conclude that the model is decelerating at an initial phase and changes from decelerating to accelerating. Hence the model is consistent with the recent cosmological observations (Perlmutter et al. [1] - [3] , Riess et al. [4] [5] , Schmidt et al. [101] , Garnavich et al. [102] ). Thus, our DE model is consistent with the results of recent observations.

3.2. Models with Variable Deceleration Parameter

We consider the deceleration parameter to be variable parameter (Pradhan et al. [76] ) as:

(variable) (24)

where R is the average scale factor.

From Equation (24), we obtain

(25)

To solve Equation (25), we assume. It is important to note here that one can assume , as R is also a time dependent function. It can be done only if there is one to one correspondence between t and R. But this is only possible when one avoid singularity like big bang or big rip because t and R are increasing function.

The general solution of (25) with assumption, is given by

(26)

To solve (26) we have to choose in such a manner that (26) be integrable. Hence we consider

(27)

is a function of R only which does not affect the nature of generality of solution.

From Equations (26) and (27), we get

(28)

The choice of in (28), is quite arbitrary but since we are looking for physically viable models of the universe consistent with observations, we consider

(29)

where is an arbitrary constant.

Integrating Equation (28) and without loss of generality assuming constants of integration to be zero, we have

(30)

Solving Equations (8) and (11), Equation (30) reduces to

(31)

With the help of (8), Equation (31) leads to

(32)

Using Equations (31) and (32), the metric (1) takes the form

(33)

Equation (33) represents Bianchi type-IX DE cosmological model in general relativity with variable deceleration parameter.

Some Physical Properties of the Model

For the cosmological model (33), the physical quantities such as spatial volume V, Hubble parameter H, expansion scalar, mean anisotropy parameter, shear scalar, energy density, EoS parameter, skewness parameter and deceleration parameter q are obtained as follows:

The spatial volume is given by

(34)

The Hubble parameter is in the form

(35)

The expansion scalar is

(36)

The mean anisotropy parameter is obtained as

(37)

The shear scalar is given by

(38)

Here

(39)

The energy density is obtained as,

(40)

The EoS parameter is,

(41)

The skewness parameter is given by,

(42)

The deceleration parameter is obtained as,

(43)

For illustrative purposes, evolutionary behaviors of some cosmological parameters are shown graphically (Figures 4-6).

Physical Behavior of the Model

From Equations (34) and (38), we observed that, the spatial volume is zero at and the expansion scalar is infinite showing that, the universe starts evolving with zero volume at and expands with cosmic time t which is big bang scenario. Also from Equations (31) and (32), the spatial scale factors are zero at the initial

epoch hence the model has a point type singularity (MacCallum [100] ). At, we have and indicating that the Hubble’s parameter is maximum and the model has fastest rate of expansion for. From Equations (37) and (39), the mean anisotropy parameter is constant and is also constant, hence the model is anisotropic throughout the evolution of the universe except at i.e. the

model does not approach isotropy. In Figure 5, the plot of energy density verses time is given which indicates

that the model starts with infinite density and as time increases the energy density tends to a finite value. Hence, after some finite time, the model approaches steady state. In Figure 6, the plot of deceleration parameter verses time is given from which we conclude that the model is decelerating at an initial phase and changes from decelerating to accelerating. Hence the model is consistent with the recent cosmological observations (Perlmutter et al. [1] - [3] , Riess et al. [4] [5] Schmidt et al. [101] , Garnavich et al. [102] ). Thus, our DE model is consistent with the results of recent observations.

3.3. Models with Linearly Varying Deceleration Parameter

We consider the linearly varying deceleration parameter (Akarsu and Dereli [80] ) as:

(44)

where R is the average scale factor, are constants.

For, Equation (44) reduces to

(45)

giving constant value of deceleration parameter.

Using this law one can generalize the cosmological solutions that are obtained via constant deceleration parameter.

After solving (45), we obtain the three different forms of the mean scale factors

(46)

(47)

(48)

where and are constants of integration. The last two Equations (56) and (57) are the solutions for constant deceleration parameter q. We are not interested in these but only on the first one, which is new. For convenience, in the following we consider the solution for and and omit the integration constant by setting. By doing this, we also set the initial time of the universe to. The reason for considering the solution only for and is not only for simplicity but also for compatibility with the observed universe. means we are dealing with increasing acceleration. Because and, the only way to shift the deceleration parameter to values higher than is to set. Under the above considerations, (46) is further reduces to

(49)

Solving Equations (8) and (11), Equation (49) reduces to

(50)

With the help of Equation (8), Equation (50) leads to

(51)

With the help of Equations (50) and (51), the metric (1) takes the form

(52)

Equation (52) represents Bianchi type-IX DE cosmological model in general relativity with linearly varying deceleration parameter.

Some Physical Properties of the Model

For the cosmological model (52), the physical quantities such as spatial volume V, Hubble parameter H, expansion scalar, mean anisotropy parameter, shear scalar, energy density, EoS parameter and Skewness parameter are obtained as follows:

The spatial volume is given by

(53)

The Hubble parameter is in the form

(54)

The expansion scalar is obtained as

(55)

The mean anisotropy parameter is

(56)

The shear scalar is given by

(57)

Here

(58)

The energy density is

(59)

The EoS parameter is obtained as

(60)

The skewness parameter is given by

(61)

For illustrative purposes, evolutionary behaviors of some cosmological parameters are shown graphically (Figures 7-9).

Physical Behavior of the Model

From Equations (53), we observed that, the spatial volume is finite i.e. the universe starts evolving with some finite volume at and expands with cosmic time t. At, the expansion scalar is infinite and obtain some finite value at late time. For the cosmological model (52), the spatial scale factors are not zero for any value of t and hence the model does not have any singularity. The parameters H, and diverge for

. The universe begins with for (decelerating expansion) and enters into the accelerating phase. At, implying that the universe experiences super-exponential expansion and ends with at. From Equations (56) and (58), the mean anisotropy parameter is constant and is also constant, hence the model is anisotropic throughout the evolution of the universe

except at i.e.the model does not approach isotropy. In Figure 8, the plot of energy density verses time is given which indicates that the model starts with infinite density and as time increases the energy density tends to a finite value. Hence, after some finite time, the model approaches steady state. In Figure 9, the plot of deceleration parameter verses time is given from which we conclude that the model is decelerating at early phase and changes from decelerating to accelerating.

3.4. Models with Special form of Deceleration Parameter

Following Singha and Debnath [85] we use a special form of deceleration parameter as:

(62)

where R is the average scale factor, is constant.

Solving Equation (62), the average scale factor R is given by

(63)

where and are constants of integration.

Solving Equations (8) and (11), Equation (63) reduces to

(64)

With the help of Equation (8), Equation (64) leads to

(65)

Using Equations (64) and (65), the metric (1) takes the form

(66)

Equation (66) represents Bianchi type-IX DE cosmological model in general relativity with special form of deceleration parameter.

Some Physical Properties of the Model

For the cosmological model (66), the physical quantities such as spatial volume V, Hubble parameter H, expansion scalar, mean anisotropy parameter, shear scalar, energy density, EoS parameter and Skewness parameter are obtained as follows:

The spatial volume is given by

(67)

The Hubble parameter is in the form

(68)

The expansion scalar is obtained as

(69)

The mean anisotropy parameter is

(70)

The shear scalar is given by

(71)

Here

(72)

The energy density is

(73)

The EoS parameter is given by

(74)

The skewness parameter is in the form,

(75)

For illustrative purposes, evolutionary behaviors of some cosmological parameters are shown graphically (Figures 10-12).

Physical Behavior of the Model

From Equation (67), the spatial volume is finite i.e. the universe starts evolving with some finite volume at and expands with cosmic time t. At, the expansion scalar is infinite and obtain some finite value at late time. From Equations (64) and (65), the spatial scale factors are not zero for any value of t and hence the model does not have singularity. From Equations (70) and (72), the mean anisotropy parameter is constant

and is also constant, hence the model is anisotropic throughout the evolution of the universe ex-

cept at i.e. the model does not approach isotropy. In Figure 11, the plot of energy density verses time is given which indicates that the model starts with infinite density and as time increases the energy density tends to a finite value. Hence, after some finite time, the model approaches steady state. In Figure 12, the plot of deceleration parameter verses time is given from which we conclude that the model is decelerating at an initial phase and changes from decelerating to accelerating. Hence the model is consistent with the recent cosmological observations (Perlmutter et al. [1] - [3] , Riess et al. [4] [5] , Schmidt et al. [100] , Garnavich et al. [101] ). Thus, our DE model is consistent with the results of recent observations.

4. Conclusions

A Bianchi type-IX cosmological model has been obtained when universe is filled with DE in general relativity. To find deterministic solution, we have considered five different models of deceleration parameter which yields time-dependent scale factors.

In model 3.1, the solution of the field equations has obtained by choosing the time dependent DP which yields time dependent scale factor. It is observed that, the model has point

type singularity. In early phase of universe, the value of deceleration parameter is positive while as, the value of. Hence the universe had a decelerated expansion in the past and has accelerated expansion at present which is in good agreement with the recent observations of SN Ia.

In model 3.2, the solution of the field equations has obtained by choosing the variable DP which yields time dependent scale factor. The model has point type singularity. The model has decelerated expansion at early stages and accelerated expansion at present.

In model 3.3, the solution of the field equations has obtained by choosing the linearly varying DP which yields time dependent scale factor. The model is non-singular. In

early phase of universe, the value of deceleration parameter is positive, after some finite time the model changes from positive to negative, while as, the value of q becomes negative.

In model 3.4, the solution of the field equations has obtained by choosing the special form of DP which yields time dependent scale factor. It is observed that, the model is

non-singular. In early phase of universe, the value of deceleration parameter is positive while as, the value of. Hence the universe had a decelerated expansion in the past and has accelerated expansion at present.

It is worth mentioning that in all cases, the models obtained are expanding, shearing, non-rotating and do not approach isotropy for large t. Further the models are anisotropic throughout the evolution. Thus, DE models are in good harmony with recent cosmological observations (Perlmutter et al. [1] - [3] , Riess et al. [4] [5] , Schmidt et al. [100] , Garnavich et al. [101] ). We hope that these models will be useful for a better understanding of dark energy in cosmology to study an inflationary behavior of the universe.

Cite this paper

H. R.Ghate,Atish S.Sontakke,Yogendra D.Patil, (2015) Bianchi Type-IX Anisotropic Dark Energy Cosmological Models with Time Dependent Deceleration Parameter. International Journal of Astronomy and Astrophysics,05,302-323. doi: 10.4236/ijaa.2015.54033

References