Received 1 October 2014; accepted 23 March 2015; published 26 March 2015

ABSTRACT

Kantowski-Sachs plane symmetric models are investigated in bimetric theory of gravitation proposed by Rosen [1] in the context of bulk viscous fluid. Taking conservation law and the equation of state, two different models of the universe are obtained. It is observed that Kantowski-Sachs vacuum model obtained in first case and bulk viscous fluid model obtained in second case. It is also observed that the bulk viscous cosmological model always represents an accelerated universe and consistent with the recent observations of type-1a supernovae. Some physical and geometrical features of the viscous fluid model are studied.

Keywords:

Bimetric Theory, Viscous Fluid, Kantowski-Sachs

1. Introduction

General relativity established by Einstein serves as a basis for constructing mathematical models of the universe. This theory has some controversies and lapses for which various alternative and modified theories of it have been proposed by authors from time to time to unify gravitation and matter fields in various forms. Most of the cosmological models based on general relativity and its modified theories such as Barber’s second self creation theory, Einstein-Cartan, Gauge theory gravity, Brans-Dicke theory, Scalar-tensor theories, Scalar theories contain an initial singularity (the big-bang) from which the universe expands. Thus to get rid of the singularities that occur in general relativity and other theories, Rosen [1] proposed his bimetric theory of relativity. Other bimetric theories of gravitation are Born-Infeld (1934) bimetric theory (according to Moffat); J Moffat’s non-symmetric gravitation theory(1979-1995); J Bekenstein’s (1992) treatment of gravitational lensing and MOND; Clayton-Moffat (1998-2003) scalar-vector-tensor theory. Rosen’s bimetric theory of relativity consists of two metric tensors at each point of the space time whose role is to determine physical situation. The first Riemannian metric tensor, which describes gravitation and the back ground metric tensor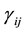, which enters into the field equations and interacts with 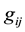but does not interact directly with matter. One can regards 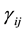as giving the geometry that would exist if there were no matter. Accordingly, at each point of the space-time one has two line elements

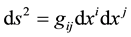(1)

and

(2)

where 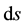is the interval between two neighbouring events as measured by a clock and a measuring rod. The interval 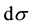is an abstract or a geometrical quantity which is not directly measurable. One can regard it as describing the geometry that exists if no matter was present. Moreover, this theory also satisfies the covariant and equivalence principles and agrees with the theory of general relativity up to the accuracy of observations made till the date.

As in general relativity, the variation principle also leads to the conservation law

(3)

where (;) denotes covariant differentiation with respect to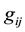. Accordingly the geodesic equation of a rest particle is the same as that of general relativity.

The field equations of Rosen’s bimetric theory of gravitation are

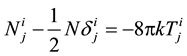(4)

where

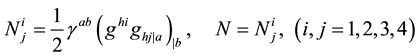
and 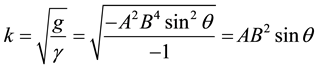together with g = determinant of 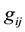and g = determinant of.

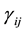Here the vertical bar (|) denotes the covariant differentiation with respect to 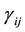and is the energy momentum tensor of the matter.

Usually the investigation of relativistic models has the energy momentum tensor of matter and generated by a perfect fluid. But to obtain more realistic models, one must consider the viscosity mechanism because the effect of bulk viscosity exhibits essential influence on the characteristic of the solution. The viscosity mechanism in cosmology has attracted the attention of many researchers as it can account for high entropy of the present universe (Weinberg [2] [3] ). High entropy per baryon and the remarkable degree of isotropy of the cosmic microwave background radiation suggests that one should analyze dissipative effects in cosmology. Moreover, there are several processes which are expected to give rise to viscous effects. These are the decoupling of neutrinos during the radiation era and the decomposition of matter and radiation during the recombination era (Kolb and Turner [4] ), decay of massive superstring models into massless models (Myung and Cho [5] ), gravitational string production (Turok [6] and Barrow [7] ) and particle creation effect in the grand unification era. Murphy [8] shows that introduction of bulk viscosity can avoid the big bang singularity. Hence one should consider the presence of material distribution other than the perfect fluid to get realistic cosmological models (see Gron [9] for a review on cosmological models with bulk viscosity) of the universe. If the present entropy is not due to bulk viscosity then perhaps it is produced by the effects of shear viscosity or heat conduction in an initially anisotropic or inhomogeneous expansion. Indeed, it may be just these dissipative processes that are responsible for smoothing out initial anisotropies and hence producing the high degree of isotropy observed in the cosmic microwave radiation background.

In general relativity, the relativists are generally using various symmetries to get physically viable information from the complicated structure of the field equations. The field equations of general relativity are non-linear in nature with ten unknowns. So it is very difficult to determine the exact solutions of the field equations. The involvement of symmetry i.e. spherical or cylindrical or plane reduces the number of gravitational potentials and thus helps one in simplifying the field equation to some extent. A space-time that admits the three- parameter group of motions of Euclidian plane is said to possess plane symmetry and is called plane symmetric space-time. The origin of structure in the universe is one of the greatest mysteries even today. The present day observations indicate that the universe at large scale is homogeneous and isotropic and it is witnessing an accelerating phase as reported recently by Gasperini and Veneziano [10] . It is well known that the exact solution of general theory of relativity for homogeneous space-time belongs to either Bianchi types or Kantowski-Sachs [11] .

Rosen [1] [12] [13] , Yilmaz [14] , Karade and Dhoble [15] , Karade [16] , Israelit [17] - [19] , Liebscher [20] , Reddy and Venkateswaralu [21] , Deo and Thengane [22] , Sahoo [23] , Mohanty, Sahoo and Mishra [24] are some of the eminent authors, who have studied various aspects of bimetric theory.

Sahoo [23] has studied Kantowski-Sachs model in presence of cosmic cloud strings coupled with electromagnetic field in bimetric theory. He has shown that there is no contribution from Maxwell’s field but established the geometric string model and vacuum model of the universe. Sahoo [25] has also studied Spherically symmetric Kantowski-Sachs space-time in bimetric theory of gravitation, considering the source of gravitation perfect fluid coupled with scalar meson field and has shown that the macro cosmological model-represented by perfect fluid does not exist, where as the micro cosmological model represented by scalar meson field exists. Sahu, Nayak and Behera [26] have found that Bianchi type-I cosmological models do not exist in bimetric theory of gravitation in presence of viscous fluid or mesonic viscous fluid with or without a mass parameter in general. Further, Kantowski-Sachs cosmological models are also studied by different authors like Tiwari and Dwibedi [27] , Rahaman, Chakraborty, Bera and Das [28] , Chaubey [29] , Rao and Neelima [30] , Adhav, Dawande and Raut [31] , Hector Martinez and Carlos Peralta [32] in different angles.

To the best of our knowledge no author has studied Kantowski-Sachs plane symmetric model in the context of bimetric theory of relativity, when source of the gravitational field is governed by bulk viscous fluid. Therefore, in this paper we are interested to study this problem for two different cases. The work reported in first case concludes that Kantowski-Sachs plane symmetric model does not accommodate bulk viscous fluid in bimetric theory of relativity. However, Kantowski-Sachs bulk viscous fluid model obtained in second case.

2. Field Equations

Consider the Kantowski-Sachs [33] metric in the form

(5)

where the metric potentials A and B are functions of cosmic time “t” only.

The background flat space-time metric is

(6)

The energy momentum tensor for bulk viscous fluid distribution is given by

(7)

with

(8)

where p is the proper pressure, is the energy density, is the effective pressure, u_i is the four velocity vector of the fluid and is the bulk viscous coefficient of the fluid.

Since the bulk viscous pressure represents only a small correction to the thermo dynamical pressure, it is reasonable assumption that the inclusion of viscous term in the energy momentum tensor does not change fundamentally the dynamics of the cosmic evolution. For the specification of, we assume that the fluid obeys an equation of state of the form

(9)

Here λ is called the adiabatic parameter.

Using comoving co-ordinate system, the field Equation (4) for the metrics (5) and (6) corresponding to the energy momentum tensor (7) can be written as

(10)

(11)

And

(12)

Equation (8) can be expressed as

(13)

Here and afterwards the suffix “4” after a field variable represents ordinary differentiation with respect to time “t” only.

3. Solution of the Field Equations

Equations (10), (11) and (12) yield

(14)

Taking last two terms of Equation (14), we get

(15)

Equations (15) and (13) yield

(16)

Case-1: From the reality conditions, we have

(17)

So from Equation (15), we find

(18)

Use of (18) in Equation (9), we obtain

(19)

By help of Equation (18), equations (10) and (11) yield

(20)

On integration, (20) yields

(21)

where are constants of integration.

Putting the values of A and B from (21), and use of Equations (18) and (19) in Equation (16), we have

(22)

Thus the metric (5) corresponding to Equations (21) & (22) takes the form

(23)

With proper choice of co-ordinates Equation (23) can be transformed to

(24)

As, so Kantowski-Sachs viscous fluid model does not survive in bimetric theory but vacuum model of the universe only exists.

It is observed from (18), (19) and (22) that

(25)

Thus the above result reduces to that of result already obtained by Sahoo [25] .

Case-2:

With help of the conservation property (3), metric (5) takes the form

(26)

By the help of (15) Equation (26) yields

(27)

To avoid complexity in the problem substituting the relation from Equation (14) in Equation (27),

we have

(28)

where is the constant of integration.

Use of (28) and value of “k” from (4) in Equation (14), we get

(29)

where (constant).

Now Equation (29) can be expressed as

(30)

Integrating (30), one can obtain

(31)

where is the constant of integration.

As we have consider the relation, so we can find

(32)

Thus (28) with the help of (32) yields

(33)

Now use of Equation (33) in Equation (15), we get

(3 )

Putting the value of from (33) in Equation (9) and assigning different values to λ, we get

(35)

(36)

and

(37)

Using (32), Equation (13) yields

(38)

By use of (35), (36), (37) separately in (38) and then using (34) in each case, we get

(39)

(40)

(41)

Therefore in view of (32), the line element (5) can be written in the form

(42)

The above model of the universe can be transformed through a proper choice of coordinates to the form

(43)

4. Physical and Geometrical Properties of the Model (43)

i. The Spatial Volume V of the Universe:

The spatial volume V of the universe is found to be

Now V → constant as t → 0 and V → 0 as t → ∞.

Thus we inferred from the results obtained above that the universe starts from a constant volume and collapse at infinite future.

ii. The Expansion Scalar θ:

The Expansion Scalar “θ” in the model is found to be

Hence as t → 0, θ → constant and as t → ∞, θ → 0.

This result shows that the model has the constant rate of expansion at initial time but as time increases the rate of expansion becomes slow and there will be no expansion at infinite future.

iii. Anisotropy of the Universe:

The shear scalar σ (Ray Choudhuri [34] ), defined by

for the model yield.

Therefore σ² → a constant as t → 0 and σ² → 0 as t → ∞. Thus it is inferred that the model is anisotropic at initial time but gradually approaches to isotropic as time increases. It is interesting that at infinite future the universe may turns to isotropic state. Since the universe in a smaller case is neither homogeneous, so the transition from anisotropic to isotropic state might have happened in the early universe which is not supported by any observed or experimental data. However there are theoretical arguments that sustain the existence of an anisotropic phase that approaches an isotropic case (Misner, [35] Chaotic Cosmology). The early universe could also be characterized by an irregular expansion mechanism. Thus it would be useful to explore models in which anisotropies existing at an early stage of expansion, are damped out in the course of evolution and such models have

received some attention (Hu & Parker, [36] ). As, the model is anisotropic at the initial

time and continues throughout the evolution.

iv. Hubble parameter:

The Hubble parameter H in the model is found to be. As H is a function of time so the model is not a steady state model.

v. Scale factor:

The scale factor S³ in the model is found to be. Thus “S” decreases as time increases.

vi. The deceleration parameter:

The deceleration parameter ‘q’ in the models defined by which has −ve sign. Hence the

model of the universe corresponds to an inflationary model. The model represents an accelerating universe in bimetric theory of gravitation and also consistent with the recent observations of type-Ia supernovae.

vii. Energy conditions for viscous fluid:

The strong, weak and dominant energy conditions i.e. are given by in the model as

, and.

It is observed from above data that the strong energy conditions is satisfied in the model. The weak and dominant energy conditions are also satisfied when. Again as t → 0, constant and as t → ∞,. Thus we inferred that the model has no singularity at t = 0 and the space time reduces to flat space time.

viii. Bulk viscous coefficient:

The bulk viscous coefficient are found in the model as given below:

and

In all the cases it is observed that as t → 0, h → ‒ve constant and as t → ∞, h → ‒∞. So it is evident from the above result that the solutions leads to unphysical situations and hence there is no singularity involved in the model.

5. Conclusion

In this paper, Kantowski-Sachs models are constructed in Rosen’s bimetric theory of gravitation when the energy momentum tensor is bulk viscous fluid. Applying the conservation equation and also the equation of state, two different models of the Kantowski-Sachs universe are obtained i.e. vacuum model and bulk viscous fluid model. It is observed that the bulk viscous cosmological model always represents an accelerated universe and also is consistent with the recent observations of type-1a supernovae. The model obtained is not of a steady state model and has no singularity. Also the model is anisotropic at initial time but approaches to isotropy at infinite future. As there is one way to avoid singularity is energy density ρ to vanish, so Rosen’s model in the context of bulk viscous fluid is only valid when the energy density ρ is not zero.

Acknowledgements

The authors thank the reverend referee for his constructive comments to bring the paper in improvement form.

References