International Journal of Astronomy and Astrophysics
Vol.3 No.3(2013), Article ID:36512,3 pages DOI:10.4236/ijaa.2013.33030
Mass as the Fifth Dimension of the Universe
1Department of Physics, Islamic Azad University (IAU)-Varamin-Pishva Branch, Tehran, Iran
2Department of Physics, University Malaya (UM), Kuala Lumpur, Malaysia
3The Indian Planetary Society (IPS), Mumbai, India
Email: nikou@um.edu.my, ips.science@gmail.com
Copyright © 2013 Bijan Nikouravan, Jitendra J. Rawal. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 21, 2013; revised June 23, 2013; accepted July 1, 2013
Keywords: Mass; 5D Universe; Einstein’s Field Equations
ABSTRACT
Newton considered three-dimensional universe endowed with flat space Euclidean geometry, and treated the time as an outside parameter and established his dynamics of the universe. Einstein along with space, considered time, and generated a four-dimensional universe endowed with non-Euclidean curved space-time geometry with time as its fourth dimension, and set up his field equations. Schwarzschild solved Einstein’s field equations around a star in space, which is, otherwise, flat, and obtained a solution. We, along with space and time, considered mass which also included energy according to Einstein’s mass-energy equivalence relation: QUOTE 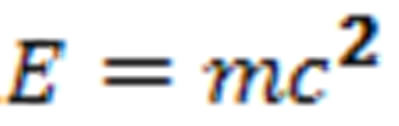
![]() E = mc2, and generated a five-dimensional universe with the mass as its fifth dimension, and solved the Einstein’s field equations, in some simple cases, and obtained solutions around a star in space, which is otherwise, flat.
E = mc2, and generated a five-dimensional universe with the mass as its fifth dimension, and solved the Einstein’s field equations, in some simple cases, and obtained solutions around a star in space, which is otherwise, flat.
1. Introduction
Though, the Newtonian dynamics is ruling the universe endowed with three dimensional flat space Euclidean geometry, it is well known that it suffers from certain serious problems in dealing with all kinds of situations that prevail in the universe. Hence, Einstein [1,2] had to put forth his theories of relativity by taking into consideration the presence of time in each and every event taking place in the universe. He took the time as the fourth dimension of the universe, on the same footing as three space dimensions, in the background of non-Euclidean curved space-time geometry, and set up his field equations. Schwarzschild [3] solved Einstein’s field equations around a star in the space, which is otherwise flat, and obtained a solution. Though, the mass is present everywhere in the universe, generally, it has been put aside as one more dimension of the universe in its physical description. When we say mass, here, we mean mass as well as energy. This is due to Einstein’s mass-energy equivalence relation: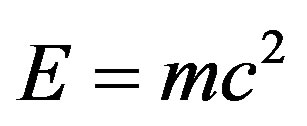 . As far back as 1920s, [4,5] and recently, this problem has caught attention of some scientists [6,7]. We, along with space and time, considered the mass as the fifth dimension of the universe, and generated five-dimensional universe and solved the Einstein’s field equations in some simple cases, and obtained solutions around a star in five-dimensional universe, which is, otherwise flat.
. As far back as 1920s, [4,5] and recently, this problem has caught attention of some scientists [6,7]. We, along with space and time, considered the mass as the fifth dimension of the universe, and generated five-dimensional universe and solved the Einstein’s field equations in some simple cases, and obtained solutions around a star in five-dimensional universe, which is, otherwise flat.
2. Solution of Einstein’s Field Equations with Mass as the Fifth Dimension
The line element in the five-dimensional Euclidean flat space-time in the spherical coordinate system with mass as the fifth dimension can be written down as:
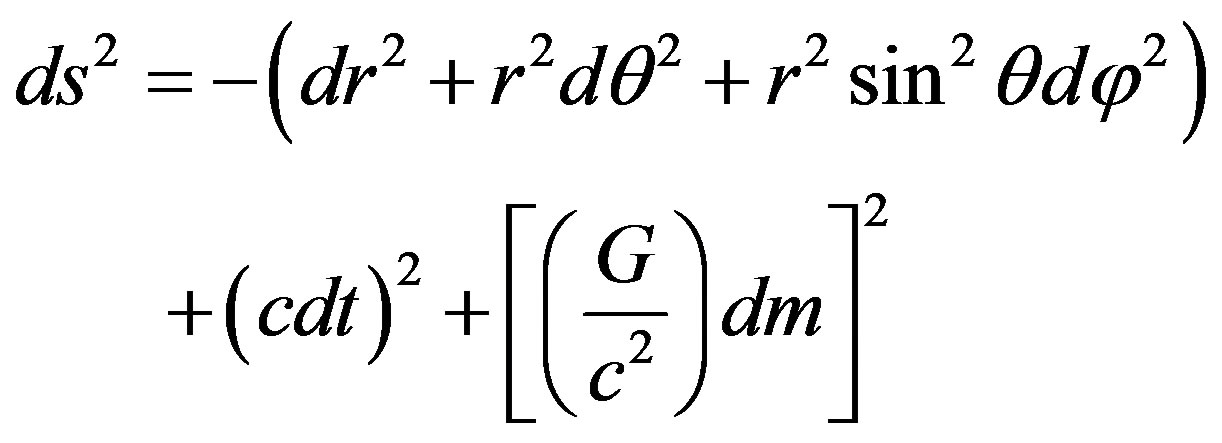 (1)
(1)
The most general line element being:
 (2)
(2)
where  is the conversion factor which is a universal constant converting mass into length. Note that its value is of the order
is the conversion factor which is a universal constant converting mass into length. Note that its value is of the order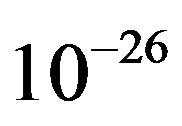 . This is the reason for the fifth-dimension being suppressed. In the region containing higher mass, the effect of the fifth-dimension in the five-dimensional universe may be revealed to an appreciable level. To begin with, we take
. This is the reason for the fifth-dimension being suppressed. In the region containing higher mass, the effect of the fifth-dimension in the five-dimensional universe may be revealed to an appreciable level. To begin with, we take 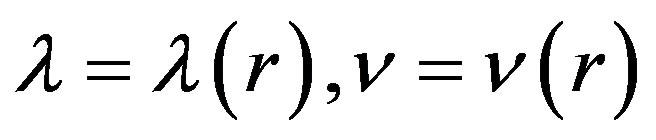 and
and 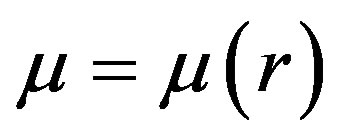 as functions of r alone, and at large distances from the attracting point mass sitting at the origin of the five-dimensional universe
as functions of r alone, and at large distances from the attracting point mass sitting at the origin of the five-dimensional universe 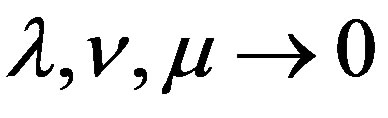 as
as 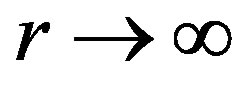 to coincide with flat space-time-mass metric Equation (1).
to coincide with flat space-time-mass metric Equation (1).
The gravitational potentials 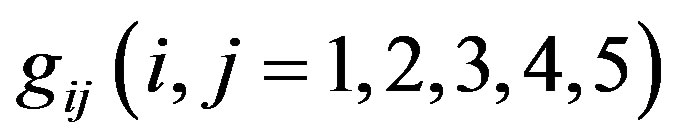 are covariant metric tensors given by
are covariant metric tensors given by
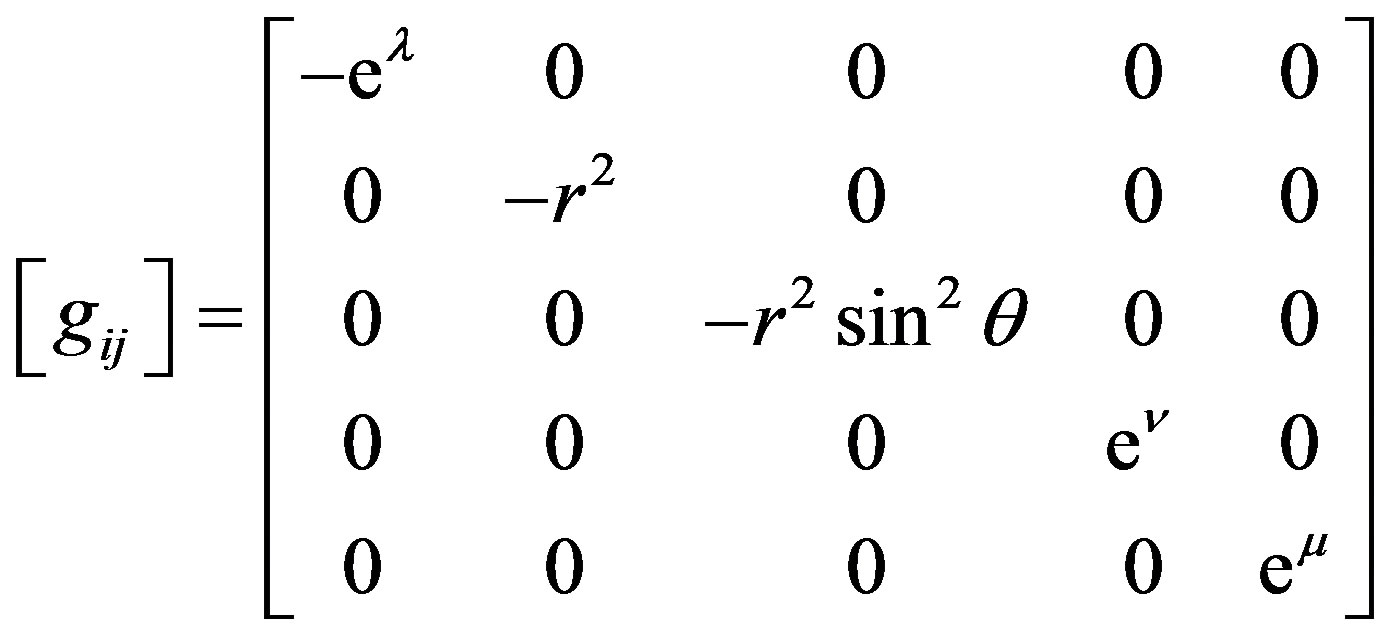 (3)
(3)
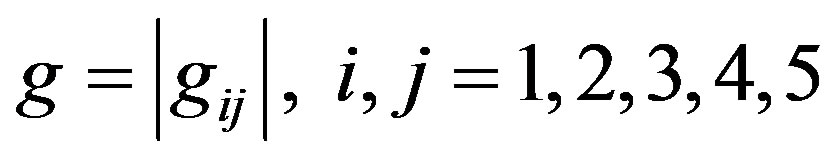 (4)
(4)
The contravariant metric tensors 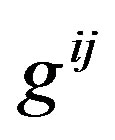 are given by
are given by
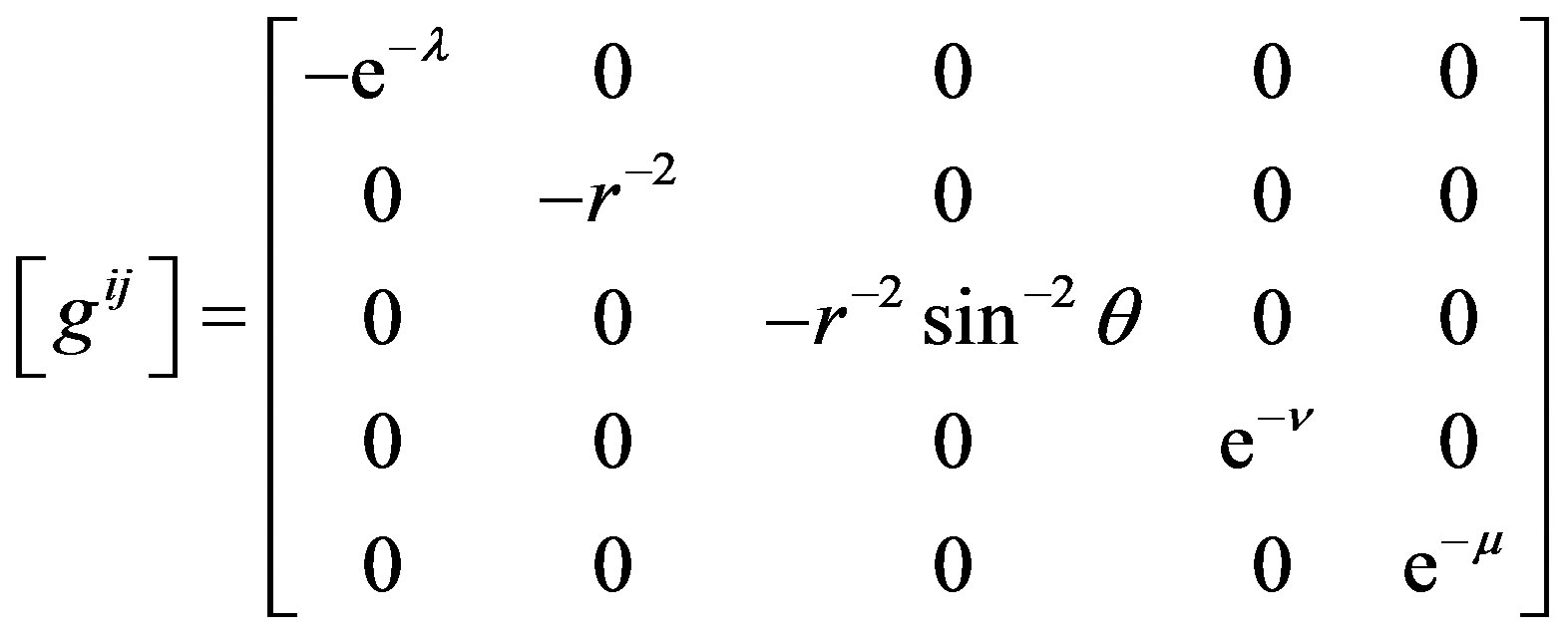 (5)
(5)
The Christoffel symbols of the second kind are given by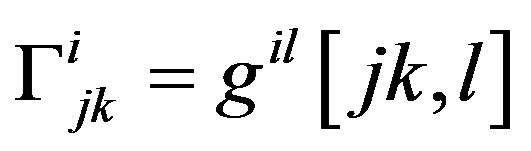 , where
, where 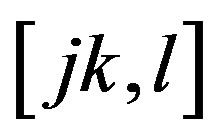 are the Christoffel symbols of the first kind, and are being given by
are the Christoffel symbols of the first kind, and are being given by
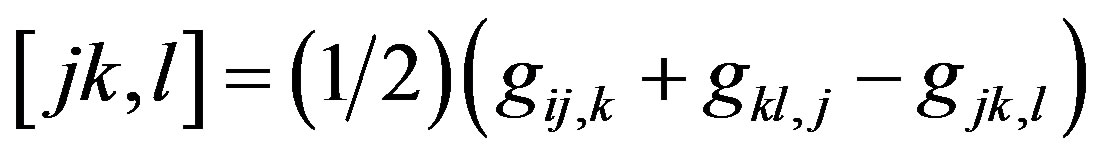
and 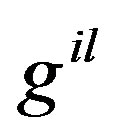 are contravariant metric tensors. We have
are contravariant metric tensors. We have .
.
There are 16 non-vanishing Christoffel symbols of the second kind which are given below:
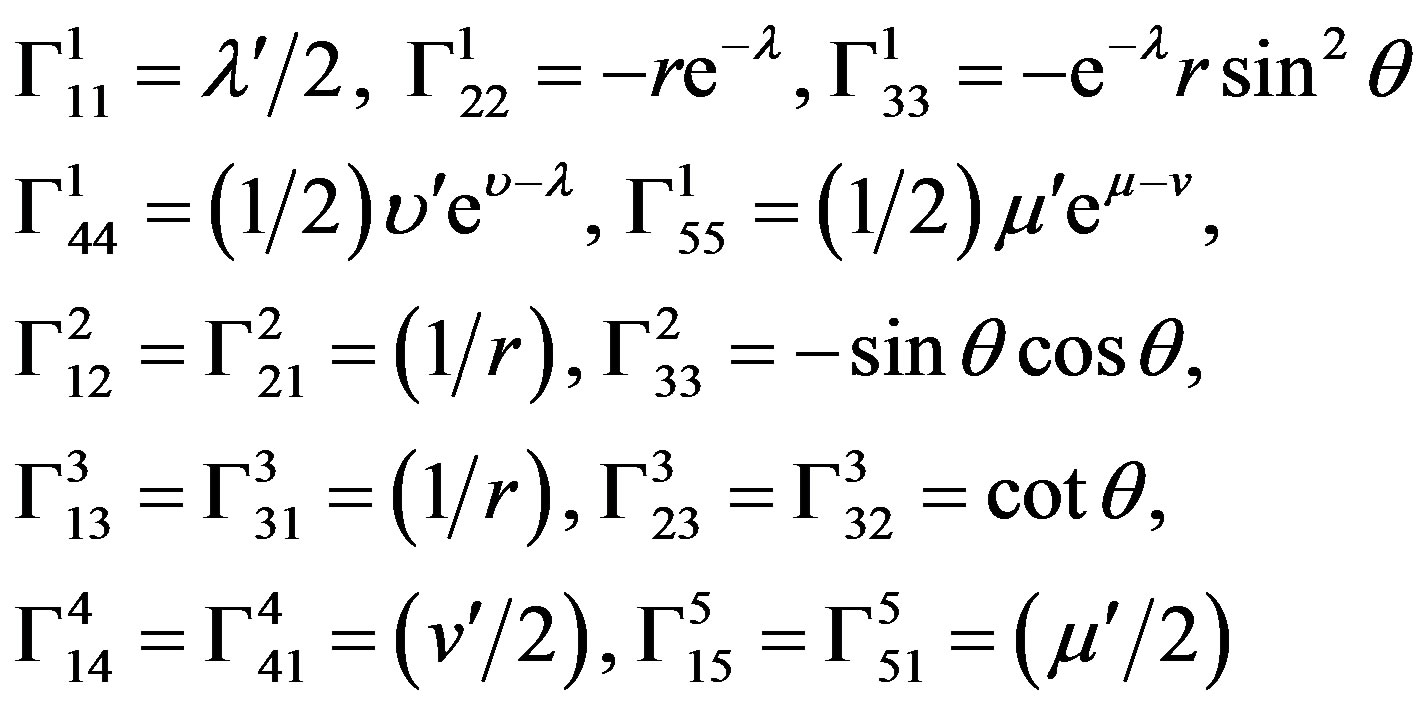 (6)
(6)
Einstein’s field equations are
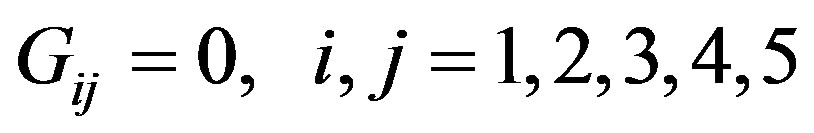 (7)
(7)
where  are given by
are given by
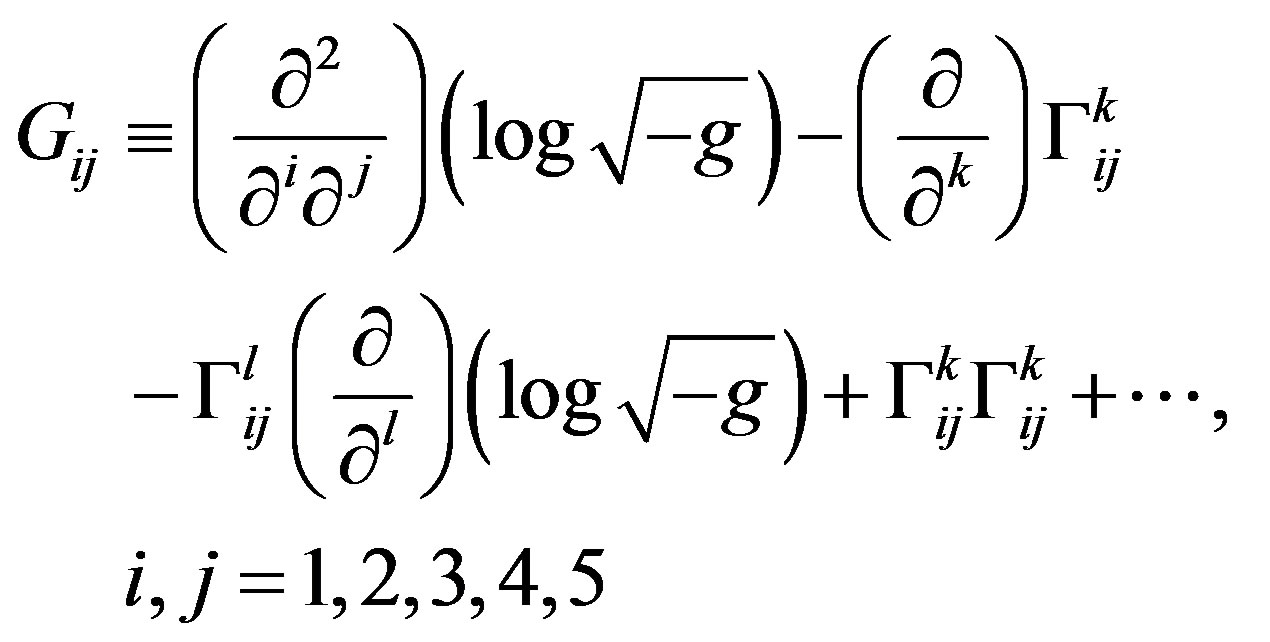 (8)
(8)
From Equations (6)-(8), we get
 (9a)
(9a)
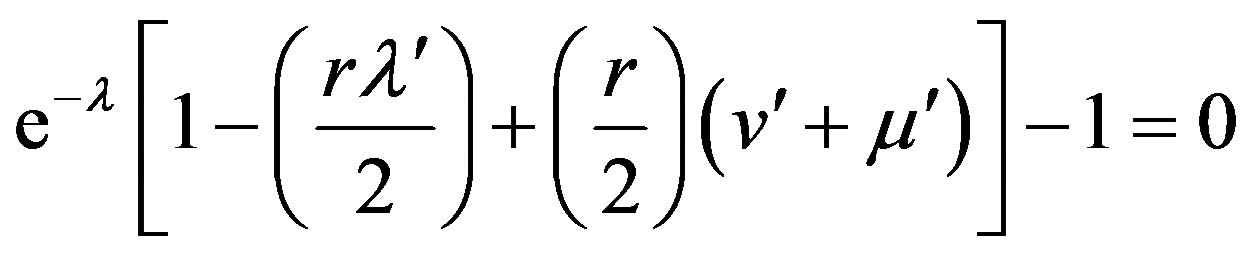 (9b)
(9b)
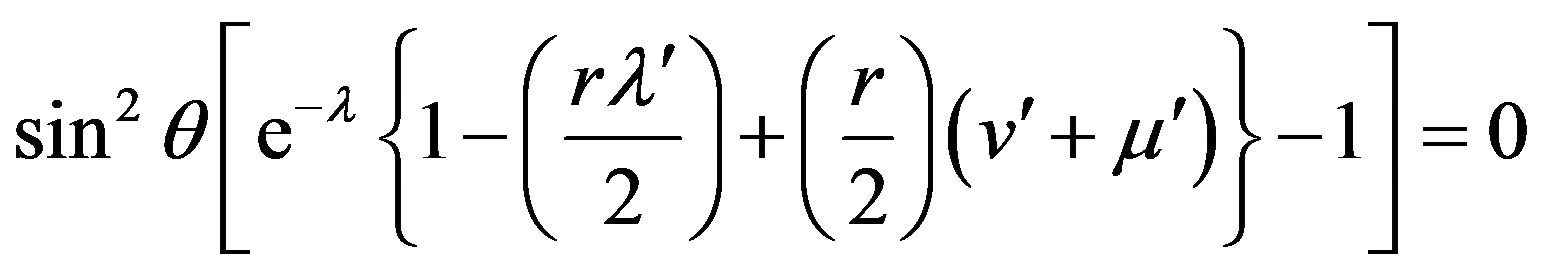 (9c)
(9c)
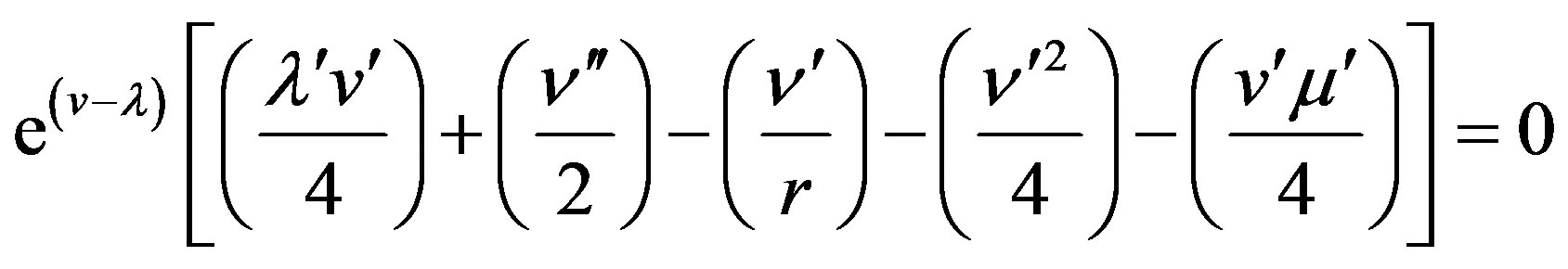 (9d)
(9d)
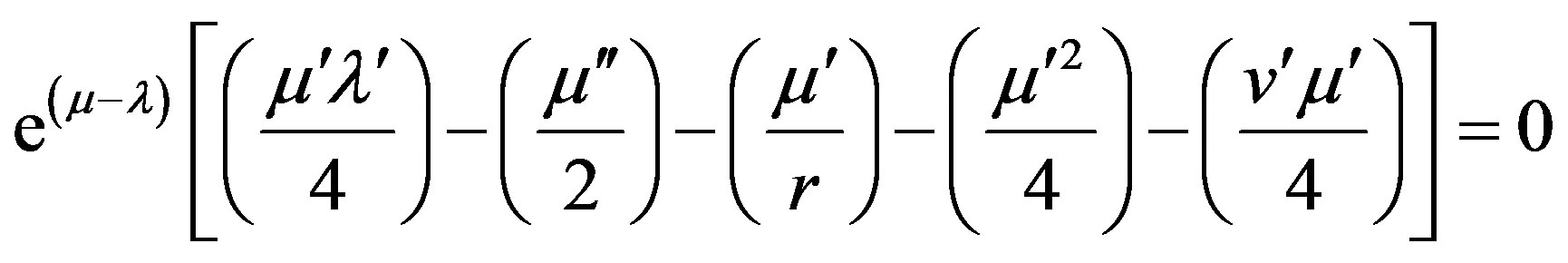 (9e)
(9e)
 (9f)
(9f)
These are equations in r alone. They are difficult to solve in their very general form. We, therefore, begin with the following simple cases:
Case (i), μ = μ(r) = constant (say) k. As μ = μ(r) → 0, as 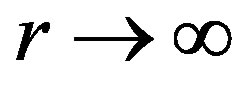 this constant must be zero. In this simple case, the Equations 9(a)-(f) reduce to the following:
this constant must be zero. In this simple case, the Equations 9(a)-(f) reduce to the following:
 (10a)
(10a)
 (10b)
(10b)
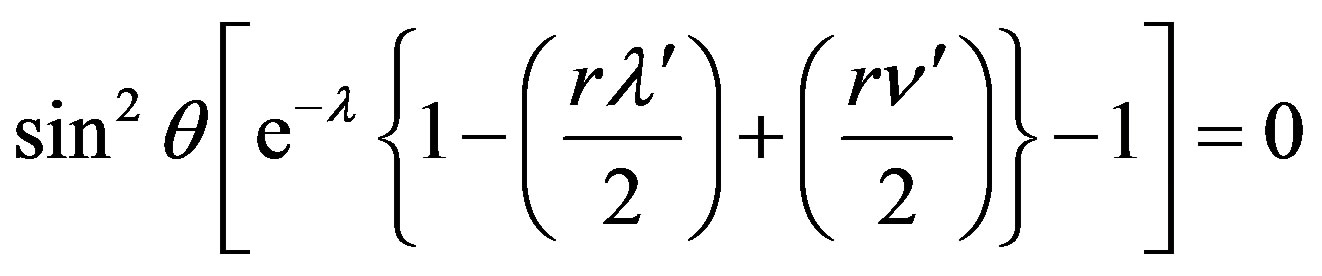 (10c)
(10c)
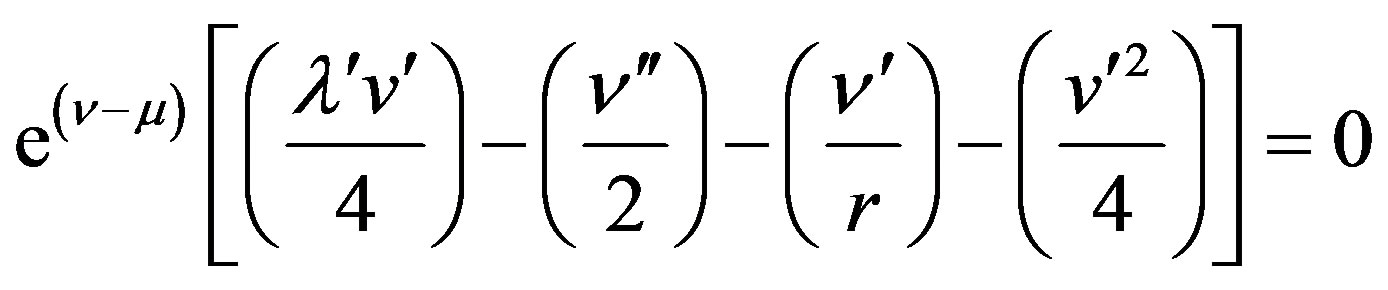 (10d)
(10d)
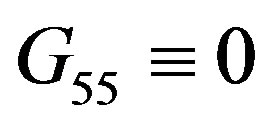 (10e)
(10e)
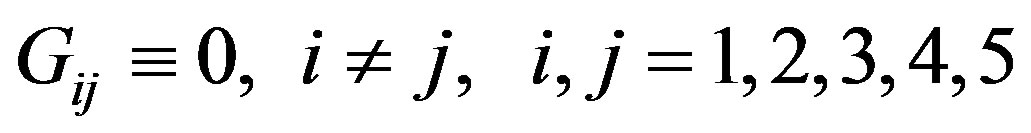 (10f)
(10f)
These are the Einstein’s field equations in five-dimensional universe with mass as its fifth dimension. The solution of these equations is:
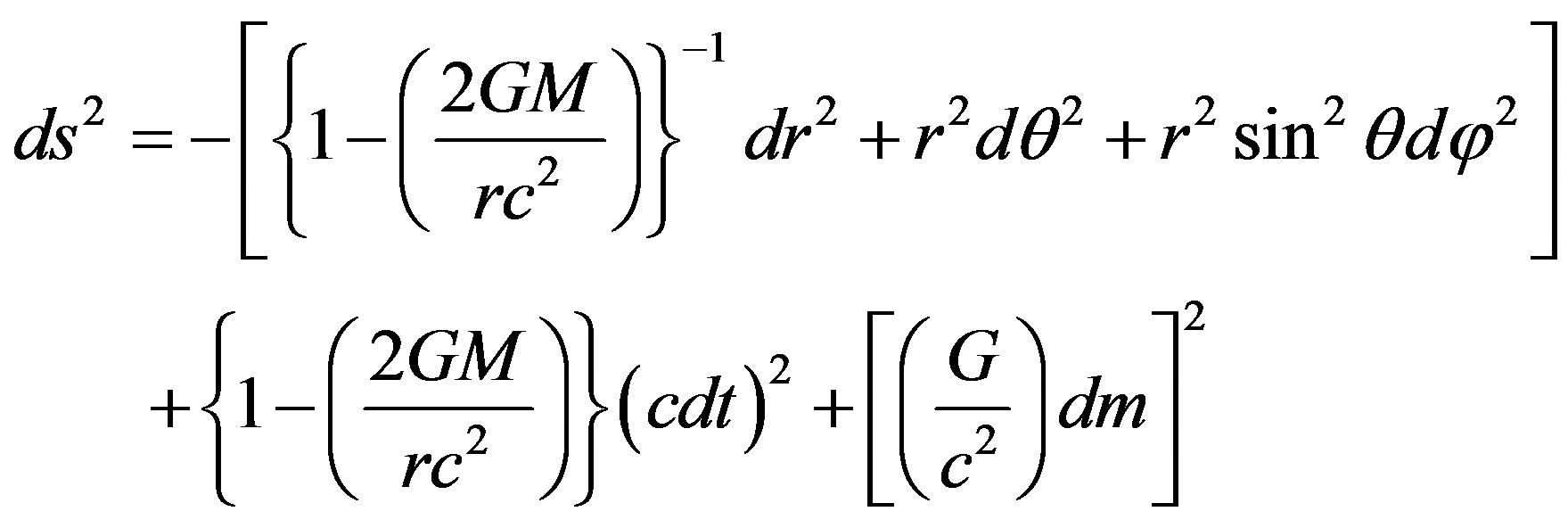 (11)
(11)
If the mass is small, the mass dimension is suppressed by the conversion factor 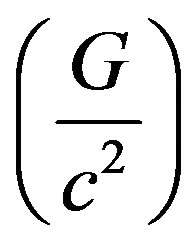 which is of the order
which is of the order
 . Therefore, in this case, we get Schwatzschild-like line element (solution) in five-dimensional universe with mass as its fifth dimension without showing much effect of mass dimension, except that it appears as one of the dimensions in the line element.
. Therefore, in this case, we get Schwatzschild-like line element (solution) in five-dimensional universe with mass as its fifth dimension without showing much effect of mass dimension, except that it appears as one of the dimensions in the line element.
Case (ii), ν = ν(r) = constant (say)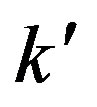 . As ν = ν(r) → 0 as
. As ν = ν(r) → 0 as , this constant must be zero.
, this constant must be zero.
In this simple case, the Equations 9(a)-(e) reduce to the following:
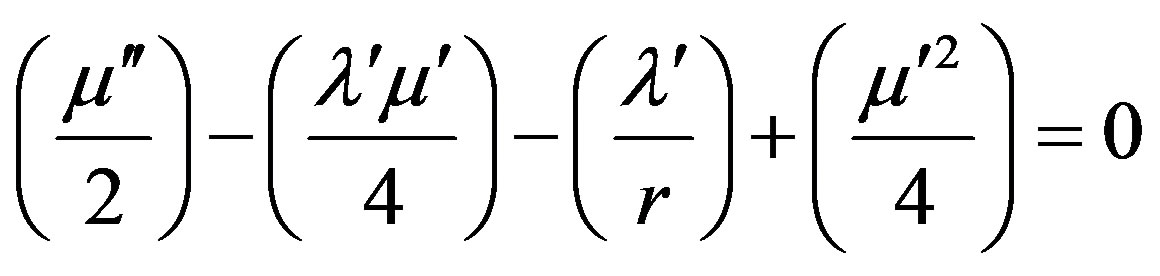 (12a)
(12a)
 (12b)
(12b)
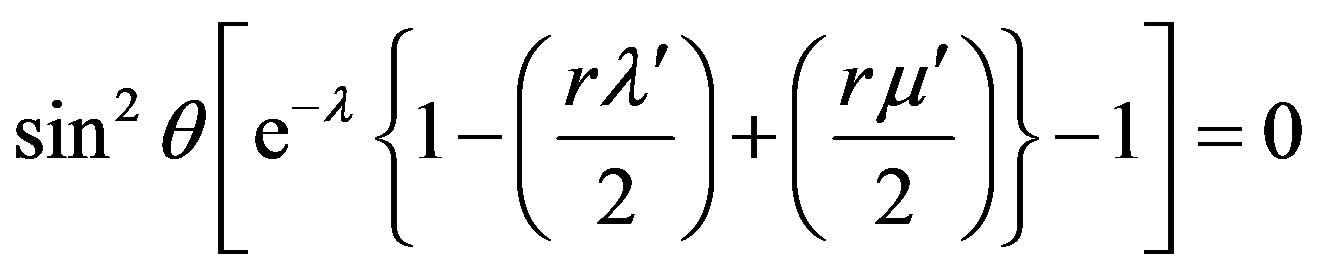 (12c)
(12c)
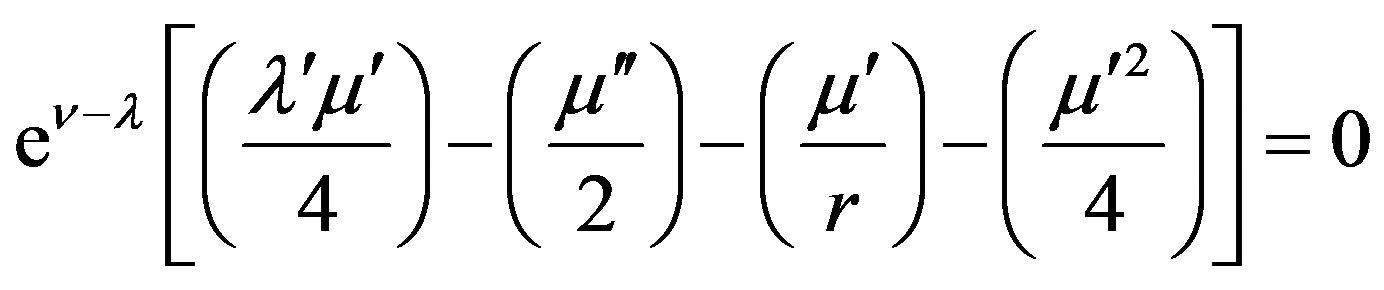 (12d)
(12d)
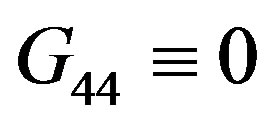 (12e)
(12e)
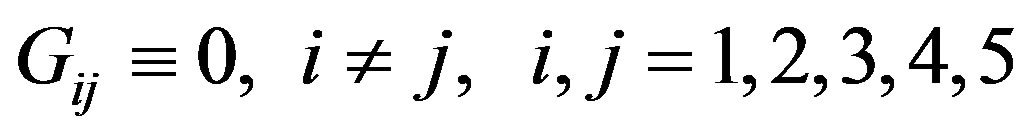 (12f)
(12f)
The solution of these equations is
 (13)
(13)
more generalized cases are under consideration.
3. Summary
In MKS (Meter-Kilogram-Second) system, Newton utilized three-dimensional space: length, breadth and height (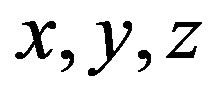 coordinates) with time as an external parameter. Einstein added one more dimension to the Universe that of time which is also everywhere present. In MKS System Kilogram (mass) remained to be utilized. We now take mass, which also includes energy due to Einstein’s energy-mass equivalence relation:
coordinates) with time as an external parameter. Einstein added one more dimension to the Universe that of time which is also everywhere present. In MKS System Kilogram (mass) remained to be utilized. We now take mass, which also includes energy due to Einstein’s energy-mass equivalence relation: , as the fifth dimension of the Universe, thereby making MKS system fully utilized, and generating five dimensional universe and solving Einstein’s field equations, in some simple cases. Work is going on to translate the whole of Maxwell’s electrodynamics into five-dimensional space to apply it to solve some problems in the general theory of relativity as well.
, as the fifth dimension of the Universe, thereby making MKS system fully utilized, and generating five dimensional universe and solving Einstein’s field equations, in some simple cases. Work is going on to translate the whole of Maxwell’s electrodynamics into five-dimensional space to apply it to solve some problems in the general theory of relativity as well.
4. Acknowledgements
This research is conducted with the support of a University Malaya Research Grant (UMRG-Project No. RG142- 11-AFR) from the University of Malaya (UM) of the first author. The second author JJR also thanks Department of Physics, University of Malaya Kuala Lumpur, Somaiya Trust, Mumbai & Saurashtra Education Foundation, Rajkot for their financial support.
REFERENCES
- A. Einstein, “On the Electrodynamics of Moving Bodies,” Annalen der Physik, Vol. 17, No. 891, 1905, p. 50.
- A. Einstein, et al., “The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity,” Dover, Kent, 1952.
- K. Schwarzschild, “On the Gravitational Field of a Mass Point According to Einstein’s Theory,” Sitzungsber. Preuss. Akad. Wiss., Phys. Math. Kl, Vol. 3, 1916, pp. 189-196.
- T. Kaluza, “Zum Unitätsproblem der Physik,” Sitz. Preuss. Akad. Wiss. Phys. Math. K, Vol. 1, 1921, p. 966.
- O. Klein, “Quantentheorie und Fünfdimensionale Relativitätstheorie,” Zeitschrift für Physik, Vol. 37, No. 12, 1926, pp. 895-906. doi:10.1007/BF01397481
- J. P. De Leon, “Cosmological Models in a Kaluza-Klein Theory with Variable Rest Mass,” General Relativity and Gravitation, Vol. 20, No. 6, 1988, pp. 539-550. doi:10.1007/BF00758909
- P. S. Wesson, “Five-Dimensional Physics: Classical and Quantum Consequences of Kaluza-Klein Cosmology,” World Scientific, Singapore City, 2006.

