International Journal of Astronomy and Astrophysics
Vol.1 No.4(2011), Article ID:16375,5 pages DOI:10.4236/ijaa.2011.14028
Application of a Probabilistic Neural Network in Radial Velocity Curve Analysis of the Spectroscopic Binary Stars ROXR1 14, RX J1622.7-2325Nw, RR Lyn, 12 Boo and HR 6169
1Department of Civil Engineering, Islamic Azad University, Anar Branch, Anar, Iran
2Department of Science and Engineering, Islamic Azad University, Marivan Branch, Marivan, Iran
E-mail: *K.Ghaderi.60@ gmail.com
Received September 20, 2011; revised October 26, 2011; accepted November 23, 2011
Keywords: Stars: Binaries: Eclipsing, Stars: Binaries: Spectroscopic
Abstract
Using measured radial velocity data of five double-lined spectroscopic binary systems ROXR1 14, RX J1622.7-2325Nw, RR Lyn, 12 Boo and HR 6169, we find corresponding orbital and spectroscopic elements via a Probabilistic Neural Network (PNN). Our numerical results are in good agreement with those obtained by others using more traditional methods.
1. Introduction
Analysis of both light and radial velocity (hereafter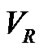 ) curves of binary systems helps us to determine the masses and radii of individual stars. One historically well-known method to analyze the
) curves of binary systems helps us to determine the masses and radii of individual stars. One historically well-known method to analyze the 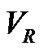 curve is that of Lehmann-Filhés [1]. Other methods were also introduced by Sterne [2] and Petrie [3]. The different methods of the
curve is that of Lehmann-Filhés [1]. Other methods were also introduced by Sterne [2] and Petrie [3]. The different methods of the  curve analysis have been reviewed in ample detail by Karami & Teimoorinia [4]. Karami
curve analysis have been reviewed in ample detail by Karami & Teimoorinia [4]. Karami 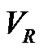 Teimoorinia [4] also proposed a new non-linear least squares velocity curve analysis technique for spectroscopic binary stars. They showed the validity of their new method to a wide range of different types of binary See Karami & Mohebi [5-7] and Karami et al. [8].
Teimoorinia [4] also proposed a new non-linear least squares velocity curve analysis technique for spectroscopic binary stars. They showed the validity of their new method to a wide range of different types of binary See Karami & Mohebi [5-7] and Karami et al. [8].
Probabilistic Neural Network (PNN) is a new tool to derive the orbital parameters of the spectroscopic binary stars. In this method the time consumed is considerably less than the method of Lehmann-Filhés and even less than the non-linear regression method proposed by Karami & Teimoorinia [4].
In the present paper we use a Probabilistic Neural Network (PNN) to find the optimum match to the four parameters of the 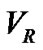 curves of the five double-lined spectroscopic binary systems: ROXR1 14, RX J1622.7- 2325Nw, RR Lyn, 12 Boo and HR 6169. Our aim is to show the validity of our new method to a wide range of different types of binary.
curves of the five double-lined spectroscopic binary systems: ROXR1 14, RX J1622.7- 2325Nw, RR Lyn, 12 Boo and HR 6169. Our aim is to show the validity of our new method to a wide range of different types of binary.
ROXR1 14 and RX J1622.7-2325Nw are very young, low-mass pre-main sequence (PMS) stars, and doublelined spectroscopic binaries that recently discovered in the Ophiuchus star forming region. The spectral type of both systems is M1 and the orbital period of ROXR1 14 is P = 5.72 days and the orbital period of RX J1622.7- 2325Nw is P = 3.23 days [9]. RR Lyn is a double-lined spectroscopic binary with a well-determined orbital inclination and primary and secondary masses of 1.927 ± 0.008 and 1.507 ± 0.004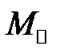 , respectively. The components have spectral classes of A3/A8/A6 and the orbital period is P = 9.945080 days [10]. 12 Boo is a double-lined eclipsing binary system with a primary and secondary masses of 1.416 ± 0.003 and 1.375 ± 0.002
, respectively. The components have spectral classes of A3/A8/A6 and the orbital period is P = 9.945080 days [10]. 12 Boo is a double-lined eclipsing binary system with a primary and secondary masses of 1.416 ± 0.003 and 1.375 ± 0.002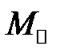 , respectively. The two components have very similar mass and the system’s combined spectral type is F8 IV and the orbital period is P = 9.6045529 days [10]. HR 6169 is a double-lined spectroscopic binary and consists of primary and secondary components. The minimum masses of the primary and secondary are 2.20 ± 0.01 and 1.64 ± 0.02
, respectively. The two components have very similar mass and the system’s combined spectral type is F8 IV and the orbital period is P = 9.6045529 days [10]. HR 6169 is a double-lined spectroscopic binary and consists of primary and secondary components. The minimum masses of the primary and secondary are 2.20 ± 0.01 and 1.64 ± 0.02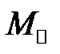 , respectively. This system have spectral classes of A2 V and the orbital period is P = 10.559435 days [10].
, respectively. This system have spectral classes of A2 V and the orbital period is P = 10.559435 days [10].
This paper is organized as follows. In Sect. 2, we introduce a Probabilistic Neural Network (PNN) to estimate the four parameters of the 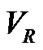 curve. In Section 3, the numerical results are reported, while the conclusions are given in Section 4.
curve. In Section 3, the numerical results are reported, while the conclusions are given in Section 4.
2. 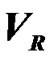 Curve Parameters Estimation by the Probabilistic Neural Network (PNN)
Curve Parameters Estimation by the Probabilistic Neural Network (PNN)
Following Smart [11], the 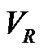 of a star in a binary system is defined as follows
of a star in a binary system is defined as follows
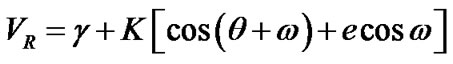 (1)
(1)
where 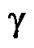 is the
is the 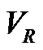 of the center of mass of system with respect to the sun. Also K is the amplitude of the
of the center of mass of system with respect to the sun. Also K is the amplitude of the 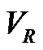 of the star with respect to the center of mass of the binary. Furthermore
of the star with respect to the center of mass of the binary. Furthermore 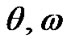 and
and 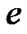 are the angular polar coordinate (true anomaly), the longitude of periastron and the eccentricity, respectively.
are the angular polar coordinate (true anomaly), the longitude of periastron and the eccentricity, respectively.
Here we apply the PNN method to estimate the four orbital parameters, 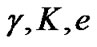 and
and 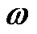 of the
of the  curve in Equation (1). In this work, for the identification of the observational
curve in Equation (1). In this work, for the identification of the observational  curves, the input vector is the fitted
curves, the input vector is the fitted 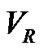 curve of a star. The PNN is first trained to classify
curve of a star. The PNN is first trained to classify  curves corresponding to all the possible combinations of
curves corresponding to all the possible combinations of 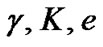 and
and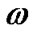 . For this one can synthetically generate
. For this one can synthetically generate 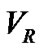 curves given by Equation (1) for each combination of the parameters:
curves given by Equation (1) for each combination of the parameters:
• 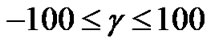 in steps of 1;
in steps of 1;
• 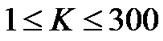 in steps of 1;
in steps of 1;
•  in steps of 0.001;
in steps of 0.001;
• 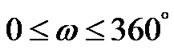 in steps of 5;
in steps of 5;
This gives a very big set of k pattern groups, where k denotes the number of different  classes, one class for each combination of
classes, one class for each combination of 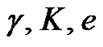 and
and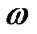 . Since this very big number of different
. Since this very big number of different 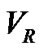 classes leads to some computational limitations, hence one can first start with the big step sizes. Note that from Petrie [3], one can guess
classes leads to some computational limitations, hence one can first start with the big step sizes. Note that from Petrie [3], one can guess 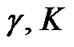 and
and 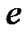 from a
from a 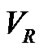 curve. This enable one to limit the range of parameters around their initial guesses. When the preliminary orbit was derived after several stages, then one can use the above small step sizes to obtain the final orbit. The PNN has four layers including input, pattern, summation, and output layers, respectively (see figure 5 in Bazarghan et al. [12]). When an input vector is presented, the pattern layer computes distances from the input vector to the training input vectors and produces a vector whose elements indicate how close the input is to a training input. The summation layer sums these contributions for each class of inputs to produce as its net output a vector of probabilities. Finally, a competitive transfer function on the output layer picks the maximum of these probabilities, and produces a 1 for that class and a 0 for the other classes [13,14]. Thus, the PNN classifies the input vector into a specific k class labeled by the four parameters
curve. This enable one to limit the range of parameters around their initial guesses. When the preliminary orbit was derived after several stages, then one can use the above small step sizes to obtain the final orbit. The PNN has four layers including input, pattern, summation, and output layers, respectively (see figure 5 in Bazarghan et al. [12]). When an input vector is presented, the pattern layer computes distances from the input vector to the training input vectors and produces a vector whose elements indicate how close the input is to a training input. The summation layer sums these contributions for each class of inputs to produce as its net output a vector of probabilities. Finally, a competitive transfer function on the output layer picks the maximum of these probabilities, and produces a 1 for that class and a 0 for the other classes [13,14]. Thus, the PNN classifies the input vector into a specific k class labeled by the four parameters 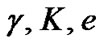 and
and  because that class has the maximum probability of being correct.
because that class has the maximum probability of being correct.
3. Numerical Results
Here, we use the PNN to derive the orbital elements for the five different double-lined spectroscopic systems ROXR1 14, RX J1622.7-2325Nw, RR Lyn, 12 Boo and HR 6169. Using measured 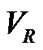 data of the two components of these systems obtained by Rosero et al. [9] for ROXR1 14 and RX J1622.7-2325Nw and Tomkin & Fekel [10] for RR Lyn, 12 Boo and HR 6169, the fitted velocity curves are plotted in terms of the photometric phase in Figures 1-5.
data of the two components of these systems obtained by Rosero et al. [9] for ROXR1 14 and RX J1622.7-2325Nw and Tomkin & Fekel [10] for RR Lyn, 12 Boo and HR 6169, the fitted velocity curves are plotted in terms of the photometric phase in Figures 1-5.
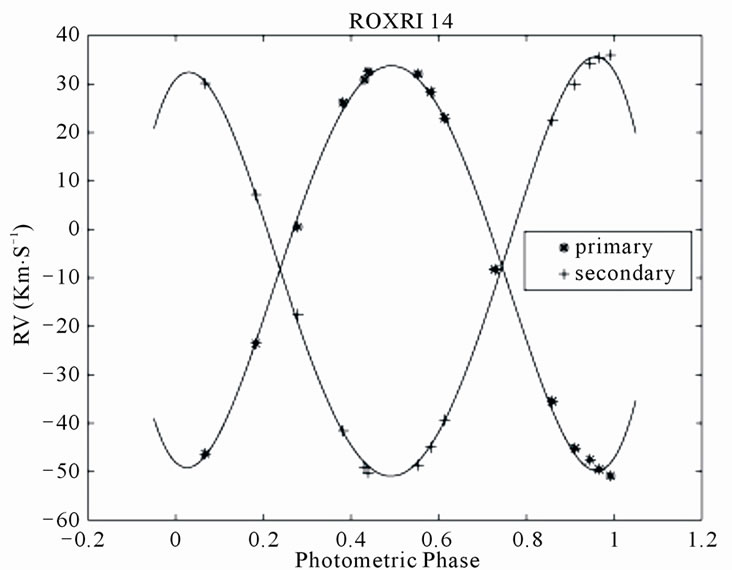
Figure 1. Radial velocities of the primary and secondary components of ROXR1 14 plotted against the photometric phase. The observational data have been measured by Rosero et al. [9].
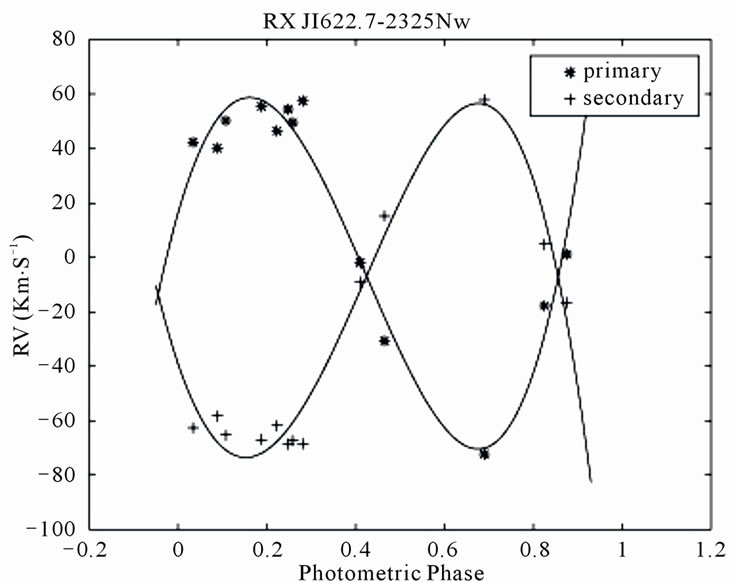
Figure 2. Radial velocities of the primary and secondary components of RX J1622.7-2325Nw plotted against the photometric phase. The observational data have been measured by Rosero et al. [9].
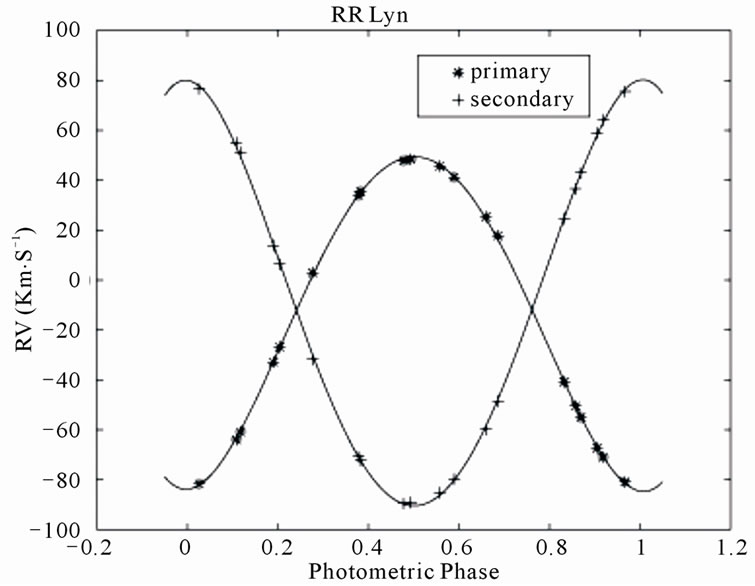
Figure 3. Radial velocities of the primary and secondary components of RR Lyn plotted against the photometric phase. The observational data have been measured by Tomkin & Fekel [10].
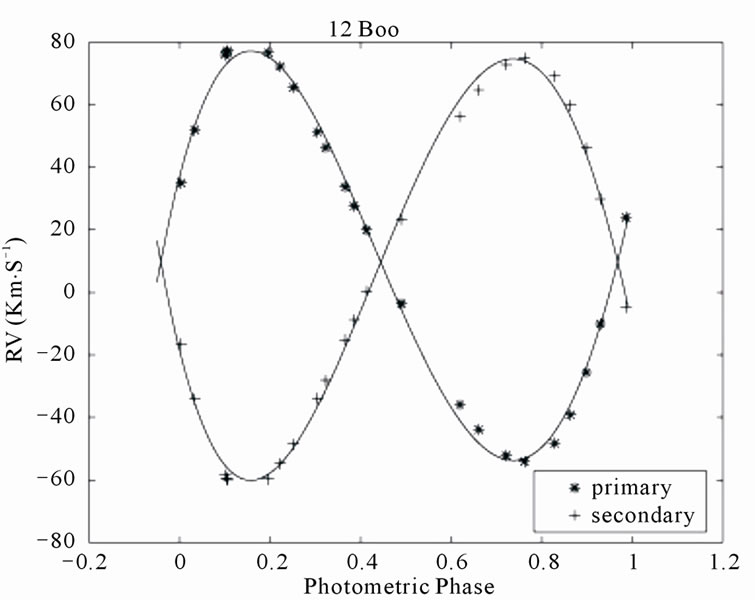
Figure 4. Radial velocities of the primary and secondary components of 12 Boo plotted against the photometric phase. The observational data have been measured by Tomkin & Fekel [10].
The orbital parameters obtaining from the PNN for ROXR1 14, RX J1622.7-2325Nw, RR Lyn, 12 Boo and HR 6169 are tabulated in Tables 1, 3, 5, 7 and 9, respectively. Tables show that the results are in good accordance with the those obtained by Rosero et al. [9] for ROXR1 14 and RX J1622.7-2325Nw and Tomkin & Fekel [10] for RR Lyn, 12 Boo and HR 6169.
Note that the Gaussian errors of the orbital parameters in Tables 1, 3, 5, 7 and 9 are the same selected steps for generating 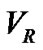 curves, i.e.
curves, i.e. 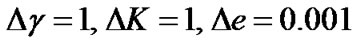 and
and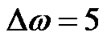 . These are close to the observational errors reported in the literature. Regarding the estimated errors, following Specht [14], the error of the decision boundaries depends on the accuracy with which the underlying
. These are close to the observational errors reported in the literature. Regarding the estimated errors, following Specht [14], the error of the decision boundaries depends on the accuracy with which the underlying
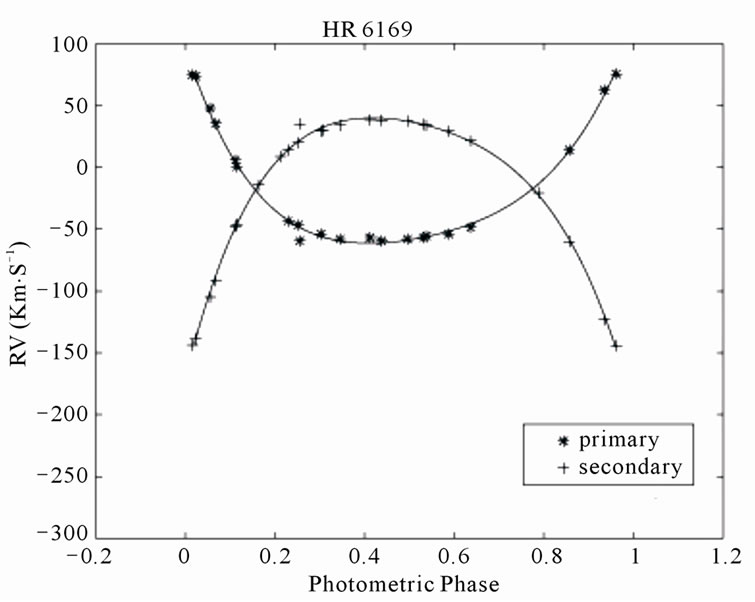
Figure 5. Radial velocities of the primary and secondary components of HR 6169 plotted against the photometric phase. The observational data have been measured by Tomkin & Fekel [10].

Table 1. Orbital parameters of ROXR1 14.
Probability Density Functions (PDFs) are estimated. Parzen [15] proved that the expected error gets smaller as the estimate is based on a large data set. This definition of consistency is particularly important since it means that the true distribution will be approached in a smooth manner. Specht [14] showed that a very large value of the smoothing parameter would cause the estimated errors to be Gaussian regardless of the true underlying distribution and the misclassification rate is stable and does not change dramatically with small changes in the smoothing parameter.
The combined spectroscopic elements including  ,
, 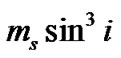 ,
,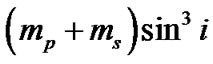 ,
, 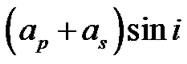 and
and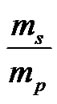 are calculated by substituting the estimated parameters
are calculated by substituting the estimated parameters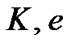 and
and 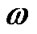 into Equations (3), (15) and (16) in Karami and Teimoorinia [4]. The results obtained for the five systems are tabulated in Tables 2, 4, 6, 8 and 10 show that our results are in good agreement with the those obtained by Rosero et al. [9] for ROXR1 14 and RX J1622.7-2325Nw and Tomkin & Fekel [10] for RR Lyn, 12 Boo and HR 6169, respectively. Here the errors
into Equations (3), (15) and (16) in Karami and Teimoorinia [4]. The results obtained for the five systems are tabulated in Tables 2, 4, 6, 8 and 10 show that our results are in good agreement with the those obtained by Rosero et al. [9] for ROXR1 14 and RX J1622.7-2325Nw and Tomkin & Fekel [10] for RR Lyn, 12 Boo and HR 6169, respectively. Here the errors
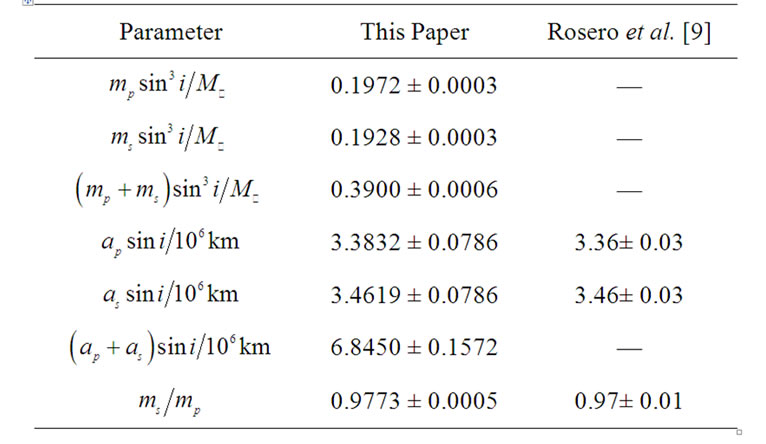
Table 2. Combined spectroscopic elements of ROXR1 14.
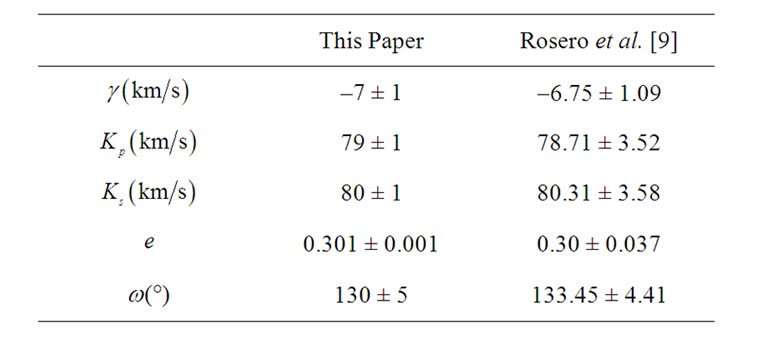
Table 3. Orbital parameters of RX J1622.7-2325Nw.
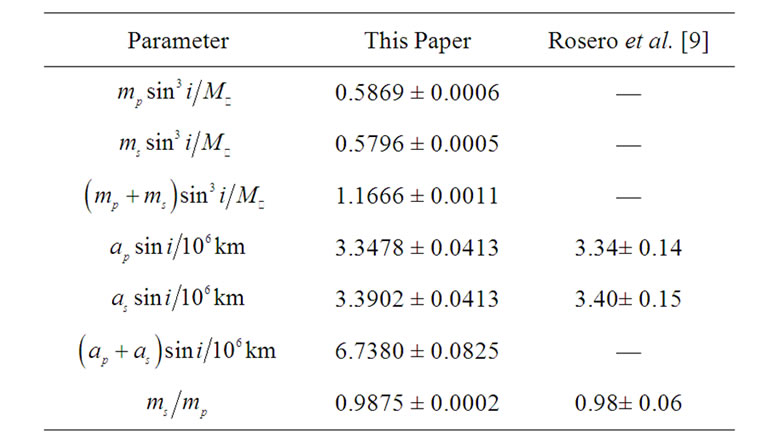
Table 4. Combined spectroscopic elements of RX J1622.7- 2325Nw.

Table 5. Orbital parameters of RR Lyn.
of the combined spectroscopic elements in Tables 2, 4, 6, 8 and 10 are obtained by the help of orbital parameters errors. See again Equations (3), (15) and (16) in Karami and Teimoorinia [4].
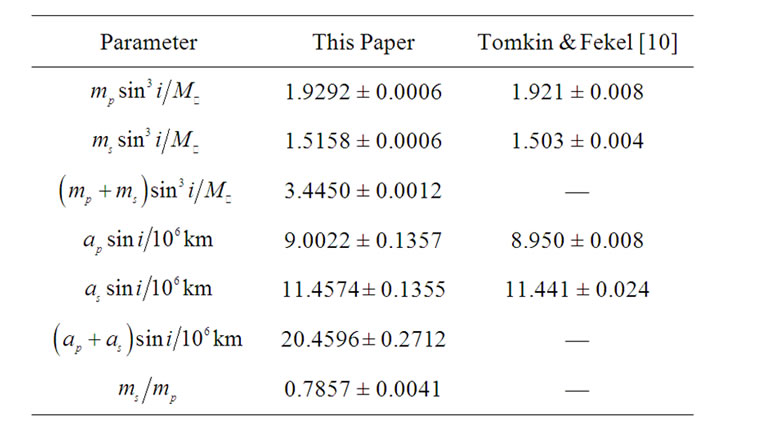
Table 6. Combined spectroscopic elements of RR Lyn.
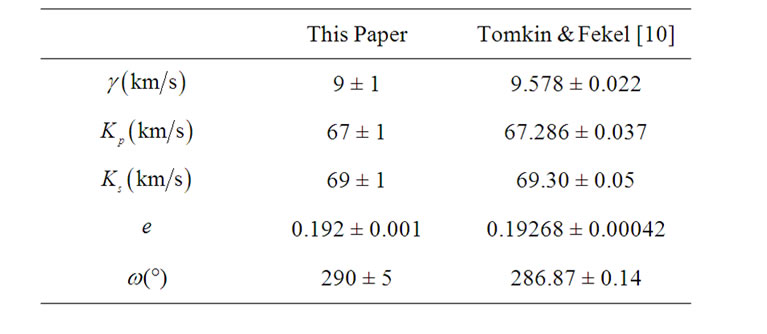
Table 7. Orbital parameters of 12 Boo.
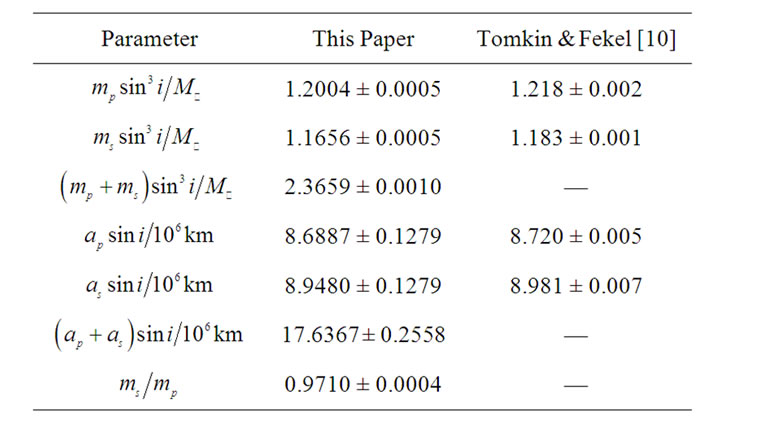
Table 8. Combined spectroscopic elements of 12 Boo.

Table 9. Orbital parameters of HR 6169.
4. Conclusions
A Probabilistic Neural Network to derive the orbital elements of spectroscopic binary stars was applied. PNNs
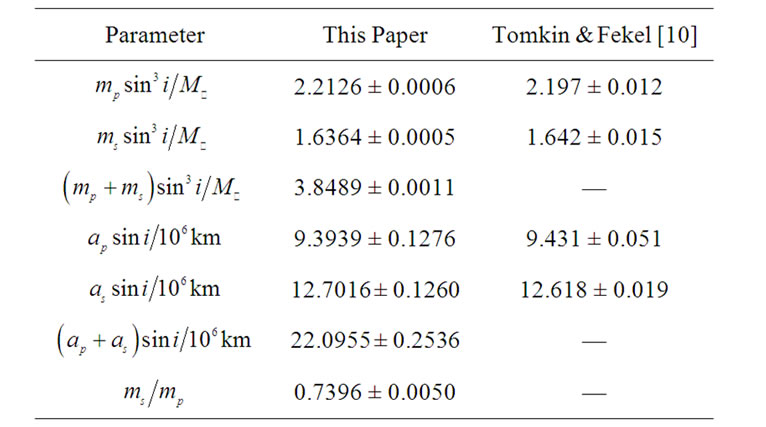
Table 10. Combined spectroscopic elements of HR 6169.
are used in both regression (including parameter estimation) and classification problems. However, one can discretize a continuous regression problem to such a degree that it can be represented as a classification problem [13,14], as we did in this work.
Using the measured 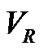 data of ROXR1 14, RX J1622.7-2325Nw, RR Lyn, 12 Boo and HR 6169 obtained by Rosero et al. [9] and Tomkin & Fekel [10], we find the orbital elements of these systems by the PNN. Our numerical results show that the results obtained for the orbital and spectroscopic parameters agree well with those obtained by others using traditional methods.
data of ROXR1 14, RX J1622.7-2325Nw, RR Lyn, 12 Boo and HR 6169 obtained by Rosero et al. [9] and Tomkin & Fekel [10], we find the orbital elements of these systems by the PNN. Our numerical results show that the results obtained for the orbital and spectroscopic parameters agree well with those obtained by others using traditional methods.
This method is applicable to orbits of all eccentricities and inclination angles. In this method the time consumed is considerably less than the method of Lehmann-Filhés. It is also more accurate as the orbital elements are deduced from all points of the velocity curve instead of four in the method of Lehmann-Filhés. The present method enables one to vary all of the unknown parameters 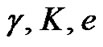 and
and 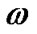 simultaneously instead of one or two of them at a time. It is possible to make adjustments in the elements before the final result is obtained. There are some cases, for which the geometrical methods are inapplicable, and in these cases the present one may be found useful. One such case would occur when observations are incomplete because certain phases could have not been observed. Another case in which this method is useful is that of a star attended by two dark companions with commensurable periods. In this case the resultant velocity curve may have several unequal maxima and the geometrical methods fail altogether.
simultaneously instead of one or two of them at a time. It is possible to make adjustments in the elements before the final result is obtained. There are some cases, for which the geometrical methods are inapplicable, and in these cases the present one may be found useful. One such case would occur when observations are incomplete because certain phases could have not been observed. Another case in which this method is useful is that of a star attended by two dark companions with commensurable periods. In this case the resultant velocity curve may have several unequal maxima and the geometrical methods fail altogether.
5. Acknowledgements
This work has been supported financially by Islamic Azad University, Marivan Branch, Iran.
6. References
[1] R. Lehmann-Filhés, “Ueber die Bestimmung einer Doppelsternbahn aus Spectroskopischen Messungen der im Visionsradius Liegenden Geschwindigkeitscomponente,” Astronomische Nachrichten, Vol. 136, No. 2, 1894, pp. 17-30.
[2] T. E. Sterne, “Notes on Binary Stars. V. The Determination by Least-Squares of the Elements of Spectroscopic Binaries,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 27, No. 3, 1941, PP. 175-181.
[3] R. M. Petrie, “Astronomical Techniques,” University of Chicago Press, Chicago, 1960.
[4] K. Karami and H. Teimoorinia, “Velocity Curve Analysis of the Spectroscopic Binary Stars by the Non-linear Least Squares,” Astrophysics and Space Science, Vol. 311, No. 4, 2007, pp. 435-442.
[5] K. Karami and R. Mohebi, “Velocity Curve Analysis of Spectroscopic Binary Stars AI Phe, GM Dra, HD 93917 and V502 Oph by Nonlinear Regression,” Chinese Journal of Astronomy and Astrophysics, Vol. 7, No. 4, 2007, pp. 558-564.
[6] K. Karami and R. Mohebi, “Velocity Curve Analysis of Spectroscopic Binary Stars PV Pup, HD141929, EE Cet and V921 Her by Nonlinear Regression,” Journal of Astrophysics and Astronomy, Vol. 28, 2007, pp. 217-230.
[7] K. Karami and R. Mohebi, “Velocity Curve Studies of Spectroscopic Binary Stars V380 Cygni, V401 Cyg, V523 Cas, V373 Cas and V2388 Oph,” Journal of Astrophysics and Astronomy, Vol. 30, No. 3-4, 2009, pp. 153-163.
[8] K. Karami, R. Mohebi and M. M. Soltanzadeh, “Application of a New Non-linear Least Squares Velocity Curve Analysis Technique for Spectroscopic Binary Stars,” Astrophysics and Space Science, Vol. 318, No. 1-2, 2008, pp. 69-71.
[9] V. Rosero, L. Prato, L. H. Wasserman and B. Rodgers, “Orbital Solutions for Two Young, Low-Mass Spectroscopic Binaries in Ophiuchus,” The Astronomical Journal, Vol. 141, No. 1, 2011, Article ID: 13.
[10] J. Tomkin and F. C. Fekel, “New Precision Orbits of Bright Double-lined Spectroscopic Binaries RR Lyn, 12 Boo, and HR 6169,” The Astronomical Journal, Vol. 131, No. 5, 2006, pp. 2652-2663.
[11] W. M. Smart, “Textbook on Spherical Astronomy,” 6th Edition, Cambridge University Press, Cambridge, 1990.
[12] M. Bazarghan, H. Safari, D. E. Innes, E. Karami and S. K. Solanki, “A Nanoflare Model for Active Region Radiance: Application of Artificial Neural Networks,” Astronomy and Astrophysics, Vol. 492, No. 1, 2008, pp. L13-L16.
[13] D. F. Specht, “Probabilistic Neural Networks for Classification, Mapping, or Associative Memory,” Proceedings of IEEE International Conference on Neural Networks, San Diego, 24-27 July 1988, pp.525-532.
[14] D. F. Specht, “Probabilistic Neural Networks,” Neural Networks, Vol. 3, No. 1, 1990, pp. 109-118. doi:10.1016/0893-6080(90)90049-Q
[15] E. Parzen, “On Estimation of a Probability Density Function and Mode,” Annals of Mathematical Statistics, Vol. 33, No. 3, 1962, pp. 1065-1076. doi:10.1214/aoms/1177704472

