International Journal of Astronomy and Astrophysics
Vol.1 No.2(2011), Article ID:5580,6 pages DOI:10.4236/ijaa.2011.12010
An Approximation Algorithm for the Solution of Astrophysics Equations Using Rational Scaled Generalized Laguerre Function Collocation Method Based on Transformed Hermite-Gauss Nodes
1Department of Computer Engineering, Islamic Azad University, Science and Research Branch, Tehran, Iran
2Department of Applied Mathematics And Computer Sciences, Shahed University, Tehran, Iran
3Department of Science, Islamic Azad University, Branch of Marivan, Marivan, Iran
E-mail: alipirkhedri @ gmail.com
Received March 12, 2011; revised April 28, 2011; accepted May 5, 2011
Keywords: Lane-Emden Equation, Generalized Laguerre Functions, Collocation Method, Hermite-Gauss Nodes, Nonlinear ODE, Semi-Infinite
Abstract
In this paper we propose a collocation method for solving Lane-Emden type equation which is nonlinear ordinary differential equation on the semi-infinite domain. This equation is categorized as singular initial value problems. We solve this equation by the generalized Laguerre polynomial collocation method based on Hermite-Gauss nodes. This method solves the problem on the semi-infinite domain without truncating it to a finite domain and transforming domain of the problem to a finite domain. In addition, this method reduces solution of the problem to solution of a system of algebraic equations.
1. Introduction
There are many problems in science and engineering arising in unbounded domains.
Spectral methods are famous ways to solve these kinds of problems. The most common approach on spectral methods, that is used in this paper too, is through the use of functions that are orthogonal over unbounded domains, such as the Hermite and the Laguerre functions [1-8].
The second approach is reformulating the original problem in the semi-infinite domain to a singular problem in a bounded domain by variable transformation and then using the Jacobi polynomials to approximate the resulting singular problem [9-11]. A third approach of spectral method is based on rational orthogonal functions, for example, Christov [12] and Boyd [13,14] developed some spectral methods on unbounded intervals by using mutually orthogonal systems of rational functions. Boyd [14] defined a new spectral basis, named rational Chebyshev functions on the semi-infinite interval, by mapping it to the Chebyshev polynomials. Guo et al. [15] proposed and analyzed a set of Legendre rational functions which are mutually orthogonal in 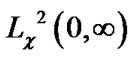 with a non-uniform weight function
with a non-uniform weight function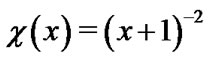 . A forth approach is replacing the semi-infinite domain with
. A forth approach is replacing the semi-infinite domain with 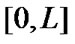 interval by choosing L, sufficiently large, this method is named as the domain truncation [16].
interval by choosing L, sufficiently large, this method is named as the domain truncation [16].
In this paper, we investigate the Generalized Laguerrecollocation method based on Hermite-Gauss Nodes which is another approach for solving ODEs on the half line. In [7] proposed spectral methods using Laguerre functions and analyzed for model elliptic equations on regular unbounded domains. It is shown that spectralGalerkin approximations based on Laguerre functions are stable and convergent with spectral accuracy in the Sobolev spaces. Siyyam [8] applied two numerical methods for solving initial value problem differential equations using the Laguerre Tau method. He generated linear systems and solved them. Maday, et al. [6] proposed a Laguerre type spectral method for solving partial differential equations. They introduced a general presentation of the method and a description of the derivation discretization matrices and then determined the optimum estimations in the adapted Hilbert norms.
2. The Lane-Emden Equation
This equation is one of the basic equations in the theory of stellar structure and has been the focus of many studies [17-21]. This equation describes the temperature variation of a spherical gas cloud under the mutual attraction of its molecules and subject to the laws of classical thermodynamics. The polytropic theory of stars essentially follows out of thermodynamic considerations, that deal with the issue of energy transport, through the transfer of material between different levels of the star. We simply begin with the Poisson equation and the condition for hydrostatic equilibrium:
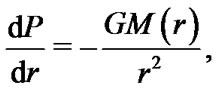 (1)
(1)
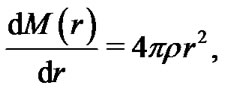 (2)
(2)
where 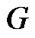 is the gravitational constant,
is the gravitational constant,  is the pressure,
is the pressure, 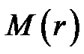 is the mass of a star at a certain radius
is the mass of a star at a certain radius , and
, and 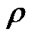 is the density, at a distance
is the density, at a distance 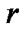 from the center of a spherical star. Combination of these equations yields the following equation, which as should be noted, is an equivalent form of the Poisson Equation.
from the center of a spherical star. Combination of these equations yields the following equation, which as should be noted, is an equivalent form of the Poisson Equation.
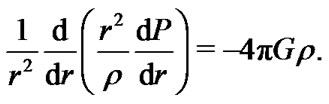 (3)
(3)
From these equations one can obtain the Lane-Emden equation through the simple supposition that the density is simply related to the density, while remaining independent of the temperature. We already know that in the case of a degenerate electron gas that the pressure and density are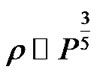 , assuming that such a relation exists for other states of the star we are led to consider a relation of the following form:
, assuming that such a relation exists for other states of the star we are led to consider a relation of the following form:
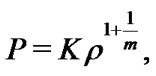 (4)
(4)
where K and m are constants, at this point it is important to note that m is the polytropic index which is related to the ratio of specific heats of the gas comprising the star. Based upon these assumptions we can insert this relation into our first equation for the hydrostatic equilibrium condition and from this rewrite equation to:
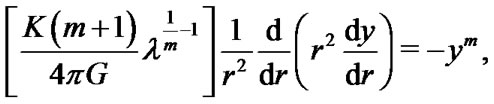 (5)
(5)
where the additional alteration to the expression for density has been inserted with 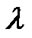 representing the central density of the star and
representing the central density of the star and 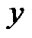 that of a related dimensionless quantity that are both related to
that of a related dimensionless quantity that are both related to 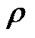 through the following relation
through the following relation
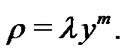 (6)
(6)
Additionally, if place this result into the Poisson equation, we obtain a differential equation for the mass, with a dependance upon the polytropic index m. Though the differential equation is seemingly difficult to solve, this problem can be partially alleviated by the introduction of an additional dimensionless variable x, given by the following:
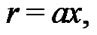 (7)
(7)
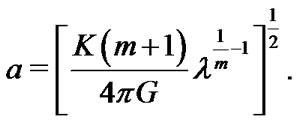 (8)
(8)
Inserting these relations into our previous relations we obtain the famous form of the Lane-Emden equation, given below:
 (9)
(9)
Taking this simple relation we will have the LaneEmden equation:
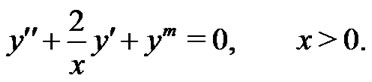 (10)
(10)
At this point it is also important to introduce the boundary conditions, which are based upon the following boundary conditions for hydrostatic equilibrium, and normalization consideration of the newly introduced quantities x and y. What follows for 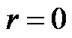 is:
is:
 (11)
(11)
As a result an additional condition must be introduced in order to maintain the condition of Equation (11) simultaneously:
 (12)
(12)
In other words, the boundary conditions are as follow:
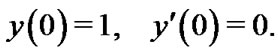 (13)
(13)
Physically interesting value of m lie in the interval [0, 5]. Exact soloution for Equation (??) are known only for  and 5. For other value of m the Lane-Emden equation is to be integrated numerically. In this paper, we solve it for
and 5. For other value of m the Lane-Emden equation is to be integrated numerically. In this paper, we solve it for 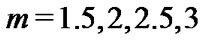 and 4.
and 4.
This paper is arranged as follows: in Section 3, we explain the formulation of rational scaled generalized Laguerre polynomials and Hermite functions required for our subsequent development. In Section 4, we summarize the application of the method for solving Lane-Emden equation and compare it with the existing methods in the literature. Finally we give a brief conclusion in the last section.
3. Rational Scaled Generalized Laguerre Polynomials and Hermite Functions Properties
This section is devoted to the introduction of the basic notions and working tools concerning orthogonal rational scaled generalized Laguerre polynomials and later we present some properties of Hermite function and Hermite-Gauss nodes.
3.1. Properties of Rational Scaled Generalized Laguerre Polynomials
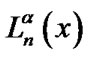 (generalized Laguerre polynomial) is the
(generalized Laguerre polynomial) is the 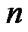 th eigenfunction of the Sturm-Liouville problem [2,22,23]:
th eigenfunction of the Sturm-Liouville problem [2,22,23]:
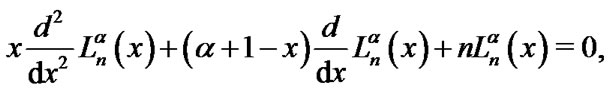
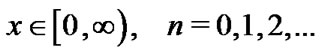 (14)
(14)
The generalized Laguerre polynomials are defined with the following recurrence formula:
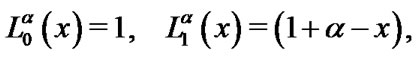
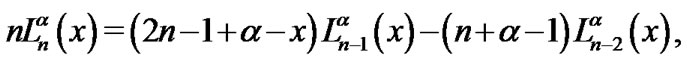
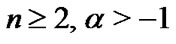 (15)
(15)
With the normalizing condition:
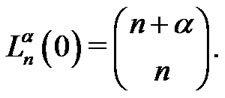 (16)
(16)
Let  denotes a non-negative, integrable, realvalued function over the interval
denotes a non-negative, integrable, realvalued function over the interval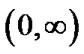 , we define
, we define
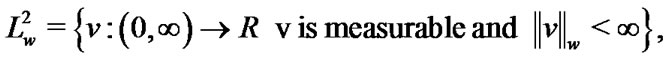
(17)
where
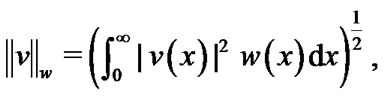 (18)
(18)
Is the norm induced by the inner product of the space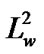 ,
,
 (19)
(19)
These are orthogonal polynomials for the weight function 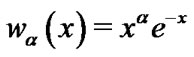 where
where 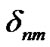 is the Kronecker delta function.
is the Kronecker delta function.
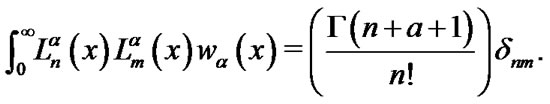
Let 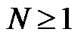 be an integer and we define
be an integer and we define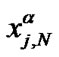 , j = 0,…,N-1 to be zeroes of
, j = 0,…,N-1 to be zeroes of 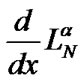 and the point x = 0. It can be shown that
and the point x = 0. It can be shown that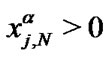 , j = 0,…,N-1 and the corresponding weights are:
, j = 0,…,N-1 and the corresponding weights are:

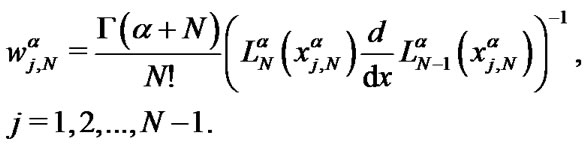
The following quadrature formula is known:

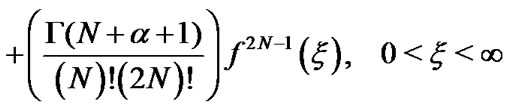 (20)
(20)
In particular, the second term on the right hand side vanishes when f is a polynomial of degree at most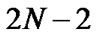 . For convenience, we shall set
. For convenience, we shall set 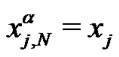 and
and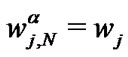 .
.
Pseudospectral approximations in unbounded domains by Laguerre polynomials lead to ill-conditioned algorithms and [24] introduced a scaling function and appropriate numerical procedures in order to limit these unpleasant phenomena.
We define scaled Laguerre functions 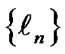 as follows:
as follows:
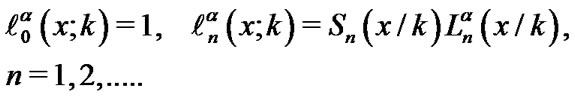 (21)
(21)
where  is a constant and
is a constant and 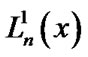 is generalized Laguerre polynomials for
is generalized Laguerre polynomials for 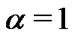 and
and 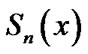 is defined as follows:
is defined as follows:
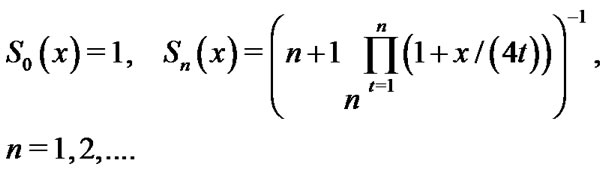 (22)
(22)
We denote scaled laguerre functions with (SLF).
Boyd [26] offered guidelines for optimizing the map parameter k where 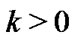 is the scaling parameter. From Equations (21) and (22), for
is the scaling parameter. From Equations (21) and (22), for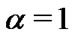 , we obtain the following formula:
, we obtain the following formula:
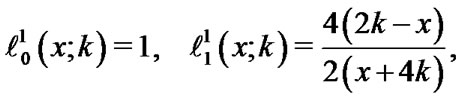
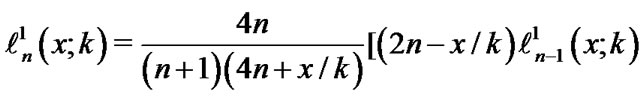
 (23)
(23)
This system is an orthogonal basis with weight function 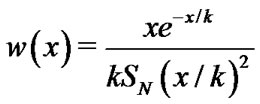 [24].
[24].
Some of the relations of scaled Laguerre functions and generalized Laguerre-Gauss-type interpolation were introduced by [24,25]. It is convenient to define the weights of 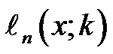 as follows:
as follows:
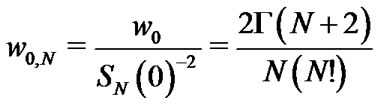
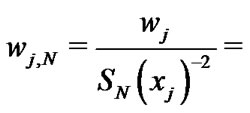
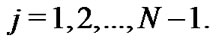
 (24)
(24)
where we noted that, for 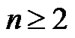
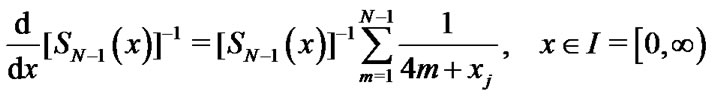
3.2. Properties of Hermite Functions
The Hermite function is defined for all 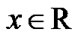 and can be written in recursive formula as follows [27-29]:
and can be written in recursive formula as follows [27-29]:
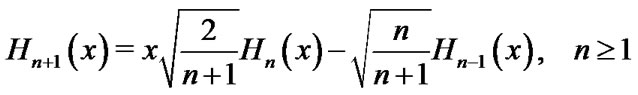
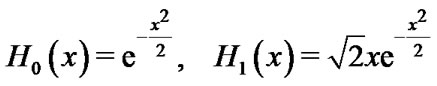 (25)
(25)
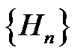 is an orthogonal system in
is an orthogonal system in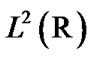 , i.e.,
, i.e.,
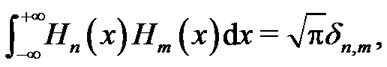 (26)
(26)
where  is the Kronecker delta function. Using the recurrence relation of Hermite polynomials and the above formula leads to
is the Kronecker delta function. Using the recurrence relation of Hermite polynomials and the above formula leads to
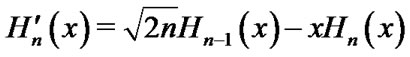
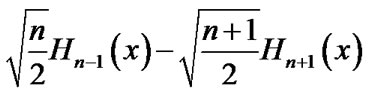
Let us define
 (27)
(27)
where 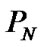 is the set of all Hermite polynomials of degree at most
is the set of all Hermite polynomials of degree at most . We now introduce the Gauss quadrature associated with the Hermite functions approach. Let
. We now introduce the Gauss quadrature associated with the Hermite functions approach. Let 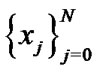 be the Hermite-Gauss nodes which can be N + 1 roots of
be the Hermite-Gauss nodes which can be N + 1 roots of 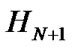 and define the weights
and define the weights
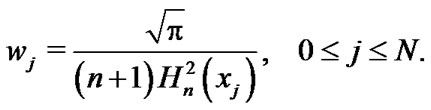 (28)
(28)
Then we have:
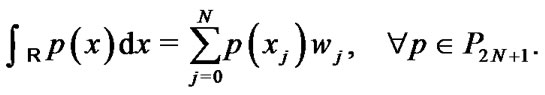
4. Solving the Lane-Emden Equation
To apply rational scaled generalized Laguerre collocation method to the standard Lane-Emden Equation introduced in Equation (10) with boundary conditions Equation (13), we define
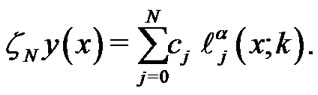 (29)
(29)
And we construct the residual function by substituting 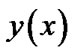 by
by 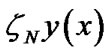 in the Lane-Emden Equation (10):
in the Lane-Emden Equation (10):
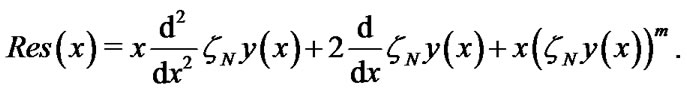
(30)
To find the unknown coefficients 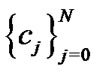 's, we equalize
's, we equalize 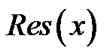 to zero at
to zero at 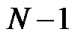 Hermite-Gauss Nodes
Hermite-Gauss Nodes
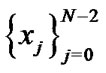 and we equalize boundary conditions in Equation (13) too, therefore we have:
and we equalize boundary conditions in Equation (13) too, therefore we have:
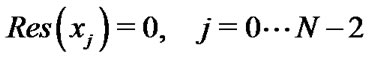
 (31)
(31)
But as mentioned before Lane-Emden equations are defined on the interval 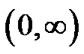 and we know properties of Hermite functions are derived in the infinite domain
and we know properties of Hermite functions are derived in the infinite domain . Also we know approximations can be constructed for infinite, semi-infinite and finite intervals. One of the approaches to construct Hermite-Gauss nodes on the interval
. Also we know approximations can be constructed for infinite, semi-infinite and finite intervals. One of the approaches to construct Hermite-Gauss nodes on the interval  which is used in the current paper, is to use a mapping, that is a change of variable of the form:
which is used in the current paper, is to use a mapping, that is a change of variable of the form:
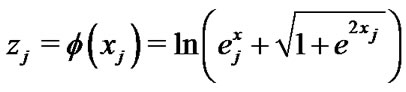 (32)
(32)
Where is the inverse map of
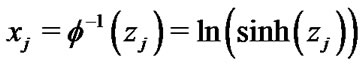 (33)
(33)
Finally to find the unknown coefficients 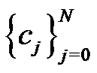 's, we have:
's, we have:
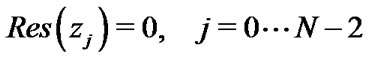 (34)
(34)
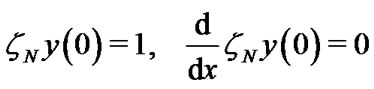 (35)
(35)
where zj is transformed root of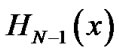 . Equations (34) and (35) gives N + 1 nonlinear algebraic equations which can be solved for the unknown coefficients
. Equations (34) and (35) gives N + 1 nonlinear algebraic equations which can be solved for the unknown coefficients 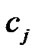 by using the well known Newton's method by Maple programming and we use
by using the well known Newton's method by Maple programming and we use

as starting points to obtain convergence of the method, consequently, 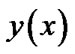 given in Equation (10) can be calculated.
given in Equation (10) can be calculated.
The resulting graph of Lane-Emden equation obtained by present method for 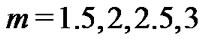 and 4 is shown in Figure 1.
and 4 is shown in Figure 1.
Tables 1 shows the comparison of the first zero of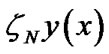 , between Padé approximation used by [17] and the present method for
, between Padé approximation used by [17] and the present method for 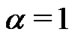 and
and 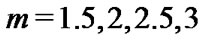 and 4 respectively.
and 4 respectively.
Tables 2 and 3 show the approximations of 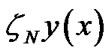 for standard Lane-Emden with
for standard Lane-Emden with  obtained by the rational scaled generalized Laguerre collocation method for
obtained by the rational scaled generalized Laguerre collocation method for  and those obtained by Horedt [20].
and those obtained by Horedt [20].
Table 4 shows the coefficients of rational scaled generalized Laguerre functions obtained by present method for the Lane-Emden equation with various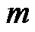 .
.
5. Summary and Conclusions
A set of rational scaled generalized laguerre orthogonal functions are proposed to solve Lane-Emden equation which is defined in the semi-infinite interval and has singularity at x = 0, by collocation method. But to approximate unknown function in Lane-Emden equation by collocation method we must equalize 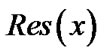 to zero at suitable points in
to zero at suitable points in  interval. Since Hermite functions are derived in the infinite domain
interval. Since Hermite functions are derived in the infinite domain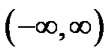 , we can't apply Hermite-Gauss nodes for equalizing
, we can't apply Hermite-Gauss nodes for equalizing 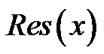 to zero, therefore we transform this nodes from
to zero, therefore we transform this nodes from 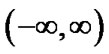 to
to
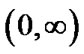 interval by a mapping
interval by a mapping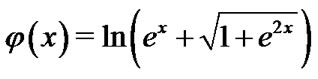 .
.

Figure 1. Lane-Emden equation graph obtained by present method for various m.
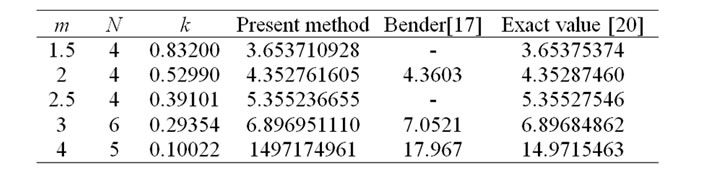
Table 1. Comparison the first zero of y(x), between Padé approximation used by [17] and the rational scaled generalized Laguerre collocation method for various m and a = 1.
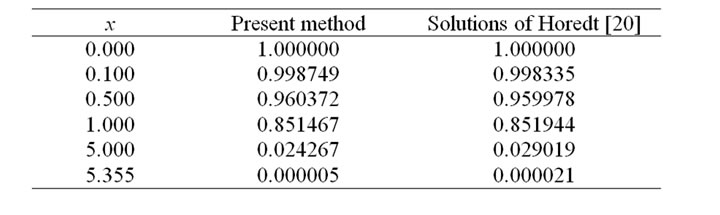
Table 2. Approximation of y(x) obtained by present method and solutions of Horedt [20] for m = 2.5 and a = 1, N = 4.
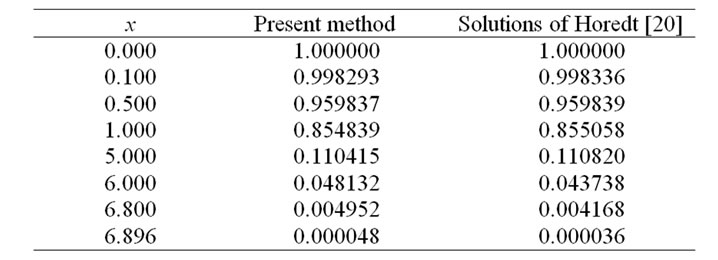
Table 3. Approximation of y(x) obtained by present method and solutions of Horedt [20] for m = 3 and a = 1, N = 6.

Table 4. Coefficients of the rational scaled generalized Laguerre functions of the Lane-Emden equation for various m.
Through the comparisons among the exact solutions of Horedt and the approximate solutions of Bender and the current work, it has been shown that the present work has provided more exact solutions for Lane-Emden equations.
6. References
[1] D. Funaro and O. Kavian, “Approximation of Some Diffusion Evolution Equations in Unbounded Domains by Hermite Functions,” Mathematics of Computation, Vol. 57, No. 196, 1991, pp. 597-619. doi:10.1090/S0025-5718-1991-1094949-X
[2] O. Coulaud, D. Funaro and O. Kavian, “Laguerre Spectral Approximation of Elliptic Problems in Exterior Domains,” Computer Methods in Applied Mechanics and Engineering, Vol. 80, No. 1-3, 1990, pp. 451-458. doi:10.1016/0045-7825(90)90050-V
[3] D. Funaro, “Computational Aspects of Pseudospectral Laguerre Approximations,” Applied Numerical Mathematics, Vol. 6, No. 6, 1990, pp. 447-457. doi:10.1016/0168-9274(90)90003-X
[4] B. Y. Guo, “Error Estimation of Hermite Spectral Method for Nonlinear Partial Differential Equations,” Mathematics of Computation, Vol. 68, No. 227, 1999, pp. 1067- 1078. doi:10.1090/S0025-5718-99-01059-5
[5] B. Y. Guo and J. Shen, “Laguerre-Galerkin Method for Nonlinear Partial Differential Equations on a Semi-Infinite Interval,” Numerische Mathematik, Vol. 86, No. 4, 2000, pp. 635-654. doi:10.1007/PL00005413
[6] Y. Maday, B. Pernaud-Thomas and H. Vandeven, “Reappraisal of Laguerre Type Spectral Methods,” La Recherche Aerospatiale, Vol. 6, 1985, pp. 13-35.
[7] J. Shen, “Stable and Efficient Spectral Methods in Unbounded Domains Using Laguerre Functions,” SIAM Journal on Numerical Analysis, Vol. 38, No. 4, 2000, pp. 1113-1133. doi:10.1137/S0036142999362936
[8] H. I. Siyyam, “Laguerre Tau Methods for Solving Higher Order Ordinary Differential Equations,” Journal of Computational Analysis and Applications, Vol. 3, No. 2, 2001, pp. 173-182. doi:10.1023/A:1010141309991
[9] B. Y. Guo, “Gegenbauer Approximation and Its Applications to Differential Equations on the Whole Line,” Journal of Mathematical Analysis and Applications, Vol. 226, No. 1, 1998, pp. 180-206. doi:10.1006/jmaa.1998.6025
[10] B. Y. Guo, “Jacobi Spectral Approximation and Its Applications to Differential Equations on the Half Line,” Journal of Computational Mathematics, Vol. 18, 2000, pp. 95-112.
[11] B. Y. Guo, “Jacobi Approximations in Certain Hilbert Spaces and Their Applications to Singular Differential Equations,” Journal of Mathematical Analysis and Applications, Vol. 243, No. 2, 2000, pp. 373-408. doi:10.1006/jmaa.1999.6677
[12] C. I. Christov, “A Complete Orthogonal System of Functions in L2 (−∞, ∞) Space,” SIAM Journal on Numerical Analysis, Vol. 42, No. 6, 1982, pp. 1337-1344.
[13] J. P. Boyd, “Spectral Methods Using Rational Basis Functions on an Infinite Interval,” Journal of Computational Physics, Vol. 69, No. 1, 1987, pp. 112-142. doi:10.1016/0021-9991(87)90158-6
[14] J. P. Boyd, “Orthogonal Rational Functions on a Semi- I nfinite Interval,” Journal of Computational Physics, Vol. 70, No. 1, 1987, pp. 63-88. doi:10.1016/0021-9991(87)90002-7
[15] B. Y. Guo, J. Shen and Z. Q. Wang, “A Rational Approximation and Its Applications to Differential Equations on the Half Line,” Journal of Scientific Computing, Vol. 15, No. 2, 2000, pp. 117-147. doi:10.1023/A:1007698525506
[16] J. P. Boyd, “Chebyshev and Fourier Spectral Methods,” 2nd Edition, Dover, New York, 2000.
[17] C. M. Bender, K. A. Milton, S. S. Pinsky, Jr. and L. M. Simmons, “A New Perturbative Approach to Nonlinear Problems,” Journal of Mathematical Physics, Vol. 30, No. 7, 1989, pp. 1447-1455. doi:10.1063/1.528326
[18] D. C. Biles, M. P. Robinson and J. S. Spraker, “A Generalization of the Lane-Emden Equation,” Journal of Mathematical Analysis and Applications, Vol. 273, No. 2, 2002, pp. 654-666. doi:10.1016/S0022-247X(02)00296-2
[19] G. Bluman, A. F. Cheviakov and M. Senthilvelan, “Solution and Asymptotic/Blow-up Behaviour of a Class of Nonlinear Dissipative Systems,” Journal of Mathematical Analysis and Applications, Vol. 339, No. 2, 2008, pp. 1199-1209. doi:10.1016/j.jmaa.2007.06.076
[20] G. P. Horedt, “Polytropes Applications in Astrophysics and Related Fields,” Klawer Academic Publishers, Dordrecht, 2004.
[21] K. Parand and A. Pirkhedri, “Sinc-Collocation Method for Solving Astrophysics Equations,” New Astronomy, Vol. 15, No. 6, 2010, pp. 533-537. doi:10.1016/j.newast.2010.01.001
[22] S. S. Bayin, “Mathematical Methods in Science and Engineering,” John Wiley & Sons, New York, 2006. doi:10.1002/0470047429
[23] G. Szegao, “Orthogonal Polynomils,” AMS, New York, 1939.
[24] D. Funaro, “Polynomial Approximation of Differential Equations,” Springer-Verlag, Berlin, 1992.
[25] V. Iranzo and A. Falques, “Some Spectral Approximations for Differential Equations in Un-Bounded Domains,” Computer Methods in Applied Mechanics and Engineering, Vol. 98, No. 1, 1992, pp. 105-126. doi:10.1016/0045-7825(92)90171-F
[26] J. P. Boyd, C. Rangan and P. H. Bucksbaum, “Pseudospectral Methods on a Semi-Infinite Interval with Application to the Hydrogen Atom: A Comparison of the Mapped Fourier-Sine Method with Laguerre Series and Rational Chebyshev Expansions,” Journal of Computational Physics, Vol. 188, No. 1, 2003, pp. 56-74. doi:10.1016/S0021-9991(03)00127-X
[27] J. Shen and L. Wang, “Some Recent Advances on Spectral Methods for Unbounded Domains,” Communications in Computational Physics, Vol. 5, No. 2, 2009, pp. 195- 241.
[28] J. Shen, T. Tang, “High Order Numerical Methods and Algorithms,” Chinese Science Press, Beijing, 2005.
[29] J. Shen, T. Tang and L. Wang, “Spectral Methods Algorithms, Analyses and Applications,” Springer, Berlin, 2010.

