Journal of Signal and Information Processing
Vol.05 No.04(2014), Article ID:51385,23 pages
10.4236/jsip.2014.54018
An Approximated Expression for the Residual ISI Obtained by Blind Adaptive Equalizer and Biased Input Signals
Nissim Panizel, Monika Pinchas
Department of Electrical and Electronic Engineering, Ariel University, Ariel, Israel
Email: nissimpanizel@gmail.com, monika.pinchas@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 August 2014; revised 18 September 2014; accepted 15 October 2014
ABSTRACT
Recently, two expressions (for the noiseless and noisy case) were proposed for the residual inter- symbol interference (ISI) obtained by blind adaptive equalizers, where the error of the equalized output signal may be expressed as a polynomial function of order 3. However, those expressions are not applicable for biased input signals. In this paper, a closed-form approximated expression is proposed for the residual ISI applicable for the noisy and biased input case. This new proposed expression is valid for blind adaptive equalizers, where the error of the equalized output signal may be expressed as a polynomial function of order 3. The new proposed expression depends on the equalizer’s tap length, input signal statistics, channel power, SNR, step-size parameter and on the input signal’s bias. Simulation results indicate a high correlation between the simulated results and those obtained from our new proposed expression.
Keywords:
Blind Adaptive Equalizers, Deconvolution, Inter-Symbol Interference (ISI), Convolutional Noise, Residual ISI

1. Introduction
Blind equalization is used in various applications such as: signal processing, digital communication, speech and image processing. Generally, a communication system may be presented by a signal transmitted via a com- munication channel added with white noise as illustrated in Figure 1. The channel is not ideal due to reflections and delays caused by the physical environment such as: ground, buildings and cables. Those reflections and delays cause distortion of the received signal which is referred as ISI. In order to overcome the irreducible
Figure 1. Block diagram of a baseband communication system.
degradation in performance caused by the ISI, a blind adaptive equalizer, may be implemented in those systems [1] - [12] . Blind de-convolution algorithms are essentially adaptive filtering algorithms designed such that they do not require the external supply of a desired response to generate the error signal in the output of the adaptive equalization filter [13] . The algorithm itself generates an estimate of the desired response by applying a non- linear transformation to sequences involved in the adaptation process [13] . Blind equalization methods are of great importance in digital signal communication systems, as they allow channel equalization at the receiver without the use of training signals which consume considerable channel capacity. In blind equalization, there is no wasted data on training symbols, therefore bandwidth is saved [6] . Since blind equalizers do not require any known training sequence for the startup period, they are also useful for point-to-multipoint network applications, such as the fiber to the curb (FTTC) systems [14] . Generally, blind methods are classified according to the location of their nonlinearity in the receiver [15] . We may classify blind equalization methods [15] as follows: 1) Polyspectral algorithms; 2) Bussgang-type algorithms; 3) Probabilistic algorithms. In the first type, the non- linearity is located at the output of the channel, right before the equalizer’s filter. The non-linearity has thus the function of estimating the channel and feeding that information to the equalizer for adaptation purposes. In the second type, the nonlinearity is found at the output of the equalizer’s filter and it is memoryless function. Among Bussgang type algorithms we may find Godard’s algorithm [7] which will also used in this paper. In the third type, the nonlinearity is combined with the data detection process. Algorithms with the third type can extract considerable information from relatively little data [15] , but this is often accomplished at a huge com- putational cost.
Up to now, the performance of a chosen equalizer (the achievable residual ISI) for biased input signals could be obtained only via simulation. According to [15] , the equalization performance depends on the nature of the equalizer (on the memoryless nonlinearity as already was mentioned before), on the channel characteristics, on the added noise, on the step-size parameter used in the adaptation process which will be explained later in this paper, on the equalizer’s tap length and on the input signal statistics. Fast convergence speed and reaching a residual ISI where the eye diagram is considered to be open are the main requirements from a blind equalizer. Fast convergence speed may be obtained by increasing the step-size parameter. But increasing the step-size parameter may lead to a higher residual ISI which might not meet any more the system’s requirements [6] . Recently [15] [16] , proposed a closed-form approximated expression for the residual ISI for the noiseless and noisy case respectively. However, those expressions [15] [16] are not applicable for biased input signals.
In this paper, we propose for the noisy and biased input signal case a closed-form approximated expression for the residual ISI that depends on the equalizer’s tap length, input signal statistics, channel power, SNR, step- size parameter and on the input signal’s bias. Since the channel power is measurable, there is no need anymore to carry out any simulation with various step-size parameters in order to reach the required residual ISI.
The paper is organized as follows: after having described the system under consideration in Section 2, the closed-form approximated expression for the achievable residual ISI is introduced in Section 3. In Section 4, simulation results are presented and the conclusion is given in Section 5.
2. System Description
The system under consideration is the same system as shown in [15] [16] and is illustrated in Figure 1. We consider the following assumptions:
1. The input sequence 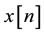 represents a two independent biased quadrature carriers case constellation input where
represents a two independent biased quadrature carriers case constellation input where 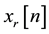 and
and  are the real and imaginary parts of
are the real and imaginary parts of 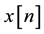 respectively.
respectively.
2. The biased input sequence mean is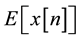 , where
, where 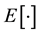 is the expectation operator.
is the expectation operator.
3. .
.
4. The unknown channel 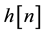 is modeled as a non-minimum phase FIR filter, which has zeros far from the unit circle.
is modeled as a non-minimum phase FIR filter, which has zeros far from the unit circle.
5.  is the equalizer’s tap-delay line.
is the equalizer’s tap-delay line.
6. The noise  is an added Gaussian white noise with zero mean and consists of
is an added Gaussian white noise with zero mean and consists of  where
where 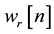 and
and  are the real and imaginary parts of
are the real and imaginary parts of 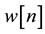 respectively as well as
respectively as well as 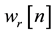 and
and 




7. The variance of 




The transmitted sequence 




where “

where D is a constant delay and 

where 






where 







where 
Substituting (4) into (5) yields:

where 

where 

Next, let us define:

where 



since



according to assumption 6 from this section,


Therefore, we may have with the help of (11):

where 



where 



equalizer’s tap length. The operator 

3. Residual ISI for the Noisy Case with Biased Input Signal
In this section, a closed-form approximated expression is derived for the residual ISI valid for biased input signals.
Theorem: Consider the following assumptions:
1. The source signal 


2. The convolutional noise





3. The convolutional noise 

4. The gain between the source and equalized output signal is equal to one.
5. The convolutional noise 

6.
7. The signal 

8. The added noise 
9. The channel 
10. 

11. The signal 
12. The equalizer’s output noise 




13.
The residual ISI expressed in dB units may be defined as:

where 



or

and

where


where 



where 





variance of 





Comments:
1. It should be noted that assumptions 2 - 5, are precisely similar to those made by [2] [13] [16] [20] .
2. It should be mentioned out that our expression for the residual ISI (14) looks quite similar to the residual ISI expression given in [16] . But, they are very different since the input signal 


Proof:
By using (5), (8) and (12), 

where 


Substituting (19) into (18) and by using (4) we obtain:

By substituting (8) into (20) and using the relation of 

Please note that





where

From (23) we obtain:

which may be written as:

By using assumptions 6, 7, 8 and 11 (from this section) we obtain:

Let us define:

Our next step is developing the following expression:

which is a part of the expression for B (27). Since the channel’s impulse response decays in time, (28) may be written as:

By substituting (29) into (27) we obtain:

Next, we turn to calculate
We recall the expression for 

Therefore, for the latter stages of the de-convolution process 

From (31), we obtain:

Next, the expectation operator is applied on (32):

By substituting 

From assumption 12 (in this section) we obtain:

It should be pointed out that (35) looks similar to the equalizer's output noise variance at [16] . But, in our case
here (35), 

Next, we turn to calculate the expression for the residual ISI applicable for the biased case. For that purpose,
we calculate first the expression for

Thus, by using (8), we obtain:

which may be written as:

From (38) we obtain:

By applying the expectation operator on both sides of (39) and using assumption 11 (from this section), we obain:

Thus, the expression for 

By using assumption 3 (from this section), (41) may be written as:

Next, we turn to calculate

Substituting (43) into (42) we obtain:

Substituting (44) into (40) leads to:

For the ideal case, 




multiplications of different index elements. Then (45) may be written as:

By using (43), we may write (46) as:

From (7), (47) may be written for 

From assumptions 2 and 13 (from this section), we may use the relation:

This completes our proof.
4. Simulation
In this section, our new proposed expression for the residual ISI (14) was tested via simulation, where we used Godard’s algorithm [7] . In our simulation we used various step-size parameters, tap length, types of channels, SNR and biased input signals. The equalizer’s taps for Godard's algorithm [7] were updated according to:

where, 







Two different input sources were considered: 1) A biased 16QAM, a modulation using ± {1, 3} levels for in- phase and quadrature components in addition to a given bias. The bias is the same for the real and imaginary axes. 2) A uniformly distributed input signal within [−0.5, 1.5] for the x and y axis where the two axis are independent. The following five different channels were used:
Channel 1: The channel parameters were taken according to [22] :

Channel 2: The channel parameters were determined according to [17] :

Channel 3: The channel parameters were determined according to [20] :
Channel 4: The channel parameters are:

Channel 5: The channel parameters were determined according to [23] :
Figures 2-9 are the simulated performance of (50) for the biased 16QAM input case, namely the ISI as a function of iteration number for various step-size parameters, channel characteristics, various SNR values and for three different biases, compared with the calculated residual ISI expression (14) proposed in this paper. According to Figures 2-9, the residual ISI obtained by (14) is very close to the simulated results.
Figure 2. A comparison between the simulated and calculated residual ISI for the 16 QAM biased source input going through channel 1 for
Figure 3. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 2 for
Figure 4. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 3 for
Figure 5. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 1 for
Figure 6. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 3 for
Figure 7. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel4 for
Figure 8. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 4 for
Figure 9. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel5 for
Figures 10-18 are the simulated performance of (50) for the biased 16QAM input case, namely the ISI as a function of iteration number for various equalizer's tap length, channel characteristics, various SNR values and for two different biases, compared with the calculated residual ISI expression (14). Figures 10-18 show a high correlation between the simulated results and those calculated with (14).
Figure 10. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 2 for 
Figure 11. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 3 for 
Figure 12. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 1 for
Figure 13. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 2 for
Figure 14. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 1 for
Figure 15. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 3 for
Figure 16. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 4 for
Figure 17. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 4 for
Figure 19 and Figure 20 illustrate the simulated performance of (50) for the biased 16QAM input case, namely the ISI as a function of iteration number for various SNR values and two different input biases and channels, compared with the calculated residual ISI expression (14). Figure 19 and Figure 20 show a high correlation between the simulated results and those calculated with (14).
Figures 21-23 illustrate the simulated performance of (50) for the biased 16QAM input case, namely the ISI as a function of iteration number for various biases, two different SNR values and three channel cases, compared with the calculated residual ISI expression (14). Figures 21-23 show a high correlation between the simulated results and those calculated with (14).
Figure 18. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 4 for
Figure 19. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 2 for tap length = 33. The averaged results were obtained in 100 Monte Carlo trials. The equalizer’s step-size and input signal mean parameters were set to 6e−6 and 2 + j2 respectively.
Figure 20. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 3 for tap length = 41. The averaged results were obtained in 20 Monte Carlo trials. The equalizer’s step-size and input signal mean parameters were set to 6e−6 and 3 + j3 respectively.
Figure 21. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 3 for tap length = 41. The averaged results were obtained in 20 Monte Carlo trials. The equalizer’s step-size and SNR parameters were set to 6e−6 and 10 [dB] respectively.
Figure 22. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 2 for tap length = 13. The averaged results were obtained in 100 Monte Carlo trials. The equalizer’s step-size and SNR para- meters were set to 6e−6 and 25 [dB] respectively.
Figure 23. A comparison between the simulated and calculated residual ISI for the 16QAM biased source input going through channel 5 for tap length = 123. The averaged results were obtained in 20 Monte Carlo trials. The equalizer’s step-size and SNR parameters were set to 4e−6 and 25 [dB] respectively.
Figures 24-26 illustrate the simulated performance of (50) for the uniformly source input, namely the ISI as a function of iteration number for three different values for the SNR, compared with the calculated residual ISI expression (14). Figures 24-26 show a high correlation between the simulated results and those calculated with (14).
Figure 24. A comparison between the simulated and calculated residual ISI for the uniformly distributed source input within [−0.5 1.5] going through channel 2 for tap length = 67. The averaged results were obtained in 20 Monte Carlo trials. The equalizer’s step-size and SNR parameters were set to 133e−6 and 40 [dB] respectively.
Figure 25. A comparison between the simulated and calculated residual ISI for the uniformly distributed source input within [−0.5 1.5] going through channel 2 for tap length = 67. The averaged results were obtained in 20 Monte Carlo trials. The equalizer’s step-size and SNR parameters were set to 133e−6 and 20 [dB] respectively.
Figure 26. A comparison between the simulated and calculated residual ISI for the uniformly distributed source input within [−0.5 1.5] going through channel 2 for tap length = 67. The averaged results were obtained in 20 Monte Carlo trials. The equalizer’s step-size and SNR parameters were set to 133e−6 and 10 [dB] respectively.
5. Conclusion
In this paper, we proposed an approximated closed-form expression for the residual ISI obtained by blind adaptive equalizer, where the error of the equalized output signal may be expressed as a polynomial function of order 3. This new expression is valid for the noisy and biased input case and depends on the step-size parameter, equalizer’s tap length, SNR, channel power and input signal statistics. This new proposed expression may be considered as a general closed-form expression for the residual ISI, where the previous proposed expressions from the literature are only special cases of it. Simulation results have shown a high correlation between the simulated results for the residual ISI and those that were calculated from our new proposed expression.
References
- Pinchas, M. (2013) Two Blind Adaptive Equalizers Connected in Series for Equalization Performance Improvement. Journal of Signal and Information Processing, 4, 64-71. http://dx.doi.org/10.4236/jsip.2013.41008
- Pinchas, M. (2013) Residual ISI Obtained by Blind Adaptive Equalizers and Fractional Noise. Mathematical Problems in Engineering, 2013, Article ID: 972174.
- Pinchas, M. and Bobrovsky, B.Z. (2006) A Maximum Entropy Approach for Blind Deconvolution. Signal Processing (Eurasip), 86, 2913-2931. http://dx.doi.org/10.1016/j.sigpro.2005.12.009
- Pinchas, M. and Bobrovsky, B.Z. (2007) A Novel HOS Approach for Blind Channel Equalization. IEEE Transactions on Wireless Communications, 6, 875-886. http://dx.doi.org/10.1109/TWC.2007.04404
- Pinchas, M. (2009) Blind Equalizers by Techniques of Optimal Non-Linear Filtering Theory. VDM Verlagsservice gesellschaft mbH.
- Pinchas, M. (2012) The Whole Story behind Blind Adaptive Equalizers/Blind Deconvolution. e-Books Publications Department, Bentham Science Publishers, Sharjah.
- Godard, D.N. (1980) Self Recovering Equalization and Carrier Tracking in Two-Dimensional Data Communication System. IEEE Transactions on Communications, 28, 1867-1875. http://dx.doi.org/10.1109/TCOM.1980.1094608
- Im, G.H., Park, C.J. and Won, H.C. (2009) A Blind Equalization with the Sign Algorithm for Broadband Access. IEEE Communications Letters, 5, 70-72.
- Reuter, M. and Zeidler, J.R. (1999) Nonlinear Effects in LMS Adaptive Equalizers. IEEE Transactions on Signal Processing, 47, 1570-1579. http://dx.doi.org/10.1109/78.765126
- Makki, A.H.I., Dey, A.K. and Khan M.A. (2010) Comparative Study on LMS and CMA Channel Equalization. 2010 International Conference on Information Society (i-Society), London, 28-30 June 2010, 487-489.
- Tucu, E., Akir, F. and Ozen, A. (2013) A New Step-Size Control Technique for Blind and Non-Blind Equalization Algorithms. Radioengineering, 22, 44-51.
- Wang, J.F. and Zhang, B. (2010) Design of Adaptive Equalizer Based on Variable Step LMS Algorithm. Proceedings of the 3rd International Symposium on Computer Science and Computational Technology, Jiaozuo, 14-15 August 2010, 256-258. http://www.academypublisher.com/proc/iscsct10/papers/iscsct10p256.pdf
- Nikias, C.L. and Petropulu, A.P. (1993) Chapter 9. Higher-Order Spectra Analysis A Nonlinear Signal Processing Framework. Prentice-Hall, Englewood Cliffs, 419-425.
- Im, G.H and Won, H.C. (2001) RF Interference Suppression for VDSL System. IEEE Transactions on Consumer Electronics, 47, 715-722. http://dx.doi.org/10.1109/30.982781
- Pinchas, M. (2010) A Closed Approximated Formed Expression for the Achievable Residual Intersymbol Interference Obtained by Blind Equalizers. Signal Processing (Eurasip), 90, 1940-1962. http://dx.doi.org/10.1016/j.sigpro.2009.12.014
- Pinchas, M. (2010) A New Closed Approximated Formed Expression for the Achievable Residual ISI Obtained by Adaptive Blind Equalizers for the Noisy Case. IEEE International Conference on Wireless Communications, Networking and Information Security WCNIS 2010, Beijing, 25-27 June 2010, 26-30. http://dx.doi.org/10.1109/WCINS.2010.5541879
- Shalvi, O. and Weinstein, E. (1990) New Criteria for Blind Deconvolution of Nonminimum Phase Systems (Channels). IEEE Transactions on Information Theory, 36, 312-321. http://dx.doi.org/10.1109/18.52478
- Pinchas, M. (2011) A MSE Otimized Polynomial Equalizer for 16QAM and 64QAM Constellation. Signal, Image and Video Processing, 5, 29-37. http://dx.doi.org/10.1007/s11760-009-0138-z
- Nandi, A.K. (1999) Blind Estimation Using Higher-Order Statistics. Chapter 2, Kluwer Academic Publishers, Boston, 78-79.
- Fiori, S. (2001) A Contribution to (Neuromorphic) Blind Deconvolution by Flexible Approximated Bayesian Estima- tion. Signal Processing (Eurasip), 81, 2131-2153. http://dx.doi.org/10.1016/S0165-1684(01)00108-6
- Pinchas, M. (2013) A Novel Expression for the Achievable MSE Performance Obtained by Blind Adaptive Equalizers. Signal, Image and Video Processing, 7, 67-74. http://dx.doi.org/10.1007/s11760-011-0208-x
- Shalvi, O. and Weinstein, E. (1993) Super-Exponential Methods for Blind Deconvolution. IEEE Transactions on Infor- mation Theory, 39, 504-519. http://dx.doi.org/10.1109/18.212280
- Arslan, G., Ding, M., Lu, B., Milosevic, M., Shen, Z. and Evans, Brian, L. (2005) UT Austin Multicarrier Equalizer Design Toolbox for Matlab. http://users.ece.utexas.edu/~bevans/projects/adsl/dmtteq/dmtteq.html




































