Journal of Signal and Information Processing
Vol. 3 No. 3 (2012) , Article ID: 22124 , 5 pages DOI:10.4236/jsip.2012.33043
Non-Stationary Signal Segmentation and Separation from Joint Time-Frequency Plane
![]()
Department of Electrical Engineering, Faculty of Engineering, King Abdulaziz University, Rabigh, KSA.
Email: ashehri@kau.eud.sa
Received May 7th, 2012; revised June 11th, 2012; accepted June 24th, 2012
Keywords: Signal Segmentation; Time-Frequency Distribution; Short-Time Fourier Transform; Non-Stationary; Wiener Masking
ABSTRACT
Multi-components sinusoidal engineering signals who are non-stationary signals were considered in this study since their separation and segmentations are of great interests in many engineering fields. In most cases, the segmentation of non-stationary or multi-component signals is conducted in time domain. In this paper, we explore the advantages of applying joint time-frequency (TF) distribution of the multi-component signals to identify their segments. The Spectrogram that is known as Short-Time Fourier Transform (STFT) will be used for obtaining the time-frequency kernel. Time marginal of the computed kernel is optimally used for the signal segmentation. In order to obtain the desirable segmentation, it requires first to improve time marginal of the kernel by using two-dimensional Wiener mask filter applied to the TF kernel to mitigate and suppress non-stationary noise or interference. Additionally, a proper choice of the sliding window and its overlaying has enhanced our scheme to capture the discontinuities corresponding to the boundaries of the candidate segments.
1. Introduction
Segmentation of multi-components or non-stationary signals has a considerable degree of importance for processing signals in many fields such as communications, biomedical, seismic and ultrasonic signals. Most of the signal segmentation approaches have been implemented and analyzed in time domain [1-3]. One of their disadvantages that they are statistical based analysis and in most cases they neglect the frequency information and its reflection on the signal dynamic changes over time. Recently, the wavelet transforms and time-frequency analysis have become a good and promise analytical methods due to their two-dimensional analysis [4-7]. Our proposed method is based on joint time-frequency analysis where both time and frequency information has been employed to obtain the desirable segmentation function.
This paper is composed of two level of analysis and its structure will be organized accordingly. The first level of this research work deals with improving time-frequency energy spectrum using the two-dimensional (2-D) Wiener masking for de-noising and mitigating any possible interferences that will affect the segmentation process. Second, is to optimize the time marginal of the masked kernel in order to obtain the desired segmentation function. For the rest of this introduction, a brief description of the short-time Fourier transform (STFT) and the 2-D Wiener filter will be provided. In Section 2, we will provide complete details of our approach including the process of denoising TF kernel and all derivations of the signal segmentation. Section 3 has the experimental work which illustrates the graphical results as depicted in the attached figures.
1.1. Short-Time Fourier Transform
In many applications such as speech, biomedical, seismic and other similar signals, we are interested in their frequency contents locally in time since their frequencies content evolve over time. These types of signal called non-stationary signals and using standard and regular Fourier Transform is not useful for analyzing such signals. The frequency information who are localized in time as the case of spikes and high frequency bursts cannot be easily detected from the regular Fourier Transform and joint time-frequency analysis becomes the right analysis tool. Recently, the time-frequency analysis methods have introduced a joint time-frequency energy distribution plane displaying the jointly both time and frequency information. Time-frequency distribution methods who do not show cross terms or negative frequency like STFT and the Discrete Evolutionary Transform (DET) provide a time-frequency distribution plane that is positive and has no cross term as well [8-10].
In STFT, time-localization is a achieved first by windowing the signal by cutting off a slice of it and then taking its Fourier Transform using Fast Fourier Transform (FFT) [9,10]. The magnitude of the STFT kernel is known as the Spectrogram. Moving or sliding the window along the time axis, the relation between the variance of time and frequency can be identified. When the time window is sufficiently narrow, each frame extracted is viewed as stationary so that Fourier transform can be used. The type and length of the sliding window has a direct effect on time and frequency resolutions.
In Continuous-time STFT, the function is multiplied by a predefined window function which is nonzero for only a short period of time. The Fourier transform of the resulting short or windowed signal will have a two-dimensional representation of the signal written as:
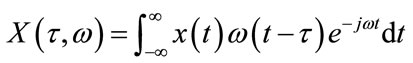 where
where 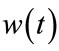 is the window function, commonly Gaussian bell shape centered around zero, and
is the window function, commonly Gaussian bell shape centered around zero, and 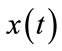 is the signal to be transformed.
is the signal to be transformed. 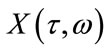 is the time-frequency kernel or the STFT resulted from the Fourier Transform of
is the time-frequency kernel or the STFT resulted from the Fourier Transform of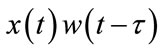 . This kernel is a complex matrix representing the magnitude and phase of the transformed signal over time and frequency domains.
. This kernel is a complex matrix representing the magnitude and phase of the transformed signal over time and frequency domains.
For the discrete representation of STFT, the data signal is broken up into equal chunks or frames. To reduce the artifacts at the boundary, these frames usually overlap each other. In similar way, each frame is Fourier transformed and output complex result will be added to get the final matrix representing the signal magnitude and phase for each point in time and frequency. This can be expressed as:
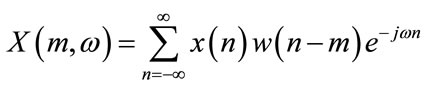 where
where 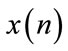 is the signal and
is the signal and  is the window. The shifting m and the frequency ω are discrete since the STFT in most typical applications is performed on a computers or microprocessors using the Fast Fourier Transform algorithm FFT.
is the window. The shifting m and the frequency ω are discrete since the STFT in most typical applications is performed on a computers or microprocessors using the Fast Fourier Transform algorithm FFT.
The magnitude squared of the STFT yields the Spectrogram of the function:
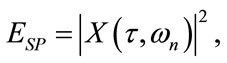
which shows the distribution of the power spectral density of the signal 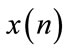 [9,10]. The time and frequency marginals of STFT were defined as
[9,10]. The time and frequency marginals of STFT were defined as
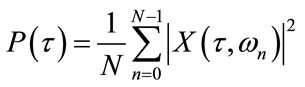 and
and
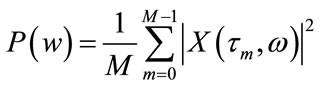 where N is the frequency samples and M is the number of time frames.
where N is the frequency samples and M is the number of time frames.
1.2. Wiener Filtering
The wiener masking is an estimate that can be found by minimizing the mean-square error [11],
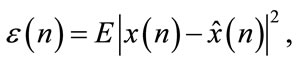
where 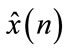 is the output of a linear time-varying mask.
is the output of a linear time-varying mask.
In order to minimized the error, the estimator was defined in [11] to have the following Wold-Cramer representation
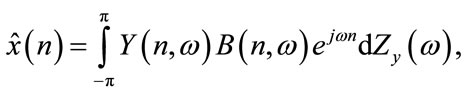
where 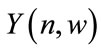 is the evolutionary time-frequency kernel of the signal
is the evolutionary time-frequency kernel of the signal , and
, and  is the masking function [12-14].
is the masking function [12-14].
According to orthogonality principles the minimization of 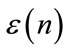 is
is
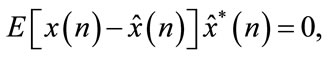
and is equivalent to

where .
.
To minimize the above equation  must equal to
must equal to

to give the mask
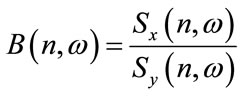 (1)
(1)
as the ratio of the spectra of the reference signal 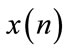 and that of the true received signal
and that of the true received signal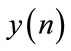 .
.
2. Signal Segmentation from Improved Time-Frequency Plane
The regular time-frequency kernel obtained from STFT or Spectrogram does not completely satisfy the time and frequency marginals of the signal. Any further improvement in terms of kernel’s time and frequency resolution will make it possible for the estimated kernel to closely satisfy time marginal condition. Theoretically, our scheme has the capability of providing the necessary improvements according to the following:
1) For constructing the Spectrogram or STFT, a prober window type with optimal length has to occur first in order to get the desirable level of time and frequency resolution. Furthermore, a high resolution of the power spectral or energy density will provide a good estimate of both time and frequency marginals who are the key success factors leading to optimal signal segmentation.
2) Improving the joint time-frequency power spectral density by means of Wiener masking scheme will suppress and mitigate any undesired non-stationary noise or interference. The wiener masking scheme has to be applied into the time-frequency kernel obtained from STFT and not directly to the signal itself.
The block diagram of the proposed system is shown in Figure 1 where a white Gaussian noise is added to the original signal to give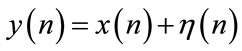 , as the real time signal.
, as the real time signal.
At the processing side, the STFT algorithm was performed to compute the time-frequency kernel for both received and reference signals as the only two required inputs for Wiener masking,
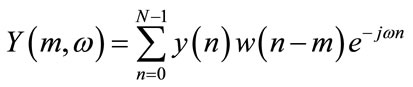 (2)
(2)
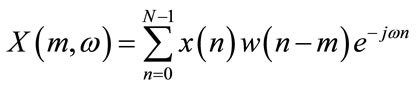 (3)
(3)
The experimental testing of several known windows shows that hamming window with a length , and time shift
, and time shift 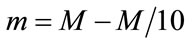 gives the highest desirable time and frequency resolution.
gives the highest desirable time and frequency resolution.
The mask  defined in (1) then can be created from the two above kernels to be
defined in (1) then can be created from the two above kernels to be
 (4)
(4)
where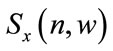 , and
, and 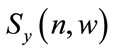 are the spectrum of the reference and received signal respectively.
are the spectrum of the reference and received signal respectively.
The improved time-frequency spectrum can be obtained using the mask 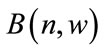 to get
to get
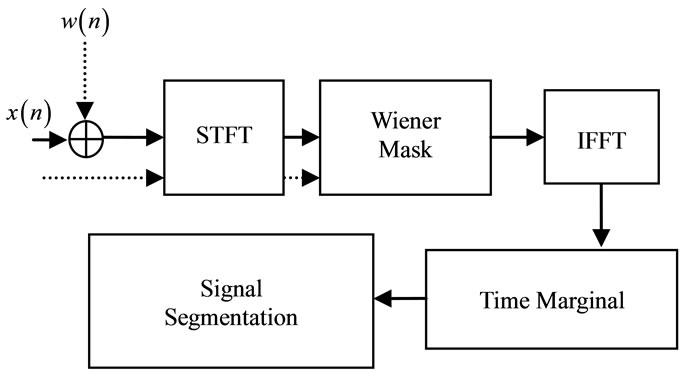
Figure 1. Signal segmentation.
 (5)
(5)
or
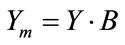 (6)
(6)
as an estimate of the original time-frequency kernel of the processed signal.
The time marginal of the improved time-frequency spectrum Ym can be obtain as
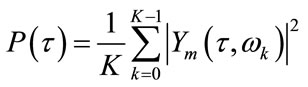 (7)
(7)
and its length equals to the total number of overlapping segments or time window frames that comes from chunking or windowing the original signal using the widow .
.
Unfortunately, in STFT the time marginal does not satisfy time marginal, 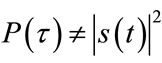 condition and therefore will not give the correct signal segmentation to indicate the boundary of its amplitude or frequency changes. Further signal processing is needed at this stage and nonlinear interpolation must be employed to interpolate the data signal to the original data points. Due to the nonlinearity of the function
condition and therefore will not give the correct signal segmentation to indicate the boundary of its amplitude or frequency changes. Further signal processing is needed at this stage and nonlinear interpolation must be employed to interpolate the data signal to the original data points. Due to the nonlinearity of the function , a second order Lagrangian interpolation polynomial is used as
, a second order Lagrangian interpolation polynomial is used as
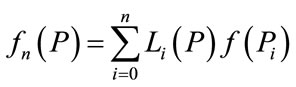 (8)
(8)
where n stands for the nth order polynomial and
 (9)
(9)
is a weighting function that includes a product on 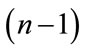 terms with terms of j = 1 omitted. The resulted interpolated function then has a time samples of length equals to the length of the original signal.
terms with terms of j = 1 omitted. The resulted interpolated function then has a time samples of length equals to the length of the original signal.
3. Simulation and Results
To prove the validity of our approach we will carry it out to a real application and running its algorithms for a multi-component signal and therefore, we will be able to display the TF kernel and its marginals. Now, let us consider the following multi-component signal ,
,

is composed of three equal segments each with different frequency. A white Gaussian noise is added to the total signal to give , and with a signal to noise ratio SNR equal to 3 dB, as one of the worst cases when the interference noise has a large power. The noisefree signal and the corrupted one are shown in Figure 4(a) and (b) respectively.
, and with a signal to noise ratio SNR equal to 3 dB, as one of the worst cases when the interference noise has a large power. The noisefree signal and the corrupted one are shown in Figure 4(a) and (b) respectively.
According to our segmentation system shown in Figure 1, the STFT is applied for both, the noise-free signal , and the reference signal
, and the reference signal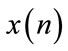 . The two spectrums are computed to be used as the input values for the Wiener mask. The TF spectrum of the noisy signal is shown in Figure 2 which displays the effect of the Gaussian noise. We notice that the energy components of the noise is spread all over the entire TF plane displaying a poor time marginal.
. The two spectrums are computed to be used as the input values for the Wiener mask. The TF spectrum of the noisy signal is shown in Figure 2 which displays the effect of the Gaussian noise. We notice that the energy components of the noise is spread all over the entire TF plane displaying a poor time marginal.
The Wiener masking scheme is applied according to the algorithm defined in (5) (6), and the estimated TF kernel obtained from the Wiener masking output is shown in Figure 3. Notice that the power of the interference noise has been mitigated allowing to estimate a noise-less TF kernel of the processed signal . As expected, this estimated/computed kernel provides a better time marginal that will enhance the segmentation process.
. As expected, this estimated/computed kernel provides a better time marginal that will enhance the segmentation process.
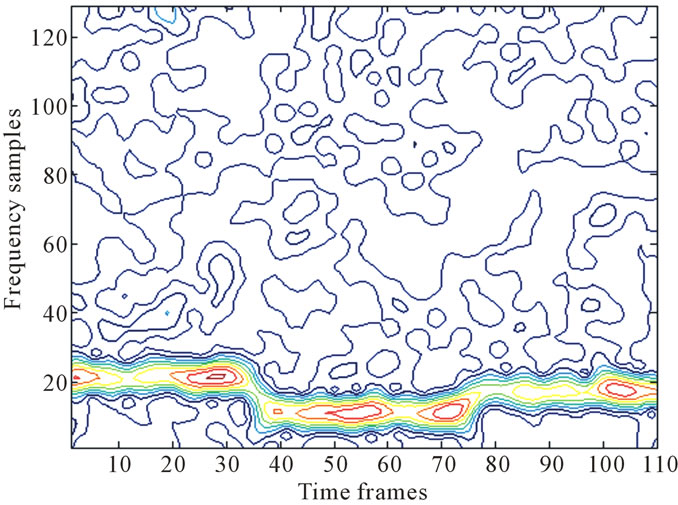
Figure 2. Time-frequency spectrum of noisy signal.
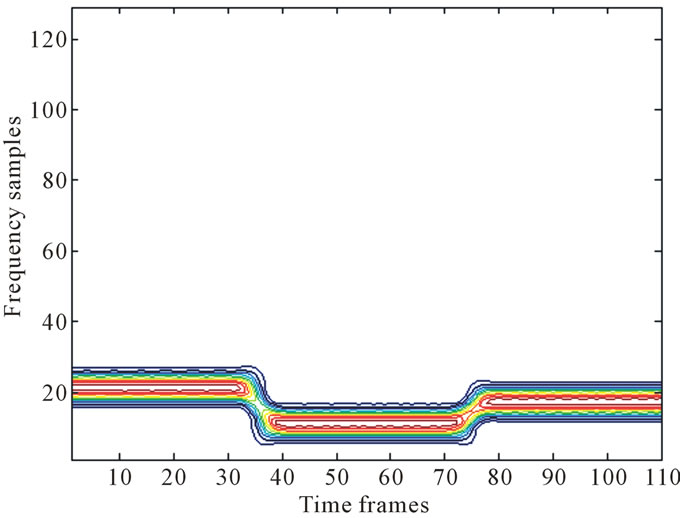
Figure 3. Estimated spectrum using wiener masking.
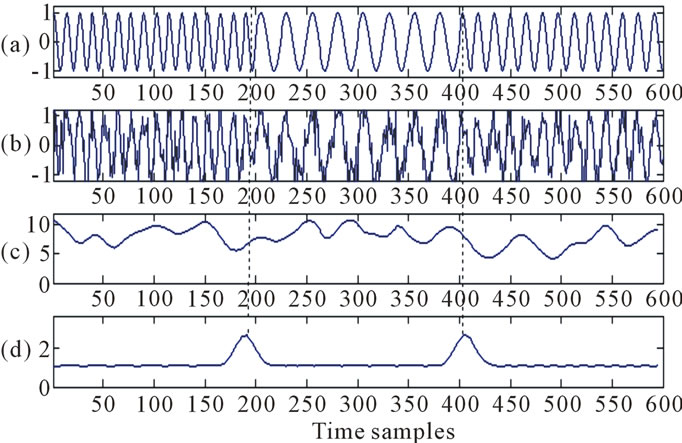
Figure 4. (a) Original non-stationary or multi-component signal x(n); (b) Noisy signal y(n); (c) Time marginal without Wiener masking, and finally (d) is the processed time marginal computed from the estimated kernel.
In fact, the estimated function which represents the time marginal defined in (7) has a length equals to the total number of signal frames or windows and is less than the signal length. Therefore, this segmentation function needs to be interpolated to equal length of the original signal as defined in (8) and (9). Figures 4(a)-(d) displays the results starting from the noise-free signal , noisy signal
, noisy signal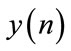 , poor time marginal function
, poor time marginal function 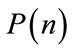 obtained from the noisy TF kernel, and finally the estimated time marginal function
obtained from the noisy TF kernel, and finally the estimated time marginal function 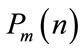 computed from the improved TF kernel. The computed time marginal function
computed from the improved TF kernel. The computed time marginal function 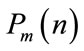 shown in Figure 4(d) provides the desired segmentations of the signal which identifies the boundaries between any two candidate segments.
shown in Figure 4(d) provides the desired segmentations of the signal which identifies the boundaries between any two candidate segments.
4. Conclusion
We have shown that with an efficient windowing for Short-time Fourier transform followed by 2-D Wiener filtering will provide a strong segmentation scheme which separates the multi-segments of non-stationary signals. In this work we have considered the 2-D Wiener masking or filtering to improve the resolution of the time-frequency kernel as crucial step which provides a good estimate of the time marginal. We should also mention that this approach depends mainly on the prober selection of the sliding window and its length for the STFT.
5. Acknowledgements
This article was funded by Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah. The author, therefore, acknowledges with thanks DSR technical and financial support.
REFERENCES
- C. Panagiotakis and G. Tziritas, “A Speech/Music Discriminator Based on RMS and Zero-Crossing,” IEEE Transactions on Multimedia, Vol. 7, No. 1, 2005, pp. 155-166. doi:10.1109/TMM.2004.840604
- S. Mahmoodi and B. Sharif, “Signal Segmentation and Denoising Algorithm Based on Energy Optimization,” Signal Processing, Vol. 85, No. 9, 2005, pp. 1845-1851. doi:10.1016/j.sigpro.2005.03.016
- H. Azami, K. Mohammadi and B. Bozorgtabar, “An Improved Signal Segmentation Using Moving Average and Savitzky-Golay Filter,” Journal of Signal and Information Processing, Vol. 3, No. 1, 2012, pp. 39-44. doi:10.4236/jsip.2012.31006
- H. Hassanpour and S. M. Anisheh, “An Improved Adaptive Signal Segmentation Method Using Fractal Dimension,” IEEE Conference on Information Science, Signal Processing and their Applications, Kuala Lumpur, 10-13 May 2010, pp. 720-723.
- S. M. Anisheh and H. Hassanpour, “Adaptive Segmentation with Optimal Window Length Scheme using Fractal Dimension and Wavelet Transform,” International Journal of Engineering, Vol. 22, No. 3, 2009, pp. 257-268.
- G. Proakis and M. Salehi, “Communication Systems Engineering,” Prentice Hall, Upper Saddle River, 1994.
- R. G. Lyons, “Digital Signal Processing,” Prentice Hall, Upper Saddle River, 2004.
- L. Cohen, “Time-Frequency Analysis,” Prentice Hall, Englewood Cliffs, 1995.
- M. H. Ackroyd, “Short-Time Spectra and Time-Frequency Energy Distributions,” Journal of Acoustical Society of America, Vol. 50, No. 5A, 1971, pp. 1229-1231. doi:10.1121/1.1912761
- R. Suleesathira, L. F. Chaparro and A. Akan, “Discrete Volutionary Transform for Time-Frequency Signal Analysis,” Journal of the Franklin Institute, Vol. 337, No. 4, 2000, pp. 347-364.
- H. Khan and L. F. Chaparro, “Formulation and Implementation of the Non-Stationary Evolutionary Wiener Filtering,” Signal Processing, Vol. 76, No. 3, 1999, pp. 243-267.
- L. F. Chaparro and A. A. Alshehri, “Jammer Excision in Spread Spectrum Communications via Wiener Masking and Frequency-Frequency Evolutionary Transform,” 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing, Vol. 4, 6-10 April 2003, pp. 473-476.
- L. F. Chaparro, R. Suleesathira, A. Akan and B. Unsal, “Instantaneous Frequency Estimation Using Discrete Evolutionary Transform for Jammer Excision,” 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, 7-11 May 2001, pp. 3525-3528.
- A. A. Alshehri, L. F. Chaparro and A. Akan, “Evolutionary Wiener Mask Receiver for Multiuser Direct Sequence Spread Spectrum,” Proceedings of EUSIPCO-2005, September 2005.

