Journal of Biomaterials and Nanobiotechnology
Vol.5 No.1(2014), Article ID:42136,8 pages DOI:10.4236/jbnb.2014.51007
On the Hyper Thermal Therapy of Tumor Tissues by Direct Laser Heating and Gold Nano Particles
![]()
Macromolecular Research Laboratory, Department of Physics, Faculty of Sciences, University Abou Bekr Belkaid, Tlemcen, Algeria.
Email: redabenmouna@yahoo.com
Copyright © 2014 Badiaa Fasla et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Badiaa Fasla et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 11th, 2013; revised December 17th, 2013; accepted January 6th, 2014
KEYWORDS
Hyper Thermal Therapy; Gold Nano Particles; Plasmon Resonance; Laser Heating



ABSTRACT
Hyper thermal therapy using lasers is emerging as a new promising route for the cancer treatment. The tumor can be directly heated by the radiation or indirectly using gold nano particles based on plasmon resonance phenolmenon. These two possibilities are explored here by solving the space and time dependent bio-heat equation under different conditions. The knowledge of temperature profiles in the tumor region helps to bypass the painful placement of sensors for monitoring tumor’s heating by the laser. Important properties which could be useful for developing an efficient tumor therapy are introduced for the first time. It is found that the effects of metabolism consist essentially in a redefinition of the blood temperature which increases proportional to the heat of metabolism. Blood perfusion in a given tissue leads to a new characteristic length of order one or two centimeters and a blood convection parameter typically of order 30 W∙m−1∙K−1. Effects of these parameters are scrutinized within the resolution of the bio-heat equation under a variety of conditions. In general, space modulations of the temperature throughout biological tissues are weak but front kinetics are quite fast. Specific examples show the way to monitor the temperature rise taking into account the tumor’s nature and size.
1. Introduction
This paper deals with the temperature modeling in connection with hyper thermal therapy using laser radiation to heat up and eliminate tumor tissues in biological organs. Cells in tumor tissues are more sensitive to heating and show compact conformations as compared to healthy ones leading to inhibition of normal circulation of nutrients and oxygen in tumor cells. In addition, this behavior can be used to develop therapy strategies with the capability of differentiating between tumor and healthy tissues and tuning interactions between lasers and biological tissues to generate adequate responses. The energy deposited into biological tissues by short wavelength high energy lasers exceeds their binding energy which means that these lasers can be used to remove micron sized tumors. Photosensitive dyes provide the possibility to turn to lasers with a lower power and wavelength is adapted to the absorption spectra of the dyes [1-4].
Hyper thermal therapy is emerging as an alternative to conventional treatments based on surgery, chemotherapy or radiotherapy with the advantages of reducing collateral effects and treatment discomfort. Its success relies on a detailed analysis of the heat transfer problem including control of time and space temperature developments throughout the tumor. In such an analysis, one should take into account the specific thermophysical parameters of tissues along with the appropriate conditions initially and at boundaries. A protocol of tumor’s heating should be designed to comply with the recommendations of the medical team according to the nature of tumor and standard regulation norms [5-8].
Laser therapy can be operated in two ways depending on whether the tumor can be exposed to a direct beam or by indirect heating via gold nano particles (GNPs). In the latter case, the capacity to reduce collateral effects is enhanced by targeting tumor tissues with a great accuracy. Therefore a good selection of an adequate distribution of GNPs together with an efficient sensing method may combine to make the particles responsive to external remote command signals helping to implement the therapy protocol. For this reason, GNPs are often used because of their specific response to lasers with given wavelengths and intensities via the surface plasmon resonance phenomenon [9-12].
The present paper is organized as follows. The celebrated Pennes bio-heat equation is firstly introduced with the necessary definitions. Then the case of direct heating of a tumor in contact with the ambient is solved before considering the case of indirect heating via GNPs for a tumor located deep inside the body. Initial temperature distributions were examined first prior to the time temperature development in terms of the laser power and the duration of exposure. Specific examples and applications were given in an effort to help develop efficient therapy strategies with the relevant thermophysical and biological parameters and a variety of biological tissues.
2. The Bio-Heat Equation
Accommodating temperature sensors throughout the tumor’s region to monitor the heating process is certainly quite painful for the patient and efforts are made to alleviate such discomforts by designing models for solving the following bio-heat equation [13] under reasonable conditions of practical interest
 (1)
(1)
The subscript b refers to blood while letter without subscript refer to the tumor unless specified otherwise.
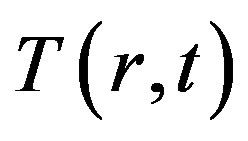 represents the temperature field at point r and time t,
represents the temperature field at point r and time t,
 is the gradient operator; letters r, c and k refer to density, heat capacity and conductivity, respectively; wb is the rate of blood perfusion and Tb the blood temperature. The metabolic heat generation of living cells is Qm while the heat produced by the laser beam is denoted
is the gradient operator; letters r, c and k refer to density, heat capacity and conductivity, respectively; wb is the rate of blood perfusion and Tb the blood temperature. The metabolic heat generation of living cells is Qm while the heat produced by the laser beam is denoted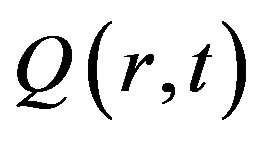 . The left hand side of Equation (1) represents the rate of thermal energy absorbed per unit volume of the biological tissue; the first term in the right hand side is the rate of heat conduction according to Fourier’s law and the second term represents the rate of heat convection through blood vessels. The convective heat exchange via blood circulation insures thermal regulation throughout the body. Blood enters the tissue at the arterial temperature Tb, exchanges a certain amount of energy which is equivalent to
. The left hand side of Equation (1) represents the rate of thermal energy absorbed per unit volume of the biological tissue; the first term in the right hand side is the rate of heat conduction according to Fourier’s law and the second term represents the rate of heat convection through blood vessels. The convective heat exchange via blood circulation insures thermal regulation throughout the body. Blood enters the tissue at the arterial temperature Tb, exchanges a certain amount of energy which is equivalent to
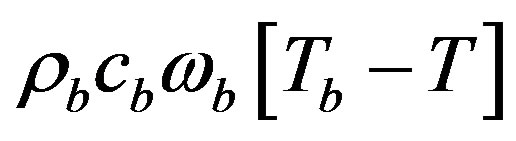 bringing the blood temperature to the level of that of the tissue. Resolution of such an equation is subject to the knowledge of initial and boundary conditions in addition to relying on appropriate values for the thermo-physical and biological parameters of the tissues, the flow rate of blood, the metabolic heat generation and the energy deposited by the laser. This problem is solved first under the conditions of a direct exposure to the incident beam before turning to the case of heating via GNPs.
bringing the blood temperature to the level of that of the tissue. Resolution of such an equation is subject to the knowledge of initial and boundary conditions in addition to relying on appropriate values for the thermo-physical and biological parameters of the tissues, the flow rate of blood, the metabolic heat generation and the energy deposited by the laser. This problem is solved first under the conditions of a direct exposure to the incident beam before turning to the case of heating via GNPs.
3. Direct Laser Heating
The heating process starts at time t = 0 by shining the laser beam on the tumor. Resolution of this problem requires first the knowledge of the initial temperature distribution
 which is sensitive to the thermophysical and biological properties of the tumor as well as to environmental conditions.
which is sensitive to the thermophysical and biological properties of the tumor as well as to environmental conditions.
3.1. The Initial Temperature Distribution T0(x)
For simplicity and without loss of generality, we consider the rectangular geometry of Figure 1(a) and a square target represented in the inset. The temperature remains constant in the yOz plane and depends on x only. Panel b of this figure concerns the case of indirect heating via GNPs as it will be discussed in a later section.
Here, the initial temperature T0(x) may be obtained by solving the following equation
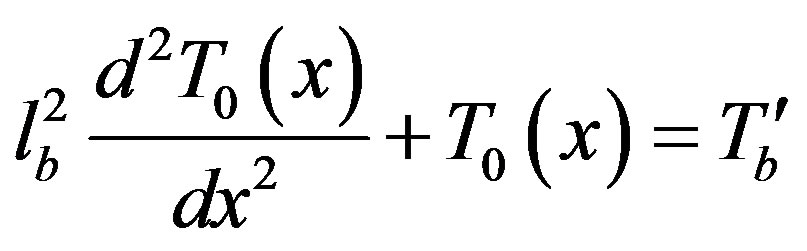 (2)
(2)
This equation exhibits the newly introduced properties such as the characteristic length lb and the effective blood temperature
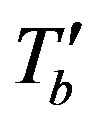 depending on the metabolic heat generation Qm
depending on the metabolic heat generation Qm
 (3)
(3)
The characteristic length lb represents the distance over which blood temperature goes from an effective value
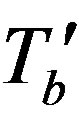 to the body temperature TB. Equation (2) can be easily solved using appropriate boundary conditions. At contact with the ambient, air convection tends to compensate the heat flux and one may write
to the body temperature TB. Equation (2) can be easily solved using appropriate boundary conditions. At contact with the ambient, air convection tends to compensate the heat flux and one may write
 (4)
(4)
where he designates the air convection parameter and Te the ambient temperature (see Figure 1(a)). On the other side of the tumor at x = L, two possibilities may arise depending on whether the interface with healthy tissues is isothermal or adiabatic. In the former case, T0(x = L) coincides with the body temperature TB while in the latter case, the derivative of T0(x) vanishes. The mathematics is
 (a)
(a) (b)
(b)
Figure 1. (a) Tumor’s volume in the rectangular coordinate system and its one dimensional representation; (b) Heating by a distribution of GNPs: Schematic representation of a spherical target with radius R by a dispersion of GNPs and amplification of the temperature distribution of a single GNP (Schematic representation of DT(r, t) versus r).
somewhat tedious in both cases and only the final results are reproduced here. For the case of an isothermal interface, it can be shown that the temperature profile is given by [14,15]
 (5)
(5)
where 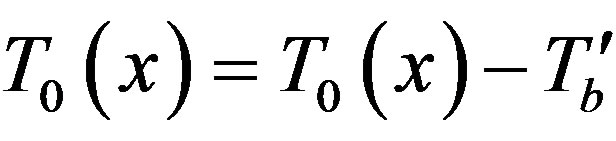 and the ratios
and the ratios
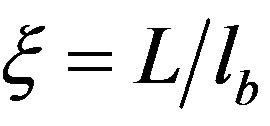 and
and
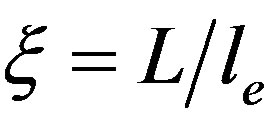 represent the tumor’s size L reduced to the blood perfusion and air convection lengths, respectively. The newly introduced characteristic length
represent the tumor’s size L reduced to the blood perfusion and air convection lengths, respectively. The newly introduced characteristic length
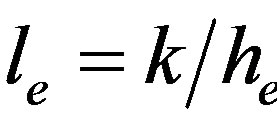 describes the distance over which the ambient temperature goes from Te to that of the surface T0(x = 0). Letting x = L in Equation (5), one gets T0(x = L) = TB while at x = 0, the temperature exhibits the effects of several parameters as one can see from the following expression
describes the distance over which the ambient temperature goes from Te to that of the surface T0(x = 0). Letting x = L in Equation (5), one gets T0(x = L) = TB while at x = 0, the temperature exhibits the effects of several parameters as one can see from the following expression
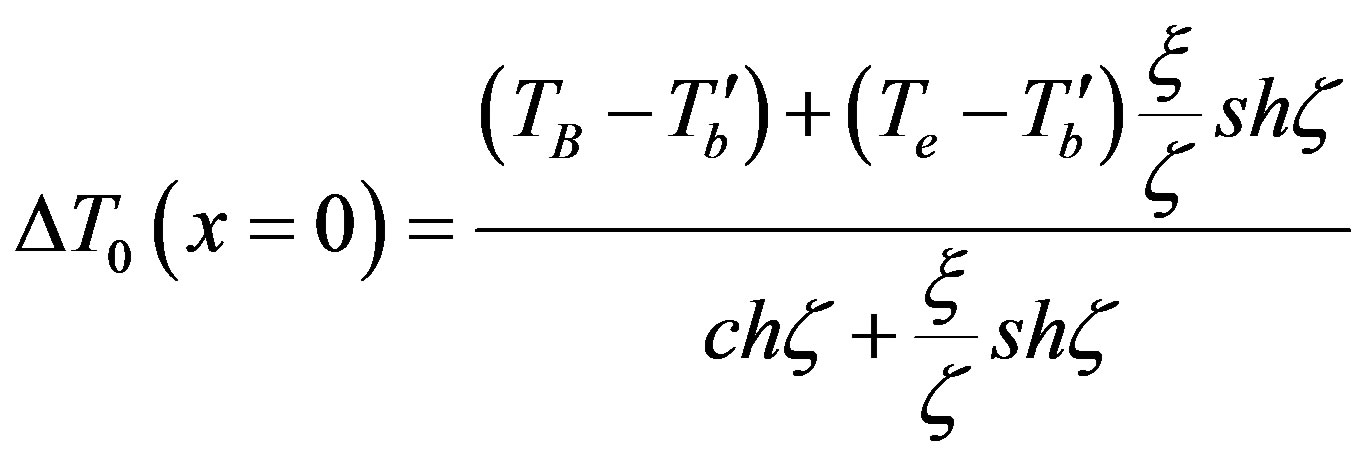 (6)
(6)
In the weak perfusion limit when z approaches zero, T0(x = 0) tends to TB independent of x. For a high convection rate, x is large and one finds the expected result T0(x = 0) = Te.
In the case where the interface at x = L is adiabatic, the solution of Equation (2) reads
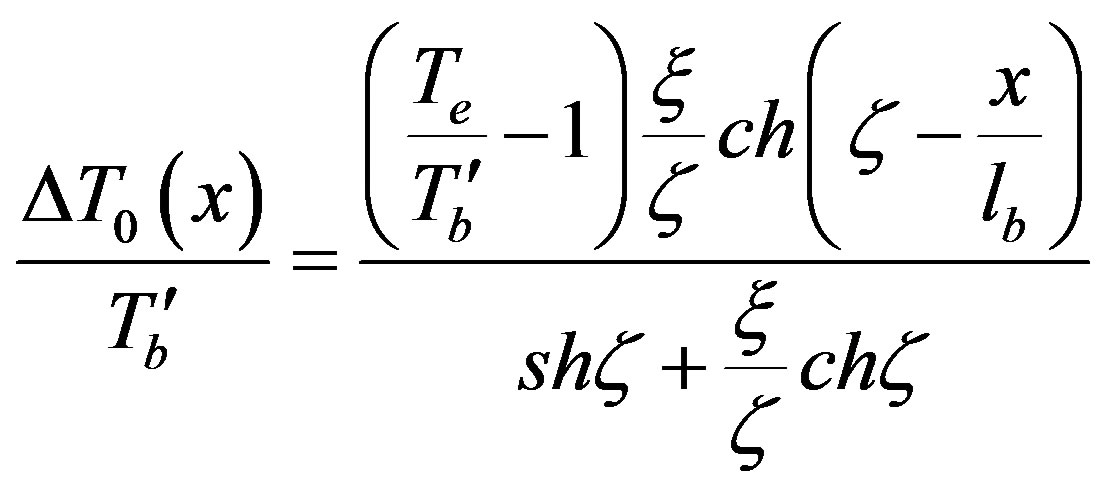 (7)
(7)
At x = L, this result reduces to
 (8)
(8)
which shows that the ratio
 is simply chz meaning that at low perfusion rates,
is simply chz meaning that at low perfusion rates,
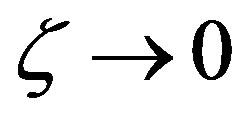 and the temperature remains constant throughout the tumor. The perfusion of blood generates throughout tissues a convection mechanism characterized by the parameter
and the temperature remains constant throughout the tumor. The perfusion of blood generates throughout tissues a convection mechanism characterized by the parameter .
.
Typical values for a case of practical interest [16,17] would be Qm =4 × 103 Wm−3, rbwb =0.5 kgm−3s−1, cb = 4 × 103 Jkg−1K−1 and k = 0.5 Wm−1K−1. Those numbers yield dTb =2 K showing that metabolic heating is not negligible. Moreover, one has lb—1.7 cm and hb—33 W−1mK−1 which means that for an air convection with he close to 33 W−1mK−1, le would be of the same order as lb while for a lower air convection (he =10 W−1mK−1) it would become much higher. Note that the ratios lb/le and he/hb are equal.
The initial temperature profile
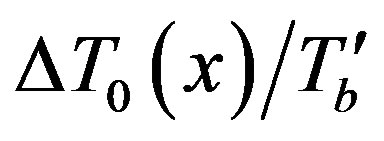 exhibits a weak space dependence over the tumor’s region but a high sensitivity to le/lb. Increasing the latter quantity makes heating less effective while decreasing it would lead to a surface temperature closer to the ambient Te.
exhibits a weak space dependence over the tumor’s region but a high sensitivity to le/lb. Increasing the latter quantity makes heating less effective while decreasing it would lead to a surface temperature closer to the ambient Te.
The knowledge of initial temperature distributions is necessary to get the complete solution subsequent to a direct heating by laser beams which is considered below through the resolution of the space and time dependent bio-heat equation.
3.2. Space and Time Temperature Profiles
Space and time temperature profiles due to a direct laser heating may be obtained by solving the following partial differential equation
 (9)
(9)
which exhibits two distinct characteristic times
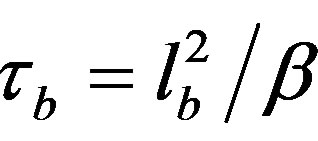 and
and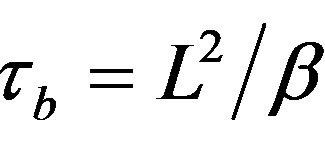 ,
,
 being the heat diffusivity. The first characteristic time tb represents the blood perfusion in the biological tissue while the second t represents the temperature relaxation over the tumor. The power laser P depends on the incident intensity q0 as P = q0L2 (see Figure 1(a)).
being the heat diffusivity. The first characteristic time tb represents the blood perfusion in the biological tissue while the second t represents the temperature relaxation over the tumor. The power laser P depends on the incident intensity q0 as P = q0L2 (see Figure 1(a)).
Shih et al. [18] reported an analytical solution of this problem assuming a constant initial temperature (i.e. T0(x) = Tb) and neglecting the effects of blood perfusion and metabolism
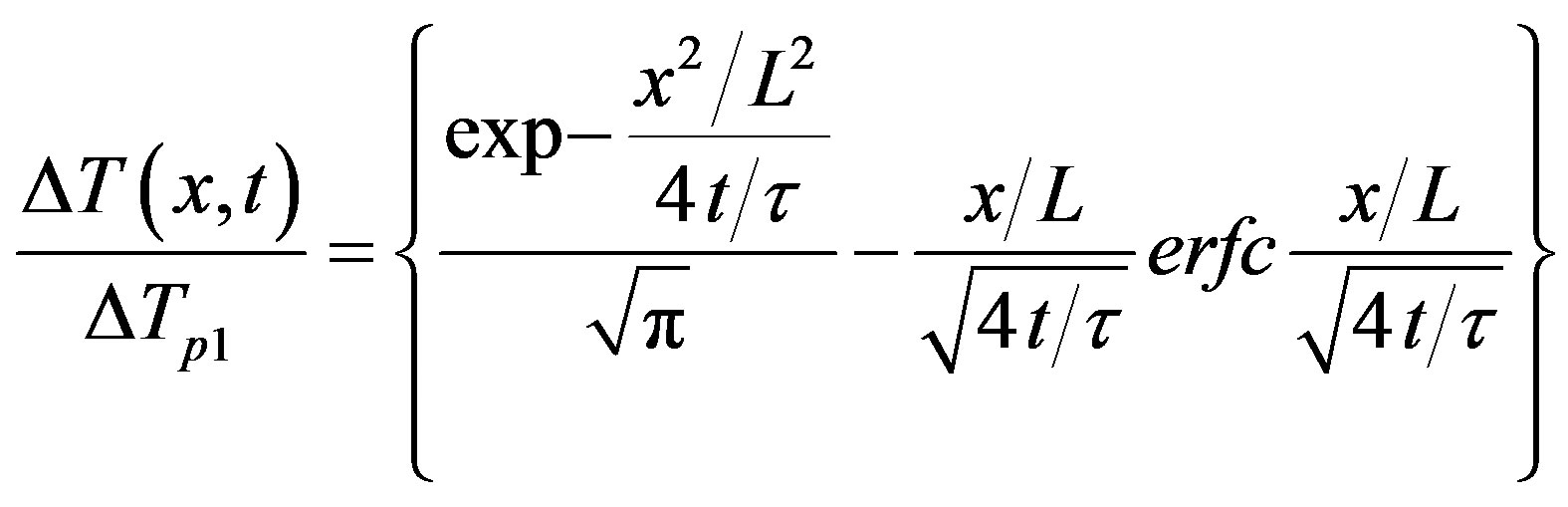 (10)
(10)
where T(x, t), TP1 and the complementary error function [19] are defined as follows
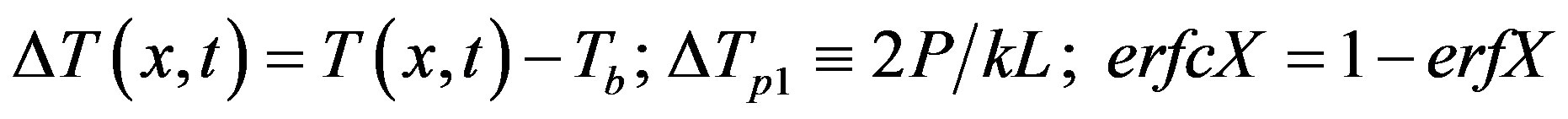 (11)
(11)
The remarkable feature here is the emergence of a single lumped parameter combining the space and time. This behavior is characteristic of a diffusion process with a mean square diffusion distance proportional to time and diffusivity as
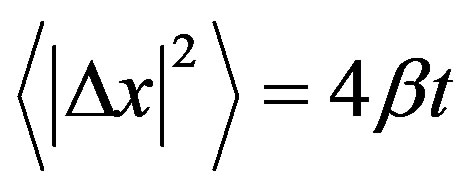 (12)
(12)
3.3. Effects of Blood Perfusion and Metabolism
Introducing the effects of blood perfusion breaks the universality and the solution becomes function of separate space and time variables, the space scaling with the length lb and time scaling with tb. Thus, the result becomes
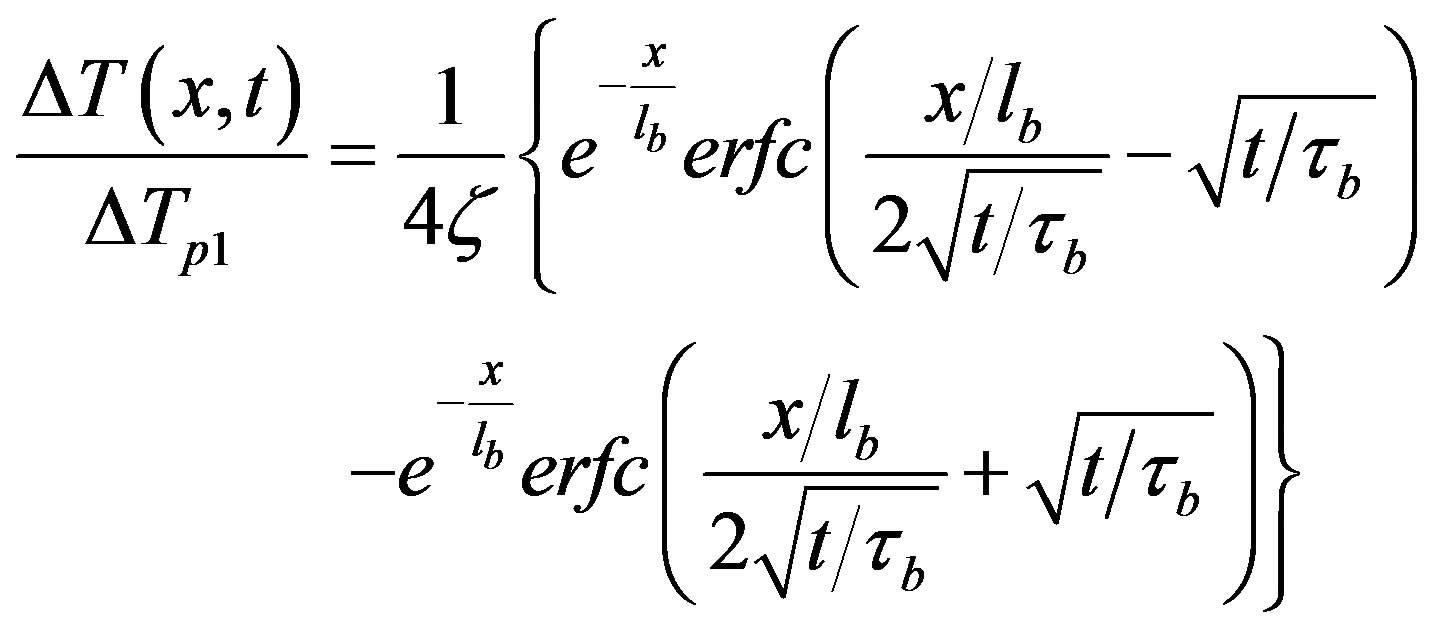 (13)
(13)
By expanding erfc(x + e) in terms of e and letting e®0, Equation (13) reduces to (10). It is remarkable to note that the metabolism can be included simply by redefining the blood temperature and using the effective value
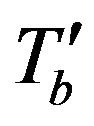 instead of Tb.
instead of Tb.
The temperature fronts shown in Figure 2 indicate that space modulations are weak but the rise of temperature with time is fast. Panels a, b illustrate the high sensitivity to the blood perfusion. At low perfusion rates, the temperature reaches quickly relatively high values but as the perfusion rate increases, a net damping of the heating process takes place and the temperature reaches a saturation limit at short times.
In Figure 3, one can better apprehend the kinetic rise of temperature since heating operates fast at short times
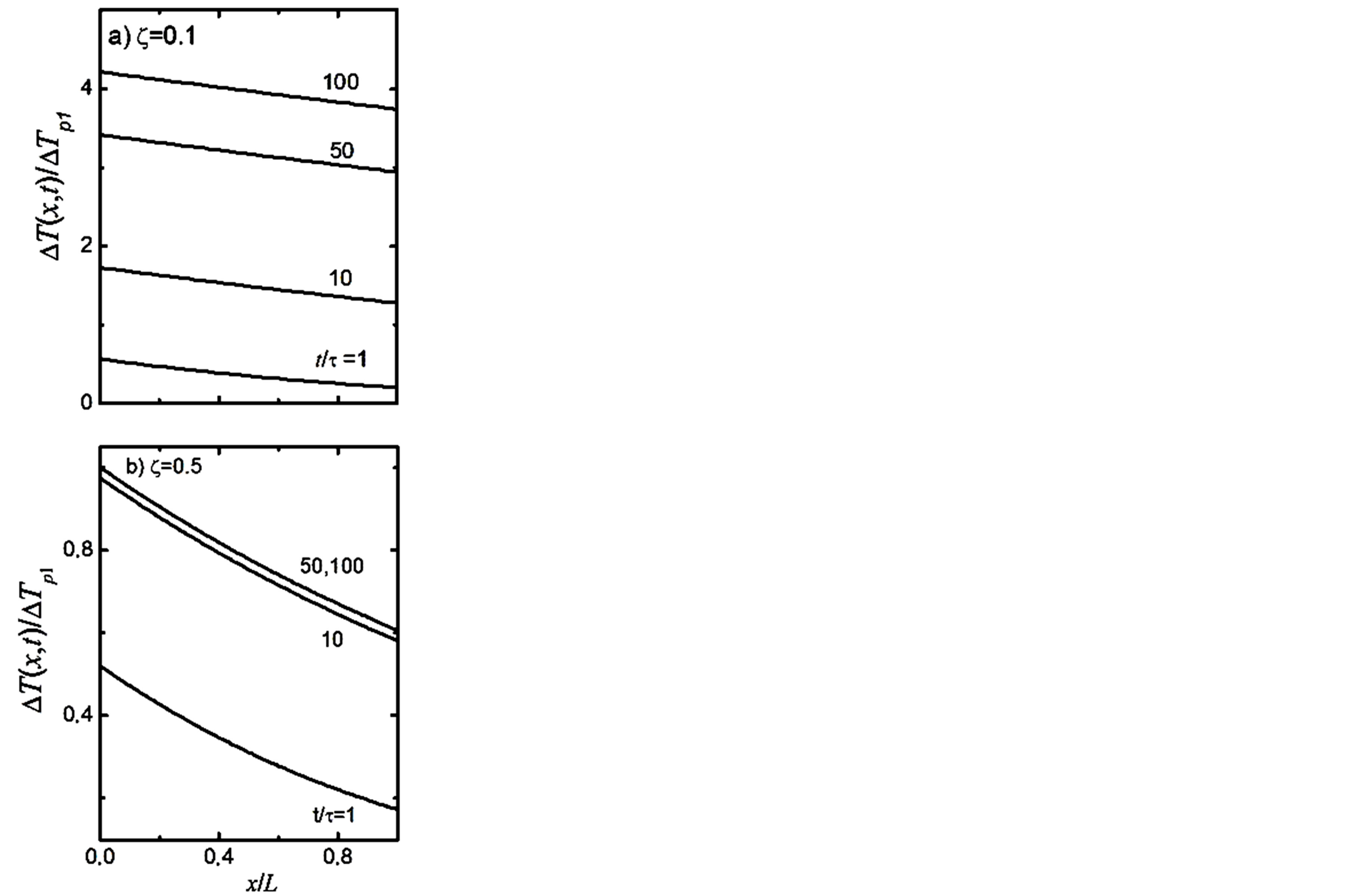
Figure 2. DT(x, t)/DTP1 versus x/L at different times t/t (see Equation (10)) for (a) z = 0.1 (weak blood perfusion), and (b) 0.5 (high blood perfusion).
undergoing a severe damping as z increases due to the blood regulation mechanism. The blood perfusion provokes some delay in early stages which can be seen in the amplified representation of panel b since the curves exhibit a horizontal initial slope (say t/t £ 0.1) before the steep rise.
4. Indirect Laser Heating via GNPs
In the case where tumors are not directly accessible to the laser beam from the ambient, the recourse to an indirect heating via GNPs turns out to be particularly useful for treatment efficiency. Panel b of Figure 1 mimics the discrete temperature distribution in a spherical tumor embedded with GNPs. One can see in the same figure, the single sphere temperature profile in the immediate vicinity of a single GNP with spherical geometry [20]. From a practical point of view, the problem may be simplified by solving the bio-heat equation in spherical coordinates assuming point sources representing the GNPs.
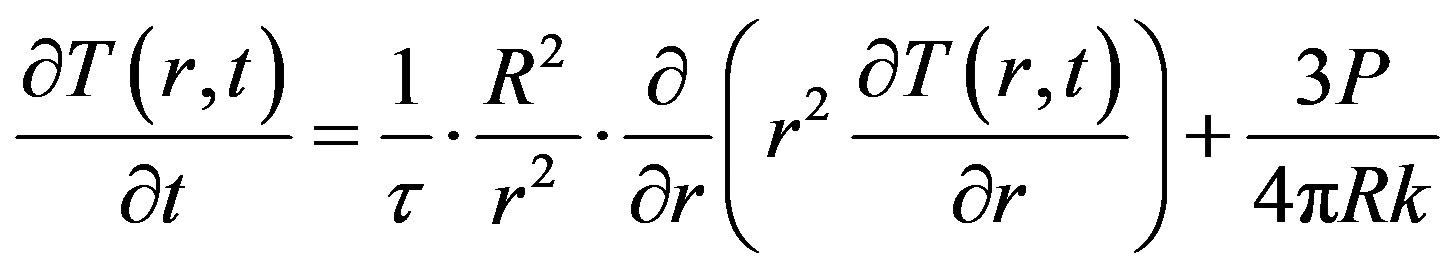 (14)
(14)
The last term in the right hand side comes from the external heat deposited in the tumor. Resolution of such a
 (a)
(a)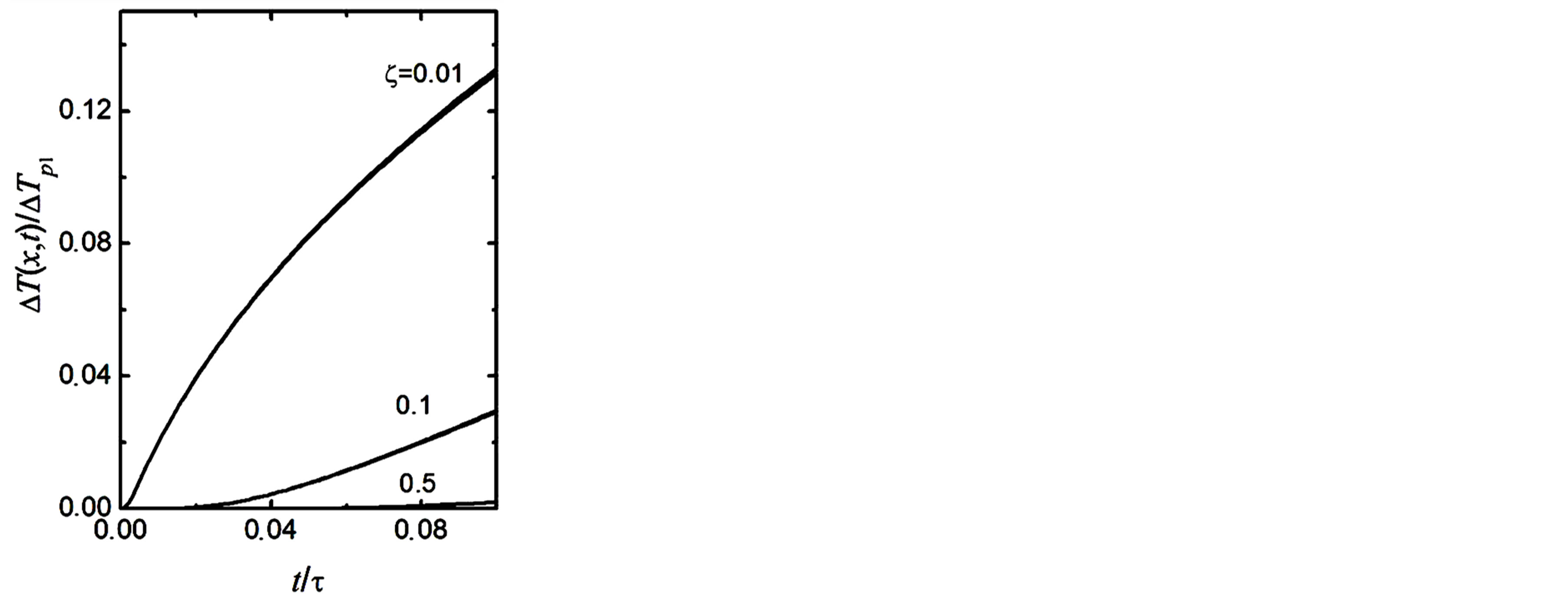 (b)
(b)
Figure 3. (a) DT(x, t)/DTP1 versus t/t for x/L = 0.5 and different values of z. (b) Amplification of DT(x, t)/DTP1 at short times (i.e., t/t < 0.1; see Equation (10)). Note the initial horizontal slope indicating perfusion induced delays in the heating process. The curves in panel (a) are weakly sensitive to x/L. For 0.1, they are slightly above and for 0.5 slightly below those shown and they all follow the same trends.
problem is subject to the knowledge of the initial distribution
 which should be determined first as stated before.
which should be determined first as stated before.
4.1. Initial Temperature Distribution for a Spherical Tumor
The initial temperature for a spherical tumor can be obtained by equating the left hand side and P in Equation (14) to zero. The spherical symmetry implies that heating is maximum at the center for r = 0. For an isothermal interface, the temperature should remain equal to the body temperature TB and the result is
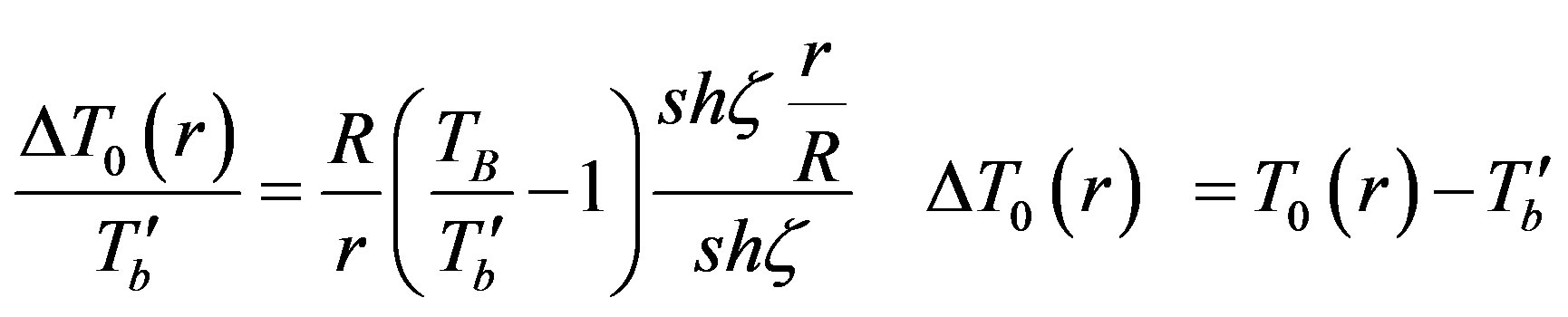 (15)
(15)
In the weak perfusion limit, z is small and the initial temperature remains equal to TB. Most authors in the literature generally assume that the initial temperature is simply the blood temperature Tb while here, we stress the point that this temperature deserves a particular attention and depends on important thermo-physical and biological parameters of both blood and tissues.
4.2. Time Temperature Fronts
Once the initial temperature is known, one may proceed to solve the kinetic problem for which the mathematics combine classical methods of Laplace transform and variation of constants. Resolution of Equation (14) yields
 (16)
(16)
where the normalizing temperature
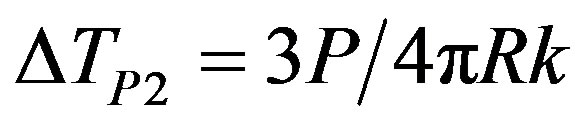 is slightly different from the one in Equations (10) and (13) for geometry considerations. The characteristic time of heat diffusion
is slightly different from the one in Equations (10) and (13) for geometry considerations. The characteristic time of heat diffusion
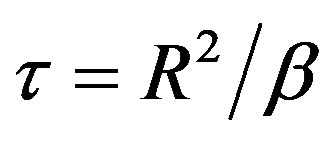 is also different for the same reason. Unlike the previous situation (see Equation (13)), space and time variables are separated and no universality is found here in spite of the fact that blood perfusion is not taken into account. Including metabolism and blood perfusion, one would have to solve the following bioheat equation
is also different for the same reason. Unlike the previous situation (see Equation (13)), space and time variables are separated and no universality is found here in spite of the fact that blood perfusion is not taken into account. Including metabolism and blood perfusion, one would have to solve the following bioheat equation
 (17)
(17)
Whose solution subject to the same initial and boundary conditions becomes
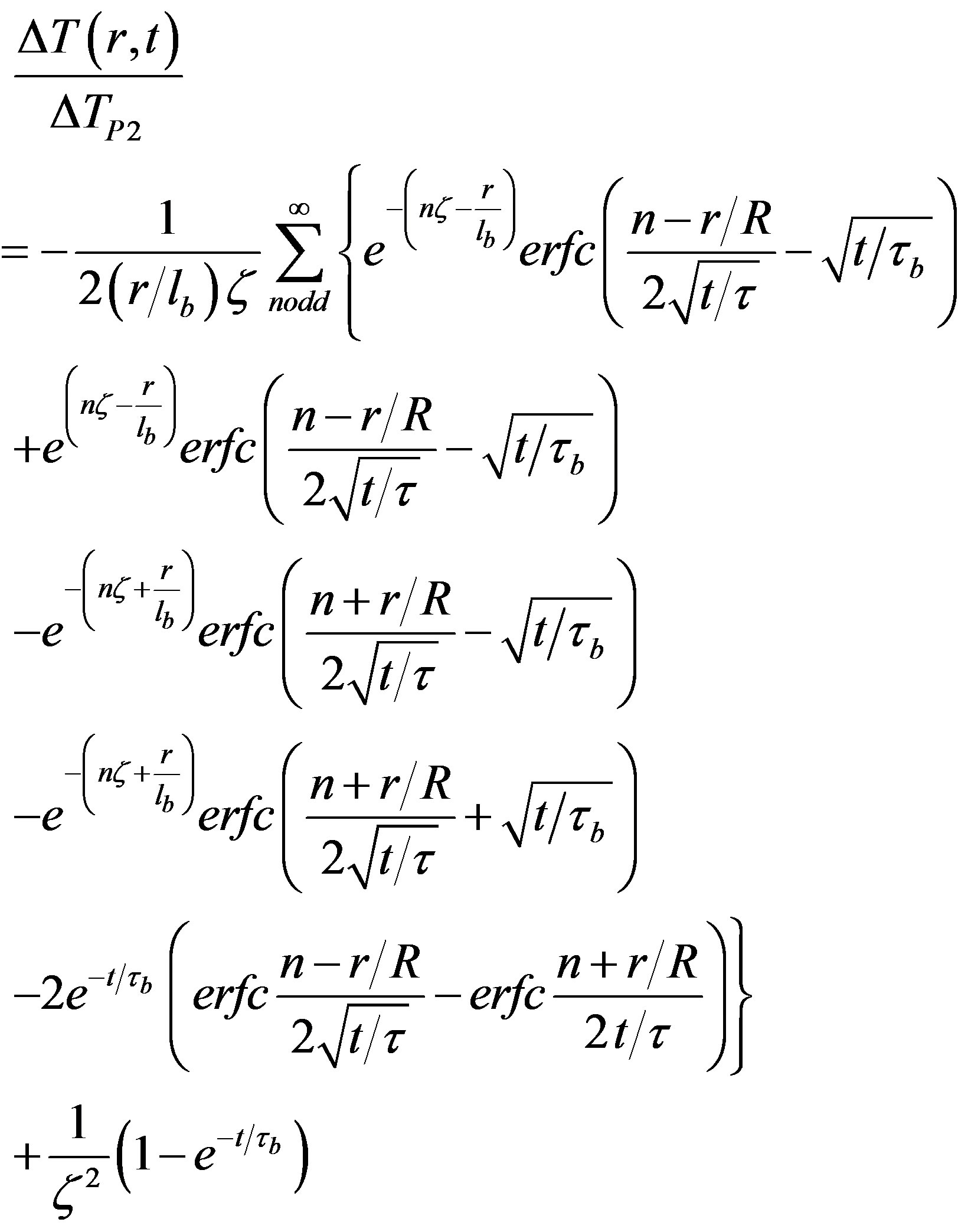 (18)
(18)
This result is quite different from that of equation 16 which is recovered only when . Formally, those results are different from those obtained in the case of the discrete distribution shown in Figure 1(b) but numerically, the temperature profiles are quite close in terms of space and time variations. Figure 4(a) confirms the very weak space dependence of temperature. Space modulations do not exceed few percents while kinetics shows a fast rise of temperature with time (see Figure 4(b)). Blood perfusion reduces both the amplitude and rate of heating. A slight enhancement of the space dependence is observed at high blood perfusion rates. The initial slope is not horizontal as in the previous case meaning that no delays in o heating should exist in early stages (see Figure 4(c)). The other qualitative trends are similar to those of Figure 3.
. Formally, those results are different from those obtained in the case of the discrete distribution shown in Figure 1(b) but numerically, the temperature profiles are quite close in terms of space and time variations. Figure 4(a) confirms the very weak space dependence of temperature. Space modulations do not exceed few percents while kinetics shows a fast rise of temperature with time (see Figure 4(b)). Blood perfusion reduces both the amplitude and rate of heating. A slight enhancement of the space dependence is observed at high blood perfusion rates. The initial slope is not horizontal as in the previous case meaning that no delays in o heating should exist in early stages (see Figure 4(c)). The other qualitative trends are similar to those of Figure 3.
5. Applications
Table 1 gives typical values for the parameters appearing in the bio-heat equation for a variety of biological tissues. No distinction is made between healthy and tumor tissues consistent with the model calculations. The density r is roughly 1 g∙cm−3 but higher by about 20% for epidermis and 50% for fat and bones. The heat conductivity k is essentially 0.5 Wm−1K−1 except epidermis and fat for which it is 20% lower and bones for which it is 20% higher. The heat capacity c is near 3.7 Jg−1K−1 except fat and bones that show a much lower heat capacity. The blood perfusion parameter wb exhibits a large dispersion of values going from 0.07 × 10−2 s−1 for fat to 6.25 × 10−2 s−1 for kidney. Epidermis is characterized by a blood perfusion rate several orders of magnitude smaller. In the literature, this parameter is often expressed by the prod-
 (a)
(a) (b)
(b) (c)
(c)
Figure 4. (a) DT(r,t)/DTP2 versus r/R for a dispersion of GNPs at different times and for z = 0.01 (see Equation (18)). The cases of z = 0.1 and 0.5 essentially yield the same qualitative behavior with lower values as illustrated in panel b; (b) DT(r,t)/DTP2 versus t/t for z = 0.01, 0.1 and 0.5; (c) Amplified version at short times. Unlike Figure 3(b), the initial slope is not horizontal.
uct rbwb in units of kg∙m−3s−1.
Table 2 gives selected data of heat transfer properties for the same biological tissues. The heat diffusivity b for most tissues is about 0.15 mm2∙s−1 but it is lower by
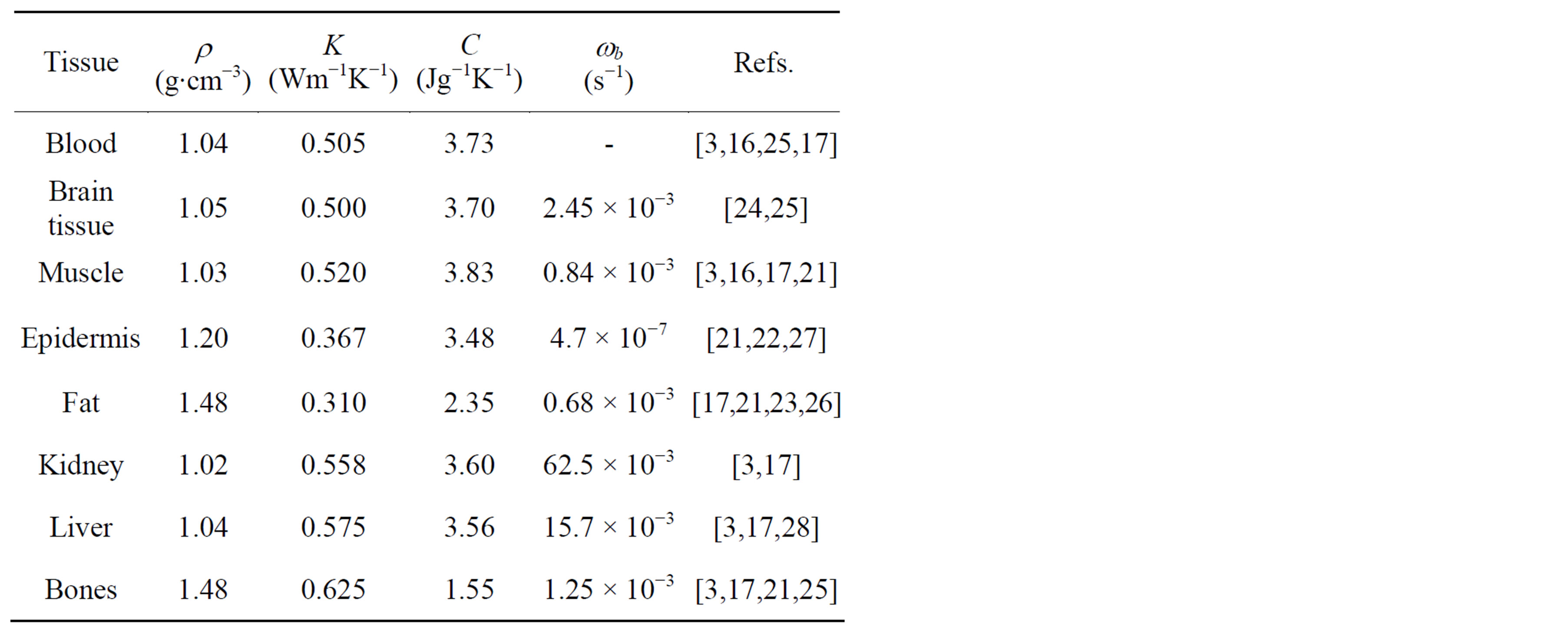
Table 1. Typical values for the thermo-physical parameters of main biological tissues.

Table 2. Selected properties of space and time temperature distributions for the same biological tissues.
nearly a factor two for epidermis and three for fat while for bone it is twice higher. The blood perfusion length lb is typically of the order of 1 to 2 centimeters while the blood perfusion time tb is typically of the order of 30 minutes. It is slightly lower for bones and slightly higher for epidermis and fat. The characteristic time of heat diffusion in tissues t is slightly above 10 min for a centimeter sized tumor except epidermis and fat for which it is much lower. The ratio t/tb = z2 increases with increasing blood perfusion rate and tumor’s size. Metabolism induces a blood temperature increase by nearly a couple of degrees. Although rough, those numbers lead to temperature rise of tumor tissues with amplitudes and times adapted for developing a strategy of hyper thermal therapy.
6. Conclusion
One of the major challenges in developing efficient hyper thermal therapy strategies resides in the precise knowledge of temperature profiles appropriate for the nature and size of the tumor. The present work is a contribution along the line of facing this challenge based on simple analytical models supplemented with typical thermophysical and biological parameters of practical interest. Effects of blood perfusion, metabolism and laser beam intensity were quantified with simple arguments starting from the resolution of the bio-heat equation with a distinction between direct laser heating and indirect heating via GNPs. The results obtained under a variety of conditions showed a systematic consistency with regard to a weak sensitivity of temperature to the position within the tumor but a strong dependence over time. Heat metabolism contributes to increasing the blood temperature by a couple of degrees while blood perfusion significantly damps the heating process. In the early stages of laser treatment, the temperature rises fast but quickly reaches an upper limit which is systematically lower as the blood flow rate is higher. New characteristic lengths are introduced and evaluated together with typical time scales characterizing the heat diffusion mechanism in tumor tissues.
REFERENCES
- J. M. Breasted, “Chirurgical Papyrus of Edwin Smith,” University of Chicago Press, Chicago, 1933.
- L. Goldman and R. J. Rockwell Jr., “Lasers Systems and Their Applications in Medicine and Biology,” Advances in Biomedical Engineering and Medical Physics, Vol. 1, 1968, pp. 317-382.
- G. Brix, S. Martin, H. Gesine and G. Jurger, “Estimation of Heat Transfer and Temperature Rise in Partial Body Regions during MR Procedures: An Analytical Approach with Respect to Safety Considerations,” Magnetic Resonance Imaging, Vol. 20, No. 1, 2002, pp. 65-76. http://dx.doi.org/10.1016/S0730-725X(02)00483-6
- J. M. Dobson, “Radiation Therapy, Hyperthermia, ImmunoTherapy, in Manual of Small Animal Oncology,” In: R. A. S. White, Ed., British Small Animal Veterinary Association, Cheltenham, 1991, pp. 161-183.
- A. P. Popov, A. V. Priezzhev and R. Myllyla, “Optimal Sizes of Gold Nanoparticles for Laser Treatment of Tumors,” 5th International Conference on Photonics and Imaging in Biology and Medicine, Proceedings of SPIE, Russia, 1 May 2007, Vol. 6534, 65343K-1-5.
- T. Avedisian, R. E. Cavicchi, P. L. McEuen and X. Zhou, “Nanoparticles for Cancer Treatment: The Role of Heat Transfer,” Cornell University, Ithaca, 2007.
- N. Harris, M. J. Ford and M. B. Cortie, “Optimization of Plasmonic Heating by Gold Nanospheres and Nanoshells,” The Journal of Physical Chemistry B, Vol. 110, No. 22, 2006, pp. 10701-10707. http://dx.doi.org/10.1021/jp0606208
- J. Liu and M. Gu, “Gold Nanoparticle-Enhanced Cancer Photo-Thermal Therapy,” IEEE Journal, Vol. 16, No. 4, 2009, pp. 989-996.
- X. Liu, M. C. Lloyd, I. V. Fedorenko, P. Bapat, T. Zhukov and Q. Huo, “Enhanced Imaging and Accelerated Photothermalysis of A549 Human Lung Cancer Cells by Gold Nanospheres,” Nanomedicine, Vol. 3, No. 5, 2008, pp. 617-626. http://dx.doi.org/10.2217/17435889.3.5.617
- I. H. El-Sayed, X. Huang and M. A. El-Sayed, “Selective Laser Photo-Thermal Therapy of Epithelial Carcinoma Using Anti-EGFR Antibody Conjugated Gold Nanoparticles,” Cancer Letters, Vol. 239, No. 1, 2006, pp. 129- 135. http://dx.doi.org/10.1016/j.canlet.2005.07.035
- D. Pissuwan, S. M. Valenzuela and M. B. Cortie, “Therapeutic Possibilities of Plasmonicall Heated Gold Nanoparticles,” Trends in Biotechnology, Vol. 24, No. 2, 2006, pp. 62-67. http://dx.doi.org/10.1016/j.tibtech.2005.12.004
- X. Huang, P. K. Jain, I. H. El-Sayed and M. A. El-Sayed, “Plasmonic Photothermal Therapy (PPTT) Using Nanoparticles,” Lasers in Medical Science, Vol. 23, No. 3, 2008, pp. 217-228. http://dx.doi.org/10.1007/s10103-007-0470-x
- H. Pennes, “Analysis of Tissue and Arterial Blood Flow Temperatures in the Resting Human Forearm,” Journal of Applied Physiology, Vol. 1, No. 2, 1948, pp. 93-122.
- Z. S. Deng and J. Liu, “Analytical Study on Bioheat Transfer Problems with Spatial or Transient Heating on Skin Surface or inside Biological Bodies,” Transactions of the ASME, Vol. 124, No. 6, 2002, pp. 638-649.
- P. R. Sharma, S. Ali and V. K. Katiyar, “Transient Heat Transfer Analysis on Skin Surface and inside Biological Tissue,” Journal of Applied Mathematics and Mechanics, Vol. 5, No. 5, 2009, pp. 36-47.
- J. C. Chato, “Fundamentals of Bioheat Transfer,” In: Gautherie, Ed., Thermal Dosimetry and Treatment Planning, Springer Verlag, Berlin, 1990, 1-56.
- B. Erdmann, J. Lang and M. Seebass, “Adaptative Solution of Nonlinear Parabolic Equations with Application to Hyperthermia Treatments,” Technical Report, KonradZuse-Zentrum fur Informationstechnik, Berlin, 1997.
- T. C. Shih, P. Yuan, W. L. Lin and H. S. Kou, “Analytical Analysis of the Pennes Bioheat Transfer Equation with Sinusoidal Heat Flux Condition on Skin Surface,” Medical Engineering & Physics, Vol. 29, No. 9, 2007, pp. 946-953. http://dx.doi.org/10.1016/j.medengphy.2006.10.008
- M. Abramowitz and I. A. Stegun, “Handbook of Mathematical Functions,” Dover Publishing Inc., New York, 1970.
- B. Fasla, R. Benmouna and M. Benmouna, “Modeling of Tumor’S Tissue Heating by Nano Particles,” Journal of Applied Physics, Vol. 108, No. 12, 2010, Article ID: 124703. http://dx.doi.org/10.1063/1.3525089
- V. L. Dragun, S. M. Damilove, Y. Tret and S. A. Gubarev, “Simulation of Reacting of Biological Tissues in the Process of Ultrahigh Frequency Therapy,” Journal of Engineering Physics and Thermophysics, Vol. 78, No. 1, 2005, pp. 109-114.
- S. C. Tiang, H. J. Ma, H. J. Li and X. Zhang, “Effect of Thermal Properties and Geometrical Dimensions on Skin Burn Injuries,” Burns, Vol. 28, No. 8, 2002, pp. 713-717. http://dx.doi.org/10.1016/S0305-4179(02)00104-3
- J. Zhang, G. A. Sandison, J. Y. Murthy and L. Xu, “Numerical Simulation for Heat Transfer in Prostate Cancer Surgery,” Journal of Biomechanical Engineering-Transactions of the ASME, Vol. 127, 2005, pp. 279-294.
- C. Diao, L. Zhu and H. Whang, “Cooling and Rewarming for Brain Ischemia or Injury: Theoretical Analysis,” Annals of Biomedical Engineering, Vol. 31, No. 3, 2003, pp. 346-353.
- L. Zhu and C. Diao, “Theoretical Simulation of Temperature Distribution in the Brain during Hypothermic Treatment for Brain Injury,” Medical and Biological Engineering and Computing, Vol. 39, No. 6, 2001, pp. 681- 687.
- A. W. Guy, “Analysis of Electromagnetic Fields in Biological Tissues by Thermographic Studies on Equivalent Phantom Models,” IEEE Transactions on Microwave Theory and Techniques, Vol. 16, No. 2, 1971, pp. 205- 214.
- J. Liu, X. Chen and L. Xu, “New Thermal Wave Aspects on Burn Evaluation of Skin Subjected to Instantaneous Heating,” IEEE Transactions on Biomedical Engineering, Vol. 46, No. 4, 1999, p. 420.
- F. Duck, “Physical Properties of Tissues,” Academic Press, London, 1990.

