Agricultural Sciences
Vol.5 No.2(2014), Article ID:42893,12 pages DOI:10.4236/as.2014.52017
Model for stock-recruitment dynamics of the Peruvian anchoveta (Eugraulis ringens) off Peru
Department of Ocean Science and Technology, Tokyo University of Marine Science and Technology, Tokyo, Japan; *Corresponding Author: sakurak@kaiyodai.ac.jp
Copyright © 2014 Ashneel A. Singh et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Ashneel A. Singh et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received 10 December 2013; revised 17 January 2014; accepted 29 January 2014
KEYWORDS:Anchoveta; Density-Dependent; Recruitment; Regimes; Reproductive Success; Sea Surface Temperature; Southern Oscillation Index; Spawning Stock Biomass
ABSTRACT
This paper was aimed at re-examining the validity of the results from Cahuin et al. (Estuar. Coast. Shelf Sci. 84, 2009) and identifying a model to describe the stock-recruitment relationship of the Peruvian anchoveta (Eugraulis ringens). Regression analysis was used to determine if density-dependent effects were present. The analysis did not show the existence of any densitydependent effects. It is important to use environmental factors and take observational and process errors into account when attempting to identify density-dependent effects in fish populations. Sea surface temperature (SST) and Southern Oscillation Index (SOI) were used as independent variables to fit the recruitment dynamics of the anchoveta. Both SST and SOI were found to be significantly important parameters in structuring anchoveta dynamics according to Akaike Information Criterion (AIC) and R2 values. The results of this study do not correlate with the findings of Cahuin et al., (2009), where density-dependent effects and the presence of regimes were detected. In conclusion, the recruitment Rt is essentially determined in proportion to spawning stock biomass St, and then environmental factors in year t further change the recruitments. This mechanism is completely same with that for Japanese sardine proposed by Sakuramoto (The Open Fish. Sci. 5, 2012).
1. INTRODUCTION
Marine ecosystems are complex and are affected by numerous intrinsic and extrinsic environmental factors. Fish populations have a tendency to fluctuate over time and the mechanisms behind these fluctuation patterns can be understood by investigating relationship of the recruitment (R) to the spawning stock biomass (SSB) and environmental factors. Jacobson and MacCall [1] have shown that the recruitment of Pacific sardine in the coastal area of North America is significantly influenced by both the SSB and the sea surface temperature (SST). SST has been shown to be correlated to anchovy population dynamics previously [2-5]. The impact of sea surface temperature on the recruitment dynamics of other species of fish has also been identified [6,7]. Climatic conditions such as wind direction index, North Atlantic oscillation and Southern oscillation index (SOI) have also been correlated with the dynamics and regimes of anchovy as well as other fish species [7-11].
Cahuin et al. [11] examined the reproductive success (RPS) and SSB relationship of the Peruvian anchoveta (Eugraulis ringens) from 1963 to 2004 and discussed their fluctuation mechanisms. They explained the longterm fluctuations by the concept of “regime shift” and separating the data series into two periods of “favorable regimes” and one period of “unfavorable regime”. Separate regression lines of ln(RPS) against SSB were calculated for each regime. They stated that the long-term dynamics of the anchoveta are caused by regime shifts and the existence of different carrying capacities or density-dependent effects during these regimes.
Wada and Jacobson [12] identified the existence of regimes in the RPS dynamics of the Japanese sardine (Sardinops melanotictus) over a long time series from 1951 to 1995. The data for the time series was divided into two and separate regression lines were constructed and identified as regimes characterized as “favorable” and “unfavorable”. Based on the slope of the regression lines for the regimes, the conclusion was drawn that densitydependent effects on recruitment do exist for Sardinops species. Density-dependent effects can only be measured for long-term data series if there is evidence of large (>1000-fold) difference between the maximum and minimum abundance in the data series [13]. Sakuramoto [14] discussed the validity of the results from Wada and Jacobson [13] and proposed a new concept for the stockrecruitment relationship of the Sardinops species. He reported that the false decreasing trend indicating the existence of density-dependent effects was due to observational error. When the data were adjusted for observational errors and regression analysis was applied to the full data series, the slope of the regression line did not differ significantly from unity indicating the absence of density-dependent effects as well as the absence of two different carrying capacities or regimes. Sakuramoto and Suzuki [15] provide a detailed report on the effect of observation and/or process error which in most cases results from environmental variables on recruitment and/ or SSB in the selection of a stock-recruitment relationship.
Cahuin et al. [11] used the General Additive Model (GAM) to model the RPS of anchovy with SSB, SST, SOI and other environmental variables. They stressed the importance of the SST, however, they identified the SOI as the environmental variable to best explain the recruitment dynamics of the Peruvian anchoveta.
The purpose of this paper is to re-examine the assessment of the Peruvian anchoveta by Cahuin et al. [11]. The objectives are to: 1) re-examine the basis of separation of the anchovy data into the two regimes; 2) test the validity of the existence of density-dependent effects; 3) find out the best model for explaining the recruitment, by using SSB, SST and SOI as the environmental variables.
2. MATERIALS AND METHODS
2.1. Data
The data on the spawning stock biomass and recruitment of the North-Central stock of anchoveta (E. ringens), was obtained from Cahuin et al. [11] (Table 1). The stock distribution of the Peruvian anchoveta is shown in Figure 1. The recruitment (R) is the number of fish at age 0 and the spawning stock biomass (SSB) is the weight of reproductive adult fish at the initialization of the spawning season. The actual raw data for R and SSB was collected by the Instituto del Mar del Peru (IMARPE). More information regarding the landings of Peruvian anchovy is available from the IMARPE database (Table 1).
The data for monthly mean sea surface temperature
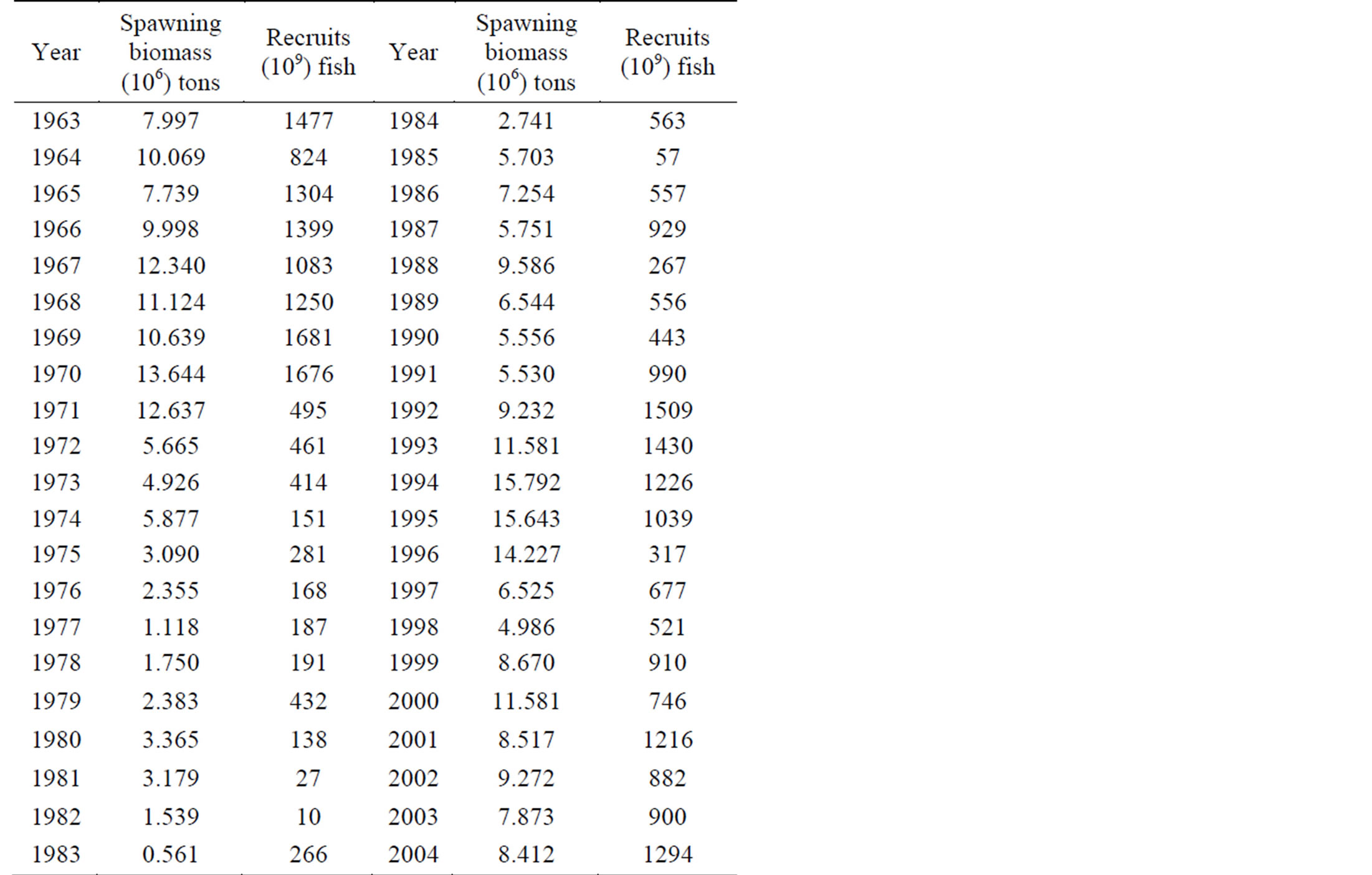
Table 1. Recruitment and spawning stock biomass of the North-Central stock of the Peruvian anchoveta Eugraulis ringens from 1963 to 2004 (source: Cahuin et al. [11]).

Figure 1. Map of Peru showing the stock distribution of the Peruvian anchoveta Eugraulis ringens off Peru (4˚ - 14˚ South). The shaded area (in blue) is the major anchovy fishing area to which the data used in this study belongs to, based on the information from Cahuin et al. [11] and IMARPE database. The fishing area is approximate and not to scale.
(SST) was obtained for the years ranging from 1963 to 2004 at Nino 1 + 2 (0˚ - 10˚ South) (90˚ West - 80˚ West), from the NOAA website. Data for the monthly Southern Oscillation Index (SOI) was also obtained from 1963 to 2004 and the annual averages were calculated from this. Both the SST and SOI data were calculated from this. The SST and SOI data as reported by the National Weather Service, Climate Prediction center were obtained from NOAA database (Table 2). The monthly anomalies from the standardized data series from 1963- 2004 were used to calculate the annual means.
Descriptions of databases that were accessed for retrieving raw datasets used for this study are shown in Table 2.
2.2. Regimes and Density-Dependent Effects
Cahuin et al. [11] reported the existence of regimes and density-dependent effect in the anchovy population dynamics. To re-examine the validity of this, we began by plotting the log of recruitment, SSB and RPS of the anchovy for the data series from 1963-2004. The data were log transformed to reduce the effects of outliers and skewness. We replicated the method of Cahuin et al. [11] to separate the data into the “favorable” and “unfavorable” regimes. Linear regression was applied to ln(RPS) against the SSB, for (a) recognizing the existence of the two regimes and (b) ignoring the regimes. In addition to this we carried out a reselection of the data based on the data points above and below the regression line for the graph of ln(RPS) against (SSB) and applied linear regression analysis to it. The coefficients of all three regression analysis were reported.
For validation of the existence of density-dependent effects, we used simple regression with least squares method. We tested the slope of the regression line for the plot of ln(RPS) against ln(SSB) for zero. This method has some limitations as the RPS is sensitive to observational errors for short data series [14,16]. To confirm the results we applied regression analysis to ln(R) against ln(SSB) to test for unity as this method is more resistant to observational errors.
2.3. Recruitment Forecasting Model
The generalized additive model (GAM) was used to explain the recruitment dynamics of the Peruvian anchoveta. The basic model was
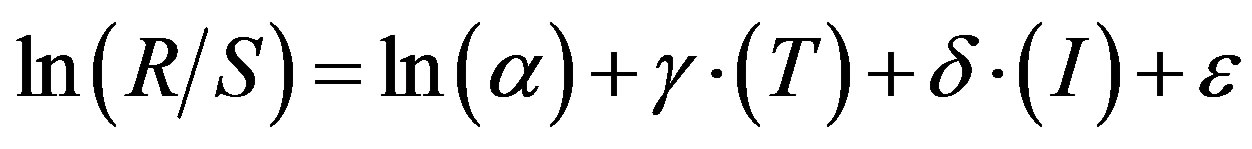 (1)
(1)
where (R/S) is the reproductive success (RPS), α is the intercept parameter, T and I are the environmental variables for SST and SOI respectively, and ε is a normally distributed random variable. The other model for the RPS that was used, was derived from a linearized Ricker [17] model and it was modified to incorporate the environmental variable
 (2)
(2)
where (R/S) is the reproductive success (RPS), and SSB is the spawning stock biomass. T and I represent the environmental variables for SST and SOI respectively. Different modifications of the two models were used for exploratory analysis to find out the best model for the recruitment fluctuations of anchoveta. The Akaike Information Criterion (AIC) was used to evaluate each model and form a basis for model selection [18]. The models exhibiting smallest AIC values and some of their parameters were reported. The actual recruitment dynamics from Table 1 and the recruitment resulting from the model was plotted.
All statistical analysis for this study was carried out using the statistical software “R”, version 3.0.1 “Good Sport”.
3. RESULTS
3.1. Regimes and Density-Dependent Effects
The fluctuations patterns for ln(R), ln(SSB) and ln(RPS)
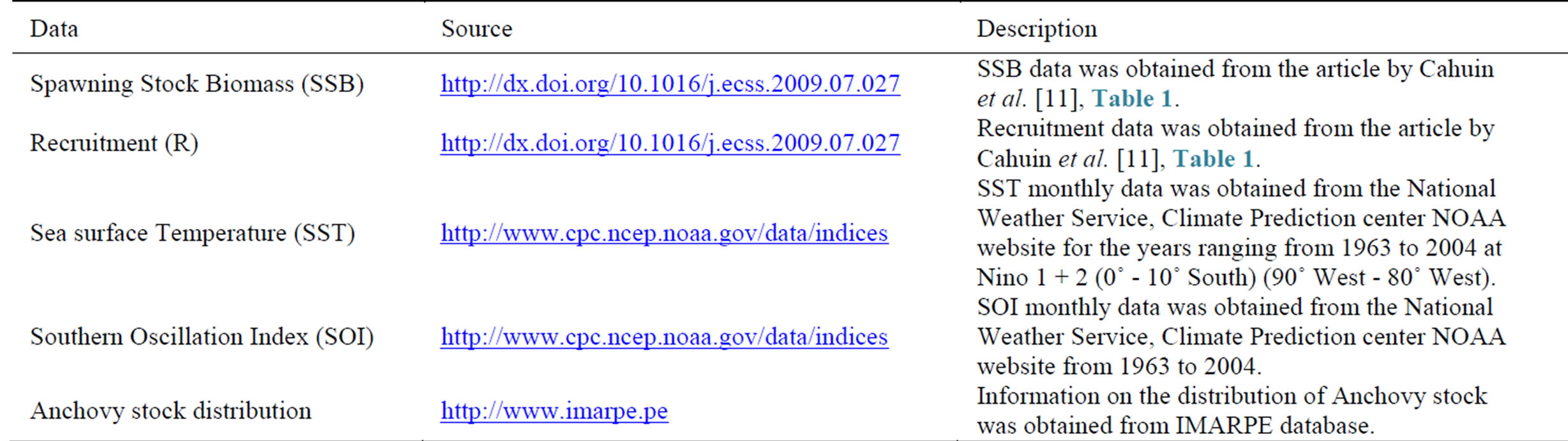
Table 2. Table showing details about the sources of the different data used for this study.
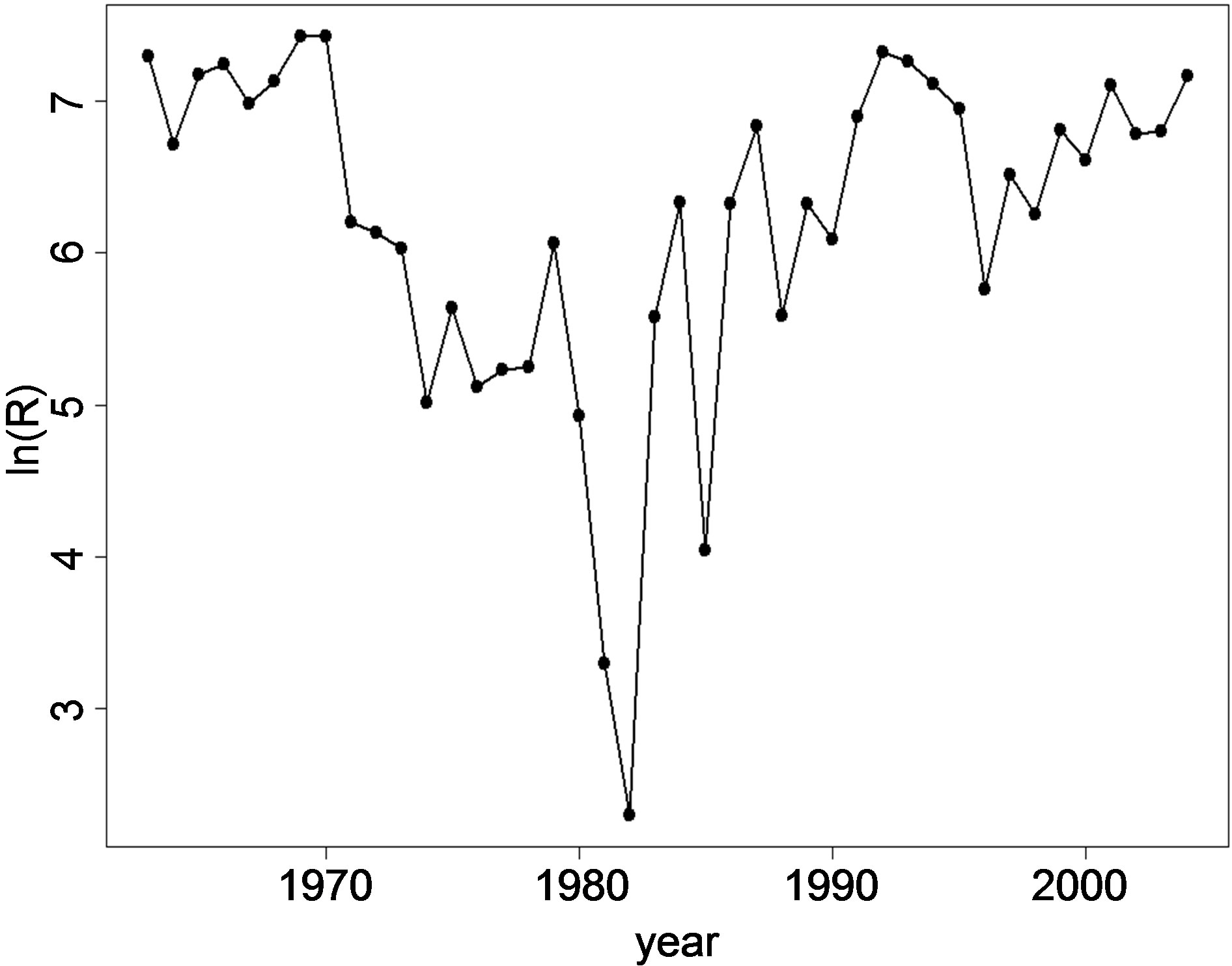
are shown in Figures 2(a), (b) and (c) respectively. The ln(R) shows a decreasing trend in the years 1970-1974, 1979-1982 and from 1992-1996. For the other years, the trend is either increasing or fluctuating with a decrease followed by an increase every following year. The fluctuation pattern for ln(R) is similar to ln(SSB). The pattern for ln(SSB) seems to be followed by ln(R) after a lag of one year. Cahuin et al. [11] identified regimes in the years 1963-1971, 1986-2004 for favorable regime and the years 1972-1985 for unfavorable regime. The plot of the ln(RPS) (Figure 2(c)) shows decreasing and increasing patterns to be randomly distributed for the range of year from 1963-2004 and does not show the regimes indentified by Cahuin et al. [11].
The plots of ln(RPS) against SSB in Figure 3 is replicated from Cahuin et al. [11]. It shows two regression lines for the data based on the favorable and unfavorable regime. We connected the data points for the two regimes following the year series. Figure 3 also shows a single regression line for the whole data series without separation into regimes. We used the regression line for the whole data series to select the data points above and below the regression line and plot separate regression lines for each in Figure 4.
The model coefficients and other parameters for the plots in Figure 3 and Figure 4 are presented in Table 3. According to Cahuin et al. [11], the model recognizing the presence of the regimes is better than a model ignoring the regimes. The AIC selects the model with regime over a model without regimes (Table 3), however, it is unclear how the selection of the data points of regimes were made. The presence of regimes is unclear from Figure 2(c), and in Figure 3, it can be observed that the RPS for the unfavorable regime does not remain continuously low for long periods of time (years). The fluctuations between low RPS and high RPS are too short to claim the existence of regimes.
The pattern is similar for the unfavorable regime. It is not clear what the basis of separation of the data into regimes really was.
If regimes do exist, then the method of separation of data by Cahuin et al. [11] in Figure 3, should be the best fit for the data points. This means that, any alternative way of separation of data should give a higher AIC value than the model of Cahuin et al. [11] (Table 3 (Model 1)). To test this, we performed an alternative selection of the data based on the data points above and below the regression line from the plot of ln(RPS) against SSB for the full data series and applied separate regression analysis to each (Figure 4).
When we compare the AIC value that was calculated for the single regression line without regimes with that of double regression lines which resulted from two different regimes, the latter AIC was smaller than the former one
 (a)
(a)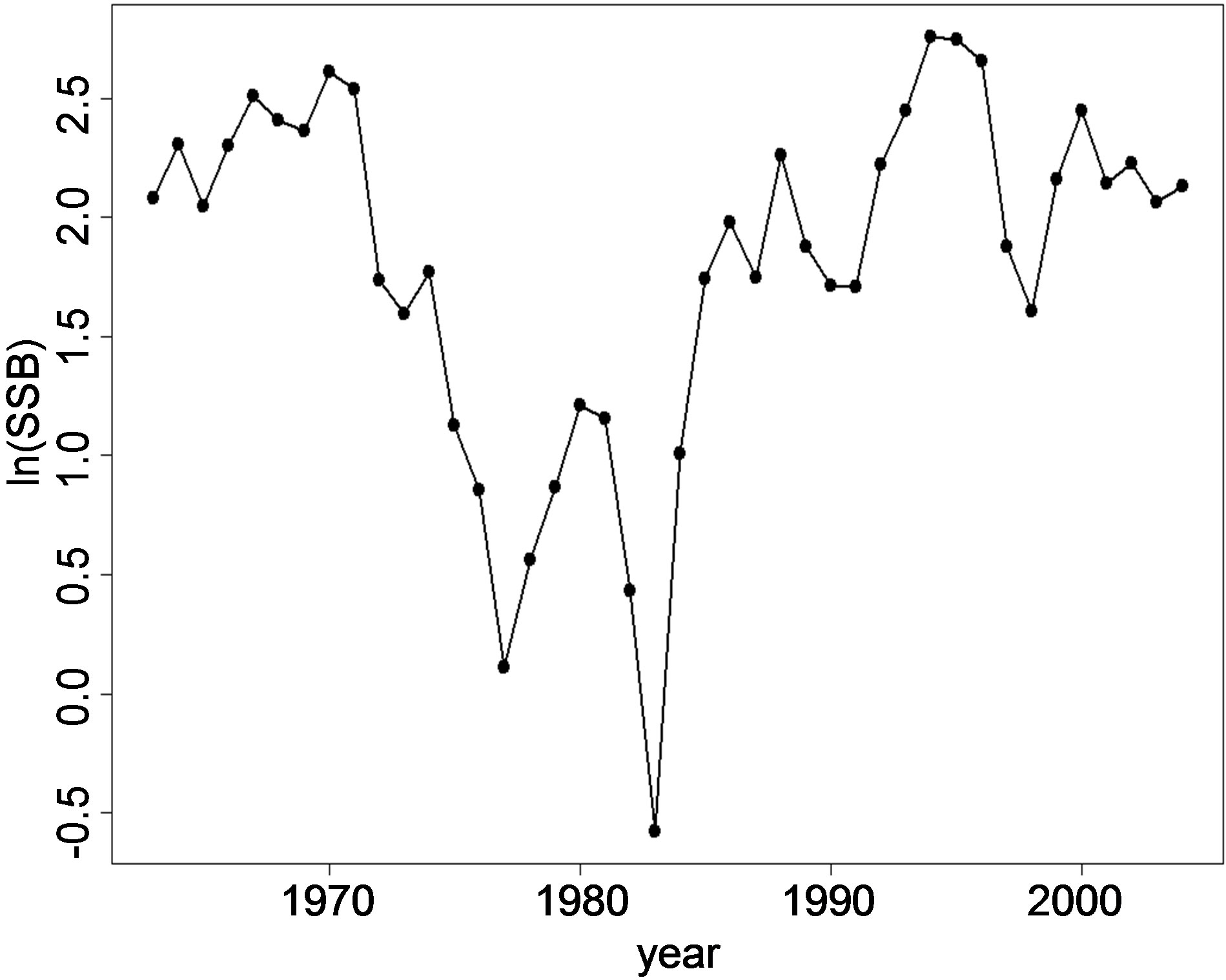 (b)
(b) (c)
(c)
Figure 2. The dynamics of Peruvian anchoveta Eugraulis ringens from 1963-2004. (a) ln(R), (b) ln(SSB), (c) ln(RPS). The fluctuations patterns are similar for ln(R) and ln(SSB). The plot ln(RPS) does not show regimes indentified by Cahuin et al. [11].

Figure 3. Graph of ln(RPS) plotted against the SSB of the Peruvian anchoveta Eugraulis ringens showing data selection based on the two regimes. The regression line in blue represents the favorable regime “F” and red represents the unfavorable regime “U” from Cahuin et al. [11]. The regression line in black represents the full data series. The lines connecting the data points for the favorable regime (in blue) and unfavorable regime (in red) show the annual variation of the data.
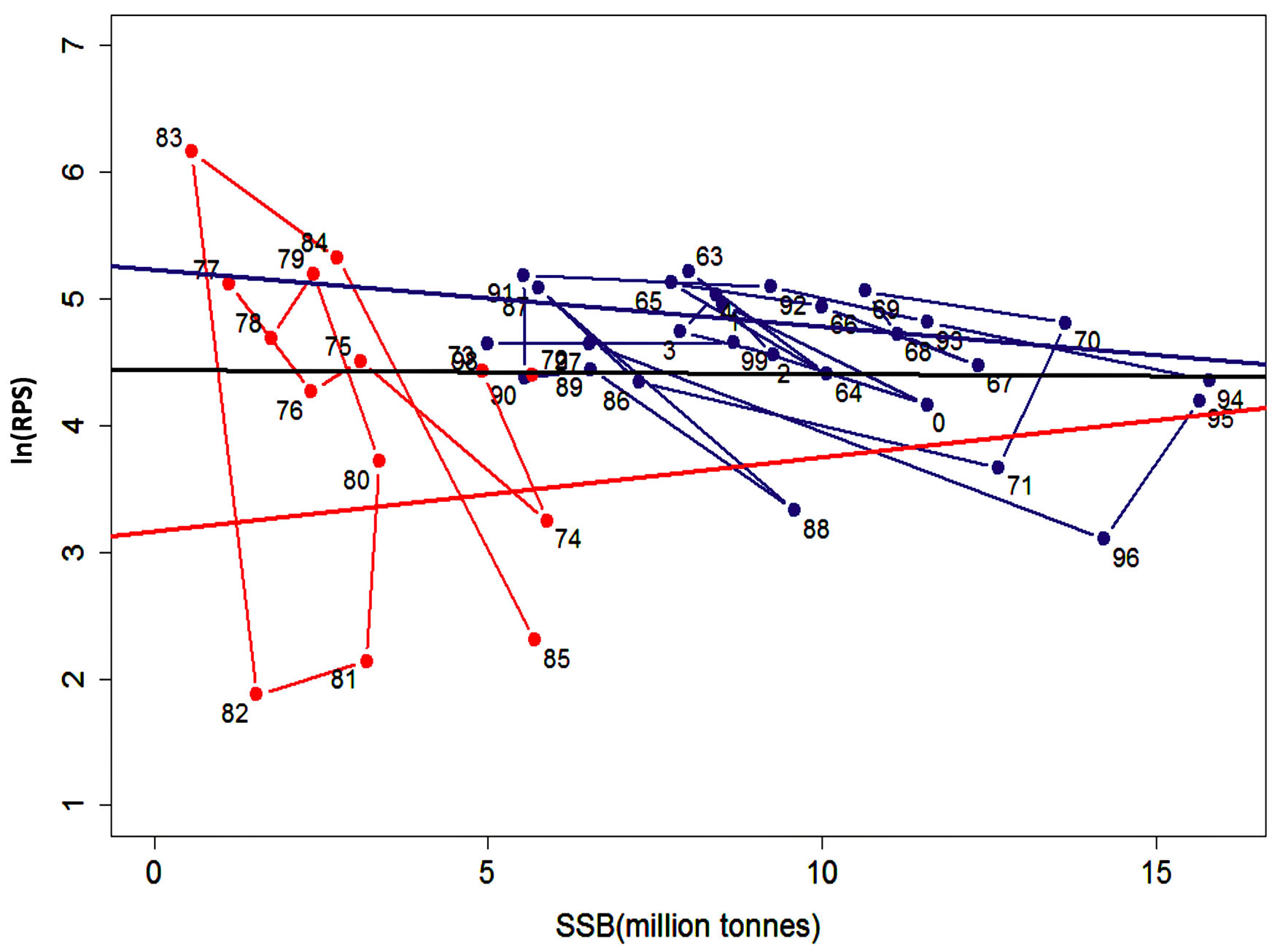
Figure 4. Graph of ln(RPS) plotted against the SSB of the Peruvian anchoveta Eugraulis ringens showing regression plots for two sets of data selected based on the data points above (regression line in blue) and below (regression line in red) the regression line for the full data series (in black). The lines connecting the data points for the favorable regime (in blue) and unfavorable regime (in red) show the annual variation of the data.

Table 3. Comparison of model coefficients for ln(RPS) as a function of the SSB for the full model without regimes, with regimes and a model with two data sets having data points selection based on points above and below the regression line for the full data series.
aReplicated model from Cahuin et al. [11]. “F” represents the favorable regime and “U” represents the unfavorable regime. bModel based on separation of data points above and below the regression line for full data series. cRegression line for data points above the regression line for full data series in Figure 4. dRegression line for data points below the regression line for full data series in Figure 4.
(Table 3). However, this does not represent the validity of the latter model as being more optimal than the former one. In other words, it is not reasonable to compare the one line model with the two lines one. We should carry out comparisons between models which consist of two lines. One example of an alternative two lines model is shown in Table 3 (Model 3). One group is constructed with the data points above the regression line for full data series in Figure 4. The other group is constructed with the data points below the regression line. The former group indicates the years when ln(RPS) was high, and the latter one indicates the years when ln(RPS) was low. When we assumed this grouping method, and calculated the AIC, the AIC of this model (Table 3 (Model 3)) was much lower than the model which considered the presence of regimes and adapted two lines (Table 3 (Model 1)). This is evidence that the proposal of the existence of density-dependent effects in each regime is questionable.
To further elucidate whether density-dependent effects exist for the Peruvian anchovy data, we adopted the method employed by Sakuramoto [14]. Regression analysis was applied to ln(RPS) against ln(SSB) for the data separated into regimes from Cahuin et al. [11]. The slope for the favorable regime (Figure 5) was (slope = −0.673) and significantly negative (p = 0.032) and for the unfavorable regime the slope was (slope = −0.878) and significantly negative (p = 0.097) under the 10% significant level. When we applied a single linear regression to the whole data series from 1963-2004 for ln(RPS) against ln(SSB), the resulting regression line (slope = −0.067) did not differ significantly from zero (p = 0.718) and density-dependent effects could not be detected (Figure 5). The pattern in Figure 5 coincided well with the simulations shown by Sakuramoto [14].
Same results can be obtained when the linear regression of ln(R) against ln(SSB) was conducted. For the plot of ln(R) against ln(SSB), the slope of the regression line
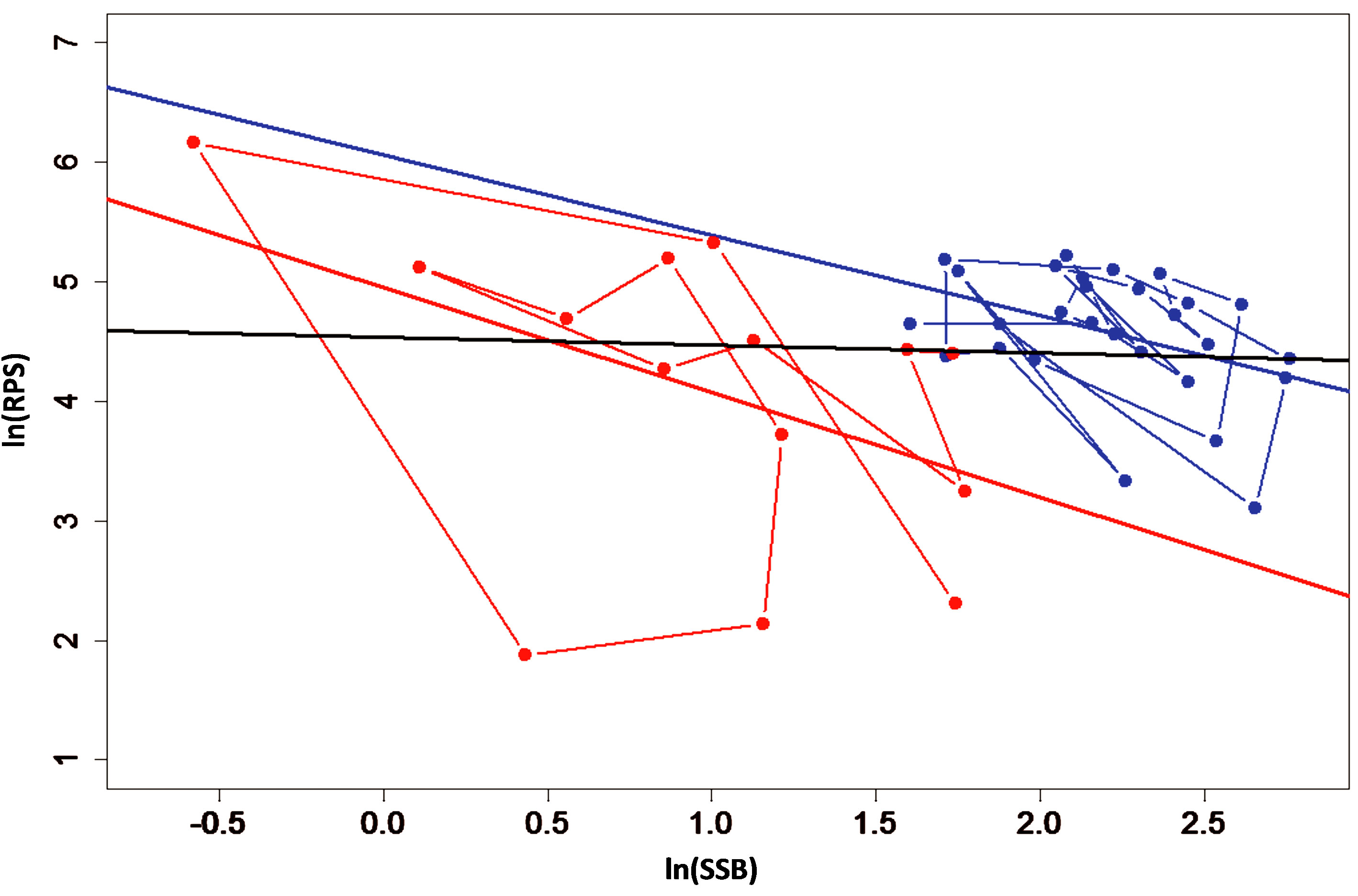
Figure 5. Graph of ln(RPS) plotted against the ln(SSB) of the Peruvian anchoveta Eugraulis ringens. The slope for the favorable regime (in blue) was (slope = −0.673) and significantly negative (p = 0.032). For the unfavorable regime (in red) the slope was (slope = −0.878) and significantly negative (p = 0.097) under 10% significant level. The slope of the regression line for full data series (in black) was (slope = −0.067) and not significantly different from zero (p = 0.718). Density-dependent effects and regime shift are not detected. The lines connecting the data points for the favorable regime (in blue) and unfavorable regime (in red) show the annual variation of the data.
for the favorable regime (slope = 0.327) was significantly different from zero and less than unity with a 95% confidence interval of (−0.282, 0.936). The slope for the unfavorable regime (slope = 0.122) was not significantly different from zero and unity with a 95% confidence interval of (−0.944, 1.188). When regression was applied to the full data set the slope for this regression was (slope = 0.923) with the 95% confidence limit of (0.561, 1.305), which is not significantly different from unity (Figure 6). According to the results, the claim of the existence of density-dependent in each regime is highly questionable for the anchovy data series.
3.2. Recruitment Forecasting Model
Cahuin et al. [11] used the Generalized Additive Model (GAM) for modeling the anchovy dynamics with the SSB and having SOI and SST as the environmental parameters. They used the full time series from 1963-2004 in one approach and came up with the following model:
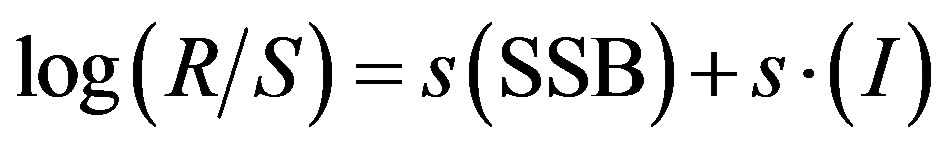 (3)
(3)
where (R/S) is the reproductive success (RPS), and SSB is the spawning stock biomass. I represent the environmental variable for SOI and s is a spline smoother parameter obtained using penalized regression splines analysis. Equation (3), when applied to full time series for anchovy data had a value of R2 = 0.251. In another approach, Cahuin et al. [11] used data only from the years 1963- 1971 and 1986-2004 which were identified as the favorable regimes. The preferred model was produced with the years of the favorable regime and SOI and SSB as the independent parameters. The resulting model was the same as Equation (3), with a value of R2 = 0.494. The difference between the two approaches is the proportion of data used for analysis. The best model by Cahuin et al. [11] was one with only the data from the favorable regimes that did not include the anchovy data for 14 years which is 33.33% of the total data. This is a major proportion of the stock-recruitment data series which was not incorporated for the modeling of the data, more importantly since the presence of regimes has now been put into question. The resulting model and the basis of selection of the best model are highly debatable.
In our approach, the fluctuation dynamics of the whole time series of the Peruvian anchovy was modeled through GAM and linearized Ricker model. We used various modifications of the models to incorporate the environmental variables of SOI and SST. In the study by Cahuin et al. [11], the SST at 4 different experimental stations across the coastal region of Peru was used. Since we did not have access to this data, in our study we used the SST from Nino 1 + 2 (0˚ - 10˚ South) (90˚ West - 80˚ West) available from the NOAA website. We used
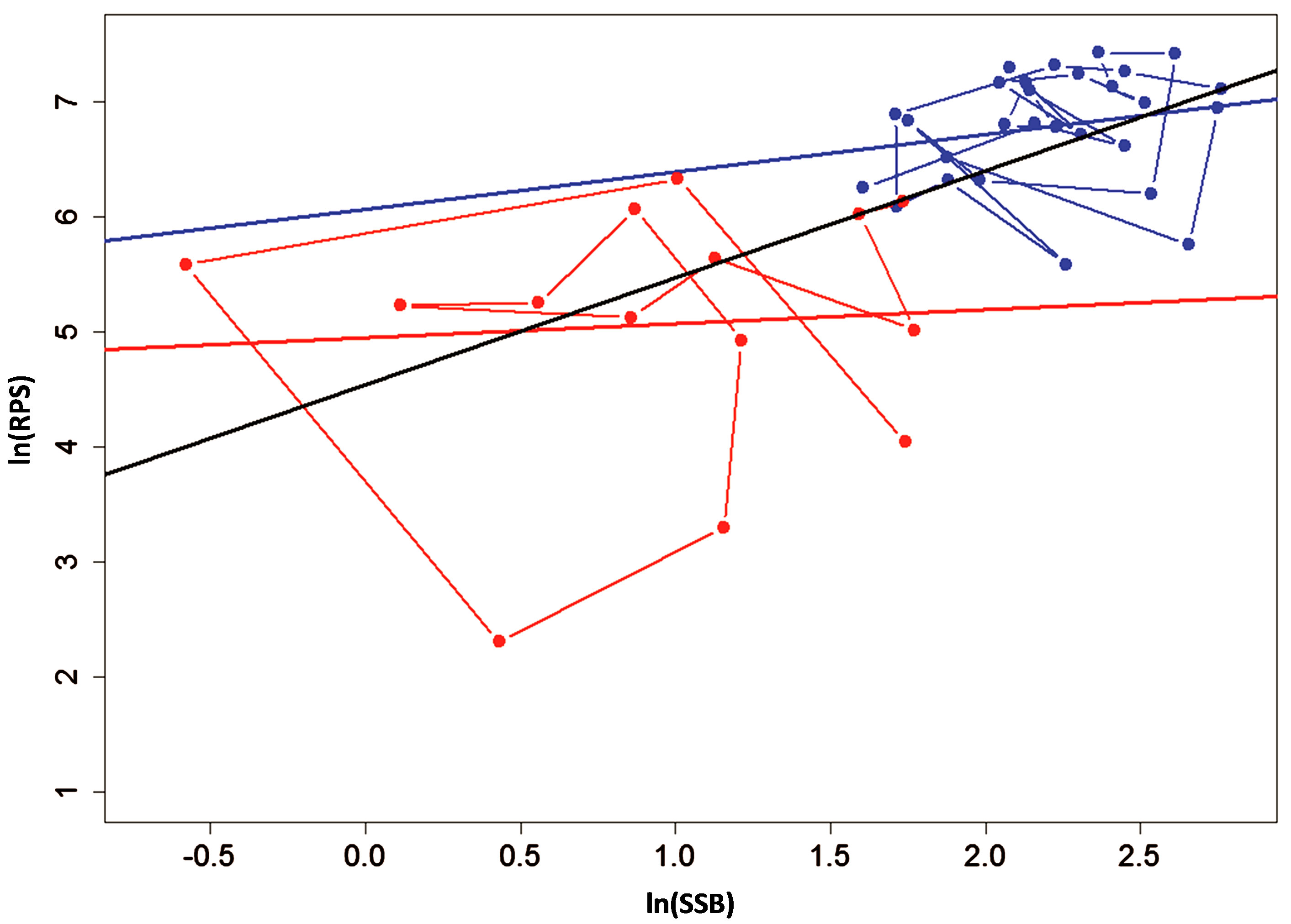
Figure 6. Graph of ln(R) plotted against ln(SSB) of the Peruvian anchoveta Eugraulis ringens. The slope of the regression line for the favorable regime (in blue) was (slope = 0.327) with a 95% confidence interval of (−0.282, 0.936). The slope for the unfavorable regime (in red) was (slope = 0.122) with a 95% confidence interval of (−0.944, 1.188). The regression line for the full data set had a slope of (slope = 0.923) with the 95% confidence limit (0.561, 1.305). This indicates the absence of density-dependent effects. The lines connecting the data points for the favorable regime (in blue) and unfavorable regime (in red) show the annual variation of the data.
the SST from the month of July as exploratory analysis showed July SST to be mostly strongly correlated to anchovy recruitment.
AIC values, R2 and significant parameter estimates were used to determine the best model for explaining the dynamics of anchovy recruitment from 1963-2004. Some of the parameters and AIC values are shown for models that exhibited strong correlations and lowest AIC values in Table 4. The table shows only the results expressed by Equation (1), as the AIC values for Equation (1) were much lower compared to Equation (2).
Models, (a), (b), (d) and (e) were the only models having significant parameter estimates with reference to their p-values. The difference in the AIC values between the models was <0.4, which is not enough to select one model over the other. We selected model (d) as it had the highest R2 value and incorporated both the SST and the SOI as the independent variables (Table 4). The best model by Cahuin et al. [11] had the SSB and SOI as the independent variables and in our case the selected model has SOI and SST as the independent variables.
The recruitment of the Peruvian anchovy was calculated from Model (d) and it was plotted against the actual recruitment from Table 1 in Figure 7. The actual recruitment dynamics seem to fit well with the model recruitment dynamics. It seems that the reproductive success of the Peruvian anchoveta Eugraulis ringens from 1963 to 2004 can be explained well by the SST and SOI.
4. DISCUSSION
Figures 3, 5 and 6 show the relationship between ln(RPS) and SSB, ln(RPS) and ln(SSB) and ln(R) and ln(SSB), respectively. In all these figures, the plots can be separated into two groups. One is the group plotted at the higher SSB or ln(SSB) and the other at the lower SSB or ln(SSB), which corresponds to Cahuin et al. [11] who defined favorable and unfavorable regimes. With reference to the SSB levels, the data can be separated into two regimes, however for the two regimes, the ln(R) and ln(RPS) fluctuated significantly above and below the regression line for the full data series. Particularly, when the SSB levels were low, the variation in the ln(RPS) levels were extremely high, which could have been produced by observational errors as was explained by Sakuramoto [14] in his simulations. On the contrary, with reference to Figure 2(c), it can be seen that the trajectory of ln(RPS) cannot be separated into the two regimes as the RPS levels fluctuate around average RPS except for the years 1981-1983 and 1985. Therefore, we agree that

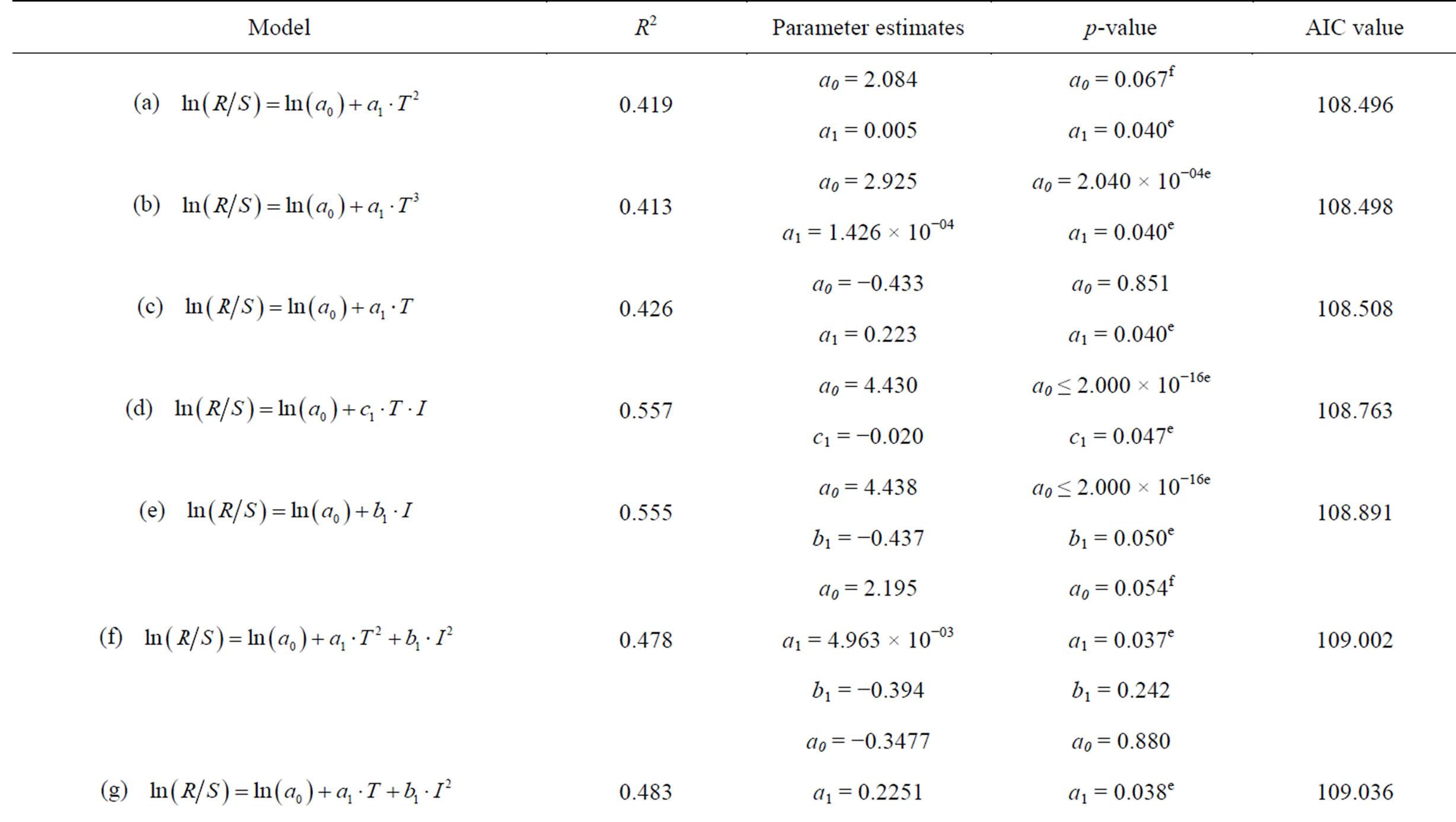
Table 4. Table showing the different models used for modeling the recruitment dynamics of the Peruvian anchoveta Eugraulis ringens and the Akaike Information Criterion (AIC) values. The model with the lowest AIC value, significant parameter estimates, highest R2 and incorporating most variables was selected. R is the recruitment, a0 is the intercept, a1, b1 and c1 are the parameter estimates for the independent variables, S is the spawning stock biomass, T is the sea surface temperature and I is the Southern Oscillation Index.
eStatistically significant at p = 0.05; fStatistically significant at p = 0.10.
the data can be separated into two different periods with high and low SSBs, however this does mean that these periods really indicate the existence of two regimes.
We did not detect the presence of density-dependent effects or regimes in our analysis of the Peruvian anchoveta through regression analysis. Sakuramoto [14] showed with simple deterministic relationships that RPS is quite sensitive to measurement errors even for small data series and can result in a false trend in the stock-recruitment relationship. For the short data series of the regimes identified by Cahuin et al. [11], we see a significant decreasing trend for ln(RPS) against ln(SSB) in Figure 5, but when the whole data series is used, there was no decreasing trend present. To confirm our results we applied regression analysis to recruitment. The results coincide well with regression analysis of the RPS and do not detect density-dependent effects. Sakuramoto [14] similarly used regression analysis on the recruitment of sardine to confirm the results of least squares regression for the RPS relationship.
Cahuin et al. [11] separated the anchovy data into two sets and applied separate regression analysis to the RPS.
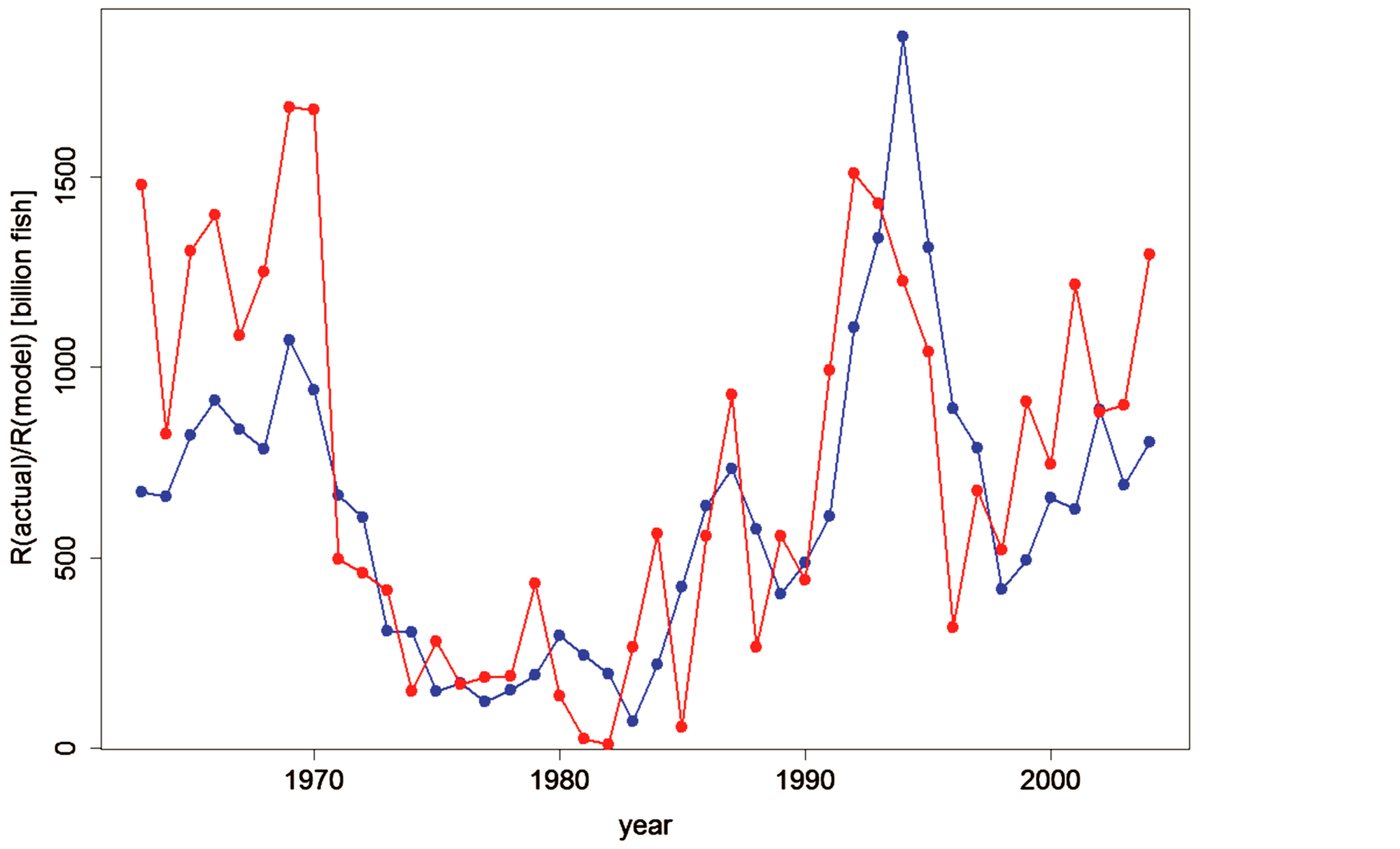
Figure 7. Graph showing the actual dynamics (in red) of the Peruvian anchoveta Eugraulis ringens from 1963 to 2004 and the dynamics resulting from model (d), (Table 4) shown in blue.
They showed that according to the AIC, the model recognizing the two regimes was better that a model with a single regression, without any separation of data (Table 3 (Models 1 and 2)). In our study, we separated the data into two sets based on the data points above and below the regression line for the RPS in Table 3 (Model 3) and Figure 4. When all three models were compared with AIC, our model was selected as the better model. In both cases, the superior model was a result of separation of the data into two sets. This may be due to the impact of the environmental factors and changes in the climatic conditions. This needs further investigation to verify why exactly this occurs and we should also be careful when using RPS to explain stock-recruitment relationships as previously stated, it is quite sensitive to observational errors [14].
Upon selection of the model with two regimes, Cahuin et al. [11] fit the RPS data with the model of Ricker. Sakuramoto and Suzuki [15] explain in detail that when the actual model for a stock-recruitment relationship is a proportional model, observational and/or process errors can result in the selection of a Ricker [17] or Beverton and Holt [19] model. On the contrary, when the actual model is a Ricker [17] or Beverton and Holt [19] model, observational and/or process errors seldom resulted in the selection of a proportional model. In this study, the expanded proportional model, which incorporated the environmental factors, SST and SOI, was selected as the optimal model, it strongly indicates a possibility that the actual stock recruitment relationship is the proportional model and does not have a density dependent effect (Figure 6).
In this study we attempted to explain the recruitment dynamics of the Peruvian anchovy from 1963-2004 with modifications of the GAM and expanded proportional model to incorporate the environmental variables. In our analysis we based our model selection through the AIC, R2 and significant parameter estimates. The R2 value for our model was much higher (R2 = 0.557) in comparison to the model with full data series (Equation (3)) by Cahuin et al. [11] (R2 = 0.251). Our selected model incorporated both the SST and SOI as the independent variables (Table 4, Model (d)). Both SST and SOI have a strong influence in structuring the dynamics of the anchoveta.
Sea surface temperature has established its importance as an environmental factor in structuring the dynamics of various fish species [2-6,20-22]. Indeed, exploratory analysis showed strong negative correlation of SOI with SST. Funamoto et al. [7] and Funamoto [23] showed that SST and wind indexes had significant bivariate relationship with fish recruitment. The SST, Pacific Decadal Oscillation and Arctic Oscillation have been shown to have significant relationship with drastic reductions in fish populations in the Kuroshio Extension [20].
Cahuin et al. [11] showed the importance of SST and SOI in modeling the dynamics of the Peruvian anchoveta. Their overall best model had SOI as the independent variable and the model selection was based on the percentage deviance. Their model did not incorporate 33.33% of the data which was stated as belonging to the unfavorable regime. However, they did show that the resulting best model was still the same when the whole range of data were used (Equation (3)). Our model show both SST and SOI as important environmental variables for modeling the recruitment dynamics of the Peruvian anchoveta. We used numerous variations of the modifications of the GAM and expanded proportional model to reach our final models, whereas the analysis of Cahuin et al. [11] do not show much variation for model selection. Also, our SST data was different from theirs and this may have affected the outcome. The variation in the fit of the model with actual data may be due to the influence of other environmental factors not incorporated in this study and is subject to further investigation.
From 1979 to 1989 rapid changes can be observed in ln(R), ln(SSB) and ln(RPS) dynamics. According to Mysak [24], the catastrophic decline in the population of the Peruvian anchoveta is a result of strong El Niño events. Klyashtorin [25], showes that strong El Niño events are followed by a sharp decline in the population of the Peruvian anchoveta. In our study, we were able to generate a suitable model for explaining the dynamics of anchovy. However, we did not incorporate El Niño as one of the modeling variables, this needs further investigation to validate the influence of El Niño in structuring the dynamics of the Peruvian anchoveta.
In conclusion, the recruitment of the Peruvian anchoveta, Eugraulis ringens off Peru Rt is essentially determined in proportion to spawning stock biomass St, and then environmental factors, SST and SOI, in year t further change the recruitments. That is, it can be written by
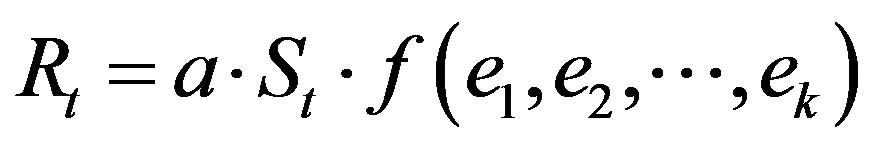 (4)
(4)
where Rt is the recruitment in year t, St is the spawning stock biomass in year t and f(.) is the function determined by environmental factors ei (i = 1, 2,···,k), where k is the number of environmental factors related to the recruitment. The mechanism shown by Equation (4) is completely same with that for Japanese sardine proposed by Sakuramoto [26,27].
ACKNOWLEDGEMENTS
We wish to thank the National Weather Service, Climate Prediction center, NOAA for providing the data on SST and SOI.
REFERENCES
- Jacobson, L.D. and MacCall, A.D. (1995) Stock-recruitment models for Pacific sardine (Sardinops sagax). Canadian Journal of Fisheries and Aquatic Sciences, 52, 566-577. http://dx.doi.org/10.1139/f95-057
- Takasuka, A., Oozeki, Y., Kubota, H. and Lluch-Cota, S.E. (2008) Contrasting spawning temperature optima: Why are anchovy and sardine regime shifts synchronous across the North Pacific. Progress in Oceanography, 77, 225- 232. http://dx.doi.org/10.1016/j.pocean.2008.03.008
- Takasuka, A. and Oozeki, Y. (2007) Optimal growth temperature hypothesis: Why do anchovy flourish and sardine collapse or vice versa under the same ocean regime? Canadian Journal of Fisheries and Aquatic Sciences, 64, 768-776. http://dx.doi.org/10.1139/f07-052
- Takasuka, A., Oozeki, Y., Kubota, H., Tsuruta, Y. and Funamoto, T. (2005) Temperature impacts on reproductive parameters for Japanese anchovy: Comparison between inshore and offshore waters, Fisheries Research, 76, 475-482. http://dx.doi.org/10.1016/j.fishres.2005.07.003
- Lluch-Belda, D., Lluch-Cota, D.B., Hernandez-Vazquez, S., Salinas-Zavala, C.A. and Schwartzlose, R.R. (1991) Sardine and anchovy spawning as related to temperature and upwelling in the California current system, CalCOFI Report, 32, 105-111. http://www.calcofi.org/publications/calcofireports/v32/CalCOFI_Rpt_Vol_32_1991.pdf
- Funamoto, T. (2007) Temperature-dependent stock-recruitment model for walleye Pollock (Theragra chalcogramma) around northern Japan. Fisheries Oceanography, 16, 515-525. http://dx.doi.org/10.1111/j.1365-2419.2007.00454.x
- Funamoto, T., Yamamura, O., Kono, T., Hamatsu, T. and Nishimura, A. (2013) Abiotic and biotic factors affecting recruitment variability of walleye Pollock (Theragra chalcogramma) off the Pacific coast of Hokkaido, Japan. Fisheries Oceanography, 22, 193-206. http://dx.doi.org/10.1111/fog.12015
- Borja, A., Uriarte, A., Valencia, V., Motos, L. and Uriarte, A. (1996) Relationships between anchovy (Engraulis encrasicolus L.) recruitment and the environment in the Bay of Biscay. Scientia Marina, 60, 179-192. http://www.icm.csic.es/scimar/pdf/60/sm60s2179.pdf
- Santojanni, A., Arneri, E., Bernardini, V., Cingolani, N., Marco, M.D. and Russo, A. (2006) Effects of environmental variables on recruitment of anchovy in the Adriatic Sea. Climate Research, 31, 181-193. http://dx.doi.org/10.3354/cr031181
- Fromentin, J. and Plaque, B. (1996) Calanus and environment in the eastern North Atlantic. II. Influence of the North Atlantic oscillation on C. finmarchicusi and C. helgolandicus, Marine Ecology Progress Series, 134, 111- 118. http://dx.doi.org/10.3354/meps134111
- Cahuin, S.M., Cubillos, L.A., Ñiquen, M. and Escribano, R. (2009) Climatic regimes and the recruitment rate of anchoveta, Engraulis ringens, off Peru. Estuarine Coastal and Shelf Science, 84, 591-597. http://dx.doi.org/10.1016/j.ecss.2009.07.027
- Wada, T. and Jacobson, L.D. (1998) Regimes and stockrecruitment relationships in Japanese sardine (Sardinops melanostictus) 1951-1995. Canadian Journal of Fisheries and Aquatic Sciences, 52, 2455-2463. http://dx.doi.org/10.1139/f98-135
- Hilborn, R. and Walters, C.J. (1992) Quantitative fisheries stock assessment: Choice dynamics and uncertainty. Chapman and Hall, New York. http://dx.doi.org/10.1007/978-1-4615-3598-0
- Sakuramoto, K. (2012) A new concept of the stock-recruitment relationship for the Japanese sardine, Sardinops melanostictus. The Open Fisheries Science Journal, 5, 60-69. http://dx.doi.org/10.2174/1874401X01205010060
- Sakuramoto, K. and Suzuki, N. (2012) Effects of process and/or observation errors on the stock-recruitment curve and the validity of the proportional model as a stock-recruitment relationship. Fisheries Science, 78, 41-54. http://dx.doi.org/10.1007/s12562-011-0438-4
- Stӧckl, D., Dewitte, K. and Thienpont, L.M. (1998) Validity of linear regression in method comparison studies: Is it limited by the statistical model or the quality of the analytical input data? Clinical Chemistry, 44, 2340-2346. http://www.clinchem.org/content/44/11/2340.full
- Ricker, W.E. (1975). Computation and interpretation of biological statistics of fish populations. Bulletin of the Fisheries Research Board of Canada, Bulletin 191, Ottawa. http://www.dfo-mpo.gc.ca/Library/1485.pdf
- Akaike, H. (1981) Likelihood of a model and information criteria. Journal of Econometrics, 16, 3-14. http://dx.doi.org/10.1016/0304-4076(81)90071-3
- Beverton, R.J.H. and Holt, S.J. (1957) On the dynamics of exploited fish populations. Fisheries Investigations, 19, 1-533.
- Sakuramoto, K., Shimoyama, S. and Suzuki, N. (2010) Relationships between environmental conditions and fluctuations in the recruitment of Japanese sardine Sardinops melanostictus in the northwestern Pacific. Bulletin of the Japanese Society of Fisheries Oceanography, 74, 88-97. http://www.jsfo.jp/contents/pdf/74-2-88.pdf
- Cianelli, L., Chan, K.S., Bailey, K.M. and Stenseth, N.C. (2004) Non-additive effects of the environment on the survival of a large marine fish population. Ecology, 85, 3418-3427. http://dx.doi.org/10.1890/03-0755
- Cianelli, L., Bailey, K.M., Chan, K.S., Belgrano, A. and Stenseth, N.C. (2005) Climate change causing phase transitions of walleye Pollock (Theragra chalcogramma) recruitment dynamics. Proceedings of the Royal Society B, 272, 1735-1743. http://dx.doi.org/10.1098/rspb.2005.3136
- Funamoto, T. (2011) Causes of walleye Pollock (Theragra chalcogramma) recruitment decline in the Northern Sea of Japan: Implications for stock management. Fisheries Oceanography, 20, 95-103. http://dx.doi.org/10.1111/j.1365-2419.2010.00570.x
- Mysak, L.A. (1986) El Nino interannual variability and fisheries in the Northeast Pacific Ocean. Canadian Journal of Fisheries and Aquatic Sciences, 43, 464-497. http://dx.doi.org/10.1139/f86-057
- Klyashtorin, L.B. (2001) Climate change and long-term fluctuations of commercial catches: The possibility of forecasting. FAO Fisheries Technical Paper, 410, 86 p. http://www.fao.org/docrep/005/y2787e/y2787e00.pdf
- Sakuramoto, K. (2013) A recruitment forecasting model for the Pacific stock of the Japanese sardine (sardinops Melanostictus) that does not assume density-dependent effects. Agricultural Sciences, 4, 1-8. http://www.scirp.org/journal/PaperInformation.aspx?PaperID=33709
- Sakuramoto, K. (2014) A common concept of population dynamics applicable to both Thrips imaginis (Thysanoptera) and the Pacific stock of the Japanese sardine (Sardinops melanostictus). Fisheries and Aguaculture Journal, in Press.

