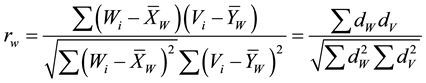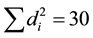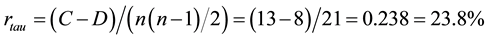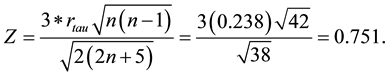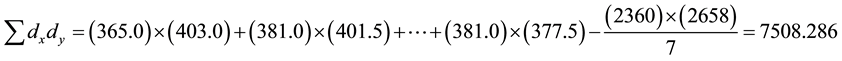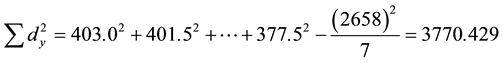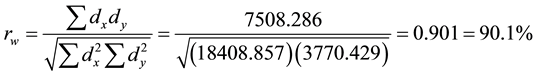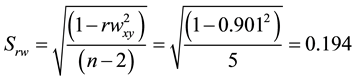Journal of Data Analysis and Information Processing
Vol.03 No.03(2015), Article ID:59197,14 pages
10.4236/jdaip.2015.33010
A Simulation Based Comparison of Correlation Coefficients with Regard to Type I Error Rate and Power
Elif Tuğran1, Mehmet Kocak2, Hamit Mirtagioğlu3, Soner Yiğit1, Mehmet Mendes1*
1Canakkale Onsekiz Mart University, Canakkale, Turkey
2University of Tennessee Health Science Center, Memphis, USA
3Yüzüncüyıl University, Van, Turkey
Email: *mmendes@comu.edu.tr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 August 2015; accepted 24 August 2015; published 27 August 2015
ABSTRACT
In this simulation study, five correlation coefficients, namely, Pearson, Spearman, Kendal Tau, Permutation-based, and Winsorized were compared in terms of Type I error rate and power under different scenarios where the underlying distributions of the variables of interest, sample sizes and correlation patterns were varied. Simulation results showed that the Type I error rate and power of Pearson correlation coefficient were negatively affected by the distribution shapes especially for small sample sizes, which was much more pronounced for Spearman Rank and Kendal Tau correlation coefficients especially when sample sizes were small. In general, Permutation- based and Winsorized correlation coefficients are more robust to distribution shapes and correlation patterns, regardless of sample size. In conclusion, when assumptions of Pearson correlation coefficient are not satisfied, Permutation-based and Winsorized correlation coefficients seem to be better alternatives.
Keywords:
Correlation Coefficient, Robustness, Type I Error Rate, Test Power, Non-Normality, Simulation

1. Introduction
In practice, researchers are often interested in investigating the linear association between two variables, where Pearson-moment correlation coefficient (r) is probably the most commonly used method [1] -[4] . This correlation coefficient, however, is only valid under the assumptions of bivariate normality, and linear relationship between and homoscedasticity of the two variables [5] -[8] . It is also highly sensitive to outliers as reported by Wilcox [5] that a single outlier can mask strong relationship between two variables. In practice, these assumptions may not be satisfied, which results in a decrease in power and a deviation of the type I error rate from the nominal level [9] -[12] . The issue of non-normality, a commonly recommended approach is to normalize the non-normal variables using an appropriate transformation and then compute Pearson correlation coefficient on the transformed data. However, in practice, transformation approach does not give satisfactory results in many experimental conditions [13] [14] . Various alternatives have been proposed, such as Spearman-Rank, Kendall-Tau, non- normal transformation based Pearson correlation coefficient, Winsorized and Permutation-based correlation coefficients when assumptions of Pearson-Moment correlation are not satisfied [5] [15] [16] , among which Spearman-Rank correlation coefficient is the next most commonly utilized approach in practice while the Winsorized and Permutation-based correlation coefficients may be even more appropriate as they both are not highly affected by distribution shape and outliers [2] [12] [16] -[19] . However, the relative performance of these different methods needs to be explored further.
In this study, we compare the performance of the Pearson-moment correlation coefficient with that of the alternatives, namely, Spearman-Rank, Kendall-Tau, Winsorized and the Permutation-based correlation coefficient under different experimental conditions through extensive simulations. In Section 2, we provide a brief description of the correlation coefficients we are comparing. In Section 3, we describe those experimentation condition, followed by the results of these simulations in Section 4. We end with a practical real-life example and discussions.
2. Materials and Methods
2.1. Simulation Setting
Three different bivariate distributions, namely, bivariate normal distribution, bivariate t-distribution with 10 degree of freedom, and bivariate log-normal distribution (skewness = 2.1), were considered, where the choices of bivariate t and log-normal distributions represents different degrees of violations of bivariate normality. All three distributions were generated as suitable transformations from a standard bivariate normal distribution with a given covariance structure.
The bivariate normal distributions  were generated according to the following transformation:
were generated according to the following transformation:

where 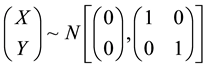 and
and 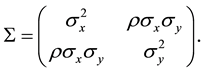
The bivariate t-distribution with 10 d.f. 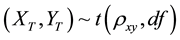 was generated as follows:
was generated as follows:
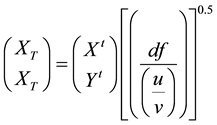
where, u and v are independent variables generated from the gamma distribution.
The log-normal distribution was generated as an exponential transformation of the bivariate normal distribution as follows:
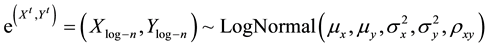 [20] -[23] .
[20] -[23] .
For each experimentation condition with sample sizes of 5, 10, 20, 30, 50, and 100, and the true correlation coefficients of 0, 0.2, 0.4, 0.6 and 0.8, 50,000 random samples were generated. Naturally, the experimental conditions with the true Pearson’s correlation coefficient of 0 (zero) correspond to the absence of any relations between two variables; thus, the rejection of the null hypothesis that ρ = 0 corresponds to the type I error rate while the rejection rate is the test power when ρ ≠ 0.
The type I error rate and test power are estimated as the rejection proportion based on the nominal alpha level of 0.05; that is, the rejection rate (R) is calculated as
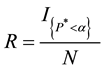
where I is the indicator function, 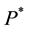 , is the permutation p-value, and N is the number of simulations. IMSL library of Fortran Power Station Developer was used for all simulations.
, is the permutation p-value, and N is the number of simulations. IMSL library of Fortran Power Station Developer was used for all simulations.
2.2. Correlation Coefficients
2.2.1. Pearson-Moment Correlation Coefficient
Given a bivariate data set of size n,  , the sample Pearson-moment correlation coefficient,
, the sample Pearson-moment correlation coefficient,  , between variables X and Y is defined by the formula
, between variables X and Y is defined by the formula
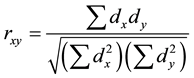
where 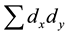 is the sum of products of the departures from the means,
is the sum of products of the departures from the means, 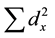 and
and 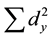 are the sum of squares of X and Y variables, respectively [24] .
are the sum of squares of X and Y variables, respectively [24] .
2.2.2. Spearman-Rank Correlation Coefficient
Spearman’s rank correlation provides a distribution free test of independence between two variables. Let R(x) and R(y) denote the ranks of a pair of variables (X and Y). In this case, Spearman-Rank correlation coefficient is calculated as
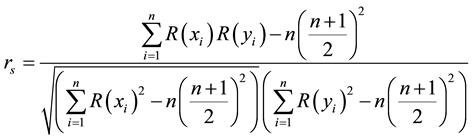 [24] .
[24] .
2.2.3. Winsorized Correlation
It is well known that the Pearson correlation coefficient is sensitive to outliers. Wilcox (2001) proposed that one of the ways of handling outliers is to compute the Winsorized correlation coefficient, which is computed after the k smallest observations are replaced by the (k + 1)st smallest observation, and the k largest observations are replaced by the (k + 1)st largest observation. Therefore, the observations are winsorizedat each end of both X and Y [5] [18] .
Let 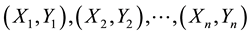



where 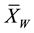
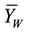
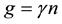
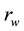
2.2.4. Permutation-Based Pearson Correlation
Principals of permutation tests consist of the following four basic steps:
1) Calculate the Pearson correlation coefficient, 
2) Find all possible permutations as: n!; if n is too large, take a large sample, say, 10,000, from all possible permutations.
3) Re-calculate the Pearson correlation coefficient for each permutation sample (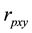
4) Compare the absolute value of the correlation coefficients from the permuted samples with the absolute value of the correlation coefficient from the original sample. The permutation-based p-value is computed by counting the number of times that correlation coefficients (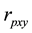

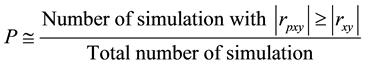
In our simulations, we used 10,000 permutations to obtain the permutation p-values to evaluate the Type-1 error and power.
2.2.5. Kendall-Tau Correlation
Let 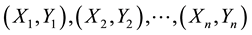
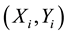
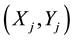

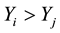
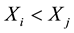
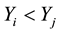
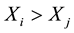
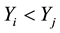
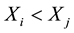
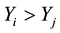
Let C and D denote the number concordant and discordant pairs, respectively. The Kendall Tau coefficient is defined as:
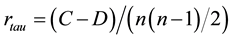
3. Results
The empirical type I error rates and power for Pearson-moment, Spearman-Rank, Kendal-Tau, Permutation- based and Winsorized correlation coefficients are presented in Tables 1-3. When samples are taken from bivariate normal distribution, which is the ideal case for Pearson-moment correlation coefficient, except for very small sample sizes such as n = 5, all correlation coefficients retain the type I error rate at the nominal. When the type I error rate and power were evaluated together Pearson, Winsorized and Permutation-based correlation coefficients are more robust when compared to the Spearman-Rank and Kendall-Tau correlation coefficients.
Empirical the type I error rates for bivariate t-distribution with 10 d.f. are given in Table 2. As seen in Table 2, the type I error rates are very similar to obtained under bivariate normality presented in Table 1, which is not surprising because bivariate t-distribution with 10 degrees of freedom is quite close to the bivariate normal distribution. Permutation-based and Winsorized correlation coefficients are the best especially when sample sizes are small (n ≤ 10) under these experimental conditions as they retain the type-I error rate while have higher power than the other approaches. On the other hand, as sample size increases, all correlations coefficient tend to give similar results as expected.
The empirical type I error rate and power of the correlation coefficients under bivariate lognormal distribution are presented in Table 3, where it is obvious that the Pearson correlation coefficient is highly negatively affected by the distribution shape. The empirical the type I error rate for Pearson correlation coefficient is estimated to be greater than 6% even when sample size is 100. Spearman-Rank and Kendall-Tau correlation coefficients are not much affected from the distribution shape where their type I error rates are quite similar to what was observed the type I error bivariate normal distribution. These two tests especially affected by the sample sizes, which is not surprising. Under these experimental conditions, the Winsorized and Permutation-based correlation coefficients, especially the Winsorized correlation coefficient, seem to be the most robust alternatives to the distribution shape, while all methods except Pearson correlation coefficient, seem to have similar the type I error rates as sample sizes are increased. When both the type I error rate and power were evaluated together, the Winsorized and Permutation-based correlation coefficients seem to be more advantageous over the Pearson, Spearman-Rank and Kendall-Tau correlation coefficients as they are more robust to the shape of the underlying distribution and sample size.
We also studied sampling distributions of the estimates for different correlation coefficients to evaluate the relative frequency of the positive estimates which provide an indirect indication of the relative test power of
Table 1. Type I error rates and test powers when samples taken from bivariate normal distribution.
Table 2. Type I error rates and test powers when samples taken from bivariate t-distribution with 10 d.f.
Table 3. Type I error rates and test powers when samples taken from bivariate log-normal distribution.
these correlation coefficients. It is expected to observe a higher frequency of positive estimates for the correla- tion coefficient which corresponds to higher power when compared to the others. As expected, the number of positive correlation coefficient estimates increase as the sample size increases (Figures 1-3). In general, the test power of Permutation-based, Winsorized and Pearson correlation coefficients are higher than those of the Spearman rank and Kendal Tau correlation coefficients. There are significant differences between these tests especially when the sample size is small.
Figures 1-3 (also these) are examples of the sampling distributions of the five correlation coefficient methods for the true correlation coefficient of 0.6 and sample sizes of 5, 20 and 100, respectively. Each sampling distribution
Figure 1. Sampling distributions of Pearson-Moment, Spearman-Rank, Kendal Tau and Winsorized correlation coefficients when samples were taken from bivariate normal distribution with ρ = 0.60.
Figure 2. Sampling distributions of Pearson-Moment, Spearman-Rank, Kendal Tau and Winsorized correlation coefficients when samples were taken from bivariate t-distribution with 10 d.f.
is obtained from 50,000 simulations. Despite the smaller range, the frequency of positive estimates of Kendall’s correlation coefficient is the least powerful of the five approaches.
4. A Real-Life Application
To illustrate the application of the five correlation coefficients discussed above. We used a data set that is obtained from an experiment to investigate the effects of three different feeding programs (AD: Adlibitum, R20:
Feed Restriction Program 1, NF6: Feed Restriction Program 2) on growth curves of male chickens (Table 4), where the association between the back weight and the chest weight was of interest to the investigator.
Figure 3. Sampling distributions of Pearson-Moment, Spearman-Rank, Kendal Tau and Winsorized correlation coefficients when samples were taken from bivariate log-normal distribution.
Table 4. Back weight (g) and chest weight (g) of chickens.
4.1. Pearson Correlation Coefficient

4.2. Spearman Rank Correlation
4.3. Kendall Tau Correlation
For this data set, the number concordant and discordant pairs are found to be 13 and 8, respectively. Thus, the Kendall Tau correlation coefficient and its significance test are calculated as follows:
4.4. Winsorized Correlation
Firstly, the data are sorted from the smallest to the largest in each cell. Then, the smallest and the largest values are replaced with the observations closest to them. Let Winsorized percentage, g, be 10.0%. In this case, the new data set would be as follows:
4.5. Permutation-Based Correlation Coefficient
For this data set, it is possible to form 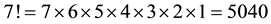
5. Discussion
In any research area, association between two variables is often of interest to the researcher; for example, the researcher may be interested in estimating the association between weight and systolic blood pressure, or plant length and yield, etc. In doing so, the researcher wishes to test for the existence of an association as well as its strength and direction if one exists. To do that, among various available methods, the researcher needs to choose the one that is most suitable to the data at hand, which may not be an easy task. Although most commonly employed in practice, many studies have shown that the Pearson-moment correlation coefficient is not robust to the violations of its assumptions, which prompts the researcher to consider alternatives such as Spearman-Rank, Kendal-Tau, and Pearson correlation-based nonlinear transformation, Permutation-based and Winsorized correlation coefficients, etc., where Spearman-Rank and Kendal-Tau correlation coefficients are the most cited alternatives. However, although the advantages of these two correlation coefficients for the ordinal and ranked data are emphasized, their performance under continuous data is not clear. In addition, the performance of the Spearman-Rank correlation coefficient has not been investigated thoroughly under many experimental conditions which the researcher faces in practice. Another practical approach is to normalize the data via a suitable transformation so to use Pearson-correlation coefficient [15] [16] [28] [29] . However, nonlinear transformations
Table 5. Correlation coefficients, the corresponding critical values, and decision about null hypothesis.
are not given satisfactory results especially when distributions are highly skewed and sample size is small. Furthermore, nonlinear transformations can cause to interpretational ambiguity [13] [14] . Thus, it necessitates using other robust alternatives such as Winsorized and Permutation-based correlation coefficients when assumptions of Pearson-moment correlation coefficient are violated. However, there has been a need to extensively investigate the performance of these two correlation coefficients under different experimental conditions commonly met in practice.
Simulation results showed that unless severe deviations from the normality assumptionexist, Pearson correlation coefficient is a method of choice, which is the case under both bivariate normal distribution and bivariate t-distribution with 10 d.f, where there is no skewness. However, it is sensitive to excessive deviations from the normality especially to skewness with small sample sizes (n < 50).
Although Spearman-Rank correlation coefficient is the most recommended when assumptions of Pearson- moment correlation coefficient is not met, in our simulations, its performance as well as the performance of Kendal-Tau are quite poor. Our findings seem to contradict with those of Fowler [10] who reported that Spearman’s correlation was more powerful than Pearson’s r across a range of non-normal bivariate distributions. Likewise, Zimmerman and Zumbo [11] reported that Spearman’s correlation was more powerful under mixed- normal and non-normal distributions. They also reported that when studying with exponential distributions, Spearman’s correlation retained the type I error rates at or below the nominal level whereas Pearson’s correlation produced inflated the type I error. Indeed, as stated in many studies, using the Spearman-Rank and Kendal Tau correlation coefficients are more appropriate when data are ordinal or ranked [24] [30] -[32] . The apparent difference between our results and those discussed above may come from the experimental conditions such as distribution shapes, sample size, number of simulations taken into considered (Note that we worked with 50,000 simulation samples per condition).
In general, Permutation-based Pearson correlation coefficient and especially the Winsorized correlation coefficient are most robust to the distribution shape, sample size, and outliers. Thus, it is possible to recommend both Permutation-based correlation coefficient and Winsorized correlation coefficient over the Spearman-Rank and Kendall-Tau correlation coefficients when assumptions of Pearson correlation coefficient are not satisfied. Hayes [2] reported that especially when normality assumption is violated, permutation tests tend to do well at controlling the type I error rate, which was similarly argued by Good [19] as well. Good [33] and Mielke and Berry [34] recommended using Permutation-based procedures, especially when sample sizes are small and the variables of interest are non-normally distributed, which are conclusions supported by our study as well. However, it must be kept in mind as suggested by Keller-McNulty and Higgins [35] , Rasmussen [15] , Hayes [2] that permutation tests do not always solve all assumption violation problems, and simulation results on this issue have been mixed.
6. Conclusion
To conclude, we recommend the use of either Winsorized correlation coefficient or Permutation-based Pearson correlation for investigating the relationship between two continuous variables of interest. Between the two, the permutation-based Pearson correlation is more computationally challenging, as it is critical to generate sufficiently large number of permutation samples to avoid misleading results [36] . For example, for n = 5, there exists 5! = 120 permutation samples, which can be generated very easily. For n = 8, we have 40,320, and for n = 10, we have 3,628,800 possible permutations. Any sample size beyond n = 10 may be too difficult to generate all possible permutations, which necessitates to sample from possible permutations, where such a sample must be sufficiently large. Although Hayes [2] [37] [38] proposed to limit the number of permutation samples to 5000, with today’s computing power, a sample of as big as 100,000 or even bigger sample size, can be easily achieved.
Cite this paper
ElifTuğran,MehmetKocak,HamitMirtagioğlu,SonerYiğit,MehmetMendes, (2015) A Simulation Based Comparison of Correlation Coefficients with Regard to Type I Error Rate and Power. Journal of Data Analysis and Information Processing,03,87-101. doi: 10.4236/jdaip.2015.33010
References
- 1. Edgell, S. and Noon, S. (1984) Effect of Violation of Normality on the t Test of the Correlation Coefficient. Psychological Bulletin, 95, 576-583.
http://dx.doi.org/10.1037/0033-2909.95.3.576 - 2. Hayes, A.F. (1996) PERMUSTAT: Randomization Tests for the MacIntosh. Behavior Research Methods, Instruments, & Computers, 28, 473-475.
http://dx.doi.org/10.3758/BF03200530 - 3. Bonett, D.G. and Wright, T.A. (2000) Sample Size Requirements for Estimating Pearson, Kendall and Spearman Correlations. Psychometrics, 65, 23-28.
http://dx.doi.org/10.1007/BF02294183 - 4. Zimmerman, D.W., Zumbo, B.D. and Williams, R.H. (2003) Bias in Estimation and Hypothesis Testing of Correlation. Psychologica, 24, 133-158.
- 5. Wilcox, R.R. (2001) Fundamentals of Modern Statistical Methods: Substantially Improving Power and Accuracy. Springer, New York.
http://dx.doi.org/10.1007/978-1-4757-3522-2 - 6. Warner, R. (2008) Applied Statistics: From Bivariate through Multivariate Techniques. Sage Publications, Inc., Thousand Oaks.
- 7. Triola, M. (2010) Elementary Statistics. 11th Edition, Addison-Wesley/Pearson Education, Boston.
- 8. Witte, R. and Witte, J. (2010) Statistics. 9th Edition, Wiley, New York.
- 9. Blair, R. and Lawson, S. (1982) Another Look at the Robustness of the Product-Moment Correlation Coefficient to Population Non-Normality. Florida Journal of Educational Research, 24, 11-15.
- 10. Fowler, R. (1987) Power and Robustness in Product-Moment Correlation. Applied Psychological Measurement, 11, 419-428.
http://dx.doi.org/10.1177/014662168701100407 - 11. Zimmerman, D. and Zumbo, B. (1993) Significance Testing of Correlation Using Scores, Ranks, and Modified Ranks. Educational and Psychological Measurement, 53, 897-904.
http://dx.doi.org/10.1177/0013164493053004003 - 12. Bishara, A.J. and Hittner, J.B. (2012) Testing the Significance of a Correlation with Non-Normal Data: Comparison of Pearson, Spearman, Transformation, and Resampling Approaches. Psychological Methods, 17, 399-417.
- 13. Osborne, J. (2002) Notes on the Use of Data Transformations. Practical Assessment, Research & Evaluation, 8.
http://pareonline.net/getvn.asp?v=8&n=6 - 14. Tabachnick, B. and Fidell, L. (2007) Using Multivariate Statistics. 5th Edition, Allyn & Bacon/Pearson Education, Boston.
- 15. Rasmussen, J. (1989) Data Transformation, Type I Error Rate and Power. British Journal of Mathematical and Statistical Psychology, 42, 203-213.
http://dx.doi.org/10.1111/j.2044-8317.1989.tb00910.x - 16. Dunlap, W., Burke, M. and Greer, T. (1995) The Effect of Skew on the Magnitude of Product-Moment Correlations. Journal of General Psychology, 122, 365-377.
http://dx.doi.org/10.1080/00221309.1995.9921248 - 17. Calkins, D.S. (1974) Some Effects of Non-Normal Distribution Shape on the Magnitude of the Pearson Product Moment Correlation Coefficient. Interamerican Journal of Psychology, 8, 261-288.
- 18. Wilcox, R.R. (1993) Some Results on a Winsorized Correlation Coefficient. British Journal of Mathematical and Statistical Psychology, 46, 339-349.
http://dx.doi.org/10.1111/j.2044-8317.1993.tb01020.x - 19. Good, P. (2009) Robustness of Pearson Correlation. Interstat, 15, 1-6.
- 20. Kotz, S., Balakrishnan, N. and Johnson, N.L. (2000) Continuous Multivariate Distributions: Volume 1: Models and Applications. 2nd Edition, John Wiley & Sons, Inc., New York.
http://dx.doi.org/10.1002/0471722065 - 21. Ruscio, J. and Kaczetow, W. (2008) Simulating Multivariate Non-Normal Data Using an Iterative Algorithm. Multivariate Behavioral Research, 43, 335-381.
http://dx.doi.org/10.1080/00273170802285693 - 22. Balakrishnan, N. and Lai, C.D. (2009) Continuous Bivariate Distributions. 2nd Edition, Springer, New York.
- 23. Chok, N.S. (2010) Pearson’s versus Spearman’s and Kendall’s Correlation Coefficients for Continuous Data. Master’s Thesis, University of Pittsburgh, Pittsburgh.
- 24. Sheskin, D.J. (2007) Handbook of Parametric and Nonparametric Statistical Procedures. 4th Edition, Chapman & Hall/CRC, Boca Raton.
- 25. Tanizaki, H. (2004) On Small Sample Properties of Permutation Tests: Independence between Two Samples. International Journal of Pure and Applied Mathematics, 13, 235-243.
- 26. Ernst, M.D. (2004) Permutation Methods: A Basis for Exact Inference. Statistical Science, 19, 676-685.
http://dx.doi.org/10.1214/088342304000000396 - 27. Knight, W. (1966) A Computer Method for Calculating Kendall’s Tau with Ungrouped Data. Journal of the American Statistical Association, 61, 436-439.
http://dx.doi.org/10.1080/01621459.1966.10480879 - 28. Kowalski, C.J. and Tarter, M.E. (1969) Co-Ordinate Transformations to Normality and the Power of Normal Tests for Independence. Biometrika, 56, 139-148.
http://dx.doi.org/10.1093/biomet/56.1.139 - 29. Rasmussen, J. and Dunlap, W. (1991) Dealing with Non-Normal Data: Parametric Analysis of Transformed Data vs. Nonparametric Analysis. Educational and Psychological Measurement, 51, 809-820.
http://dx.doi.org/10.1177/001316449105100402 - 30. Siegel, S. (1957) Nonparametric Statistics. The American Statistician, 11, 13-19.
- 31. Lieberson, S. (1964) Limitations in the Application of Non-Parametric Coefficients of Correlation. American Socio-logical Review, 29, 744-746.
http://dx.doi.org/10.2307/2091428 - 32. Khamis, H. (2008) Measures of Association: How to Choose? Journal of Diagnostic Medical Sonography, 24, 155-162.
http://dx.doi.org/10.1177/8756479308317006 - 33. Good, P. (2005) Permutation, Parametric and Bootstrap Tests of Hypotheses. 3rd Edition, Springer-Verlag, New York.
- 34. Mielke, P.W. and Berry, K.J. (2007) Permutation Methods. A Distance Function Approach. 2nd Edition, Springer, New York.
- 35. Keller-McNulty, S. and Higgins, J.J. (1987) Effect of Tail Weight and Outliers on Power and Type-I Error of Robust Permutation Tests for Location. Communications in Statistics B-Simulation and Computation, 16, 17-35.
http://dx.doi.org/10.1080/03610918708812575 - 36. Akkartal, E., Mendes, M. and Mendes, E. (2010) Determination of Suitable Permutation Numbers in Comparing Independent Group Means: A Monte Carlo Simulation Study. Journal of Scientific & Industrial Research, 69, 422-425.
- 37. Hayes, A.F. (1998) SPSS Procedures for Approximate Randomization Tests. Behavior Research Methods, Instruments, & Computers, 30, 536-543.
http://dx.doi.org/10.3758/BF03200687 - 38. Hayes, A.F. (2000) Randomization Tests and the Equality of Variance Assumption When Comparing Group Means. Animal Behaviour, 59, 653-656.
http://dx.doi.org/10.1006/anbe.1999.1366
NOTES
*Corresponding author.