International Journal of Geosciences
Vol.05 No.10(2014), Article ID:50156,11 pages
10.4236/ijg.2014.510096
Locating the Focus of a Starting Earthquake
Alexander Ivanchin
Institute of Monitoring of Climatic and Ecological Systems (IMCES SB RAS), Tomsk, Russia
Email: alex_ivanchin@mail.ru
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 July 2014; revised 23 August 2014; accepted 15 September 2014
ABSTRACT
This article describes a method of locating the focus of a starting earthquake based on the use of the elastic interaction energy. The method allows determining the focus location and its energy class as well as evaluating the stresses caused by it and observing its evolution.
Keywords:
Earthquake Forecasting, Locating the Focus of Earthquake, Stresses of Earthquake

1. Introduction
An earthquake is always an unexpected phenomenon. Modern science is not able to predict the time or the place or the earthquake strength. The problem of locating the focus of a starting earthquake has not even been set due to the poor level of understanding the processes preceding its start. At present the main earthquake hypothesis is the “explosive” relaxation of the high elastic stresses accumulated in the lithosphere. A serious objection to the above hypothesis is the stress relaxation caused by the plastic flow whose rate grows exponentially with temperature and stress [1] . In the lithosphere the temperature and the pressure increase with the depth and, therefore, models of the earthquake focus with no elastic stress concentrations, such as the Inertial Earthquake Focus (IEF) model, are more probable [2] - [4] .
Nowadays, geophysical measurements can be performed only on the surface or in the thin subsurface layer of the Earth, so all the earthquake hypotheses are purely theoretical. Although some data can be obtained from seismic waves, their amount is far from sufficient, since the waves are long and provide little information. Therefore, there remains only one way of locating the focus of a starting earthquake―to develop a method using the elastic stress field of a starting earthquake focus. This method is suggested in the present work.
2. Inertial Earthquake Focus
In the lithosphere tectonic plates move and turn relative to each other. Due to the Earth’s rotation each plate possesses the moment of momentum  parallel to the axis of rotation of the Earth’s body [5]
parallel to the axis of rotation of the Earth’s body [5]
 .
.
Here 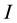 is the moment of inertia,
is the moment of inertia, 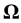 is the vector of the angular velocity of the Earth’s rotation. There can be two types of change of the angular velocity of rotation illustrated in Figure 1 by the example of a rotating cylinder. One is precession, when by the action of the external moment, that is perpendicular to the axis of rotation , the orientation of the axis of rotation in space changes, whereas the angular velocity value does not change in magnitude. The direction of the axis of rotation changes from the vertical orientation in Figure 1(а) into the horizontal one, as is shown in Figure 1(b), its position relative to the material points of the cylinder does not change, and the external moment does not perform work. The other type of change of the angular velocity of rotation is shown in Figure 1(c), where the position of the axis of rotation relative to the material points of the cylinder changes.
is the vector of the angular velocity of the Earth’s rotation. There can be two types of change of the angular velocity of rotation illustrated in Figure 1 by the example of a rotating cylinder. One is precession, when by the action of the external moment, that is perpendicular to the axis of rotation , the orientation of the axis of rotation in space changes, whereas the angular velocity value does not change in magnitude. The direction of the axis of rotation changes from the vertical orientation in Figure 1(а) into the horizontal one, as is shown in Figure 1(b), its position relative to the material points of the cylinder does not change, and the external moment does not perform work. The other type of change of the angular velocity of rotation is shown in Figure 1(c), where the position of the axis of rotation relative to the material points of the cylinder changes.
For a cylinder to change the orientation of the rotation axis relative to the points of the body, it is necessary, first, in the horizontal rotation position of a cylinder (b) to apply the external moment of force directed opposite to the angular velocity vector 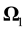 and stop the rotation. Then, it is necessary to apply the external moment of force directed along the axis and make the cylinder rotate around and along the axis (Figure 1(c)).
and stop the rotation. Then, it is necessary to apply the external moment of force directed along the axis and make the cylinder rotate around and along the axis (Figure 1(c)).
For simplicity, let us consider the IEF in the form of a sphere. As a result of tectonic movement, the direction of axis will deviate by an angle 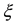 from the Earth’s axis of rotation. If the turn occurred in a vacuum, the direction of the angular velocity would deviate by the angle
from the Earth’s axis of rotation. If the turn occurred in a vacuum, the direction of the angular velocity would deviate by the angle  and its value would be
and its value would be  . At the same time, the equality
. At the same time, the equality 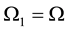 would be satisfied. However, the IEF is located in the solid lithosphere and rotates together with the Earth, so the angular velocity cannot differ in value or direction from the Earth’s angular velocity
would be satisfied. However, the IEF is located in the solid lithosphere and rotates together with the Earth, so the angular velocity cannot differ in value or direction from the Earth’s angular velocity 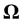 . Here there occurs a change in the position of the axis of rotation relative to the IEF points. Therefore, first we stop the IEF rotation applying elastic stresses with the moment of force
. Here there occurs a change in the position of the axis of rotation relative to the IEF points. Therefore, first we stop the IEF rotation applying elastic stresses with the moment of force  inclined at the angle of
inclined at the angle of 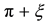 to the Earth’s rotation axis, with the IEF kinetic energy wholly turning into the potential energy of the elastic stresses occurring around it in the lithosphere. Then we make the IEF rotate reaching the angular velocity
to the Earth’s rotation axis, with the IEF kinetic energy wholly turning into the potential energy of the elastic stresses occurring around it in the lithosphere. Then we make the IEF rotate reaching the angular velocity  applying to it the elastic stress with the moment of force
applying to it the elastic stress with the moment of force 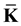 directed along the Earth’s rotation axis. The kinetic energy of rotation completely turns into the potential energy of the elastic stresses and vice versa, which means that the following equality will be satisfied
directed along the Earth’s rotation axis. The kinetic energy of rotation completely turns into the potential energy of the elastic stresses and vice versa, which means that the following equality will be satisfied
 (2.1)
(2.1)
The resulting vector is
 (2.2)
(2.2)
hence

Thus, the IEF gets its own moment of force 

Figure 1. The orientation change of the rotating axis is displayed.
ertial systems, whereas the rotating Earth is not such a system. If the Earth did not rotate, there would be no moment of force .
The stress field of the moment of force 
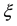

3. The Elastic Field of the Moment of Force
The equation of elastic equilibrium for the displacement vector 

The deformation tensor is
and the stress tensor is

Here 





and the moment of force is

Here 



since for a sphere with the center in the origin of coordinates the vector 




Then (3.1) is reduced to the equation

since the first term in (3.1) becomes zero. For the moment of force 




Here 

Here the displacement vector is written first in the Cartesian system of coordinates and then in the spherical one. The sequence of writing the spherical vector components is as follows: radial 


Differentiating (3.9) we obtain that

The potential vector 

The stress tensor has the same

The values (3.9), (3.11), (3.12) are not zero only outside the IEF. Let us choose a system of coordinates so that the moment of force had only one component along the axis 

hence

If a source is produced by inertial effects, that is the IEF, then multiplying (3.14) by 

Similarly,



The elastic energy density will be written as
The elastic energy of the stresses of the moment of force (2.3) is

The unknown constant 


and the energy will be

The constant 
into the potential energy of the elastic stresses (3.12). The inertial moment of a sphere is

As a result, we obtain

Substituting (3.22) into (3.15) we derive the value of the moment of force

The stress field according to (3.18) looks like

Substituting (3.22)into (3.19) we obtain an expression for the IEF

On the IEF surface the stresses are

As is shown in [7] , in order to derive a general solution for the elasticity problem, a nonpotential solution should be added the potential solution (3.16). However, in the Appendix it is shown that the interaction energy of the potential and nonpotential solutions is zero. Addition of the nonpotential solution to the potential one (3.16) will increase the system energy, and for this reason it is excluded from consideration.
4. Interaction of Focuses. Locating an Earthquake Focus
If there exist two torque regions, there is energy of elastic interaction between them, that can be used to locate the focus of a starting earthquake. For this purpose, it is necessary to create an artificial TR in the lithosphere applying shear stresses to the surface of the artificial cavity. Let us designate the values relating to the artificial TR by one point at the top (further referred to as the first TR), and the IEF by two points (further referred to as the second TR). The centres of these focuses are located on the abscissa at point 





Here

The zenith angles 



















The displacement vectors in the laboratory system of coordinates can be represented like this

The displacements (4.2) determine the deformation tensors


The total deformation tensor is

The total elastic energy density is written as

Substituting here (4.5) we find that the total density energy is the sum of the following components: the density of the energy of the first focus
the energy density of the second focus
and the density of the interaction energy of the focuses
Integrating 


For integrating turn to the bipolar coordinates in (4.7). The elastic energy density is a scalar, and the change to the bipolar coordinates is performed by replacing the Cartesian coordinates by the bipolar ones (4.7) using the formulas [8] :

The coordinate surface for 

with the center on the abscissa at the point






The elastic interaction energy (4.7) in the bipolar coordinates is written as

Here it is designated

Since the first TR is an artificial source of the moment of force, the distance to the focus will always be much larger than its size 
hence
For the second TR the following relation can be true 
As a result, we derive from (4.10)
The total energy will be written as

Here, instead of 




If 

coefficient 


between the focuses

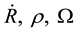












The force 



Here 
We have
The potential 
is
The vector
is the solution of the Equation (3.1). Here the vector 



This force is directed along the line connecting the IEF centers. Equating the forces (4.13) and (4.14) we obtain the value of the arbitrary constant

The displacement vector component 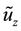

It consists of two terms. The first term is the displacement of the radius sphere r as a whole without deformation. The second term is the deformation component. Substituting the coefficient B with the change of 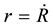

Measuring 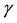



















To locate an IEF, it is necessary to determine the displacement of an artificial TR with an accuracy up to a millimeter and better. In order to create the moment of force, one can use precession. Between the moment of force 


The above method can be the simplest one. It allows achieving an arbitrary orientation of the moment of force, which is necessary to perform measurements.
5. Conclusions
In the present work a method of locating the focus of a starting earthquake is suggested. The existence of the IEF is the effect of the Earth’s rotation. Its analogue is the Coriolis force. Cyclones and anticyclones are caused by the Earth’s rotation. In the lithosphere they are analogous to the IEF. Undoubtedly, the IEF evolution takes much longer than a cyclone, and the rates of gas flows in the atmosphere are by orders of magnitude higher than tectonic rates. However, it should not lead to denying or ignoring inertial effects in the lithosphere.
The existence of tectonic plates with localization of elastic stresses is the main hypothesis of earthquake focuses. The reasons for stress localization can be different as well as their space dependence. If there exist two regions with a similar space distribution of stresses, then between them there is the energy of elastic interaction. Using the above energy it is possible to locate the focus of a starting earthquake creating artificially a region with a specified stress profile. Mathematical calculation of other models of earthquake focuses will be somewhat different from the one discussed here, which is not a problem.
Cite this paper
AlexanderIvanchin, (2014) Locating the Focus of a Starting Earthquake. International Journal of Geosciences,05,1137-1148. doi: 10.4236/ijg.2014.510096
References
- 1. Lothe, J. and Hirth, J.P. (1967) Theory of Dislocations. McGraw-Hill Book Company, New York.
- 2. Vikulin, A.V. and Ivanchin, A.G. (1997) Seismic Process Model. Computing Technologies, 2, 35-54.
- 3. Vikulin, A.V. and Ivanchin, A.G. (1998) Rotational model of Seismic Process. Pacific Geology, 17, 18-29.
- 4. Vikulin, A.V., Ivanchin, A.G., et al. (2012) Data-Processing and a Computing System of Simulation of Seismic and Volcanic Processes as a Basis for Studying Wave Geodynamic Phenomena. Computer Technologies, 3, 34-54.
- 5. Landau, L.D. and Lifshitz, E.M. (1960) Mechanics. Pergamon Press Ltd., Oxford/London
- 6. Landau, L.D. and Lifshits, E.M. (1986) Theory of Elasticity. 3rd Edition, Elsevier Butterworth-Heimenann, Oxford.
- 7. Ivanchin, A. (2010) Potential. Solution of Poisson’s Equation, Equation of Continuity and Elasticity. http://arXiv.org/abs/1011.4723
- 8. Korn, T.M. and Korn, G.M. (1968) Mathematical Handbook for Scientists and Engineers. McGraw-Hill Book Company, New York.
- 9. Ivanchin, A. (2008) Nonpotential Solution of the Electron Problem. http://arXiv.org/abs/0902.1286
Appendix. Nonpotential Solution
As is known, along with the potential solution there can also be a nonpotential one [7] [9] . A general solution will be their linear combination, whose coefficients are determined from the condition of the total energy minimum.
To derive the nonpotential solution take the vector
The rotor is

One must find the solenoidal vector 

then the vector

is the solution (3.1). For simplification, let us integrate (6.1) over 

Here it is designated

Since 




Integrate (6.4) over and (6.5) over 
Here it is designated
In the spherical coordinates we have
Its solution is
Differentiating we obtain the components of the vector 

The vector divergence is

which means that the vector 


hence

The nonpotential solution (6.2) is written in Cartesian and spherical coordinates as
In the deformation tensor for the displacement 





























