Received 25 February 2015; accepted 11 April 2015; published 15 April 2015

ABSTRACT

Purpose: The CyberKnife system equipped with multileaf collimator (MLC) has been shown promising in treatment-time reduction and plan-quality improvement, because of the enhanced coverage of larger lesions and the improved target conformity. In this study, we aim to develop an efficient non-coplanar beam selection program for CyberKnife-based IMRT. Method: The candidate beam set in this study consists of 94 non-coplanar beams, each defined by a vector connecting a CyberKnife node and a target point. Our goal is to choose an adequately small number of beams that will allow the generation of high quality IMRT plans. We use the beam coverage of patient- surface as a surrogate for the solution space of beamlet-based inverse planning. Based on body- surface coverage and beam-projection overlap on the surface, a beam-selection program was developed. To evaluate the effectiveness of the beam selection method, IMRT plans with the selected beams for different treatment sites were generated using the Varian Eclipse treatment planning system and compared with the IMRT plans with conventional coplanar beams. Results: Our pro- gram efficiently selected a subset of relatively small number of non-coplanar beams, while pre- serving the body-surface coverage and therefore the solution space for inverse planning optimiza- tion. For example, a set of 17 beams were selected for a pancreatic cancer case, covering 92.5% of the surface area which was covered by all the 94 candidate beams with the same field size. The IMRT plans with the selected beams show superior quality with dramatically improved critical structure sparing, as compared with the clinically approved IMRT plans. Conclusion: One can efficiently select effective sets of non-coplanar beams with our program, which allow the generation of high-quality plans for MLC-based robotic radiotherapy.

Keywords:

Robotic Radiotherapy, Beam Selection, CyberKnife

1. Introduction

Currently, the only robotic radiosurgery/radiotherapy device available commercially is the Accuray CyberKnife system. The system possesses two essential features which differentiate it from other radiotherapy/radiosurgery systems [1] : 1) a 6 MV photon treatment head is mounted on an industrial robotic arm, which allows the agile delivery of a relatively large number of non-coplanar beams; and 2) it incorporates an advanced image guidance system, which allows (almost) real-time tumor tracking in combination with the robotic beam delivery.

Although the CyberKnife system has shown excellent local control of tumors in clinical trials for a broad range of treatment sites, there are still some drawbacks associated with the system, such as long treatment times and the inefficient coverage of large lesions with irregular shapes. The CyberKnife system equipped with MLC has been introduced recently. The 12 cm × 10 cm MLC opening (defined at 80 cm SAD) of the new system improves the treatment for large, irregular lesions. More importantly, with proper inverse planning optimization for the new system, one will be able to achieve a significant reduction in the treatment time and further improvement in critical structure sparing while achieving excellent tumor control. In the current Accuray MultiPlan treatment planning system (TPS) for cone or Iris-based CyberKnife, the beam selection is integrated into the MU weight optimization in the linear programming-based algorithm [2] [3] . The candidate beam set in the MultiPlan TPS consists of a few thousand beams. However, this approach is not feasible for implementing beamlet-based optimization for the MLC-based system, since the solution space is now a few hundred times as large as it was for the previous models.

As the first step toward a viable solution for implementing a beamlet-based inverse planning algorithm for the MLC-based CyberKnife system, we address the beam selection issue in this work. As an essential component for external beam treatment planning and optimization, beam selection is of fundamental importance and can affect the final quality of a treatment plan. Different approaches for beam orientation selection for the MLC- based CyberKnife system have been reported recently [4] - [7] . Fan et al. manually selected 23 beams based on the frequency distribution of typical CyberKnife node usage in IRIS collimator plans and used the selected beams to generate IMRT plans [4] . Heijmen’s group (Netherlands) presented “Cycle” and “iCycle” algorithms for beam selection which were integrated in the 3D conformal and IMRT planning procedures, respectively [5] - [7] .

In this work, we propose a novel beam selection method based on the beam coverage and the overlap of the beam projections on the patient body surface. It is recognized that when delivering the same amount of dose to a target, the larger the covered surface area, the lower the surface dose. Furthermore, the beam coverage of patient surface (on the entrance side) can be used as a convenient surrogate for the size of solution space, considering the fact that the useful beamlets which could contribute dose to the target will have to go through the patient surface first. A larger solution space for inverse planning optimization tends to allow the generation of IMRT plans with better quality in principle. On the other hand, a smaller number of selected beams will lead to higher treatment efficiency. Hence, our goal is to choose an adequate number of beams that allow both the production of high quality IMRT plans and efficient treatment delivery.

2. Material and Methods

The candidate beam set in our study consists of 94 non-coplanar beams, each defined by a vector connecting one CyberKnife node from a chosen body path set and a target point. The MLC leaves are configured to approximate a circle only for the beam-selection simulation, which is separate from the beamlet-based optimization. During the beam selection procedure, the field size can be chosen such that the cross-section of each candidate beam fully covers the planning target volume (PTV) and hence, most beamlets from the selected beams will contribute to the PTV dose. These potentially useful beamlets will have to enter the patient surface before they can deposit dose to the PTV. Therefore, to certain extent, the surface coverage by the circular beams mentioned above reflects the number of useful beamlets which form the solution space for the following step of beamlet-based optimization. Theoretically speaking, with a more complete solution space, one can achieve better critical structure sparing and PTV coverage.

Keeping all candidate beams can offer us maximal surface coverage and, in principle, the maximal potential of critical structure sparing. However, in this case the treatment efficiency will be extremely low, not to mention that even with the state-of-the-art computation technology it is intractable to realize beamlet-based optimization for so many beams each containing hundreds of beamlets (~10 cm × 12 cm/(0.5 cm × 0.5 cm) = 480). Fortunately, it is possible to reduce the number of beams without sacrificing excessive surface coverage and hence, the potential of critical structure sparing, if there are significant overlaps between the projections of individual beams on the surface.

We have developed a MATLAB program to select the beam orientations automatically, based on the patient surface coverage and beam projection overlap on the surface. To parameterize the field size of the candidate beams for our simulation, we used a radius R which specifies the radius of the beam cross section projected onto the plane perpendicular to the beam orientation at D = 80 cm. The radius can be chosen such that each beam fully covers the PTV. When adding each beam sequentially, one will increase the surface coverage and/or the beam overlap on the surface. The surface coverage due to the selected beams is parameterized by N_c, namely the number of surface voxels which are covered by the ray of at least one of the selected beams, while the overlap is parameterized by N_o, the number of surface voxels which are in the ray paths of two or more selected beams.

Given the coordinate of a surface voxel center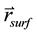, the coordinate of a CyberKnife node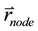, and the coordinate of the target point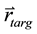, it is straightforward to determine whether or not the voxel is within the ray of the beam defined by 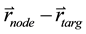via ray tracing. Specifically, in our program, we calculate the angle 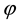formed by the vectors and, then compare it with the beam divergence angle 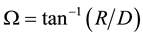of the circular beams. If and (the beam enters the body through the voxel,

instead of exiting), we consider the voxel as covered by the ray of the beam.

During the i-th iteration (with i > 1) of the sequential beam selection from a set of N beams, we calculate 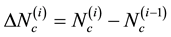and 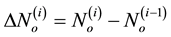for all remaining [N − (i − 1)] beams. We then rank these candidate beams according to the ascending order of 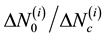and choose the top one to add to the list of se-

lected beams. The selection process continues until the overlap just exceeds a pre-set limit in the (f + 1)-th round. The quality of the selected beam sets can be evaluated by the surface coverage 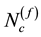and the number of selected beams f. We note that with our current method, the selected set of beams is not unique even for the same patient, because during the first few steps of our sequential selection method one has the freedom of selecting different beams which do not overlap on the surface. For the sample cases in this study, we have selected hundreds of sets of beams and we have chosen the sets which provide the best surface coverage.

To evaluate the dosimetric effectiveness of our beam selection scheme, we have generated IMRT plans based on the selected beams and compared the plan quality with the conventional IMRT (with up to 8 coplanar beams) plans for one prostate (without lymph node involvement) and one pancreatic case. For the prostate and pancreatic cases, we have selected 25 and 17 noncoplanar beams respectively using our program, from the above mentioned set of 94 candidate beams. The target point for the noncoplanar beams for each case was chosen to be the isocenter of the approved treatment plan. The directions of the selected beams were converted to the gantry and couch angles according to the arrangement of the Varian linear accelerator, assuming that the patient setup is head-in and supine. Using the converted gantry and couch angles, we generated IMRT plans for the sample cases with the Varian Eclipse treatment planning system (Version 10.0).

3. Results

We show the beam coverage and overlap on two patient-body surfaces for one prostate case and one pancreatic case (Figure 1). The color map reflects the number of beams covering each surface voxel. The surface contour for panels (a) and (b) is obtained from the CT image of a prostate case. The radius R specifying the field size at D = 80 cm is chosen to be 4 cm and the target point is chosen to be the isocenter used in the actual clinical plan for this patient. The surface contour for panels (c) and (d) is obtained from the CT image of a pancreatic case and the beam radius R is set to be 5 cm at D = 80 cm. The target point is chosen in the same way as in the prostate case. In panels (a) and (c), we show the coverage and overlap of the beam projections of all 94 candidate beams and one can clearly see the tremendous overlap of the beam projections on the surfaces. For both cases, there are many surface voxels which are covered by more than 10 beams if we keep all of the existing candidate beams. In panel (b), we show the results for a set of 25 beams, which were selected using our program. The coverage and overlap are 93.2% and 19.1% (normalized so that the coverage is 100% when all 94 beams are selected) respectively. In panel (d), we show the beam coverage and overlap for a set of 17 selected beams. For this case,

the coverage and overlap are 92.5% and 19.9% respectively. The overlap constraint for the numerical simulation is 20% for both cases. From the figure, we can see clearly that with the selected beams the beam overlap on the patient surface for both cases is greatly reduced, while the surface coverage is preserved fairly well.

In Figure 2, we show the dose-volume histograms (DVH) of the conventional coplanar IMRT plans and the noncoplanar IMRT plans with the selected beams for the same prostate case (panels (a) and (b)) and pancreatic case (panels (c) and (d)) as shown in Figure 1. The solid and dash-dotted curves correspond to the IMRT plans with the selected noncoplanar beams (S-NCP) and the plans with coplanar beams (CP) respectively. The doses are normalized so that 95% of the PTV is covered by 100% prescription dose, which is 80 Gy for the prostate case and 50.4 Gy for the pancreatic case, respectively. The S-NCP plan for the prostate case is based on a set of 25 selected beams while that for the pancreas case is generated with 17 selected beams. The CP plans were clinically approved and delivered with manually selected coplanar beams. Specifically, the CP plan for the prostate case was generated with 8 beams at gantry angles of 135˚, 110˚, 70˚, 30˚, 0˚, 310˚, 270˚ and 245˚, while the CP plan gantry angles for the pancreatic case are 180˚, 150˚, 90˚, 30˚, 320˚, 280˚, and 200˚. A more detailed comparison between the CP and S-NCP plans can be found in Table 1. We can see from both Figure 2 and Table 1 that the PTV doses are comparable between the NCP and CP plans, while the NCP plans lead to more favorable dosimetric parameters for most of the critical structures under consideration.

4. Discussion

In principle, optimal sparing of critical structures without sacrificing the target coverage can be achieved when the solution space for the beamlet-based inverse optimization contains all the beamlets which can contribute to the PTV dose. In our beam-selection scheme, selecting fewer beams while preserving the body surface coverage provides a practical method to preserve the solution space while reducing the computational complexity and the treatment time. In our approach, the beam selection is separate from the inverse plan optimization. To avoid confusion, we stress that the body surface coverage calculation is based on the circular beams, which are used solely for the beam selection simulation. The intensity modulation is achieved by a separate inverse optimization program (the Varian Eclipse TPS) and the shapes of real segments obtained after leaf-sequencing can be very irregular and very different from the circular configuration.

The results of our beam selection program presented in this study depend on the location of the target and the size of the circular beams, as well as the constraint on the allowed beam overlap. In the example prostate and pancreatic cancer cases, the target points are both close to the midline of the body. When the target point gets closer to the body surface, generally speaking one will tend to obtain a lesser number of beams using our method, with other parameters remaining the same. One will also attain a lesser number of beams selected, if using a larger beam size. A more stringent constraint on the allowed beam projection overlap on patient surface also leads to a smaller number of selected beams.

For certain sites of treatment, the geometry of the target and organs at risk is more or less similar for individual patients. In this situation, the same set of beams could be used for the IMRT generated-plans for different patients, without sacrificing the quality of the plans. For example, we have used 13 selected beams to generate

IMRT plans for 10 prostate and pancreatic cases and found that the plan quality is in general superior to the conventional coplanar IMRT plans and the Rapid Arc plans with up to two arcs [8] . This implies that for certain treatment sites one may only need a small number of nodes (for example 30 nodes or so as compared with 94 or 117 nodes in certain path sets of the current CyberKnife system). If the robotic arm can be programmed to travel through only the selected nodes for such sites (designing new “path”), the treatment time can be further dramatically reduced. We also note that the MLC-based CyberKnife system has different set of nodes comparing with the cone or IRIS collimator based systems. For example, with the new configuration of nodes, certain beams could enter the body from the back of a patient in a supine setup. We expect that selecting beams with our method from the new node set could further improve the plan quality as compared with the S-NCP plans we have generated.

Finally, we briefly discuss the computational efficiency of our program. We carried out the MATLAB simulation using a PC with 2.33 GHz Intel Core 2 Duo CPU and 3.23 GB of RAM. Currently, we have not made intentional efforts to optimize the efficiency of our code. With our existing program, reading and saving information from aconverted CT data file (with 128 × 128 matrix resolution) takes about 14 seconds; determining the beam coverage of all surface voxels takes about 80 seconds; sequentially selecting one set of beams takes less than 10 seconds.

5. Conclusion

Utilizing the coverage and overlap of the beam projections on patient surfaces as references, we have developed a beam selection method for MLC-based CyberKnife IMRT. With our program, one can efficiently select effective sets of non-coplanar beams. The selected beams allow the generation of high-quality IMRT plans for MLC-based robotic radiotherapy with optimal delivery efficiency.

References