American Journal of Plant Sciences
Vol.5 No.13(2014), Article
ID:46599,15
pages
DOI:10.4236/ajps.2014.513200
Pitfalls and Uncertainties of Using Potentiometric Titration for Estimation of Plant Roots Surface Charge and Acid-Base Properties
Grzegorz Jozefaciuk, Alicja Szatanik-Kloc, Malgorzata Lukowska, Justyna Szerement
Institute of Agrophysics of Polish Academy of Sciences, Lublin, Poland
Email: jozefaci@ipan.lublin.pl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 April 2014; revised 19 May 2014; accepted 29 May 2014
ABSTRACT
Amount and properties of roots surface charge are important for nutrient uptake and balance in plants. Roots surface charge markedly varies at different rizosphere conditions (particularly pH and ionic strength), which can markedly alter during vegetation season. Among recently available measuring methods, surface charge-pH dependence of roots (as well as other biological objects) is most easily evaluated by potentiometric titration. Use of this method is also easy at different ionic strengths. Potentiometric titration also allows for estimation of the distribution of charge generating surface groups. However, many applications of this method seem to be based either on incorrect methodical or theoretical approaches. In this paper we discuss the methodical and theoretical backgrounds of the titration method. Basing on experimental titration curves of roots of barley grown in nutrient solution, we show inconsistency of surface charge results obtained at different measuring conditions. Limitations of theoretical interpretations of the results are outlined also.
Keywords:Charge, Density, Dissociation, Method, Plant, Root, Surface, Titration

1. Introduction
Probably the simplest and most convenient method used for estimation of plants root charge versus pH characteristics and to characterize acidic strength of surface charge generating groups is back-titration [1] -[8] . In this method the root suspension is adjusted to a low pH and titrated upwards with the added base. The base added to a solid/liquid suspension is consumed by acids present on solid surface and by acids present in the supernatant, therefore additional titration of the supernatant is performed. At any pH, the amount of base consumed by the roots themselves can be found by subtracting the amount of base consumed by the supernatant from this consumed by the whole suspension. In this way the titration curve of the roots solid phase is obtained which serves for estimation of roots charge-pH dependence and for characterization of acidic strength (dissociation or proton binding constants) of charge-generating surface functional groups. These groups have been usually modeled as one or more negatively charged biotic ligands. Usually models involving discrete rather than continuous distributions of their dissociation constants are preferred. However, due to high heterogeneity of acidic properties of charge generating groups, occurrence of their discrete distributions seems hardly probable. Moreover, proper defining of discrete dissociation constants requests the titration curves exhibiting one or more well established inflexion points (polysigmoidal curve shape) that, from our experience, frequently results from improper titration conditions, which of course give also uncertain results of roots surface charge. In the present paper we show proper conditions for estimation of experimental back-titration curves of plant roots and show a simple background for their theoretical analysis using continuous site-distribution model. Obviously the back-titration method may be applied for studies of any solids including plant tissues, biological membranes, microorganisms etc. In this paper we consider plant roots as an example.
2. Methodical Aspects of Titration Measurements
2.1. Expression of Raw Titration Data
Classically, the titration curves are expressed as dependencies of the pH of the titrated sample on the amount (mol) of the added titrant (base). As mentioned earlier, to find the roots titration curve, the amount of base consumed by the supernatant at any pH should be subtracted from this consumed by the whole suspension at the same pH. To do this instead of classical titration curves one should construct plots showing the amount of the titrant as a function of pH (change x and y axis) for both the suspension and supernatant, interpolate the amounts of base consumed by both of them to the same pH values (preferably with a constant step) and finally calculate their differences. For any purpose, the amount of the base consumed by the unit mass of the roots should be estimated, therefore the mass of the roots present in the titrated suspension should be known.
2.2. Estimation of the Mass of the Titrated Sample
Since roots always contain some amount of water depending on their initial moisture, laboratory temperature and air humidity that may also vary due to different root structures developed at different plant growth conditions, expressing the titration data basing on actual roots weight may lead to considerable uncertainty. Therefore as a reference state the mass of completely dry roots should be preferred that may be found after heating the roots by 24 h at 105˚C. Such procedure removes physically bound water and is well reproducible [9] . Therefore we suggest estimating the dry mass of the titrated roots basing on 105˚C drying of the material subsample.
2.3. Origin of the Investigated Roots
Most interesting for a researcher is the behavior of plant roots under natural conditions, so studying of roots harvested directly from a soil seems to be a preferred option. However in this case the finest roots may be adhered to soil grains and removed with the soil at harvesting and/or some finest soil components adhered to the roots may be taken together with the experimental material that may strongly affect the results [10] . Therefore studies of roots coming from more clear environments as hydroponics or aeroponics should be preferred, if possible.
2.4. Sample State
In general the roots charge (and CEC value) depends, except of plant type, age and growth conditions, on the state of the material used (living, fresh or dried) [11] -[18] . Thus selection of the sample state is generally a matter of choice, however it must be the same for any comparison purposes. For comparison of roots grown at different conditions and harvested at the same time, we prefer air-dried roots that are cheapest and very convenient method allowing for longer storage of the experimental material. The titrated roots must be equilibrated with the suspension medium what is particularly important if dry (or lyophilized) material is to be titrated. Therefore the roots suspension should be prepared some time earlier before the titration—we equilibrate suspensions of air dry roots overnight. Difficulties in titration of the whole roots may occur, particularly if mechanical stirrer is used for mixing (roots wrap around the stirrer) therefore cutting of roots to around 1 - 2 mm length pieces is recommended. The cut material can be much better homogenized.
2.5. Standardizing Ionic Composition of the Root Suspension
Different cations present on the root surfaces may markedly change the ionic strength of the titrated suspension that should be kept constant during the titration. Some cations, particularly aluminum, iron and heavy metals, may buffer the pH in various ranges altering the titration curves. Therefore prior to the titration the ionic composition of the sample should be standardized that is particularly important for comparison of roots coming from various growing conditions. The electrodialysis method has frequently been employed for this purpose, however it is a drastic process that removes organic materials from the interior of the roots and affects the measured CEC in close relation to the severity of the treatment [19] . The acid washing method has been used alternatively. In this method the root-exchange sites must be completely saturated with H+, however it may not be satisfied if acid washing causes leakage of metal cations from inside of tile root cells. In our studies we rinse the roots 3 times in 0.01 moldm−3 HCl and 5 times in distilled water. Because basic cations in the third HCl extract were not detectable by AAS, we assumed that the homoionic hydrogen form of the roots is obtained.
2.6. Preventing Contact with Laboratory Air
Very important is preventing the laboratory air contact with the titrated sample. Absorbed carbon dioxide is titrated simultaneously strongly altering the results. To prevent this gaseous nitrogen is passed through the sample for some time before and during the whole experiment. Similar restrictions should be applied for preparation of the reagents. Outgassed water (or salt solution) and the reagent free of carbonates should be used for preparing the titer solution. The contact of the titrant with laboratory air should be prevented prior and during the titration.
2.7. Estimation of Base Consumption by Supernatant
The supernatant can be extracted from concurrently prepared or from the same suspension. In the latter case half of the supernatant to be titrated is extracted from the studied suspension prior to its titration. We tried to separate supernatants from root suspensions after 15 min centrifuging at 6000 rpm. Large amount of base was consumed by the separated supernatants that we attributed to not complete settling of low-density hydrophilic organic particles. Further increase in the centrifuging time to 30 min and rate to 8000 rpm did not improve the situation or even lead to an increase of the amount of base consumed by the separated supernatants. Most probably during centrifuging root cells break evolving organic compounds from their interior as was postulated in [20] . However, this is worth to mention that in [21] any marked release of root organic compounds during centrifuging of soil samples amended with 14C labeled roots was observed. To avoid the uncertain step of supernatant separation, instead of measuring the supernatant titration curve we prefer to use the titration curve of the suspension medium i.e. the titration curve of the solution applied for the suspension preparation.
2.8. Salt and Base Concentration Effects
Buffering ionic strength during the titration may be also important since dependence of plant materials exchange properties on salt concentration is frequently observed [22] , however any dependence has been also reported [23] . Changes in ionic strength may occur during titration due to the suspension dilution with the added base, therefore the titrant should contain that same salt concentration as the titrated suspension, which is frequently forgotten in many studies. The pH of a suspension depends on solid-liquid ratio that changes during titration due to addition of the titrant what may be minimized applying high base concentration, however too high concentrations may decrease precision of base dosing.
2.9. Titration Equilibrium
The ideal titration curve should be registered maintaining acid-base equilibrium conditions. To do this several parallel root samples may be treated with different increments of NaOH and pH of each suspension should be measured till constant value, however this needs huge amount experimental material. Using single sample, equilibrium conditions may be approached either by stepwise titration (manual or automatic) allowing the suspension to reach pH stability prior to the addition of the next aliquot of base or by automatic titration at extremely low titration speed (that can be manipulated also by varying sample mass or base concentration). All equilibrium titrations need much time so their results may be affected by bacterial or fungi attack, or by tissue maceration.
3. Interpretation of Titration Data
3.1. Evaluation of Surface Charge of Roots
Surface charge of plant roots is generated by dissociation of ionogenic functional groups occurring on various molecules from which the root tissue is composed. There can be several types of such groups of varied proton binding strengths e.g. amine, carboxyl, phenolic, phosphate [4] [5] [17] . The dissociation of such surface groups, SG, can be described by two general reactions:
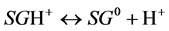 (1)
(1)
for principally neutral surface groups which are actually protonated (e.g. amines at low pH values), and by:
 (2)
(2)
for acidic type groups.
The addition of a base hydroxyls to the above systems during titration results in neutralization of surface protons in the reactions:
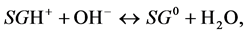 (3)
(3)
 (4)
(4)
that leads either to decrease of positive surface charge (reaction 3) or to increase of negative charge (reaction 4).
Positive surface charging of at low pH values is certified by occurrence of the isoelectric point (IEP) of some plant components: for thylakoid membranes it is 4.1 - 4.7 [24] and for barley roots plasmalemma vesicles is 3.6 - 3.7 [25] . Since this is extremely difficult to quantify charges associated to surface groups of both above types, and both these groups are proton donors (acids), in titration experiments one usually assumes that only surface acids, SAH are present both and reactions are unified to:
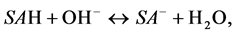 (5)
(5)
Now all changes in surface charge due to base addition are formally treated as increase in negative surface charge so the amount [Mol] of base consumed by the solid phase of the roots, Nroots(pH), during titration of the roots suspension from any pH1 value up to any other pH2 value (a difference of the base consumed by the suspension and the supernatant) is assumed to be equivalent to the increase of the negative surface charge of the roots themselves in the considered pH range, DQV(pH):
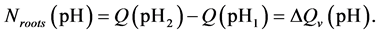 (6)
(6)
At the beginning of the titration (for initial pH1 = pHini) the surface charge has the value of Qini which value is not measured during titration. Due to rather low dissociation constants of root surface acidic groups, an amount of negative charge generated by them at low value of pHini should be really small and therefore one frequently assumes that Qini = 0. However, protonation and positive charging of other surface groups (see Equation (1)) increases with pH decrease, so the amount of positive charge may be significant at initial low pH of the titration. In this case significant portion of the added base can be in fact used for neutralization (decrease) of positive surface charge and not to increase of negative charge.
Among various methods applied to estimate the CEC of plant materials, retitration of acid washed material to a neutral pH [26] has been probably most common one. This method is equivalent to titration of plant root suspension to pH = 7. We hypothesize that the existence of root positive charge may be responsible for frequently reported overestimation of CEC of roots measured by the above methods in respect to CEC measured in other ways at the same pH values (DQV from titration includes initial positive charge and increase of negative charge while CEC is a measure of cations adsorbed only on negative charges).
3.2. Evaluation of Dissociation Constants of Roots Surface Acids
Because of various chemical character and/or various locations in the macromolecules the acidic strength (and dissociation constants) of surface acids can differ markedly. The charge-generating dissociation reaction of any acid kind i located on root surface, SAHi, can be written as:
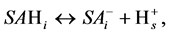
where  denotes proton at the plane of dissociation.
denotes proton at the plane of dissociation.
Since the dissociation takes place near the surface, it is described by the intrinsic dissociation constant, Kintr, which for each of i-th surface acid may be written as:
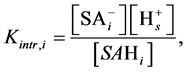 (7)
(7)
where the brackets denote surface activities.
The surface protons concentration is affected by electrostatic interactions with charged surface. The activity of the hydrogen ion at the plane of dissociation [Hs+] is related to the proton concentration in the bulk solution (H+) by the Boltzman expression:
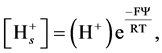 (8)
(8)
where Ψ is the difference in electrostatic potential between the surface (plane of dissociation) and the bulk of the solution, F is Faraday s constant, R is the universal gas constant and T is the absolute temperature.
Since determination of the value of Ψ is not easy [27] , and it undergoes continuous changes during the titration due to changes in surface charge, one usually neglects the electrostatic effects and places:
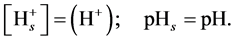 (9)
(9)
Under such assumption, instead of the intrinsic, the apparent surface dissociation constants, Kapp, are considered:
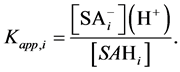 (10)
(10)
This is worth noting that at high ionic strengths the concentration of any ion near the charged surface approaches its concentration in the bulk solution due to shrinking of diffuse double layer. Therefore it is preferable to maintain higher neutral salt concentrations of the supernatant during the titration process, because in this case 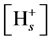 is closer to (H+) and K,intr is better approximated by Kapp. High ionic strength allows also for a better development of variable surface charge because at high ionic strengths dissociation of surface groups is less hindered by electrostatic effects.
is closer to (H+) and K,intr is better approximated by Kapp. High ionic strength allows also for a better development of variable surface charge because at high ionic strengths dissociation of surface groups is less hindered by electrostatic effects.
Let us consider the root surface as being a mixture of n surface acids kind i of initial concentrations (activities) ci. The apparent dissociation constant of each acid may be written as:
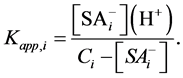 (11)
(11)
The dissociation of water is:
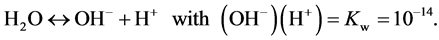 (12)
(12)
At any point of the titration the electrostatic balance for the whole titrated system requests that sum of charges carried by all cations is equal to the sum of charges of all anions. Assuming no soluble acids are present in the supernatant (i.e. considering titration curve of roots solid phase only), the amount of base BOH added to the system equal to the amount of its B+ cations, the ionic balance may be written as:
 (13)
(13)
where v denotes the actual volume of the titrated system, assumed further to be constant during the whole titration process (that is equivalent to titration with base of extremely high concentration).
Dividing Equation (1) by v and introducing (OH−) calculated from Kw, and [Ai−] values calculated from apparent dissociation constants Kapp,i of the respective acids one has:
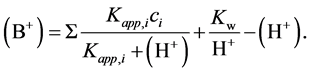 (14)
(14)
The latter equation can be used to simulate titration curves of the mixture of surface acids. The simplest way to do this is to calculate the amount (concentration) of the added base i.e. (B+) for different concentrations of H+ (different pH’s) with arbitrarily assumed surface acids composition i.e. their ci and Kapp,i values. Results of such simulations using MS Excel for different number n of surface acids are shown in Figure 1. The titration curves in Figure 1 were drawn within pH 3 to 10 range (that corresponds to rationale experimental titration window) assuming the Kapp,i values range from 10−4 to 10−9; Kapp,i/Kapp,i+1 is constant for a given set of n acids; and ci =1/n (the sum of concentrations of all acids is equal to 1).
Figure 1 illustrates important features of titration curves: for 3 acids (and of course for 1 and 2 acids, as well) one can distinguish very well defined inflection points that is due to high differences between dissociation constants of particular acids (For n = 3 this is around over 2 orders of magnitude). Inflection points in titration curves of four acids are still visible, however distinguishing of inflection points for mixture of five and more acids appears to be very problematic.
The inflection points of the titration curve of any acid, including surface acid SAH, occurs when the buffering capacity of the system acid/anion is the highest i.e. where concentration of nondissociated acid equals the concentration of its anion (salt):
 (15)
(15)
Having in mind the above circumstance, at the inflection point one has:
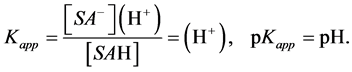 (16)
(16)
Therefore pH at any inflection point corresponds to –log of dissociation constant of the respective surface acid present in the titrated system.
Inflection points (and pKapp,i values) can be determined from pH values at which peaks of the first derivative of the titration curve on pH are located, which for the Figure 1 mixtures are presented in Figure 2.
Figure 2 shows that discrimination of dissociation constants of 7 (and more) individual acids present together in the titrated mixture is not possible even for ideal (computer-generated) titration data. This also shows impos




Figure 1. Simulated using Equation (11) titration curves of of 3, 4, 5 and 7 different surface acids of various ratios of dissociation constants (given within each plot). On y axis the amount of the base used for titration (B) is plotted.
sibility of distinguishing acids of dissociation constants differing by around one order of magnitude (in our case they differ by a factor of 7:Ki/Ki+1 = 7 that only accidentally meets the number n of titrated acids). Distinguishing dissociation constants from experimental titration data of acid mixtures is much more complicated. Even if we have titration data measured with extremely high precision, finding inflection points is hardly possible in most cases. Figure 3 (analogically to Figure 2) shows first derivatives of titration curves for mixtures of 3, 4 and 5 acids from Figure 1 with arbitrarily introduced ± random errors of pH readings of maximally 0.01 pH unit (it is almost impossible to reach so high precision in practice).
Figure 3 shows that discrimination between dissociation constants of only four surface acids basing on experimental titration curves may cause serious difficulties due to severe data scattering. Looking on the problem from the opposite side—one can simulate (reconstruct) any experimental titration curve assuming that it results from titration of a mixture of not more than four acids of arbitrarily selected dissociation constants and of concentrations ci found as best-fit parameters.
Since estimation of apparent surface dissociation constants of a mixture of a few surface acids is practically possible only for titration curves exhibiting well developed inflection points, for majority of real roots titration curves one should find another approach to characterize strength of surface acids. This is usually done by estimation of average value of surface dissociation constants. The curves presented in Figure 2 and Figure 3 may be interpreted in terms of the frequency χ of occurrence of various pKapp values within the titrated acids mixture:
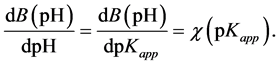 (17)
(17)
where f is the fraction of neutralized acids.
The χ(pKapp) versus pKapp dependence is thus the (nonnormalized) distribution function of acid dissociation



Figure 3. First derivatives of titration curves of mixtures of n acids from Figure 1 with introduced ± random errors not higher than 0.01 pH unit (points). Solid line is a running average for five subsequent data points.
constants. Dividing χ(pKapp) by the total amount of acids present in the mixture, ∑ci, (that in the present case is equal to 1) one obtains normalized distribution function, υ(pKapp):
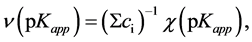 . (18)
. (18)
The average apparent surface dissociation constant is defined as:
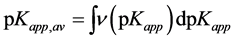 . (19)
. (19)
As this is seen, estimation of both normalized pKapp distribution function and pKapp,av value needs having ∑ci value, equal to the amount of base requested for total neutralization of all surface acids, Ntot Since experimental determination of Ntot is hardly possible, for practical purposes one usually assumes that it is equal to Nmax, i.e. the maximal value of the base (Nsusp-Nsol) used for titration within the whole experimental window. Moreover, since distinguishing between groups of surface acids differing in dissociation constants by less than one order of magnitude makes no sense, using experimental titration data to calculate the distributions of surface dissociation constants one should rather rely not on continuous but rather on discrete distribution functions, thus Equation (17) should be replaced by stepwise dependencies. Now one has:
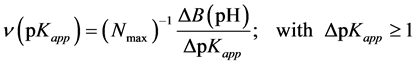 (20)
(20)
where:  and so, average value of apparent dissociation constant for the whole root is calculated as:
and so, average value of apparent dissociation constant for the whole root is calculated as:
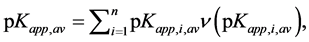 (21)
(21)
where the number of surface acids n is now defined by pH range of the experimental widow pHini to pHmax (that is equal to the range of pKapp values considered): 
4. Experiments
4.1. Material
Roots of barley Hordeum (Ars) Stratus grown in the Marshner and Romheld nutrient solution [28] , harvested at the occurrence of a Flag Leaf, washed thrice with excess of 0.01 Mol∙dm−3HCl, fivefold with distilled water, and stored in the air-dry state were used for titration. The detailed description of plants growth conditions, root harvesting and acid washing is described in [9] .
4.2. Sample Pretreatment
At first the air dry roots were cut to around 1mm pieces and carefully homogenized. Next the dry mass content in the air-dry roots was estimated after 105˚C drying by 24 h. Each sample of air-dry (nonheated) roots to be titrated was suspended overnight in 20 ml volume of a supernatant in a closed titration vessel. As the supernatants NaCl solutions of different concentrations: 0 (water), 0.01, 0.1 and/or 1.0 Mol∙dm−3 were used. Prior to the titration each roots suspension was adjusted to pH » 2.95 by additions of small increments of 1 mol∙dm−3 HCl. If the final pH did not change more than by 0.01 pH unit by 5 min, the suspension was weighed (for precise determination of the supernatant volume) and the titration was started.
4.3. Static Titration
Four series of root suspensions prepared as described above were titrated in triplicate. Each from the series contained eleven root samples of 0.1 ± 0.001 g (weighed with the precision of 0.0001 g). Different 1.00 Mol∙dm−3 NaOH aliquots (with accuracy of 1 μl) were added to each of the suspension. NaOH was dissolved in NaCl solution of the concentration equal to this of the respective supernatant. The vessels were closed, placed on a rotary shaker and the suspensions pH after various time intervals were registered. Similarly 20 ml aliquots of the supernatants were titrated.
4.4. Automatic Titration
The automatic titrations were performed in triplicate using Titrino autotitration unit provided by Mettler Toledo equipped with Orion Research combined electrode. The continuous flux of nitrogen through titrated medium was applied starting 60min before the titration. Suspensions containing around 0.025, 0.05, 0.10 and 0.25 g of air dry roots (exact weight estimated with a precision of 0.0001 g) were titrated using 1.00 mol∙dm−3 NaOH dissolved in the respective NaCl solution. The titrations were proceeded with 10 ml aliquots of NaOH allowing the suspension to reach a stability of 0.001 pH units−1 prior to the addition of the next aliquot of base. The titration curves of the supernatants (the respective NaCl solutions) were determined in similar way.
4.5. Data Elaboration
Each of three replicates of most of titrations curves differed not more than 3.2%. Higher variations (up to 6%) were noted only for static titration curves registered after two extreme equilibration times (24 and 48 h).The data presented further are arithmetical averages from triplicate measurements, for which only standard deviations were calculated.
5. Results and Discussion
5.1. Titration Curves
Figure 4 shows exemplary static titration curves for the studied roots suspensions.
Initially the pH of the suspensions decreases in the whole range of the base added that may be attributed to slow kinetics of neutralization of surface acidic groups and after longer equilibration times the pH increases at lower base doses, that cannot occur if only neutralization of acids takes place. The latter phenomenon is most probably due to growth of microorganisms within roots suspensions since the roots samples were not disinfected. The observed pH increase is largest in root-water suspension and decreases with NaCl concentration, that may be due to inhibiting effect of salt level on microorganisms development. Due to the above effect we further consider the static titration curves measured after 8h equilibration as equilibrium titration curves.
Figure 5 shows exemplary titration curves measured by automatic titration for suspensions of roots samples of various masses.
The shape of the automatic titration curves depends on the mass of the root sample. For small sample masses two inflection points can be distinguished while only one inflection point is observed for higher masses. This is most probably connected with nonequilibrium titration conditions. The same titrant aliquot added to smaller root mass results in higher titration rate per unit mass of the roots than for higher root mass. Certainly, even the applied condition of titration pH stability is not enough to preserve similar pseudo equilibria of neutralization of surface acids during automatic titration of suspensions of different solid: liquid ratios. It shows another important problem of titration: using small samples one can erroneously interpret the roots behavior.
5.2. Variable Charge vs. pH Dependencies
Variable charge vs. pH dependencies for the studied roots calculated according to Equation 6 are presented in Figure 6. In this Figure surface charge developed by unit mass of 105˚C heated roots is presented basing on estimation of moisture content of the titrated air dry roots equal to 89.6% w/w. The experimental window between pH 3.0 and 10.0 was selected and the amounts of base consumed by a given suspension and supernatant during titration to different common pH values were estimated from best-fit polysigmoidal curves (curvexpert program by D.G. Hyams). Having much more experimental data from autotitration than from static titration, we interpolated pH data with the step of 0.2 and 1.0 pH unit, respectively.
The higher mass of the root sample the better the coincidence of the charge calculated from automatic titration and the equilibrium charge. Automatic titration with higher rates (lower sample masses) appear to produce unrealistic results of charge-pH curves in pH > 7 range. High charge-salt concentration effect is observed. In water the total surface charge of the roots (at pH = 10) is around 1.6 and it consecutively increases up to around 2.0 in 1 M NaCl.
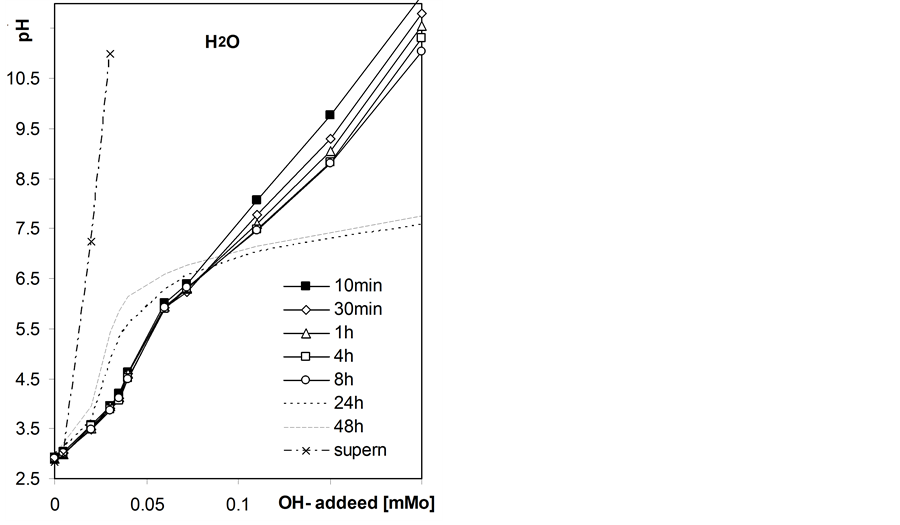
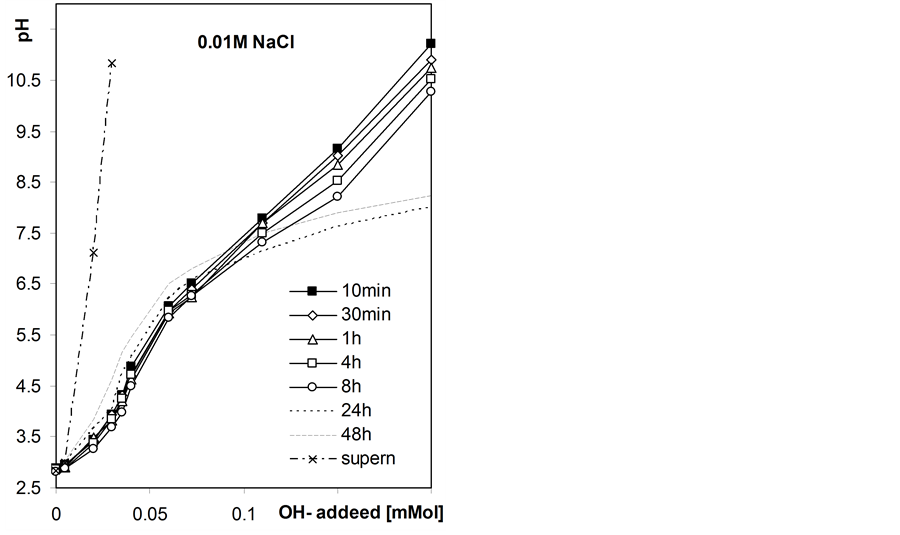
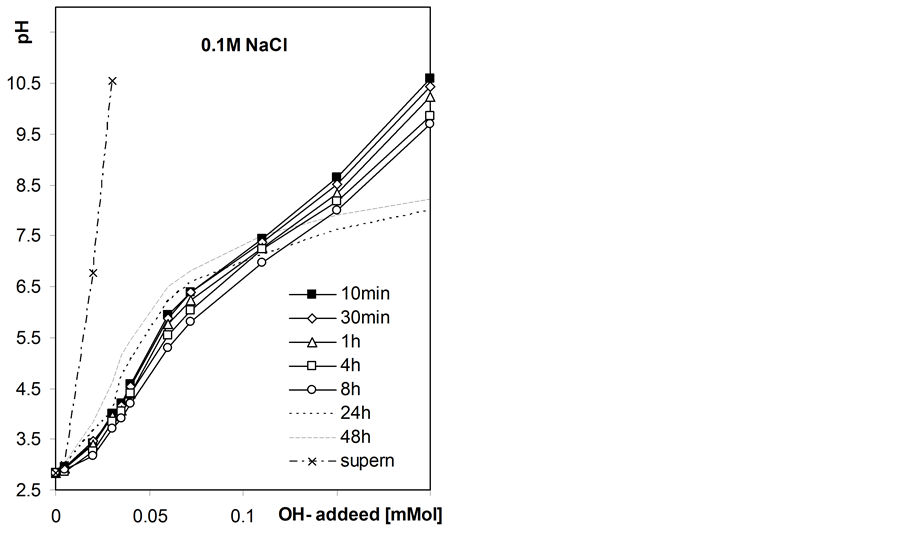
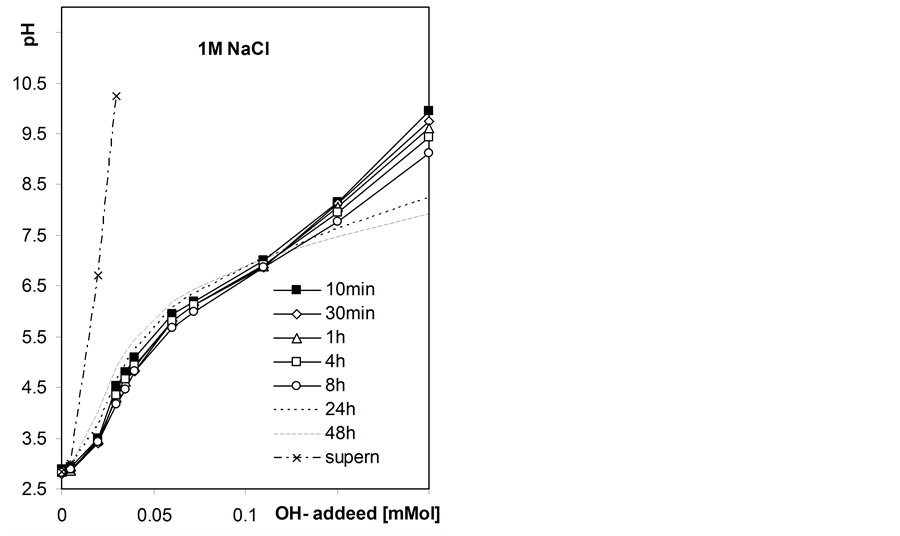
Figure 4. Exemplary static titration curves of the studied barley roots suspensions in water and in NaCl solutions of different concentrations measured after various quilibration time given within the figure. The curves presented for supernatants were not time-dependent.
5.3. Distributions and Average Values of Surface Dissociation Constants
Normalized apparent surface dissociation constants distribution functions calculated from Equation (20) for variable charge vs. pH data (Figure 6) are presented in Figure 7.
The pKapp distributions calculated from static titration data are almost identical to these calculated from automatic titration for maximum root mass (Figure 7, left plot) that indicates applicability of low speed autotitration
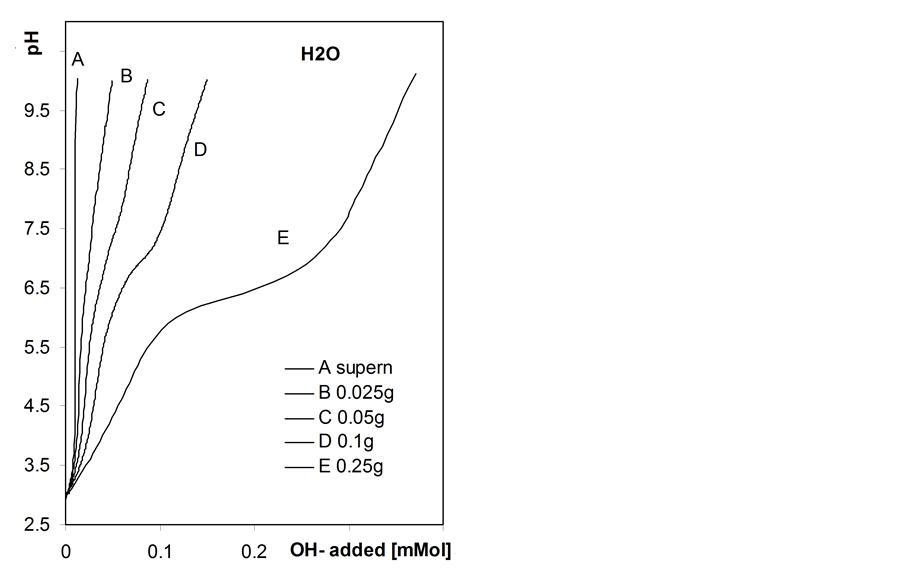
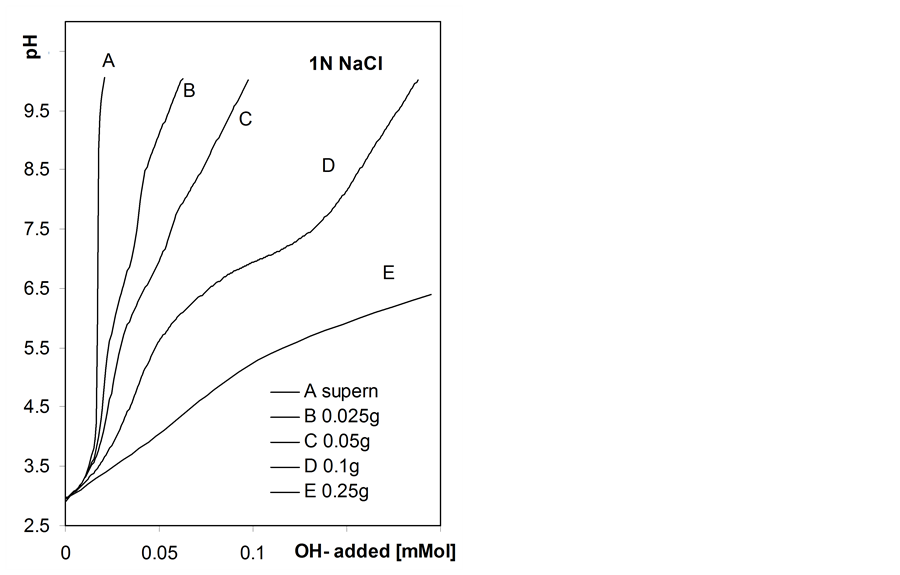
Figure 5. Automatic titration curves of the studied barley roots suspensions in water and in 1M NaCl solution measured for various weights of the root samples given within the Figure, and of the respective supernatants. To show more details of the curves the x-axes in left and right plots are not proportional.
to roots surface charge studies. From this plot one can see that roots titrated in water exhibit significant amount of strongly acidic surface groups (pKapp = 3.5) that may reflect exchangeable protons adsorption on negative part of the initial surface charge. Increasing salt concentration in the supernatant leads to replacing of exchangeable protons by sodium ions and an apparent decrease in strong acids fraction. Generally, one-peak distributions are calculated at quasi-equilibrium titration conditions. Right plot in Figure 7 illustrates differences in pKapp distributions calculated from automatic titration data for different masses of titrated roots (here the first derivatives of titration data with a step of 0.2 pKapp unit are plotted). For low masses of root samples one obtains two-peak distributions that are due to improper titration conditions and not to the nature of the studied roots surface.
Values of negative logarithms of average surface dissociation constants calculated from Equation (21) using data illustrated in Figure 7 are presented in Table1
The values of average pKapp, reflecting the overall acidity of the root surface appear not to exhibit any welldefined trend with changes in supernatant salt concentration, however we expected that they would decrease with increasing ionic strength due to evident decrease in the amount of strongly acidic surface groups, as seen from distribution functions. The expected trend is better pronounced for static titration (EQ) data, however in general, the average pKapp value seems not to be a good indicator of root surface acidic character and one should better rely on interpretation of behavior of distribution functions. Even drastic differences in distributions of surface acidic groups as revealed for automatic titration of different root sample masses are not much reflected in changes of average pKapp.
5.4. Addendum: Surface Charge Density
Surface charge density, SCD, of the root surface governs primarily the uptake of all mineral ions into the plant, however it can also influence the transport ATPases in root cells, fluidity of cell membranes and many other plant processes and properties [29] -[31] . The root SCD is defined as an amount of charge located on unit area of the roots. Having known the root surface charge at a given pH, Q (Mol∙g−1), the SCD (C∙m−2) may be calculated as:
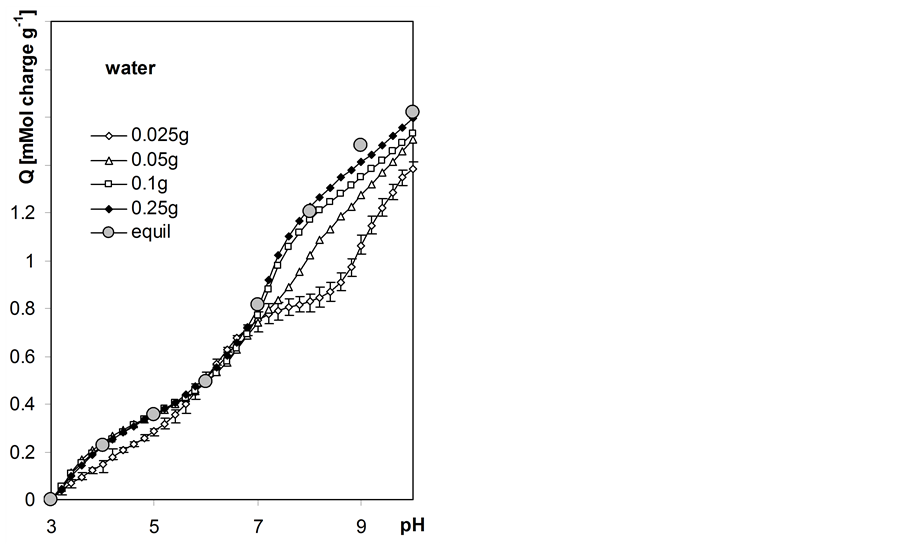
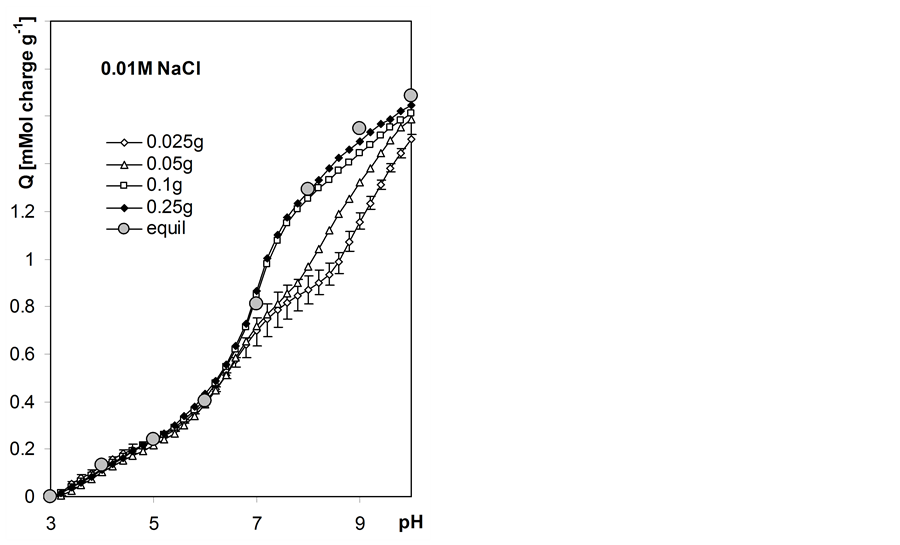

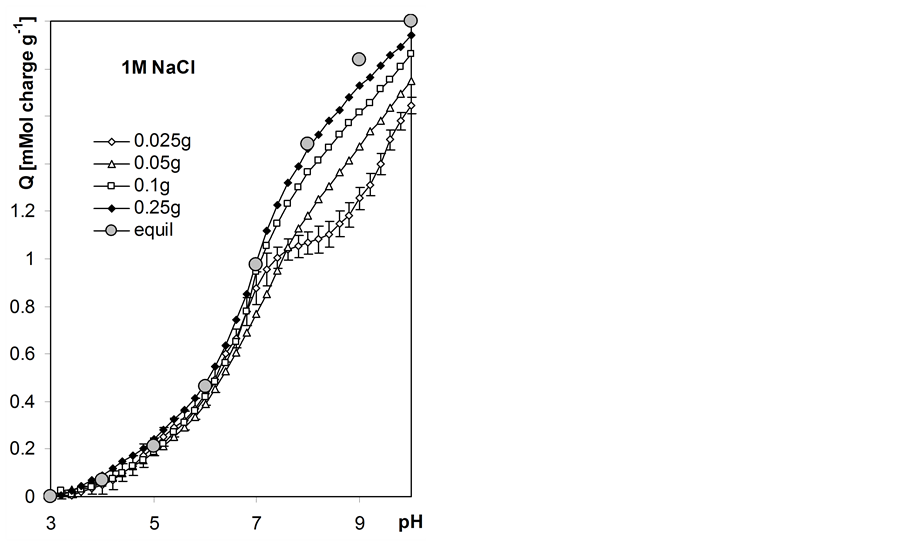
Figure 6. Root surface charge vs. pH dependence at various concentrations of NaCl calculated from titration curves measured for various weights of the root samples given within the Figure. Equil denotes equilibrium charge calculated from 8h static titration data. The curves show average data calculated from three titration replicates. Not to shadow details only the largest error bars (standard deviations) are included for charge calculated for the sample of the smallest mass.
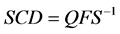 , (22)
, (22)
where F (C∙Mol−1) is the Faraday constant and S (m2×g−1) is the specific surface area of the roots.
Since in [9] we estimated the surface area of the same roots as these studied in the present paper, being around
Table 1 . Average pK values of surface dissociation constants of the studied barley roots calculated from distribution functions presented in Figure 7.
Abbreviations: AT-automatic titration of root mass given after the letters, EQ-8h static titration. Note: values in first two columns calculated from distribution functions presented in the left plot in Figure 7 and in next four columns from data in the right plot. Average data ± standard deviations, calculated from three titration replicates are presented.
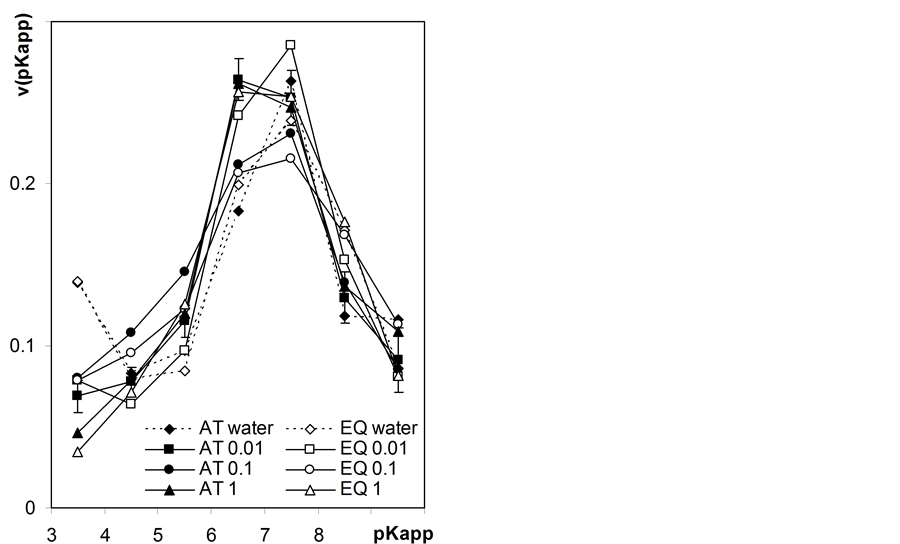
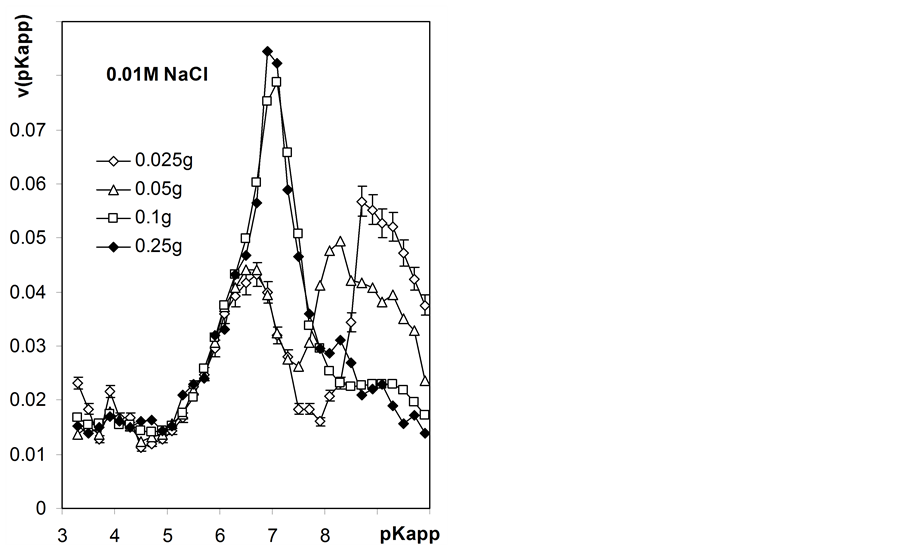
Figure 7. Normalized distribution functions of apparent surface dissociation constants of the studied roots. Left picture includes functions calculated from automatic titrations (AT) for maximum mass samples (0.25 g) and from 8 h static titrations (EQ) at various concentrations of NaCl (numbers after AT or EQ). Right picture shows functions calculated from titration curves measured in 0.01 M NaCl for various weights of the root samples given within the plot. The curves show average data calculated from three titration replicates. Not to shadow details only the largest error bars (standard deviations) are shown.
400 m2∙g−1, we took this value to calculate SCD of the studied roots. The value of roots surface charge at pH = 7 (1 mMol∙g−1) was taken for calculations.
The resulting surface charge density value equals 241 mC∙m−2 that is around one order of magnitude higher than SCD values (from 17 to 29 mC∙m−2) measured also at pH = 7 for different components of plant roots (microsomes, plasma membranes, plasmalemma vesicles, different membrane fractions extracted from roots of seedlings) using 9-aminoacridine fluorescence [29] -[32] , that is considered as a standard method. The above discrepancy may be explained at least in two manners. The first is high heterogeneity in location of surface charged groups on the surface: in this case large aminoacridine molecule covers a few charged groups and screens them from further electrostatic adsorption of the next aminoacridine molecules (thus the remaining charged groups present “under” the adsorbed aminoacridine molecule are neutralized by small basic cations). The second explanation lies in high geometric heterogeneity of the root surface and occurrence of very thin pores (of charged walls) into which large aminoacridine molecule cannot penetrate. Assuming that the area of one aminoacridine molecule equals 70 square Angstroms (here we rely on the area of its analogue anthracene, being around 68 square Angstroms, as found in http://www.chemicalize.org/structure) the 1 m2 of flat and homogeneously charged surface may be covered by maximum 1.4 × 1018aminoacridinemolecules present in monolayer. Such value gives surface charge density of around 230 mC∙m−2 that means that if the studied roots surface is flat, the aminoacridine method can measure all root charges developed at pH 7 (of course if charging of the whole roots is similar to its components).
6. Conclusions
Since titration results have to be expressed on unit mass of the roots, we propose to use the mass of 105˚C dried roots for this purpose.
The most important element in measurements of titration curves of plant roots is maintaining acid-base equilibrium, however it is not easy to get it in practice, even for long time static titration.
Inflection points on titration curves used commonly for estimation of dissociation constants of surface acidic groups may result from nonequilibrium titration conditions.
Plant roots surface charge seems to be very heterogeneous thus common attempts to describe it using discrete-site distribution models seem to be a tacit over interpretation of experimental data.
Salt concentration strongly influences the measured surface charge therefore buffering ionic strength of the supernatant during titration is also necessary.
Using surface charge from titration and surface area from water vapor adsorption, one determines surface charge density around 10 times higher than that evaluated by 9-aminoacridine fluorescence.
Acknowledgements
This work was supported by the European Regional Development Fund through the Innovative Economy Program for Poland 2007-2013, project WND-POIG.01.03.01-00-101/08 POLAPGEN-BD, “Biotechnological tools for breeding cereals with increased resistance to drought”. The project is realized by POLAPGEN Consortium coordinated by Institute of Plant Genetics, Polish Academy of Sciences in Poznan. Further information about the project can be found at www.polapgen.pl.
References
- Ginn, B.R., Szymanowski, J.S. and Fein, J.B. (2008) Metal and Proton Binding onto the Roots of Fescue Rubra. Chemical Geology, 253, 130-135. http://dx.doi.org/10.1016/j.chemgeo.2008.05.001
- Cheng, T. and Allen, H.E. (2001) Prediction of Uptake of Copper from Solution by Lettuce Lactuca sativa Romance). Environmental Toxicology & Chemistry, 20, 2544-2551. http://dx.doi.org/10.1897/1551-5028(2001)020<2544:POUOCF>2.0.CO;2
- Meychik, N.R., Honarmand, S.J., Nikolaeva, Y.I. and Yermakov, I.P. (2007) Ion Exchange Properties of Cicer arietinum L. Root Cell Walls under Different Environmental Salt Conditions. Biologija, 53, 75-79
- Meychik, N.R. and Yermakov, I.P. (2001) Ion Exchange Properties of Plant Root Cell Walls. Plant and Soil, 234, 181-193. http://dx.doi.org/10.1023/A:1017936318435
- Sentenac, H. and Grignon, C. (1981) A Model For Predicting Ionic Equilibrium Concentrations in Cell Walls. Plant Physiology, 68, 415-419. http://dx.doi.org/10.1104/pp.68.2.415
- Kaulbach, E.S., Szymanowski, J.E.S. and Fein, J.B. (2005) Surface Complexation Modeling of Proton and Cd Adsorption onto an Algal Cell Wall. Environental Science and Technology, 39, 4060-4065. http://dx.doi.org/10.1021/es0481833
- Wu, Y. and Hendershot, W.H. (2009) Cation Exchange Capacity and Proton Binding Properties of Pea (Pisum sativum L.) Roots. Water, Air, and Soil Pollution, 200, 353-369. http://dx.doi.org/10.1007/s11270-008-9918-2
- Zhou, Z., Zhou, J., Wang, H. and Wang, J. (2008) Preparation and Surface Characteristics of Root Cell Walls of Soybean and Maize Seedlings. Plant Nutrition and Fertilizer Science, 14, 392-397.
- Jozefaciuk, G. and Lukowska, M. (2013) New Method for Measurement of Plant Roots Specific Surface. American Journal of Plant Sciences, 4, 1088-1094. http://dx.doi.org/10.4236/ajps.2013.45135
- Lukowska, M. and Jozefaciuk, G. (2013) Unknown Mechanism of Plants Response to Drought: Low Soil Moisture and Osmotic Stresses Induce Severe Decrease in CEC and Increase in Acidity of Barley Roots. Journal of Agricultural Science, 5, 204-213
- Graham, E.R. and Baker, W.L. (1991) Ionic Saturation of Plant Roots with Special Reference to Hydrogen. Soil Science, 72, 435-442. http://dx.doi.org/10.1097/00010694-195112000-00003
- Epstein, E. and Leggett, J.E. (1954) The Absorption of Alkaline Earth Cations by Barley Roots. Kinetics and Mechanism. American Journal of Botany, 41, 785-791. http://dx.doi.org/10.2307/2438542
- Ram, L.C. (1980) Cation Exchange Capacity of Plant Roots in Relation to Nutrients Uptake by Shoot and Grain as Influenced by Age. Plant and Soil, 55, 215-224. http://dx.doi.org/10.1007/BF02181801
- Rengel, Z. and Robinson, D.L. (1989) Aluminum and Plant Age Effects on Adsorption of Cations in the Donnan Free Space of Ryegrass Roots. Plant and Soil, 116, 223-227. http://dx.doi.org/10.1007/BF02214551
- Grignon, C. and Sentenac, H. (1991) pH and Ionic Conditions in the Apoplast. Annual Review of Plant Physiology and Plant Molecular Biology, 42, 103-128. http://dx.doi.org/10.1146/annurev.pp.42.060191.000535
- Shomer, I., Novacky, A.J., Pike, S.M., Yermiyahu, U. and Kinraide, T.B. (2003) Electrical Potentials of Plant Cell Walls in Response to the Ionic Environment. Plant Physiology, 133, 411-422. http://dx.doi.org/10.1104/pp.103.024539
- Kinraide, T.B. (2004) Possible Influence of Cell Walls upon Ion Concentrations at Plasma Membrane Surfaces. Toward a Comprehensive View of Cell-Surface Electrical Effects upon Ion Uptake, Intoxication, and Amelioration. Plant Physiology, 136, 3804-3813. http://dx.doi.org/10.1104/pp.104.043174
- Kinraide, T.B. and Wang, P. (2010) The Surface Charge Density of Plant Cell Membranes (σ): An Attempt to Resolve Conflicting Values for Intrinsic σ. Journal of Experimental Botany, 61, 2507-2518. http://dx.doi.org/10.1093/jxb/erq082
- Bartlett, R.J. (1964) Measurement of Cationand Anion-Exchange Capacities of Roots Using NaCl Exchange. Soil Science, 98, 351-357. http://dx.doi.org/10.1097/00010694-196412000-00001
- Vedy, J.C. and Bruckert, S. (1982) Soil Solution; Composition and Pedogenic Significance. In: Bonneau, M. and Souchier, B., Eds., Constituents and Properties of Soils, Academic Press, New York, 184-214.
- Zabowski, D. (1989) Limited Release of Soluble Organics from Roots during the Centrifugal Extraction of Soil Solutions. Soil Science Society of America Journal, 53, 977-979. http://dx.doi.org/10.2136/sssaj1989.03615995005300030058x
- Arsova, A. (2002) Cation-Exchange Characteristics of Wheat, Barley and Pea Depending on the Osmotic Pressure in Nutrient Solutions of Low pH. Bulgarian Journal of Plant Physiology, 28, 35-45.
- Van De Geijn, S.C. and Petit, C.M. (1979) Transport of Divalent Cations: Cation Exchange Capacity of Intact Xylem Vessels. Plant Physiology, 64, 954-958. http://dx.doi.org/10.1104/pp.64.6.954
- Korner, L., Moller, I.M., Kjellbom, P. and Larsson, C. (1984) Surface Properties of Plasmalemma Vesicles from Barley Roots and Shoots. 4th Congress of FESPP, Strasbourg, 29 July-3 August 1984, 515-516.
- Akerlund, H.E., Andersson, B., Persson, A. and Albertsson, P.A. (1979) Isoelectric Points of Spinach Thylakoid Membrane Surfaces as Determined by Cross Partition. Biochimica et Biophysica Acta, 552, 238-246. http://dx.doi.org/10.1016/0005-2736(79)90280-3
- Crooke, W.M. (1964) The Measurement of the Cation-Exchange Capacity of Plant Roots. Plant and Soil, 21, 43-49. http://dx.doi.org/10.1007/BF01373871
- McBride, M. (1997) A Critique of Diffuse Double Layer Models Applied to Colloid and Surface Chemistry. Clays and Clay Minerals, 45, 598-608. http://dx.doi.org/10.1346/CCMN.1997.0450412
- Marschner, H. and Romheld, V. (1983) In Vivo Measurement of Root-Induced pH Changes at the Soil-Root Interface: Effect of Plant Species and Nitrogen Source. Zeitschrift für Pflanzenphysiologie, 111, 249-251.
- Barczi, A., Moller, I.M., Lundborg, T. and Kylin, A. (1984) The Surface Charge Density of Wheat Root Membranes. Physiologia Plantarum, 61, 535-540. http://dx.doi.org/10.1111/j.1399-3054.1984.tb05166.x
- Moller, I.M., Lundborg, T. and Barczi, A. (1984) The Negative Surface Charge Density of Plasmalemma Vesicles from Wheat and Oat Roots. FEBS Letters, 167, 181-185. http://dx.doi.org/10.1016/0014-5793(84)80857-1
- Dahlin, C. (2003) Surface Charge Densities and Membrane Fluidities in Thylakoids with Different Degrees of Thylakoid Appression after Norflurazon Treatment. Photosynthetica, 41, 635-639. http://dx.doi.org/10.1023/B:PHOT.0000027532.55335.a7
- Korner, L.E., Kjellbom, P., Larsson, C. and Moller, I.M. (1985) Surface Properties of Right Side-Out Plasma Membrane Vesicles Isolated from Barley Roots and Leaves. Plant Physiology, 79, 72-79. http://dx.doi.org/10.1104/pp.79.1.72






