American Journal of Climate Change
Vol.06 No.01(2017), Article ID:74680,16 pages
10.4236/ajcc.2017.61007
Trend Analysis of Rainfall in Ganga Basin, India during 1901-2000
Suman Bera
Department of Geography and Environment Management, Vidyasagar University, Midnapore, India

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 22, 2016; Accepted: March 10, 2017; Published: March 13, 2017
ABSTRACT
Shortage of water in the river in relation to rainfall change plays a pivotal role in water sharing like Ganga. In attempt to understand the rainfall changes, Mann-Kendall test and Sen’s slope estimation on hundred years’ (1901-2000) rainfall data of 236 districts in entire Ganga basin were run. Half of the districts showed a decreasing trend in annual rainfall in which 39 districts were statistically significant. During pre-monsoon (Jan.-May), 78% of the total districts showed the decreasing trend with the significance of 54 districts. A majority of the districts under the Kosi, Gandak and Sone sub-basins showed the significant negative trend in annual, pre-monsoon and post-monsoon season. So, there need some districts’ and sub-basins’ wise strategies to cope with the situation in the context of climate change.
Keywords:
Mann-Kendall Test, Sen’s Slope Estimator, Climate Change

1. Introduction
Rainfall, the most important form of precipitation, is the principal element of hydrological cycle on earth surface. But this hydrological element has potentially been threatened by the climatic change along with snow accumulation and melts- water, evapo-transpiration and ground water table [1] . Besides, annual river run- off and water availability will likely decline by 10% - 30% in tropics and mid- latitudes and 10% - 40% in high latitudes and wet tropics due to global climatic changes [2] . As a result, almost two-thirds of the world population will be under water paucity in future decades [3] [4] [5] [6] . This scenario will affect the trans- boundary river and its sharing. Ganga, as a transboundary river, flows through India (79.10%), Bangladesh (4.26%), China (3.08%) and Nepal (13.56%). The inadequate availability of water flow on main river has caused difficulties in water sharing between the nations during lean season. Unequal rainfall distribution, irregularities in pre-monsoon, monsoon and post-monsoon rainfall etc., seem to be more common factors to control seasonal water availability at Ganga River. There- fore, the rainfall trend is more appropriate to examine as the most dominant input to the systems of water discharge in river. In India, nearly 80% of annual rainfall occurs during monsoonal period (June to September), but decline of rainy days with increasing rainfall intensity have resulted in serious threats on required wa- ter availability [7] . Proper understanding of long term rainfall trend, magnitudes and variability is useful to estimate the water resource availability in rivers. Va- rious scientific studies show that the spatial and temporal variations of water resources in the basins are closely related to precipitation changes [8] [9] . Decreasing precipitation, ensuring the decline of fresh water availability occurs in many Indian rivers [10] [11] . There are several researches about long term rainfall changes over India. Some studies indicated, no trend in monsoon rainfall [12] - [21] explored some pockets of significant long term rainfall changes in India. Using Mann-Kendall rank statistical test for 90 years’ (1901-1990) observed daily rainfall data from 151 observatory stations, [22] found increasing trend of rain in monsoon but decreasing trends in pre- and post-monsoon periods. [11] studied long term trends in monthly, seasonal and annual rainfall of 30 meteorological sub-divisions over India during the period from 1871 to 2005. The analysis revealed decrease in annual and monsoon rainfall except Haryana and Gangetic West Bengal. Similarly, [23] showed the declining trend of precipitation over north-western Himalaya from 1860s to 2000s whereas, post-monsoon rain did not show any trend. [24] examined the trend through Modified Mann- Kendall test (MMK) and Pettitt-Mann-Whitney (PMW) methods using 80 years’ data (1901-1980) of annual precipitation in Ganges tributaries in Uttarakhand and results showed the decline of precipitation. [25] analyzed rainfall data from 316 rain gauge stations in India and found an increasing trend of annual rain in Ganga basin. Regionally, [26] found increasing trend in rainfall over Ganga, Indus, Brahmaputra, Krishna and Cauvery basins. [27] found increasing trend in summer monsoon over western Indo-Gangetic plains (170 mm/100years) from 1900 and statistically insignificant decreasing trend (5 mm/100years) over central part of the plain using the rainfall data for the period of 1829-1999 over Indo-Gangetic plain. [28] observed mild decrease in wet season rainfall during 1963-2006 compared with the period of 1914-1962 and also decrease in surplus rainfall from 1972. [29] evaluated 124 years’ (1871-1994) sub-divisional rainfall data and concluded that except 2 sub-divisions, the annual precipitation over Ganga basin showed stable. Similarly, [7] analyzed basin wise trends of rainfall, rainy days and temperature over India with the help of Mann-Kendall test and Sen’s slope estimator. The result revealed increasing trend in rainy days and no trend in annual rainfall over Ganga basin.
Plethora of studies revealed rainfall changes over Ganga basin. Results of these studies contradict each other. In the present study, season wise district level ana- lysis of rainfall trend is considered to be essential in better understanding of climatological and hydrological situation of the Ganga basin. Two of the mostly cited methods (Mann-Kendall test and Sen’s slope estimator) for long term trend analysis have been used in the present study.
2. Study Area and Data Used
The study is carried out in the Ganga basin of India (Figure 1), which lies approximately between 21˚6'N to 31˚21'N latitude and between 73˚2'E and 89˚5'E longitude, have maximum length and width of approximately 1543 km and 1024 km respectively. It has a total area of about 8,61,452 sq∙km and occupied 26.3% of the total geographical area of the country. Generally 70% - 80% of the total annual rainfall occurs during the month of July to September. The average annual rainfall for this basin varies from 400 to 2000 mm. and every sq∙km of land surface area receives an average of 1 Million Cubic Meter of water annually through rainfall [30] (CWC and NRSC, 2014). The distribution of average annual, pre-monsoon, monsoon and post-monsoon rainfall during the study is depicted here (Figure 2).
The study concentrates on the rainfall analysis from 1901 to 2000 for 236 districts of eleven states that fall under the Ganga basin. Monthly rainfall data are
Figure 1. Ganga River Basin with its 19 sub-basins.
Figure 2. Average rainfall during 1901-2000. (a) Annual, (b) Pre-monsoon, (c) Monsoon and (d) Post-monsoon.
obtained from the India Meteorological Department (IMD), Pune, India. Some missing data are filled up by the data collected from India Water Portal (http://indiawaterportal.org/met_data/). Present analysis attempts to concentrate on rainfall distribution in pre-monsoon (January-May) season along with monsoon (June-September), post-monsoon (October-December). So, monthly rainfall series are used to form annual, pre-monsoon, monsoon and post-monsoon series, over the river Ganga.
3. Methodology
In the study, non-parametric methods, Mann-Kendall (MK) test [31] [32] and Sen’s estimator [33] are used to detect the nature of trends in the time series. Mann-Kendall’s method is applied to test the presence of a monotonic trend and the statistical significance of the trend and Sen’s slope estimator for estimating true change per year in the time series. No pre-whitening of the data series is carried out.
3.1. Mann-Kendall (MK) Test
MK test is not only used for rainfall trends, but also widely used for analysing different climatic variables [23] [34] - [46] and analysis of various environmental data [47] . World Meteorological Organisation recommended MK test to measure the significant monotonic trends in hydrological series [48] . [49] analyzed the temporal and spatial rainfall distribution trend and variation by asymmetrical factor method and Mann-Kendall test method. [50] used Mann-Kendall test to determine the trends of long-term annual precipitation and stream flow series of eastern Black Sea Region in Turkey. The low sensitivity in homogeneous time series [51] and non requirement of normally distributed data series are two great advantages of MK test [52] .
The Mann-Kendall test is appropriate in cases when the data values xi of a time series can be assumed to follow the model:
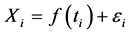 (1)
(1)
where 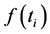 is a continuous monotonic increasing or decreasing function of time and the residuals εi can suppose to be from the same distribution with zero mean. It is therefore assumes that the variance of the distribution is constant in time.
is a continuous monotonic increasing or decreasing function of time and the residuals εi can suppose to be from the same distribution with zero mean. It is therefore assumes that the variance of the distribution is constant in time.
The null hypothesis of no trend, H0, assumes that the observations xi are independently distributed in time and the alternative hypothesis, H1, denoted an increasing or decreasing monotonic trend. The number of annual values in the considered data series is designated by n. Missing values are allowed and n can thus be smaller than the number of years in the time series. The Mann-Kendall test statistic S is determined using the following formula:
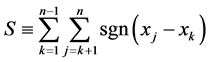 , (2)
, (2)
where, xj and xk are the annual values in years j and k, j > k, respectively, and
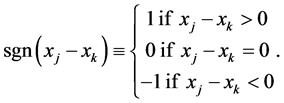 (3)
(3)
The variance of S is computed by the following equation which takes into account that ties may be present:
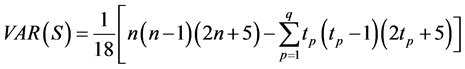 (4)
(4)
where, n is the number of data points, q is the number of tied groups and tp is the number of data values in the pth group. Z statistics or Normal Approximation test generally used when the sample size is greater than 10. The Normal appro- ximation test (Z test) is developed by both the values of S and VAR(S) (Equa- tion (5)).
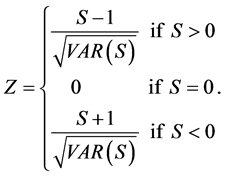 (5)
(5)
The statistically significant trend is assessed by this Z value. The positive and negative values of Z denotes increasing and decreasing trend respectively. The statistic Z has a normal distribution. To test for either an increasing or decreasing monotone trend (a two-tailed test) at α level of significance, H0 is rejected if the absolute value of Z is greater than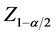 , where
, where 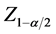 is acquired from the standard normal cumulative distribution tables [52] .
is acquired from the standard normal cumulative distribution tables [52] .
3.2. Sen’s Slope Estimator
To estimate the true slope of an existing trend (as change per year) the Sen’s nonparametric method is used. It can be in cases where the trend can be assumed to be linear. This means that 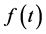 in Equation (1) is equal to
in Equation (1) is equal to
 (6)
(6)
where, Q is the slope and B is a constant.
To get the slope estimate Q in Equation (6), we first calculate the slopes of all data value pairs:
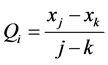 (7)
(7)
where, xj and xk are the data scores at times j and k (j > k) respectively. If there are n values xj in the time series we get as many as 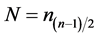 slope estimates of Qi. The Sen’s estimator of slope is the median of these N values of Qi. The N values of Qi are ranked from the smallest to the largest and the Sen’s estimator is
slope estimates of Qi. The Sen’s estimator of slope is the median of these N values of Qi. The N values of Qi are ranked from the smallest to the largest and the Sen’s estimator is
 (8)
(8)
Q is tested with a two-sided confidence interval at 100(1 − α)% and the slope estimate is obtained by the nonparametric method.
The confidence interval at two different confidence levels; α = 0.01 and α = 0.05 as follows:
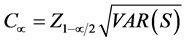 (9)
(9)
where, VAR(S) has been defined in Equation (4), and 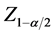 is obtained from the standard normal distribution.
is obtained from the standard normal distribution.
After that, 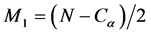 and
and 

4. Results and Discussion
4.1. Magnitude of Trend
The magnitude of the trend of this time series (1901-2000) is determined using Sen’s estimator method. Annual rainfall trend shows a large variability in the magnitude. The spatial pattern of annual rainfall in Ganga basin experienced positive trend in eastern and western margin along with a vast areas of negative trend in between. The districts, situated in West-South west and East-South east part, showed positive trend (Figure 3). More than half of the districts have shown a decreasing trend. Out of total 236 districts, maximum reduction was experienced by Dehradun (−8.35 mm/year) and the maximum increase was witnesses by South 24 Parganas (4.99 mm/year).
Annual total rainfall amount cannot fully address the complex hydrological, political and socio-economic situation of the Ganga basin unless detailed distribution of rain in different seasons is considered. Analysis of seasonal trends showed that pre-monsoon (January to May) rainfall increased over 52 districts (22% of total No. of districts) but decreased over 184 (78%); monsoon (June to September) rainfall increased over 103 (44%) and decreased over 133 districts (56%); and post-monsoon (October to December) rainfall increased and decreased over 147 (62%) and 89 districts (38%) respectively.
Pre-monsoon rain, although constitutes a smaller part (about 10%) of average
Figure 3. Trend and magnitude of annual rainfall changes (mm/year). Significant trends are showed in circles.
annual rainfall, is immensely important for the area under study. Present analysis shows that maximum districts (185 districts) under the Ganga basin have registered negative trend in pre-monsoon rain mainly in northern and central zones. The maximum increase is of the order of 1.95 mm/year for Uttarkashi followed by Tehri Garhwal (1.52 mm/year), Kinnaur (0.82 mm/year), Pithoragarh (0.50 mm/year) etc., whereas the maximum decrease is in Pauri Garhwal (−1.53 mm/year) followed by Champawat (−1.47 mm/year), Nadia (−1.43 mm/year), Annupur (−1.29 mm/year) etc. Though maximum districts have negative rainfall changes, almost all of the sub-basins have such negative trend also. The upper riparian sub-basins of Farakka point like Kosi, Ghaghara, Gomti, Tons, Gandak, Sone and Ramganga have been affected by the negative rainfall trend (Figure 4).
The monsoon rainfall trend analysis shows that the maximum value of increasing trend is found in South 24 Parganas (4.36 mm/year) followed by Champawat (4.14 mm/year). Whereas, the minimum value of negative trend is found in Dehradun (−7.33 mm/year). Besides, Solan (−5.37 mm/year), Rudraprayag (−5.27 mm/year), Nainital (−5.25 mm/year), Khushinagar (−4.72 mm/year) etc., showed the high magnitude of decreasing trend. The distribution
Figure 4. Trend and magnitude of pre-monsoon rainfall changes (mm/year). Significant trends are showed in circles.
of monsoon rainfall trend shows (Figure 5) negative trend over the districts under Kosi, Ghaghara, Gomti, Tons and Sone basins.
In post-monsoon period, the highest value of increasing trend is found over Koriya district (0.88 mm/year). In opposite side, the highest value of negative trend is −0.42 mm/year over Champawat district. The result shows that the magnitude of the change is comparatively very small (Figure 6). An extensive zone of almost no trend lies in the middle of the basin running almost along the main stream. Increasing trend with small magnitude is observed in the northern districts of Uttar Pradesh, Bihar, West Bengal and Haryana and north-eastern districts of Madhya Pradesh.
4.2. Significance of Trend
To find out the significance of trends in seasonal and annual rainfall, Mann Kendall test is applied here. The result of increasing annual rainfall trend (Table 1) indicated that 12 districts have found statistically significant at ≥95% confidence level. Among the districts, Purnia (Bihar), Ratlam, Mandsaur and Ujjain (Madhya Pradesh), Tehri-Gharwal and Uttarkashi (Uttarakhand), Aligarh,
Figure 5. Trend and magnitude of monsoon rainfall changes (mm/year). Significant trends are showed in circles.
Figure 6. Trend and magnitude of post-monsoon rainfall changes (mm/year). Significant trends are showed in circles.
Gorakhpur, Goutam Budh Nagar and Moradabad (Uttar Pradesh), Kolkata and South 24 Parganas (West Bengal) have shown the significant positive change. Contrary, the significant negative trend at ≥95% confidence level have detected over 39 districts like in Lakhisarai, Madhubani, Gaya, Darbhanga, Samastipur, Rohtas, Aurangabad, (Bihar); Aallahabad, Banda, Basti, Bareily, Kaushambi, Sant Kabir Nagar, Mahoba, Sharavasti, Bareilly, Chandauli, Gazipur, Rae Barelia, Sonbhadra, Ballia, Pilbhit (U.P); Nainital, Pauri Garhwal, Rudraprayag, Bagesh- war, Almora, Dehra Dun, Udham Singh Nagar (Uttarakhand); Saharsa, Sidhi, Shahdol, (M.P.); Palamu, Gumla, Lohardaga, (Jharkhand); Solan, Simla (H.P) and Surguja, Korea, Raigarh (Chhattisgarh).
Among 236 districts, only 4 districts (Saran and Goutam Budh Nagar, Uttarkashi and Tehri Garhwal) have indicated significant at ≥95% confidence level in pre-monsoon rainfall. Table 2 is indicated, significant (≥95% confidence level) negative rainfall trend in pre-monsoon season is found over 54 districts out of which 9 districts fall in Bihar (Banka, Khagaria, Begusarai, Gaya, Rohtas, Sahar- sa, Jamui, Madhubani, Lakhisarai), 5 districts in Chhattisgarh (Bilaspur, Korea, Jashpurnagar, Surguja, Korba), 9 districts in Jharkhand (Purba Singbhum, Latehar,
Table 1. Significant values of sen estimator of slope, Q (mm/year) for annual rainfall.
Trends significant at 95% (*), 99% (**) and 99.9% (***).
Table 2. Sen estimator of slope, Q (mm/year) for pre-monsoon rainfall.
Trends significant at 95% (*), 99% (**) and 99.9% (***).
Lohardaga, Chatra, Gumla, Hazaribag, Ranchi, Garhwa, Palamau), 12 districts in Madhya Pradesh (Annupur, Dhar, Jabalpur, Narshingpur, Satna, Shivpuri, Tikamgarh, Shahdol, Dindori, Umaria, Katni, Rewa), 3 in Rajasthan (Baran, Bun- di, Sikar), 4 in Uttarakhand (Almora, Rudraprayag, Pauri Garhwal, Champa- wat), 9 in Uttar Pradesh (Gaziabad, Gonda, Mathura, Meerut, Sant Kabir Nagar, Pilbhit, Sonbhadra, Bareilly, Rae Bareilly), 2 in West Bengal (Nadia, Barddhaman) and 1 in Haryana (Faridabad).
During the monsoon season, the increasing rainfall at on 16 districts and decreasing rainfall at 35 districts are detected statistically significant at ≥95% confi- dence level (Table 3). Several districts fall in Kosi, Sone, and Ramganga subba- sins have showed significant negative trend.
It can be noted from Table 4 that 13 districts have indicated significant at ≥95% confidence level, in which 8 are positive and 5 are negatively significant in post-monsoon season.
Table 3. Sen estimator of slope, Q (mm/year) for monsoon rainfall.
Trends significant at 95% (*), 99% (**) and 99.9% (***).
Table 4. Sen estimator of slope, Q (mm/year) for post-monsoon rainfall.
Trends significant at 95% (*) and 99% (**).
5. Conclusions
The present study on district wise monthly rainfall data on entire Ganga basin from 1901 to 2000 using Mann-Kendall and Sen’s slope estimator methods aimed to have clear understanding about the rainfall trends over the basin and its sub-basins. More than half of the districts of the Ganga basin that comes under Kosi, Ghaghara, Gandak, Gomti, Tons, Sone have shown a decreasing trend in annual rainfall.
In seasonal trend analysis, pre-monsoon (Jan.-May) rainfall decreases over major part of Ganga basin. 78% of the total districts showed the decreasing trend with significance of 54 districts. This seasonal rainfall decreased over the districts covered by the sub-basins like Kosi, Gandak, Ghaghara, Gomti, Tons, Sone and Ramganga. Here, the maximum decrease is −1.53 mm/year. The districts over Kosi, Ghaghara, Tons, Gomti, Sone basins showed decreasing rainfall in mon- soon period. Besides, the distribution of post-monsoon rainfall trend indicates almost neutral trend (−0.1 mm/year to +0.1 mm/year) in maximum districts of the total basin.
Significance testing showed that the pre-monsoon rainfall had significant negative changes over the maximum districts of the basin in comparison to the other seasons. Most of districts falling in Kosi, Sone, Ramganga, Gandak, Ghag- hara and Tons have registered as significant negative rainfall change. Though 35 districts have a negative trend in Monsoon season, only 5 districts are detected significantly for post-monsoon period. The annual and monsoon rainfall indicated the same direction of trend for the maximum of the districts over the Gan- ga basin.
Therefore, the study indicates the large spatial and temporal variability in the annual and seasonal rainfall trends over the Ganga basin and its sub-basin areas. The majority of the districts over Kosi, Gandak and Sone sub-basins indicated the significant negative trend for annual, pre-monsoon and even in monsoon season. These sub-basins have significantly played their major role in the seasonal fluctuation of water flow in the river Ganga. So there need some districts’ and sub-basins’ wise strategies to deal with this climate change condition.
Acknowledgements
The author would like to thank Prof. Ramkrishna Maiti for his cooperation and the Indian Meteorological Department (IMD), Pune, India for providing the rainfall data.
Cite this paper
Bera, S. (2017) Trend Analysis of Rainfall in Ganga Basin, India during 1901-2000. American Journal of Climate Change, 6, 116-131. https://doi.org/10.4236/ajcc.2017.61007
References
- 1. IPCC (1995) Climate Change 1995: Economic and Social Dimensions of Climate Change. Contribution of Working Group III to the Second Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge.
- 2. Milly, P.C.D., Dunne, K.A. and Vecchia, A.V. (2005) Global Pattern of Trends in Stream Flow and Water Availability in a Changing Climate. Nature, 438, 347-350.
https://doi.org/10.1038/nature04312 - 3. Seckler, D., Amarasinghe, U., Molden, D.J., de Silva, R. and Barker, R. (1998) World Water Demand and Supply, 1990 to 2025: Scenarios and Issues. Research Report 19, International Water Management Institute, Colombo.
- 4. Vorosmarty, C., Green, P., Salisbury, J. and Lammers, R.B. (2000) Global Water Resources: Vulnerability from Climate Change and Population Growth. Science, 289, 284-288.
https://doi.org/10.1126/science.289.5477.284 - 5. Rijsberman, F.R. (2006) Water Scarcity: Fact or Fiction? Agricultural Water Management, 80, 5-22.
https://doi.org/10.1016/j.agwat.2005.07.001 - 6. Basu, M. and Shaw, R. (2013) Water Policy, Climate Change and Adaptation in South Asia. International Journal of Environmental Studies, 70, 175-191.
https://doi.org/10.1080/00207233.2013.781736 - 7. Jain, S.K. and Kumar, V. (2012) Trend Analysis of Rainfall and Temperature Data for India. Current Science, 102, 37-49.
- 8. Zhang, Q., Xu, C.Y., Zhang, Z.X., Chen, Y.Q. and Liu, C.L. (2008) Spatial and Temporal Variability of Extreme Precipitation during 1960-2005 in the Yangtze River Basin and Possible Association with Large Scale Circulation. Journal of Hydrology, 353, 215-227.
https://doi.org/10.1016/j.jhydrol.2007.11.023 - 9. Yang, T., Zhang, Q., Chen, Y.D., Tao, X., Xu, C.Y. and Chen, X. (2008) A Spatial Assessment of Hydrologic Alteration Caused by Dam Construction in the Middle and Lower Yellow River, China. Hydrological Processes, 22, 3829-3843.
https://doi.org/10.1002/hyp.6993 - 10. Gosain, A.K., Rao, S. and Basuray, D. (2006) Climate Change Impact Assessment on Hydrology of Indian River Basins. Current Science, 90, 346-353.
- 11. Kumar, V., Jain, S.K. and Singh, Y. (2010) Analysis of Long-Term Rainfall Trends in India. Hydrological Sciences Journal, 55, 484-496.
https://doi.org/10.1080/02626667.2010.481373 - 12. Mooley, D.A. and Parthasarthy, B. (1984) Fluctuations of All India Summer Monsoon Rainfall during 1871-1978. Climatic Change, 6, 287-301.
https://doi.org/10.1007/BF00142477 - 13. Sarker, R.P. and Thapliyal, V. (1988) Climate Change and Variability. Mausam, 39, 127-138.
- 14. Thapliyal, V. and Kulshreshtha, S.M. (1991) Climate Changes and Trends over India. Mausam, 42, 333-338.
- 15. Lal, M. (2001) Climatic Change—Implications for India’s Water Resources. Journal of Indian Water Resources Society, 21, 101-119.
- 16. Koteswaram, P. and Alvi, S.M.A. (1969) Trends and Periodicities in Rainfall at West Coast Stations in India. Current Science, 38, 229-231.
- 17. Jagannathan, P. and Parthasarathy, B. (1973) Trends and Periodicities of Rainfall over India. Monthly Weather Review, 101, 371-375.
https://doi.org/10.1175/1520-0493(1973)101<0371:TAPORO>2.3.CO;2 - 18. Chaudhary, A. and Abhyankar, V.P. (1979) Does Precipitation Pattern Foretell Gujarat Climate Becoming Arid. Mausam, 30, 85-90.
- 19. Kumar, V., Singh, P. and Jain, S.K. (2005) Rainfall Trends over Himachal Pradesh, Western Himalaya, India. Conference on Development of Hydro Power Projects— A Prospective Challenge, Shimla, 20-22 April 2005.
- 20. Dash, S.K., Jenamani, R.K., Kalsi, S.R. and Panda, S.K. (2007) Some Evidence of Climate Change in Twentieth-Century India. Climatic Change, 85, 299-321.
https://doi.org/10.1007/s10584-007-9305-9 - 21. Kumar, V. and Jain, S.K. (2010) Trends in Seasonal and Annual Rainfall and Rainy Days in Kashmir Valley in the Last Century. Quality International, 212, 64-69.
https://doi.org/10.1016/j.quaint.2009.08.006 - 22. Sinha Ray, K.C. and Srivastava, A.K. (1999) Is There Any Change in Extreme Events Like Droughts and Heavy Rainfall? INTROPMET-97, IIT New Delhi, 2-5 December 1997.
- 23. Bhutiyani, M.R., Kaleb, V.S. and Pawar, N.J. (2010) Climate Change and the Precipitation Variations in the Northwestern Himalaya: 1866-2006. International Journal of Climatology, 30, 535-548.
- 24. Basistha, A., Arya, D.S. and Goel, N.K. (2009) Analysis of Historical Changes in Rainfall in the Indian Himalayas. International Journal of Climatology, 29, 555-572.
https://doi.org/10.1002/joc.1706 - 25. Singh, P., Kumar, V., Thomas, T. and Arora, M. (2007) Changes in Rainfall and Relative Humidity in River Basins in Northwest and Central India. Hydrological Processes, 22, 2982-2992.
https://doi.org/10.1002/hyp.6871 - 26. Parthasarathy, B. and Dhar, O.N. (1976) A Study of Trends and Periodicities in the Seasonal and Annual Rainfall of India. Indian Journal of Meteorology, Hydrology and Geophysics, 27, 23-28.
- 27. Singh, N. and Sontakke, N.A. (2002) On Climatic Fluctuations and Environmental Changes of the Indo-Gangetic Plains, India. Climate Change, 52, 287-313.
https://doi.org/10.1023/A:1013772505484 - 28. Ranade, A., Singh, N., Singh, H.N. and Sontakke, N.A. (2008) On Variability of Hydrological Wet Season, Seasonal Rainfall and Rainwater Potential of the River Basins of India (1813-2006). Journal of Hydrological Research and Development, 23, 79-108.
- 29. Mirza, M.Q., Warrick, R.A., Ericksen, N.J. and Kenny, G.J. (1998) Trends and Persistence in Precipitation in the Ganges, Brahmaputra and Meghna River Basins. Hydrological Sciences Journal, 43, 845-858.
https://doi.org/10.1080/02626669809492182 - 30. CWC and NRSC (2014) Ganga Basin Report. Ministry of Water Resource, Version 2.
- 31. Mann, H.B. (1945) Nonparametric Tests against Trend. Econometrica, 13, 245-259.
https://doi.org/10.2307/1907187 - 32. Kendall, M.G. (1955) Rank Correlation Methods. Charles Griffin, London.
- 33. Sen, P.K. (1968) Estimates of the Regression Coefficient Based on Kendall’s Tau. Journal of the American Statistical Association, 63, 1379-1389.
https://doi.org/10.1080/01621459.1968.10480934 - 34. Hirsch, R.M., Slack, J.R. and Smith, R.A. (1982) Techniques of Trend Analysis for Monthly Water Quality Data. Water Resources Research, 18, 107-121.
https://doi.org/10.1029/WR018i001p00107 - 35. Hirsch, R.M. and Slack, J.R. (1984) A Nonparametric Trend Test for Seasonal Data with Serial Dependence. Water Resources Research, 20, 727-732.
https://doi.org/10.1029/WR020i006p00727 - 36. Lettenmaier, D.P., Wood, E.F. and Wallis, J.R. (1994) Hydro-Climatological Trends in the Continental United States 1948-1988. Journal of Climate, 7, 586-607.
https://doi.org/10.1175/1520-0442(1994)007<0586:HCTITC>2.0.CO;2 - 37. Lins, H.F. and Slack, J.R. (1999) Streamflow Trends in the United States. Geophysical Research Letters, 26, 227-230.
https://doi.org/10.1029/1998GL900291 - 38. Douglas, E.M., Niyogi, D. and Frolking, S. (2006) Changes in Moisture and Energy Fluxes Due to Agricultural Land Use and Irrigation in the Indian Monsoon Belt. Geophysical Research Letters, 33, 1-5.
https://doi.org/10.1029/2006GL026550 - 39. Burn, D.H. and Elnur, M.A.H. (2002) Detection of Hydrologic Trends and Variability. Journal of Hydrology, 255, 107-122.
https://doi.org/10.1016/S0022-1694(01)00514-5 - 40. Yue, S., Pilon, P. and Cavadias, G. (2002) Power of the Mann-Kendall and Spearman’s Rho Test for Detecting Monotonic Trends in Hydrological Series. Journal of Hydrology, 259, 254-271.
https://doi.org/10.1016/S0022-1694(01)00594-7 - 41. Yue, S. and Pilon, P. (2004) A Comparison of the Power of the T-Test, Mann-Kendall and Bootstrap Tests for Trend Detection. Hydrological Sciences Journal, 49, 21-37.
https://doi.org/10.1623/hysj.49.1.21.53996 - 42. Burn, D.H., Cunderlink, J.M. and Pietroniro, A. (2004) Hydrological Trends and Variability in the Liard River Basin. Hydrological Sciences Journal, 49, 53-67.
https://doi.org/10.1623/hysj.49.1.53.53994 - 43. Zhang, Q., Jiang, T., Gemmer, M. and Becker, S. (2005) Precipitation, Temperature and Runoff Analysis from 1995-2002 in the Yangtze Basin, China. Hydrological Sciences Journal, 50, 65-80.
- 44. Aziz, O.I.A. and Burn, D.H. (2006) Trends and Variability in the Hydrological Regime of the Mackenzie River Basin. Journal of Hydrology, 319, 282-294.
https://doi.org/10.1016/j.jhydrol.2005.06.039 - 45. Chen, H., Guo, S., Xu, C.Y. and Singh, V.P. (2007) Historical Temporal Trends of Hydro-Climatic Variables and Runoff Response to Climate Variability and Their Relevance in Water Resource Management in the Hanjiang Basin. Journal of Hydrology, 344, 171-184.
https://doi.org/10.1016/j.jhydrol.2007.06.034 - 46. Gan, T.Y. (1998) Hydroclimatic Trends and Possible Climatic Warming in the Canadian Prairies. Water Resources Research, 34, 3009-3015.
https://doi.org/10.1029/98WR01265 - 47. Hipel, K.W. and McLeod, A.I. (1994) Time Series Modelling of Water Resources and Environmental Systems. Elsevier, Amsterdam.
- 48. Mitchell, J.M., Dzerdzeevskii, B., Flohn, H., Hofmeyr, W.L., Lamb, H.H., Rao, K.N. and Wallen, C.C. (1966) Climate Change. WMO Technical Note No. 79, World Meteorological Organization.
- 49. Zhang, J.Y., Huang, G.R., Wang, Z.J. and Chen, Q.X. (2011) Analysis of Temporal and Spatial Variation of Rainfall in Guangzhou City at Recent Years. Water Resources and Power, 29, 5.
- 50. Eris, E. and Agiralioglu, N. (2012) Homogeneity and Trend Analysis of Hydrometeotological Data of the Eastern Black Sea Region, Turkey. Journal of Water Resource and Protection, 4, 99-105.
https://doi.org/10.4236/jwarp.2012.42012 - 51. Jaagus, J. (2006) Trends in Sea Ice Conditions in the Baltic Sea near the Estonia Coast during the Period 1949/1950-2003/2004 and Their Relationships to LargeScale Atmospheric Circulation. Boreal Environment Research, 11, 169-183.
- 52. Tabari, H. and Talaee, P.H. (2011) Temporal Variability of Precipitation over Iran: 1966-2005. Journal of Hydrology, 396, 313-320.
https://doi.org/10.1016/j.jhydrol.2010.11.034 - 53. Salmi, T., Maatta, A., Anttila, P., Ruoho-Airola, T. and Amnell, T. (2002) Detecting Trends of Annual Values of Atmospheric Pollutants by the Mann-Kendall Test and Sen’s Slope Estimates—The Excel Template Application MAKESENS. Ilmatieteen laitos, Meteorologiska Institutet, Finnish Meteorological Institute, 1-35.








