Received 7 September 2014; revised 12 October 2014; accepted 30 October 2014

ABSTRACT

The aim of this work is to introduce some weak forms of continuity in bitopological spaces. Then we use these new forms of weak continuity to give many decompositions of 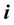-continuity and pairwise continuity.

Keywords:

Relative Continuity, Decompositions of Continuity, Bitopological Spaces, 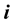-Continuity, Pairwise Continuity

1. Introduction

The concept of bitopological spaces has been introduced by Kelly [1] . Functions and continuous functions stand among the most important notions in mathematical science. Many different weak forms of continuity in bitopological spaces have been introduced in the literature. For instance, we have pairwise almost and pairwise weakly continuity [2] , pairwise semi-continuity [3] , pairwise pre continuity [4] , pairwise ρ-continuity [5] , pairwise α-continuity [5] and many others, see ([6] [7] ). N. Levine, in [8] introduced decomposition of continuity in topological spaces. In 2004 [9] Tong introduced twenty weak forms of continuity in topological spaces. In this paper, we generalize the results obtained by Tong to the setting of bitopological spaces.

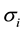Throughout this paper and (or briefly, X and) always mean bitopological spaces on which no separation axioms are assumed unless explicitly stated. Let be a subset of X, by (resp.) we denote the closure (resp. interior) of A with respect to (or) and 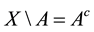will denote the complement of. Here and.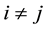

2. Preliminaries

We recall some known definitions

Definition 1 ([3] ) A subset 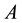of a bitopological space 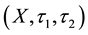is called -semi open if there is an - open set U in X such that.

Definition 2 ([3] ) A function is called -semi continuous if is - semi open in X for each -open set V of Y.

Definition 3 ([2] ) A function is called -weakly (resp. -almost) continuous if for each point and each -open set V of Y containing, there exists an -open set U of X con- taining such that (resp..

Definition 4 ([5] ) A subset A of a bitopological space is called ij-α-open if

.

Definition 5 ([5] ) A function is called -continuous if is - open in X for each i-open set V of Y.

Definition 6 ([4] ) A subset A of a bitopological space is called ij-pre open if.

Definition 7 ([4] ) A function is called pre continuous if is -pre open in X for each i-open set V of Y.

The relations of the above weak forms of continuity are as follows:

[Diagram 1]

3. Classification of ij-Weak Continuity

Lemma 1 For a subset of a bitopological space, we have

1);

2);

3);

4).

Proof (1) and (2) are obvious. (3) Since, then. Therefore,. On the other hand,

, then (4) Similar to (3).

Proposition 1 Let be a function. Then

1) is -continuous if and only if for each -open set in;

2) is -pre continuous if and only if for each -open set in;

3) f is -continuous if and only if for each -open set in.

It is known [2] that a function is -weakly continuous if and only if for each

-open set of,. From this we define the following.

Definition 8 Let be a function. Then

1) is -pre weakly continuous if and only if for each -open set V in Y;

2) is -weakly continuous if and only if for each - open set V in Y.

It is well known [2] that is -almost continuous if and only if

. From this we define the following group of definitions.

Definition 9 Let be a function. Then

1) is -pre-almost continuous if and only if for each - open set V in Y;

2) f is ij-α-almost continuous if and only if for each i-

mopen set V in Y.

Lemma 2 A function is -semi continuous if and only if for each -open set

of,.

Proof Let be an -semi continuous function. Then is -semi open in for each -open set of. Since is a -semi open set in, there exist an -open set such that.

Since we have. Hence, , and therefore,.

Conversely, assume that for each -open set. Now

. Put. Then there exists an -open set such that. It means is -semi open in for each -open set

of. Hence, is an -semi continuous function.

In view of the above lemma we define the following:

Definition 10 Let be a function. Then

1) is -weak semi continuous if and only if for each -open set V in Y;

2) is -almost semi continuous if and only if for each - open set V in Y.

Definition 11 Let be a function. Then:

1) is -pre semi continuous if and only if for each -open set V

in Y;

2) is -pre weak semi continuous if and only if for each i- open set V in Y;

3) is -pre almost semi continuous if and only if for each -open set V in Y.

The following diagram gives the relations between all the weak forms of continuity

[Diagram 2]

Proof (Proof of some relations in Diagram 2).

1) -weak continuity -weak continuity

Let be an -weak continuous function. Then

for each -open set of. Since,

. Hence, is -weak continuous;

2) -weak continuity -pre weak continuity.

Let. This implies hence. Assume is -weak continuous. Then for each -open set of.

Since,.

Hence, f is ij-pre weak continuous.

We could use similar ways to prove other relations in Diagram 2.

4. Classification of Relative Continuity

Let be a function. Then is -continuous if and only if is an -open set in for each -open set in. If we change the requirement on from being -open in to being -open in a subspace, then we can obtain many new weak forms of continuity.

Definition 12 Let be a function. Then

1) is -continuous if and only if is an -open set in the subspace for each -open set in;

2) f is ij-pre continuous if and only if is an -open set in the subspace for each i- open set in;

3) f is -continuous if and only if is an -open set in the subspace for each -open set in.

Proposition 2 Any function f is an i^#-continuous function.

Proof Let be a function. For each i-open set V in Y we have

, then is an i-open set in the subspace. Hence, is -continuous function.

Definition 13 Let be a function. Then

1) f is -weak continuous if and only if is an i-open set in the subspace for each i-open set V in Y;

2) f is ij-pre weak continuous if and only if is an i-open set in the subspace for each -open set V in Y;

3) is -weak continuous if and only if is an i-open set in the subspace

for each -open set V in Y.

Definition 14 Let be a function. Then

1) f is -almost^#continuous if and only if is an i-open set in the subspace for each -open set in;

2) is -pre almost continuous if and only if is an -open set in the subspace

for each -open set in;

3) is -almost continuous if and only if is an -open set in the subspace

for each -open set in.

Definition 15 Let be a function. Then

1) is a -pre-semi continuous if and only if is an -open set in the subspace

for each -open set in;

2) is a -pre weak semi continuous if and only if is an -open set in the subspace

for each -open set in;

3) is a -pre-almost semi continuous if and only if is an -open set in the subspace

for each -open set in.

Lemma 3 Let and be a bitopological space. Then for.

Proof Let. Then there exists an i-open set V in the subspace such that. We

can write, where is an -open set in. Therefore,. Hence, is an -open set in the subspace Z.

Conversely, assume that. Then there exists an -open in such that. Since

, where is an -open set in the subspace. Hence.

Lemma 4 If and is an -open set in then is also -open relative to for.

Proof The proof follows immediately from where is an -open in.

The following diagram gives the relations between all the weak forms of continuity

[Diagram 3]

Proof (Proof of some relations in Diagram 2).

1) -pre weak semi continuity -pre almost semi weak continuity;

Let be an -pre weak semi^# continuous. Then is an i-open set in the

subspace. Now

. By Lemmas 4.6 and 4.7, we

obtain is an -open in the subspace. Hence,

is pre almost semi continuous.

2) -pre almost semi continuity -pre semi continuity;

Let be -pre almost semi continuous. Then is an -open set in. Since,

. Therefore,

. By Lemmas 4.6 and 4.7, we obtain

is an i-open in the subspace. Hence,

is -pre semi^# continuous.

3) -pre^#continuity pre semi^# continuity;

Let be -pre continuous function. Then is -open set in the

subspace. Since, then by using Lemma 4.6

and Lemma 4.7, we obtain is an -open in the subspace. So

is -pre semi^# continuous.

4) -pre almost^# continuity -pre^# continuity;

Let be -pre almost^# continuous function. Then is -open set in. Since,. So

, by using Lemmas 4.6 and 4.7, we obtain is -open

in the subspace. Then is an -pre continuous.

5) -pre almost^#continuity -pre semi^#continuity;

Let be pre almost continuous function. Then is -open set in

. Since, then, therefore. This implies, so

. Then

. By using Lemmas 4.6 and 4.7, we obtain is -open in the subspace. So is an -pre semi continuous.

We could also use the similar ways to prove other relations in Diagram 3.

The following examples show that the reverse implications of Diagram 3 is not true.

Example 1 Let, , , , and

Define a map by, ,

. The map is 12-pre weak continuous but not 12--weak continuous because

which is not 1-open in the subspace.

Example 2 Let, , , , and

. Define a map by,

Then the map f is 12-pre weak^# continuous but not 12-pre weak semi^# continuous, because

which is not 1-open set in the subspace.

Example 3 Let, , ,

and Define a map by, ,

and. The map f is 21-pre almost^# continuous but not 21-pre almost semi^# continuous because

is not 2-open in the subspace.

5. Decompositions of i-Continuity and Pairwise Continuity

For a property of a function, we say that is pairwise if is 12- and 21-. For example, is called pairwise weakly continuous if it is 12-weakly continuous and 21-weakly continuous. is pairwise continuous if and are continuous.

In this section we will give eight decompositions of -continuity and pairwaise continuity.

Lemma 5 Let be a mapping with and let be another

mapping with for each -open set of. Let be a function such that for each - open set V in Y,

1);

2) There is an -open set G of X such that.

Then is -continuous.

Proof Since, then. Therefore,

. We have

proved that is an -open set and hence is -continuous.

Now we turn to the decomposition of -continuity and pairwise continuity.

Theorem 1 Let be a function. Then each of the following conditions implies that is -continuous.

1) is -pre continuous and -pre-continuous;

2) is -continuous and -continuous;

3) is -weakly continuous and -weak-continuous;

4) is -pre weakly continuous and -pre weak-continuous;

5) is -weakly continuous and -weak-continuous;

6) is -almost continuous and -almost-continuous;

7) is -it pre-almost continuous and -pre-almost-continuous;

8) is -almost continuous and -almost-continuous.

Proof

1) Since f is ij-pre continuous,. Since f is ij-pre^#-continuous, , where O is i-open set in X. By Lemma 5.1, f is continuous, where

and;

2) Since is -continuous,. Since is -continuous,

, where is -open set in. By Lemma 5.1, is continuous, where

and;

3) Since is -weakly continuous,. Since is -weak-continuous,

, where is -open set in. By Lemma 5.1, is continuous, where and;

4) Since is -pre weakly continuous,. Since is -pre weak-

continuous, where is -open set in. By Lemma 5.1, is con- tinuous, where and;

5) Since is -weakly continuous,. Since is -

weak^#-continuous, , where is -open set in. By Lemma 5.1, is continuous, where and;

6) Since is -almost continuous,. Since is -almost- continuous, , where is -open set in. By Lemma 5.1, is

continuous, where and;

7) Since is -pre-almost continuous,. Since is -pre- almost-continuous, , where is -open set in. By Lemma

5.1, is continuous, where and;

8) Since is -almost continuous,. Since is ij-α-almost-continuous, so, where is -open set in X.

By Lemma 5.1, is continuous, where and.

Corollary 1 Let be a function. Then each of the following conditions implies that is pairwise continuous.

1) is pairwise pre continuous and pairwise pre-continuous;

2) is pairwise -continuous and pairwise -continuous;

3) is pairwise weakly continuous and pairwise weakly-continuous;

4) is pairwise pre weakly continuous and pairwise pre weak-continuous;

5) is pairwise -weakly continuous and pairwise -weak-continuous;

6) is pairwise almost continuous and pairwise almost-continuous;

7) is pairwise pre-almost continuous and pairwise pre-almost-continuous;

8) is pairwise -almost continuous and pairwise -almost-continuous.

Proof The proof follows immediately from Theorem 5.3.

Acknowledgements

This work was funded by the Deanship of Scientific Research (DSR), king Abdulaziz University, Jeddah, under grat No. (363-006-D1433). The author, therefore, acknowledge with thanks DSR technical and financial support.

References