Open Journal of Fluid Dynamics
Vol.3 No.3(2013), Article ID:37049,7 pages DOI:10.4236/ojfd.2013.33025
Numerical Hydrodynamic of Multihull Tunnel Vessel
Department of Ocean Engineering, Amirkabir University of Technology, Tehran, Iran
Email: morteza_ghassab@yahoo.com, gasemi@aut.ac.ir
Copyright © 2013 Morteza Ghassabzadeh, Hassan Ghassemi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 26, 2013; revised July 25, 2013; accepted August 10, 2013
Keywords: Multi-Hull; Tunnel Vessel; Hydrodynamic Simulations; Finite Volume Method
ABSTRACT
The research described in this paper was carried out to predict the numerical hydrodynamic of multihull tunnel vessel at various speeds. The hull form of vessel is fairly generated by the tunnel hull form generator (THFG) code using the Non Uniform Rational B-Spline (NURBS) method. Then, the hydrodynamic simulation of high speed vessel is carried out based on finite volume discretization method using volume of fluid (VOF) model to consider free surface between water and air phases around the vessel. A dynamic mesh restructuring method is applied for grid generation regarding to the heave and pitch motions of vessel in each time step. Calculated drag and trim angles at various speeds are in good agreement with experimental data. More results are carried out at the speed 15 knots to understand the convergency of the pitch and heave motions.
1. Introduction
Tunnel vessels are especial types of the advanced planing vessels that have complexity hull forms. Tunnel form, the main part of this hull form, significantly affects hydrodynamic behavior. Access to an automated quickly precise method for generating this hull form is an essential task based on the least input control parameters, but till now a few researches have been studied on these hull form design.
Some researchers have worked on the generation of different simple hull forms and most of them are based on Spline curves. For instance, Hinatsu [1] and Sariouz [2] developed a method to generate the surface of vessel hull using the Fourier series and non-uniform. The boundary curves such as centerline, chins and sheer lines of a vessel were modeled by B-Spline curves [3]. The parametric geometry generation in curved bilge fishing vessels was proposed based on the non-uniform B-Spline surfaces by Perez & Clemente [4]. Ventura et al. [5] developed a methodology for the computation of the intersect on of parametric surfaces using NURBS. Calkins et al. [6] focused on the mono-hull and catamaran planing vessels hull form design. They developed a computational automated method to create the hull form of a planing vessel using a mathematical procedure in the conceptual design step. Recently, authors developed a new software code, namely THFG, to generate automatically the hull form of planing tunnel vessel by various mathematical functions [7].
The existing techniques for analysis of high-speed planing hulls are classified into two major categories, i.e. analytical-experimental and numerical techniques. The numerical techniques are further divided into methods for boundary value problems such as boundary element method (BEM) and domain-dependent problems such as Finite volume method (FVM).
Hydrodynamic behavior of tunnel vessels is similar to general planing vessel and most changes are happened due to the increasing speed. The physical conditions (draft and trim) of the vessel which are significantly changing from displacement condition to planing condition could be significantly high.
So far, some researchers carried out both experimental and numerical work in this field. Most works have been done for the planing hull by Savitsky. His studies included the prismatic high speed vessel via definition of systematic model tests focusing mainly on the effects of design parameters, such as location of the centre of gravity, forward speed, and other geometric parameters of the planing hull (Savitsky & Brown [8], Savitsky et al. [9], Savitsky & Morabito [10]).
Numerical methods such as boundary element method (BEM) and finite volume applying a volume of fluid (VOF) model have been employed to determine the planing vessel hydrodynamic behavior. Ghassemi and Ghiasi [11] developed a combined method consisting of a potential-based boundary element method (BEM) for the induced pressure resistance, the boundary layer theory for the frictional resistance and practical method for the spray resistance to determine the hydrodynamic characteristics of planing vessels in calm water. As a complementary research, Ghassemi & Yu-min [12] extended this method to determine hydrodynamic forces on a planing hull in steady motion.
The VOF model is a surface-tracking technique applied to a fixed Eulerian mesh to study a multiphase problem. It is designed for two or more immiscible fluids where the position of the interface between the fluids is of interest [13]. Since the analysis of air-water interface changes is essential to investigate the hydrodynamics behavior of planing vessels, the VOF model seems to be an adequate method to simulate planing vessels. Yumin et al. [14] presented a new CFD method based on Reynolds-Averaged Navier-Stokes (RANS) equations and volume of fluid (VOF) method and the six-degrees-offreedom equations were applied to calculate hydrodynamic forces of planing vessels.
The hydrodynamic effect of propeller tunnels in high speed vessel was studied by way of modified resistance and pressure distribution, using both numerically CFD method and experimentally geometric scaled models [15]. Width and depth parameters of channel for numerical or experimental analyses of high speed hull and hydrofoil vessels have most effect on resistance test results studied in a Froude number range of 0.3 - 1.0 using experimental results and theoretical work [16,17].
Most of researches have been studied on the simple hull form, not complex multi-hull tunnel vessels because of their complicated nature. Complementary to our previous work, an innovative quick precise method is proposed to generate the tunnel hull form automatically using the least control and hull form adjustment input parameters. Then, hydrodynamic behavior of tunnel vessel analyzed via finite volume method by using VOF model. A four-tunnel vessels model is tested experimentally so that the numerical results are compared by towing test resistance results. Finally, a full scale tunnel vessel is studied completely and various numerical results are presented.
2. Modeling and Simulation Methods
2.1. Geometry Modeling Method
The hull form geometry is generated using our developed new mathematical procedure to automatically generation of the planing tunnel vessels hull form. The THFG code is an efficient and applicable method in complex bodies like multihull shape to produce the hull geometrical models [7].
In the THFG code, minimum number of input control parameters has been used to design the geometry. At first, four longitudinal guidelines functions are defined by polynomial functions and NURBS curves. Next, using specified key points, the sections’ curves are generated. Then, the fair transverse sections, the fair surfaces and the solid models could be generated consecutively. In Figure 1, the steps of hull form generation are shown.

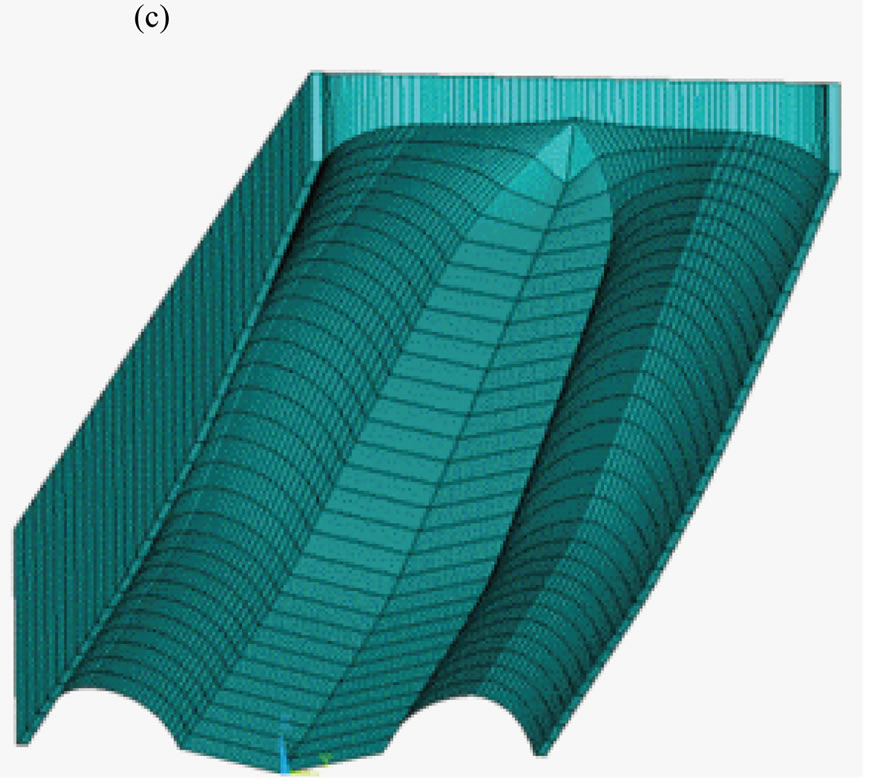
Figure 1. Generation of the hull form by THFG code. (a) Generate point with guidelines; (b) Generate curve of sections; (c) Generate hull form.
In THFG code, to produce guidelines and tunnel sections, the third order NURBS curves are used. The relations applied for this method are expressed as follows [18]:
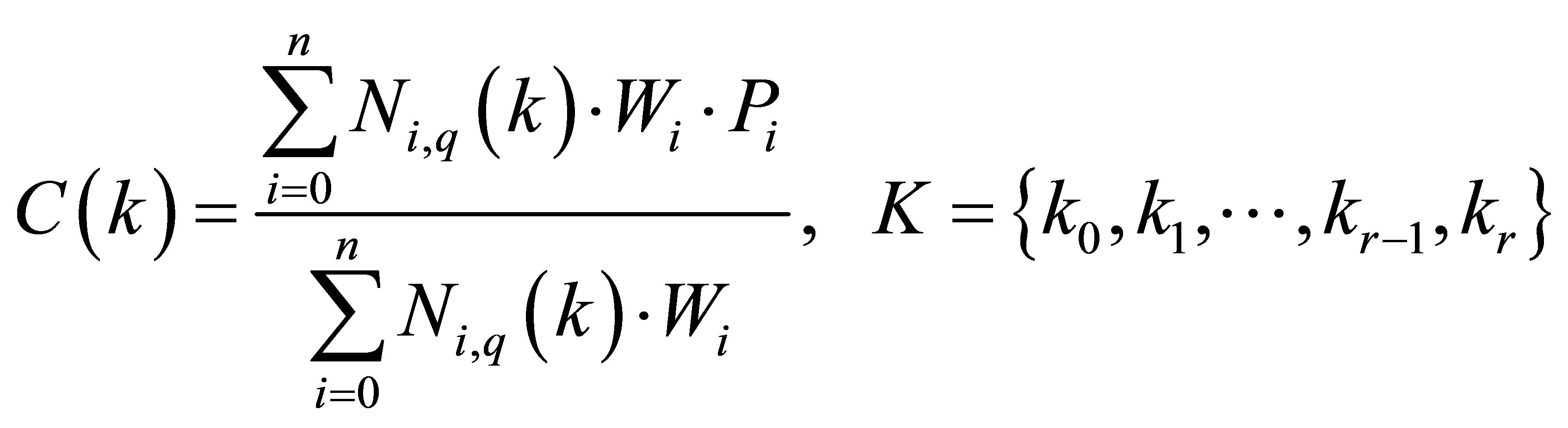 (1)
(1)
In Equation (1), q is assumed to 3; n + 1 is 6 for guidelines and 3 for sections in each part of tunnel; r + 1 is fixed to 10 for guidelines and 8 for sections in each part of the tunnel. The knot vector values (ki), the control points (Pi) and their weights (Wi) are assumed as optional values for each guideline or section curve of the tunnel. The shape of the curve can be properly adjusted by controlling these parameters.
To control the shape, the number of control points is fixed to 6 and also uniform knot vectors are used. The knot vectors values of guidelines and sections are shown in Equation (2).
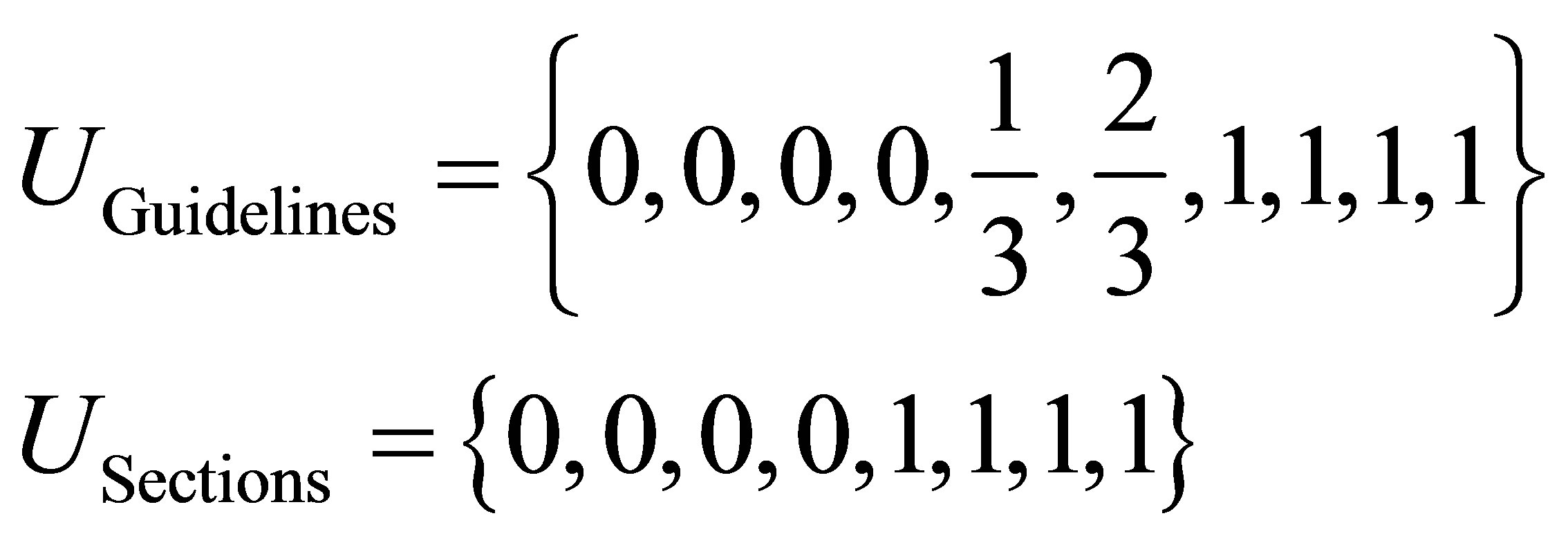 (2)
(2)
2.2. Calculation Domain
In order to reduce computations and because of the symmetry existence in the analyses domain, half of the body vessel is considered in the multiphase (air and water) domain. The dimensions of computational domain and under studied vessel position inside it are shown in Figure 2. To prevent from reaching the wave motion of vessel to outflow boundary, the outflow boundary is adjusted too far (72.5 m) from behind the vessel. Furthermore, a distance of 40 meters between the vessel and
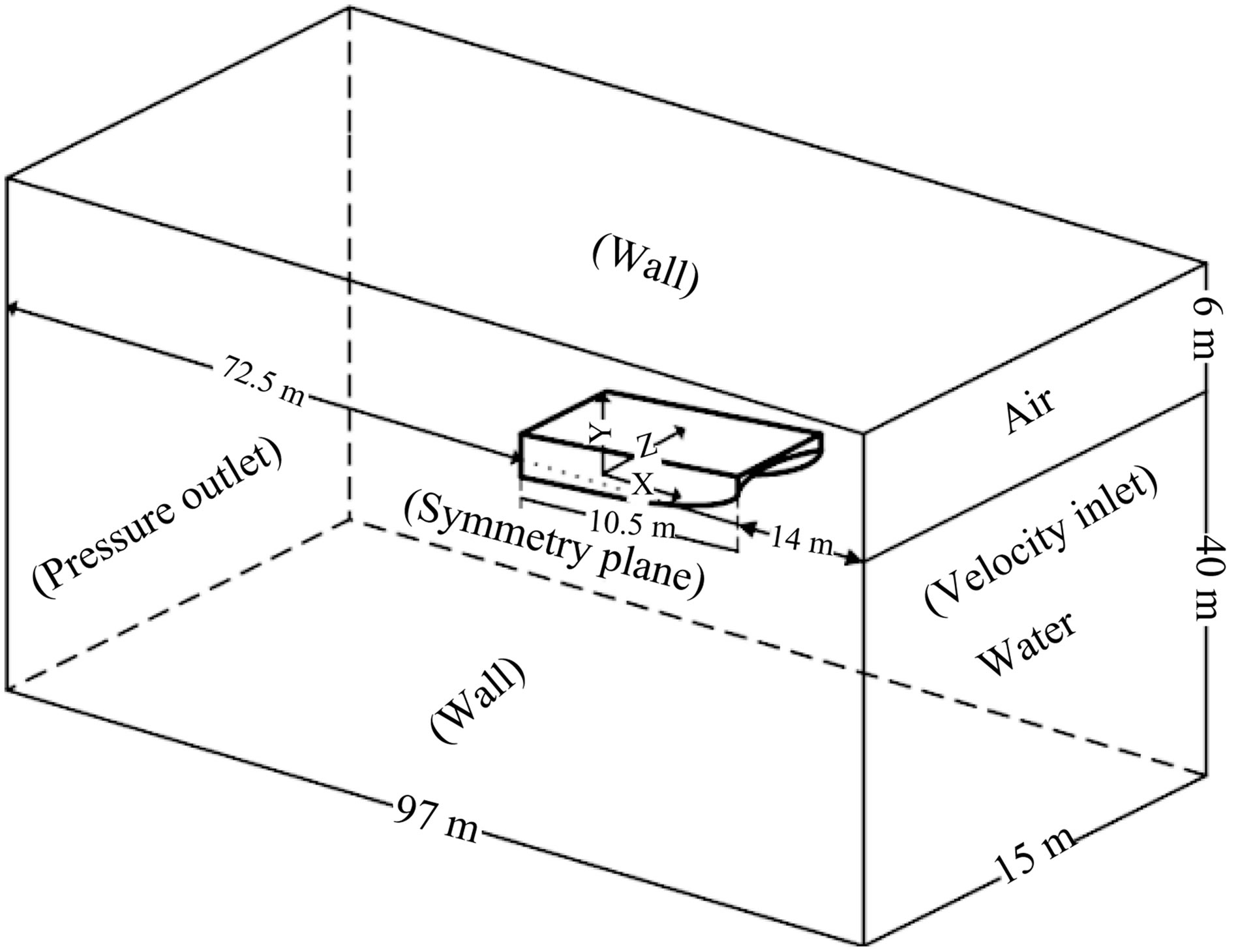
Figure 2. Computational domain of the vessel in real data.
bottom of domain is because of observance of deep water condition. The created sub domain containing vessel inside it at initial position is divided to two parts by water surface. For suitable simulation to make a precise calculation of free surface and around the vessel, the calculation domain is divided by air-water interface to two separate parts and also the sub domain is divided to two boxes; a small box around vessel and another out of that.
The constructed vessel by THFG code and divided domain are applied to the commercial grid generation tool, GAMBIT 2.3 (Fluent Inc.), to generate the desirable calculation control volumes structure. To divide the calculation space into adequate discrete control volumes, threedimensional tetrahedral computational cells were used. In addition, triangular elements were used for surface boundaries, including: the vessel, walls, interface, inlet and outlet of the domain.
During solving procedure, a dynamic mesh restructuring method is applied regarding to the heave and pitch motion of vessel. The grid section around body near the free surface between air and water is refined to achieve a desirable meshing structure for interface zone to remain similarly in all time steps. This is carried out while the outer section of grid away from body is unchanged all the time.
2.3. Hydrodynamic Numerical Method
In present work, to solve the hydrodynamic behavior of high speed vessel, the longitudinal position of vessel is fixed then air and water pass through the vessel body with constant speed. This process is similar to cavitation or wind tunnel test processes.
The local and global coordinate systems are fixed at the vessel gravity center and in the first position of gravity center before motion, respectively. The degrees of freedom of vessel in this method are pitch and heave motions as shown in Figure 3. In this method, draft and trim angle of vessels at a constant speed are adjusted while balancing the lift force with weight.
The procedure algorithm of numerical method for hydrodynamic analyses of high speed vessel is shown in Figure 4. The termination criteria of method are determined as when the variation of vessel movement diminishes to zero or velocity vector approaches zero in consecutive steps. So, the vessel is achieved a balanced state in which sum of forces and moments become zero.
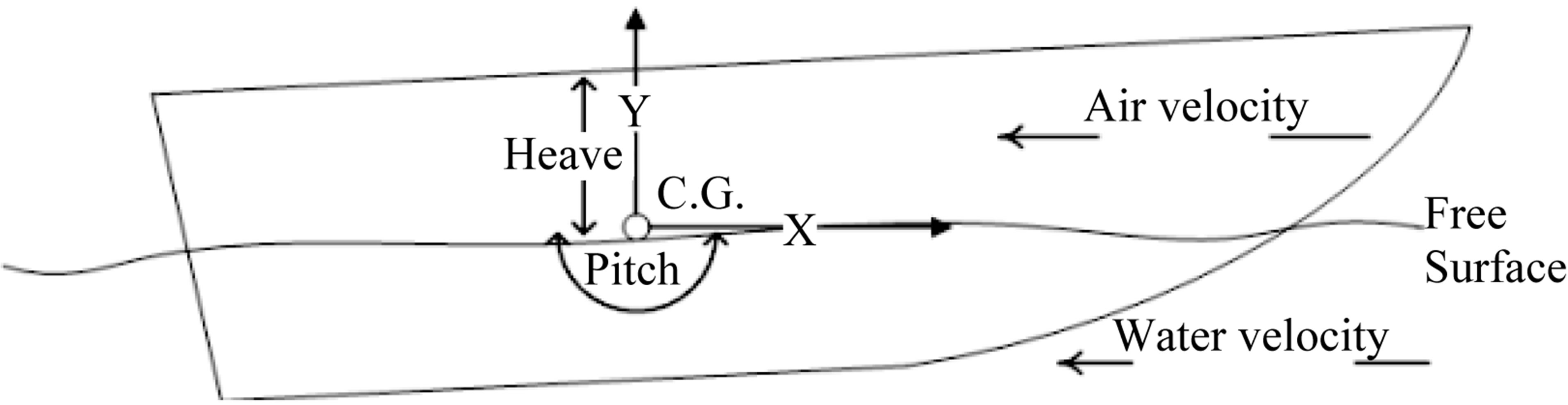
Figure 3. Degrees of freedom of vessel.

Figure 4. Solution algorithm of present methods.
At the first time step, the Navier-Stokes and Continuity equations in all nodes of domain are solved, and then by integration of pressure field around the vessel surface, the forces and moments acted on body are calculated. Then, by solving the motion of body, velocity vector of vessel gravity center is obtained. When the difference of displacement vectors (heave and pitch) and velocity vectors for previous and present time steps diminishes to zero (less than ε) and lift force equals to weight, the calculation process is terminated and the vessel becomes stable as described by Equation (3). Achieving this condition, the trim, draft and drag of vessel is fixed. If it does not happen, the vessel is moved to the new draft and trim angle based on results of solution of equilibrium equation. Then, the grid near the free surface around the vessel (small box) is restructures and more steps are iterated consecutively.
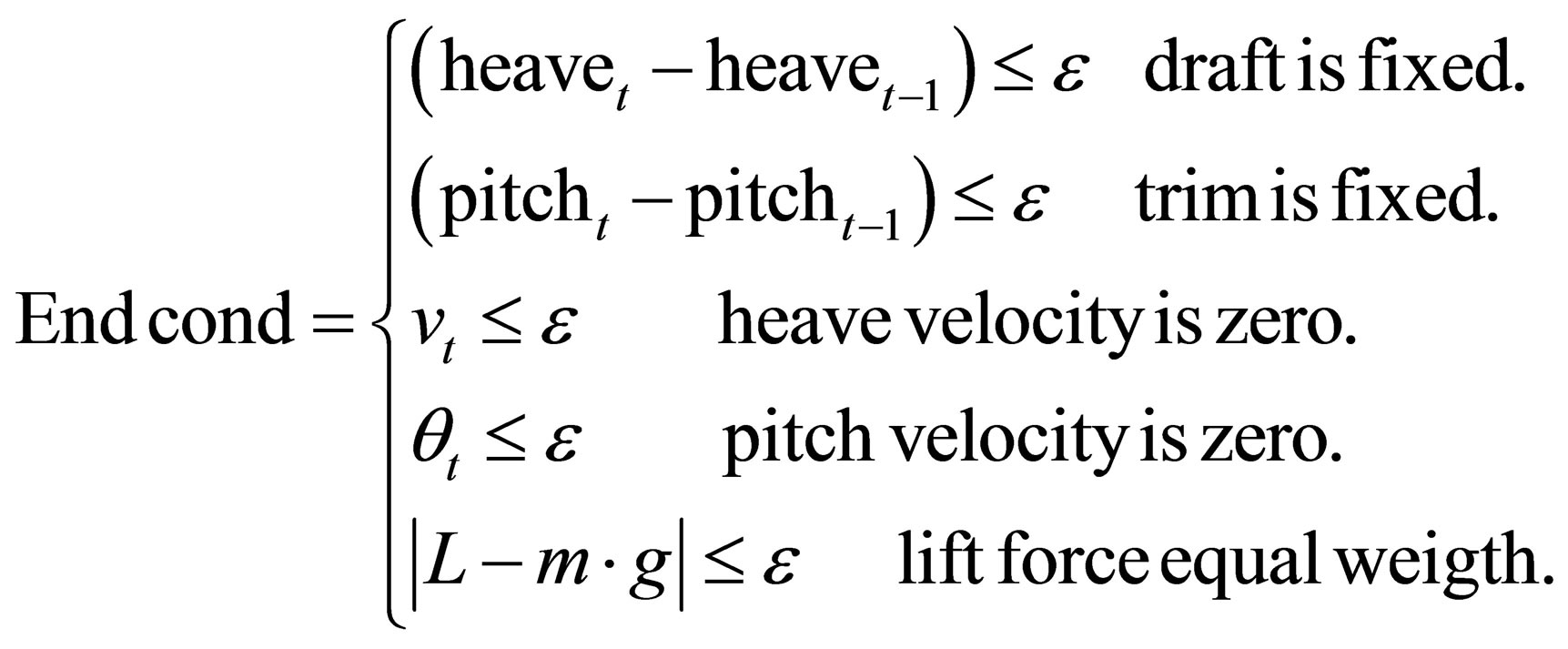 (3)
(3)
As described earlier, the VOF approach is used for free surface modeling. In this case, the volume fraction, density and dynamic viscosity of two existent phases (air and water) are solved using following equations in each control volume for all time steps:
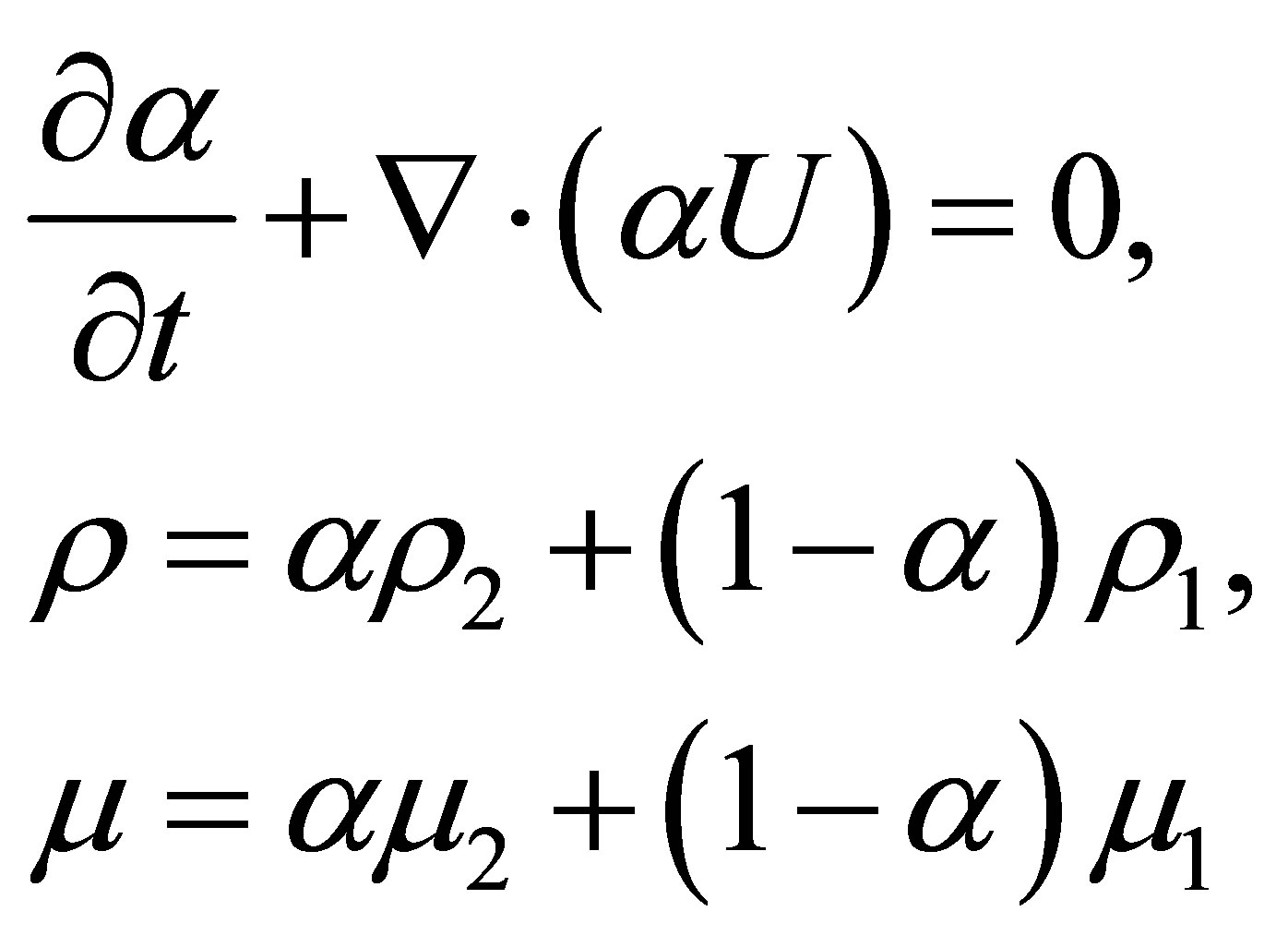 (4)
(4)
And the corresponding equations for conservation of momentum (Navier-Stokes) are given as:
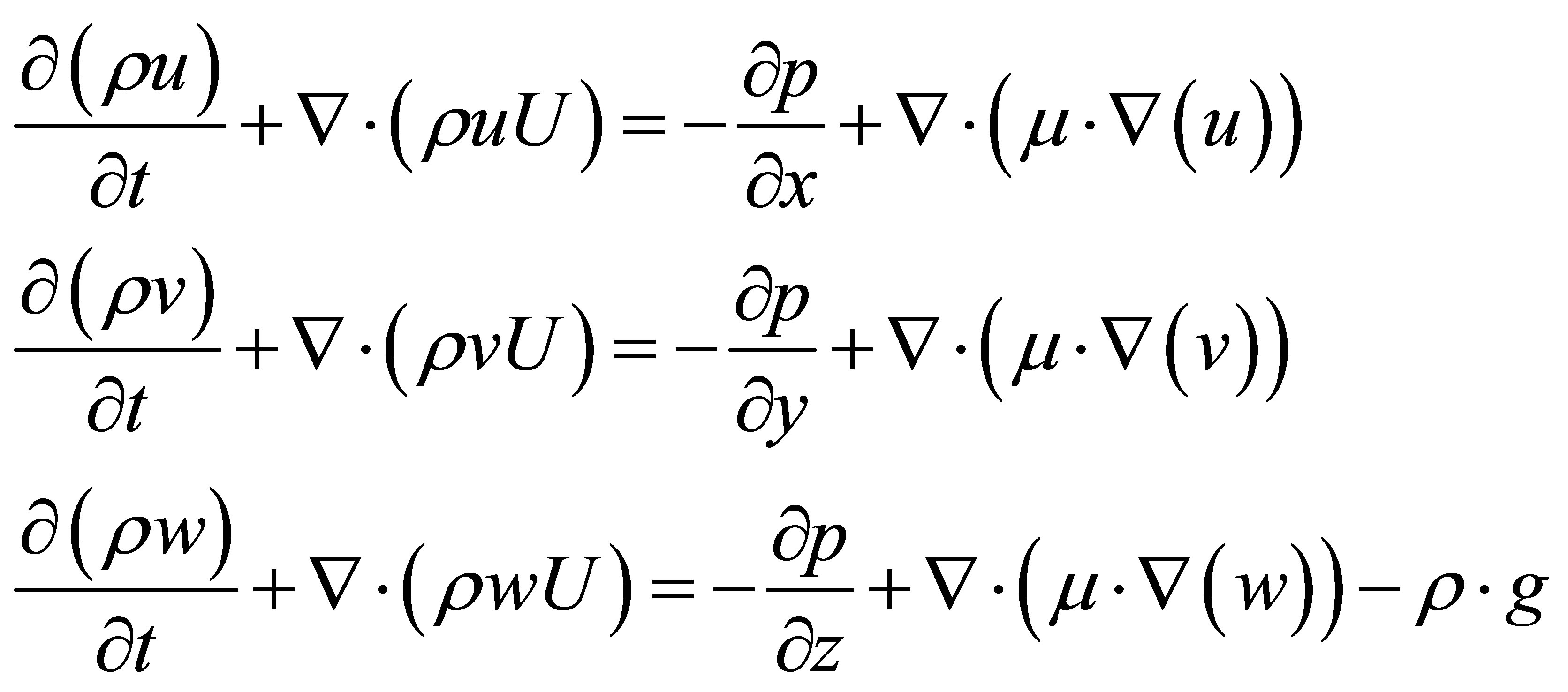 (5)
(5)
For movement estimation of the vessel based on velocity and pressure fields in the flow domain, the equations of linear and angular momentums at each time step are solved as following:
To reduce calculation time, the initial draft and trim angle of vessel is assumed near to the final dynamic draft and trim angle of vessel at stable condition.
In order to turbulence modeling, additional conservation equations for kinetic turbulence energy (κ) and turbulence energy dissipation (ε) are solved. In this study, Standard k-ε model has been used.
To solve hydrodynamic equations as described above, a commercial software (FLUENT 6.3) assisted by an external User Defined Function (UDF) is used for numerical calculations at each time step less than of 0.001 s. The simple discretization method is used for the NavierStokes system (velocity-pressure coupling) applying the first order implicit method for solving unsteady formulation of the problem.
3. Result and Discussion
3.1. Grid Independency and Validation Results
Applying the first validation approach, the comparison between experimental and CFD simulation results for vessel drag is shown in Figure 5. It should be noticed that dimensions of CFD model and tested model are the same, so there is no scale effect in results. It is observed that the obtained curves are in good agreement and accordance so that the maximum difference between resulted data through experiment and CFD methods is about 7% therewith validity of CFD code is approved.
As the second approach, the resulted trim angles in comparison with experimental data reported by Subramanian and Subramanyam [15] are presented in Figure 6 based on volume Froude numbers. It can be seen that the CFD code applies in accordance with the experiments. It is confirmed that the maximum error of CFD code is smaller than 6%.
To ensure the grid independency, different grids numbers have been chosen. Finally, it is found that with the number 2.4 million grids all parameters such as resistance and trim angle are converged. The important values y+ is less than 50 for all speed when the resistance is converged. Gird number, resistance and its y+ values are shown in Table 1.
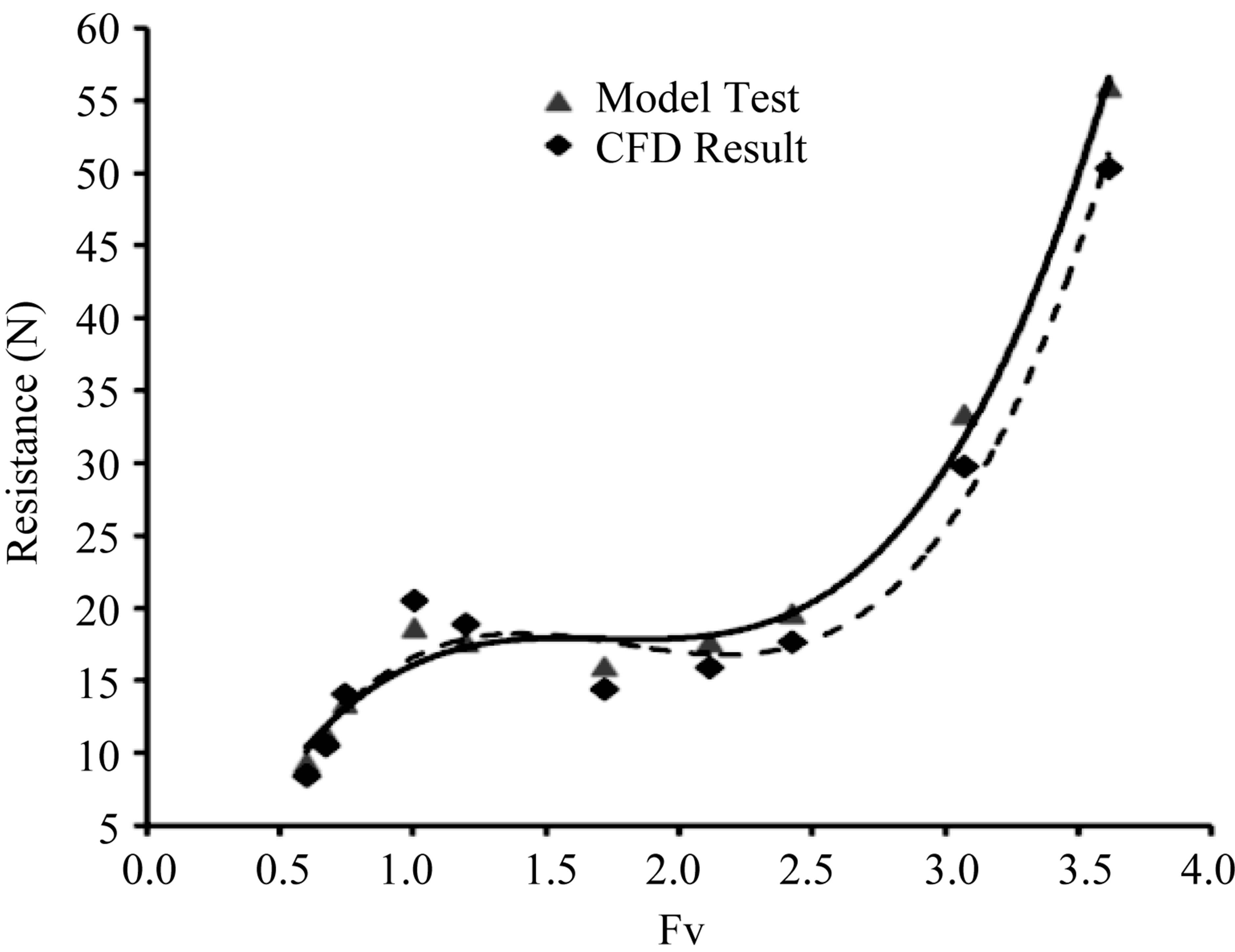
Figure 5. Comparison of drag.

Figure 6. Comparison of trim angle.
3.2. Hydrodynamics Studies
In this study, a two-tunnel vessel with specifications according to data summarized in Table 2 is generated which is illustrated in Figure 7. Masses distribution and equipments arrangement are considered according to data of Table 3.

Table 1. Grid number, resistance and its y+ values (FV = 2.5).
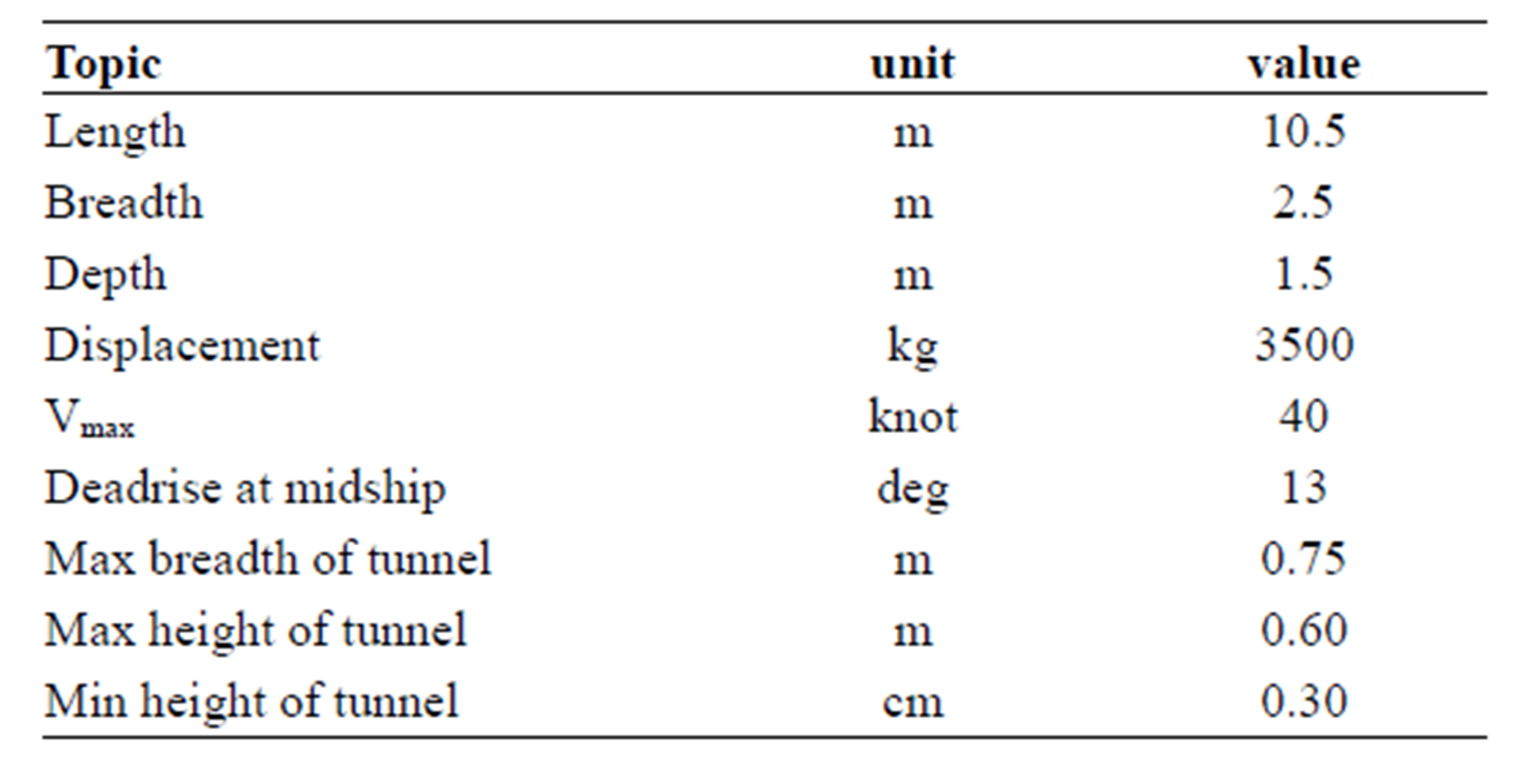
Table 2. Main specifications of the vessel.

Table 3. Weight specifications of the vessel.

Figure 7. Bottom view of tunnel vessel hull form.
3.2.1. Variations of Heave and Pitch
The vessel is running at various speeds. Here, we focused at the speed 15 knots. The results of spray, pressure, pitch and heave motions distinguished. Figure 8 shows the spray area and the pressure area at 15 knots. The angle between keel and stagnation line and the angle between keel and whisker spray are named as α and θ having values of 10˚ and 21.5˚, respectively. Savitsky et al. [9] presented following equation for calculation of α and θ in prismatic body:
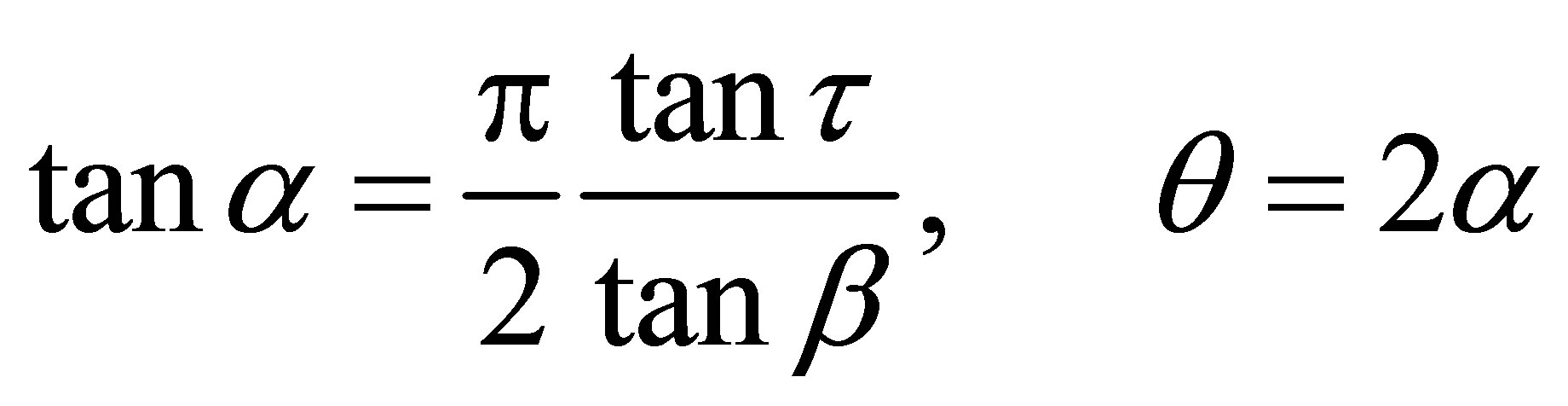 (6)
(6)
where β and τ are deadrise and trim angles, respectively. At 25 knots, τ is 2.7˚ and in this longitudinal position, β equals to 21˚. Assuming the middle V-shape body independent of tunnel body and similar to prismatic body, α and θ can be calculated based on Equation (6) as presented in Table 4.
Comparing these values for α and θ with numerical results, the hypothesis of similarity of middle part of tunnel vessel with simple prismatic is approved.
As previously mentioned, the pressure field around the vessel, hydrodynamic forces and momentums acted on it, are obtained for each time step. The vessel is moving up and down and rolling about transverse axis until the body would be stable and the lift force equals to weight so that the resultant momentum of them diminishes to zero. In this situation, the pitch angle, draft and drag of vessel become fixed and the vertical and angular velocities are approached to zero. In the procedure of stabilizing the vessel motions, the numerical hydrodynamic analysis of vessel is repeated for more than 8000 iterations. Figures 9-12 show the convergency of heave, pitch, pitch and heave velocities in hydrodynamic analyses of tunnel vessel at 15 knots. It can be seen from Figure 9 that variations of heave decrease rapidly to reach a small constant value of 0.05. It is observed from Figure 10 that pitch angle is increased during time passing to achieve a
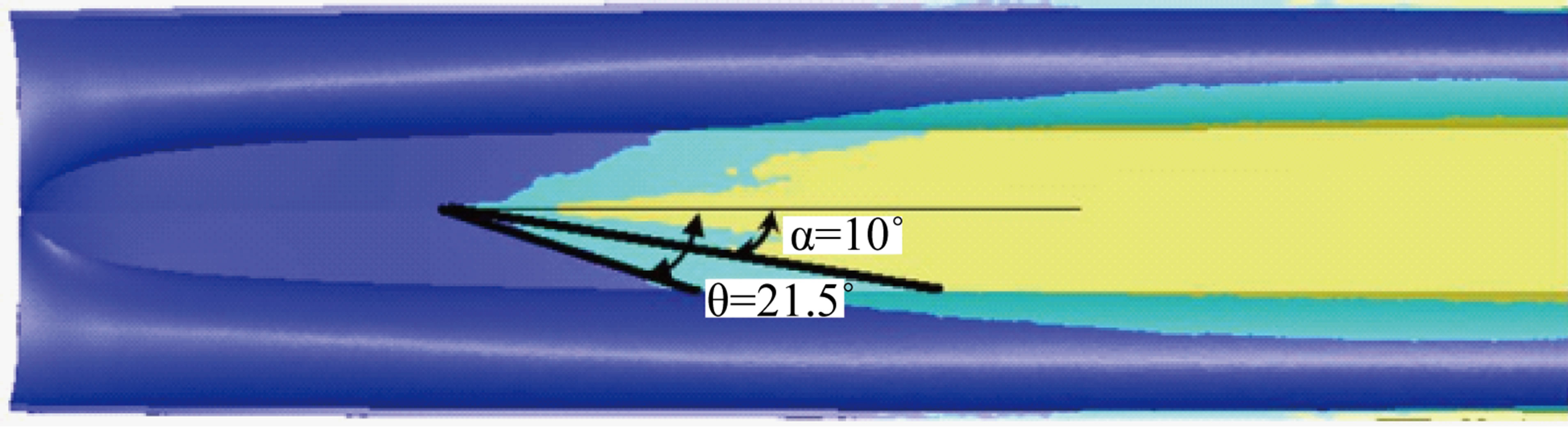
Figure 8. Spray (in green color) and pressure (in yellow color) area in prismatic body at 15 knots.
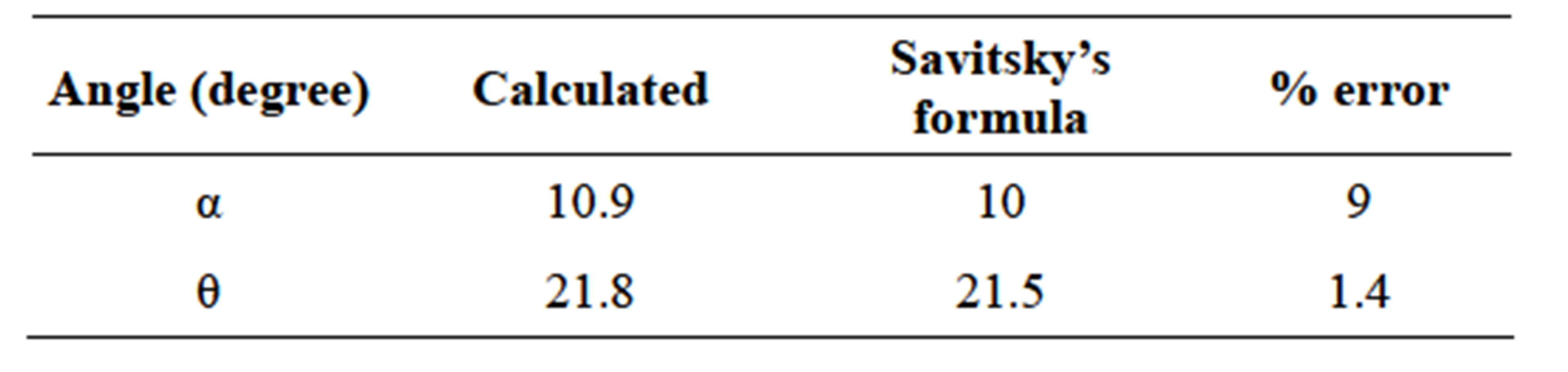
Table 4. Comparison of the spray angle between Savitsky’s formula and presented calculated.

Figure 9. Variation of heave based on time steps.
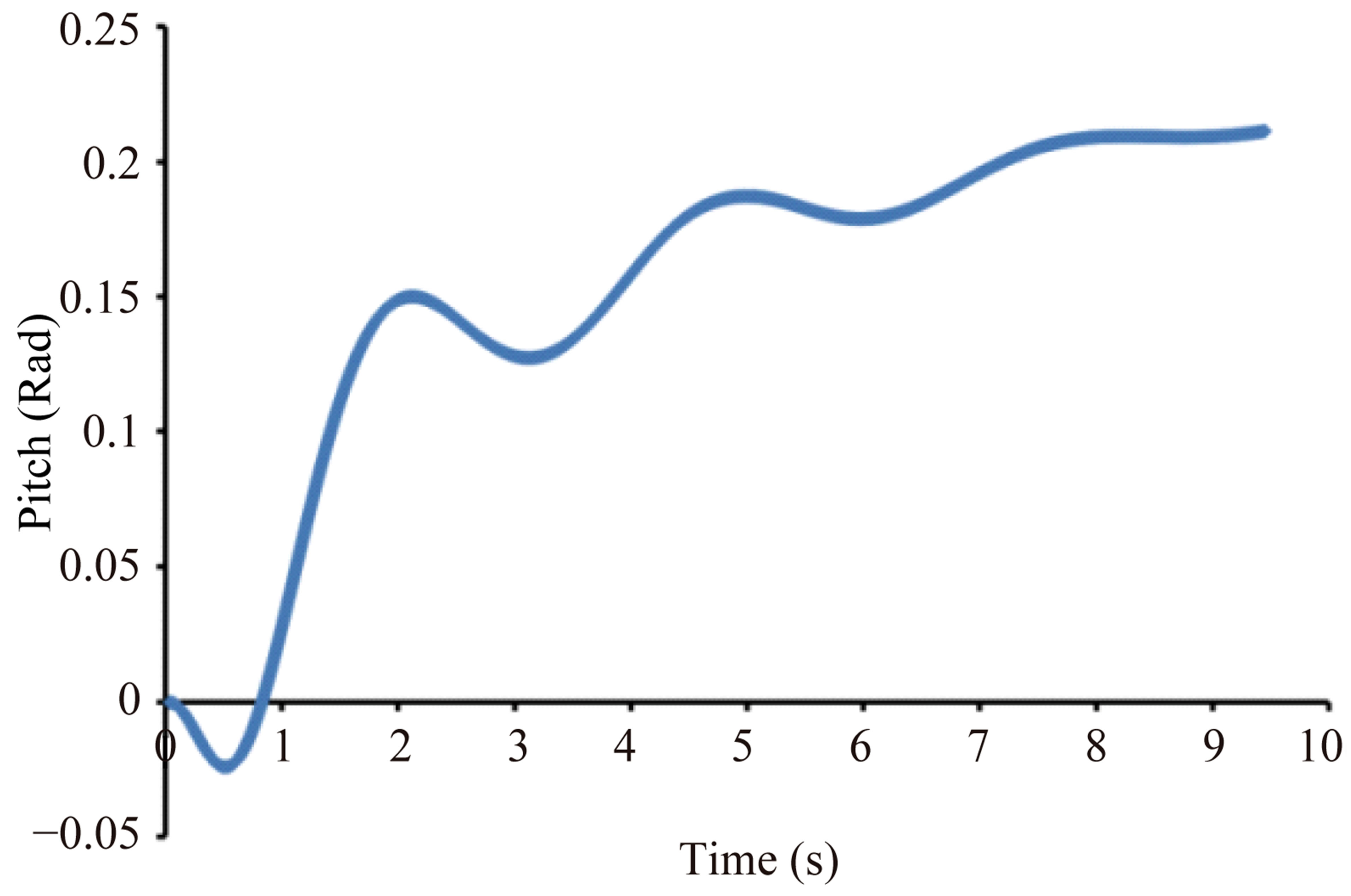
Figure 10. Variation of pitch angle based on time steps.
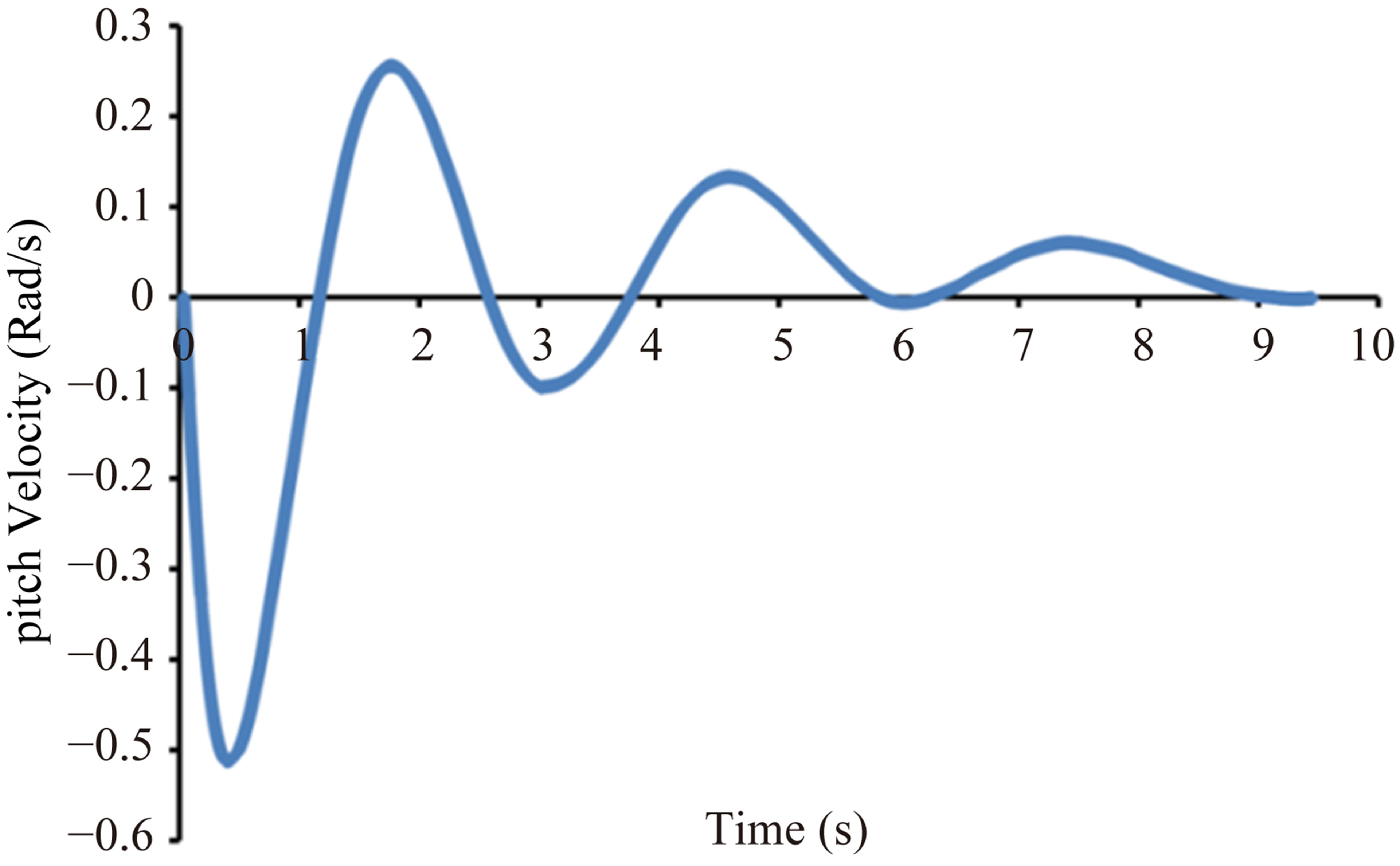
Figure 11. Variation of pitch angle velocity based on time steps.
constant level after 9.45 seconds. A damping trend also can be observed for pitch and heave velocities from Figures 11 and 12, respectively. The pitch velocity diminishes to −0.002 rad/s and heave velocity becomes about 0.004 m/s. Hence, considering the equality of weight and lift forces, all five termination conditions are satisfied.
4. Concluding Remarks
In this paper, a multihull tunnel vessel hull form was
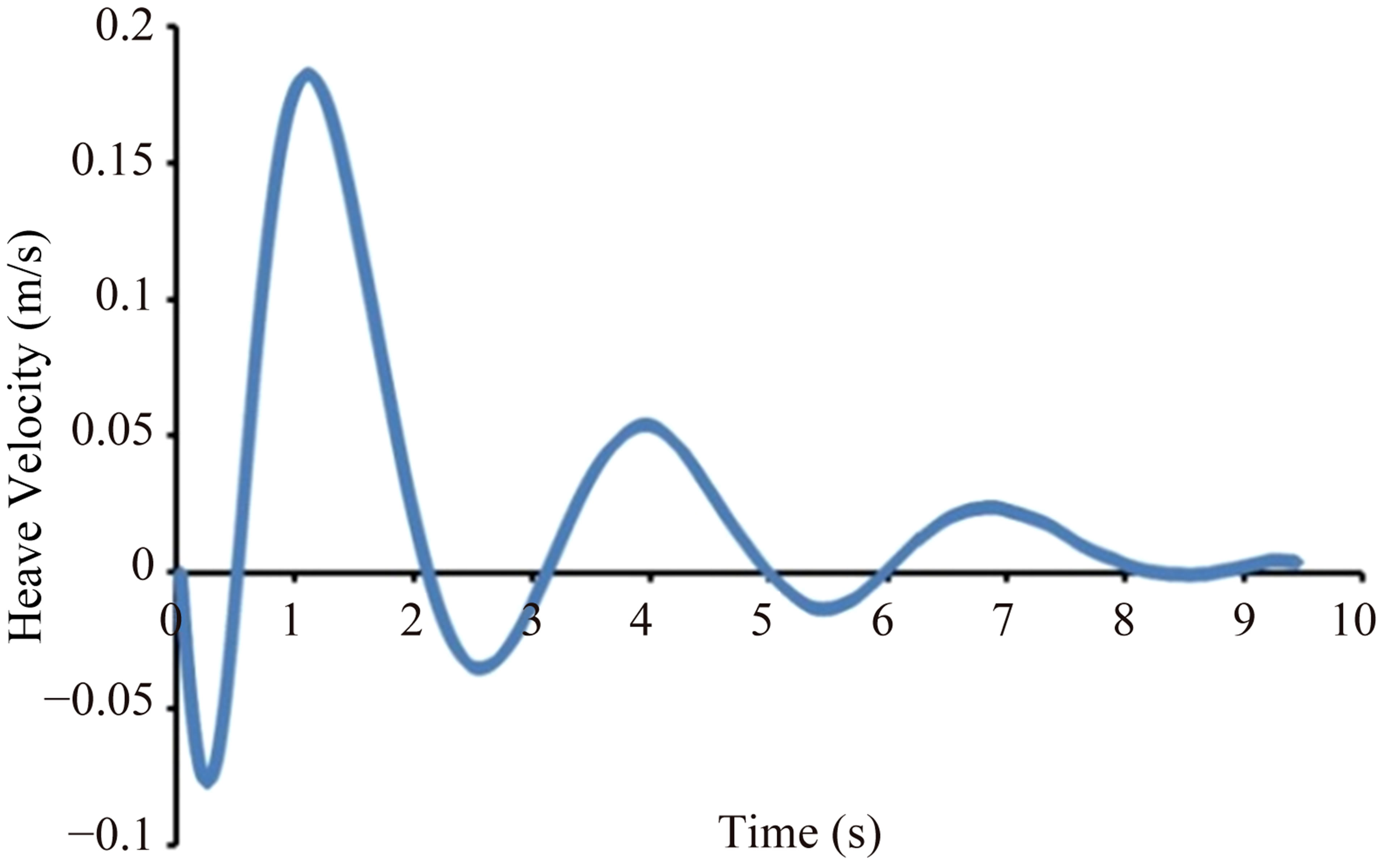
Figure 12. Variation of heave velocity based on time steps.
successfully generated by our developed THFG code. Then, a numerical approach was used to hydrodynamic study of the designed vessel. The THFG code is a suitable tool for hull form design of tunnel vessels that can be used for experimental model building and numerical hydrodynamic analyses and predictions. Its fast and precise procedure suggests its utilization for parametric study and using as an optimization approach for hull form of tunnel vessel types. Entering twenty geometry control parameters in THFG code by using NURBS curve can generate fair tunnel vessel hull form at the minimum time.
Continuously, a case study of 10.5 m tunnel vessel was designed by THFG code and studied via hydrodynamic analyses method. At 15 knots speed, angle of spray line and stagnation line is in a good accordance with Savitsky’s reported experimental data. Also, at this speed, convergency of motion parameters, including pitch angle, heave, pitch and heave velocity, during iterations of solving procedure are presented.
REFERENCES
- M. Hinatsu, “Fourier NUBS Method to Express Ship Hull Form,” Journal of Marine Science and Technology, Vol. 9, 2004, pp. 43-49. doi:10.1007/s00773-003-0166-2
- E. Sarioz, “An Optimization Approach for Fairing of Ship Hull Forms,” Ocean Engineering, Vol. 33, No. 13, 2006, pp. 2105-2118. doi:10.1016/j.oceaneng.2005.11.014
- F. Perez and J. A. Suarez, “Quasi-Developable B-Spline Surfaces in Ship Hull Design,” Computer-Aided Design, Vol. 39, No. 10, 2007, pp. 853-862. doi:10.1016/j.cad.2007.04.004
- F. L. Perez and J. A. Clemente and J. A. González, “Parametric Generation, Modeling, and Fairing of Simple Hull Lines with the Use of Non-Uniform Rational BSpline Surfaces,” Journal of Ship Research, Vol. 52, No. 1, 2008, pp. 1-15.
- M. Ventura and C. Guedes Soares, “Surface Intersection in Geometric Modeling of Ship Hulls,” Journal of Marine Science and Technology, Vol. 17, No. 1, 2012, pp. 114- 124. doi:10.1007/s00773-011-0145-y
- D. Calkins, R. D. Schachter and L. T. Oliveira, “An Automated Computational Method for Planing Hull Form Definition in Concept Design,” Ocean Engineering, Vol. 28, No. 3, 2001, pp. 297-327. doi:10.1016/S0029-8018(99)00069-4
- M. Ghassabzadeh and H. Ghassemi, “An Innovative Method for Parametric Design of Planing Tunnel Vessel Hull Form,” Ocean Engineering, Vol. 60, No. 4, 2013, pp. 14- 30. doi:10.1016/j.oceaneng.2012.11.015
- D. Savitsky and P. W. Brown, “Procedures for Hydrodynamic Evaluation of Planing Hulls in Smooth and Rough Water,” Marine Technology, Vol. 13, No. 4, 1976, pp. 381-400.
- D. Savitsky, M. F. Delorme and R. Datla, “Inclusion of Whisker Spray Drag in Performance Prediction Method for High-Speed Planing Hulls,” Maine Technology, Vol. 44, No. 1, 2007, pp. 35-56.
- D. Savitsky and M. Morabito, “Surface Wave Contours Associated with the Forebody Wake of Stepped Planing Hulls,” Marine Technology, Vol. 47, No. 1, 2010, pp. 1- 16.
- H. Ghassemi and M. Ghiasi, “A Combined Method for the Hydrodynamic Characteristics of Planing Crafts,” Ocean Engineering, Vol. 35, No. 3-4, 2008, pp. 310-322. doi:10.1016/j.oceaneng.2007.10.010
- H. Ghassemi and S. Yumin, “Determining the Hydrodynamic Forces on a Planing Hull in Steady Motion,” China Ocean Engineering, Vol. 7, 2008, pp. 147-156.
- FLUENT Inc., “Fluent 6.3 User’s Guide,” 2006.
- S. Yumin, C. Qingtong, S. Hailong and L. Wei, “Numerical Simulation of a Planing Vessel at High Speed,” Journal of Marine Science and Application, Vol. 11, No. 2, 2012, pp. 178-183. doi:10.1007/s11804-012-1120-7
- A. V. Subramanian, P. V. V. Subramanyam and A. N. Sulficker, “Pressure and Drag Influences Due to Tunnels in High-Speed Planing Craft,” International Shipbuilding Progress, Vol. 54, No. 1, 2007, pp. 25-44.
- A. Millward, “The Effect of Channel Width and Depth on the Resistance of a High Speed Hull,” International Shipbuilding Progress, Vol. 51, No. 4, 2004, pp. 377-394.
- M. Reichel and A. Bednarek, “The Experimental Studies on Hydrofoil Resistance,” Archives of Civil and Mechanical Engineering, Vol. 7, No. 3, 2007, pp. 167-175. doi:10.1016/S1644-9665(12)60024-7
- L. Piegl and W. Tiller, “The NURBS,” Springer, Berlin, 1997.

