Open Journal of Fluid Dynamics
Vol.2 No.4(2012), Article ID:25721,13 pages DOI:10.4236/ojfd.2012.24017
Dufour Effects on Unsteady Hydromagnetic Radiative Fluid Flow past a Vertical Plate through Porous Medium
1Department of Mathematics, University of Botswana, Gaborone, Botswana
2Department of Mathematics, Sree Vidyanikethan Engineering College (Autonomous), Tirupati, India
3Department of Mathematics, S.V. University, Tirupati, India
Email: *prakashj@mopipi.ub.bw, agvijaykumar1729@gmail.com, svijayakumarvarma@yahoo.co.in
Received July 23, 2012; revised September 1, 2012; accepted September 9, 2012
Keywords: MHD; Heat and Mass Transfer; Diffusion-Thermo (Dufour Number); Vertical Plate; Porous Medium
ABSTRACT
The objective of the present study is to investigate diffusion-thermo (Dufour effect) and radiation effects on unsteady MHD free convection flow past an impulsively started infinite vertical plate with variable temperature and uniform mass diffusion in the presence of transverse applied magnetic field through porous medium. At time t > 0, the plate is given an impulsive motion with constant velocity 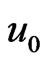 in the vertical upward direction against to the gravitational field. At the same time the plate temperature is raised linearly with time t and the level of concentration near the plate is raised to
in the vertical upward direction against to the gravitational field. At the same time the plate temperature is raised linearly with time t and the level of concentration near the plate is raised to . A magnetic field of uniform strength
. A magnetic field of uniform strength 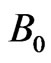 is applied normal to the direction to the flow. The dimensionless governing equations are solved in closed form by Laplace-transform technique. The effect of flow parameters on velocity, temperature, concentration, the rate of heat transfer and the rate of mass transfer are shown through graphs.
is applied normal to the direction to the flow. The dimensionless governing equations are solved in closed form by Laplace-transform technique. The effect of flow parameters on velocity, temperature, concentration, the rate of heat transfer and the rate of mass transfer are shown through graphs.
1. Introduction
In nature, there exist flows which are caused not only by the temperature differences but also the concentration differences. These mass transfer differences do affect the rate of heat transfer. In industries, many transport processes exist in which heat and mass transfer takes place simultaneously as a result of combined buoyancy effect in the presence of thermal radiation. Hence, radiative heat and mass transfer play an important role in manufacturing industries for the design of fins, steel rolling, nuclear power plants, gas turbines and various propulsion device for aircraft, missiles, satellites, combustion and furnace design, materials processing, energy utilization, temperature measurements, remote sensing for astronomy and space exploration, food processing and cryogenic engineering, as well as numerous agricultural, health and military applications. If the temperature of surrounding fluid is rather high, radiation effects play an important role and this situation does exist in space technology. In such cases, one has to take into account the combined effect of thermal radiation and mass diffusion.
Boundary layer flow on moving horizontal surfaces was studied by Sakiadis [1]. The effects of transversely applied magnetic field on the flow of an electrically conducting fluid past an impulsively started isothermal vertical plate were studied by Soundalgekar et al. [2]. MHD effects on impulsively started vertical infinite plate with variable temperature in the presence of transverse applied magnetic field were studied by Soundalgekar et al. [3]. The dimensionless governing equations were solved using Laplace transform technique. Kumari and Nath [4] studied the development of the asymmetric flow of a viscous electrically conducting fluid in the forward stagnation point of a two-dimensional body and over a stretching surface with an applied magnetic field. The governing equations were solved using Laplace transform technique.
England and Emery [5] studied the thermal radiation effects of an optically thin gray gas bounded by a stationary vertical plate. Soundalgekar and Takhar [6] considered the radiation free convection flow of an optically thin gray gas past a semi-infinite vertical plate. Radiation effects on mixed convection along isothermal vertical plate were studied by Hossain and Takhar [7]. In all above studies, the stationary vertical plate is considered. Raptis and Perdikis [8] studied the effects of thermal radiation and free convection flow past a moving vertical plate. The governing equations were solved analytically. Das et al. [9] analyzed radiation effects on flow past an impulsively started infinite isothermal vertical plate. The governing equations were solved by the Laplace transform technique. Muthucumaraswamy et al. [10] and Rajesh and Varma [11] studied radiation and mass transfer effects on exponentially accelerated isothermal vertical plate. Recently, Kumar and Varma [12] studied thermal radiation and mass transfer effects on MHD flow past an impulsively started exponentially accelerated vertical plate with variable temperature and mass diffusion.
Free convection flows that occurs in nature and in engineering practice is very large and has been extensively considered by many authors. When heat and mass transfer occurs simultaneously between the fluxes the driving potentials are more intricate in nature. An energy flux is generated not only by temperature gradients but by composition gradients as well. Temperature gradients can also create mass fluxes and this is the Soret or Thermal-diffusion effect. Generally, the thermal-diffusion and diffusion-thermo effects of smaller order magnitude than the effects prescribed by Fourier’s or Fick’s laws and are often neglected in heat and mass transfer processes. Due to the importance of thermal-diffusion and diffusionthermo effects for the fluids with very light molecular weight as well as medium molecular weight many investtigators have studied and reported results for these flows and the contributors such as Eckert and Drake [13], Dursunkaya and Worek [14], Anghel et al. [15], Postenlnicu [16] are worth mentioning. Alam and Rahman [17] studied the Dufour and soret effects on steady MHD free convective heat and mass transfer flow past a vertical porous plate embedded in a porous medium. Alam et al. [18] investigated the Dufour and Soret effects on unsteady free convection and mass transfer flow past an impulsively started infinite vertical plate embedded in a porous medium under the influence of transverse magnetic field.
In this paper, it is proposed to study diffusion-thermo and radiation effects on MHD free convection flow past an impulsively started infinite vertical plate with variable temperature through porous medium in the presence of transverse applied magnetic field. The dimensionless governing equations are solved using Laplace transform technique. And the solutions are expressed in terms of exponential and complementary error functions.
2. Mathematical Formulation
Diffusion-thermo and radiation effects on unsteady MHD free convection of flow of a viscous incompressible, electrically, conducting, radiating fluid past an impulsively started infinite vertical plate with variable temperature and uniform mass diffusion in the presence of transverse applied magnetic field through porous medium have been studied. The 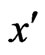 -axis is taken along the plate in vertical upward direction and
-axis is taken along the plate in vertical upward direction and 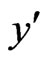 -axis is taken normal to it in the direction of applied transverse magnetic field. Initially, it is assumed that the plate and surrounding fluid are at the same temperature and concentration in stationary condition for all the points in entire flow region
-axis is taken normal to it in the direction of applied transverse magnetic field. Initially, it is assumed that the plate and surrounding fluid are at the same temperature and concentration in stationary condition for all the points in entire flow region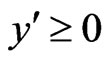 . At time
. At time , the plate is given an impulsive motion with constant velocity
, the plate is given an impulsive motion with constant velocity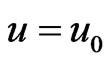 . At the same time, the plate temperature is raised linearly with time t and the concentration levels near the plate are raised to
. At the same time, the plate temperature is raised linearly with time t and the concentration levels near the plate are raised to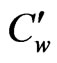 . A magnetic field of uniform strength
. A magnetic field of uniform strength 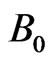 is assumed to be applied normal to the flow. For free convection flow, it is also assumed that1) The induced magnetic field is assumed to be negligible as the magnetic Reynolds number of the flow is taken to be very small.
is assumed to be applied normal to the flow. For free convection flow, it is also assumed that1) The induced magnetic field is assumed to be negligible as the magnetic Reynolds number of the flow is taken to be very small.
2) The viscous dissipation is neglected in the energy equation.
3) The effects of variation in density 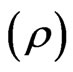 with temperature and species concentration are considered only on the body force term, in accordance with usual Boussinesq approximation.
with temperature and species concentration are considered only on the body force term, in accordance with usual Boussinesq approximation.
4) The fluid considered here is gray, absorbing/emitting radiation but a non-scattering medium.
5) Since the flow of the fluid is assumed to be in the direction of 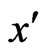 axis, so the physical quantities are functions of the space co-ordinate
axis, so the physical quantities are functions of the space co-ordinate 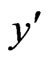 and
and  only.
only.
Then by usual Boussinesq’s approximation, the flow is governed by the following equations.
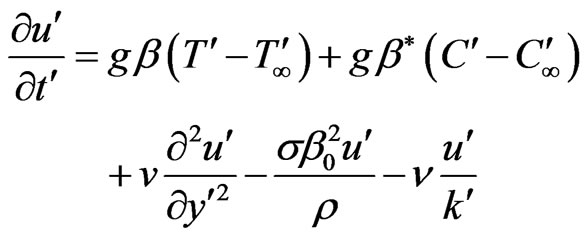 (1)
(1)
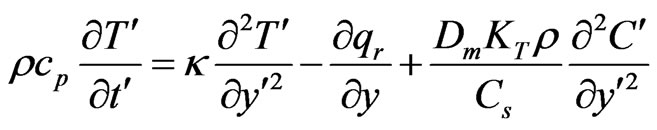 (2)
(2)
 (3)
(3)
with the following initial and boundary conditions
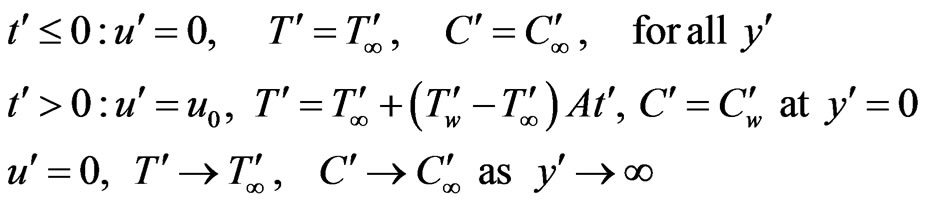 (4)
(4)
where 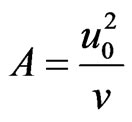 The local radiant for the case of an optically thin gray gas is expressed by
The local radiant for the case of an optically thin gray gas is expressed by
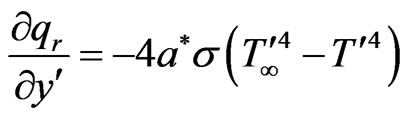 (5)
(5)
It is assumed that the temperature differences within the flow are sufficiently small and that 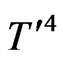 may be expressed as a linear function of the temperature. This is obtained by expanding
may be expressed as a linear function of the temperature. This is obtained by expanding  in a Taylor series about
in a Taylor series about  and neglecting the higher order terms, thus we get
and neglecting the higher order terms, thus we get
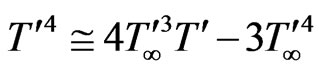 (6)
(6)
From Equations (5) and (6), Equation (2) reduces to
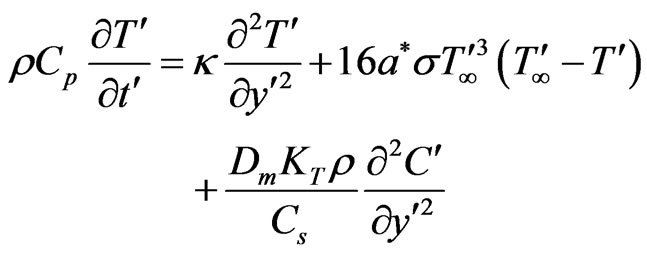 (7)
(7)
On introducing the following non-dimensional quantities
 (8)
(8)
We get the following governing equations which are dimensionless
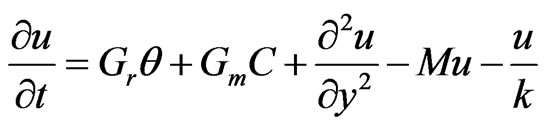 (9)
(9)
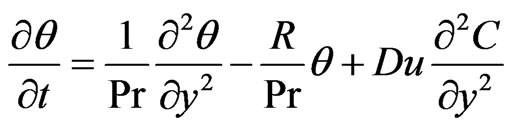 (10)
(10)
 (11)
(11)
The initial and boundary conditions in dimensionless form are as follows:
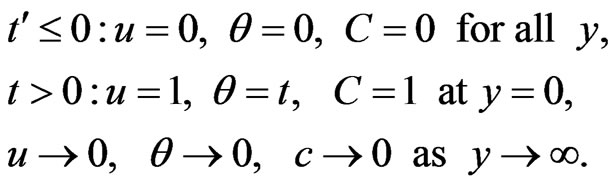 (12)
(12)
3. Solution of the Problem
The appeared physical parameters are defined in the nomenclature. The dimensionless governing equations from (9) to (11), subject to the boundary conditions (12) are solved by usual Laplace transform technique and the solutions are expressed in terms of exponential and complementary error functions.
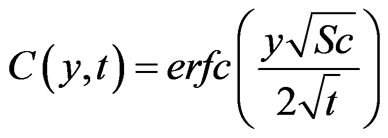 (13)
(13)
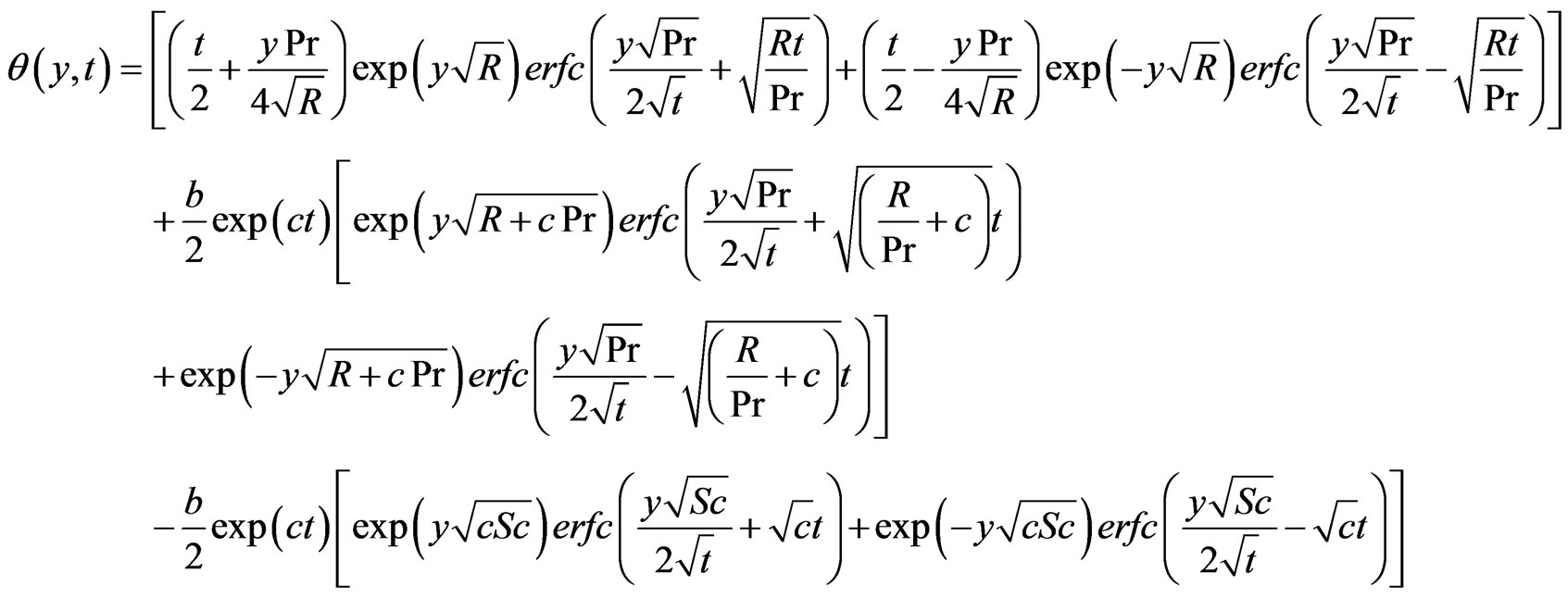 (14)
(14)
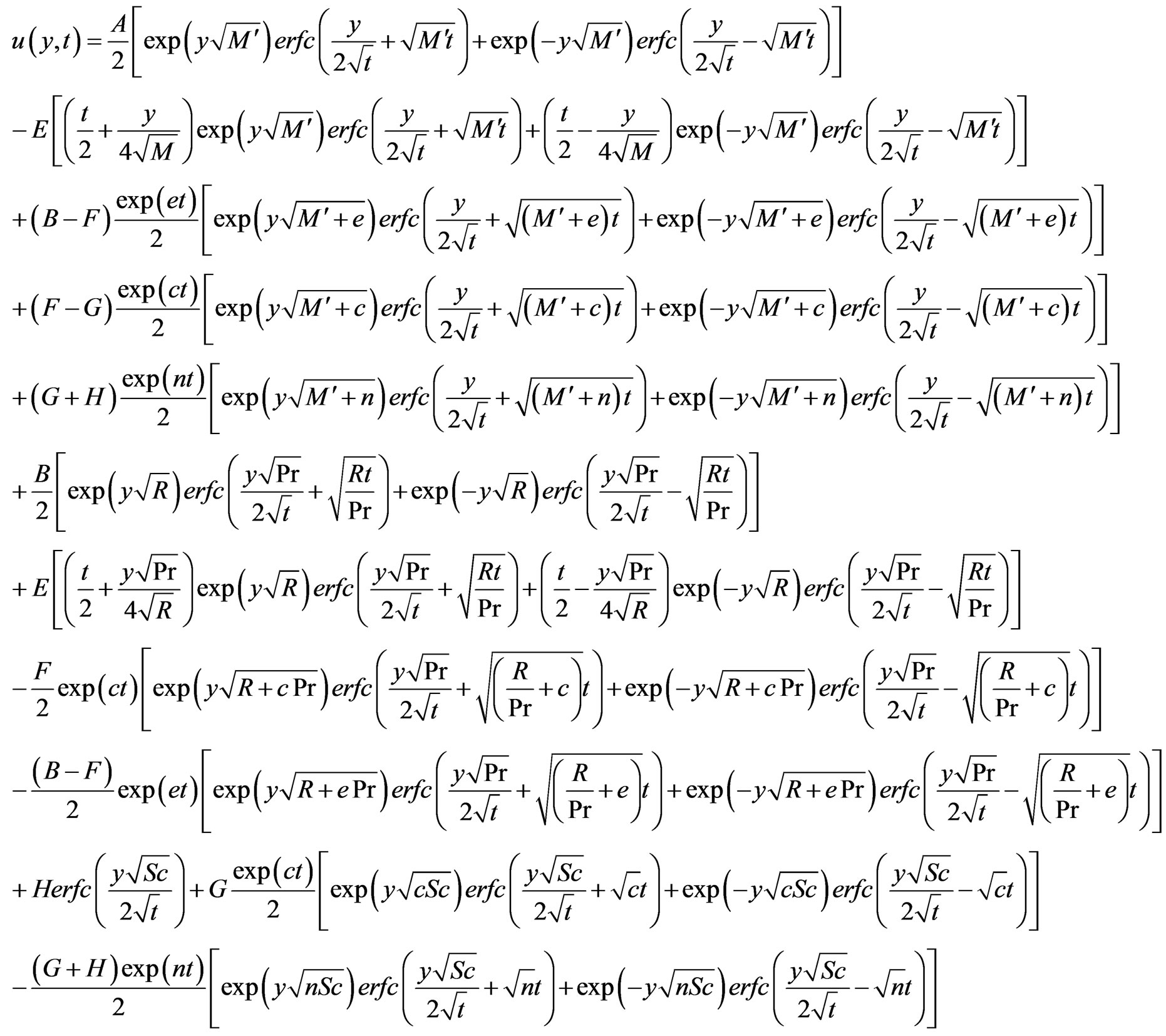 (15)
(15)
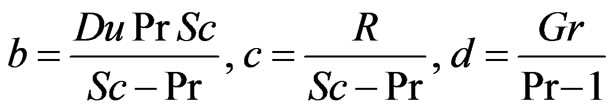 ,
,

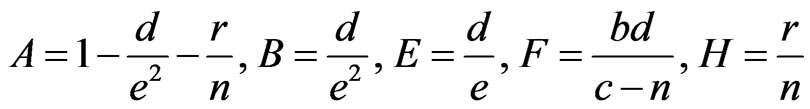
4. Nusselt Number
From temperature field, now we study Nusselt number (rate of change of heat transfer) which is given in nondimensional form as
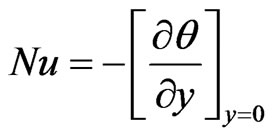 (16)
(16)
From Equations (14) and (16), we get Nusselt number as follows:

5. Sherwood Number
From concentration field, now we study Sherwood number (rate of change of mass transfer) which is given in non-dimensional form as
 (17)
(17)
From Equations (13) and (17), we get Sherwood number as follows:
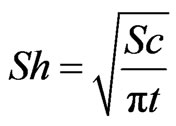
6. Results and Discussions
In order to get a clear insight of the physical problem the velocity, temperature, concentration, the rate of heat transfer and the rate of mass transfer have been discussed by assigning numerical values to the parameters like radiation parameter (R), magnetic parameter (M), Schmidt parameter (Sc), Prandtl number (Pr), Dufour number (Du), thermal Grashof number (Gr), mass Grashof number (Gm) and time t from Figures 1-13 for the cases of cooling (Gr > 0, Gm >0) and heating (Gr < 0, Gm < 0) of plate. The heating and cooling takes place by setting up free convection currents due to temperature and concentration gradient.
Figure 1 depicts the effect of magnetic field parameter on the fluid velocity and we observed that an increase in magnetic field parameter the velocity decreases in case of cooling of the plate while it increases in case of heating. Figures 2-4 show the effects of R, Du, Gr and Gm on the velocity field u. From these figures, it is observed that the velocity u increases as the radiation parameter R or Dufour number Du or thermal Grashof number Gr or mass Grashof number Gm increases in case of cooling of the plate and a reverse effect is noticed in the case of heating. The velocity profiles for different values of Schmidt number are shown in Figure 5. From this it is seen that the velocity decreases with increasing values of Schmidt number in the case of cooling of the plate but increases in the case of heating of the plate. Figure 6 reveals the velocity variation with time t for the cases of both cooling and heating. From this we observed that the velocity increases as time t increases for the case of cooling and the trend is just reversed for the case of heating of the plate. The effect of permeability parameter k on the velocity field is shown in Figure 7. It is seen from this figure that the velocity increases with increase of permeability parameter k in both cases of cooling and heating of the plate.
The influence of various flow parameters on the fluid temperature are illustrated in Figures 8-10. Figure 8 depicts that the effects of the Dufour number on the fluid temperature. It can be clear seen from this figure that the diffusion thermal effects slightly affect the fluid temperature. As the values of Dufour number increase, the fluid temperature is also increases. The effect of thermal radiation R on the temperature field is illustrated in Figure 9. It is obvious that the radiation parameter restricts the fluid temperature. Therefore, using radiation we can control the fluid temperature. In Figure 10, we depict the
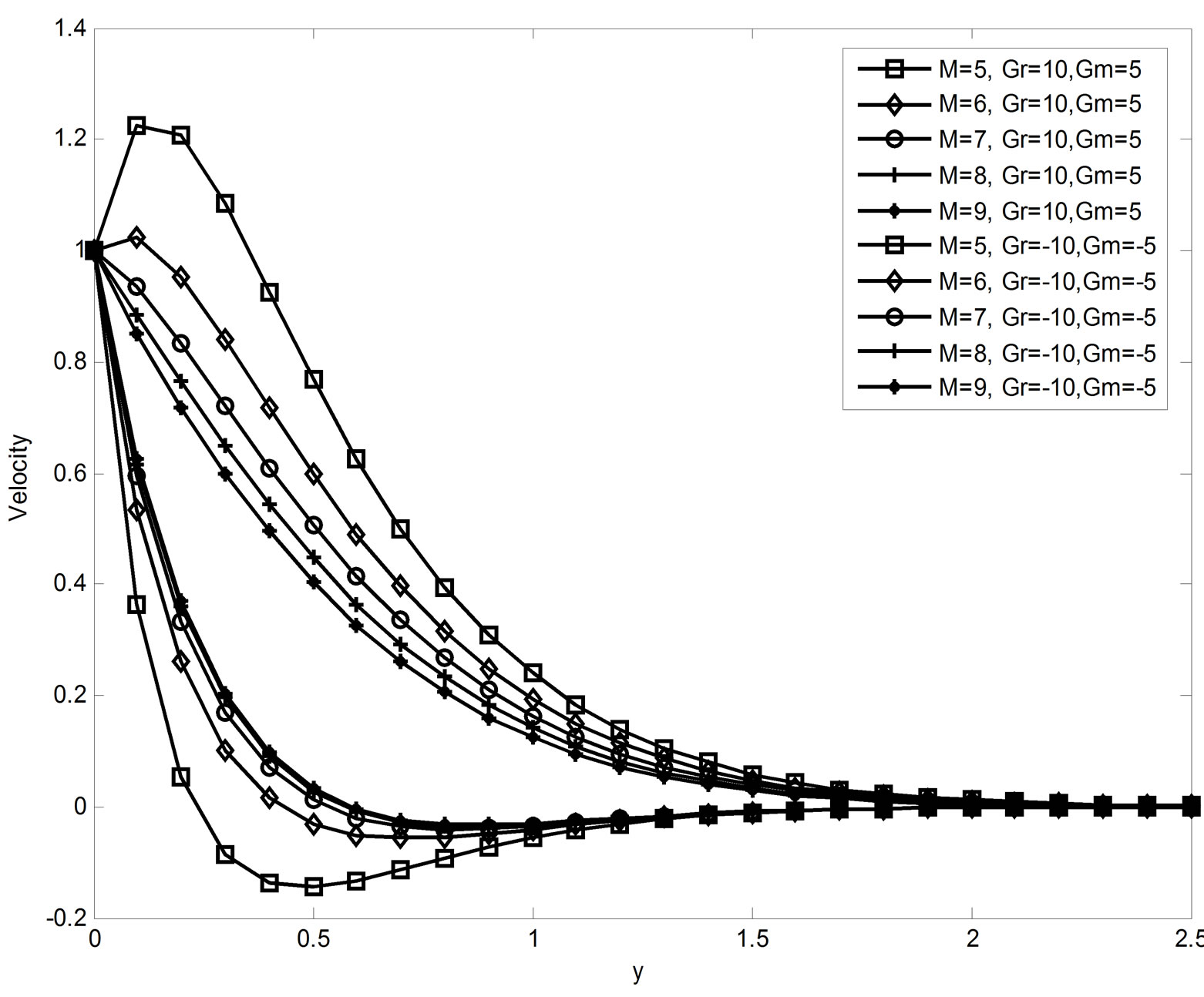
Figure 1. Velocity profiles when Sc = 2.01, Pr = 0.71, R = 10, k = 5, Du = 0.03 & t = 0.4.
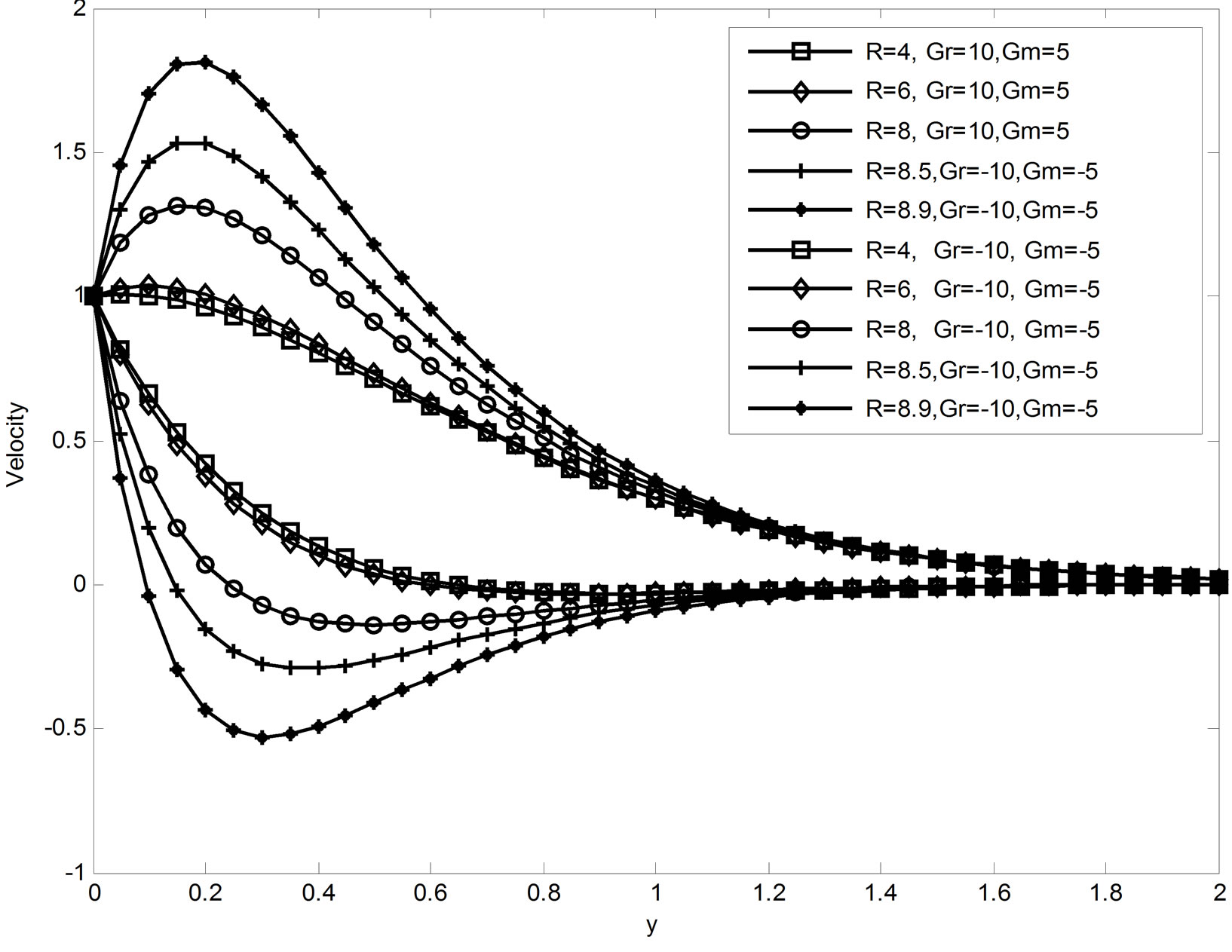
Figure 2. Velocity profiles when Sc = 2.01, Pr = 0.71, M = 3, k = 5, Du = 0.03 & t = 0.4.

Figure 3. Velocity profiles when Sc = 2.01, Pr = 0.71, R = 10, k = 5, M = 3 & t = 0.4.
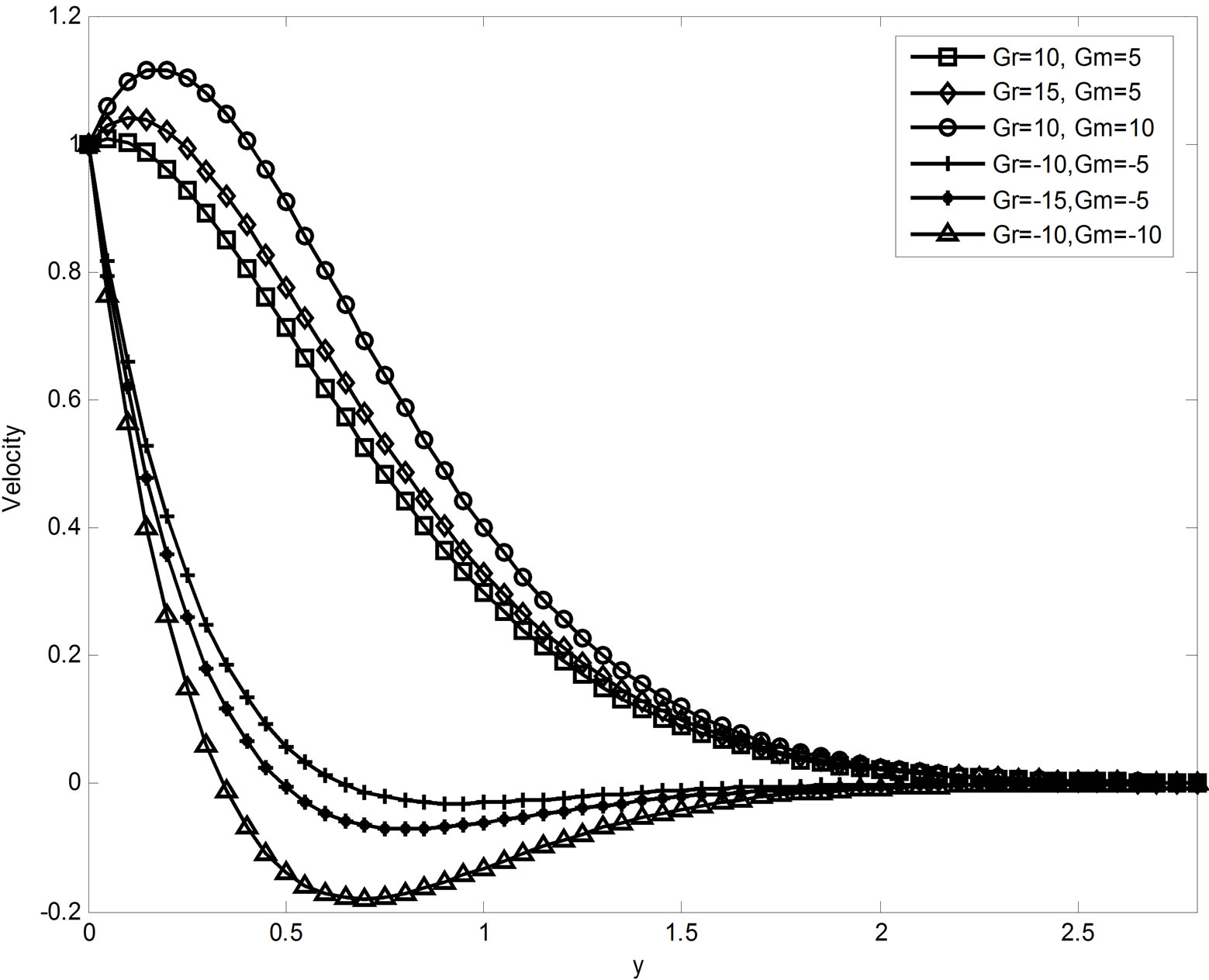
Figure 4. Velocity profiles when M = 3, Pr = 0.71, Sc = 2.01, R = 10, k = 5, Du = 0.03 & t = 0.4.
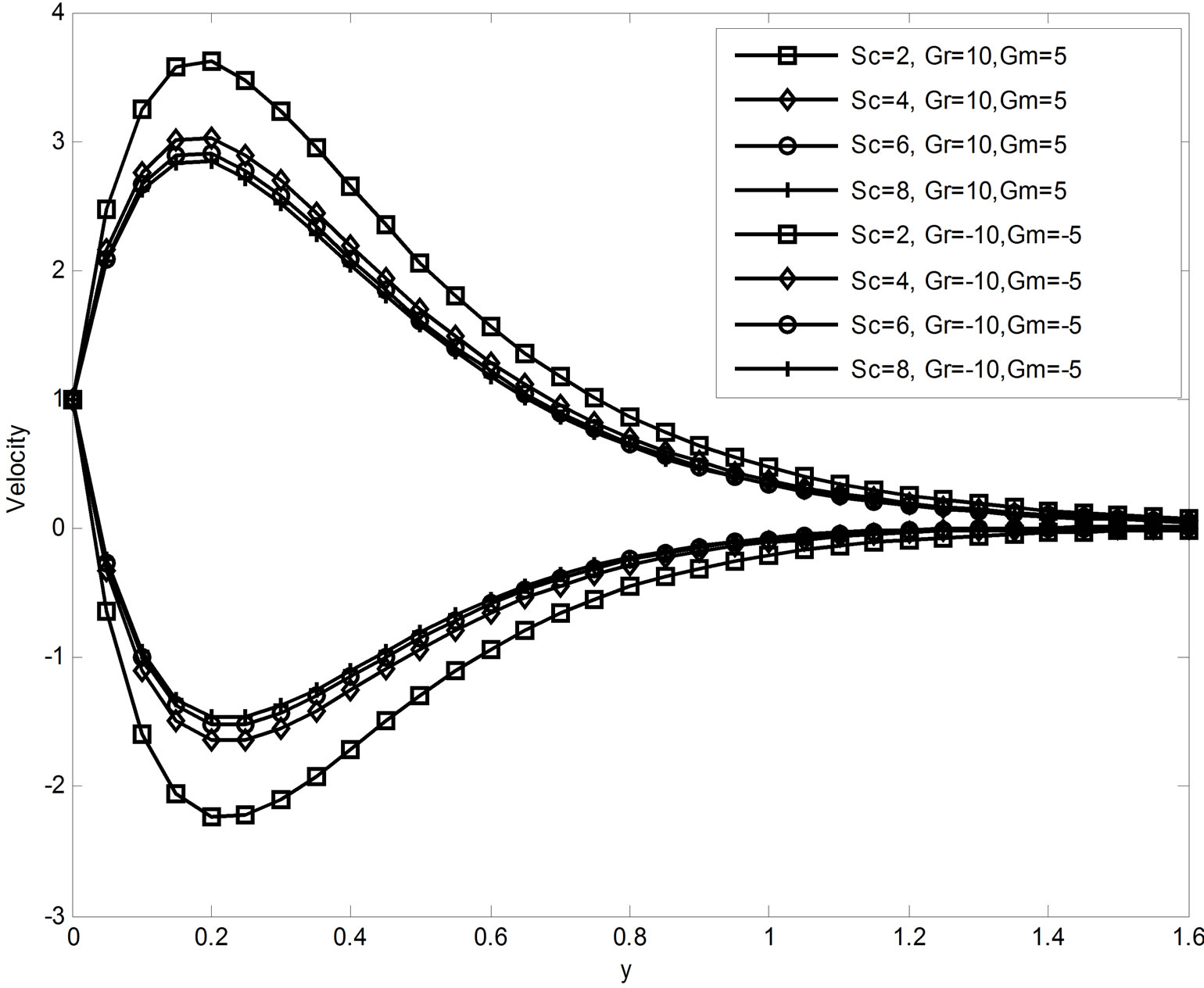
Figure 5. Velocity profiles when M = 4, Pr = 0.71, R = 10, k = 5, Du = 0.03 & t = 0.4.

Figure 6. Velocity profiles when Sc = 2.01, M = 3, Pr = 0.71, R = 10, k = 5, Du = 0.03.

Figure 7. Velocity profiles when Sc = 2.01, Pr = 0.71, R = 10, M = 3, Du = 0.03 & t = 0.4.
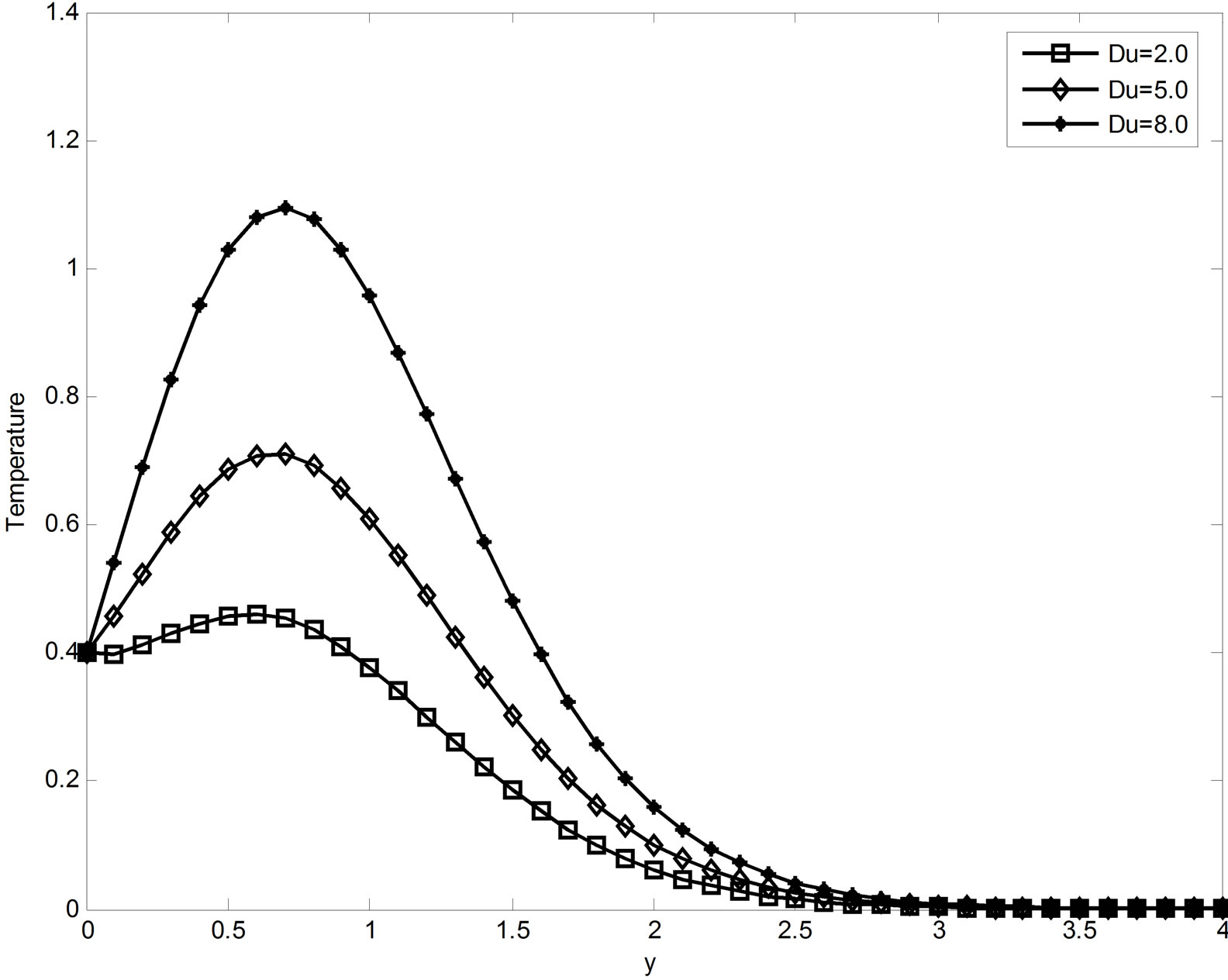
Figure 8. Temperature profiles when R = 4, Pr = 0.71 & Sc = 2.01.
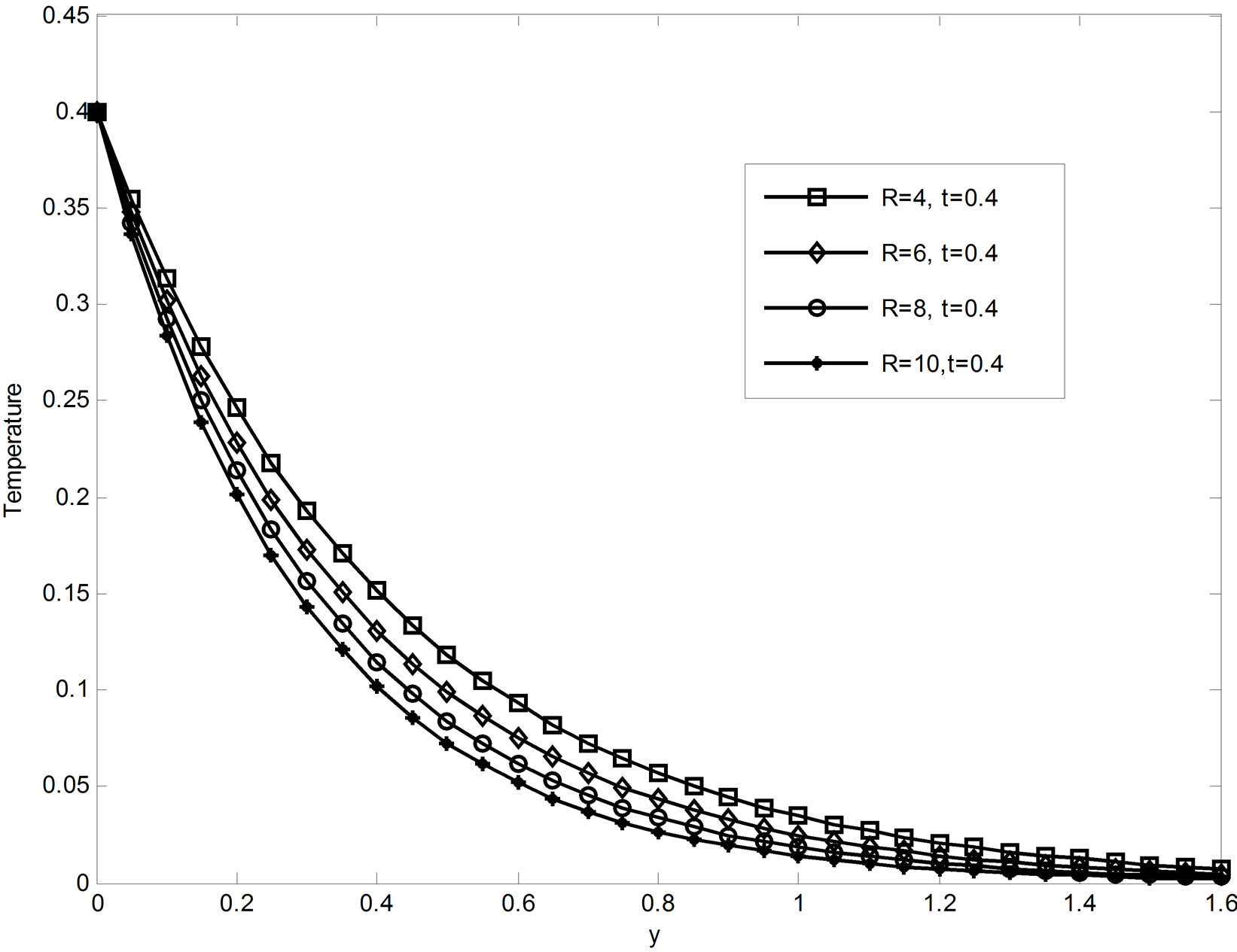
Figure 9. Temperature profiles when Du = 0.03, Pr = 0.71 & Sc = 2.01.
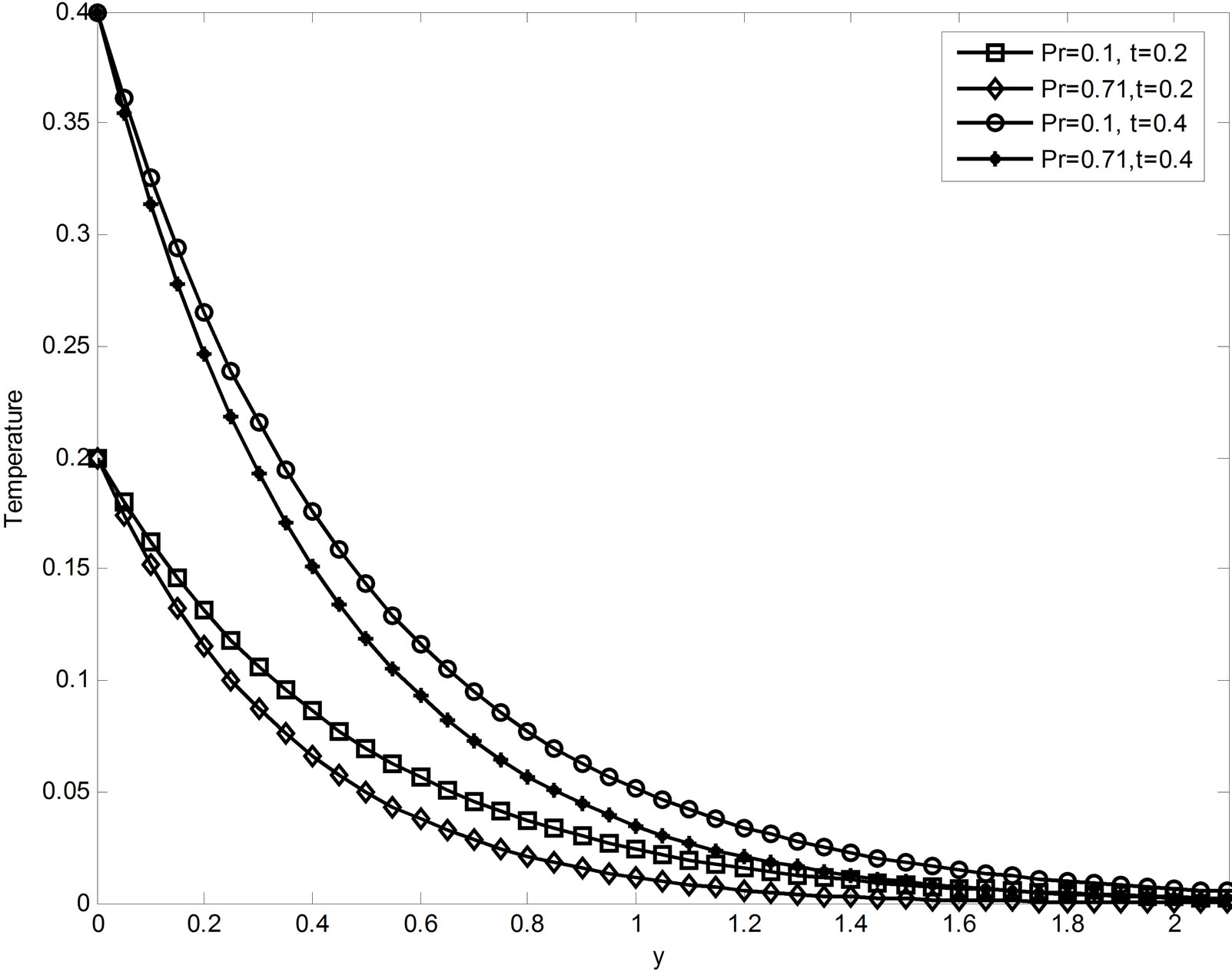
Figure 10. Temperature profiles when R = 4, Du = 0.03 & Sc = 2.01.

Figure 11. Concentration profiles.

Figure 12. Nusselt number.
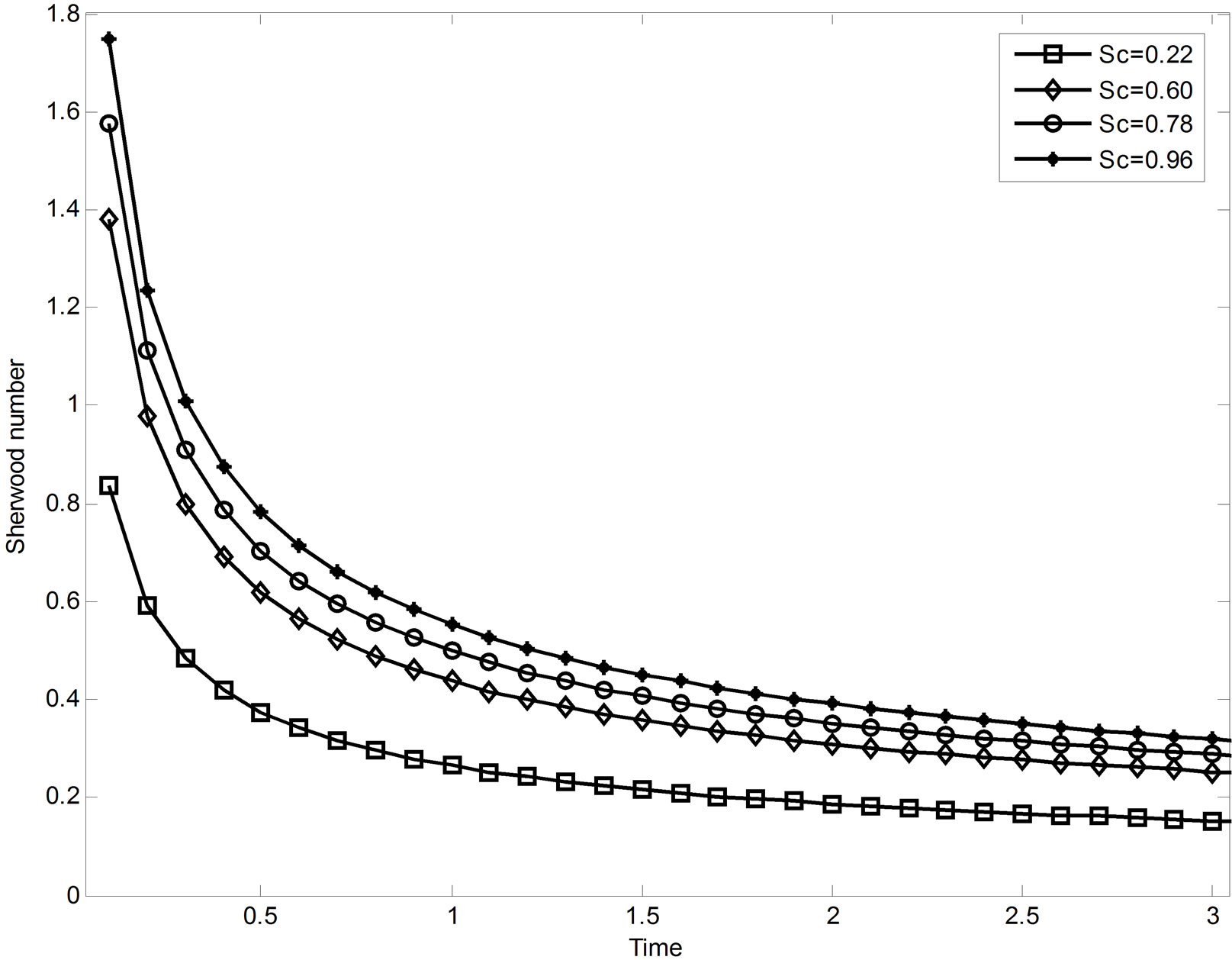
Figure 13. Sherwood number.
effects of Prandtl number Pr on the temperature field. It is observed that an increase in the Prandtl number leads to decrease in the fluid temperature. It is due to the fact that thermal conductivity of the fluid decreases with increasing Pr, resulting a decrease in thermal boundary layer thickness.
The concentration profiles for different values of Schmidt number (Sc) and time t are presented in Figure 11. From this figure it is seen that the concentration decreases with increase in Sc while it increases with time t. Figure 12 reveals the rate of heat transfer coefficient in terms of Nusselt number for different values of radiation parameter R, Prandtl number Pr and Dufour number Dr respectively. It is observed that Nusselt number increases with increasing values of R or Pr but decreases as Du increases. Finally, from Figure 13 it is seen that Sherwood number increases with increase of Sc.
REFERENCES
- B. C. Sakiadis, “Boundary Layer Behavior on Continuous Solid Surfaces: II. Boundary Layer on a Continuous Solid Flat Surfaces,” AIChE Journal, Vol. 7, No. 2, 1961, pp. 221-225. doi:10.1002/aic.690070211
- V. M. Soundalgekar, S. K. Gupta and N. S. Birajdar, “Effects of Mass Transfer and Free Convection Currents on MHD Stokes Problem for a Vertical Plate,” Nuclear Engineering and Design, Vol. 53, No. 3, 1979, pp. 339-346.
- V. M. Soundalgekar, M. R. Patil and M. D. Jahagirdar, “MHD Stokes Problem for a Vertical Plate with Variable Temperature,” Nuclear Engineering and Design, Vol. 64, No. 1, 1981, pp. 39-42. doi:10.1016/0029-5493(81)90030-3
- M. Kumari and G. Nath, “Development of Two Dimensional Boundary Layer with an Applied Magnetic Field Due to an Impulsive Motion,” Indian Journal of Pure and Applied Mathematics, Vol. 30, No. 7, 1999, pp. 695-708.
- W. G. England and A. F. Emery, “Thermal Radiation Effects on the Laminar Free Convection Boundary Layer of an Absorbing Gas,” Journal of Heat Transfer, Vol. 91, No. 1, 1969, pp. 37-44. doi:10.1115/1.3580116
- V. M. Soundalgekar and H. S. Takhar, “Radiation Effects on Free Convection Flow past a Semi-Infinite Vertical Plate,” Modeling, Measurement and Control, Vol. 51, 1993, pp. 31-40.
- M. A. Hossain and H. S. Takhar, “Radiation Effect on Mixed Convection along a Vertical Plate with Uniform Surface Temperature,” Heat and Mass Transfer, Vol. 31, No. 4, 1996, pp. 243-248. doi:10.1007/BF02328616
- A. Raptis and C. Perdikis, “Radiation and Free Convection Flow past a Moving Plate,” International Journal of Applied Mechanics and Engineering, Vol. 4, No. 4, 1999, pp. 817-821.
- U. N. Das, R. K. Deka and V. M. Soundalgekar, “Radiation Effects on Flow past an Impulsively Started Vertical Infinite Plate,” Journal of Theoretical Mechanics, Vol. 1, 1996, pp. 111-115.
- R. Muthucumaraswamy, K. E. Sathappan, and R. Natarajan, “Mass Transfer Effects on Exponentially Accelerated Isothermal Vertical Plate,” International Journal of Applied Mathematics and Mechanics, Vol. 4, No. 6, 2004, pp. 19-25.
- V. Rajesh and S. V. K. Varma, “Radiation and Mass Transfer Effects on MHD Free Convection Flow past an Exponentially Accelerated Vertical Plate with Variable Temperature,” ARPN Journal of Engineering and Applied Sciences, Vol. 4, No. 6, 2009, pp. 20-26.
- A. G. Vijaya Kumar and S. V. K. Varma, “Thermal Radiation and Mass Transfer Effects on MHD Flow past an Impulsively Started Exponentially Accelerated Vertical Plate with Variable Temperature and Mass Diffusion,” Far East Journal of Applied Mathematics, Vol. 55, No. 2 2011, pp. 93-115.
- E. R. G. Eckert and R. M. Drake, “Analysis of Heat and Mass Transfer,” McGraw-Hill, New York, 1972.
- Z. Dursunkaya and W. M. Worek, “Diffusion-Thermo and Thermal-Diffusion Effects in Transient and Steady Natural Convection from Vertical Surface, International Journal of Heat Mass Transfer, Vol. 35, No. 8, 1992, pp. 2060-2065. doi:10.1016/0017-9310(92)90208-A
- M. Anghel, H. S. Takhar and I. Pop, “Dufour and Soret Effects on Free Convection Boundary Layer over a Vertical Surface Embedded in a Porous Medium,” Mathematics, Vol. 11, No. 4, 2000, pp. 11-21.
- A. Postelnicu, “Influence of a Magnetic Field on Heat and Mass Transfer by Natural Convection from Vertical Surfaces in Porous Media Considering Soret and Dofour Effects,” International Journal of Hear and Mass Transfer, 47, No. 6-7, 2004, pp. 1467-1472.
- M. S. Alam, M. M. Rahman and M. A. Smad, “Dufour and Soret Effects on Unsteady MHD Free Convection and Mass Transfer Flow past a Vertical Porous Plate in a Porous Medium,” Nonlinear Analysis: Modelling and Control, Vol. 11, No. 3, 2005, pp. 217-226.
- M. S. Alam and M. M. Rahman, “Dufour and Soret Effects on MHD Free Convection Heat and Mass Transfer Flow past a Vertical Flat Plate Embedded in a Porous Medium,” Journal of Navel Architecture and Marine Engineering, Vol. 2, No. 1, 2005, pp. 55-65.
Nomenclature
 Absorption coefficient
Absorption coefficient
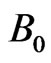 External magnetic field
External magnetic field
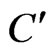 Species concentration
Species concentration
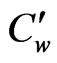 Concentration of the plate
Concentration of the plate
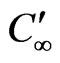 Concentration of the fluid far away from the plate
Concentration of the fluid far away from the plate
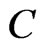 Dimensionless concentration
Dimensionless concentration
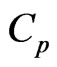 Specific heat at constant pressure
Specific heat at constant pressure
 Concentration susceptibility
Concentration susceptibility
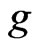 Acceleration due to gravity
Acceleration due to gravity
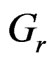 Thermal Grashof number
Thermal Grashof number
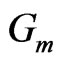 Mass Grashof number
Mass Grashof number
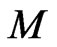 Magnetic field parameter
Magnetic field parameter
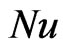 Nusselt number
Nusselt number
 Prandtl number
Prandtl number
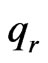 Radiative heat flux in the y-direction
Radiative heat flux in the y-direction
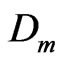 Coefficient of mass diffusivity
Coefficient of mass diffusivity
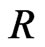 Radiative parameter
Radiative parameter
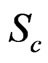 Schmidt number
Schmidt number
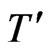 Temperature of the fluid near the plate
Temperature of the fluid near the plate
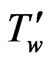 Temperature of the plate
Temperature of the plate
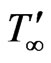 Temperature of the fluid far away from the plate
Temperature of the fluid far away from the plate
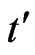 Time
Time
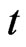 Dimensionless time
Dimensionless time
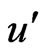 Velocity of the fluid in the
Velocity of the fluid in the  -direction
-direction
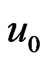 Velocity of the plate
Velocity of the plate
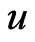 Dimensionless velocity
Dimensionless velocity
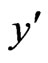 Co-ordinate axis normal to the plate
Co-ordinate axis normal to the plate
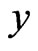 Dimensionless co-ordinate axis normal to the plate
Dimensionless co-ordinate axis normal to the plate
Greek Symbols
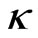 Thermal conductivity of the fluid
Thermal conductivity of the fluid
 Thermal diffusivity
Thermal diffusivity
 Volumetric coefficient of thermal expansion
Volumetric coefficient of thermal expansion
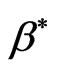 Volumetric coefficient of expansion with concentration
Volumetric coefficient of expansion with concentration
μ Coefficient of viscosity
ν Kinematic viscosity
r Density of the fluid
ρ Electric conductivity
σ Dimensionless temperature
erf Error function
erfc Complementary error function
Subscripts
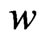 Conditions on the wall
Conditions on the wall
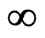 Free stream conditions
Free stream conditions
NOTES
*Corresponding author.

