ABSTRACT

In this work, we studied the performance of modified techniques of Adomian method applied to non-linear Volterra integral equations of the second kind. This study shows that the modified techniques are reliable, efficient and easy to use through recursive relations that involve simple integrals. Furthermore, we found that the right choice and the proper implementation of the modified techniques reduce the computational difficulties and increase the speed of convergent, comparing with the standard Adomian method.

1. Introduction

In recent years, many works have been focusing on the developing and applying of advanced and efficient methods for integral equations such as implicitly linear collocation methods [1], product integration method [2], Hermite-type collocation method [3] and analytical (semianalytical) techniques such as Adomian decomposition method [4,5]. In this work, we investigate the performance of modified techniques of Adomian decomposition method applied to non-linear Volterra integral equations of the second kind. This type of integral equations has the following form

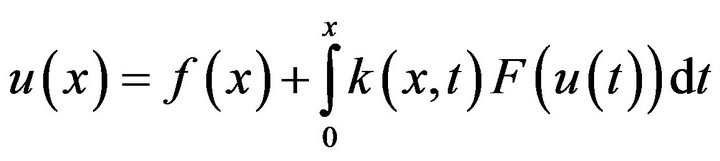. (1.1)

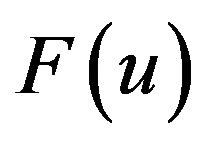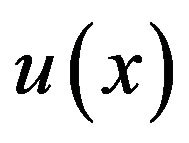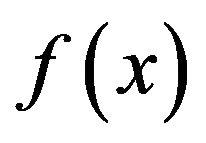Equation (1.1) represents a nonlinear Volterra integral equation of second kind with unknown function and is a non-linear function of, and we assumed that, the kernel and the function are analytical functions on 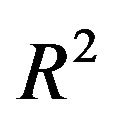and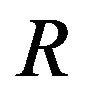, respectively. Hence, Equation (1.1) classifies as a linear Volterra integral equation of second kind if is a linear function of the unknown function.

2. Standard Adomian Method

The standard technique for the non-linear integral Equation (1.1), starts by decomposing into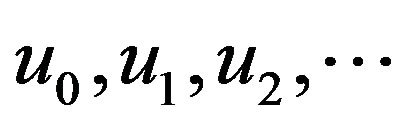, and assuming that

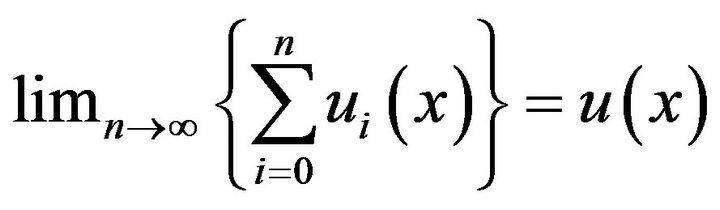. (2.1)

For the non-linear function, we set

(2.2)

In (2.2), 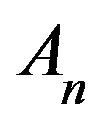, 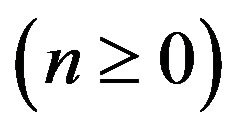are special polynomials known as Adomian polynomials. In ref. [6], close formulas of these polynomials, for any non-linear function, introduced in the terms of the Kronecker delta. With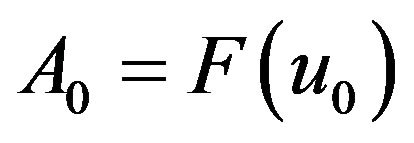, these formulas for read

(2.3)

where

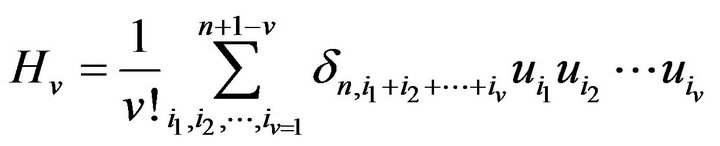
Now Equation (1.1) becomes,

, (2.4)

Now and the can be completely determined by using the recurrent formula

(2.5)

Consequently the solution of the integral Equation (1.1), in a series form, can be immediately determined by using (2.5).

Recently, ref. [7] claims that the choice of the initial data plays an essential rule on improving the performance and the speed of the convergence of the Adomian method. Furthermore, for a complicated function, we can see immediately from the recurrent Formula (2.5) that the standard Adomian method will encounter computational difficulties. To see that, we applied the recurrent Formula (2.5) on the nonlinear Volterra integral equation

. (2.6)

If we choose, then the other components can be found from (2.5) as follows:

Note that, with the help of the Mathematica Packages, we can deduce that these calculations will lead to the exact solution, which is quit hard to see immediately from the above calculations.

3. Modified Techniques

To reduce the computational difficulties of the standard method and accelerate the convergence of this method, we introduce modified techniques of the standard Adomian method [8,9].

First Modified Technique:

In the first modified technique, we assume that the function 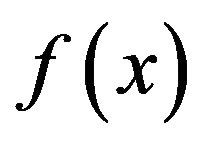can be split as follows

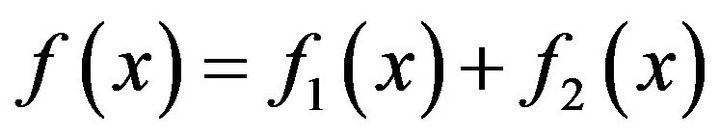. (3.1)

Based on this assumption, we can introduce a slight change for the choice of the components 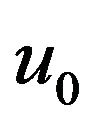and as following

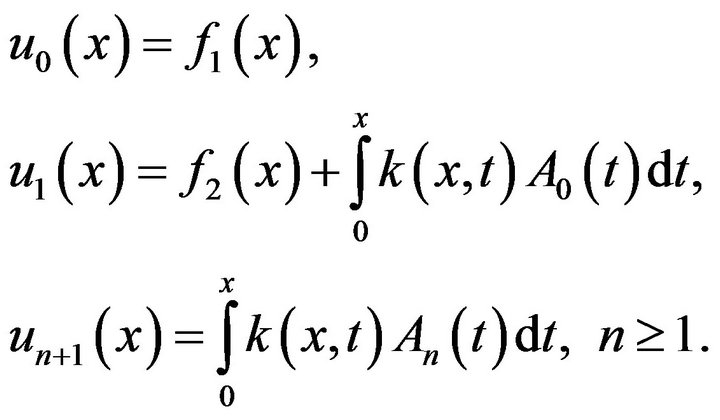(3.2)

As we will see in the next section, this change reduces, the computational difficulties of finding other components and accelerate the convergence of the standard Adomian method procedure. Furthermore, the improvement of the standard Adomian decomposition method, uses the first modified recursive Formula (3.2), depends mainly on the splitting (3.1). In addition, we recommend, to apply the first modified technique, when is given in term of a polynomial or a combination of polynomial and trigonometric, or transcendental, functions.

Second Modified Technique:

The main idea of the second modified technique is replacing the non-homogeneous function by a series of infinite components. Ref. [9] expresses in term of the Taylor series and introduces the recursive formula

(3.3)

In (3.3),; represents the Taylor series components of. Note that, it is easily to observe that the second modified recursive Formula (3.3) minimizes the size of the calculations which produced in the standard Adomian decomposition method. In addition, it is clear that the reduction in each iteration of (3.3), will ease the construction of Adomian polynomials for the non-linear term.

4. Comparison Study

In this section, we compare the modified techniques against the standard Adomian decomposition method. To do that, let us study the following examples of non-linear Volterra integral equations.

Example 1: Consider the nonlinear Volterra integral equation

(4.1)

To investigate the first modified technique, we split into two parts, say

. (4.2)

The modified recursive Formula (3.2) reads

,

This implies, for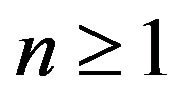. This leads to the exact solution and hence by deploying the right splitting of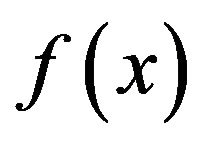, we can avoid the calculation difficulties of Adomian polynomials required for the non-linear term as we will see later.

To investigate the second modified technique, let us first expand the function 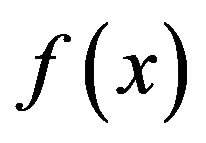in term of Taylor series expansion. This reads

(4.3)

Next, the second modified recursive Formula (3.3) gives

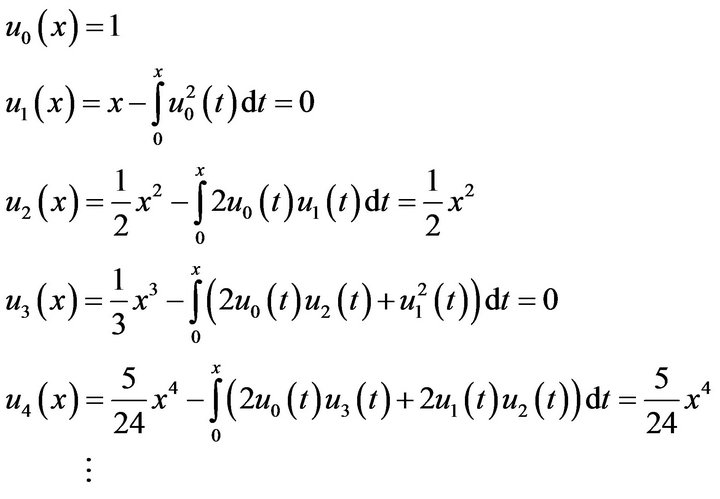(4.4)

This leads to

(4.5)

This is the Taylor series expansion of secx, where 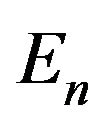represents the 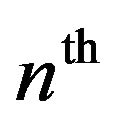Euler number. This study shows that the second modified technique eases the construction of Adomian polynomials for the non-linear term and hence reduces each term of the recursive Formula (3.3). This also shows that the second modified technique, for some cases, improves the performance of the standard method.

To investigate the performance of the standard Adomian method, we use the recurrent Formula (2.5). For the integral Equation (4.1), this reads

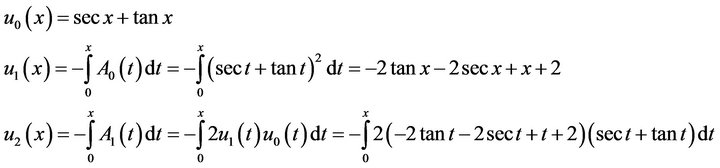(4.6)

This leads to computational difficulties.

Example 2: Consider the nonlinear Volterra integral equation

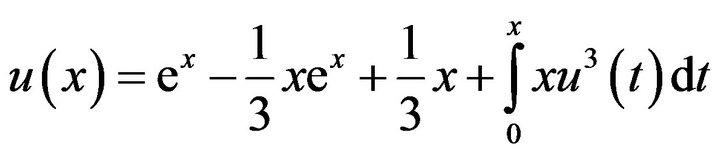(4.7)

To investigate the performance of the standard Adomian method, we use the recurrent Formula (2.5). For the integral Equation (4.7), this reads

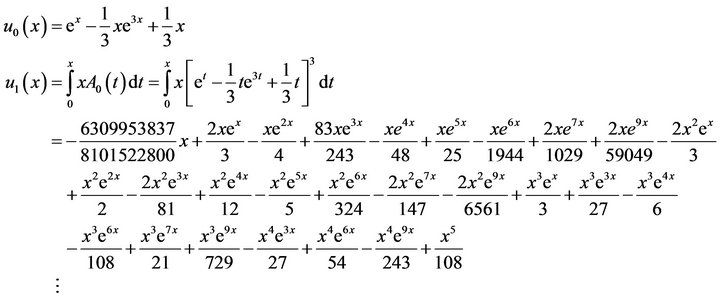(4.8)

To apply the first modified technique, we split into two parts, say

. (4.9)

The modified recursive Formula (3.2) reads

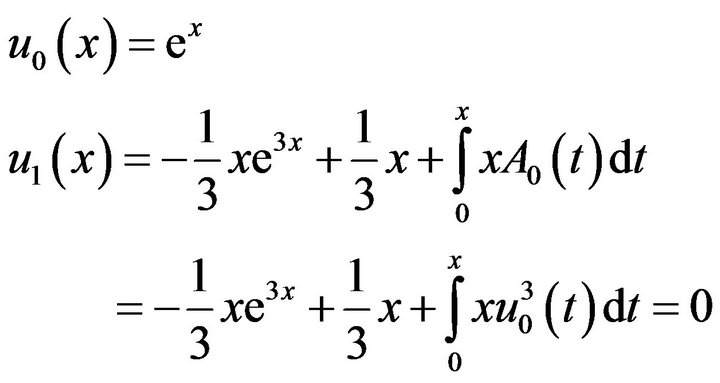(4.10)

This implies that

, (4.11)

which leads to the exact solution.

To apply the second modified technique, let us first expand the function in term of Taylor series expansion, which reads

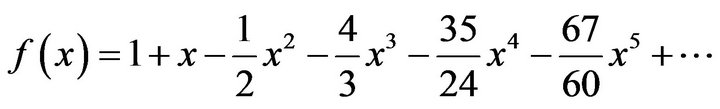(4.12)

Next, the second modified recursive Formula (3.3) gives

(4.13)

This leads to the Taylor series of the exact solution.

Example 3: Consider the non-linear Volterra integral equation

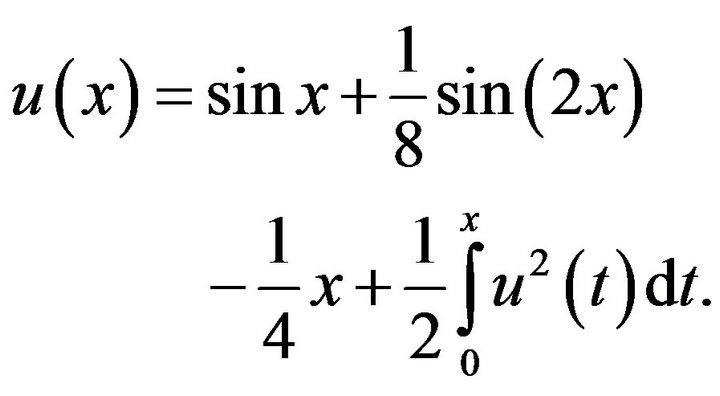(4.15)

To investigate the performance, we first apply the modified technique. To do that, we split 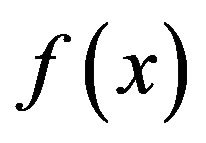into two parts, as

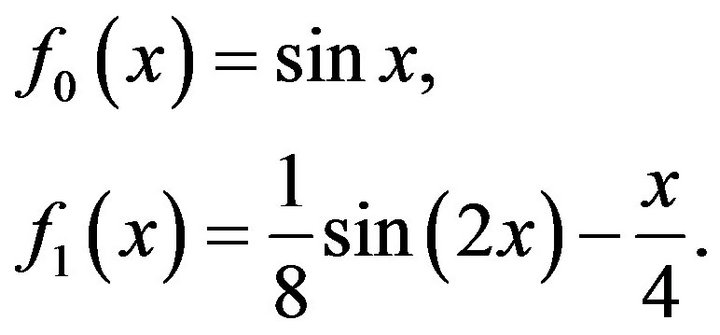(4.16)

The modified recursive Formula (3.2) gives

This implies that

, (4.17)

which leads to the exact solution

To apply the second modified technique, let us first expand the function in term of Taylor series expansion. This reads

(4.18)

Next, the second modified recursive Formula (3.3) gives

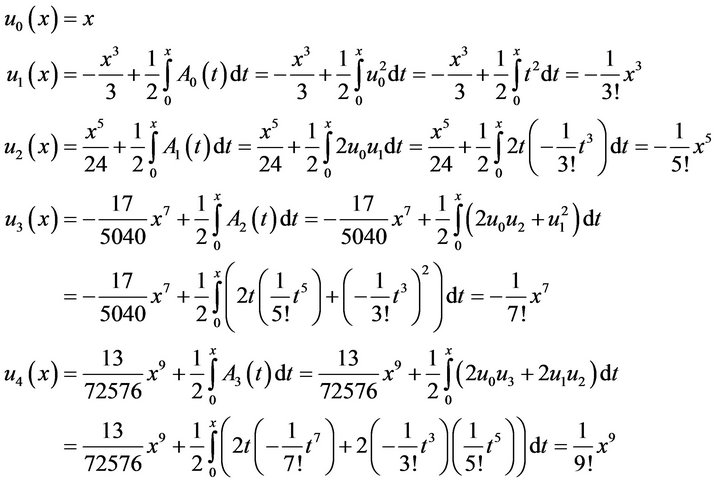(4.19)

This leads to exact solution

To show the computational difficulties of the standard Adomian method, we use the recurrent Formula (2.5). For the integral Equation (4.15), this reads

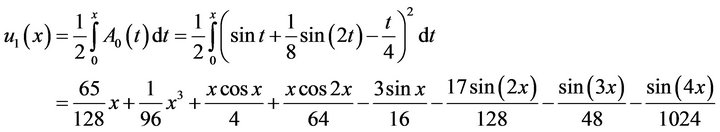
This gives

This shows, the computational difficulties of the standard Adomian decomposition method comparing with the modified techniques.

5. Conclusion

In this work we showed the accuracy, applicability and simplicity of modified techniques of Adomian method applied to non-linear Volterra integral equations. A compression study against the standard Adomian method showed the applicability and the accuracy of the modified techniques. For the modified techniques, this study showed that the first modified technique requires choosing the right splitting of the function. Hence, by using the right splitting, we can avoid the calculation difficulties of using the Adomian polynomials required for the non-linear term. In addition, this study also showed that the second modified technique overcomes the difficulty of the splitting of the function 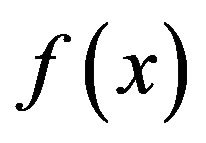and eases the difficulties construction of the Adomian polynomials required for the non-linear term.

REFERENCES