American Journal of Analytical Chemistry
Vol.05 No.05(2014), Article ID:45029,14 pages
10.4236/ajac.2014.55042
Statistical Studies of the Physicochemical Analytic Results of a Series of Synthetic Calcium Hydroxyapatite Containing Carbonate and Sodium
Faouzia Rockh B. Hadj Yahia, Ismail Khattech
Faculty of Science, Chemistry Department, Applied Thermodynamics Laboratory, Tunis El Manar, Tunisia
Email: faouziarockh1@Gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 March 2014; revised 7 April 2014; accepted 15 April 2014
ABSTRACT
The objective of this study is to present a simple method of statistical calculation that allowed us to determine the relationship between the different data obtained from the characterization of the synthetic carbonated apatites containing sodium, in order to find the fundamental substitution mechanism(s) for incorporation of Na+ and 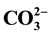 and to establish the general formula. For that, a series of hydroxyapatites containing carbonate and sodium (Na-CO3HAps) has been obtained by the precipitation method. All the compounds were characterized by infrared spectra (IR), powder X-ray diffraction (PXRD) and elemental analysis. The statistical treatment of the experiment result allows us to determine the relationship between one variable and the change in the other and to found the fundamental substitution mechanism(s) for incorporation of Na+ and
and to establish the general formula. For that, a series of hydroxyapatites containing carbonate and sodium (Na-CO3HAps) has been obtained by the precipitation method. All the compounds were characterized by infrared spectra (IR), powder X-ray diffraction (PXRD) and elemental analysis. The statistical treatment of the experiment result allows us to determine the relationship between one variable and the change in the other and to found the fundamental substitution mechanism(s) for incorporation of Na+ and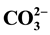 . Analysis of variance (ANOVA) allows us to test the models proposed.
. Analysis of variance (ANOVA) allows us to test the models proposed.
Keywords:
Carbonated Calcium Hydroxyapatite Containing Sodium Na-CO3HAps, Statistical Studies, Multiple Linear Regression, Analysis of Variance (ANOVA)

1. Introduction
Carbonated calcium hydroxyapatite containing sodium and/or potassium, magnesium etc. is the most important mineral compound in human dental, enamel and bone [1] [2] . We can also found this type of apatite in sedimen- tary phosphate apatite [3] . Consequently, these materials have necessitated studies of the effects of ions, such as 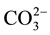 Na+, Mg2+, on the physicochemical properties and especially the mode of
Na+, Mg2+, on the physicochemical properties and especially the mode of 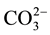 Na+ incorporation in apatite structure. But, the complexity of biological and sedimentary phosphates apatite has returned these studies very difficultly.
Na+ incorporation in apatite structure. But, the complexity of biological and sedimentary phosphates apatite has returned these studies very difficultly.
For this reason, multiple techniques have been used to prepare these products, with wet chemical methods and solid-state reactions [4] -[14] . Carbonate incorporation in synthetic carbonated calcium hydroxyapatites “CO3 HAp” has been classified as either type A or type B depending on the mode of 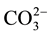 substitution:
substitution: 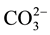 for
for  type A substitution and
type A substitution and 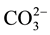 for
for 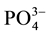 type B substitution [10] [11] .
type B substitution [10] [11] .
In the precipitation of “CO3HAps”, different products are obtained if the calcium solution is added to the phosphate plus carbonate solution “direct” rather than vice versa “inverse” apatite [6] [8] [12] -[14] . All these products are B-Apatite, but it seems that the maximum possible carbonate content was greater in the “direct” apatite compared with “inverse” apatite [13] . Na-free B-type “CO3HAps” has been prepared with a maximum 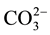 content between 10 wt% at 14 wt%. In the presence of ions such as (Na+, K+ or Mg2+), we have a coupled substitution. With Na+ for Ca2+, B-type apatite “Na-CO3HAps” contains up to 22 wt%
content between 10 wt% at 14 wt%. In the presence of ions such as (Na+, K+ or Mg2+), we have a coupled substitution. With Na+ for Ca2+, B-type apatite “Na-CO3HAps” contains up to 22 wt% 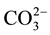 [14] .
[14] .
Based on some studies, such as EPR and IR spectroscopy, X-ray and neutron diffraction, chemical analyses, infrared and Raman spectroscopy, the crystallite size, chemical composition and physicochemical nature of synthetic apatite have been determinated. But there have been multiple studies, speculations and controversy about the mechanism(s) by which 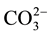 and alkali metal(s) are incorporated in the apatite lattice [15] -[20] . According to De Maeyer et al., the fundamental substitution mechanisms for the incorporation of Na+ and
and alkali metal(s) are incorporated in the apatite lattice [15] -[20] . According to De Maeyer et al., the fundamental substitution mechanisms for the incorporation of Na+ and 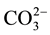 in hydroxyl apatite “HAp” can be described using six basic processes [21] .
in hydroxyl apatite “HAp” can be described using six basic processes [21] .
1) 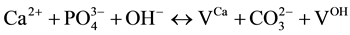
2) 
3) 
4)
5)
6)
where VX is the vacancy on a regular apatite lattice site occupied by X.
Moreover, these authors propose a coupling of different fundamental mechanisms in a fixed proportion, lead- ing to the definition of apparently new mechanisms. The composition of B-type of Na-CO3HAps is determined by the occurrence of one or more of these fundamental mechanisms. Thus, these authors suggest that the stoi- chiometry would be given by:
where a, b, c, d and e are the contribution per unit cell of basic substitutions (I to V) resulting in the fundamental substitution mechanisms for incorporation of Na+ and 
The aim of the present study is to present a statistical method which allows us to determine the relationship between the obtained values and experimental conditions and to estimate the change in one variable from the given increase or decrease in another. The analysis of variance (ANOVA) allows us to test the mathematical model. Finally, the statistical method allows us to find the fundamental substitution mechanism(s) for incorpora- tion of Na+ and
2. Experimental Procedure
2.1. Preparation of Na-CO3HAps
The preparation method is described in detail elsewhere [12] [13] , In brief, The precipitated Na-CO3HAps were prepared by dripping calcium solution 0.03 M (Ca(NO3)2×4H2O) into a phosphate solution 0.008 M of (Na2HPO4×12H2O) which contains also different concentrations of (Na2CO3) such as the molar ratio R:




After hydrolysis which took 3 h, the precipitates were filtered, washed abundantly with hot distilled water (95˚C), dried for 12 h at 70˚C and then heated at 400˚C in air for 24 h in order to eliminate inter- and intra- crystalline water.
2.2. Characterization
2.2.1. Infrared Spectroscopy and X-Ray Diffraction
Na-CO3HAps samples are characterized by IR absorption spectroscopy and X-ray diffraction. In infra-Red, we use pellets of absorption. They are prepared using the usual KBr disk technique. It consists in mixing 1 mg of powder of a sample of Na-CO3HAp with 300 mg KBr then pressed at 6 psi. The pellets so prepared were then scanned on a Shimadzu IR spectrometer in the range (4000 - 400) cm−1.
Powder X-ray diffraction analysis for the Na-CO3HAps samples were carried out using an X-ray diffractome- ter MRD with a generator (40 kV and 40 mA). After indexation of the full pattern, cell parameters were refined using the program “WINCELL”
2.2.2. Chemical Analysis and Density Measurements
The dehydrated samples were subjected to a chemical analysis. The phosphorus content of precipitates is deter- mined by colorimetry after complexation with vanado-molybdate [22] . The sodium and calcium content are ob- tained by atomic absorption spectroscopy and the carbonate content was determined by coulometry method (re- lease of CO2 by dissolution in acid). The hydroxide content % OH was calculated on the basis of electro neutral- ity. Density of the solids was measured by a flotation method [13] .
3. Results
3.1. Physical Analysis
The infra-Red spectrums presented in Figure 1 show that they are typical of apatite containing B-type carbonate [13] . The assignment of absorption bands was made according to the studies [12] [13] . IR analyses of the sam- ples show the effect of increasing 



Figure 1. Absorption Spectra of Na-CO3Haps obtained from solutions with: (A) R = 5, (B) 15 AND (C) 25.
In Figure 2 we presented the X-ray diffraction patterns. The peaks are relatively sharp and well resolved and can all attributed to the hexagonal crystal form of hydroxyapatite, but some shifts of peaks position can be ob- served, reflecting a change in unit cell dimensions due to incorporation of 
3.2. Chemical Results
The compositions of samples in Weight % determined by chemical analysis are displayed in Table 2. The results of quantitative analysis of phosphorus, calcium and sodium were determined with standards deviations 0.17; 0.03 and 0.09 respectively and the amount of CO3 was determined on relative uncertainty 2%.
The results of the chemical and physical analysis (Table 1 and Table 2) allowed us to calculate the number of each ion X per unit cell, nx according to:

where M (r×Vcell×N) is the molar mass, Vcell is the unit cell volume, Mx is the atomic or ionic mass of X and N Avogadro’s constant. The amount of OH ions was calculated taking into account the electroneutrality of each compound. Table 3 gathers the calculation results.
4. Discussion
As in the case of the reference [23] , the last column of Table 3 shows that the sum of the number of phosphate and carbonate per unit cell 



Figure 2. XRD patterns of synthetic apatites obtained from solutions with: (A) R = 5, (B) 15, (C)25.
Table 1. Values of lattice parameters “a”, “c” and volume molar; density and weight (Mw) of the prepared samples.
Table 2. Chemical composition (weight %) and total mass balance S% of Na- CO3HAps prepared from solutions with

Similarly, we have calculated the number of vacancies on Ca2+ and OH− lattice sites respectively:

and

The results of these calculations are summarized in Table 4. The errors in Table 4 were estimated by means of error propagation theory.
Table 3. Unit cell composition of Na-CO3AHps calculated on the basis of the chemical composition and by means of Equa- tion (1).
Table 4. Unit cell compositions of Na-CO3Aaps calculated on the basis of the chemical composition and by means of fol- lowing Equation (2).
Comparing our experiment data with the data available in the literature [24] -[26] , we can found that the presents results are in agreement with those of reference [25] , though, this series was prepared by hydrolysis of monetite in solution with varied 
So, it may be said in the present study, that the fundamental substitution mechanisms (I, III and IV) could ac- count for the incorporation of 


and

and the generic formula has the following expression:
5. Statistical Studies
The objective of this study is to construct a mathematical model which allows us to estimate the change in Y the dependent variable from a given increase or decrease in X the independent variable and to determine which me- chanism(s) is related with experimental conditions.
The mathematical model is expressed as:

where ei is the random variable drawn from N(0, s2), b0 and bj are the estimated regression coefficients. The model assumes that their deviation ε from the line is normally distributed with means 0 and constant variances s2.
Least square method [26] allows calculating the regression and correlation coefficients, the variance of the b parameters and to test the null hypothesis H0: bj = 0 and their significances level. The analysis of variance for the linear regression or the F test allows us to be confident that at least one of X-variable contributes to the regression. The theoretical basis of these calculations is given in references [12] [26] .
5.1. Multiple Linear Regression of Y = c/a Crystallographic Parameters Ratio on 
In attempts to disentangle and to measure the effects of the insertion of 

The multiple linear regression (Table 5(a)) indicates that the ratio of the hexagonal lattice dimensions of Na-CO3Aps “c/a” vary linearly with the carbonate and sodium content according to:

The analysis of variance (Table 5(b)/ANOVA) shows further that F-test = 100.5 is higher than criterion F(5%; 2.9) = 4.26. This allowed us to rejet H0: b1 = b2 = 0 and affirm that at least one of the predictors is linearly asso- ciated to the response.
T-test of of the estimated regression coefficients b1 and b2 has shown that b2 and b1 are significant at 70% level.
5.2. Multiple Linear Regression of 

To understand the influence of the experimental conditions on the composition of these apatites (data Table 4), we conducted a multiple linear regression [22] on two X-variables where, X1 and X2 are the Na+ and 
Table 5. calculation for fitting a multiple linear regression analysis of the estimated Y = c/a the ratio of the lattice parameters of Na-CO3HApson carbonate and sodium contents X1 = wt% CO3, X2 = wt% Na. (a) Calculation of regression, correlation coefficients and variances, (b) F-test: Analysis of Variance.
concentrations in solution and Y is the estimates molar ratios of 
The multiple linear regression (Table 6(a)) indicates that the molar CO3/P ratio of the Na-CO3HAps vary linearly with the concentrations of carbonate and sodium in solution according to:

The result of the F-test (Table 6(b)) F = 635.5 and the individual t-test of the b’s Table 6 b for b1, t = −7.82. For b2, t = 8.26 confirm that the molar CO3/P ratio of Na-CO3HAps solid is significantly depends on both con- centrations of carbonate 


CO3/P molar ratio is constant. This shows that for 
increase on molar 


The multiple linear regression (Table 7(a)) indicates that the molar Na/P ratio of Na-CO3HAps vary linearly with the carbonate content according to:

An analysis of variance (Table 7(b)/ANOVA), further shows that F-test = 43.5 is higher than criterion F(1%, 2.10) = 7.56, this allowed us to rejet H0: b1 = b2 = 0 and affirm that at least one of the predictors is linearly as- sociated to the response. T-test of the regression coefficients b1 and b2 has shown for b1, t = −0.45 signifiant at 30% level. For b2, t = 1.67 signifiant at 80% level.
5.3. Multiple Linear Regression of the Estimated Molar Content of Calcium 


The examination of Table 4 showed too that nCa molar content of the solid decreases when 
From Table 8, the multiple linear regression analysis shows that the relationship between these quantities is given by equation:
Table 6. Calculation for fitting a multiple linear regression of the estimated 

Table 7. Calculation for fitting a multiple linear regression analysis of the estimated Y = nNa/nP molar ratio in Na-CO3HAps solid on X1 = [Na+] and 

From the intercept of the following equation it can seen that, within experimental error, a carbonate-free apa- tite 


The analysis of variance (Table 8(b)), further shows that F-test = 379.4 is higher than criterion F(5%, 2.9) = 4.26, this allowed us to rejet H0: b1 = b2 = 0 and affirm that at least one of the predictors is linearly associated to the response. T-tests of the regression coefficients b1 and b2 show that the value of: b1 is signifiant at 80% level and for b2 is signifiant at 90% level.
5.4. Multiple Linear Regression of Y = a, c or d the Contributions of Mechanisms I, III and IV on X1 = [Na+] and 
For determine which mechanism(s) is related with experimental conditions, we have undertaken a statistical analysis [26] of the values of a, c and d the contribution of the mechanisms I, III and IV (Table 9) calculated according to the following Equations (5)-(7) as a function of Na+ and 
Table 8. Calculation for fitting a multiple linear regression of the estimated 


Table 9. Values of (a, c and d) the estimated contribution of the mechanism I, II and IV.
From Table 10, the multiple linear regression analysis shows that the relationship between these quantities is given by equation:

An analysis of variance (Table 10(b)/ANOVA), further shows that F-test = 25.36 is higher than criterion F (5%, 2.9) = 4.26, this allowed us to rejet: is linearly H0: b1 = b2 = 0 and affirm that at least one of the predictors associated to the response. The individuals t-test of the regression show that for b1, t = 0.79 signifiant at 60% level and for b2, t = −0.70 signifiant at 50% level.
Table 10. Calculation for fitting a multiple linear regression of the estimated 

Table 11. Calculation for fitting a multiple linear regression of the estimated 

From Table 11, the multiple linear regression analysis shows that the relationship between these quantities is given by equation:

An analysis of variance (Table 11(b)/ANOVA), further shows that F-test = 163.55 is higher than criterion F(5%, 2.9) = 4.26, this allowed us to rejet H0: b1 = b2 = 0 and affirm that at least one of the predictors is linearly associated to the response. The individual t-tests on the regression coefficients b1 and b2 and, Hence, for b1, t = 10, for b2, t = −9.8 t(b1) and t(b2) are signifiants at P > 99.9% level.
From Table 12, the multiple linear regression analysis shows that the relationship between these quantities is given by equation:

An analysis of variance (Table 12(b)/ANOVA), further shows that F-test = 0.10 is lower than criterion F(5%, 2.9) = 4.26, this test affirm that mechanism IV is unrelated to experiment conditions. The result of the present study provide that mechanisms I and III are the main in incorporation of Na+ and 
5.5. Multiple Linear Regression Analysis for the Determination of Formula of Unit Cell
The determination of unit cell has been realized by a multiple linear regression between the variables Y = nCa and X1 = a, X2 = c, X3 = d. Least square allows calculating the regression and correlation coefficients. The sample regression (prediction equation) is:



where n is sample size, m is number of parameters and 
From Table 13, the multiple linear regression analysis shows that the relationship between these quantities is given by equation:

Table 12. Calculation for fitting a multiple linear regression of the estimated Y = d = nNa ? c the contribution of the mechanism IV on the concentration of Na+: X1,i and the concentration of
Table 13. Calculation for fitting a multiple linear regression of the estimated Y = nCa =Y in Na-CO3HAps on the contribution of mechanism I a: X1i, contribution of mechanism III c: X2i contribution of mechanism IV d: X3i.
An analysis of variance (ANOVA), further shows that F-test = 2018.9 is higher than criterion F(5%, 2.9) = 4.26, this allowed us to rejet H0: b1 = b2 = b3 = 0 and affirm that at least one of the predictors is linearly asso- ciated to the response.
for testing the regression coefficients b1, b2 and b3 and discovering with variable(s) is related to estimate Y = nCa, we conduct on the one hand individual t-tests on the b’s, Hence, for b1, t = −5.28, for b2, t = −28.3 and for b3, t = −1.2 t(b1) and t(b2) are signifiants at P > 99.9% level. Thus, the molar nCa of Na-CO3Aps solid is signifi- cantly depends on both a and c contributions of mechanisms I and III. The general formula can be written as fol- lows:
Also, structural study for two samples obtained under comparable conditions [28] has been investigated ex- tensively by physicochemical analysis and by Rietveld method refinements. The results of unit cell content cal- culated from the occupations of the atomic sites and the data of chemical composition 
(The sum of mechanism II and III)

These results show that we cannot consider unique and well defined substitution mechanisms resulting in apa- tites, especially for homogeneous precipitation methods in aqueous solutions, because the lack of control of the reaction parameters as well as incomplete analyses of the solids could result in erroneous interpretations of the substitution mechanism.
On the other hand El Feki et al. [28] confirm that no vacancies of OH− are observed by Rietveld refinements. But, small fraction of vacancies is undetectable by this method and was ignored in the structure refinements.
6. Conclusion
The different statistical analyses present in this review mainly focused on original and new approaches of the knowledge of the substitutions mechanisms. However, in biological calcifications, part of lattice ions of Hap are substituted to considerable extent ions. Consequently, these substitutions have an important influence on several processes (the growth, the dissolution, the mineralization and the demineralization processes. In order to derive the fundamental thermodynamic properties of the solid which determine the course of these processes, the stoi- chiometry of the apatite and especially of the mechanisms by which 
References
- LeGeros, R.Z. (1981) Apatites in Biological Systems. Progress in Crystal Growth and Characterization of Materials, 4, 1-45. http://dx.doi.org/10.1016/0146-3535(81)90046-0
- Nagy, G., Lorand, T., Patonai, Z., Montsko, I., Bajnoczky, G., Marcsik, A. and Marka, L. (2008) Analysis of Patholo- gical and Non-Pathological Human Skeletal Remains by FT-IR Spectroscopy. Forensic Science International, 175, 55- 60. http://dx.doi.org/10.1016/j.forsciint.2007.05.008
- Follmi, K.B. (1996) The Phosphorus Cycle, Phosphogenesis and Marine Phosphate-Rich Deposits. Earth-Science Reviews, 40, 55-124. http://dx.doi.org/10.1016/0012-8252(95)00049-6
- Frank-Kamenetskaya, O., Kol’tsov, A., Kuz’mina, M., Zorina, M. and Poritskaya, L. (2011) Ion Substitutions and Non- Stoichiometry of Carbonated Apatite-(CaOH)) Synthesized by Precipitation and Hydrothermal Methods. Journal of Molecular Structure, 992, 9-18. http://dx.doi.org/10.1016/j.molstruc.2011.02.013
- Larson, P.R., Madden, A.S. and Tas, A.C. (2013) Non-Stirred Synthesis of Na- and Mg-Doped, Carbonated Apatitic Calcium Phosphate. Ceramics International, 39, 1485-1493. http://dx.doi.org/10.1016/j.ceramint.2012.07.095
- Lafon, J.P., Champion, E. and Bernache-Assollant, D. (2008) Processing of AB-Type Carbonated Hydroxyapatite Ca10−x(PO4)6−x(CO3)x(OH)2−x−2y(CO3)y Ceramics with Controlled Composition. Journal of the European Ceramic Soci- ety, 28, 139-147. http://dx.doi.org/10.1016/j.jeurceramsoc.2007.06.009
- Apfelbaum, F., Diab, H., Mayer, I. and Featherstone, J.D.B. (1992) An FTIR Study of Carbonate in Synthetic Apatites. Journal of Inorganic Biochemistry, 45, 4277-4282. http://dx.doi.org/10.1016/0162-0134(92)84016-G
- Zendah, H., Khattech, I. and Jemal, M. (2013) Thermochemical and Kinetic Studies of The Acid Attack of “B” Type Carbonate Fluorapatites at Different Temperatures 25˚C - 55˚C. Thermochimica Acta, 565, 46-51. http://dx.doi.org/10.1016/j.tca.2013.04.033
- Yao, F. and LeGeros, R.Z. (2010) Carbonate and Fluoride Incorporation in Synthetic Apatites: Comparative Effect on Physico-Chemical Properties and in Vitro Bioactivity in Fetal Bovine Serum. Materials Science and Engineering C, 30, 3423-3430. http://dx.doi.org/10.1016/j.msec.2009.12.011
- Schramm, D.U. and Rossi, A.M (2000) Electron Spin Resonance (ESR) Studies of CO2-Radicals in Irradiated A and B-Type Carbonate-containing Apatites. Applied Radiation and Isotopes, 52, 1085-1091. http://dx.doi.org/10.1016/S0969-8043(00)00046-4
- Fleet, M.E. and Liu, X. (2007) Coupled Substitution of Type A and B Carbonate in Sodium-Bearing Apatite. Bi- omaterials, 28, 916-926. http://dx.doi.org/10.1016/j.biomaterials.2006.11.003
- Bel Hadj Yahia, F. and Jemal, M. (2010) Structural Analysis and Thermochemistry of B-Type Carbonate Apatites. Thermochimica Acta, 505, 22-32. http://dx.doi.org/10.1016/j.tca.2010.03.017
- El Feki, H. (1990) Synthèse et Etude de la Décomposition Thermique d’Hydroxy et de Fluorapatites Carbonatées Pho- sphocalciques Sodées. Ph.D. Dissertation, Tunis II University, Tunis.
- Elliott, J.C. (1994) Structure and Chemistry of the Apatites and Other Calcium Orthophosphates. Elsevier, Amsterdam.
- Labarthe, J.C., Bonel, G. and Montel, G. (1973) Sur la Structure et les propriétés des Apatites Carbonatés de type B Pho- sphocalciques. Annali di Chimica, 8, 289-301.
- Vignoles, M., Labarthe, J.C. and Vignoles, C. (1978) Contribution à L’étude Structurale des Apatites Carbonatées de type B. Colloques Internationaux du CNRS, 230, 117-125.
- Vignoles, M., Bonel, G., Labarthe, J.C. and Bacquet, G. (1982) Etude Physico Chimique des Apatites Carbonatées Phosphocalciques Semblables à la Francolite. Bull. Minéral., 105, 307-311.
- Khattech, I. and Jemal, M. (1985) Etude de la Décomposition Thermique de Fluorapatites Carbonatées. Thermochi- mica Acta, 95, 119-128. http://dx.doi.org/10.1016/0040-6031(85)80039-3
- Khattech, I. and Jemal, M. (1987) Décomposition Thermique de Fluorapatites Carbonatées de Type B “Inverses”. Thermochimica Acta, 118, 267-275. http://dx.doi.org/10.1016/0040-6031(87)80090-4
- El Feki, H., Khattech, I., Jemal, M. and Rey, C. (1994) Decomposition thermique d’hydroxyapatites carbonatées so- dées Thermal decomposition of carbonated hydroxyapatites containing sodium ions. Thermochimica Acta, 237, 99- 110. http://dx.doi.org/10.1016/0040-6031(94)85188-3
- De Maeyer, E.A.P. and Verbeeck, R.M.H. (1993) Possible Substitution Mechanisms for Sodium and Carbonate in Cal- ciumhydroxyapatite. Bulletin des Sociétés Chimiques Belges, 102, 601-609. http://dx.doi.org/10.1002/bscb.19931020907
- Charlot, G. (1966) Les Méthodes de la Chimie Analytique. Masson, Paris.
- De Maeyer, E.A.P., Verbeeck, R.M.H. and Nassens, D.E. (1994) Effect of Heating on the Constitution of Na+- and
Containing Apatites Obtained by Hydrolysis of Monetite. Inorganic Chemistry, 33, 5999-6006. >http://html.scirp.org/file/7-2200818x140.png" class="200" /> Containing Apatites Obtained by Hydrolysis of Monetite. Inorganic Chemistry, 33, 5999-6006. http://dx.doi.org/10.1021/ic00104a006
- De Maeyer, E.A.P., Verbeeck, R.M.H. and Nassens, D.E. (1994) Optimalization of the Preparation of Na+- and
Containing Hydroxyapatites by the Hydrolysis of Monetite. Journal of Crystal Growth, 135, 539-547. >http://html.scirp.org/file/7-2200818x141.png" class="200" /> Containing Hydroxyapatites by the Hydrolysis of Monetite. Journal of Crystal Growth, 135, 539-547. http://dx.doi.org/10.1016/0022-0248(94)90145-7
- De Maeyer, E.A.P., Verbeeck, R.M.H. and Pieters, I.Y. (1996) Influence of the Solution Composition on the Stoichi- ometry of Na+- and of K+-Containing Carbonated Apatites Obtained by The Hydrolysis of Monetite. Journal of Crystal Growth, 169, 539-547. http://dx.doi.org/10.1016/S0022-0248(96)00424-1
- Snedecor, G.W. and Cochran, W.G. (1980) Statistical Methods. 7th Edition, The Iowa State University Press, Ames.
- Borcard, D. (2009) Régression Multiple. Université de Montréal. http://biol09.biol.umontreal.ca/BIO2042/Regr_mult.pdf
- El Feki, H., Savariault, J.M., Ben Salah, A. and Jemal, M. (2000) Sodium and Carbonate Distribution in Substituted Calcium Hydroxyapatite. Solid State Sciences, 2, 577-586. http://dx.doi.org/10.1016/S1293-2558(00)01059-1













 Containing Apatites Obtained by Hydrolysis of Monetite. Inorganic Chemistry, 33, 5999-6006. >http://html.scirp.org/file/7-2200818x140.png" class="200" /> Containing Apatites Obtained by Hydrolysis of Monetite. Inorganic Chemistry, 33, 5999-6006.
Containing Apatites Obtained by Hydrolysis of Monetite. Inorganic Chemistry, 33, 5999-6006. >http://html.scirp.org/file/7-2200818x140.png" class="200" /> Containing Apatites Obtained by Hydrolysis of Monetite. Inorganic Chemistry, 33, 5999-6006.  Containing Hydroxyapatites by the Hydrolysis of Monetite. Journal of Crystal Growth, 135, 539-547. >http://html.scirp.org/file/7-2200818x141.png" class="200" /> Containing Hydroxyapatites by the Hydrolysis of Monetite. Journal of Crystal Growth, 135, 539-547.
Containing Hydroxyapatites by the Hydrolysis of Monetite. Journal of Crystal Growth, 135, 539-547. >http://html.scirp.org/file/7-2200818x141.png" class="200" /> Containing Hydroxyapatites by the Hydrolysis of Monetite. Journal of Crystal Growth, 135, 539-547.