Modeling and Numerical Simulation of Material Science
Vol.4 No.1(2014), Article ID:42129,16 pages DOI:10.4236/mnsms.2014.41007
Modelling of the Quantum Transport in Strained Si/SiGe/Si Superlattices Based P-i-n Infrared Photodetectors for 1.3 - 1.55 µm Optical Communication
1Department of Physics, Faculty of Sciences of Monastir, Laboratory of Condensed Matter and Nanosciences (LMCN), Monastir, Tunisia
2Interdisciplinary Nanoscience Centre of Marseille (CINaM), Aix-Marseille University, Marseille, FranceEmail: *sfina_fsm@yahoo.fr
Copyright © 2014 Noureddine Sfina et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Noureddine Sfina et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 16, 2013; revised December 16, 2013; accepted December 23, 2013
Keywords:Strained SiGe/Si Quantum Wells; Band Structure; Device Engineering; P-i-n Infrared Photodetectors
ABSTRACT
In this paper, a p-i-n heterojunction based on strain-compensated Si/Si1−xGex/Si multiple quantum wells on relaxed Si1−yGey is proposed for photodetection applications. The Si1−yGey/Si/Si1−xGex/Si/Si1−yGey stack consists in a W-like potential profile strain-compensated in the two low absorption windows of silica fibers infrared (IR) photodetectors. These computations have been used for the study of p-i-n infrared photodetectors operating at room temperature (RT) in the range 1.3 - 1.55 μm. The electron transport in the Si/Si1−xGex/Si multi-quantum wells-based p-i-n structure was analyzed and numerically simulated taking into account tunneling process and thermally activated transfer through the barriers mainly. These processes were modeled with a system of Schrödinger and kinetic equations self-consistently resolved with the Poisson equation. Temperature dependence of zero-bias resistance area product (R0A) and bias-dependent dynamic resistance of the diode have been analyzed in details to investigate the contribution of dark current mechanisms which reduce the electrical performances of the diode.
1. Introduction
Although III-V compounds, such as InGaAs latticematched to InP, offer superior optical performance over the Si-based ones in photodetectors at wavelengths near 1.3 and 1.55 µm for optical fiber communications [1], the compatibility of silicon materials with the state-of-the-art VLSI technology stimulates a great number of research efforts to take advantage of the feasibility of photodetectors with wavelengths beyond the limitation of the Si band gap, to 1.3 µm and even to 1.5 µm [2,3]. Recent advances in Si low-temperature epitaxy such as molecular beam epitaxy (MBE) and ultra-high vacuum chemical vapor deposition (UHV-CVD) enable the incorporation of Ge into Si to form high quality SiGe alloys, and thus to extend the spectral response to this wavelength range [4-6]. Because of the large lattice mismatch between Si and Ge, the critical thickness for a strained SiGe layer with a high Ge content exceeding 60% is limited to less than 100 Å. This limitation prevents the use of strained SiGe materials for photodetector applications operating at normal incidence since a sufficiently large absorption depth is required to achieve appreciable quantum efficiency. Although Si/Si0.4Ge0.6/Si multiple-quantum wells (MQWs) strained layers have been demonstrated in electro-optical modulators involving interband transitions for normal incidence operation [7], so far only waveguide structures with laterally-injected light have been reported for photodetectors thanks to their enhanced light absorbing length [8]. Therefore, a larger Ge content is necessary to generate sufficient optical absorption at 1.3 or 1.5 µm wavelengths. This will require a thicker graded buffer to reduce the threading dislocation density in the relaxed absorber layer [9]. It is apparent that for large Ge contents, this approach would be applicable only with very thick buffer layers, and will not suit industrial applications on one hand. On the other hand, if multiple SiGe/Si strained layers are used for light absorption instead of a single strained layer, the total absorbing layer thickness will increase to the critical thickness with a Ge content equivalent to the average composition of the overall multilayer. Together with the strain induced band gap narrowing (to increase the absorption coefficient at a given wavelength), it is expected that photodetectors with an appreciable sensitivity at normal incidence is possible by using such strained layer super lattices [10]. In this work, we report the theoretical simulation of Si/Si0.4Ge0.6/Si p-i-n infrared photodetectors operating at room temperature around 1.3 - 1.55 μm. The active layer of the infrared photodetector consists of alternating layers of strain-compensated Si/Si0.40Ge0.60/Si MQWs grown on relaxed Si0.75Ge0.25 virtual substrates. The design of such quantum wells having a W-like alignment of the conduction and valence bands has been proposed earlier [11]. The active photodetector absorption layer consists of seven W cells separated by 10-nm-thick Si0.75Ge0.25 spacers. The aim of this work is the presentation of a comprehensive model of electron and hole quantum transport mechanisms through the strain-compensated Si0.75Ge0.25/Si/Si0.4Ge0.6/Si/Si0.75Ge0.25 MQWs. We investigated dark current contributing mechanisms through the temperature dependence of zero-bias resistance area product (R0A) and the bias dependence of dynamic resistance of the diode. The dark current versus the bias voltage and temperature dependence of zero-bias resistance area product of the diode are studied with numerical simulations.
2. Presentation of the Structure
The energy minima of the valence-band in compressively strained Si0.4Ge0.6 and tensile Si layers are given by the strain-splitted heavy-holes and light-holes bands respectively, while the fourfold  and the twofold
and the twofold  strain-splitted bands set the energy minimum of the conduction band respectively. The corresponding valence and conduction band offsets at pseudomorphic Si0.75 Ge0.25/Si and Si/Si0.40Ge0.60 heterointerfaces are
strain-splitted bands set the energy minimum of the conduction band respectively. The corresponding valence and conduction band offsets at pseudomorphic Si0.75 Ge0.25/Si and Si/Si0.40Ge0.60 heterointerfaces are ;
; ,
,  and
and , respectively. The transverse and in-plane electron effective masses are nearly independent of the composition being
, respectively. The transverse and in-plane electron effective masses are nearly independent of the composition being  and
and  for strained Si (and relaxed Si0.75Ge0.25) and
for strained Si (and relaxed Si0.75Ge0.25) and  and
and  for strained Si0.40Ge0.60. The transverse and in-plane heavy-hole effective masses are strain independent with
for strained Si0.40Ge0.60. The transverse and in-plane heavy-hole effective masses are strain independent with , 0.26, and 0.23 and,
, 0.26, and 0.23 and,  , 0.13, and 0.08 for Si, Si0.75Ge0.25 and Si0.40Ge0.60 layers, respectively. The transverse and in-plane light-hole effective masses are
, 0.13, and 0.08 for Si, Si0.75Ge0.25 and Si0.40Ge0.60 layers, respectively. The transverse and in-plane light-hole effective masses are  0.17, 0.11, and 0.12, and
0.17, 0.11, and 0.12, and  0.29, 0.19, and 0.09 for Si, Si0.75Ge0.25 and Si0.40Ge0.60 strained layers, respectively. Figure 1(a) shows the Band profiles, energy levels and wave functions of fundamental electron e1 and heavyhole hh1 levels for the Si(2 nm)/Si0.4Ge0.6(3 nm)/Si(2 nm) W quantum well (QW) cell designed for infrared (IR) detection at 1.55 μm. The fundamental sample design consists of a p-i-n infrared photodetector with MQW embedded in the intrinsic region, as shown in Figure 1. The highly n-doped and p-doped buffer regions are composed of 75% Si and 25% Ge (Si0.75Ge0.25) and the nominally strain-balanced QW structure consists of pure Si wells with Si0.4Ge0.6 barriers. The band structures of the W-like potential profile, used to form the device, are sketched in Figure 1(b). Since Si and Ge are both indirect band gap materials, the global conduction band minima are not at the zone center. Si indirect gap is at the Δ valleys along the (001) crystal directions and Ge’s is at the L points in the (111) directions [12,13]. Tensile strained Si wells and compressive strained Si1−xGex barriers are designed to give an overall strain-balanced MQWs structure with an average material composition of the adjacent Si1−yGey regions. The edges of the valence and the conduction bands of the p-i-n heterojunction based on the seven W-period MQWs with the Fermi level and the quantum levels are drawn with their relative wave function at zero bias as shown in Figure 1(a).
0.29, 0.19, and 0.09 for Si, Si0.75Ge0.25 and Si0.40Ge0.60 strained layers, respectively. Figure 1(a) shows the Band profiles, energy levels and wave functions of fundamental electron e1 and heavyhole hh1 levels for the Si(2 nm)/Si0.4Ge0.6(3 nm)/Si(2 nm) W quantum well (QW) cell designed for infrared (IR) detection at 1.55 μm. The fundamental sample design consists of a p-i-n infrared photodetector with MQW embedded in the intrinsic region, as shown in Figure 1. The highly n-doped and p-doped buffer regions are composed of 75% Si and 25% Ge (Si0.75Ge0.25) and the nominally strain-balanced QW structure consists of pure Si wells with Si0.4Ge0.6 barriers. The band structures of the W-like potential profile, used to form the device, are sketched in Figure 1(b). Since Si and Ge are both indirect band gap materials, the global conduction band minima are not at the zone center. Si indirect gap is at the Δ valleys along the (001) crystal directions and Ge’s is at the L points in the (111) directions [12,13]. Tensile strained Si wells and compressive strained Si1−xGex barriers are designed to give an overall strain-balanced MQWs structure with an average material composition of the adjacent Si1−yGey regions. The edges of the valence and the conduction bands of the p-i-n heterojunction based on the seven W-period MQWs with the Fermi level and the quantum levels are drawn with their relative wave function at zero bias as shown in Figure 1(a).
3. Theoretical Model
The model of quantum transport is developed for a p-Si1−yGеy/Si1−yGеy/Si/Si1−xGеx/Si/Si1−yGеy/n-Si1−yGеy device in which external p-Si1−yGеy/Si1−yGеy and Si1−yGеy/n-Si1−yGеy regions act as electron injector and collector for internal Si1−yGеy/Si/Si1−xGеx/Si/Si1−yGеy quantum well. The lower energy conduction band is solely considered, that corresponds to the six-fold , four-fold
, four-fold  and two-fold
and two-fold  degenerated valleys for Si1−yGеy injecting contacts, Si1−xGеx potential barriers and Si quantum wells region, respectively (see Ref. [11]). The band diagram of the single W structure under an external applied voltage
degenerated valleys for Si1−yGеy injecting contacts, Si1−xGеx potential barriers and Si quantum wells region, respectively (see Ref. [11]). The band diagram of the single W structure under an external applied voltage  and possible mechanisms of electron transport are shown schematically in Figure 2. The tunneling process in this structure between Si quantum wells is supposed to be a general carrier transfer mechanism (mechanism 1 in Figure 2). The pre-confinement Si regions forward and afterwards the Si1−xGеx barrier stack accumulate electrons. They fill the states possessing energy close to the bottom of the
and possible mechanisms of electron transport are shown schematically in Figure 2. The tunneling process in this structure between Si quantum wells is supposed to be a general carrier transfer mechanism (mechanism 1 in Figure 2). The pre-confinement Si regions forward and afterwards the Si1−xGеx barrier stack accumulate electrons. They fill the states possessing energy close to the bottom of the


Figure 1. (a) Conduction and valence bands profile along the strained Si1−yGey/Si/Si1−xGex/Si/Si1−yGey structure with straininduced energy-splitted bands. In insert are shown the six iso-energetic ellipsoidal surfaces of conduction for unstrained Si1−yGеy; (b) Schematic diagram of a p-i-n photodetectors. The cross-sectional view shows the structure of strained SiGe/Si W-multiple quantum wells grown on silicon on relaxed SiGe direct buffers.

Figure 2. Energy band diagram of p-Si1−yGеy/Si1−yGеy/Si/ Si1−xGеx/Si/Si1−yGеy/n-Si1−yGеy (y = 0.25, x = 0.60) stack under an external bias, and carrier behavior inside the structure: 1 is the tunneling transfer from extended states, 2 is the tunneling transfer from the localized states in preconfinement region, and 3 is the thermally activated carrier transport.
silicon well, which can be identified as localized states. Electron tunneling from these states through the stack provides an additional component to the charge flow through the device (mechanism 2 in Figure 2). The relatively low potential barriers for electrons and “relaxed type” of injecting contacts open a possibility for thermally activated emission over the barrier, which can be very efficient depending on the temperature, the doping, and the interface quality (mechanism 3 in Figure 2). The model of quantum transport takes into consideration the thermally activated transfer through the MQWs structure. The presence of opposite components of this transfer provides a predominate charge carrier flow from preconfinement region back to the injecting contact over the flow of these charge carriers through the Si1−yGеy/ Si/Si1−xGеx well, that depends on band discontinuities between Si/Si1−yGеy and Si/Si1−xGеx paths [14]. The height of the potential barrier, the doping, and the quality of interfaces mainly define a prevalence of one of the above mechanisms. For modeling reason, the electron charges are supposed to flow in z direction that is the normal to the growth direction, as it is shown in Figure 1(b). The charge distribution in the injecting contacts is defined within the Boltzmann approximation of the Fermi-Dirac statistic [15]:
 (1)
(1)
 (2)
(2)
where  and
and  are the respective effective equilibrium concentrations of electrons and holes at zero bias,
are the respective effective equilibrium concentrations of electrons and holes at zero bias,  is the elementary charge,
is the elementary charge, 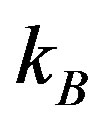 is the Boltzmann constant,
is the Boltzmann constant,  is the temperature,
is the temperature,  is the electrostatic potential extension along z direction, and
is the electrostatic potential extension along z direction, and  is the Fermi energy. The electrons fill all available states in active zone of the structure according to the Fermi-Dirac
is the Fermi energy. The electrons fill all available states in active zone of the structure according to the Fermi-Dirac  distribution [16]. The Fermi level is linearly varying from
distribution [16]. The Fermi level is linearly varying from  at the P region contact to
at the P region contact to  at the N contact region. The electron and hole densities in the active part of the device are described in the following way:
at the N contact region. The electron and hole densities in the active part of the device are described in the following way:
 (3)
(3)
 (4)
(4)
where the factor 2 stands for the spin degeneracy and a summation is performed over all conduction-band valleys  and all available values of the wave vector
and all available values of the wave vector ;
;  being one electron wave function. Because of the spatial invariance in the xy-plane, the wave function of the electron is separable
being one electron wave function. Because of the spatial invariance in the xy-plane, the wave function of the electron is separable , where the transverse wave function is described by plane waves as
, where the transverse wave function is described by plane waves as
 . The longitudinal wave function
. The longitudinal wave function  along z direction corresponding to wave vector value
along z direction corresponding to wave vector value  is one solution of the Schrödinger equation [17]:
is one solution of the Schrödinger equation [17]:
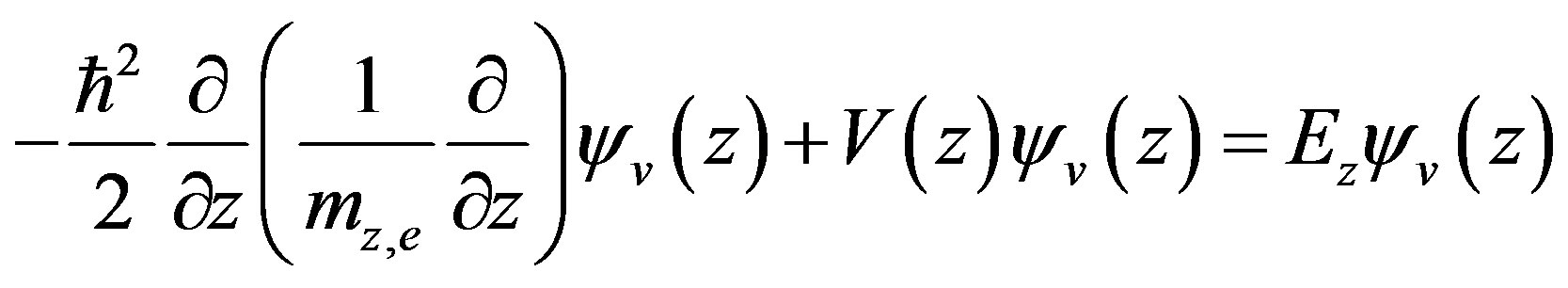 (5)
(5)
 (6)
(6)
where  is the reduced Plank’s constant;
is the reduced Plank’s constant;  and
and  are the effective masses of electron and hole in the conduction and valence band respectively along the z direction.
are the effective masses of electron and hole in the conduction and valence band respectively along the z direction.  is the potential energy of electron and hole defined as follows:
is the potential energy of electron and hole defined as follows:
 (7)
(7)
 (8)
(8)
where  and
and  are the conduction and valence band profiles along the structure.
are the conduction and valence band profiles along the structure.
Assuming a parabolic dispersion relation in the case of iso-energetic elliptic surface for the different conduction valleys along the total structure, and after performing integration over the transverse component of the momentum for the total electron density, the charge distribution expressions are found to be:
 (9)
(9)
 (10)
(10)
where the first term of  describes the contribution from the two valleys b, e; whereas the second term corresponds to the contribution from the rest four valleys a, d and f, c (see Figure 1). In the above expressions, the summation over momentum has been replaced by the integration index. Factors
describes the contribution from the two valleys b, e; whereas the second term corresponds to the contribution from the rest four valleys a, d and f, c (see Figure 1). In the above expressions, the summation over momentum has been replaced by the integration index. Factors  and
and  stand for the valley degeneracy. For an analysis of the thermally activated carrier transport, the electron transfer components in two opposite directions from the confinement silicon regions are included. While the above currentdensity equations correspond to the steady state conditions, the continuity equations deal with time-dependent phenomena such as low-level injection, generation and recombination. Qualitatively, the net change of carrier concentration is the difference between generation and recombination, added to the net current flowing in and out of the region of interest. The continuity equations are [18]:
stand for the valley degeneracy. For an analysis of the thermally activated carrier transport, the electron transfer components in two opposite directions from the confinement silicon regions are included. While the above currentdensity equations correspond to the steady state conditions, the continuity equations deal with time-dependent phenomena such as low-level injection, generation and recombination. Qualitatively, the net change of carrier concentration is the difference between generation and recombination, added to the net current flowing in and out of the region of interest. The continuity equations are [18]:
 (11)
(11)
 (12)
(12)
where  and
and  are the electron and hole generation rates respectively,
are the electron and hole generation rates respectively,  and
and  are the electron and hole free carrier concentrations at thermodynamic equilibrium,
are the electron and hole free carrier concentrations at thermodynamic equilibrium, 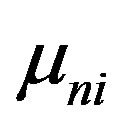 and
and  are respectively the electron and hole mobilities,
are respectively the electron and hole mobilities,  et
et  are the electron and hole respective diffusion coefficients,
are the electron and hole respective diffusion coefficients,  and
and  are the electron and hole free carrier concentration in the ith mesh point (
are the electron and hole free carrier concentration in the ith mesh point ( , where N is the number of mesh points) and
, where N is the number of mesh points) and  and
and  are the electron and hole recombination lifetimes respectively. In the absence of the optical excitation with photons
are the electron and hole recombination lifetimes respectively. In the absence of the optical excitation with photons , and these other current densities are given by:
, and these other current densities are given by:
i) The conduction and diffusion current densities in conduction and valence bands respectively
 (13)
(13)
 (14)
(14)
The conduction and diffusion current density in conduction and valence band respectively are written using the rates of electron and hole ,
,  concentrations in the ith point of mesh as following [19]:
concentrations in the ith point of mesh as following [19]:
 (15)
(15)
 (16)
(16)
ii) The recombination and band-to-band tunneling current densities in conduction and valence bands respectively The tunneling current density along the z-direction between two conducting regions through a forbidden region can be written as [20]:
 (17)
(17)
 (18)
(18)
Together with known tunneling probability, the tunneling current J can be calculated from the product of the number of available carriers in the origin (Region A), and the number of empty states in the destination (Region B) as highlighted in Figure 3, where fA, fB, NA, and NB represent the Fermi-Dirac distributions and densities of states in the corresponding regions and Tt is the tunneling probability:
 (20)
(20)
 (21)
(21)
For an analysis of the thermally activated carrier transport, the electron transfer components in the two opposite directions from the pre-confinement silicon regions are included. The rates of electrons and holes ,
,  concentrations in the ith point of mesh are written as [6]:
concentrations in the ith point of mesh are written as [6]:
 (22)
(22)
 (23)
(23)

Figure 3. Energy band diagrams showing breakdown mechanisms of tunneling band to band in Si1−yGеy/Si/Si1−xGеx/ Si/Si1−yGеy MQW strain compensated photodetector device.
where ,
,  are the electron and hole concentrations in the ith mesh point (
are the electron and hole concentrations in the ith mesh point ( , where N is the number of mesh points) and the
, where N is the number of mesh points) and the  are the rates of carrier transfer from i to i+1 mesh point and in the opposite direction. This rate that we have defined within the thermally activated transport theory includes the image-force effect in the following way [15,16]:
are the rates of carrier transfer from i to i+1 mesh point and in the opposite direction. This rate that we have defined within the thermally activated transport theory includes the image-force effect in the following way [15,16]:
 (24)
(24)
 (25)
(25)
where  is the relative permittivity of the materials,
is the relative permittivity of the materials,  is the permittivity in vacuum,
is the permittivity in vacuum,  is the step of the mesh, and
is the step of the mesh, and  and
and  are the frequency of the local carrier oscillations in the quantum well the expression of
are the frequency of the local carrier oscillations in the quantum well the expression of  and
and , and are given by (see Appendix A):
, and are given by (see Appendix A):
 (26)
(26)
 (27)
(27)
where  and
and  are the carrier lifetimes for electron and hole respectively,
are the carrier lifetimes for electron and hole respectively,  and
and  are the mobilities for electron and hole respectively, T refers to the temperature, kB is the constant of Boltzmann, and q is the charge of electron. All variables
are the mobilities for electron and hole respectively, T refers to the temperature, kB is the constant of Boltzmann, and q is the charge of electron. All variables  and
and  have been attached to discrete mesh. The system of kinetic equations has been solved for stationary case. Charge accumulation in the quantum wells is non-uninform and defines the potential distribution in the structure. To evaluate the potential
have been attached to discrete mesh. The system of kinetic equations has been solved for stationary case. Charge accumulation in the quantum wells is non-uninform and defines the potential distribution in the structure. To evaluate the potential  drop along z direction, the Poisson equation is solved:
drop along z direction, the Poisson equation is solved:
 (28)
(28)
where  and
and 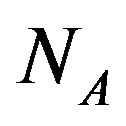 are the ionized donor and acceptor doping concentration.
are the ionized donor and acceptor doping concentration.
The finite-difference method has been applied for Schrödinger and Poisson equations’ solutions. The real space along the stack has been divided into discrete uniform mesh points and equations have been solved within those discrete spacing. Then, the three-diagonal matrix has been used to extract eigenvalues and corresponding eigenvectors according to:
 (29)
(29)
where  is the three-diagonal matrix;
is the three-diagonal matrix;  is the eigenvector including the values
is the eigenvector including the values  of discrete mesh and
of discrete mesh and  is the eigenvalue of energy. The same finite-difference method with an identical mesh has been used for Poisson Equation (28) solver. This means that we have solved a system of differential equations in their discretization form within the three-point finite difference scheme [20,21].
is the eigenvalue of energy. The same finite-difference method with an identical mesh has been used for Poisson Equation (28) solver. This means that we have solved a system of differential equations in their discretization form within the three-point finite difference scheme [20,21].
The interaction procedure is used to obtain a self-consistent solution of the Schrödinger equation (5 and 6), the kinetic equation system for the thermally activated carrier transport (22, 23, 24 and 25) and the Poisson equation (28). (i) Starting with a trial potential  with an original potential distribution which can be assumed within the equilibrium conditions, (ii) assuming the justified Boltzmann approximation for valence electrons and (iii) considering the constancy of the quasi-Fermi level in the contact region and its linear spreading in the active part of device, the wave functions and their corresponding eigenvalues of energy have been defined from the solution of the Schrödinger equation. These parameters are used to calculate the electron density distribution (Equations (9) and (10)) with additional accounting for the thermally activated contribution (Equations (22) and (23)), followed by computation of the potential distribution using the Poisson equation (28). The new potential energy
with an original potential distribution which can be assumed within the equilibrium conditions, (ii) assuming the justified Boltzmann approximation for valence electrons and (iii) considering the constancy of the quasi-Fermi level in the contact region and its linear spreading in the active part of device, the wave functions and their corresponding eigenvalues of energy have been defined from the solution of the Schrödinger equation. These parameters are used to calculate the electron density distribution (Equations (9) and (10)) with additional accounting for the thermally activated contribution (Equations (22) and (23)), followed by computation of the potential distribution using the Poisson equation (28). The new potential energy  is then obtained from Equations (7) and (8). After extracting the self-consistent solutions of the Schrödinger and Poisson equations providing the potential distribution to be known, the distribution of charge carrier density along the structure is again defined. The described method of the Schrödinger equation solver is effective for a charge distribution considering all charge states with the energy above and below the Fermi energy at the injecting contact. However, this method does not allow finding out a probability of tunneling. For this reason, the description of carrier transport by a system of wave function equations have been applied considering the incident and reflected waves in every points of the discrete mesh and including the boundary conditions at the points 1 and N [22,23], according to:
is then obtained from Equations (7) and (8). After extracting the self-consistent solutions of the Schrödinger and Poisson equations providing the potential distribution to be known, the distribution of charge carrier density along the structure is again defined. The described method of the Schrödinger equation solver is effective for a charge distribution considering all charge states with the energy above and below the Fermi energy at the injecting contact. However, this method does not allow finding out a probability of tunneling. For this reason, the description of carrier transport by a system of wave function equations have been applied considering the incident and reflected waves in every points of the discrete mesh and including the boundary conditions at the points 1 and N [22,23], according to:
 (30)
(30)

where A, B are the amplitude coefficients. Thus, the transmission coefficient for tunneling is given by:
 (31)
(31)
This transmission coefficient includes 3D to 2D from injecting contacts to the active part of p-i-n heteostructure, where quantum effects prevailed. Yet, calculation of the potential profile along the whole structure within this method misses the current from localized states in preconfinement regions, which are occupied according to the Fermi-Dirac distribution. The contribution of the localized states to the total current is supposed to be significant in the case of positive energy gap between the injecting contact and the bottom of the quantum well in the pre-confinement region. For this cause the procedure of probability calculation has been used for the active part of the device excluding the potential profile at the contact regions that allows accounting the contribution of 2D-2D current from localized states in pre-confinement regions seen Ref. [24].
4. Results and Discussion
To create the conditions for a well-organized photodetection effect, the I-V characteristics were calculated within the above model. The used parameters are summarized in Table 1. The donor and the acceptor concentrations in the n-type and p-type respectively were fixed to ND = NA = 1 × 1018 cm−3. At room temperature, the Fermi level positions 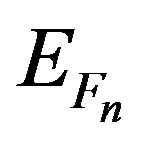 and
and  are 0.05969 eV and 0.04219 eV below the conduction and valence bands respectively. The calculations of the transmission probability in Si0.75Ge0.25/Si/Si0.4Ge0.6/Si/Si0.75Ge0.25 MQW for the conduction and valence bands have shown the presence of multiple peaks for the transverse and longitudinal effective masses of electrons and light-holes and heavy-holes effective masses for fourteen quantum wells Si layer under tensile strain on the relaxed Si0.75Ge0.25 and seven potential barriers Si0.4Ge0.6 layers compressively strained on the relaxed Si0.75Ge0.25 respectively. Transmission coefficients are calculated using the transfer matrix method all over the length of the structure. The results are demonstrated in Figure 4 where the transmission coefficient is plotted. (a) Transmission coefficient versus electron energy for the transverse and longitudinal effective masses for seven “W” periods strained quantum wells, forming the active zone of p-i-n junction. (b) Transmission coefficients for a multi-quantum wells in the p-i-n structure versus energy for light-hole and heavy-hole incidence. In one hand the great value of the longitudinal effective mass of electrons causes the related low transmission coefficient and the multi-levels appearance. This is the reason of the significant domination of the transmission component relative to the transverse mass. In the other hand, the large value of the heavy-hole effective mass origins is correlated with the low transmission coefficient by comparison with light-holes transmission coefficient. The vertical dash line separates the energy range that is not considered for the modeling of the 3D-2D resonant tunneling transfer. The parameters of Figure 4 correspond to a conduction and valence bands offsets at injecting contacts
are 0.05969 eV and 0.04219 eV below the conduction and valence bands respectively. The calculations of the transmission probability in Si0.75Ge0.25/Si/Si0.4Ge0.6/Si/Si0.75Ge0.25 MQW for the conduction and valence bands have shown the presence of multiple peaks for the transverse and longitudinal effective masses of electrons and light-holes and heavy-holes effective masses for fourteen quantum wells Si layer under tensile strain on the relaxed Si0.75Ge0.25 and seven potential barriers Si0.4Ge0.6 layers compressively strained on the relaxed Si0.75Ge0.25 respectively. Transmission coefficients are calculated using the transfer matrix method all over the length of the structure. The results are demonstrated in Figure 4 where the transmission coefficient is plotted. (a) Transmission coefficient versus electron energy for the transverse and longitudinal effective masses for seven “W” periods strained quantum wells, forming the active zone of p-i-n junction. (b) Transmission coefficients for a multi-quantum wells in the p-i-n structure versus energy for light-hole and heavy-hole incidence. In one hand the great value of the longitudinal effective mass of electrons causes the related low transmission coefficient and the multi-levels appearance. This is the reason of the significant domination of the transmission component relative to the transverse mass. In the other hand, the large value of the heavy-hole effective mass origins is correlated with the low transmission coefficient by comparison with light-holes transmission coefficient. The vertical dash line separates the energy range that is not considered for the modeling of the 3D-2D resonant tunneling transfer. The parameters of Figure 4 correspond to a conduction and valence bands offsets at injecting contacts ,
,
 and
and . This confirms the requirements of the additional calculations of 2D-2D tunneling from localized states in the pre-confinement quantum well for adequate current simulations. Figure 5 shows the dark current density (J) of the p-i-n heterojunction based on Si0.75Ge0.25/Si/Si0.4Ge0.6/Si/Si0.75Ge0.25 MQW strain-compensated strained structures versus biased voltage (V) which sweeps from −6.5 V to 6.5 V, as a function of temperature in the range of 50 - 350 K. We also notice that the dark current versus voltage curve is not symmetric to the zero voltage. This result clearly shows the carrier blocking effect of the Si0.4Ge0.6 layer between the silicon quantum wells. The dark current is lower at forward bias. The carriers in the quantum wells have to overcome the Si0.4Ge0.6 barrier to get out when the device is forward biased but only the Si0.75Ge0.25 and Si0.4Ge0.6 barriers when the device is reversed biased. The increase of the dark current with temperature is mainly due to its exponential dependence on temperature, the values increase with temperature T and V as expected [29,30]. Figure 6 shows the calculated total dark current density-bias voltage curves using the above model of the photodetectors at 300 K with four distinct regimes with different dominant mechanisms, the conduction current density, diffusion current density, recombination current density, and tunneling band-to-band current density. It is observed that the thermal diffusion and the conduction current densities describe very well the forward current characteristics of the MQW photodetector. The recombination current density and tunneling band-to-band current density contributions to the reverse bias current are
. This confirms the requirements of the additional calculations of 2D-2D tunneling from localized states in the pre-confinement quantum well for adequate current simulations. Figure 5 shows the dark current density (J) of the p-i-n heterojunction based on Si0.75Ge0.25/Si/Si0.4Ge0.6/Si/Si0.75Ge0.25 MQW strain-compensated strained structures versus biased voltage (V) which sweeps from −6.5 V to 6.5 V, as a function of temperature in the range of 50 - 350 K. We also notice that the dark current versus voltage curve is not symmetric to the zero voltage. This result clearly shows the carrier blocking effect of the Si0.4Ge0.6 layer between the silicon quantum wells. The dark current is lower at forward bias. The carriers in the quantum wells have to overcome the Si0.4Ge0.6 barrier to get out when the device is forward biased but only the Si0.75Ge0.25 and Si0.4Ge0.6 barriers when the device is reversed biased. The increase of the dark current with temperature is mainly due to its exponential dependence on temperature, the values increase with temperature T and V as expected [29,30]. Figure 6 shows the calculated total dark current density-bias voltage curves using the above model of the photodetectors at 300 K with four distinct regimes with different dominant mechanisms, the conduction current density, diffusion current density, recombination current density, and tunneling band-to-band current density. It is observed that the thermal diffusion and the conduction current densities describe very well the forward current characteristics of the MQW photodetector. The recombination current density and tunneling band-to-band current density contributions to the reverse bias current are
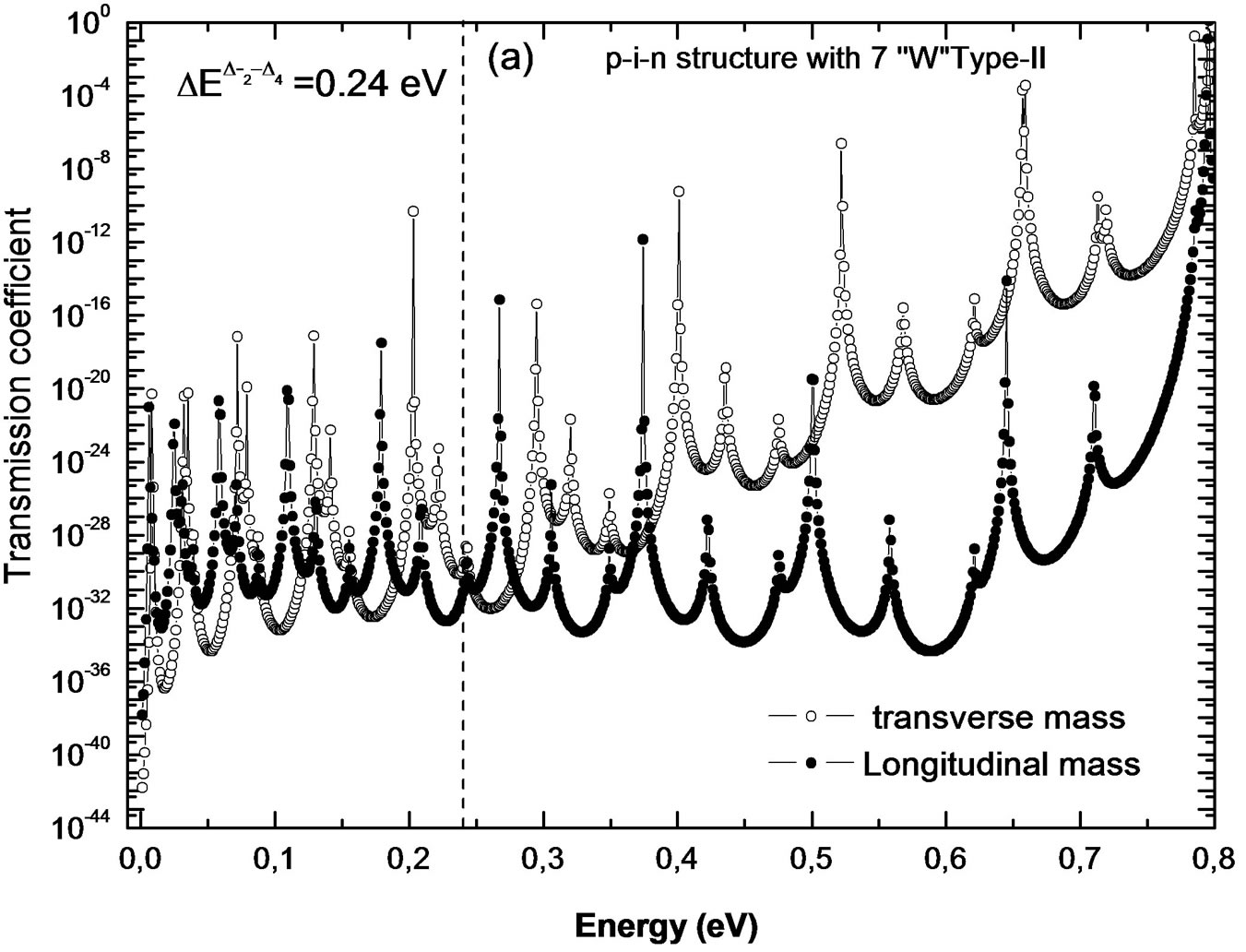

Figure 4. Transmission coefficients versus electron energy for seven W-period strained quantum wells for: (a) the transverse and longitudinal effective masses, the active zone of p-i-n junction; (b) the light-hole and heavy-hole incidence.

Figure 5. Dark current density of the p-i-n heterojunction based on Si0.75Ge0.25/Si/Si0.4Ge0.6/Si/Si0.75Ge0.25 MQW strain-compensated strained structures of 100 µm in diameter versus bias voltage for temperatures from 50 to 350 K. The current is nearly symmetric to zero voltage.

Figure 6. Total dark current density at 300 K as a function of bias voltage from −6.5 V to 6.5 V is shown with four distinct regimes with different dominant mechanisms, the conduction current density, diffusion current density, recombination current density and band to band tunneling current density.

Table 1. The parameters used in the simulation of the total dark current density in order to obtain the optimal agreement between experimental values and numerical simulation.
also described thoroughly the behavior of total dark current density with reverse bias application. Note that the resulting reverse bias current and the current conducted through the shunt resistance overlap each other in Figure 6. Thus, it is the current flowing through the shunt resistance that dominates the reverse characteristics of the diode. It is suggested that the degradation of the dynamic resistance and a dominant shunt current in the reverse bias are related. Current-voltage (I-V) calculation was performed using the above model at 300 K. Figure 7 shows the I-V characteristics of a typical diode. The breakdown voltage was 5.75 V at 300 K. As shown in the inset, a low dark current of 4.7 × 10−4 A/cm2 at −1 V was obtained at 300 K. This is one order of magnitude lower than that reported in Ref. [31]. However, it is still much higher than the ideal dark current of pure silicon diodes. This may be due to additional generation processes in the silicon quantum wells and the Si0.75Ge0.25 layers, i.e., the emission of carriers from the potential wells formed by these regions and the silicon layers. The surface states can also contribute to the dark current for the description of the diffusion, generation-recombination, and the barriers tunneling affect. At 50 K, the dark current density was in range of 1 × 10−3 A/m2 corresponding to a differential-resistance-area-product at zero bias of 136 W∙cm2. The profile of the R0A versus 1000/T curve in Figure 8 establishes that the details of modeled values to be reported elsewhere indicate that the dark current is dominated by four different mechanisms in four different temperature regimes. From 50 to 100 K, the device per formance is limited by the temperature-insensitive barriers tunneling effect [32] that causes the device performance not to be good more than 100 K, the thermally generated carriers produce a stronger generation-recombination and diffusion current. From 100 to 125 K, the device is limited by the generation-recombination with an interesting recombination lifetime in the depleted region while above 125 K, the diffusion current becomes the dominant component. In this regime, the device performance is approaching those III-V devices [33]. The differential-resistance-area-product at zero bias as a function of 1000/T for 7 and 35 W-periods have been calculated and are shown in Figure 8. Simulation of I-V characteristics of Si1−yGey/Si/Si1−xGex/Si/Si1−xGex/Si/Si1−yGey structure has shown that the electron tunneling current is higher than the hole tunneling current. This is because of the large difference in the barrier heights for electrons and holes. Figure 9 shows the dark current density without excitation and the current density with excitation caused by external influences such as the optical excitation with photons or impact ionization under large electric fields of a typical device shown in Figure 1(b). In order to obtain the best agreement between experimental values and numerical simulation, we showed that the performed calculations have good correlation with experimental results [34,35], and the weak dependence of dark current peak shift are explained by the difference of offset values in each devices. Figure 10 shows the calculated energy

Figure 7. I-V characteristics of the Si0.75Ge0.25/Si/Si0.4Ge0.6/Si/Si0.75Ge0.25 MQW “W” p-i-n diode at 300 K. The breakdown voltage at 300 K is about 5.75 V. In the inset log-scale plot, a dark current at 300 K from −6.5 V to 6.5 V is shown.

Figure 8. Zero-bias resistance area product of the p-i-n heterojunction based on Si0.75Ge0.25/Si/Si0.4Ge0.6/Si/Si0.75Ge0.25 MQW strain-compensated strained structures for 7 W-periods and 35 W-periods versus the inverse temperature 1000/T relation shows five distinct regimes with different dominant mechanisms: Thermally activated, conduction, diffusion, generation-recombination, and barriers tunneling effect.

Figure 9. Current densities versus the bias current with and without optical excitation at room temperature. The excitation is caused by external influences such as the optical excitation with photons or impact ionization under large electric fields at 300 K.

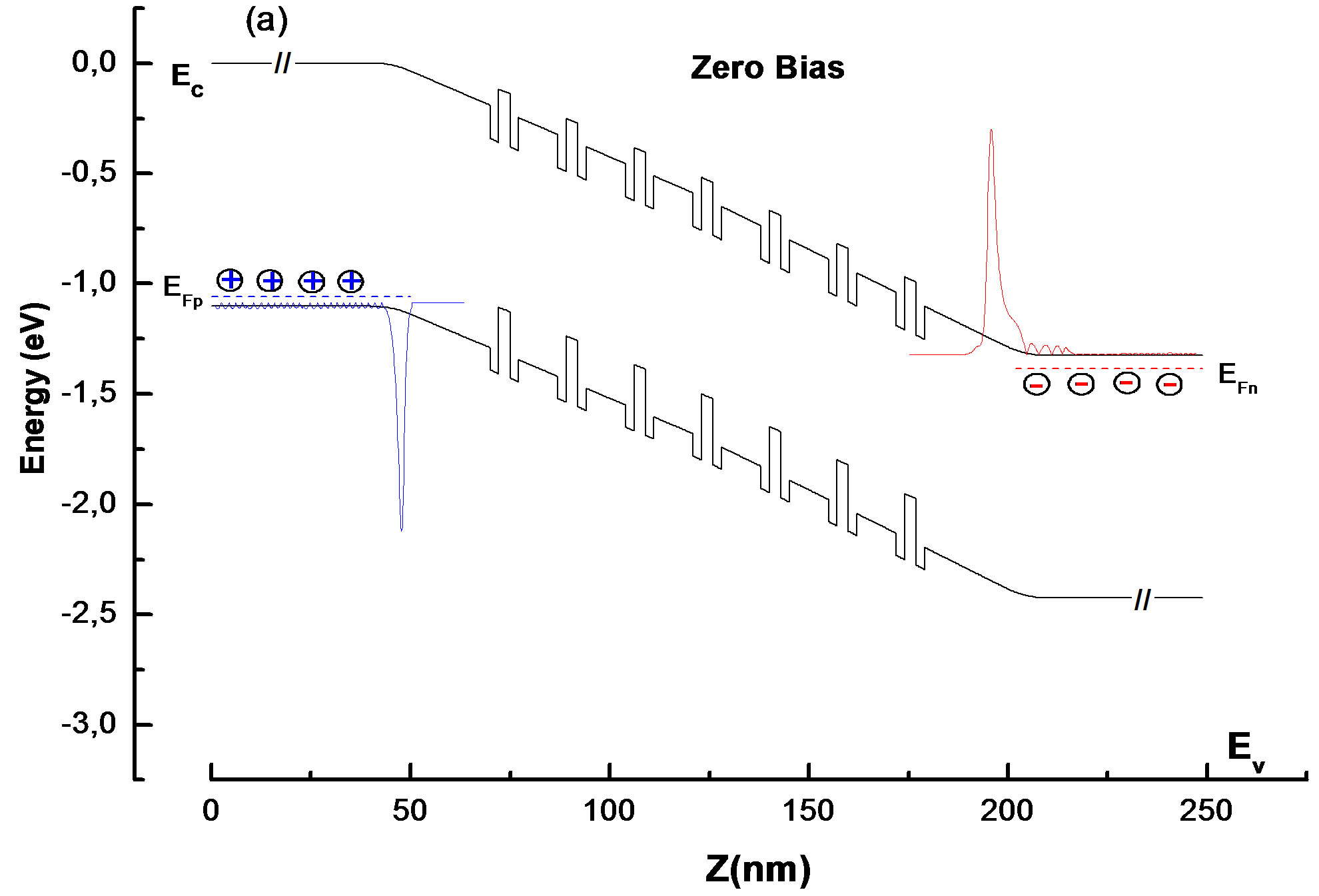


Figure 10. (a) Edges of the conduction and valence bands of the Si0.75Ge0.25/Si/Si0.4Ge0.6/Si/Si0.75Ge0.25 MQW strain-compensated strained structures optimally designed for 1.55 μm detection. The Fermi levels are drawn with their wave functions at zero bias; (b) Band diagram for a p-i-n photodetector under a reverse bias (−0.6V) at room temperature. EFp and EFn are the Fermi levels of conduction and valence bands; (c) The p-i-n heterojunction at direct bias (+0.6V) with the Fermi levels and wave functions; (d) The modeling heterostructure at the mode of the plat band under Vbias = 1.25V. The Fermi levels and the e1 and hh1 quantum levels are drawn with their relative wave functions.
band diagrams of the p-i-n photodetectors with and without applied bias voltage. In Figure 10(a), the edges of the conduction and valence bands of the Si0.75Ge0.25/ Si/Si0.4Ge0.6/Si/Si0.75Ge0.25 MQW strain-compensated strained structures optimally designed for 1.55 μm detection are illustrated. The Fermi levels are drawn with their wave functions at zero bias. Figure 10(b) presents the band diagram for a p-i-n photodetector under a reverse bias Vbias = −0.6V at room temperature; EFp and EFn are the Fermi levels of conduction and valence bands. Figure 10(c) shows the p-i-n heterojunction at direct bias Vbias = 0.6 V with the Fermi levels and wave functions, while Figure 10(d) illustrates the modeling heterostructure at the mode of the plat band under Vbias = 1.25 V. The Fermi levels and the e1 and hh1 quantum levels are drawn with their relative wave functions. The device performances such as threshold current density, external quantum efficiency, optical confinement, carrier confinement, thermal sensitivity, and the absorption region are all crucially dependent on the thicknesses and/or energy band gap of the pseudo substrate layer Si0.75Ge0.25 for both single and multiple quantum well photodetectors [14]. There have been few reported results showing the contribution of the pseudo substrate layer to the photodetectors [36,37]. From these results, one can speculate that the pseudo substrate layer with an advanced band discontinuity provides a barrier height to prevent the carriers from surmounting it and reduces the leakage current. When a reverse bias is applied across the device, the entire i-region becomes depleted. Due to high resistivity and total depletion of the i-layer, almost all the electric field appears across it. The applied reverse bias should not be so high that the breakdown could take place. The dark current is independent of applied reverse bias. Since the light arises from the top surface, most of the photon flux passes through the relatively thin top layer. The absorbed photons generate electron-hole pairs which drift towards the electrodes due to the existing electric field to give rise to a photocurrent in the external circuit. One of the advantages of heterojunction p-i-n photodiodes is that the device characteristics are tunable by changing the composition of the i-layer. For multi-quantum wells used in Si1−yGey/Si/Si1−xGex/Si/Si1−xGex/Si/Si1−yGey structures, in order to increase the photoelectron current, the applied voltage is equally dropped in all QWs so that only the current at small voltages remains significant and the total current is equal to the current of a single well multiplied by the number of wells. The currents for both thin and thick additional barrier in MQWs structures are also estimated. The sequential tunneling current may be considered not only between D-like states but also transferring sequentially to different states in another well. SiGe/Sisuperlattice p-i-n photodetectors are finding extensive applications in long haul and high bit rate optical communication systems and in local area networks for operation in the infrared region (1.3 - 1.55 μm) [38]. In addition to optical communication, these devices are also useful for sensing applications as they have superior electro-optical characteristics, namely low dark current, high quantum efficiency, greater sensitivity and high speed of response.
5. Conclusion
The carrier transport in p-i-n Si1−yGey/Si/Si1−xGex/Si/Si1−xGex/Si/Si1−yGey MQW device has been modeled on the basis of a self-consistent solver of the Schrödinger, Poisson, and kinetics equations. We have found the range of the structural parameters, thickness, and composition providing a realistic epitaxy of the optimized Si/Si1−xGex/Si photodetectors built-on strained Si0.75Ge0.25/Si/Si0.4Ge0.6/Si/Si0.75Ge0.25 quantum wells embedded in p-Si0.75Ge0.25 and n-Si0.75Ge0.25 that act as pre-confinement regions of the electronic charge. The computer simulation has shown insignificant contribution of the 2D-2D carries transfer from states localized in the pre-confinement silicon well due to the high potential barrier at Si/Si0.4Ge0.6 interface. The electrical characterristics J-V of the infrared p-i-n photodetector have been modeled by using our quantum transport model. It has shown four distinct regimes with different dominant mechanisms, the conduction current density, diffusion current density, recombination current density, and tunneling band-to-band current density. The reverse bias characteristics are, however, limited by the shunt resistance and the band-to-band tunneling contribution. Zero-bias resistance area product of the diode is calculated and found to be limited by four distinct regimes at room temperature for 7 and 35 Si1−xGex/Si W-periods. This heterostructure can be used to create a photodetector that is sensitive to 1.55-µm-light when grown directly on silicon with using virtual SiGe virtual substrate.
REFERENCES
- B. Movaghar, S. Tsao, S. Abdollahi Pour, T. Yamanaka, and M. Razeghi, “Gain and Recombination Dynamics in Photodetectors Made with Quantum Nanostructures: The Quantum Dot in a Well and the Quantum Well,” Physical Review B, Vol. 78, 2008, Article ID: 115320. http://dx.doi.org/10.1103/PhysRevB.78.115320
- R. Apetz, L. Vescan, A. Hartmann, C. Dieker and H. Lüth, “Photoluminescence and Electroluminescence of SiGe Dots Fabricated by Island Growth,” Applied Physics Let= ters, Vol. 66, No. 4, 1995, p. 445. http://dx.doi.org/10.1063/1.114051
- T. Stoica and L. Vescan, “Quantum Efficiency of SiGe LEDs,” Semiconductor Science and Technology, Vol. 18, No. 6, 2003, pp. 409-416. http://dx.doi.org/10.1088/0268-1242/18/6/303
- B. Levine, “Quantum-Well Infrared Photodetectors,” Journal of Applied Physics, Vol. 74, No. 8, 1993, p. R1. http://dx.doi.org/10.1063/1.354252
- K. K. Choi, “The Physics of Quantum Well Infrared Photodetectors,” World Scientific, Singapore City, 1997.
- H. C. Liu, M. Buchanan, J. Li, Z. R. Wasilewski, P. H. Wilson, P. A. Marshall, R. A. Barber, P. Chow-Chong, J. W. Fraser and J. Stapledon, “Applications of Photonic Technology 2,” In: G. A. Lampropoulos and R. A. Lessard, Eds., Applications of Photonic Technology 2, Plenum, New York, 1997, pp. 311-318.
- Z. Lo, R. Jiang, Y. Zheng, L. Zang, Z. Chen, S. Zhu, X. Cheng and X. Liu, “Staircase Band Gap Si1−xGex/Si Photodetectors,” Applied Physics Letters, Vol. 77, No. 10, 2000, p. 1548. http://dx.doi.org/10.1063/1.1286958
- P. Rauter, T. Fromherz, C. Falub, D. Grützmacher and G. Bauer, “SiGe Quantum Well Infrared Photodetectors on Pseudosubstrate,” Applied Physics Letters, Vol. 94, No. 8, 2009, Article ID: 081115. http://dx.doi.org/10.1063/1.3089817
- I. Bormann, K. Brunner, S. Hackenbuchner, G. Zandler, G. Abstreiter, S. Schmult and W. Wegscheider, “Midinfrared Intersubband Electroluminescence of Si/SiGe Quantum Cascade Structures,” Applied Physics Letters, Vol. 80, No. 13, 2002, p. 2260. http://dx.doi.org/10.1063/1.1465131
- P. Boucaud, M. E. Kurdi and J. M. Hartmann, “Photoluminescence of a Tensilely Strained Silicon Quantum Well on a Relaxed SiGe Buffer Layer,” Applied Physics Letters, Vol. 85, No. 1, 2004, p. 46. http://dx.doi.org/10.1063/1.1766073
- N. Sfina, J. Lazzari, J. Derrien, F. A. d’Avitaya and M. Said, “Strain-Balanced Si1−xGex/Si Type II Quantum Wells for 1.55 μm Detection and Emission,” The European Physical Journal B, Vol. 48, No. 2, 2005, pp. 151- 156. http://dx.doi.org/10.1140/epjb/e2005-00389-6
- N. J. Ekins-Daukes, K. Kawaguchi and J. Zhang, “StrainBalanced Criteria for Multiple Quantum Well Structures and Its Signature in X-Ray Rocking Curves,” Crystal Growth & Design, Vol. 2, No. 4, 2002, pp. 287-292. http://dx.doi.org/10.1021/cg025502y
- C. G. Van de Walle and R. M. Martin, “Theoretical Calculations of Heterojunction Discontinuities in the Si/Ge System,” Physical Review B, Vol. 34, No. 8, 1986, p. 5621. http://dx.doi.org/10.1103/PhysRevB.34.5621
- F. Ben Zid, A. Bouri, H. Mejri, R. Tlili, M. Said, F. A. D’Avitaya and J. Derrien, “Stark Effect Modeling in Strained n-Type Si/Si1−xGex Resonant Tunneling Heterostructures,” Journal of Applied Physics, Vol. 91, No. 11, 2002, p. 9170. http://dx.doi.org/10.1063/1.1473213
- S. M. Sze, “Physics of Semiconductor Devices Academic,” John Wiley and Sons, Hoboken, 1981.
- J. A. Berashevich, A. L. Danilyuk, A. N. Kholod and V. E. Borisenko, “Carrier Transport and Related Phenomena in Nanosize Periodic Silicon/Insulator Structures,” Materials Science and Engineering: B, Vol. 101, No. 1-3, 2003, pp. 111-118. http://dx.doi.org/10.1016/S0921-5107(02)00664-5
- G. Bastard, “Wave Mechanics Applied to Semiconductor Heterostructures,” Les Editions de Physique, Les Ulis, 1988.
- W. Shockley, “Electrons and Holes in Semiconductors,” D. Van Nostrand, Princeton, 1950.
- A. S. Grove, “Physics and Technology of Semiconductor Devices,” Wiley, New York, 1967.
- E. H. Nicollian, “Electrical Properties of the Si-SiO2 Interface and Its Influence on Device Performance and Stability,” Journal of Vacuum Science & Technology, Vol. 14, No. 5, 1977, p. 1112. http://dx.doi.org/10.1116/1.569343
- I.-H. Tan, G. L. Snider, L. D. Chang and E. L. Hu, “A Self-Consistent Solution of Schrödinger-Poisson Equations Using a Nonuniform Mesh,” Journal of Applied Physics, Vol. 68, No. 8, 1990, p. 4071. http://dx.doi.org/10.1063/1.346245
- K. Araki, “Analysis of Barrier Transmission in Resonant Tunneling Diodes,” Journal of Applied Physics, Vol. 62, No. 3, 1987, p. 1059. http://dx.doi.org/10.1063/1.339736
- R. Tsu and L. Esaki, “Tunneling in a Finite Superlattice,” Applied Physics Letters, Vol. 22, No. 11, 1973, p. 562. http://dx.doi.org/10.1063/1.1654509
- N. Sfina, J.-L. Lazzari, F. Ben Zid, A. Bhouri and M. Said, “Wave Function Engineering in W Designed StrainedCompensated Si/Si1−xGex/Si Type II Quantum Wells for 1.55 μm Optical Properties,” Optical Materials, Vol. 27, No. 5, 2005, pp. 859-863. http://dx.doi.org/10.1016/j.optmat.2004.08.073
- M. M. Rieger and P. Vogl, “Electronic-Band Parameters in Strained Si1−xGex Alloys on Si1−yGey Substrate,” Physical Review B, Vol. 48, No. 19, 1993, pp. 14276-14287. http://dx.doi.org/10.1103/PhysRevB.48.14276
- R. People and S. K. Sputz, “Band Nonparabolicities in Lattice-Mismatch-Strained Bulk Semiconductor Layers,” Physical Review B, Vol. 41, No. 12, 1990, pp. 8431-8439. http://dx.doi.org/10.1103/PhysRevB.41.8431
- B. V. Kamenev, L. Tsybeskov, J.-M. Baribeau and D. J. Lockwood, “Coexistence of Fast and Slow Luminescence in Three-Dimensional Si/Si1−xGex Nanostructures,” Physical Review B, Vol. 72, No. 19, 2005, Article ID: 193306. http://dx.doi.org/10.1103/PhysRevB.72.193306
- J. Millman and A. Grabel, “Dispositifs à Semiconducteurs,” Jacob Millman, Livres, 1989.
- J. Phillips, K. Kamath and P. Bhattacharya, “Far-Infrared Photoconductivity in Self-Organized InAs Quantum Dots,” Applied Physics Letters, Vol. 72, No. 16, 1998, p. 2020. http://dx.doi.org/10.1063/1.121252
- V. Ryzhii, “The Theory of Quantum-Dot Infrared Phototransistors,” Semiconductor Science and Technology, Vol. 11, No. 5, 1996, p. 759. http://dx.doi.org/10.1088/0268-1242/11/5/018
- F. Y. Huang, X. Zhu, M. O. Tanner and K. L. Wang, “Normal-Incidence Strained-Layer Superlattice Ge0.5Si0.5/Si photodiodes near 1.3 μm,” Applied Physics Letters, Vol. 67, 1995, p. 566. http://dx.doi.org/10.1063/1.115171
- I. M. Baker and C. D. Maxey, “Summary of HgCdTe 2D Array Technology in the UK,” Journal of Electronic Materials, Vol. 30, No. 2, 2001, pp. 682-689. http://dx.doi.org/10.1007/BF02665856
- Y. Wei, A. Hood, H. Yau, A. Gin, M. Razeghi, M. Z. Tidrow and V. Nathan, “Uncooled Operation of Type-II InAs/GaSb Superlattice Photodiodes in the Midwavelength Infrared Range,” Applied Physics Letters, Vol. 86, No. 23, 2005, Article ID: 233106. http://dx.doi.org/10.1063/1.1947908
- D. Ali, P. Thompson, J. DiPasquale and C. J. K. Richardson, “A Silicon-Germanium W-Structure Photodiode for Near-Infrared Detection,” Journal of Vacuum Science & Technology B, Vol. 27, No. 1, 2009, p. 23. http://dx.doi.org/10.1116/1.3039688
- A. I. Yakimov, A. V. Dvurechenskiï, A. I. Nikiforov, S. V. Chaïkovskiï and S. A. Tiïs, “Ge/Si Photodiodes with Embedded Arrays of Ge Quantum Dots for the near Infrared (1.3 - 1.5 µm) Region,” Semiconductors, Vol. 37, No. 11, 2003, pp. 1345-1349. http://dx.doi.org/10.1134/1.1626222
- H. Presting, T. Zinke, A. Splett, H. Kibbel and M. Jaros, “Room-Temperature Electroluminescence from Si/Ge/Si1−x Gex Quantum—Well Diodes Grown by Molecular— Beam Epitaxy,” Applied Physics Letters, Vol. 69, 1996, p. 2376. http://dx.doi.org/10.1063/1.117642
- H. Presting, T. Zinke, A. Splett, H. Kibbel and M. Jaros, “Room-Temperature Electroluminescence from Si/Ge/Si1−x Gex Quantum-Well Diodes Grown by Molecular-Beam Epitaxy,” Applied Physics Letters, Vol. 69, No. 16, 1996, p. 2376. http://dx.doi.org/10.1063/1.117642
- M. Wolf, R. Brendel, J. H. Werner and H. J. Queisser, “Solar Cell Efficiency and Carrier Multiplication in Si1−xGex Alloys,” Journal of Applied Physics, Vol. 83, No. 8, 1998, p. 4213. http://dx.doi.org/10.1063/1.367177
- J. A. Berashevich, V. E. Borisenko, J.-L. Lazzari and F. A. D’Avitaya, “Resonant Tunneling versus Thermally Activated Transport through Strained Si1−xGex/Si/Si1−xGex Quantum Wells,” Physical Review B, Vol. 75, No. 11, 2007, Article ID: 115336. http://dx.doi.org/10.1103/PhysRevB.75.115336
6. Appendix A
In the following, we determine the conduction and the diffusion current densities in conduction band respectively; these currents are given by:
 (A.1)
(A.1)
 (A.2)
(A.2)
 (A.3)
(A.3)
We consider a system of rate equations describing the elastic tunneling carrier transfer mechanism, the charge flow through the device and the thermally activated emission over the barrier. In this case, Equation (A3) is replaced by:
 (A.4)
(A.4)
The expression of  is taken from the works of Julia A. Berashevich et al. [39]:
is taken from the works of Julia A. Berashevich et al. [39]:
 (A.5)
(A.5)
Using the first approximation of the expression of  taking
taking , the second member (the image-force effect) of
, the second member (the image-force effect) of  tends to 1:
tends to 1:
 (A.6)
(A.6)
Within the approximation, the carrier transport is described by kinetic equations. The rates of electron in the ith point of mesh  become:
become:
 (A.7)
(A.7)
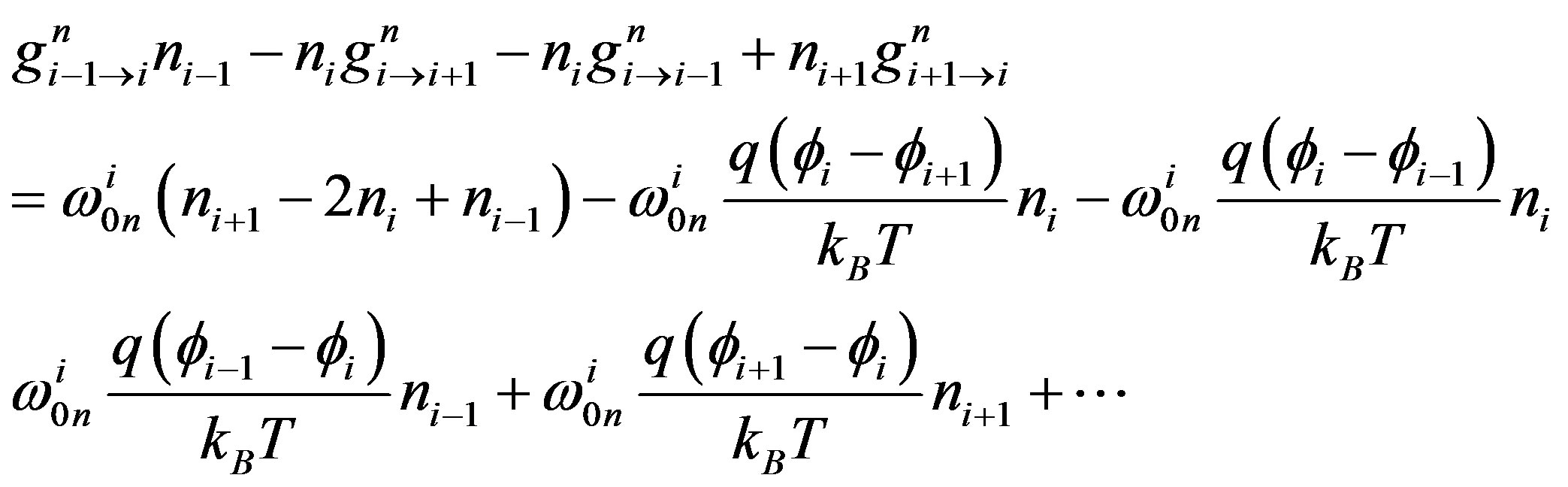 (A.8)
(A.8)
 (A.9)
(A.9)
The following development of Equation (A.3) in one order gives the same terms than Equation (A.9).
 (A.10)
(A.10)
 (A.11)
(A.11)
With simple identification between equations (A.9) and (A.11) we can obtain:

With this development we can prove that the frequency of the rates in the conduction band is:
 (A.12)
(A.12)
Using the same calculation for the conduction and diffusion currents respectively in the valence band we can prove that the frequency of the rates in the valence band is given by:
 (A.13)
(A.13)
NOTES
*Corresponding author.

