Modeling and Numerical Simulation of Material Science
Vol.3 No.4(2013), Article ID:37534,3 pages DOI:10.4236/mnsms.2013.34019
The Correctional Model of Population Development Equation
1Department of Basic Courses, Air Force Logistics College, Xuzhou, China
2Department of Training, Air Force Logistics College, Xuzhou, China
Email: *liuman8866@163.com
Copyright © 2013 Man Liu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 2, 2013; revised July 2, 2013; accepted July 10, 2013
Keywords: population development equation; the correctional population model; discrete population model
ABSTRACT
The problem of population development has always been the key problem of restricting the development of our country. In order to increase the prediction accuracy, we analyze the exponential model, logistic model and continuous model. Also, the improved discrete population development model is provided to control the quantity and improve the quality of population.
1. Introduction
Population problem is a common concern to countries around the world. China is a populous country and the population problem is the key problem to restrict the development of our country. The essence of China is to develop. In order to solve the population problem now, we should not only keep the birthrate low, but also plan the quantity, quality, structure and distribution of population. On the base of promoting all-round development of people, we realize that the coordination and positive interaction are beneficial in the population development. At present, the methods of population prediction mainly have simple linear regression [1], multiple linear regression [2], grey forecasting method [3-5], time series method [6], neural network method [7] and so on. In many methods, the population development equation model is the most widely used and successful one put forward by Song Jian and Yu Jingyuan [8,9].
2. Models of Population Growth
2.1. Exponential Growth Model—Malthusian Model of Population Growth
Two hundred years ago, an English demographer named Thomas Malthus (1766-1834) surveyed the demographic data of British population more than one hundred years, and found the hypothesis of the population growth rate was costant. On the basis of the hypothesis the famous population exponential growth model was established.
Noting the time , the quantity of population is
, the quantity of population is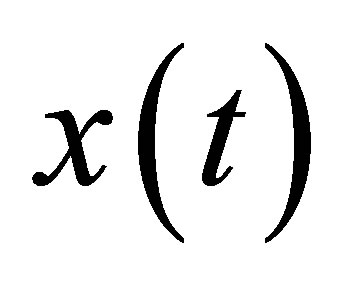 , the quantity of population is
, the quantity of population is  when the initial time
when the initial time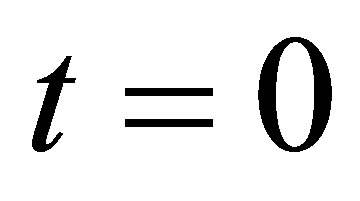 , we suppose the population growth rate is constant
, we suppose the population growth rate is constant , i.e., the increment of
, i.e., the increment of 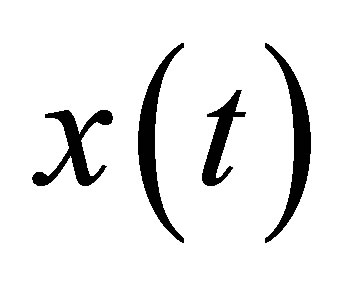 per unit time is equal to
per unit time is equal to  multiply by
multiply by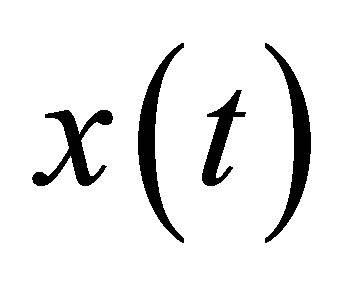 . Therefore we set up the following differential equation [10]
. Therefore we set up the following differential equation [10]

By solving the equation we can obtain
 .
.
In other words, the population will be infinitely increase over time exponentially, it is called exponential growth model.
The exponential growth model is good for the population prediction of short-term forecast, but in the long run, the population growth is impossible unlimited at any region, the exponential model can’t predict the population evolution process over a long period of time, in fact, the population growth rate is constantly changing, so we have the following population prediction models.
2.2. The Model of Retardant Population Growth—Logistic Model
Considering the factors such as natural resources, environment conditions for blocking the population growth, and with the increase of population, the retardant effect is more and more big. Let 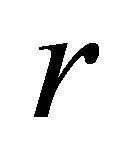 be natural growth rate, it denotes that the growth rate of population is low. Let
be natural growth rate, it denotes that the growth rate of population is low. Let
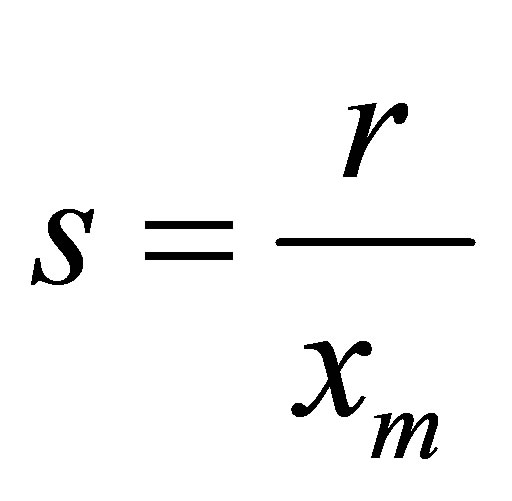 ,
,
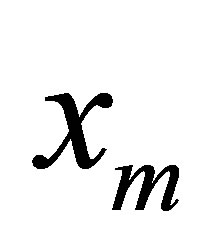 is the largest population. That is to say, when
is the largest population. That is to say, when 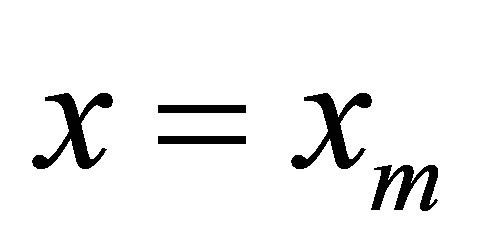 the population is no longer growth, i.e., the rate
the population is no longer growth, i.e., the rate . We can obtain the following population development equation
. We can obtain the following population development equation
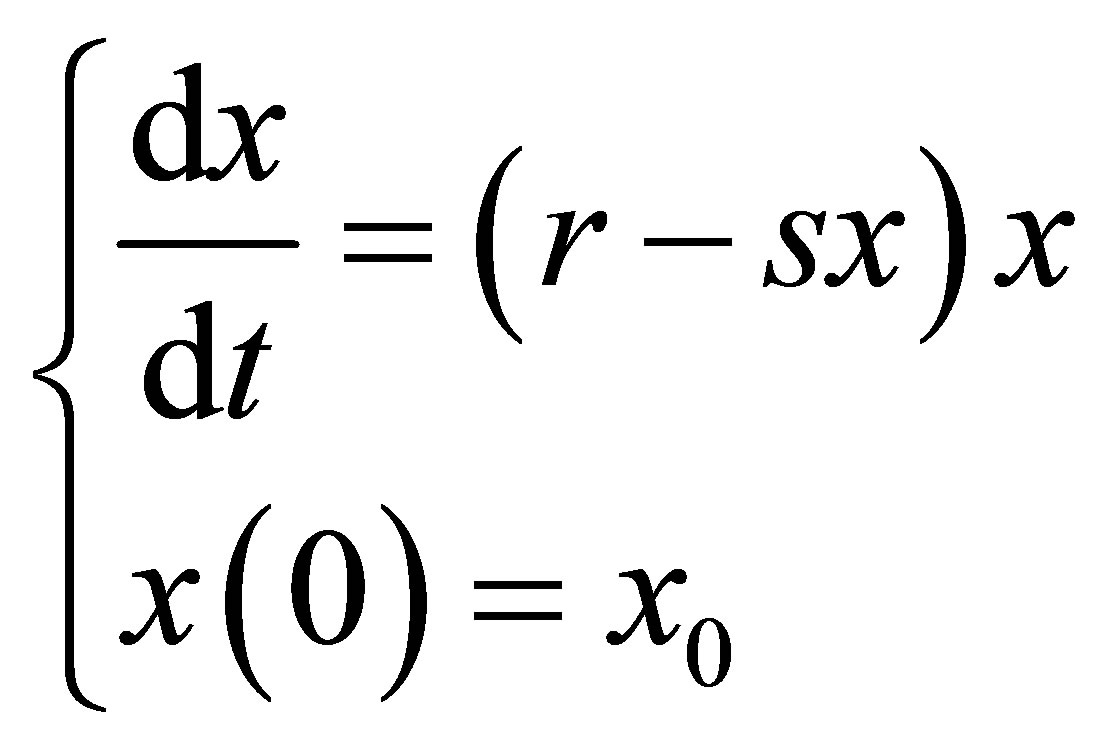
By separating variables, we found
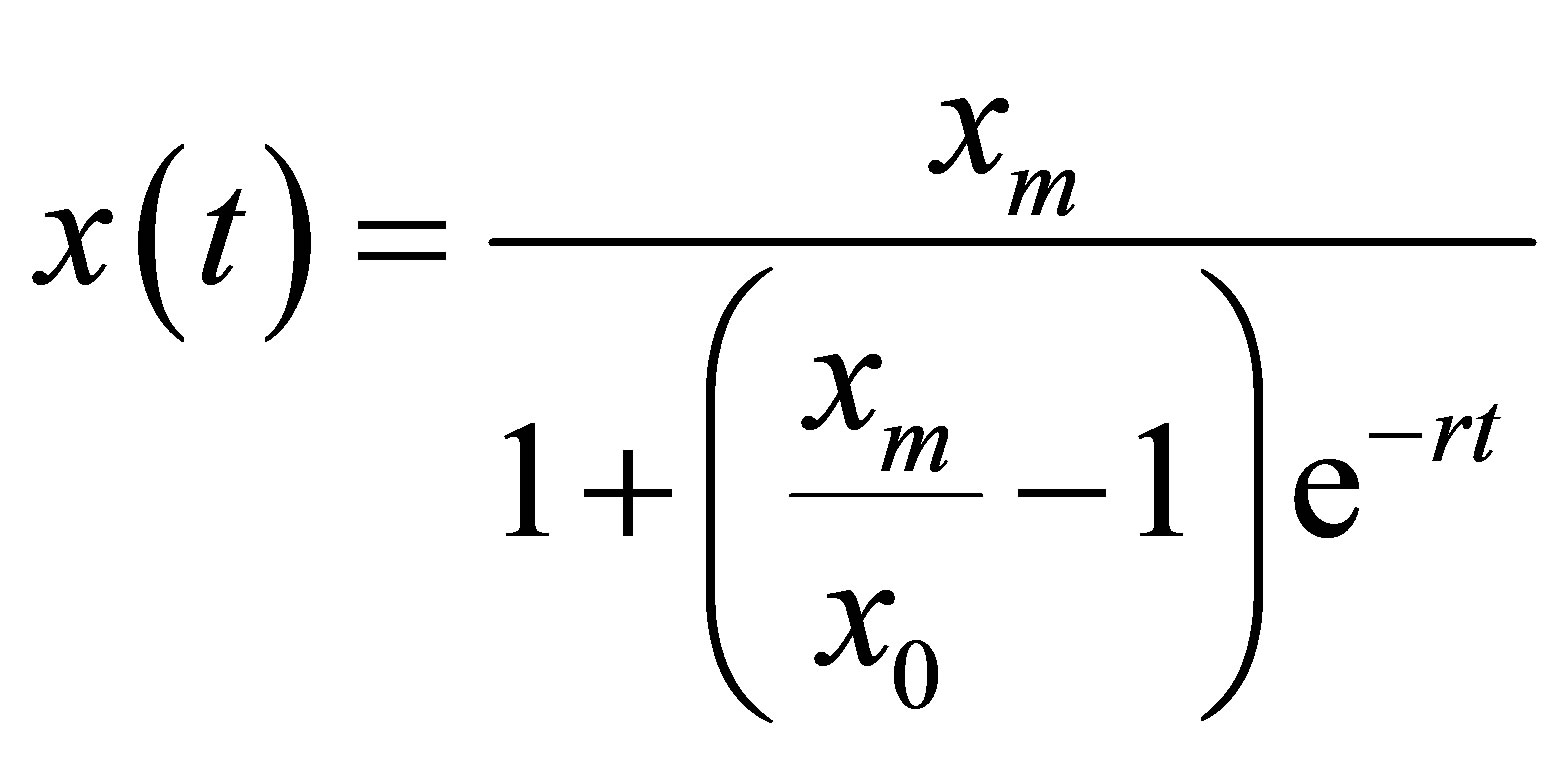 .
.
The graph of population development over time is a S-shaped curve, at the beginning of the increment 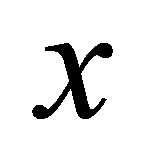 is slow, when
is slow, when
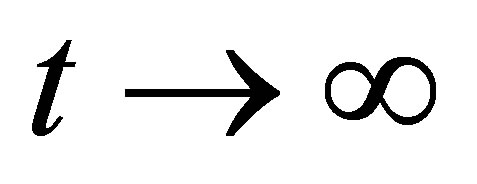 ,
,  ,
, 
is point of inflexion.
2.3. Continuous Mathematical Model of Population Development
Multhus model and Logistic model fail to take into account the age structure of population, they are only adapted not to the population prediction at future but to the past data. In fact, in order to study the future population growth, the population age structure is the important factor that cannot be ignored. Because the fertility and mortality rates of women at different age will cause the very big difference on the population. For example, two countries or regions have the same total population at present, if a country or a region is higher proportion of young people than another country or a region, then the population development status will be very different later.
Considering the age structure of the first order partial differential equation. One is continuous, it is described to use a partial differential equation with boundary control.
Let  be the total population whose age are less than
be the total population whose age are less than  when the time
when the time ,
,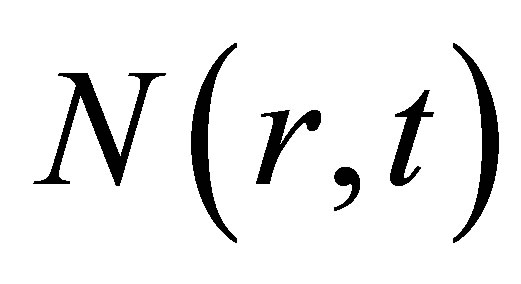 is called population function.
is called population function. 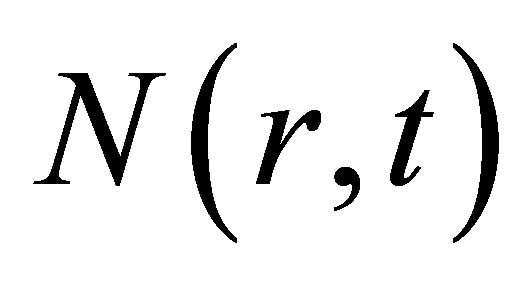 is the non-negative function of two variables and is the increasing function for
is the non-negative function of two variables and is the increasing function for . When
. When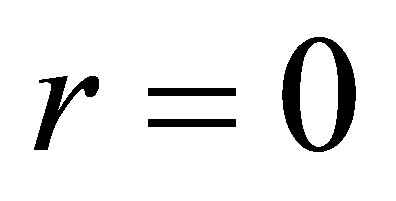 ,
, . Let
. Let 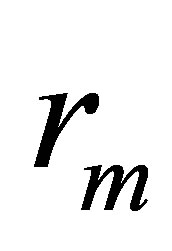 be the biggest age people can live. Then
be the biggest age people can live. Then
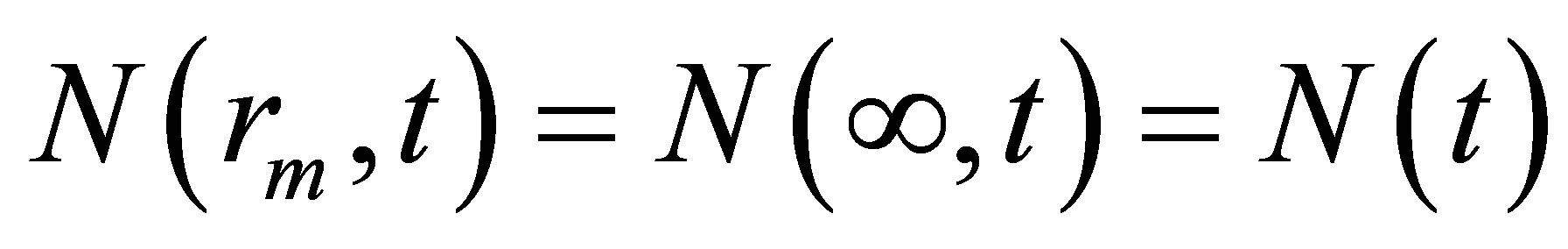 .
.
Let
 ,
,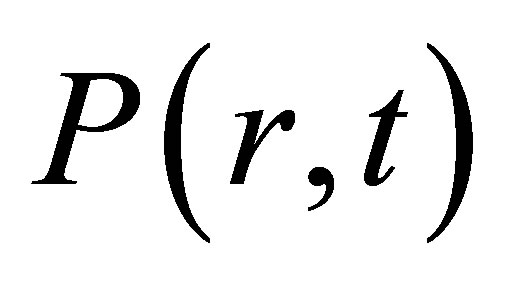
is called population density function (Also known as the population composition by age, or population state), . So we have
. So we have

The continuous model of population is as follows
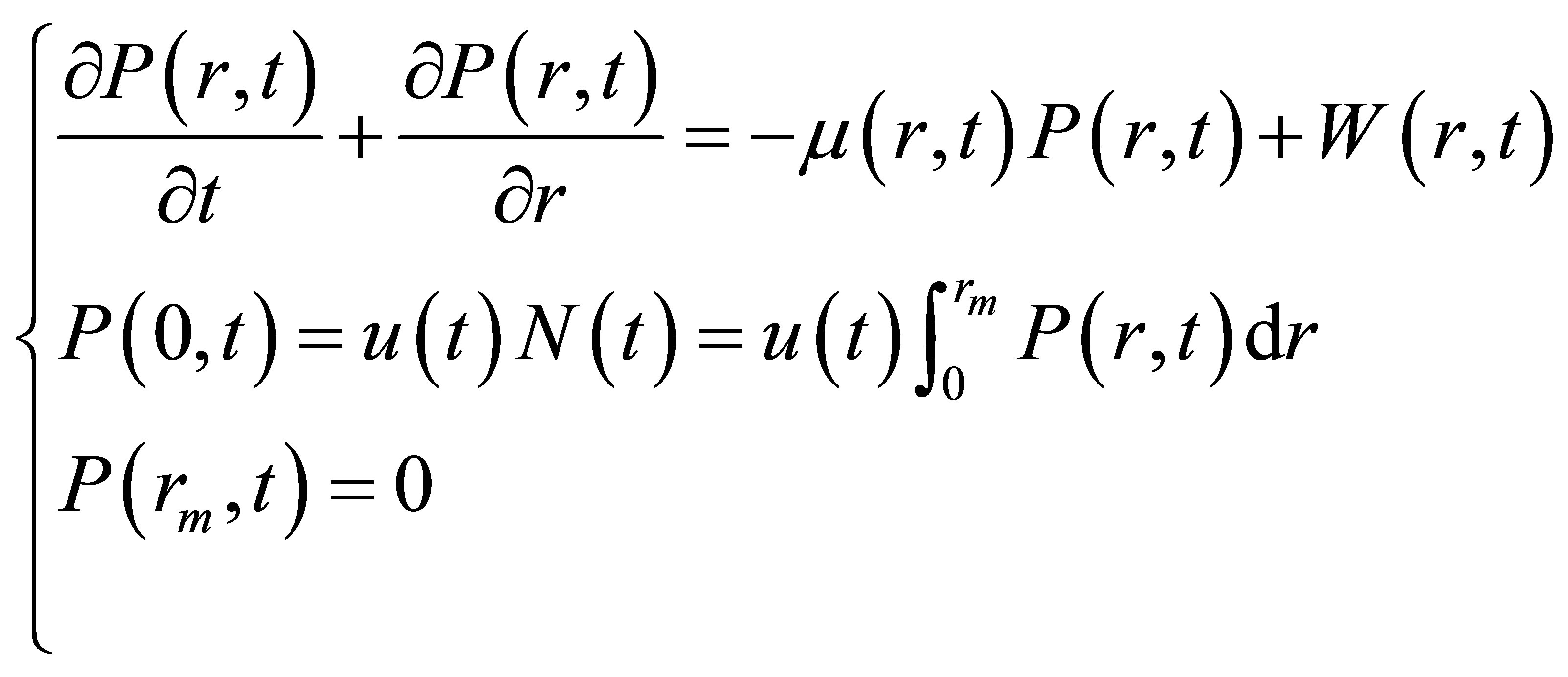
 is the ratio of the total number of births per unit time and the total population at moments
is the ratio of the total number of births per unit time and the total population at moments ,
, 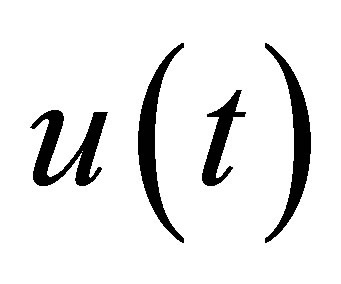 is called the relative fertility function.
is called the relative fertility function.
Defining the relative mortality
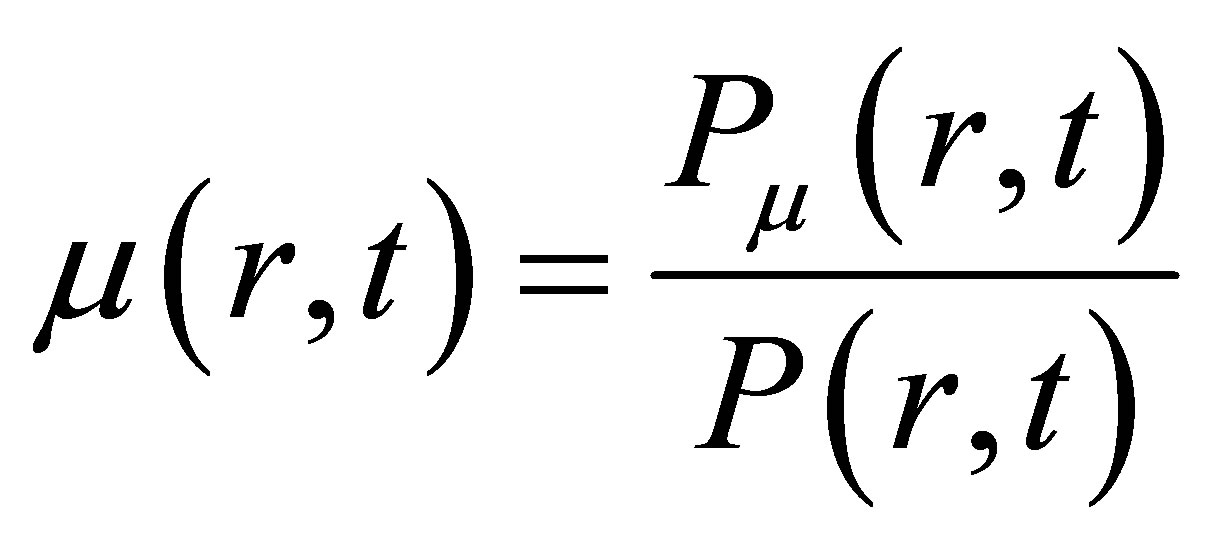
 denotes the population density function of death.
denotes the population density function of death.  can be calculated by the statistics according to the population mortality distribution at moments
can be calculated by the statistics according to the population mortality distribution at moments .
.
 denotes the perturbation of population caused by migration, natural disasters, war, etc.
denotes the perturbation of population caused by migration, natural disasters, war, etc.
By the method of statistics we can obtain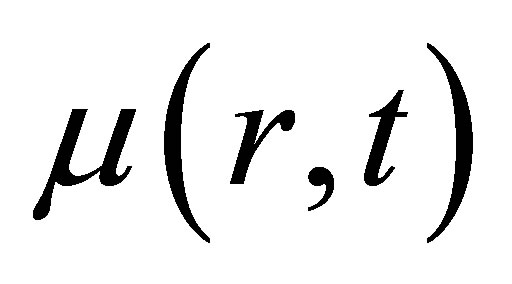 ,
, 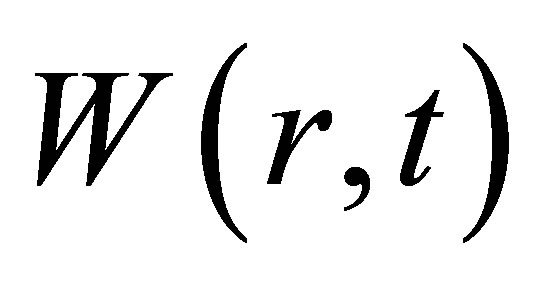 ,
, 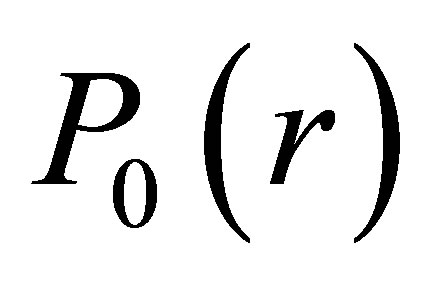 , the relative fertility function
, the relative fertility function  is given, we can get
is given, we can get 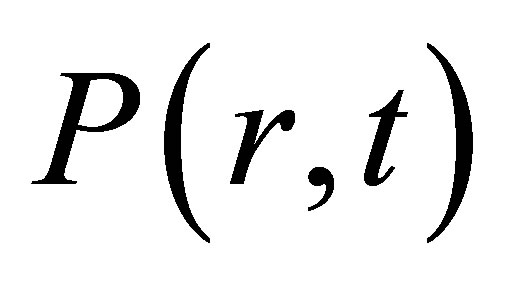 by solving the equation set, it reflects the process of population development is changing along with age and time.
by solving the equation set, it reflects the process of population development is changing along with age and time.
3. Discrete Model of Population Development
Continuous model is not very convenient in practical application, because the known conditions of statistical data are discrete, such as one year the fertility, mortality, sex ratio of each age female etc. Secondly, as a result, people hope the data is discrete. Third the expression of solution in continuous model contains the unknown function, it is difficult to get the solution, so we need to set up a corresponding discrete model. We use the state transition matrix to describe here.
Assuming age calculated by one full year of life, time is year. In discrete model we only consider birth, aging and death caused of population evolution, and ignore the influence such as migration, war etc.
Let  be the number of people for
be the number of people for  year
year  years old, the maximum year is
years old, the maximum year is ,
,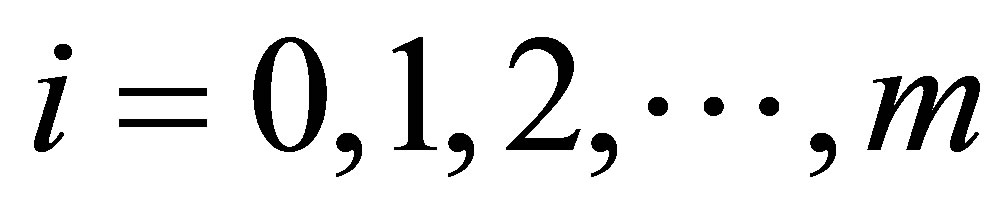 . Let
. Let 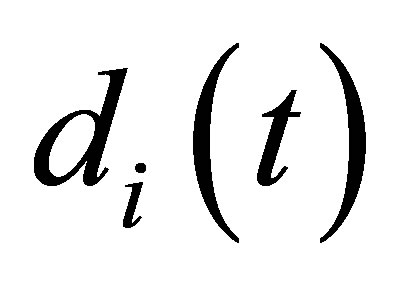 be the death rate for
be the death rate for  year
year  years old,
years old,  be the survival rate. Let
be the survival rate. Let  be the female fertility at the right age for
be the female fertility at the right age for  year
year  years old,
years old,  be the ratio of women in the population for
be the ratio of women in the population for  year
year  years old. Let
years old. Let

be the average women of childbearing age giving birth to the number of baby.
Let
 ,
,
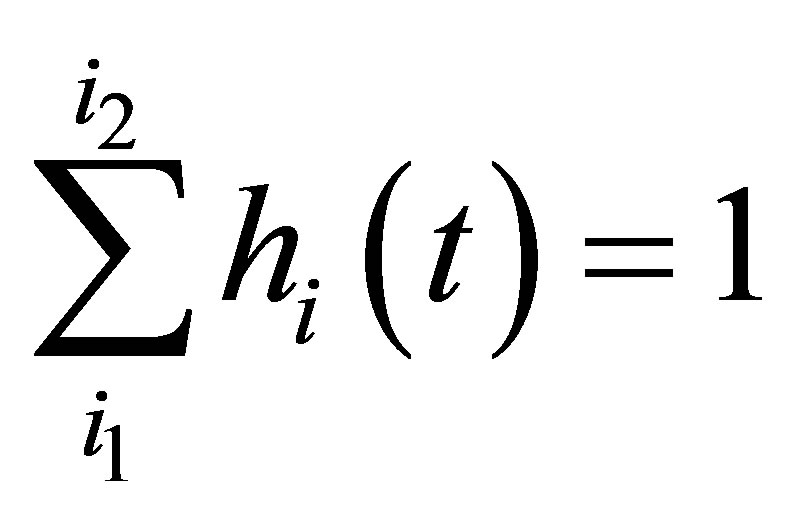 ,
,
 is called fertility pattern.
is called fertility pattern.
Introducing the vector and matrix
 ,
,


there

In control theory  is called state vector,
is called state vector,  is called state-transition matrix,
is called state-transition matrix,

are called controlled quantity.
We can set up the population development equation—first-order difference equation
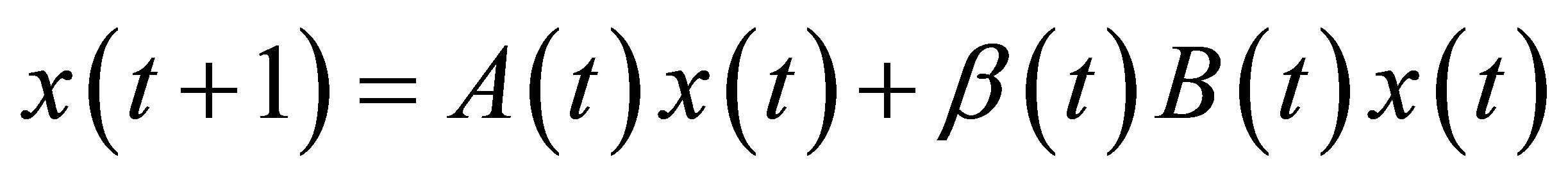 because
because  and
and  are linear respectively, the equation is a bilinear equation.
are linear respectively, the equation is a bilinear equation.
We can determine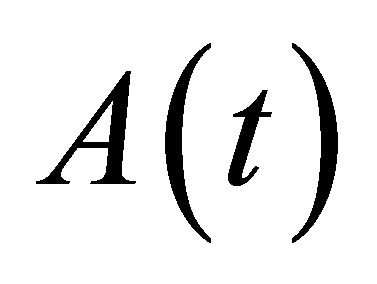 ,
,  by statistics, when the total fertility rate
by statistics, when the total fertility rate 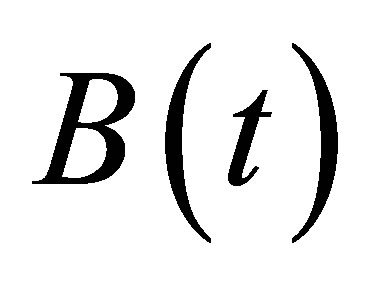 is given, we may forecast the process of the population development.
is given, we may forecast the process of the population development.
4. Summary
Before setting up the model of population development and forecast population, it is important for us to determine the main target population. Usually a lot of indicators reflect the status of population, such as total population, birth rate, mortality rate and the total fertility rate and so on. According to the needs, there are other important target population, for example:
1) The aging rate. The aging rate is the population over 60 years in the total population. It is different from the aging index, which is equal to the ratio of average age in average life expectancy.
2) The rate of urbanization. It is the ratio of the urban population in the total population, which is an important index of population distribution.
3) Sex ratio at birth by the number of the baby boys when the number of girls is 100.
Today, stepping into aging society gradually, the gender gap of China is more and more big. After studying the effect of different indicators for population development, we conclude that it is very important to control the population quantity and improve population quality.
REFERENCES
- A. Latengtuya and J. Liang, “Model of Population Forecasting,” Inner Mongolia Science and Technology and Economy, Vol. 4, 1994, pp. 21-22.
- Y. H. Hao and X. M. Wang, “Grey Dynamic Model and Its Application in Population Prediction,” Mathematics in Practice and Theory, Vol. 32, No. 5, 2002, pp. 813-820.
- J. G. Qi, “Research of Population Economics Prediction,” Dalian University of Technology Library, Dalian, 2006.
- K. P. Men, L. L. Guan and X. Z. Yi, “Research of China’s Population Development Prediction,” Statistics and Decision, Vol. 22, 2007, pp. 6-9.
- R. N. Wang and D. S. Tang, “Based on the Improved Grey GM (1, 1) Model of Population Prediction,” Statistics and Decision, Vol. 20, 2007, pp. 93-95.
- X. J. Chang, “Time Series Analysis,” Higher Education Press, Beijing, 1993.
- J. J. Wu, “Population Forecast Model Based on BP Neural Network Research,” Statistics & Information Forum, Vol. 19, No. 2, 2004, pp. 44-46.
- J. Song and J. Y. Yu, “Population Cybernetics,” Science Press, Beijing, 1985.
- J. Song, “Corpus. Century Gue: Song Jian Draft Pick,” Atomic Energy Press, Beijing, 2001.
- Q. Y. Jiang, J. X. Xie and J. Ye, “Mathematical Model,” Higher Education Press, Beijing, 2003, pp. 162-166.
NOTES
*Corresponding author.

