Received 4 June 2016; accepted 27 June 216; published 30 June 2016

ABSTRACT

A possible explanation about some puzzling aspects of quasars is proposed. Moreover, using the red shifts of spectral lines picture, a simple method to calculate Hubble’s constant is presented.

Keywords:

About the Quasars

1. Introduction

Quasars were originally discovered as intense sources of radio emission. A quasar is by definition a starlike body with a large red shift. Such property is characteristic of quasars and gives them their mysterious nature. By 1974, the spectra of over two hundred quasars had been analyzed, and all of them had very large red shifts. The simplest way to explain the quasars’ red shifts is to assume that they are extremely distant bodies that follow Hubble’s law; in such a way that they are the most distant objects known. Moreover [1] [2] , if the red shifts of quasars are caused by the expansion of the Universe, they are very luminous bodies indeed. In fact, the galaxies are not the most luminous objects in the Universe; because that honor belongs to the quasars, which are hundreds of times as luminous as galaxies. As the name indicates, many quasars are intense radio sources. The total amount of energy emitted in the radio range is somewhat less than the optical luminosity; in such a way that the quasars emit a lot of optical radiation, too. Thus, the most puzzling of all quasars’ problems is the energy source. Another puzzling aspect of quasars comes from their small size; problem which is encounter when the investigators try to explain the optical radiation which comes from the rapidly varying sources. Those observations have been made in the optical part of the spectrum, and according to the results obtained, it is well known at present that the continuous radiation from quasars is variable with time. Most quasars vary relatively slowly increasing and decreasing their luminosities over periods of about a year, but a few of them are over much violent in their variation increasing dramatically their luminosities in periods of a day or so. When the size of quasars was first pointed out in 1966, some scientists thought that the problem was serious enough so that the cosmological distances of quasars should be questioned; because if the quasars were brought closer, they would not need to be as luminous and the size problem could be solved. However, according to recent observations the source of the radiation comes from a very small region; in such a way that it is quite puzzling that so much radiation comes from such a small volume of space. The question is how such a small volume can produce so much energy.

2. The Size and the Energy Emission of Quasars

If some results of Einstein’s Special Theory of Relativity [3] are taken into account, it is possible to propose a solution to the size and the large luminosity of quasars. According to that theory no material body could possible travel with a velocity greater than the velocity of light in vacuum. Thus it becomes obvious that none of them could accelerate beyond the light barrier. This argument still stands. Concerning the quasars, all of them are material bodies which have a proper mass different from zero [3] [4] . In other words, they are objects which can only travel at velocities smaller than the velocity of light in the empty space; and clearly, the only way by which they can move is by means of an acceleration process. However, in its original paper, Einstein said that there is an upper limit of the velocity for the material bodies. In fact, the total energy of those objects would get infinitely large upon approaching the velocity toward the light barrier; as it is easy to see from the following relativistic transformation equation [5]

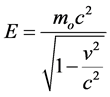(1)

This very important relativistic result shows, in particular, that the total energy of a free body does not go to zero for v = 0 but rather takes on a finite value.

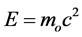(2)

where is the proper mass. This last quantity is called the rest energy of the body.

On the other hand, there is another relativistic transformation equation for the volume of the material bodies. Since the transverse dimensions do not change because of the motion, the volume V of a body decreases according to the following formula.

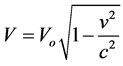(3)

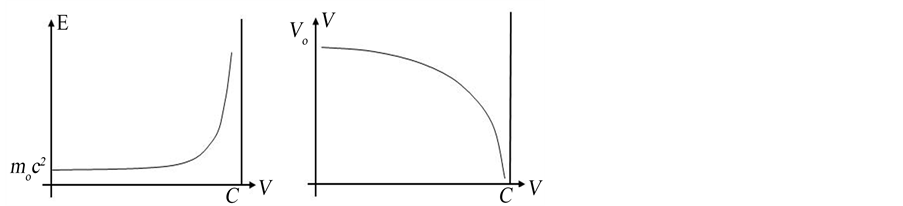
where V_o is the proper volume of the body. An examination of the Equations (1) and (3) shows that when v → c, E → ¥; and V → 0. Thus as the velocity of a body, as a quasar, increases toward the velocity of light in the empty space, the quasars’ total energy increases toward infinity and its volume or size decreases toward zero. Since it is absurd for any quasar with finite proper mass m_o to have infinite energy, and at the same time volume zero, it must conclude that it is impossible for any quasar to move with the light velocity in vacuum. Nevertheless, the relativistic transformation Equations (1) and (3) show that in one case an increase of the total energy, and in the other case a decrease in the size of quasars are produced when their velocity v goes toward c, in such a way that taking into account their great red shifts; those conclusions are enough to explain the quasars’ large luminosity, and at the same time its small size; as it is easy to see in the following graphics (see Figure 1).

3. The Relativistic Lens

The relativistic effect over the total energy emission, and the size of the quasars, apparently, acts as a kind of lens: In fact, according to the formula (3) the volume V decreases when the quasar’s velocity v increases toward c. At the same time the quasar’s total energy, and also its mass, increases toward infinity when v → c.

On the other hand, it is well known from Optics that the ratio of the image size q, to the object size p is what is called the magnification M; so that, M = q/p. According to the relativistic transformation Equation (3), it could be considered that V is the volume image, and V_o is the volume object; in such a way that

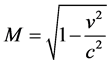(4)

Since v < c always, M < 1; and we have that V < V_o always. That means that the effect of the increasingly velocity of recession v is to diminish the size of the volume image. On the other hand, from the other relativistic transformation equation; that is to say, the Equation (1); E will be the total energy image, and E_o = m_oc² the total energy object; and then.

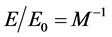(5)

Since M < 1, M⁻¹ > 1 always, so that, the increasingly velocity of recession v produces in this case, an effect of magnification; in such a way the total energy image E is always greater than the total energy object E_o.

Because of the enormous velocities of recession of the quasars, and also due to the relativistic effect, the image of the total energy emitted, appears amplified, and at the same time, and because of the same reasons, the image of the size appears diminished.

4. The Red Shifts and Hubble’s Constant

The red shift of a quasar is usually denoted by the letter z; that is to say

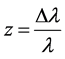(6)

where ∆l is the shift in wavelength of a spectral line, and l is the wavelength that that line had when it left the quasar. Quasar red shifts range from relatively small numbers, like 0.158 for 3C 273, to large, like 3.53 for OQ 172, the most distant quasar known at this time. The red shifts can also be expressed as a velocity by means of the Doppler shift formula. However, if the velocity is small compared to the velocity of light, the following simple form of that formula is normally used.

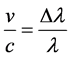(7)

where v is the velocity, and c the velocity of light. Given that the quasars have very large red shifts; showing that these objects are moving at relativistic recession velocities; it is necessary to use the exact formula for the relativistic Doppler shift [5] - [7]

(8)

From this equation, one gets that

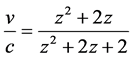(9)

where z is the red shift measured from the spectra.

Let

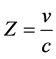(10)

be, the relativistic red shift corresponding to a velocity of recession v, which always is small compared to the velocity of light in the empty space.

According to the evolutionary phenomenon called the Expansion of the Universe [1] , the velocity of recession and the distance are correlated. The larger the distance is, the greater the velocity is. This relationship is known as the law of red shifts, or also Hubble’s law, and can be written as follows: Velocity of recession equals Hubble’s constant times distance

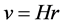(11)

where H Hubble’s constant. Hence, substituting (10) in (11), the following result is obtained

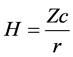(12)

In this case, it is possible to compare any couples of quasars, and consider one of them as a measure unit; in such a way that

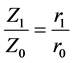(13)

where Z_o and r_o, are the relativistic redshift and the distance, respectively, of the measure unit; as long as, Z₁ and r₁ are the relativistic red shift and the distance of the other quasar. Thus, to calculate extragalactic distances, only one need the Equation (9) to obtain the relativistic red shifts from the red shifts measured directly from the respective spectra, and then, the following relationship can be used

(14)

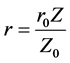
Although is not possible to use the local group of galaxies for measuring the Hubble constant; because of a such a distances their random velocities may interfere with the motion because of to the Expansion of the Universe, can still be used as a previous step to obtain the data for the measure unit. As it is well known, the nearest large cluster of galaxies is the Virgo Cluster; 23.9 Megaparsecs distant, and according to the red shift measured from its spectrum, the velocity of recession of that cluster is equal to 1200 km∙sec⁻¹. Given that this velocity is small compared to the velocity of light, the Equation (7) is used to obtain that z = 0.4 × 10⁻². On the other hand, the red shift obtained directly from the spectrum of the quasar 3C 273 is z = 0.158; so that, from the Equation (9), it is easy to calculate the following relativistic redshift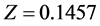. 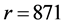In that case, using the previous data of the Virgo Cluster, and the relationship (14) one gets that Megaparsecs.

Let’s consider the quasar 3C 273 as a measure unit, from which we have that

(15)

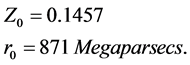
Using those data in the Equation (14), and also the formula (9) to obtain the relativistic red shifts from the red shifts measured directly in the respective spectra, which are reported in the specialized literature, the following results are obtain.

Finally, from the relationship (12), and with the use of the former data, a value of 50.2 kilometers per second per Megaparsec for Hubble’s constant is obtained in every case; and, this is the exact value for that constant.

5. Conclusions

With all that have been previously mentioned, there are enough reasons to believe that quasars seem to be N- galaxies or Seyfert galaxies which are so far away that only their central core is visible. The N-galaxies are the optical equivalents, in a sense, of the compact radio source, having most of their luminosity contained in small, brilliant, almost stellar nuclei. Their properties read very much like quasars’ properties. On the other hand, the N-galaxies are distinguished by their photographic appearance and the Seyfert galaxies by their spectra. Nevertheless, not all the N-galaxies have spectra with Syefert characteristics; but in general, the spectra of N-galaxies and Seyfert galaxies can be explained in the same way that the spectra of quasars can be.

Also, it is possible to assume that the rapidity of the variations in the luminosity of some quasars, maybe the most distant, can be explained with the aid of the relativistic effect over the size of those objects.

Finally, with the use of the red shifts of the spectral lines picture, it is possible to propose another way to calculate Hubble’s constant.

Cite this paper

Angel Fierros Palacios, (2016) About the Quasars. Journal of High Energy Physics, Gravitation and Cosmology,02,323-327. doi: 10.4236/jhepgc.2016.23030

References