Received 28 May 2015; accepted 23 June 2015; published 26 June 2015

ABSTRACT

This paper proposes a quantum-inspired evolutionary algorithm with neighborhood search (call- ed QEANS) to solve the project portfolios optimization problem with limited multiple resources and bounded risks for each project portfolio. The decision concerns how to find an optimal or best assignment of projects to a set of project portfolios that maximizes the total profit. The studied problem is formulated by a 0-1 linear programming model, and a quantum-inspired evolutionary algorithm with neighborhood search is proposed to solve it. In specific, each problem solution is encoded by a Q-bits matrix, which is updated by quantum-rotation gate. In addition, crossover and mutation operators are integrated so as to increase the population diversity. Furthermore, an effective repairing procedure is proposed for dealing with the generated infeasible solutions. To prevent the local optimum, a specific neighborhood search procedure is also proposed. Randomly generated instances are used to test and justify the effectiveness of the proposed QEANS. The obtained results indicate that the proposed QEANS is effective.

Keywords:

Project Portfolio, Optimization, 0-1 Linear Programming, Quantum Evolutionary Algorithm

1. Introduction

With the fast development of technology and the changing consumer behavior, most enterprises or companies have to face an ever experienced complicated competition environment. This is because that, in the Internet Age, lots of new ideas and concepts are emerged around the world each day or in a short period of time, and some of them may be quickly transformed into new products (services) or new technologies, which are then widely spread across the world. Due to this reason, new markets or services will be created and new companies or enterprises are founded. Therefore, all companies have to compete with each other and suffer from uncertain operational risks as well as relatively small profit margins. Hence, almost all the great or powerful enterprises adopt the market diversification strategy and expect to mitigate risks, improve competitiveness, maintain company’s sustainability and obtain considerable profits from different marketing fields.

In practice, only minority companies had achieved their expectations and most of them had failed. The reasons were generally from two aspects. One aspect was that companies had made wrong market diversification strategies because of many reasons, so company’s resources (i.e., money, technologies, human resources and so on) were used in wrong places and wasted. The other was that companies had made proper diversification strategies but they lacked sufficient ability or resources to implement them, because the diversification strategy generally belonged to macroscopical level, and it must be reflected in the specific business activities. From this point, we can know how to choose specific business activities from numerous possible ones for achieving company’s long-term strategy and how to assign existing limited resources to each chosen activity as well as how to manage them to effectively play a key role in the success of strategy implementation.

To tackle the above mentioned problems, it is a good choice to implement the diversification strategy by using the methodology of Project Portfolio Management (PPM). According to [1] and [2] , project portfolio management refers to the process for effectively identifying, assessing, selection, and optimizing the collection of projects in order to meet some certain expectations and needs (such as long-term strategic objectives) of an enterprise or a company. From above descriptions, we can know that company’s strategy implementation can be seen as project management process, as company’s new businesses can be seen as projects, and project portfolio management is an important tool to effectively manage and implement these projects in strategy implementation. A key issue to the project portfolio management is the portfolio selection and resource allocation problem.

Motivated by the above descriptions, this paper proposes a novel meta-heuristic approach (called Quantum- inspired Evolutionary Algorithm with Neighborhood Search, QEANS) to solve the strategy-oriented project portfolio optimization problem under bounded risks and with the consideration of resources sharing in different projects. This problem is NP-complete. Our objective is to find an optimal projects selection scheme such that the overall revenues of selected projects are maximized.

The rest of this paper is arranged as follows. Section 2 presents the literature review. The problem description and its formulation are given in Section 3. In Section 4, we introduce the proposed solution method, i.e., Quantum-inspired Evolutionary Algorithm with Neighborhood Search (QEANS). In Section 5, randomly generated instances are used to test the effectiveness of the proposed algorithm. At last, Section 6 concludes this paper and discusses some possible future research directions.

2. Literature Review

This section presents a literature review of related project portfolio problems and Quantum-inspired Evolutionary Algorithm (QEA). Studies on different kinds of project portfolio problems have been reported by researchers. For example, Arcjer and Ghasemzadeh [3] developed a decision support system consisted by a multi-stage integrated framework for the project portfolio selection process. Dickinson et al. [4] proposed a nonlinear integer program model for optimizing the portfolio of new technology projects selection problem with considering the interdependencies between different projects. Girotra et al. [5] investigated the structure and effect of multiple projects targeting the same market at the portfolio level. Chen and Askin [6] developed a general mathematical formulation for the joint problem of selecting and scheduling projects with maximizing the present worth of profit. Besides, Coffin and Taylor [7] developed a beam search procedure for solving the R&D projects selection and scheduling problem. Heidenberger [8] developed an MILP (mixed integer linear programming) approach for dynamic projects selection problem. In addition, some researchers also proposed effective approaches for the projects selection problem from very specific background. For instance, Badri et al. [9] formulated a 0 - 1 goal programming model for IS (Information System) project selection problem. Eilat et al. [10] developed a DEA (Data Envelopment Analysis) model embedded in the BSC (Balanced Score Card) approach for funding suitable projects from new R&D portfolios.

Since 1990, QEA has been received much attention from engineers and researchers due to its excellent optimization ability. According to Hey [11] , QEA can be regarded as a probability optimization algorithm because it is based on the principle and concept of quantum computing, i.e., quantum bit (Q-bit) representation, quantum parallelism and quantum updating gate. It has showed very good performance in terms of solution quality and computation time in solving many famous combinatorial optimization problems. For instance, Narayanan and Moore [12] and Talbi et al. [13] proposed different QEAs to optimize the travelling salesman problem (TSP) and obtained better performance compared to traditional approaches. Han and Kim [14] and Zhao et al. [15] developed various effective QEAs for knapsack problems. Besides, some researchers have also developed different kinds of QEA for flowshop/jobshop scheduling problem [16] [17] .

Viewing from the above descriptions, we can see that project portfolio optimization problem with limited risks and multiple kinds of resources have rarely been studied in the literature. In addition, various efficient QEAs have been applied in several research fields except for optimizing project portfolio problem. Therefore, this work tries to connect this research gap.

3. Problem Description, Notation and Formulation

3.1. Problem Description

In this paper, we consider the following problem. Suppose that a company decides to use the methodology of project portfolio management to achieve its strategic objectives. And according to its strategic objectives, the company intends to invest some idle resources (including money, technology, human resource and so on) to N new projects which had been evaluated by professional experts and are considered to have great investment value, that is, the success of implementing these new projects can effectively help the company improve its competitiveness, maintain high sustainability, maximize its incomes and so on. Here, we suppose that all resources required for implementing these new projects are available or the company has the ability to get the required resources for carrying out these new projects. Furthermore, it is supposed that each project has its own expected revenue and potential risk of failure. We also suppose that some different projects may use the same type of resources (such as technology or equipment), which is called resource-sharing. Besides, due to resource limitations, the company can only implement at most M project portfolios at a certain period of time, that is to say, each project portfolio has a maximum resource allocation quantity. In order to control risk in an acceptable range or level, each project portfolio must have a maximum risk tolerance. That is to say, the overall risks of projects belonging to a same project portfolio cannot exceed the pre-defined maximum risk setting.

Based on the above descriptions, this paper studies how to optimize the project portfolio selection problem with satisfaction of bounded portfolio-risks and resource limitations. The decision concerns how to select the projects among a given set of projects for each project portfolio such that the total profits of selected projects in all portfolios are maximized. To facilitate the problem formulation, we give the following notation and decision variables:

N: the number of total projects.

M: the number of project portfolios.

K: the types of available resources.

R_j: the maximum risk acceptance degree of project portfolio j, 1 £ j £ M.

v_i: the expected revenue or profit of project i, 1 £ i £ N.

r_i: the failure risk of project i, 1 £ i £ N.

C_{k, j}: the maximum quantity of resource k assigned to project portfolio j, 1 £ k £ K, 1 £ j £ M.

q_{k, i}: the quantity of resource k assigned to project i, 1 £ i £ N, 1 £ k £ K.

j_k: the sharing-degree of resource k, and j_k Î [0, 1], 1 £ k £ K. If j_k = 0, it means that resource k cannot be shared or used by different projects; Otherwise, resource k (such as equipment and buildings) can be completely used by different projects.

m_i: the projects similarity of project portfolio i, and m_i Î (0, 1), 1 £ i £ M. For m_i » 0, it implies that all projects in portfolio i are different, and for m_i » 1, it implies that all projects in portfolio i are nearly the same ones. It should be noted that, since there does not exit the same projects, we have m_i ¹ 1.

The decision variables are the following:

V: the total profits of M project portfolios.

x_{i, j}: 0-1 variable. If x_{i, j} = 1, it means that project i belongs to project portfolio j; Otherwise (i.e., x_{i, j} = 0), project i does not belong to project portfolio j, for 1 £ i £ N, 1 £ j £ M.

3.2. Mathematical Model

Based on the above descriptions and notation, the mathematical model for project portfolio optimization problem with limited resources and bounded risks can be formulated as follows:

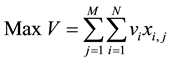(1)

subject to:

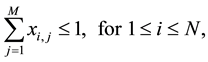(2)

. (3)

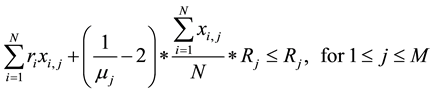. (4)

In the above model, the problem objective is formulated as (1), i.e., maximization of the total profit of all portfolios. Constraint (2) indicates that each project i can only be assigned to at most one project portfolio j, because it cannot be divided. From this definition, we can know that each project is either be selected for a project portfolio or not be selected. Furthermore, constraint (3) defines that the total resource of type k required by all projects in a portfolio j cannot exceed its pre-allocated quantity C_{k, j}. Finally, constraint (4) defines that the overall risk of all projects in a project portfolio j cannot exceed its pre-defined maximum risk acceptance level R_j.

4. Solution Method

In this section, due to the NP-complete characteristic of our studied problem, we introduce a novel meta-heuris- tic approach to solve it. That is called as Quantum-inspired evolutionary algorithm (QEA) with neighborhood search procedure. In what follows, we first introduce the Q-bits representation, and then describe other components of the proposed algorithm in details.

4.1. Representation

QEA is formulated according to the principles of quantum computing [11] [14] . The smallest unit of information in QEA is called Q-bit, which is usually defined as follows [14] :

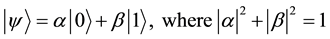. (5)

In Equation (5), complex numbers a and b respectively denote the probability amplitudes of Q-bit y in state “0” and state “1”. From this definition, we can know that each Q-bit would be found in state “0” with probability |a|² or in state “1” with probability |b |². In order to determine its final state, a random-key observation way is generally applied to each Q-bit. In specific, a number rd is randomly generated from uniform distribution [0, 1). If rd > |a|², then Q-bit is in state “1”; otherwise, Q-bit is in state “0”. Due to this reason, QEA can be regarded as a probabilistic algorithm.

As mentioned above, the value of integer decision variable x_{i, j} belongs to 0 or 1. Hence, it has a same characteristic with Q-bit. Inspired by this fact, the chromosome is defined as follows:

,

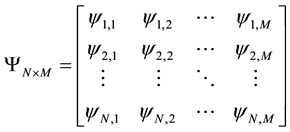where

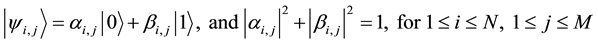. (6)

By using the above mentioned random-key way, the final state of each Q-bit y_{i, j} can be determined. If Q-bit y_{i, j} is in state “0”, we let it represent that project i is not in portfolio j, i.e., x_{i, j} = 0; Otherwise, project i is in portfolio j, i.e., x_{i, j} = 1. Finally, all values of decision variables x_{i, j} (hereafter we called binary matrix X) are known, and correspondingly, the objective value (i.e., V) can also be calculated.

4.2. Feasibility Checking Procedure

For each obtained binary matrix X (i.e., values of decision variables x_{i, j}) associated with a Q-bits chromosome, it may be an infeasible solution. Therefore, we need to check whether it satisfies the problem constraints (2), (3) and (4). If it does not satisfy the problem constraints, then we repair it. To do this, consider the following:

Step (A): Check constraint (2). Because each project can only be assigned to at most one project portfolio, for any project i (1 £ i £ N), if it is assigned to more than one project portfolio, we randomly remove it from one of portfolios (i.e., reset x_{i, j} = 0, 1 £ j £ M), until constraint (2) is satisfied.

Step (B): Check constraint (3). Suppose that maximum resource (type k) quantity of project portfolio j (i.e., C_{k, j}) is exceeded, then we remove project i with the minimum ratio value of v_i/q_{k, i} from project portfolio j until the total required resources of projects in portfolio j are smaller than or equal to C_{k, j}.

Step (C): Check constraint (4). Suppose that the maximum risk acceptance degree (i.e., R_j) of portfolio j is exceeded, then we remove project i with the minimum ratio value of v_i /r_i from project portfolio j until the overall risk of portfolio j is satisfied.

Based on the above works, each obtained problem solution (i.e., binary matrix X) is either proved or repaired to be feasible. Hence, the corresponding objective value can be easily calculated.

4.3. Updating Q-Bits Individuals

For each Q-bit y_{i, j} in a quantum chromosome Y, it is updated by the well-known quantum rotation gate, which is usually defined as the follows [14] :

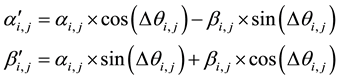for. (7)

In (7), Dq_{i, j} is the rotation angle, which decides the rotation direction and magnitude in the process of updating Q-bit y_{i, j}. We first define q₀ be the initial rotation angle, and then suppose that V_Y represents the objective value related to quantum chromosome Y, and V_B represents the objective value of the best chromosome (denoted by B) found in population. Similar to [14] , the rotation angle Dq_{i, j} is determined based on the values of decision variable x_{i, j} in individual Y (marked as Y-x_{i, j}) and in the best one (marked as B-x_{i, j}). If V_Y < V_B, then consider the following cases:

(a) For Q-bit y_{i, j} in the 1^st or 3^rd quadrant, if Y-x_{i, j} = 1 and B-x_{i, j} = 0, then we set Dq_{i, j} = q₀, which aims to increase the probability of Q-bit y_{i, j} in state “0”; else if Y-x_{i, j} = 0 and B-x_{i, j} = 1, then we set Dq_{i, j} = (-q₀), which aims to increase the probability of Q-bit y_{i, j} in state “1”; else, Dq_{i, j} = ±0.002p, which aims to let Q-bit search its neighborhood area.

(b) For Q-bit y_{i, j} in the 2^nd or 4^th quadrant, if Y-x_{i, j} = 1 and B-x_{i, j} = 0, then we set Dq_{i, j} = (-q₀), which aims to increase the probability of Q-bit y_{i, j} in state “0”; else if Y-x_{i, j} = 0 and B-x_{i, j} = 1, then we set Dq_{i, j} = q₀, which aims to increase the probability of Q-bit y_{i, j} in state “1”; else, Dq_{i, j} = ±0.002p, which aims to let Q-bit search its neighborhood area.

4.4. Chromosome Mutation

To increase the population diversity, mutation operation is applied to quantum chromosome according to certain probability. In particular, four points p, q, g, h (they can be the same or different) are randomly generated for each chosen chromosome, 1 < p, q < N, 1 < g, h < M, then, for each Q-bit y_{i, j}, p £ i £ q, g £ j £ h, we swap its amplitudes of states “0” and “1”, that is, the original Q-bit y_{i, j} is defined as: |y_{i, j}ñ = a _{i, j} |0ñ + b _{i, j}|1ñ, after mutation operation, it becomes: |y_{i, j}ñ = b_{i, j} |0ñ + a _{i, j}|1ñ.

4.5. Binary Matrix Variation

To further increase the solution diversity, crossover and mutation operations are applied to the selected problem solutions (i.e., values of decision variable x_{i, j}) according to their respective probabilities. In specific, binary tournament method is used to select individuals for crossover. At first, four different points p, q, g, h are randomly generated, 1 < p, q < N, 1 < g, h < M. For generating offspring1, the value of x_{i, j} (p £ i £ q, g £ j £ h) is copied from parent 2, and the values of other x_{i, j} (i Ï [p, q], j Ï [g, h]) is copied from parent 1; similarly, for offspring2, the value of x_{i, j} (p £ i £ q, g £ j £ h) is copied from parent 1, and values of other x_{i, j} (i Ï [p, q], j Ï [g, h]) is copied from parent 2.

Furthermore, mutation operator is applied to each chosen problem solution X. More precisely, four different points p, q, g, h are randomly generated, 1 < p, q < N, 1 < g, h < M. For p £ i £ q, g £ j £ h, if x_{i, j} in X is equal to 1 (i.e., project i is in project portfolio j), then we set x_{i, j} = 0; else (i.e., project i is not in project portfolio j), then we set x_{i, j} = 1.

4.6. Neighborhood Search Procedure

For improving the solution quality as many as possible, neighborhood search procedure is applied to the obtained binary matrix at each generation. In specific, for a binary matrix X, if there exists a project i which does not be assigned for any of project portfolios (i.e., for each j, we have x_{i, j} = 0), then we randomly put it into project portfolio j (1 £ j £ M), i.e., setting x_{i, j} = 1; else, if project i is in project portfolio j (i.e., x_{i, j} = 1), then we randomly put it into project portfolio j − 1 or j + 1 (i.e., setting x_{i, j} = 0 and x_{i, j-1} = 1 or x_{i, j+1} = 1). Finally, evaluate all the generated new solutions, and update the best solution.

4.7. Quantum Population Re-Initialization

Although several effective variation ways have been proposed to increase the diversity of quantum population and problem solutions, it still has some possibilities to enhance the diversity in order to prevent the algorithm falling into the local optimum. To do this, we re-initialize all the quantum chromosomes at every l generation.

4.8. Steps of the Proposed Algorithm

Input: Pops (size of the quantum chromosomes); Maxgen (maximum number of iterations); c_p (crossover probability); m_p (mutation probability); l (population re-initialization period); q₀ (the initial rotation angle).

Output: the best solution V_B and x_{i, j}.

Step (I): Randomly initialize quantum chromosomes and set t = 0.

Step (II): Determine Q-bits state, and assign the corresponding value to decision variable x_{i, j}.

Step (III): Evaluate individuals, i.e., check the feasibility of the obtained solutions x_{i, j}.

Step (IV): Store the best solution among all the solutions and related values of variables x_{i, j}.

Step (V): Let t = t + 1.

Step (VI): if t > Maxgen, then go to stop and output the stored best solution; else, go to Step (VII).

Step (VII): Apply Q-gate to update each quantum chromosome.

Step (VIII): Apply mutation operator to quantum chromosomes.

Step (IX): Determine Q-bits state, evaluate individuals, and finally update the best solution.

Step (X): Apply crossover and mutation operators to obtained binary matrixes (i.e., x_{i, j}).

Step (XI): Evaluate individuals and update the best solution.

Step (XII): Apply neighborhood search procedure.

Step (XIII): At every l generation, re-initialize all the quantum chromosomes. Then, determine the Q-bits state, evaluate individuals, and finally update the best solution .After that, go to Step (V).

5. Computational Results

In this section, randomly generated instances are used to evaluate the performance of our proposed quantum- inspired evolutionary algorithm with neighborhood search (QEANS). The experimental study is carried out on a HP personal computer with an Inter Core i5-2400 Processor 3.10 GHz (Windows 7 environment). The proposed QEANS is implemented in C++ programming language. The random instances are generated by the following way. We set N Î {100, 200, 500}, M Î {15, 20}, K Î {5, 10}, and let U (a, b) be a uniform distribution between parameters a and b. The expected revenue or profit of project i is set as: v_i = U (30, 100); the risk of project i is set as: r_i = U (0.1, 0.5), for 1 £ i £ N. The projects similarity of project portfolio j is set as: m_j = U (0.1, 0.9); the maximum risk acceptance level of project portfolio j is set as: R_j = U (0.85, 1), for 1 £ j £ M. Moreover, the sharing-degree of resource k is set as j_k = U (0.1, 0.95), for 1 £ k £ K. For each given values of N, M and K, five instances are randomly generated. Furthermore, the algorithm parameters are set as follows: Maximum generations: Maxgen = 500; Population size: Pops = 500; Crossover probability: c_p = 0.8; Mutation probability: m_p = 0.1; Population re-initialization period: l = 20.

Table 1 reports the computational results on the randomly generated instances. Note that the “B.P.” and the “CPU” respectively refer to the average best profit and the average computation time of the five randomly generated instances (for each given values of N, M and K). Since the rotation angle (i.e., q₀) has positive effect to the performance of QEANS, we set q₀ Î {0.01p, 0.03p, 0.05p, 0.08p} in our experimental study to further test its influence to the algorithm. From Table 1, we can see that both the average total profit (i.e., B.P.) and the CPU time (i.e., CPU) increase with the problem size (i.e., the value of N and M). We also notice that the CPU times gaps of different rotation angle settings for each given value of N, M and K are generally small and in the range of 0 s - 6 s, which can be neglected. Besides, we can also see from Table 1 that our proposed QEANS with q₀ = 0.08p has a better performance than that with other rotation-angle settings, for almost all the tested instances except for the one with setting N = 500, M = 15 and K = 10. Moreover, for random instance with N = 500, M = 15 and K = 5, our algorithm with q₀ = 0.03p has a better solution quality than that with q₀ = 0.08p, please see the bold font in Table 1. Figure 1 illustrated the results curves of different parameter settings. From above descriptions, we can conclude that our proposed QEANS is effective for solving the studied optimization problem in terms of solution quality and computation time.

6. Conclusion

This paper first formulated an integer programming model and then proposed a quantum-inspired evolutionary algorithm with neighborhood search (QEANS) for project portfolios optimization problem with limited resources and bounded risks for each project portfolio. The objective of the studied problem is to maximize the total profit. Each decision variable is directly encoded by a Q-bit, which is updated by the quantum-rotation gate. To increase the diversity of the population, crossover and mutation operators were implemented into the proposed QEANS. To further improve the solution quality, a specific neighborhood search procedure was proposed. Com- putational results on randomly generated instances with different parameter settings showed that the proposed QEANS was effective for solving the studied problem in terms of solution quality and CPU time. Future research directions include the extension of the proposed mathematical model and optimization algorithm to solve the problem with bi-objective or triple-objective, such as maximization of the total profits and minimization of the overall risks at the same time.

References

NOTES

^*Corresponding author.