American Journal of Industrial and Business Management
Vol.4 No.7(2014), Article
ID:48076,9
pages
DOI:10.4236/ajibm.2014.47046
Model of 4PL’s Outsourcing Logistics Coordination Based on Service Quality
Bin Ding, Hui Zheng
School of Management, University of Science and Technology of China, Hefei, China
Email: zhengh566@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 May 2014; revised 16 June 2014; accepted 18 July 2014
ABSTRACT
The paper establishes a supply chain coordinating model based on single 4PL-multy 3PL. Considering goods loss and damage, it comes to the conclusion that the fixed revenue-sharing contract couldn't be coordination when the yields was relative to the efforts of 3PL and 4PL. In order to get the coordination, we first model a fixed revenue-sharing contract based on side payment using L-F model and the theory of principal-agent on the premise of symmetric information. Then, we analyze the application of this model when the information is asymmetric. The result shows that the symmetric model can get the coordinating while the optimal efforts of asymmetric information model depend on the 3PL’s performance. At last, we check the analysis using a traditional sample.
Keywords:Fixed Revenue-Sharing Contract, Side Payment, 3PL Coordination, Principal-Agent Model, L-F Game Theory

1. Introduction
The third party logistics (3PL) has developed rapidly since 1980s, including the supply inventory management, the procurement, the transportation, the information management and other logistics services. As the trend of economic globalization strengthens, more and more products are produced and circulated in different areas of the world. The logistics activities have becoming more and more complicated and the diversity arises among different logistics entities. As a good way to integrate resources, the fourth party logistics (4PL) can both improve efficiency and decrease the operation cost of logistics service.
However, a variety of risks relating to 3PL have been reported in literatures. There are many problems in the outsourcing logistics service to 3PL such as inadequate provider expertise, inadequate employee quality, inability of 3PL to deal with special products and emergency circumstances. The main risk that customers are exposed to is goods loss and damage. The data show that 32% of complain is caused by goods loss and damage. As an integrator, 4PL carries out the majority of the administrative activities but leaves the physical activities to contracted 3PL service providers. Therefore, 4PL has the ability and responsibility to manage outsourcing logistics quality risk for its clients.
In the existing literature, the incentive 4PL offered to 3PL is mainly adopted by the mixed revenue-sharing mechanism. Hoong Chuin Lau [1] established the multi-agent intelligent system to support the 4PL’s transportation network; Xiu Li [2] tried to design implement of 4PL; Gülçin [3] researched on the evaluation of 4PL operating models with 2-additive Choquet integral; W. S. Lim [4] designed an optimal contract to incentive 3PL to supply the high-level logistics service level under the asymmetric quality and cost information. Huang Min [5] worked on modeling and optimizing of 4PL routing optimization based on goal programming. MC Chen [6] applied loss aversion to investigate the service quality in logistics, and discussed a moderating effect of service convenience. Y. Zhang [7] researched on 4PL management services based on Horizontal Supply Chain. J. Li [8] designed an intelligent model of the cluster supply chain with the horizontal cooperation. Many other researchers have done a lot of work in the field of 3PL and 4PL [9] -[15] . However, they seldom considered the optimal incentive problem based on the quality risk of goods loss and damage [16] -[20] . In this paper, we establish a 4PL-n3PL model to design a side-payoff mechanism to guide the 3PL to offer an optimal quality effort level to guarantee the coordination of the supply chain with the symmetric information and asymmetric information. And we analyze the 4PL’s effort level and the expected profit in those different conditions.
2. Problem Description and Traditional Models
2.1. Problem Description
One manufacturer outsources logistic transaction to n-3PL. But it is difficult for the manufacturer to maintain a good relationship with so many 3PLs in order to satisfy the high standard logistic service. On the contrary, too many 3PLs would greatly increase the production enterprise logistics subcontract and the difficulty of the management of logistics service quality. In practice, there are two main solutions. One is a self-built 4PL. Another is that the manufacturer delegates a 4PL to deal with the 3PL logistic service outsourcing transaction, manage the relationship between 4PL and 3PL, and control the quality risk.
The joint efforts among 4PL and 3PLs can increase the output of logistics services. Considering goods loss and damage, the logistic quality level is determined by the 3PLS’ efforts. Before the logistic operation process, the 4PL can’t monitor the 3PLS’ efforts. But when the logistics service finished, the 4PL can estimate 3PLS’ efforts with the good loss and damage level. The 3PLS should take the effort cost when exerting efforts. More efforts will generate fewer loss and damage level. In practice, the supply chain can’t get coordination because of 3PLS’ lower efforts than optimal level. The aim of this paper is to develop the 3PLS’ optimal effort with L-F game theory and Principal-agent theory.
Based on L-F game theory and principal-agent theory, the paper researches on examining the benefit relationship between the 4PL and 3PL.We assume that 4PL is a leader, playing a leading role in the process of the whole game, 3PLS are followers, always trying to decide whether or not to accept a contract parameters of the 4PL. Hypothesis 4PL and 3PLS are risk neutral and perfectly rational, namely, they will make decisions according to the expected profit maximization principle.
2.2. Model Assumption
We set 2 continuous variables 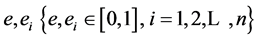 to measure the effort of 4PL and 3PLS. The quality effort cost of them separates as
to measure the effort of 4PL and 3PLS. The quality effort cost of them separates as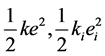 , where k and ki are cost parameters. The measure
, where k and ki are cost parameters. The measure
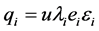 is the service quality index, which stands for the logistics service quality influence of 3PLS’ effort; So
is the service quality index, which stands for the logistics service quality influence of 3PLS’ effort; So 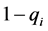 is the goods loss and damage Ratio.
is the goods loss and damage Ratio. ![]() is an random variable that affecting the logistics service quality which is exponential distribution.
is an random variable that affecting the logistics service quality which is exponential distribution.  is the ith parameter and
is the ith parameter and ![]() is a constant. When the goods loss and damage happens, the 4PL will suffer
is a constant. When the goods loss and damage happens, the 4PL will suffer 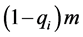 punishment, where m is the punishment parameter. The output function is
punishment, where m is the punishment parameter. The output function is , where
, where 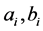 are the parameters of 4PL and 3PL and
are the parameters of 4PL and 3PL and ![]() is an standard normality random variable. The 4PL offers and 2-part linear contact to 3PL in the form of
is an standard normality random variable. The 4PL offers and 2-part linear contact to 3PL in the form of  where is the fixed shift and
where is the fixed shift and 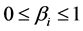 is a quality revenue parameter.
is a quality revenue parameter.
2.3. Virtual Centralized Decision Model and Mixed Revenue Sharing Decision Model
1) Virtual Centralized Decision The aim of Supply Chain Coordination is to maximize the supply chain profit. In virtual centralize decisionmaking, the 4PL and 3PLs form an integrated company, which means 4PL choose 3PLs to execute logistics services. In order to get the best profit level, the decision maker determines the efforts of 4PL and 3PLs. The expected profit of the integrated company ![]() is as followed.
is as followed.
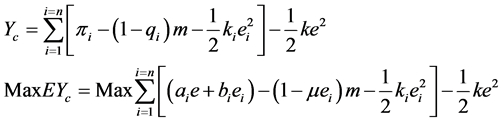
The function is jointly concave in each effort level of e and ei, so we can get the optimal effort level e* and ![]() with derivation.
with derivation.
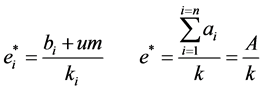 (1)
(1)
Substituting the optimal solution (1) into the objective function, we can get the optimal profit.
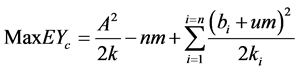
2) Mixed Revenue Sharing Decision Model In the Mixed Revenue Sharing subcontracting mechanism, 4PL offer every 3PL a fixed pay  and
and 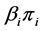 based the 3PLi’s profit. The expected profit of 4PL
based the 3PLi’s profit. The expected profit of 4PL 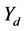 is as followed.
is as followed.

We introduce  as the ith logistics revenue,
as the ith logistics revenue,  is his retained revenue. The 3PL make decision according to the aim to get the maximum revenue. Based on the principal-agent theory, the incentive compatibility constraints
is his retained revenue. The 3PL make decision according to the aim to get the maximum revenue. Based on the principal-agent theory, the incentive compatibility constraints
(IC) and Participatory constraints (IR) are
(IC) 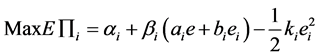
(IR) 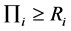
As the leader of the game process, the 4PL choose his decision according to the L-F game theory. By solving IC, we get the optimal ei
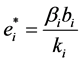 (2)
(2)
Considering IR, in order to get the maximum revenue, 4PL will always decrease 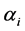 to optimal
to optimal
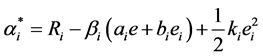 . Then substitute to the objective function, we get
. Then substitute to the objective function, we get
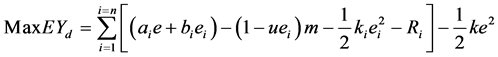
The function is jointly concave, so we make derivation
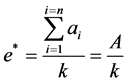 (3)
(3)
So the ith expected profit is 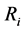 and the 4PL’s expected profit is
and the 4PL’s expected profit is
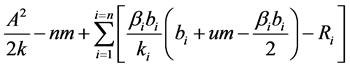
As for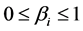 , we compare (2) and (3) to get the coordination outcome
, we compare (2) and (3) to get the coordination outcome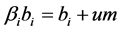 . The equation is conflicted, so the supply chain cannot balance the coordination. And the 3PL’s effort level is lower than in the Virtual Centralized Model.
. The equation is conflicted, so the supply chain cannot balance the coordination. And the 3PL’s effort level is lower than in the Virtual Centralized Model.
3. Coordination Model Base on Side-Payoff with Symmetric Information
In the Mixed Revenue Sharing Decision Model, the supply chain cannot get the coordination just because the 3PL pay the quality effort cost and do not have the chance to share profit added value. So in this section, 4PL offer a side-payoff contract to give the 3PL effort incentive. The side-payoff incentive function must eliminate the influence of 4PL, and the incentive function is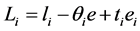 , where
, where 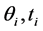 are side-payoff parameters. Considering the symmetric information, the 4PL can observe the cost information of 3PL
are side-payoff parameters. Considering the symmetric information, the 4PL can observe the cost information of 3PL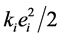 , the expected profit of 4PL is
, the expected profit of 4PL is

Based on the principal-agent theory, the incentive compatibility constraints (IC) and participatory constraints (IR) are
(IC) 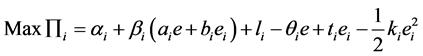
(IR) 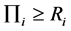
Based on L-F game theory, we solve the IC to get
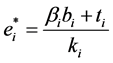 (4)
(4)
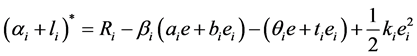 (5)
(5)
Substituting  into the objective function and derivate
into the objective function and derivate 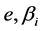
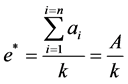 (6)
(6)
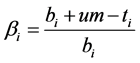 (7)
(7)
So the supply chain can get coordination, the coordination constrain is (7). The ith profit of 3PLi is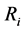 . The profit of 4PL is
. The profit of 4PL is 
4. Coordination Model Base on Side Payoff with Asymmetric Information
Considering asymmetric information and goods loss and damage level, 4PL will offer more shift to the 3PL whose operation capability is stronger. According to the symmetric model, the revenue of 3PL has a negative correlation with the parameter ki. So the low-cost 3PL disguised as high-cost 3PL to get more revenue. In this scenario, we consider the cost parameter 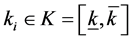 as the 3PL’s private information. The 4PL cannot get the specific value, but Probability distribution function
as the 3PL’s private information. The 4PL cannot get the specific value, but Probability distribution function  and Probability density function
and Probability density function 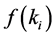 by analysis the history data. 4PL offer a contract
by analysis the history data. 4PL offer a contract  to collect the cost information of 3PL and 3PLchosse his effort level
to collect the cost information of 3PL and 3PLchosse his effort level ![]() by accepting the contract. Once the 3PL choose the menu contract
by accepting the contract. Once the 3PL choose the menu contract , he transfer his information to 4PL. But the 3PL may transfer the wrong information based on his revenue. The 4PL will design an optimal contract to guarantee the 3PL’s truth-telling about cost information.
, he transfer his information to 4PL. But the 3PL may transfer the wrong information based on his revenue. The 4PL will design an optimal contract to guarantee the 3PL’s truth-telling about cost information.
Based on the Corbett (2000) assumption, ![]() conforms monotonous risk condition
conforms monotonous risk condition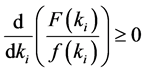 , and the 4PL’s objective function is
, and the 4PL’s objective function is
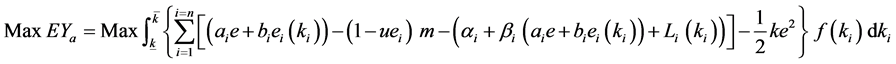 The incentive compatibility constraints(IC)and Participatory constraints (IR) of 3PLs are
The incentive compatibility constraints(IC)and Participatory constraints (IR) of 3PLs are
(IC1) 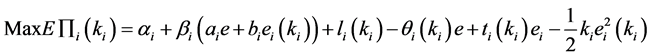
(IC2) 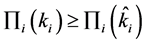
(IR) 
where 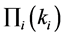 is 3PL’s expected revenue in normal way, and
is 3PL’s expected revenue in normal way, and  is his expected revenue declaring the cost parameter
is his expected revenue declaring the cost parameter![]() . IC1 shows that 3PL always choose his efforts level on the aim of maximizing expected revenue, which is an adverse selection problem. IC2 shows that 3PL’s truth-telling revenue is greater that the liestelling revenue, which is a moral hazard problem. IR shows the 3PL’s minimum revenue.
. IC1 shows that 3PL always choose his efforts level on the aim of maximizing expected revenue, which is an adverse selection problem. IC2 shows that 3PL’s truth-telling revenue is greater that the liestelling revenue, which is a moral hazard problem. IR shows the 3PL’s minimum revenue.
Based on the incentive theory, the 3PL get the optimal revenue when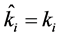 , and in practice, the optimal decision is that 3PL declare the true cost parameter. So IC1 and IC2 can be replaced by 2 constrains (1)
, and in practice, the optimal decision is that 3PL declare the true cost parameter. So IC1 and IC2 can be replaced by 2 constrains (1)
 when
when 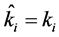 (2)
(2)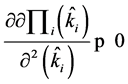 . So
. So
 . We derivate k and substitute to, with the Corbett (2001) [9] [10] conclusion, we get
. We derivate k and substitute to, with the Corbett (2001) [9] [10] conclusion, we get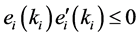 .
.
We set 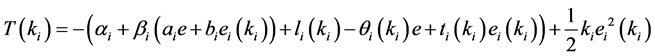 and the equation will be
and the equation will be
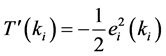 (8)
(8)
The coordination model base on side payoff with asymmetric information is as followed.


Equation (8) shows that 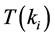 is decreasing function and when
is decreasing function and when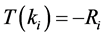 , it gets the optimal value. So we substitute the equation
, it gets the optimal value. So we substitute the equation 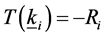 into the constrain (9), the outcome is
into the constrain (9), the outcome is
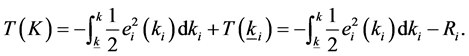 Not considering the constrain (10), the objective function is an unconstrained problem. So we get
Not considering the constrain (10), the objective function is an unconstrained problem. So we get
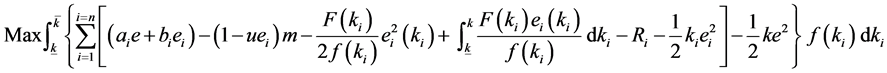 derivate
derivate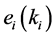 , we get
, we get
 (12)
(12)
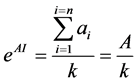 (13)
(13)
And considering assumption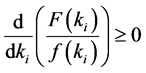 , the constrain (10) is satisfied. So we get the following conclusion.
, the constrain (10) is satisfied. So we get the following conclusion.
Conclusion: 3PL’s effort level under asymmetric information is not more than the effort level under symmetric information. The asymmetric information lowers the 3PL’s effort level and prevents the coordination of the supply chain, but not the 4PL’s.
We know that 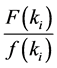 is and decreasing function, its maximum value and minimum value are respectively
is and decreasing function, its maximum value and minimum value are respectively 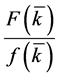 and 0. So the maximum and minimum expected profit of 4PL is as followed.
and 0. So the maximum and minimum expected profit of 4PL is as followed.

5. Discussion and Sample
5.1. Discussion
1) From Equation (4), We know that 3PLs’ effort level has an positive corelative with incentive parameter 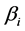 and side-payoff parameter
and side-payoff parameter , The larger value the 4PL offer to
, The larger value the 4PL offer to 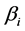 and
and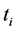 , the higher effort level the 3PLs choose. 3PLs’ effort level has a negative correlative with the cost parameter ki which stands for the operation capability of logistics service level. The stronger capability the 3PLs have, the lower goods loss and damage level is.
, the higher effort level the 3PLs choose. 3PLs’ effort level has a negative correlative with the cost parameter ki which stands for the operation capability of logistics service level. The stronger capability the 3PLs have, the lower goods loss and damage level is.
2) The Equation (7) shows that 4PL’s incentive parameter  and the side-payoff parameter
and the side-payoff parameter 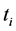 has a negative correlative with the operation capability. 4PL will offer more shifts to 3PLs whose operation capability are stronger. The incentive effect is determined by the punishment parameter m, if 4PL gives more punishment, the 3PLs will give more effort to decrease the goods loss and damage ratio.
has a negative correlative with the operation capability. 4PL will offer more shifts to 3PLs whose operation capability are stronger. The incentive effect is determined by the punishment parameter m, if 4PL gives more punishment, the 3PLs will give more effort to decrease the goods loss and damage ratio.
3) The Equation (6) shows that 4PL’s effort level ![]() has a positive correlative with its cost control capability of decrease loss and damage level. 4PL is regard as leader in the supply chain, forcing him to keep an optimal effort level to guarantee the coordination. If the yield parameter is higher, the 4PL will choose higher effort level to decrease the loss and damage.
has a positive correlative with its cost control capability of decrease loss and damage level. 4PL is regard as leader in the supply chain, forcing him to keep an optimal effort level to guarantee the coordination. If the yield parameter is higher, the 4PL will choose higher effort level to decrease the loss and damage.
4) 3PL s’ effort level under asymmetric information is not more than the effort level under symmetric information. The asymmetric information lowers the 3PL s’ effort level and prevents the coordination of the supply chain, but not the 4PL’s. When we just consider asymmetric information, the 3PL’s effort level has a positive correlative with the yield parameter which stands for the operation efficiency of the logistics service capability. The stronger operation efficiency the 3PLs have, the more effort level they will offer. Under asymmetric information, the 3PL s’ effort level has a negative correlative with the ratio of probability distribution function and probability density function. The larger the ratio is, the higher effort level distortion caused by asymmetric information is. So the 4PL must try its best to collect the true information to make the right decision.
5) From Equations (1) (3) (6) (13), we can get the conclusion that the 4PL’s quality effort level keeps constant in virtual centralized model, non-coordination, symmetric information and asymmetric information modes. The reason is that, the owner of 4PL entity is the manufacturer who has enough capital and supply 4PL logistics themselves. To guarantee high efficient logistics service, they always keep optimal effort and the main job of them is to guide 3PLs to offer enough quality to decrease loss goods and damage as well as timely delivery.
5.2. Profit Distribution between 3PL and 4PL
It is very important to identify the profit distribution between 3PL and 4PL. In virtual centralized decision, there is no profit distribution because 3PL and 4PL are regarded as an integrated entity. In decentralized decision making process with Mixed Revenue Sharing Decision Model, the 4PL can extract all system profits and leave 3PLs with just enough profit to ensure their participation, in other words, the 3PLs can only get their reservation profit Ri. When the cost information is asymmetric, the 4PL’s expected profit declines. This implies that the cost information is important to 4PL. Consequently, the 4PL should collect cost information of 3PLs to reduce the expected profit loss and improve logistics service quality. Certainly, there should be new cost in the process of collecting information.
5.3. Sample
3PLs’ quality effort level determines the goods loss and damage level. By comparison, we find that the 3PLs’ quality effort levels in mixed revenue-sharing decision and revenue-sharing with side-payoff decisions with symmetric cost information are the same, which means that there is no difference between the two kinds of decision model. The reason for this is that, though 4PL cannot monitor 3PLs’ quality effort, 4PL can design suitable contract parameters to drive 3PL exerting optimal effort level for maximizing his own profit. The 4PL is effectively the only decision maker. However, when the cost information is asymmetric, the 3PLs’ quality effort level is distorted by the asymmetric information.
We set a sample to identify the effort level and expected profit in different models. The value of the parameters is as follows.
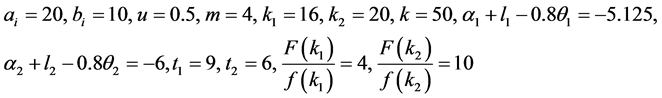
Table 1 illustrates the comparative results of different decisions, where the “VC”, “M”, “S”, “A” “L-L” and “H-L” represent “Virtual Centralized”, “Mixed Revenue-sharing model”, “side-payoff with symmetric information” and “side-payoff with asymmetric information”, “Low cost 3PL declare low cost” and “High cost 3PL declare low cost” respectively.
Table 1 shows that both 3PL1 and 3PL2 offer the optimal quality effort level in virtual centralized decision, side-off with symmetric information and truth-telling with asymmetric information. In the mixed revenue-sharing model, it is only when 4PL offer 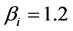 can that the supply chain gets coordination. So the 4PL must offer excessive shift to 3PLs, which is not exist in practice. In the side-payoff with asymmetric information model, the truth-telling mode can make supply chain coordination. However, the profit of 4PL declines in the lie-telling
can that the supply chain gets coordination. So the 4PL must offer excessive shift to 3PLs, which is not exist in practice. In the side-payoff with asymmetric information model, the truth-telling mode can make supply chain coordination. However, the profit of 4PL declines in the lie-telling
Table 1 . Profit distribution in different model.
mode. Consequently, the 4PL should collect cost information of 3PLs to reduce the expected profit loss and improve logistics service quality. Certainly, there should be new cost in the process of collecting information. If the collecting cost is less than the expected profit loss 0.52, 4PL will collect information.
6. Conclusions
In this paper, we consider a class of quality of risk called goods loss and damage. By using the contract design method and the game theory, we establish a single 4PL-n3PL logistics service outsourcing model to guide the 3PLs to offer an optimal quality effort level. The conclusion is as followed: with symmetric information, the traditional revenue-sharing contract can’t guide the 3PLs to offer an optimal quality effort level, and the supply chain can’t make the coordination automatically. Therefore, we design a new coordination model based on side-payoff, by using incentives which 4PL can guide the 3PL choose the optimal quality effort level to decrease the level of goods loss and damage with symmetric information. We prove that the asymmetric information can distort the effort level. 3PLs and 4PL should spend some cost to collect information of the 3PLs. At the end of the paper, we set a sample to make a comparison between the traditional revenue-sharing model and the new side-payoff model.
The paper just considers the short-term integration problem between 4PL and 3PLs. In the future, we will consider the long-term multi-game problems among 4PL and 3PLs and consider the problem when 4PL also carry out logistics service. The research has been proceeding.
7. Funding
This work is supported by the National Natural Science Foundation of China (No. 71110107024).
References
- Hoong, C.L. and Yam, G.G. (2002) An Intelligent Brokering System to Support Multi-Agent Web-Based 4th-Party Logistics. The International Conference on Tools with Artificial Intelligence, 154-164.
- Li, X., Liu, W.H., et al. (2003) The Design and Realization of Four Party Logistics. The IEEE International Conference on Systems, Man and Cybernetics, 1, 838-842
- Buyukozkan, G., Feyzioglu, O. and Ersoy, M.S. (2009) Evaluation of 4PL Operating Models: A Decision Making Approach Based on 2-Additive Choquet Integral. International Journal of Production Economics, 121, 112-120. http://dx.doi.org/10.1016/j.ijpe.2008.03.013
- Lim, W.S. (2000) A Lemons Market? An Incentive Scheme to Induce Truth-Telling in Third Party Logistics Providers. European Journal of Operational Research, 125, 519-525.
http://dx.doi.org/10.1016/S0377-2217(99)00210-6 - Min, H., Liang, R., Ming, C., et al. (2013) Modeling and Optimizing of 4PL Routing Optimization Problem Based on Goal Programming. Control and Decision Conference (CCDC), 2013 25th Chinese, Guiyang, 25-27 May 2013, 2348-2352.
- Hsu, C L., Chen, M.C. and Chang, K.C. (2010) Applying Loss Aversion to Investigate Service Quality in Logistics: A Moderating Effect of Service Convenience. International Journal of Operations & Production Management, 30, 508-525. http://dx.doi.org/10.1108/01443571011039605
- Zhang, Y. and Xie, Y. (2010) Research on 4PL Management Services Platform Based on Horizontal Supply Chain. ICLEM 2010@s Logistics for Sustained Economic Development: Infrastructure, Information, Integration, ASCE, Chengdu, 8-10 October 2010, 4518-4524.
- Li, J., Xiong, N., Park, J.H., et al. (2012) Intelligent Model Design of Cluster Supply Chain with Horizontal Cooperation. Journal of Intelligent Manufacturing, 23, 917-931.
http://dx.doi.org/10.1007/s10845-009-0359-6 - Corbett, C.J. (2001) Stochastic Inventory Systems in a Supply Chain with Symmetric Information: Cycle Stocks, Safety Stocks and Consignment Stock. Operations Research, 49, 487-500.
http://dx.doi.org/10.1287/opre.49.4.487.11223 - Corbett, C.J. and de Groote, X. (2000) A Supplier’s Optimal Quantity Discount Policy under Asymmetric Information. Management Science, 46, 444-450.
http://dx.doi.org/10.1287/mnsc.46.3.444.12065 - Kaya, M. and Ozer, M. (2009) Quality Risk in Outsourcing: Noncontractable Product Quality and Private Quality Cost Information. Naval Research Logistics, 56, 669-685.
http://dx.doi.org/10.1002/nav.20372 - Yen, Y.C., Ho, R.G., Laio, W.W., et al. (2012) An Empirical Evaluation of the Slip Correction in the Four Parameter Logistic Models with Computerized Adaptive Testing. Applied Psychological Measurement, 36, 75-87. http://dx.doi.org/10.1177/0146621611432862
- Leina, Z., Tiejun, P. and Guoqing, Y. (2010) Research of Mobile Security Solution for Fourth Party Logistics. 2010 6th International Conference on Semantics Knowledge and Grid (SKG), Beijing, 1-3 November 2010, 383-386.
- Tsai, Y.T. (2013) The Study of Service Innovation of 4PL. http://ethesys.lib.mcu.edu.tw/ETD-db/ETD-search/view_etd?URN=etd-0529113-230542
- Trappey, A.J.C., Trappey, C.V., Chang, A.C., et al. (2013) Global Logistic Management for Overseas Production Using a Bulk Purchase 4PL Model. 20th ISPE International Conference on Concurrent Engineering, 451-460.
- Li, F., Li, L., Jin, C., et al. (2012) A 3PL Supplier Selection Model Based on Fuzzy Sets. Computers & Operations Research, 39, 1879-1884. http://dx.doi.org/10.1016/j.cor.2011.06.022
- Joo, S.J., Keebler, J.S. and Hanks, S. (2013) Measuring the Longitudinal Performance of 3PL Branch Operations. Benchmarking: An International Journal, 20, 251-262.
http://dx.doi.org/10.1108/14635771311307704 - Coltman, T.R., Devinney, T.M. and Keating, B.W. (2011) Best-Worst Scaling Approach to Predict Customer Choice for 3PL Services. Journal of Business Logistics, 32, 139-152.
- Mothilal, S., Gunasekaran, A., Nachiappan, S.P., et al. (2012) Key Success Factors and Their Performance Implications in the Indian Third-Party Logistics (3PL) Industry. International Journal of Production Research, 50, 2407-2422. http://dx.doi.org/10.1080/00207543.2011.581004
- Wong, J.T. (2012) DSS for 3PL Provider Selection in Global Supply Chain: Combining the Multi-Objective Optimization Model with Experts’ Opinions. Journal of Intelligent Manufacturing, 23, 599-614. http://dx.doi.org/10.1007/s10845-010-0398-z


