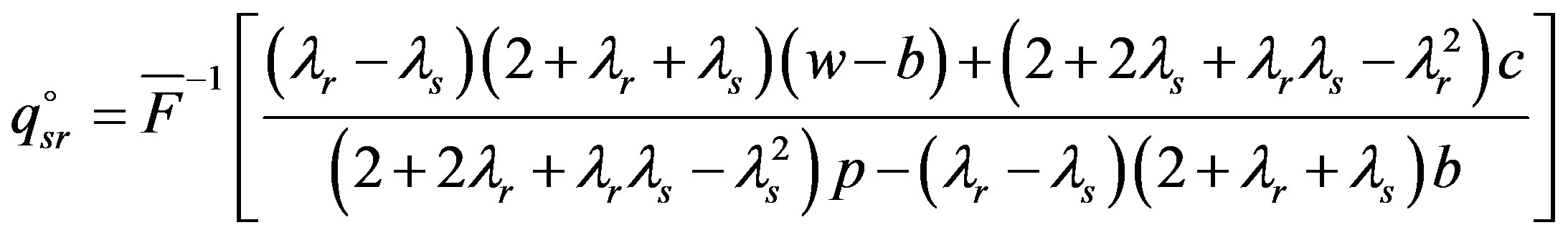American Journal of Industrial and Business Management
Vol.4 No.1(2014), Article ID:42316,5 pages DOI:10.4236/ajibm.2014.41007
Buy-Back Contract Incorporating Fairness in Approach of Stackelberg Game
![]()
School of Management, Chongqing Jiaotong University, Chongqing, China.
Email: wgx777@126.com, *yinyaxian90@126.com
Copyright © 2014 Guangxing Wei, Yaxian Yin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Guangxing Wei, Yaxian Yin. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received December 6th, 2013; revised January 3rd, 2014; accepted January 9th, 2014
KEYWORDS
Fairness; Stackelberg Game; Wholesale Price; Buy-Back Contract; Supply Chain Coordination
ABSTRACT
This paper develops the basic model of the buy-back contract by introducing the fairness to investigate how the dominant supplier decides the wholesale price, whether the buy-back contract can achieve coordination and how the fairness influences the wholesale price. It is found that, under Stackelberg game between the retailer and the dominant supplier, the buy-back contract cannot coordinate the supply chain whether the fairness is incorporated or not. Furthermore, the optimal wholesale price under Stackelberg game is larger than the initial wholesale price, which can achieve coordination. Moreover, the optimal wholesale price decreases with the retailer’s fairness, while it increases with the supplier’s fairness.
1. Introduction
Generally, the members in the supply chain make decisions to maximize their payoffs. However, the decisions may damage the whole supply chain’s payoffs. This phenomenon was called double marginalization. In order to mitigate or even eliminate this phenomenon, the supply chain contracts were emerged. Some supply chain contracts such as the wholesale price contract, the buy-back contract, the revenue sharing contract, and the quantity flexibility contract, were introduced by Cachon [1]. The buy-back contract can be expressed as: suppliers charge the wholesale price for per unit product, but they return the buy-back price for the left per unit product to the retailer at the end of the season. The buy-back price is smaller than the wholesale price. Some literatures indicated that the buy-back contract can coordinate the supply chain and the use of the buy-back contract is benefit to supply chain members [2-4]. Traditional supply chain contracts assume that the participants are rational agents. However, the recent research found that the participants are not rational agents, their decisions may be affected by some other factors. First, the supply chain members’ status and strengthen are inconsistent, which leads to the situations of the dominant retailer supply chain and the dominant supplier supply chain. Also the dominant enterprise can get better payoffs in this way [5]. The literature established the buy-back contract’s model under Stackelberg game between the dominant supplier and the retailer to research how they distribute the payoffs. And the result found that the retailer can only gain the reserved payoffs, while the supplier can obtain all the left payoffs [6]. The literature investigated a model of the buy-back contract with the dominant retailer, and pointed out that the supply chain cannot achieve the coordination [7]. Second, decision makers’ behaviors will be affected by some other factors such as fairness, loss aversion, sympathy, disgust and so on in the real operation of business. The decision makers not only pay attention to their payoffs, but also concern about whether the distribution of the payoffs is fair or not. Also, fairness will affect the decision makers’ behaviors [8,9]. Some literatures researched the impact of the fairness on the supply chain coordination [10-13]. In this paper, when we investigate the buy-back contract, two factors will be considered. First, we research a two-stage supply chain including the retailer and the dominant supplier under Stackelberg game. So the sequence of the decision is: the supplier makes a decision first; then the retailer makes a decision; at last, the supplier makes the optimal decision. Second, fairness was incorporated. By establishing the models under Stackelberg game incorporating fairness to investigate whether the supply chain can achieve the coordination, how the supplier formulates the optimal wholesale price and how the fairness influences the supplier’s optimal wholesale price.
The rest of the paper is organized as follows. In Section 2, the basic model for the buy-back contract is employed. In Section 3, the Stackelberg game model is established. In Section 4, the improved model incorporating fairness is investigated. Finally, conclusions are given in section 5.
2. Basic Model
Considering a two-stage supply chain where the retailer buys the product at the wholesale price 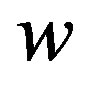 from the supplier, while sells the product at the retail price
from the supplier, while sells the product at the retail price 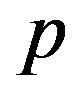 to the customers. To produce a production the supplier’s cost is
to the customers. To produce a production the supplier’s cost is , and
, and 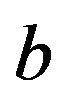 is the buy-back price. The market demand is
is the buy-back price. The market demand is 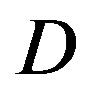 and the average demand is
and the average demand is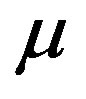 ,
,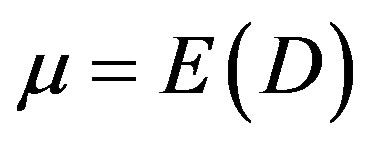 . Denoting
. Denoting  as probability density function, and denoting
as probability density function, and denoting 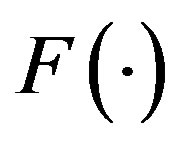 as cumulative distribution function. Respectively, F is a continuous, differentiable and strictly increasing function, and
as cumulative distribution function. Respectively, F is a continuous, differentiable and strictly increasing function, and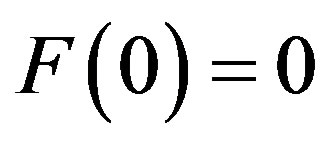 ,
, . From these settings, we can calculate the expectation quantity of the retailer is:
. From these settings, we can calculate the expectation quantity of the retailer is:
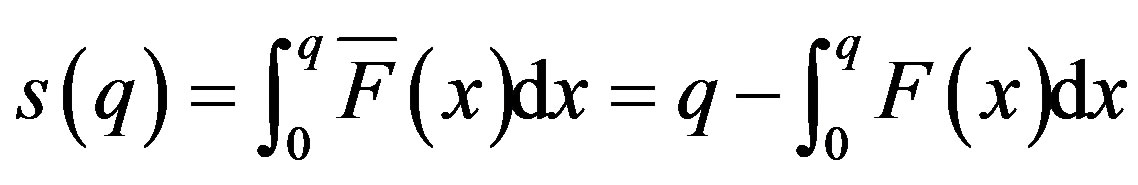
So the expectation payoffs’ functions of the retailer, the supplier and the system are as follows:
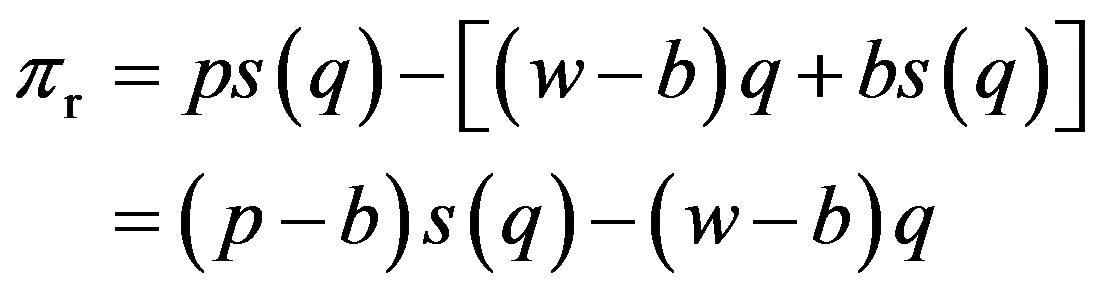 (1)
(1)
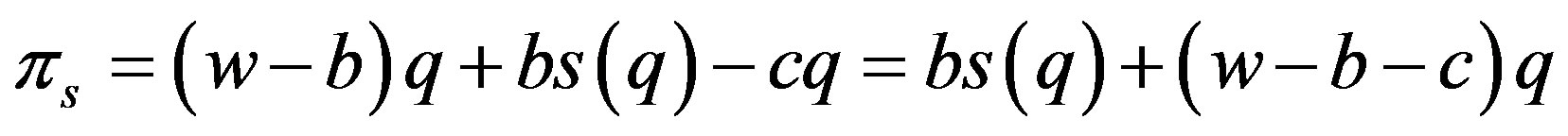 (2)
(2)
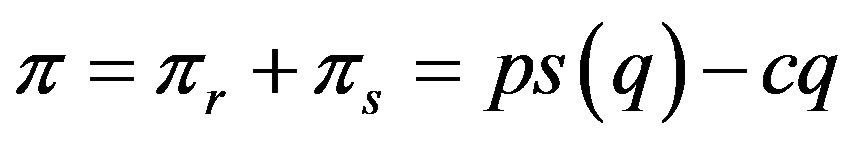 (3)
(3)
By calculating derivation of the above equations, it is found that, the buy-back contract can achieve the coordination of supply chain when the equation
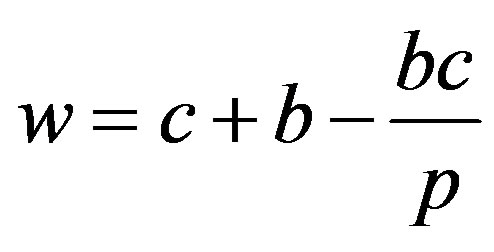 was satisfied.
was satisfied.
3. Stackelberg Game Model
Under Stackelberg game, the sequence of the decision between the dominant supplier and the retailer is: first, the supplier decides the wholesale price and the buy-back price, then, the retailer decides order quantity according to the wholesale price and the buy-back price. At last, the supplier decides the optimal wholesale price and the optimal buy-back price. The supplier’s choice of the optimal wholesale price and buy-back price are made by observing the retailer’s order quantity. Therefore, the supplier’s wholesale price and buy-back price is a function of the retailer’s ordering strategy. When the retailer makes a decision of order quantity, the supplier will formulates the wholesale price and the buy-back price relatively. This is a dynamic Stackelberg game where the participants grasp the perfectly information. So the backward induction method can be used to solve this problem. To simplify the research, we argue that the buy-back price was given and unchanged. So the supplier only makes a decision of the wholesale price.
Proposition 1: Under Stackelberg game, the retailer’s optimal order quantity 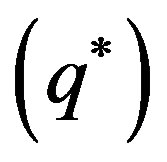 satisfies the equation of
satisfies the equation of
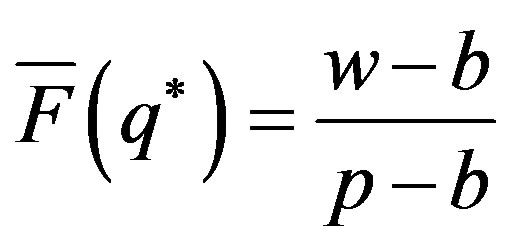 . And the dominant supplier’s optimal wholesale price
. And the dominant supplier’s optimal wholesale price 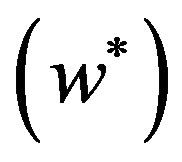 subjects to equation of
subjects to equation of
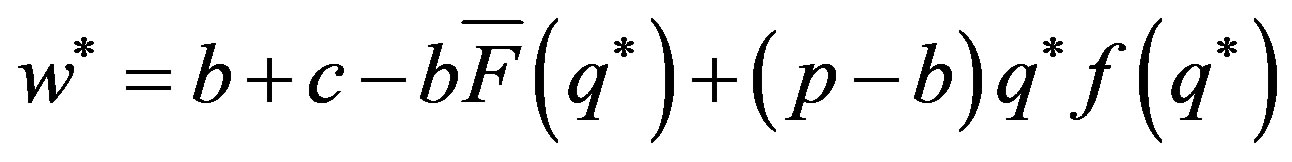 .
.
Proof: We use the method of backward induction to solve this problem.
First, according to the given information, the retailer will decides order quantity, which satisfies the equation of 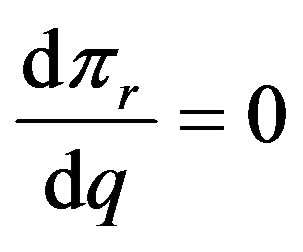 to maximizing his payoffs, from this equation we can get that the retailer’s order quantity
to maximizing his payoffs, from this equation we can get that the retailer’s order quantity 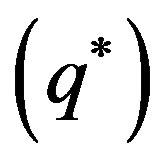
satisfies the equation of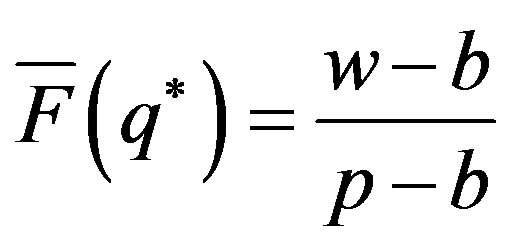 , which can be denoted as
, which can be denoted as 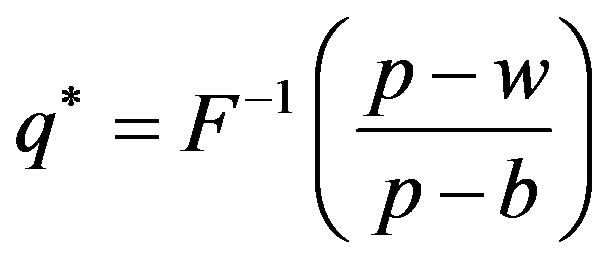 .
.
Then the supplier will chooses the optimal wholesale price to maximizing payoffs according to the retailer’s optimal order quantity. Substituting the above equation into the supplier’s payoffs function, so the following equation can be got:

According to the equation of , we can get that:
, we can get that:
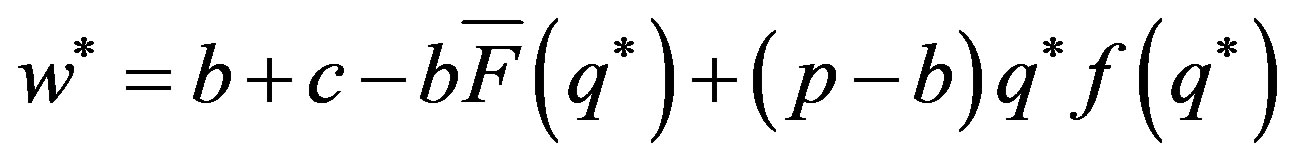 . Q.E.D.
. Q.E.D.
Proposition 2: If the initial wholesale price satisfies the coordination of the buy-back contract, but under Stackelberg game, the buy-back contract cannot achieve coordination.
Proof: according to the buy-back contract’s basic model, we know that when 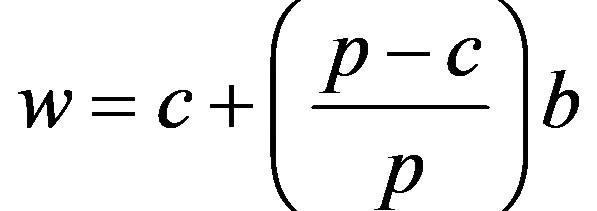 the supply chain can realize the coordination initially.
the supply chain can realize the coordination initially.
According to the method of decentralized decision, the supplier’s optimal wholesale price satisfies the equation of 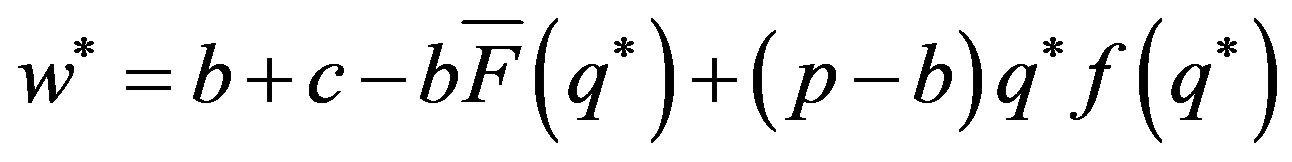 Simplify the equation,
Simplify the equation,
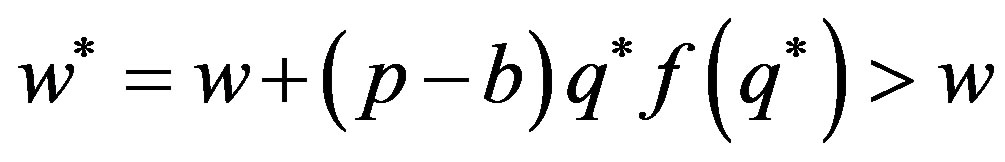 . Q.E.D.
. Q.E.D.
Obviously, under Stackelberg game, the optimal wholesale price is larger than the wholesale price, which can coordinate the buy-back contract. So the buy-back contract can’t achieve coordination. This is because, first, under Stackelberg game the dominant supplier sets the wholesale price by considering his payoffs rather than supply chain system payoffs. Second, the supplier sets the wholesale price after observing the retailer’s order quantity in which the decision is benefit to maximizing his payoffs.
4. Improved Model
When the fairness was incorporated, the fair solution of Nash barging was introduced, because the fairness is relative, the status and the contribution of the two parties will affect the distribution of payoffs, so the two sides argued for their own fair payoffs as a criterion of whether the trade is fair or not. Donating 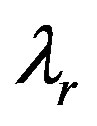 and
and 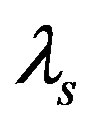 as the fairness of the retailer and the supplier respectively, which
as the fairness of the retailer and the supplier respectively, which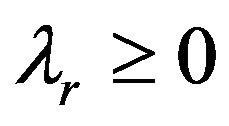 ,
,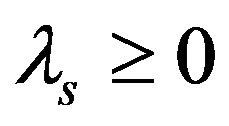 . Equation
. Equation 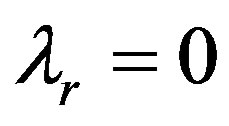 means that the retailer doesn’t care fairness and equation
means that the retailer doesn’t care fairness and equation 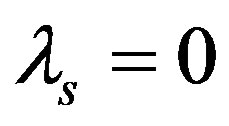 means that the supplier doesn’t care fairness. And
means that the supplier doesn’t care fairness. And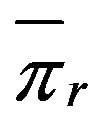 ,
, 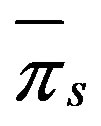 represent the fair solution of Nash barging in which,
represent the fair solution of Nash barging in which,
 [11].
[11].
The utility functions of the retailer, the supplier and the supply chain system are as follows:
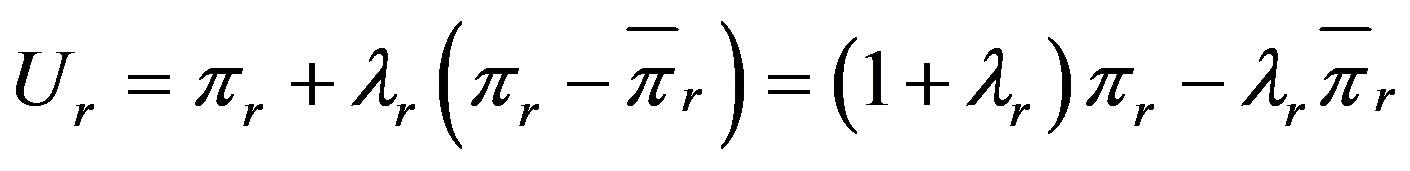 (4)
(4)
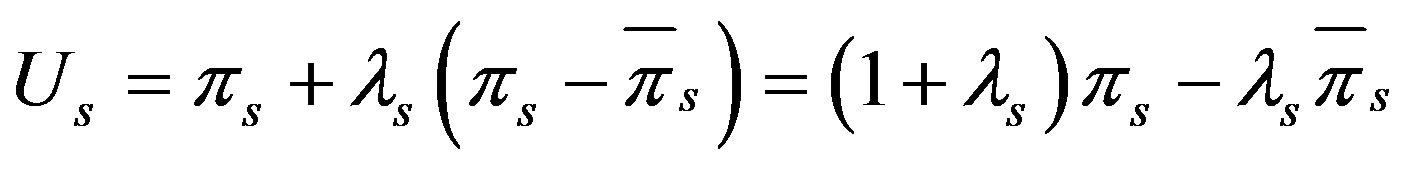 (5)
(5)
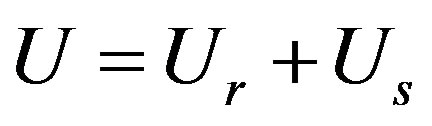 (6)
(6)
4.1. Only Retailer Incorporates Fairness
When the retailer incorporates fairness and the supplier doesn’t incorporate fairness. Namely that 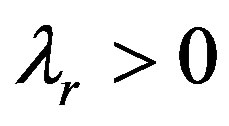 and
and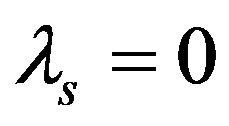 . Putting these equations into the utility function of the retailer, the supplier and the supply chain system, the following equations can be got:
. Putting these equations into the utility function of the retailer, the supplier and the supply chain system, the following equations can be got:
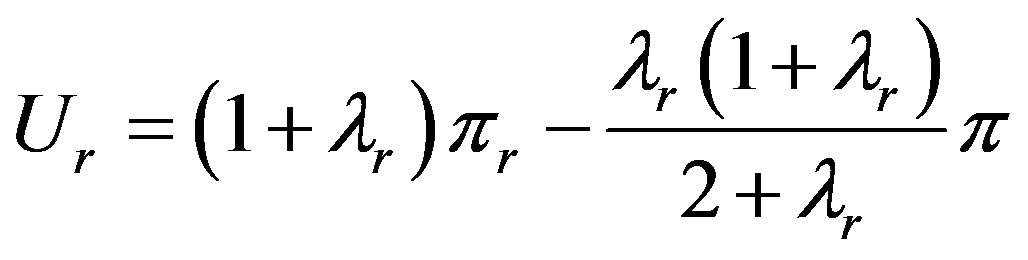 (7)
(7)
 (8)
(8)
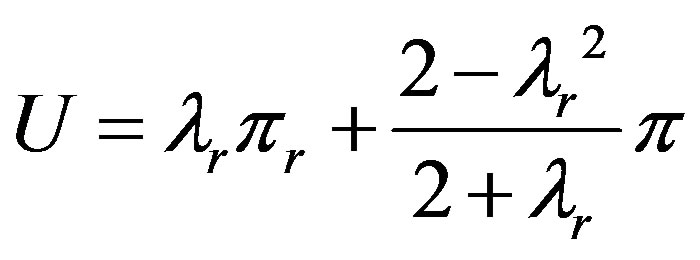 (9)
(9)
Proposition 3: When only retailer incorporates fairness, under Stackelberg game, the retailer’s order quantity  satisfies the equation of
satisfies the equation of
 . And the dominant supplier’s optimal wholesale price
. And the dominant supplier’s optimal wholesale price 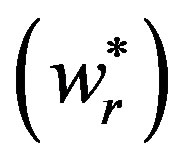 satisfies the equation of
satisfies the equation of
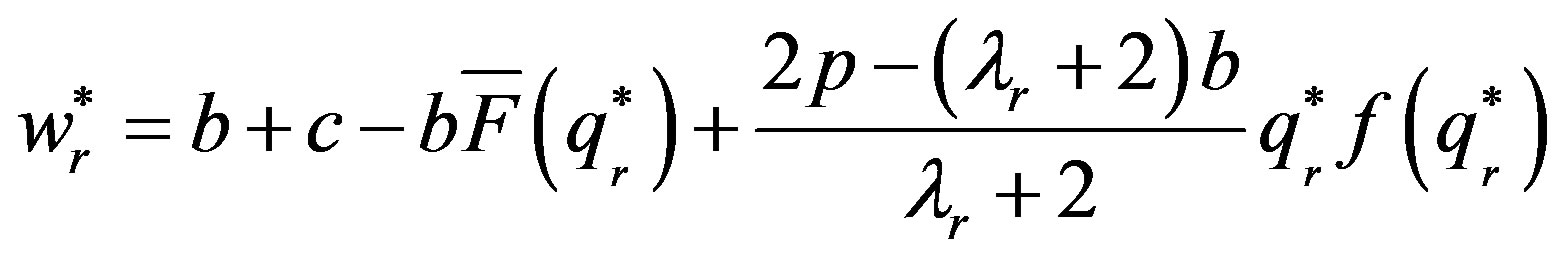 . When the decision is centralized, the order quantity satisfies the equation of:
. When the decision is centralized, the order quantity satisfies the equation of:
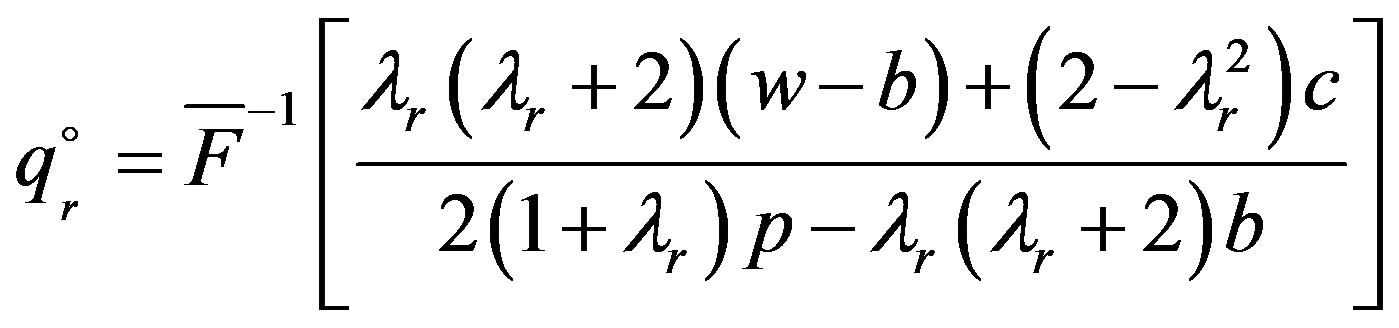 .
.
Proof: we use the method of backward induction to solve this problem.
First, according to the given information, in order to maximize utility, the retailer’s order quantity subjects to the equation of , from this equation, we can get that the retailer’s order quantity
, from this equation, we can get that the retailer’s order quantity 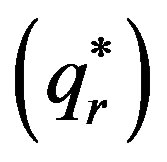 satisfies the equation of
satisfies the equation of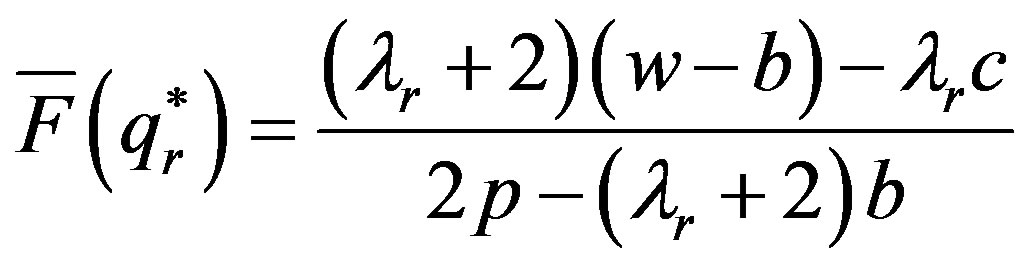 , simplify the above equation, we can get that
, simplify the above equation, we can get that
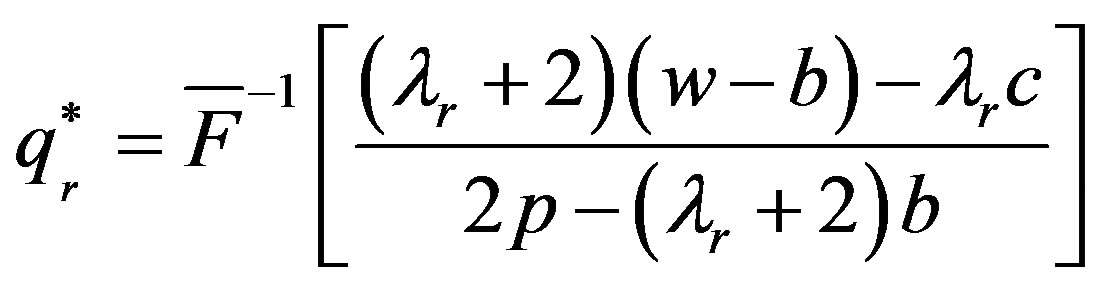 .
.
Then the supplier sets the optimal wholesale price to maximizing utility according to the retailer’s order quantity. Substituting it into the equation of the supplier’s utility function, the following equation can be got:
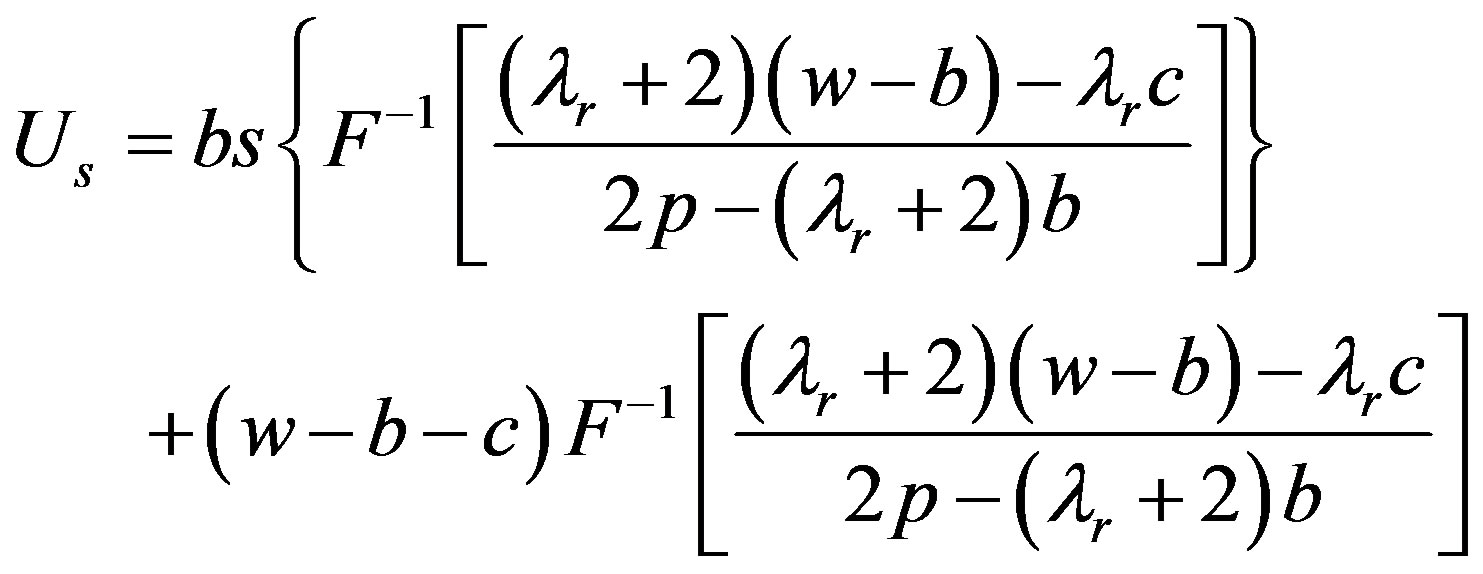
According to the equation of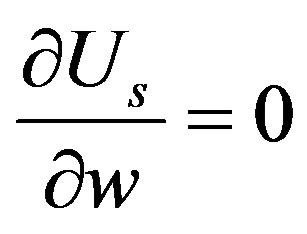 , we can get that:
, we can get that:
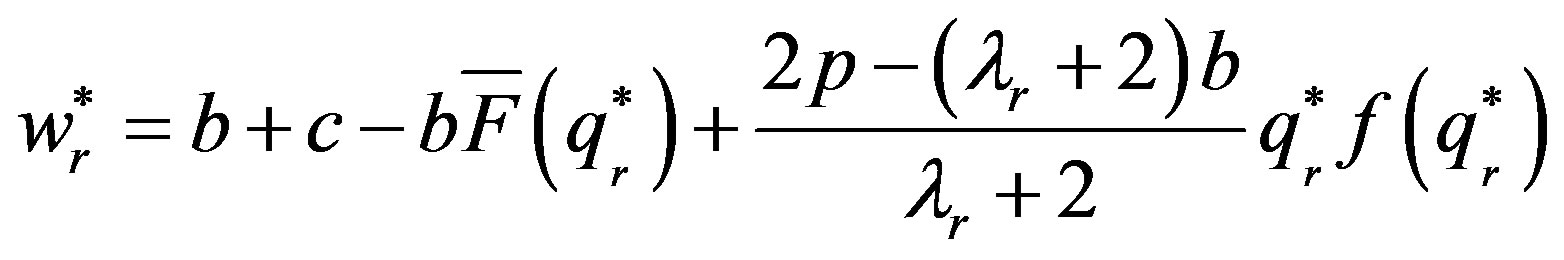
Now considering the centralized decision, the supply chain system’s utility function is:
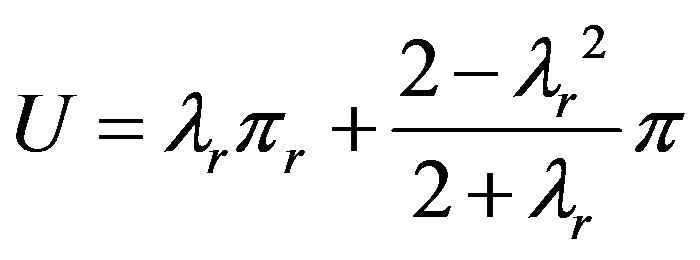
To get the optimal quantity of the supply chain, the equation of

should be satisfied. So the system’s optimal quantity 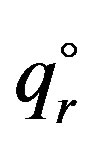 satisfies the equation of
satisfies the equation of
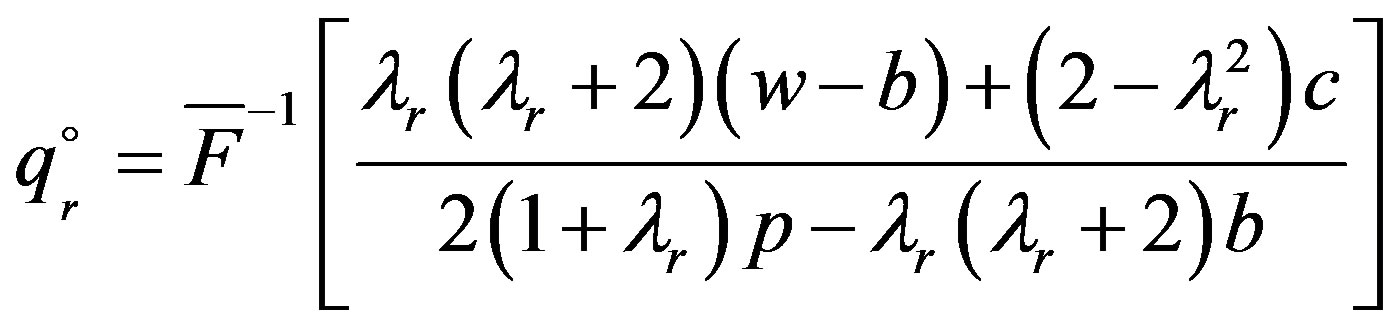 Q.E.D.
Q.E.D.
Proposition 4: When only the retailer incorporates fairness and the dominant supplier formulates a wholesale price, which can coordinate the buy-back contract initially, but under the game, the buy-back contract can’t achieve coordination and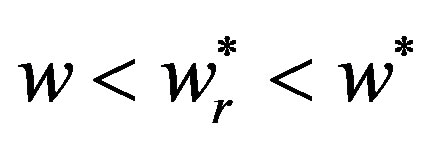 . Moreover, the optimal wholesale price
. Moreover, the optimal wholesale price 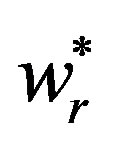 decreases with the retailer’s fairness.
decreases with the retailer’s fairness.
Proof: when the buy-back contract can coordinate supply chain system, the equation of 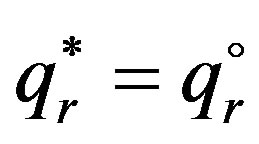 should be satisfied, simplify the equation, we can get that
should be satisfied, simplify the equation, we can get that
 , from this, we can further get
, from this, we can further get
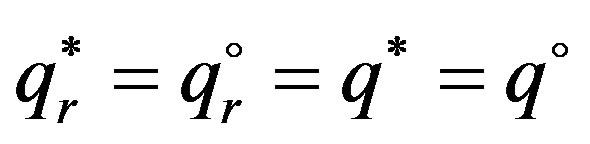 .
.
The optimal wholesale price satisfies the equation:

So the buy-back contract can’t achieve coordination.
Also 
Combining it with the Proposition 2, we can easily get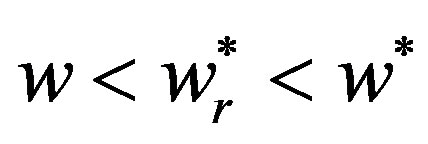 .
.
According to the theory of implicit function, we can obtain that:
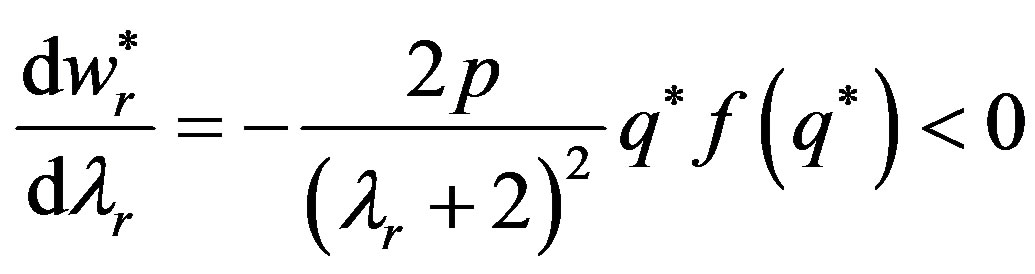 Q.E.D.
Q.E.D.
So the optimal wholesale price 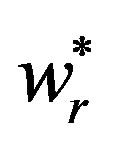 decreases with the retailer’s fairness.
decreases with the retailer’s fairness.
When only the retailer incorporates fairness, the supplier formulates the wholesale price, which can coordinate the buy-back contract initially, under Stackelberg game, the supplier will sets the optimal wholesale price, which is larger than the initial wholesale price, so the buy-back contract cannot achieve coordination. When the retailer incorporates fairness, the retailer will not only pays attention to his utility but also concerns about the supplier’s utility, when the optimal wholesale price is lower, the retailer will believes that he gets a relative fair treatment. However, the supplier sets the optimal price to maximizing his utility according to the retailer’s order quantity. So the optimal wholesale price is smaller than the optimal wholesale price, which the members of supply chain don’t incorporate fairness.
4.2. Retailer and Supplier all Incorporate Fairness
When the retailer and the supplier all incorporate fairness, namely that 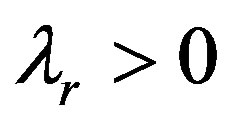 and
and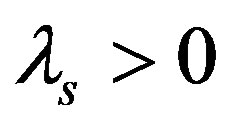 . Putting these equations into the utility function of the retailer, the supplier and the supply chain system, the following equations can be got:
. Putting these equations into the utility function of the retailer, the supplier and the supply chain system, the following equations can be got:
 (10)
(10)
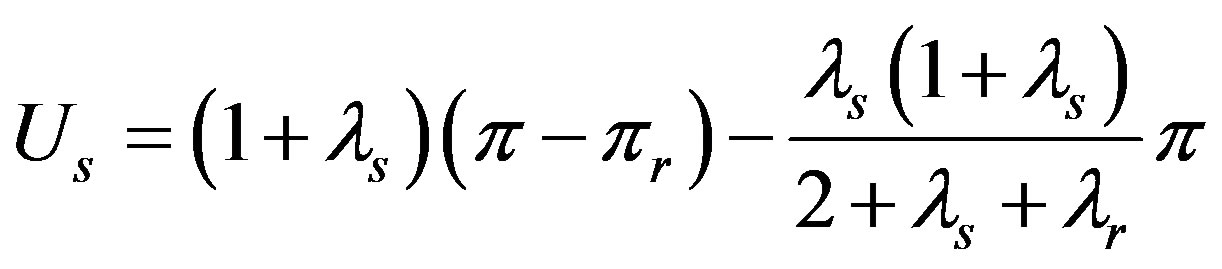 (11)
(11)
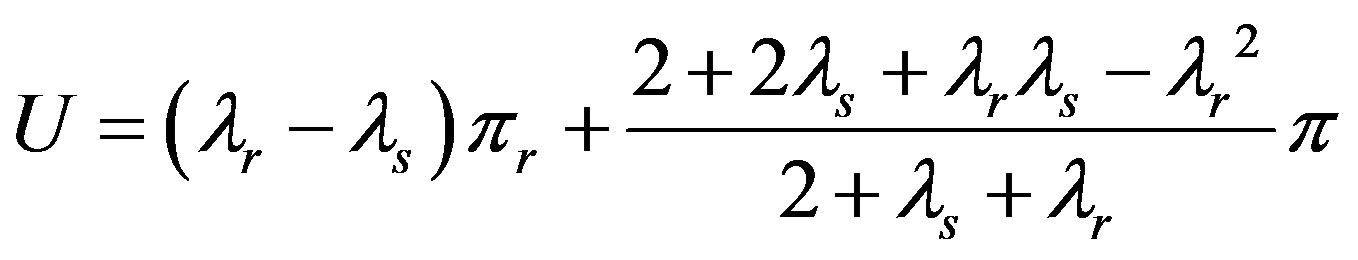 (12)
(12)
Proposition 5: When the retailer and the supplier all incorporate fairness, and decisions are decentralized, the retailer’s order quantity 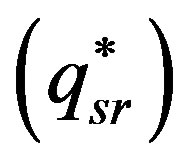 satisfies the equation of
satisfies the equation of
 . And the dominant supplier’s optimal wholesale price
. And the dominant supplier’s optimal wholesale price  satisfies the equation of
satisfies the equation of
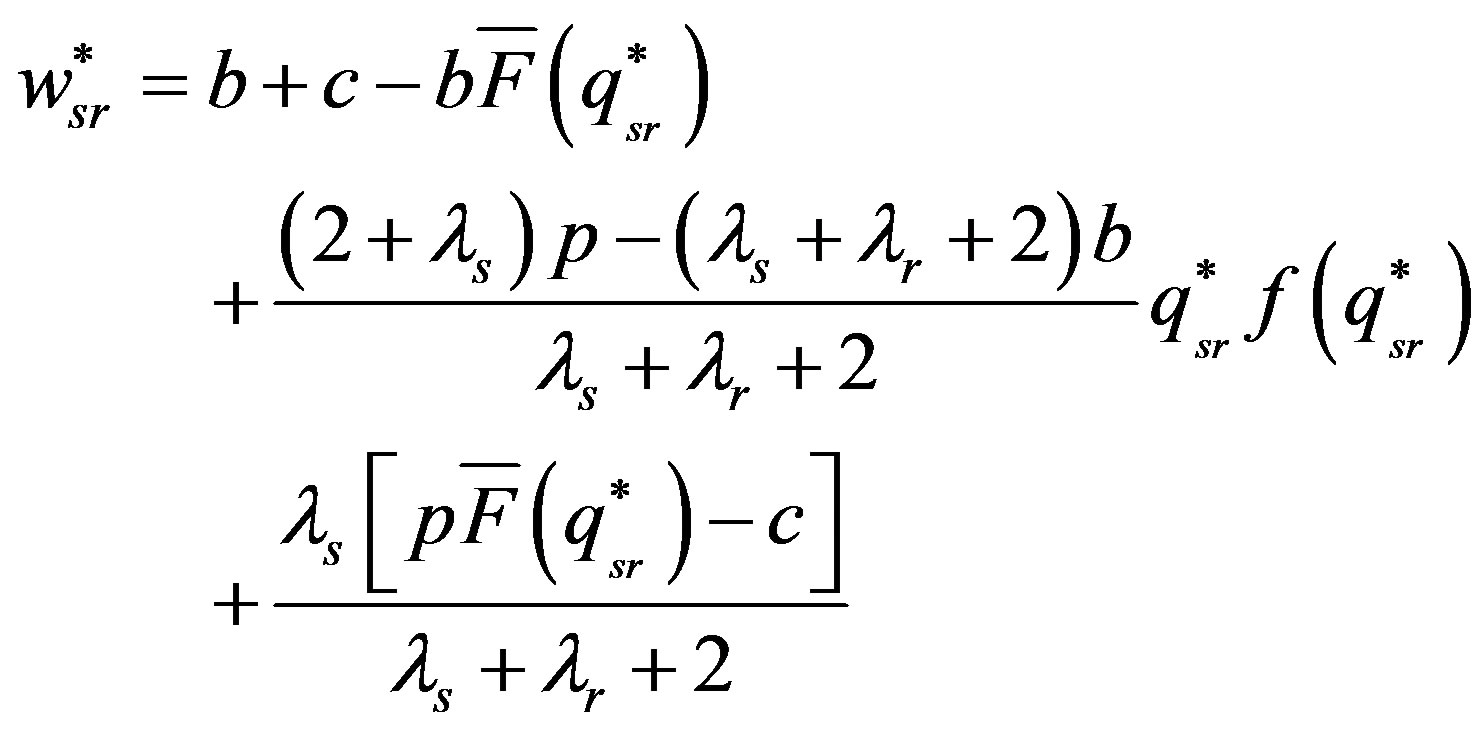
When decision is centralized, the optimal order quantity satisfies the following equation (see foot of page).
Proposition 6: When the retailer and the supplier all incorporate fairness and the supplier formulates the wholesale price, which can coordinate the buy-back contract initially, but under Stackelberg game, the buy-back contract can’t achieve coordination and . Moreover, the optimal wholesale price
. Moreover, the optimal wholesale price 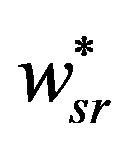 decreases with the retailer’s fairness, while increases with the supplier’s fairness.
decreases with the retailer’s fairness, while increases with the supplier’s fairness.
|
|
Proposition 5 and proposition 6 can be proofed similarly as proposition 3 and proposition 4. So we simplify that here.
When the retailer and the supplier all incorporate fairness and the supplier formulates the wholesale price, which can coordinates buy-back contract firstly, under Stackelberg game the dominant supplier will sets the optimal wholesale price, which is larger than the initial wholesale price, so the buy-back contract cannot achieve coordination. The optimal wholesale price 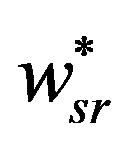 increases with the supplier’s fairness. That is because when the retailer’s order quantity is unchanged and the retailer’s fairness coefficient is larger, the supplier will maximizes his utility by using the method of raising the wholesale price.
increases with the supplier’s fairness. That is because when the retailer’s order quantity is unchanged and the retailer’s fairness coefficient is larger, the supplier will maximizes his utility by using the method of raising the wholesale price.
5. Conclusions
This paper investigates the buy-back contract incorporating fairness under Stackelberg game between the dominant supplier and the retailer based on newsvendor model. By establishing models, we research how the dominant supplier sets the wholesale price, whether the buy-back contract can achieve coordination and how the fairness influences the wholesale price. The results show that the buy-back contract can’t coordinate the supply chain under Stackelberg game whether the two parties incorporate fairness or not. And the retailer’s order quantity is unchanged. Moreover, we obtain that the optimal wholesale price decreases with the retailer’s fairness, while it increases with the supplier’s fairness.
However, there are still some limitations in this paper. First, we consider a two-stage supply chain including a retailer and a supplier, in another words, we did not consider the competition among the supply chain members. So the future research can extend the supply chain. Second, we only incorporate fairness, but in real life, people will incorporate a variety of factors, such as reciprocity, empathy, jealousy, so the future research can investigate the supply chain with a variety of behavioral tendencies.
REFERENCES
- G. P. Cachon, “Supply Chain Coordination with Contracts,” Handbooks in Operations Research and Management Science, Vol. 11, No. 2003, 2003, pp. 227-339.
- H. M. Gilbert, “The Role of Returns Policies in Pricing and Inventory Decisions for Catalogue Goods,” Management Science, Vol. 44, No. 2, 1998, pp. 276-283. http://dx.doi.org/10.1287/mnsc.44.2.276
- K. L. Donohue, “Efficient Supply Contracts for Fashion Goods with Forecast Updating and Two Production Modes,” Management Science, Vol. 46, No. 11, 2000, pp. 1397-1411. http://dx.doi.org/10.1287/mnsc.46.11.1397.12088
- J. G. Liu and C. Wu, “Study of a Tow-Level Supply Chain Returns Policy Model Based on the Newsboy Model,” Chinese Journal of Management Science, Vol. 18, No. 4, 2010, pp. 73-78.
- G. L. Zhang and Z. X. Liu, “A Stackelberg Game of Profit Division in Supply Chains with Dominant Firms,” Systems Engineering, Vol. 24, No. 10, 2006, pp. 19-23.
- Q. H. Pang, “Research on Profit Division in Supply Chains Based on Stackelberg Game with Buyback Contract,” Science Technology and Engineering, Vol. 9, No. 16, 2009, pp. 4873-4876.
- F. Wang, Q. Z. Wu and C. S. Cui, “A Study on the Retailer-Leading Supply Chain Buyback Contract,” Transactions of Beijing Institute of Technology, Vol. 30, No. 2, 2010, pp. 245-248.
- E. Fehr and K. M. Schmidt, “A Theory of Fairness, Competition and Cooperation,” The Quarterly Journal of Economics, Vol. 114, No. 3, 1999, pp. 817-868. http://dx.doi.org/10.1162/003355399556151
- C. H. Loch and Y. Wu, “Social Preferences and Supply Chain Performance: An Experimental Study,” Management Science, Vol. 54, No. 11, 2008, pp. 1835-1849. http://dx.doi.org/10.1287/mnsc.1080.0910
- O. Caliskan-Demirag, Y. H. Chen and J. B. Li, “Channel Coordination under Fairness Concerns and Nonlinear Demand,” European Journal of Operational Research, Vol. 207, No. 3, 2010, pp. 1321-1326. http://dx.doi.org/10.1016/j.ejor.2010.07.017
- C. Du, “Supply Chain Contracts Considering Fairness Concerns,” Dissertation, University of Science and Technology of China, 2011.
- T. H. Cui, J. S. Raju and Z. J. Zhang, “Fairness and Channel Coordination,” Management Science, Vol. 53, No. 8, 2007, pp. 1303-1314. http://dx.doi.org/10.1287/mnsc.1060.0697
- W. Xing, S. Y. Wang and Q. H. Zhao, “Impact of Fairness on Strategies in Duel-channel Supply Chain,” Systems Engineering-Theory & Practice, Vol. 31, No. 7, 2011, pp. 1249-1256.
NOTES
*Corresponding author.