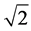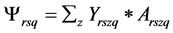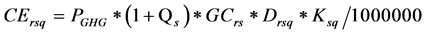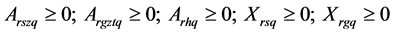Received 30 November 2015; accepted 23 January 2016; published 26 January 2016

ABSTRACT

Biorefineries are keen to design optimal biomass supply chains to minimize production, harvest, transport, and other costs. Such a design problem is challenging with the availability of multiple feedstocks (agricultural residues, perennials such as energy crops, short rotation woody crops), sourced from multiple harvest sheds, and transported across multiple modes (trucks, rails, and barges). This paper presents a multi-period optimization model to analyze the feasibility of collection from multiple harvest sheds. The results are demonstrated for a case study location in Alpena, MI served by truck and water transport. The model results suggest that: i) perennial biomass with higher yields would be preferred due to higher biomass production per unit area; ii) transport from farther locations are warranted only if the biomass production costs in the farther harvest sheds are cheaper by 20% - 30% compared to the adjacent harvest shed; and iii) the local situations of a biorefinery―characterized by the parametric inputs in the model―play a key role in determining the optimal feedstock composition across multiple harvest sheds. The results also support long term contracts associated with high yielding perennial feedstocks such as energy crops and short rotation woody crops.

Keywords:

Biomass, Supply Chain, Harvest Shed, Cellulosic Biofuel, Biorefinery

1. Introduction

The Renewable Fuels Standard mandate in Energy Independence and Security Act (EISA) 2007 established annual targets for cellulosic and advanced biofuels totaling at 137 GL (137 giga liters or 36 billion gallons) by 2022. But the actual production has consistently fallen short of the targets due to technological hurdles and difficulty in sourcing biomass raw materials in a cost effective manner [1] - [3] . The biomass raw materials account for almost half of the biofuel production costs and the commercial cellulosic biorefineries, including pilot cellulosic biofuel plants that have begun operations in 2014, are seeking to reduce the costs associated with biomass procurement [4] .

Logistic problems associated with biomass procurement have been analyzed extensively (See [5] and [6] for an overview). The main research questions addressed include assessment of regional biomass potential, transportation of spatially distributed biomass, and temporal aspects of sourcing biomass [5] and [6] . Other related research questions include selection of optimal location of biorefineries within a state, optimal pattern of growing, harvesting, storing, and delivering different feedstocks to a selected biorefinery. The major drawback of these studies is that these issues are evaluated in isolation or limited to only one biomass harvest shed. The feasibility of procuring a variety of biomass feedstocks from multiple locations (by adopting a hub-and-spoke model) using multiple modes of transport (e.g. combining truck transport with water based shipping) to expand the reach to multiple harvest sheds has not been adequately explored.

This paper evaluates the feasibility of procuring biomass feedstocks from multiple harvest sheds, using multi-modal transport. Such decisions involve several tradeoffs. Costs of biomass production and harvesting can vary geographically and by the type of biomass (e.g. agricultural residues, perennial grasses or woody biomass). Biomass suppliers are likely to demand long term contracts for supply of dedicated energy crops such as perennial grasses and short rotation woody biomass, but may be willing to supply agricultural residues and woodchips on short term contracts. The transport costs depend the distance, the mode of transport and required intermediate handling [7] - [10] . Mathematical programming models are widely used to analyze the costs of the above factors [11] -[14] . Further, environmental externality costs of biofuels, e.g. greenhouse gas footprint depend on the type of biomass, its production system, as well as the transport distance and the transportation mode employed. For example, previous studies report that perennial feedstocks such as hybrid poplar and switchgrass are preferable to aspen wood or corn stover in terms of both economic and environmental performance [15] [16] . Yemshanov and McKenney [17] find that using transport modes other than trucks can reduce greenhouse gas (GHG) emissions associated with biomass supply chains. Similarly other studies find that substituting truck transport with other modes, especially water based shipping, reduces GHG emissions associated with biomass procurement [18] [19] .

This study develops a multi-period mathematical optimization model with the objective to minimize the total biomass procurement costs, including external costs of GHG emissions, while sourcing biomass from multiple locations. It extends of the model developed earlier by Kumarppan and Joshi [10] for analyzing some of these tradeoffs with respect to a single biorefiney and a single mode of transport. Their analysis for a case study location in Kansas, indicated that most of the biomass would be collected within a 32 - 48 km (20 - 30 mile) radius from around the biorefinery. Further, despite the long term contractual requirements perennials grasses were preferred feedstock and the annual feedstocks were mainly used only as buffer feedstocks to meet the shortfalls in perennial feedstock availability during transition periods. The environmental GHG emission costs were a minor factor compared to the production, harvest, and transport costs. The optimization model used in this study extends the model by including more than one transport mode (truck and water based shipping) and more than one harvest shed to collect biomass. In addition to spatial and temporal optimization within the harvest shed considered in the before-mentioned model [10] , this analysis also addresses the tradeoff between extending the collection radius within the adjacent harvest shed, versus starting a new collection point in a distant but better connected harvest shed. Feedstocks that can be procured on the spot market, e.g. forestry chips, are also included in this analysis.

The application of the model is demonstrated by presenting the analyses for a case study biorefinery located in Alpena, Michigan, a port city on the Great Lakes. The case study considers two harvest sheds: one adjacent to the biorefinery in Alpena, and another farther harvest shed located at various distances (96 - 965 km or 60 to 600 miles) from Alpena; and water shipping would connect the farther harvest shed with Alpena. Four different feedstocks are considered potentially available in each harvest shed. Analysis using typical parameter values from extant literature (shown in Table 1) suggests that the adjacent harvest shed closer to the biorefinery continues to supply a predominant proportion (upto 83%) of the biorefinery feedstock mix due to transport and double handling costs associated with the biomass from the farther harvest shed. The feedstocks from farther

harvest sheds would enter the optimal feedstock mix only if the farmgate prices are cheaper by at least 20% - 30% compared to biomass from the adjacent harvest shed. However, the overall procurement costs are lower compared to the previous estimate by Kumarappan and Joshi [10] , which indicates that the option of using multiple harvest-sheds and multi-modal transport is value adding.

The rest of the paper is organized as follows: the next section presents the generic mathematical optimization model that includes multiple harvest sheds and transport modes. Section three outlines the case study analysis for Alpena. Sections four and five discuss the results and broader implications for cellulosic biorefineries.

2. Generic Mathematical Model

Consider a generic biorefinery with a biofuel production capacity PC. It can potentially procure biomass from the harvest shed adjacent to it or from a number of other potential harvest-sheds located afar but connected by a potentially cheaper mode of transport e.g. waterways or rail (Figure 1). Each of these harvest-sheds is assumed to be circular with either the biorefinery or a collection point (railhead or a port) located in the center. Each of the harvest sheds consists of series of concentric circular zones of both agricultural and non-agricultural land. A sector of the harvest shed may also be covered by water (e.g. a lake or sea) but that doesn’t affect the model applicability since it only constrains the available land in each harvest shed.

Each harvest shed is assumed capable of supplying three types of feedstocks: 1) Perennial feedstocks such as energy crops or short rotation woody feedstocks (g) that require long term contracts. Their yield levels fluctuate temporally depending on the type; for instance, energy crops such as miscanthus produce biomass each year for 10 years, while short rotation woody crops yield substantially large amounts of biomass once every 5 - 7 years. The perennial feedstocks are assumed to require longer term contracts because the landowners produce their biomass primarily to meet the demands of the cellulosic biorefinery and will not be willing to plant in the absence of long term contracts because of hold-up concerns. 2) Annual feedstocks e.g. agricultural residues (s) that are supplied on an annual contract basis. 3) Feedstocks that are delivered on a spot market basis without any contracts such as wood chips (h).

The decision variables are the area of land contracted for growing perennial feedstocks (g) and agricultural residues (s) in each of the concentric circular areas of the different harvest sheds, and the quantity of spotmarket purchases of feedstock in each planning period over the entire planning horizon. The objective is to minimize the net present value of all biomass procurement costs including, farmer payments, mutltimodal transport and material handling costs, storage costs, and external environmental costs, subject to constraints relating to land availability in each zone of the harvest sheds, biomass yields and availability, desired procurement contract lengths, harvest windows, biofuel production capacity and mass balance. The planning horizon is 20 years and the decisions are made on a quarterly basis, i.e. 80 quarters.

Some key features of the model are presented below and the complete model is provided in the Appendix.

The price/ton (CX) paid to the biomass supplier to cover costs of production, harvesting etc. are considered exogenous but vary across feedstock type (g, s) and harvest shed (r) reflected by corresponding subscripts. The contract prices for feedstock type (h) delivered directly to the refinery without any contracts are denoted by CC_rh that can vary by the harvest shed (r). The total transport costs (CT), Storage costs (X), environmental externality costs (CE) will be endogenously determined in the model because these costs depend on the decisions on the spatial and temporal patterns of biomass procurement contracts.

The objective is to minimize the net present value of the total costs over the planning horizon which is given by:

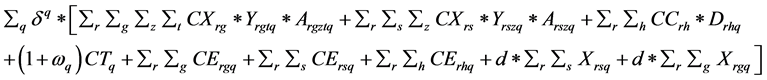
where δ refers to the discount rate, Y refers to the yield/unit area of the particular feedstock (s, g), t refers to the year the perennial feedstock is initially planted; A refers to area contracted for and harvested with subscripts referring to harvest shed (r), feedstock (s, g), zone (z), quarter (q). Once planted, perennials are assumed to produce biomass for τ_g years with a specific temporal yield pattern and the biorefinery is contractually obligated to collecting all this biomass. The decision variables of the cost minimization problem are the area A_rgztq contracted for perennial feedstock (g), area A_rszq contracted for feedstock (s), and spot market purchase quantity (D_rhq) of feedstock h during each quarter q.

The transport costs for annual and perennial feedstocks are endogenously determined based on the choice of the primary decision variables of land area contracted in different zones for different feedstocks. Transport costs (CT) and associated environmental emissions (CE) costs vary with the distance and the location of the field within the harvest shed and the mode of transport. The truck transport costs are computed as a linear function of the amount of biomass and distance to the biorefinery. There are additional loading and unloading costs (L_r) when the feedstock is transferred between truck and barges. Water based shipping costs from each harvest shed to the port where biorefinery is located is calculated as (ξ *B_r). The parameter B_r is the distance between the farther port where biomass is collected and the biorefinery location. The per-unit cost for water based shipping (ξ) is estimated using the reported barge transportation costs published by USDA Agricultural Marketing Service [20] (USDA).

The total transport costs are given by the relation:

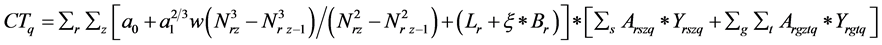
where a₀ and a₁ refer to the fixed and variable components of truck transport respectively, N_rz is the outer radius of zone z in harvesthed r, L_r refers to per unit material transfer costs.

The environmental GHG emissions for each feedstock are calculated based on the FEAT model [21] . The GHG emissions associated with the production (fertilizers, herbicide, and insecticides use; on farm fuel use) and transportation of cellulosic biomass are included. The amount of emissions is multiplied by an estimated price for GHG (P_GHG) to calculate the total emissions costs (CE) for each feedstock. The emissions costs are also endogenously determined since they vary with the biomass feedstock mix chosen.

The optimization model minimizes the total cost, subject to the above accounting relationships and other constraints. The land area constraint ensures that the land area contracted is less than or equal to the total land area available for contracting for different types of feedstock in each zone of various harvest-sheds. The parameters σ_rgz and σ_rsz represent the geographical area available to grow biomass g and s, in zone z, in the harvest shed r. The biofuel production constraint ensures that enough biomass is available and used in each of the quarters to meet the biofuel production target. The mass balance constraint ensures that the biomass procured in the current period plus the carry over inventory from previous period is either converted to biofuel in that period or stored for the next periods.

The full model for equations, constraints, and explanations for parameters are given in the Appendix.

3. Case Study

The case study biorefinery location chosen is Alpena, Michigan which is a port city located on Lake Huron with access to the St Lawrence River (Figure 2). Alpena biorefinery can access biomass from the lower peninsular (LP) region of Michigan using truck transport, and biomass from and from upper peninsular (UP) region of Michigan and other regions in NewYork and Canada across the Great Lakes using water barge transport. These potential harvest sheds are located at a distance ranging from 52 - 520 nautical miles (60 - 600 miles), respectively, from the biorefinery.

The circle indicates the adjacent harvest shed near Alpena, MI; the stars indicate the possible locations of biomass harvest sheds; the numbers correspond to approximate transport distance in nautical miles.

Each harvest shed is assumed to supply four types of biomass feedstocks that differ in their yield patterns and levels: i) dedicated energy crops such as miscanthus can produce 2.94 Mg/ha/year (8 t/ac/year) biomass over a

decade except during the initial establishment phase; ii) short rotation woody crops (SRWC) such as poplar yield substantially higher biomass, estimated at 14.69 Mg/ha (40 t/ac), once in seven years. Both these feedstocks are considered to be delivered on long term contract because landowners grow these feedstocks primarily to meet the needs of the biorefinery (Loveridge, et al). Two other feedstocks available are iii) agricultural residues such as corn stover with estimated yields 0.46 Mg/ha/year (1.25 t/ac/year) available on annual contracts transported by the birefinery; and iv) wood chips (from forestry) purchased on spot markets and delivered at the biorefinery gate. Parameter values used for the case study are summarized in Table 1.

The harvest shed is assumed to be circular in both adjacent and farther locations. The harvest sheds extend up to 100 miles around the collection point, divided into six concentric circular zones. Since the harvest sheds are located near ports, only a portion of the land will be available for biomass harvest: for the adjacent and farther harvest sheds, 75% and 50% of the concentric circular areas are assumed to be available for biomass sourcing, respectively. Based on the local agricultural and forestry patterns around Alpena, the land suitable for each feedstock is estimated at 10% for agricultural residues, 22% for energy crops, and 10% for SRWC. Since the wood chips are delivered on an individual load basis, there is no land restriction associated with it. Various scenarios are developed to evaluate the impact of each of these parametric values on the optimal composition of biomass.

The biorefinery is assumed to be in operation for 20 years, divided into 80 quarters; the net present value of all costs is calculated using a discount rate of 2%. The seasonal changes in transport costs due to differences in energy prices are normalized at 0% for the first quarter of each year (Jan-Mar), and computed at 5%, 8%, and 9% for each of the subsequent quarters. These seasonal value parameters are estimated from the seasonal price changes for diesel which is a key determinant of transport costs.

4. Results and Discussion

Our reference case is that only the biomass feedstocks from the adjacent harvest shed are featured in the optimal feedstock mix, i.e. biomass from farther locations are not available, which is the case analyzed previously in Kumarappan and Joshi [10] . For the reference case we hike up the loading and unloading costs very high at $5.5/Mg (or $5/ton) per loading or unloading instanceto eliminate any biomass transport from farther harvest sheds. These assumptions are relaxed (Table 2) as part of scenario analysis. For the reference case parameters, the

^arefers to Lower Peninsular Michigan in the case study; ^blocated at 60 miles distance in the reference case.

average cost of biomass raw material would be $0.15/l ($0.56/gallon) of biofuel. At a conversion rate of 291 liters per Mg (70 gallons/ton), the biorefinery can expect to pay $43/Mg ($39/ton) of biomass in real terms without inflation. Upon adjusting for inflation at 2%, the price for biomass can reach up to $62.7/Mg ($57/ton) in nominal terms at the end of 20 year production time frame. This cost estimate is well within the range quoted in the existing literature (Aden et al.). This case study with four feedstocks show slightly lower costs than that reported in Kumarappan and Joshi (2014) where only two feedstocks―energy crops and agricultural residues―were considered. Hence, biorefineries will have opportunities to reduce biomass raw material costs by using multiple sources of biomass.

The first two columns in Table 2 show that the short rotation woody crops and energy crops would supply, over 20 years, 43% and 29% of biomass required by the biorefinery respectively. The preferences for these feedstocks arise due to higher biomass yields and the ability to harvest them during lean winter (off-peak) seasons. Even though, there were contractual obligations to harvest perennial feedstocks over longer time frames, they help reduce raw material costs due to harvesting flexibilities, higher yields and resulting lower transport distances and costs.

The implication for the biorefineries is to opt for perennial feedstock contracts to reduce biomass feedstock costs. The annual feedstocks such as agricultural residues and wood chips (no-contract feedstock) from the adjacent harvest shed would supply 20% and 8% of biomass respectively. In spite of lower yields, the agricultural residues are still provide biomass sources when the perennial feedstocks are not available in sufficient quantities; the prevalence of agricultural land in the harvest shed is also a reason for their cost effective supply.

The last two columns in Table 2 present the biomass feedstock composition for a more realistic scenario where the loading costs are $1.1/Mg ($1/ton) per incident. With lower loading costs, biomass from the farther harvest shed becomes a part of the optimal feedstock mix: about 17% of biomass would be contracted from the farther location and the remaining 83% from the adjacent harvest shed. The feasibility of farther harvest shed helps reduce the biomass raw material cost further down to $0.13/liter ($0.52/gallon) of biobutanol, which is an equivalent of $9.5/Mg ($36/ton) in real dollar terms; upon adjusting for inflation of 2%, the biomass would cost up to $14.3/Mg ($54/ton) at the end of 20 year time frame. The techno-economic studies predict that biofuel production costs will be competitive with crude oil if the delivered biomass costs remain in the range of $9.2 - 14.55/Mg ($35 - 55/ton). Our results suggest that under the parametric values shown in Table 1, procurement from multiple harvest sheds using a hub and spoke system might be feasible for harvest sheds connected by waterways or railways.

Table 3 presents the changes to optimal biomass portfolio when the non-contractual feedstock (wood chips) are available at prices lower than $66/Mg ($60/ton) assumed in the reference case. When the delivered costs of chips fall from $66/Mg to $55/Mg and $44/Mg in both harvest sheds (adjacent and farther), the proportion of wood chips in the adjacent harvest shed increase in the optimal feedstock mix from 7% to 27% and 91% respectively. The lower costs for wood chips at $44/Mg makes it much more competitive such that almost all of the biomass (91%) is derived from the adjacent harvest shed without any biomass transported from the farther harvest shed. The optimal composition of biomass indicates that biomass raw materials derived from the farther harvest shed will be economical in certain conditions.

4.1. Distance of Farther Harvest Shed

Differences in production costs (i.e. farmgate price paid to the biomass producers) in different regions can affect the proportion of a particular feedstock in the optimal mix. Particularly, a feedstock that has lower production costs in the farther harvest shed, can offset the additional costs due to loading/unloading and water shipping. To assess how the feedstock composition changes when feedstock from farther harvest sheds are relatively cheaper, the exogenous production and harvesting costs (CX) were reduced by −10% to −50% in the farther harvest shed. As expected, with lower production costs in the farther harvest shed, the proportion of that feedstock increases in the optimal feedstock mix (Figure 3). The reduction in production costs for the farther harvest sheds are represented along the horizontal axis. The top solid line shows the proportion of energy crops from the farther harvest shed located at 52 nautical mile distance; the second, third, and fourth lines (from the top) shows the proportion of the feedstock from farther harvest sheds located at 173, 346, and 520 nautical mile distance from the biorefinery, respectively. The curves show effects on the selected feedstock from the farther harvest shed, but not the changes in optimal proportions of other feedstocks, which also vary as a result of overall cost minimization.

The four panels in Figure 3 suggest that long distance water transport from the farther harvest shed is desirable only if the feedstock production costs are lower by at least 20% - 30% in the farther harvest shed. The energy crops (top left) have to be cheaper by at least 20% to be transported 173 nautical miles (200 miles). Transporting from even farther locations will require substantial savings in production costs ranging 30% - 50%.

For the case study parameters, the perennial poplar (top right) from the farther harvest shed is generally competitive within a 173 nautical miles (200 miles); for poplar to be transported 346 - 520 nautical miles (400 - 600 miles), its production costs have to be substantially cheaper at 40-50% in the farther harvest sheds. The production costs of other feedstocks such as wood chips (bottom left) and agricultural residues (bottom right) in the farther harvest sheds have to be at least 20% - 30% cheaper to warrant water transport of 346 - 520 nautical miles (400 - 600 miles). The cost savings in the farther harvest shed can have the biggest influence with wood chips that do not require any contracts and the least impact in case of agricultural residues which have the lowest biomass yields.

4.2. Role of Environmental Costs

Every stage in the production, harvest, and transport of cellulosic biomass supply entails GHG emissions. When these GHG emissions are included in the optimization problem as external costs ($16.5 - 33/Mg), they can affect the optimal composition of cellulosic biomass feedstocks. However, the model runs indicate that considering GHG costs at $16.5/Mg, may not have a significant impact on the optimal biomass composition. The estimated transport cost is $0.19/Mg-km ($0.28/ton-mile) which is substantially higher than the estimated GHG cost of $0.0007/Mg-km ($0.001/ton-mile) when GHGs are valued at $16.5/Mg. These are not big enough to cause significant changes in the biomass portfolio, and mostly resulted in shifting small proportions of biomass from the

farther to the adjacent harvest shed. It helps save on GHG emissions associated with longer distances. Nevertheless, the GHG costs can play a substantially bigger role at higher prices for GHG emissions.

5. Conclusions and Implications

The cellulosic biomass raw materials contribute to more than half of biofuel production costs. The biorefineries are keen to design optimal supply chain that can minimize production, harvest, transport, and other costs associated with biomass supply. The design of an optimal harvest shed becomes more challenging with the availability of multiple feedstocks (agricultural residues, perennials such as energy crops, short rotation woody crops), sourced from multiple harvest sheds, and transported across multiple modes (trucks and barges). A multi-period optimization model was developed to minimize the costs of cellulosic biomass supply.

The results and implications of the model are described for a case study location in Alpena, MI which can support water transport across the Great Lakes and along the rivers. Under representative parameter values the model results suggest that most of the biomass would be sourced from the adjacent harvest shed. For the feedstocks to be transported 52 - 520 nautical miles, the feedstock production costs have to be substantially lower in the farther harvest shed. The results also indicate that i) perennial biomass with higher yields would be preferable due to higher biomass production per unit area; ii) greater transport distances are warranted only if the biomass production costs in the farther harvest sheds are cheaper by 20% - 30% compared to their counterparts in the adjacent harvest shed; and iii) the actual conditions―characterized by the parametric inputs in the model―play a key role in determining the optimal feedstock composition across harvest sheds. When multiple harvest sheds are involved, the attractiveness in one feedstock due to lower production costs can alter the preferences for all other feedstocks as well. The results also indicate that the biorefineries can reduce their costs in the long run by signing up long term contracts to harvest high yielding perennial feedstocks (energy crops and short rotation woody crops).

Acknowledgements

The authors are grateful for the support of the USDA-NIFA, Grant No. 2012-67009-19693.

Cite this paper

SubbuKumarappan,SatishJoshi, (2016) Optimal Cellulosic Biomass Contracting with Multiple Feedstocks and Locations, and Multi-Modal Transport. Natural Resources,07,69-82. doi: 10.4236/nr.2016.71007

References

Appendix

Subscript notation:

s = Annual agricultural residue feedstocks such as straw or stover []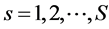

g = Perennial grass feedstocks such as miscanthus, poplar []

h = Contracted feedstock such as chips delivered on an individual load basis []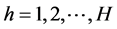

z = Concentric circular production zone []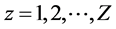

q = The production/harvesting time period (quarter) []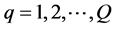

t = Year in which perennial crops are planted [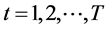]. Perennial crop g is assumed to supply biomass for τ_g years following establishment; hence, the perennial crop g established in year 3 (t = 3) will supply biomass starting in year 3 until 3 + τ_g

r = harvest shed []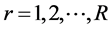

Parameters:

CM_rs, CM_rg = Unit material cost of feedstocks s and g (dollars per ton, price paid to farmers)

CC_rh = Delivered cost of feedstocks h at the biorefinery location (dollars per ton)

CH_rs, CH_rg = Unit harvest cost of feedstocks s and g (dollars per ton)

CT_z = Unit transport cost of feedstock from zone z to the collection zone (dollars per ton-mile)

CS_rsq, CS_rgq = Unit storage cost of feedstocks s and g in quarter q (dollars per ton per quarter)

CE_rgq = Unit environmental cost of perennial feedstock g from harvest shed r in quarter q (dollars per ton)

CE_rsq = Unit environmental cost of annual feedstock s from harvest shed r in quarter q (dollars per ton)

CE_rhq = Unit environmental cost of contractual feedstock h from harvest shed r delivered in quarter q (dollars per ton)

CX_rszq = Total exogenous costs of annual feedstocks s processed in quarter

(, dollars per ton)

CX_rgzq = Total exogenous costs of perennial feedstocks g processed in quarter

(, dollars per ton)

Y_rgtq = Yield of perennial feedstock g, planted in year t, for quarter q[Fixed pattern of yields in tons per acre per quarter] [for example, miscanthus crop planted in year t = 3 will yield 746 g/m² (3.33 tons/acre) in quarter 12; 1495 g/m² (6.67 tons/acre) in quarter 16; 2241 g/m² (10 tons/acre) every fourth quarter during quarters 20 - 36; 1793 g/m² (8 tons/acre) every fourth quarter during quarters 40 - 48; and 0 tons in all other quarters. If miscanthus crop were planted in year t = 5, then the same yield pattern will be shifted from quarters 20 through 56. The amount of biomass available in quarter q depends on the planting year (t) of miscanthus]

Y_rszq = Yield of annual feedstockss that remains constant?harvested only once in a year either during the third or during the fourth quarter)

Y_rhq = Amount of biomass h per delivery/contract?the feedstock h is contracted and delivered entirely on the basis of loads without any long term obligations

Ψ_rsq, Ψ_rgq = Quantity of feedstock (s, g) produced within each harvest shed (r) during quarter q (tons)

Ψ_rhq = Quantity of feedstock h available through contract in each quarter q from each harvest shed r (tons)

D_rsq, D_rgq, D_rhq = Quantity of feedstock s, g, and h from harvest shed r processed at the biorefinery during quarter q (tons)

ω_q = Factor to compute seasonal costs related to transporting; second quarter is taken as the reference season, i.e. ω_q=2 is normalized at 1

δ = Quarterly discount factor

d = Storage cost parameter (dollars per ton per quarter)

ε_s = Rate of loss of agricultural residue in storage (percentage per quarter)

ε_g = Rate of loss of perennial grasses in storage (percentage per quarter)

ε_h = Rate of loss of chips in storage (percentage per quarter)

PC_q = Quarterly ethanol processing capacity (gallons)

K_s, K_g, K_h = Ethanol output for feedstock s, g, and h respectively (gallons per ton)

MIR = Minimum Inventory Requirement (tons)

Q = Terminal time period

P_GHG = Price for one ton of greenhouse gas ($ per ton of CO₂ equivalent)

GC_rg = Greenhouse gas credit with the use of perennial feedstock g (tons of GHG per million gallon of cellulosic ethanol)

GC_rs = Greenhouse gas credit with the use of annual feedstock s (tons of GHG per million gallon of cellulosic ethanol)

GC_hs = Greenhouse gas credit with the use of feedstock h obtained through individual loads without contracts (tons of GHG per million gallon of cellulosic ethanol)

a₀ = Fixed component of transport costs ($ per ton of feedstock)

a₁ = Variable component of transport costs, includes the GHG emissions costs as well ($ per ton-mile)

σ_rsz = Fraction of total land area available in zone z to harvest annual feedstock s (in percentage)

σ_rgz = Fraction of land area available in zone z to harvest all perennial feedstocks g (in percentage)

ZA_rz = Total geographic area within zone z (acres)

N_rz = Outer radius of zone z in harvest shed r (miles)

L_r = Transfer costs from trucks to barge in harvest shed r, if applicable ($ per ton)

ξ =per mile cost of water transport ($ per ton-mile)

B_r = Distance between the port r and biorefinery location (miles)

w = factor to convert radial distance to road distance; with perpendicular road network, w equals

Ϙ = Amount of emissions when feedstocks involve water based transportation Objective function:

Minimize discounted cumulative feedstock procurement costs over Q quarters:

where CX refers to exogenous costs of cellulosic biomass, CT refers to endogenously determined transport costs and d *X refers to storage costs

with respect to decision variables:

A_rszq = Acreage contracted to harvest annual feedstock s in quarter q, zone z, harvest shed r (in acres)

A_rgztq = Acreage planted with perennial feedstock g in year t, zone z, harvest shed r (in acres)

X_rsq, X_rgq, X_rhq = Storage levels (stock variable, either at the biorefinery or on farm fields) of feedstock s, g, and h, in each harvest shed r, at the end of quarter q (in tons)

D_rsq, D_rgq, D_rhq = Quantity of feedstock (annualss, perennials g, no-contract feedstocksh) processed/demanded in quarter q from harvest shed r―which are implicitly determined as residuals upon choosing X_rsq, X_rgq, and X_rhq subject to the following accounting relationships (E1-E4) and constraints (E5-E10):

Accounting relationships:

E1: Zone area ZA_rz (in acres) around the biorefinery extending from zonal radius N_{r z−1} to zonal radii N_rz (in miles); the constant 640 converts square miles of area to acres

E2: Total biomass produced during every quarter (Ψ_rq) is computed by multiplying the acreage harvested (A_rszq, A_rgztq) with yield (Y_rszq, Y_rgtq); Ψ_rhq refers to the amount of chips h delivered from harvest shed r during quarter q

E3: Transport costs:

E4: Environmental costs of perennial feedstocks (CE_rgq) and annual feedstocks (CE_rsq) are computed based on expected GHG prices (P_GHG) and GHG credit (GC)¹.

Constraints:

E5: Land availability constraints for perennial feedstocks:

The acreage harvested with grasses (A_rgztq) and agricultural residues (A_rszq) should be less than the available area from crop lands (σ_rszZA_rz) and marginal (σ_rgzZA_rz) croplands. This constraint has to be satisfied in every quarter q across all zones z in all harvest sheds r. The land availability constraint is not applicable to feedstock h, for example chips that are delivered on contractual basis of individual loads.

Land availability constraints for annual feedstocks

E6: Biomass mass balance constraints: Biomass supplied from fields and storage should equal the sum of biomass processed and inventoried in each quarter:

Biomass produced in quarter q (Ψ_rq) + Stocks from previous quarter (q − 1) = Biomass used for biofuel conversion in quarter q (D_rgq + D_rsq + D_rhq) + Ending stock for quarter q

E7: Biofuel produced has to meet or exceed the processing capacity (PC_q) in every quarter:

E8: Biomass stored at the biorefinery has to meet the minimum inventory required (MIR) at the biorefinery―only this quantity of biomass incurs storage costs. The excess biomass, if any, would be stored on field without storage costs.

E9: Terminal conditions for the last quarter (Q) are imposed by restricting the final period storage to zero after meeting the biomass processing requirements

Biomass supplied from the fields in final quarter Q + supply from the storage in quarter (Q − 1)―Biomass used for conversion in Q = Ending stock for quarter Q = 0

E10: Non negativity constraints of acreage and storage decision variables:

NOTES

¹The division by 1,000,000 is for unit conversion.