Open Journal of Epidemiology
Vol.06 No.01(2016), Article ID:63638,30 pages
10.4236/ojepi.2016.61007
Dynamic Modelling of Dengue Epidemics in Function of Available Enthalpy and Rainfall
Hugo Abi Karam1*, Julio Cesar Barreto da Silva2, Augusto José Pereira Filho3, José Luis Flores Rojas3
1Instituto de Geociências, IGEO-CCMN-UFRJ, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brasil
2Departmento de Estatística, CCET-UFRN, Universidade Federal do Rio Grande do Norte, Natal, Brasil
3Instituto de Astronomia, Geofísica e Ciências Atmosféricas, IAG-USP, Universidade de São Paulo, SP, Brasil

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 December 2015; accepted 20 February 2016; published 23 February 2016
ABSTRACT
In this work, we present results of an investigation of environmental precursors of infectious epidemic of dengue fever in the Metropolitan Area of Rio de Janeiro, RJ, Brazil, obtained by a numerical model with representation of infection and reinfection of the population. The period considered extend between 2000 and 2011, in which it was possible to pair meteorological data and the reporting of dengue patients worsening. These data should also be considered in the numerical model, by assimilation, to obtain simulations of Dengue epidemics. The model contains compartments for the human population, for the vector Aedes aegypti and four virus serotypes. The results provide consistent evidence that worsening infection and disease outbreaks are due to the occurrence of environmental precursors, as the dynamics of the accumulation of water in the breeding and energy availability in the form of metabolic activation enthalpy during pre-epidemic periods.
Keywords:
Modelling Dengue Epidemics, Environmental Enthalpy, Environmental Precursors of Dengue Epidemics

1. Introduction
Dengue fever is an acute viral disease of fast dissemination, featured by an infirmity that is caused by the Dengue fever virus, an arbovirus of the family Flaviviridae, genus Flavivirus, which comprises 4 immunological types (i.e. serotypes) which are activelly circulating among humans (DENV-1, DENV-2, DENV-3 and DENV-4) [1] . Surprisiling, a new type (DENV-5) was identified by Nikos Vasilakis in 2013 [2] . Nowadays, Dengue fever epidemics is a serious public health global issue [1] .
In Brazil, Dengue fever infections have been reported since 1986 [3] , but only after 2015, the 4 serotypes have been found in Brazil [4] - [6] .
The primary infection caused by any one of the serotypes can provide permanent protection against reinfec- tion by the same serotype and temporary protection against the remaining serotype [7] . In general, the natural growth of population exposes a new group of humans to primary infection of the viruses [8] .
According to the 2005 technical relatory from the Brazilian Wealth Surveilance Service (Serviço de Vigilân- cia em Saúde) [9] , the epidemic situation was of the most severe among countries of tropics, in highly urbanized regions where the Aedes aegypti, the mosquito vector of Dengue fever, can easily breed.
The viremia period on humans is of seven days, being shorter on other primates [10] . The Dengue may occur as Dengue Fever, the most benign and frequent form of Dengue, but it can also occur as Dengue Haemorrhagic Fever, a much more severe manifestation, causing death in approximately 5% of the reinfected patients [11] .
The Dengue vector is the Aedes aegypti mosquito that has two distinct phases in its life cycle: aquatic, which comprehends the stages of egg, larva and pupa; and winged, also known as adult phase [12] . In each of those phases and stages specific mortality occurs. There are also distinct transition times from a stage to another.
When the mosquito transmits the disease to a human, through the inoculation of the virus, an incubation period called viremia starts in the human organism. After the contamination, the virus remains in the human blood from the day before the fever to the sixth day of disease. In this period, a non-infected female Aedes aegypti that bites the infected human, also contaminates itself, initiating the extrinsic incubation process [10] . The Dengue virus is not harmful to the mosquito, and once infected it becomes a permanent vector.
The life cycle of the Dengue vector is well known. For a extensive description see Christophers (1960) [12] . A simple description was given by the researchers of Fundação Oswaldo Cruz (FIOCRUZ) in Rio de Janeiro-RJ [13] [14] .
In a summarized form, only the virus infected female Aedes aegypti mosquitoes are able to transmit the disease to men. The specificity of females as a vector of the virus is due to the haematophagous nutrition necessary to mature the eggs [12] . The regular nutrition of male and female Aedes aegypti is based on liquids containing sugars and sap from plants. The virus presence in the salivary glands of the vector occurs after the extrinsic incubation period, which lasts from the blood ingestion to the moment in which the mosquito will be able to transmit the virus, which will be largely replicated in its salivary glands and nervous system. This period varies from 8 to 14 days, from the moment the female mosquito bites an infected human, takes the human blood and receives the virus that goes to its pharynx. The virus then is absorbed and spread to the insect organism until the virus is concentrated in the salivary glands and brain of the mosquito. Then the virus replicates, enabling the inoculation on a human. In high temperatures this incubation period can be shortened in three days. In some cases the virus may replicate in the ovary and other reproductive system tissues of the mosquito. When this happens part of the female mosquito cubs are born with the virus, which can be transmitted by hereditary. Because of this Aedes aegypti mosquitoes may be flying around infected without register of human infections [13] [14] .
According to Brigdman and Oliver (2006) [15] , projections from the first half of the XXI century suggest a mean urban population growth of 2% per year; thus in 2050 it is estimated that 65% of the world population will live in cities, with incresing higher temperatures, associated with the global warming and also the development of Urban Heat Islands (UHI).
In the present work, a numerical model was proposed in the form of a set of coupled non-linear partial differential equations used to simulate the epidemic dynamics in the human population, vectors and virus. The model equations were designed to permit representation of Dengue fever infections, as also the assimilation of atmospheric observed data, including air temperature, pressure, umidade, precipitation, shortwave irradiance, etc. The simulated period was between Jan./2000 and Dec./2011, when Dengue fever epidemics were observed on the Metropolitan Area of Rio de Janeiro (MARJ).
The distribution and intensity of the precipitation events in a tropical location are important during the dengue epidemics development. A complex relationship exists between the rainfall occurrences and the Dengue vector development such as exemplyfied by Campos (2009) [16] and Rocha et al. (2012) [17] , which shows that rainfall rates above 50 (mm∙h−1) are able to remove by washing the eggs from the walls of the breeding, hence- forth limiting the epidemic occurrences.
The dataset used in this work were obtained from surface weather stations located at the international airport of Rio, for 12 years (2000-2011). Also data from the public health service of Brazil (called SUS) were used. The SUS data are records of notifications of patients who were diagnosed with dengue fever. The frequency of the dengue notifications by SUS was of fortnight in the used period. Additionally, atmospheric data such as the density of the flux of global solar radiation (i.e., the shortwave irradiance) has been considered to estimate the potential evapotranspiration [18] [19] . The Surface Energy Budget (SEB) in the model was closed considering an equal number of equations and unknowns. The SEB was obtained following the physical meaning recom- mended by micro and hydrometeorology [20] - [22] .
The efficiency of a prognostic model for Dengue epidemic dynamics can be evaluated by comparing the predicted number of re-infections with the number of reported notifications by SUS.
The results obtained seem suggest the atmospheric thermodynamic variables such as the rate of variation and accumulation of the environmental enthalpy can be assimilated in a epidemic model of Dengue, as a way to make estimations about the population of vectors, in such a way, that epidemics outbreak can be predicted seasonally for a tropical metropole, as MARJ in Brazil.
2. Methods
2.1. Thermodynamic State of the Environment
The entomological parameters, the parameters that characterize the stages of a insect life, depend upon the conditions of the insect, as well on environmental factors. The dependence on air temperature is known (e.g., Otero et al., 2006) [23] , as well as the threshold amount of water in the breeding sites, for the maintenance of the mosquito life cycle. After the hatching (eclosion) of the larva, that is follows a period of replenishment of the reservoir from rain, the water quantity and the food available in the site must be enough for the survival of the larva. In general, 40 to 60 larva of Aedes aegypti need a water volume on the reservoir of above 10 mm for survival and posterior development of the aquatic cycle as pupa (Christophers, 1960) [12] . Other factors are also important, such as illumination, related to the circadian cycle, and the infection itself, related to the activity level of the mosquito. Experimental results from Lima-Câmara et al. (2011) [24] show a growth in the movement rate of infected female Aedes aegypti in relation to non-infected ones.
There is also which consider that for the increase and maintenance of the epidemic cycles of Dengue, the environmental thermodynamic variables as the enthalpy, entropy and degree-day index, all must accumulate large values, as precondition or concomitant occurrence.
Based on the laws that govern thermodynamics, it is considered that any living organism constitutes a system of chemical reactions and physio-chemical processes in a continuous non-equilibrium state. The maintenance of this state is reached through the consumption of energy, withdraw from the environment. Together with cellular work there dissipation of part of this energy. This energy dissipated as heat is used by animals in the most diverse systemic processes involving the organism, from metabolism to functional activities. Hence, through the variation of enthalpy, entropy and degree day, in a closed system, it is possible to relate the influence of the functions of state in the functional activities of a living being using the dissipation o energy.
The word entropy was first used by Clausius, in 1865, to determine the quantity of dissipative energy, through the transformation oh heat in work. Entropy is a function of state associated with a system in thermodynamic equilibrium. It explains that an isolated physic system evolves to a state of thermodynamic equilibrium when maximum entropy is reached. This maximum entropy corresponds to a systemic disorder, which in turn, is related to a completely random distribution of objects in a statistically homogeneous form. So the order is related to heterogeneity, corresponding to a bigger diversity and smaller systemic redundancy (Atlan, 1992) [25] .
According to Murphy and O’Neill (1997) [26] , Schrödinger postulates that the thermodynamics applicable to biologic systems is in a non-equilibrium state, where a organism survives in its highly organized state withdrawing high quality energy from the external mean and processing it to produce, in itself, a more organized state.
Life is a system away from equilibrium, that in turn keeps its local organization level in expense of a bigger global entropy budget. One of the ways to relate temperature to biologic development is using the thermal units system or degree day, according to Brunini et al. (1976) [27] .
The employ of Degree-Day Index (DG) permits to define a linear relation between increases in air tempera- ture and the ratio of metabolic development, which in despite the simplification hypothesis, allows to determine the basal temperature or even the insect phase duration.
In this work, we propose three thermodynamic variables to stablish the relationships between the environment conditions and the population dynamic. Really, under simplification hypothesis (i.e., associated to barotropy) these variables as quite interchangeable, from the point of view of a equal-finality parametrization. The variables are the degree-day index, the accumulated entropy change, and the accumulated enthalpy change. Therefore, we have considered:
• Atmospheric degree-day index―Lets  to be the basal temperature for mosquitoes metabolic performance, assumed equal to the mean temperature of July 1st, actualized each year. So we can write
to be the basal temperature for mosquitoes metabolic performance, assumed equal to the mean temperature of July 1st, actualized each year. So we can write
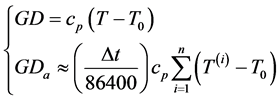 (1)
(1)
where 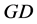 represents the degree-day index, measured here in energy units by mass unity (J∙kg−1), and defined by the difference between the actual (
represents the degree-day index, measured here in energy units by mass unity (J∙kg−1), and defined by the difference between the actual (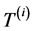 ) and the basal temperature (
) and the basal temperature ( ), multiplied by the specific heat at constant pressure of the air,
), multiplied by the specific heat at constant pressure of the air,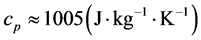 . The associated accumulated diurnal variation is repre-
. The associated accumulated diurnal variation is repre-
sented by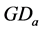 , with initial value reset to zero at the initial time (each July, 1st). The integer n indicates the number of observations since July, 1st. The integer index i is the observation counter along the data series.
, with initial value reset to zero at the initial time (each July, 1st). The integer n indicates the number of observations since July, 1st. The integer index i is the observation counter along the data series.
• Atmospheric entropy change―The diurnal variation of enthalpy, entropy and degree-day index are com- puted. The accumulated diurnal variation of the entropy ( ) can be obtained as
) can be obtained as
 (2)
(2)
where 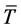 is a typical scale of the air temperature, usually assumed equal to 300 (K),
is a typical scale of the air temperature, usually assumed equal to 300 (K),  is the latent heat capacity of the air at constant pressure,
is the latent heat capacity of the air at constant pressure,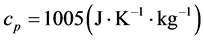 .
. 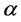 is the specific volume of air (i.e., the inverse of air density) and
is the specific volume of air (i.e., the inverse of air density) and  is the median value of
is the median value of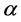 , here estimated by
, here estimated by







• Atmospheric enthaphy change―Formally the enthaply (H) is the sum of the internal energy (U) plus the work (W), i.e., 



since the state relation can be written as

Inspecting Equations (1)-(3), the relationship between



With this relationships at hand, it is possible to verify the relation between the air environment thermody- namics and the performance of the kinetic rate of enzymatic reactions, the duration of the maturation-emergency period for the different phase of the mosquito life.
In the MARJ, the variation of enthalpy (numerically equal to the variation of accumulated degree day) at the end of a winter-to-summer period of 180 days is approximately equal to 





These estimations were obtained by integration of a cos-sin function representing the first harmonic of mean air temperature in Rio de Janeiro city, along 180 days (i.e., 







Without considering the details of the diurnal variation, we can estimate a value of same order to the inter-seasonal variation of enthalpy, i.e.,

is comparable to the average value of variation computed from observations to Rio de Janeiro city (Figure 7). This diurnal evaluation can be then multiplied by 180 days (i.e., approximately half year) in order to obtain the estimation of the inter-seasonal variation, i.e., considering the period of 6 months, started in
2.2. Known Precursors of Dengue Epidemics
There are some investigations on the epidemics precursors. For instance, a comprehensible one was provided by Descloux et al. (2012) [28] which have investigated the epidemic dynamics of dengue in Noumea, that is essentially driven by the climate of previous forty years. In accord to theses authors the maximal temperature and relative humidity thresholds and their persistence were determinant in outbreak occurrences. For epidemics in Noumea, the best explicative variables were the number of days with maximal temperature exceeding 32˚C during Jan-Feb-Mar and the number of days with maximal relative humidity exceeding 95% during Jan. The best predictive variables were the maximal temperature in Dec and maximal relative humidity during Oct-Nov- Dec of the previous year.
In the present work, the enthalpy change and seasonal accumulation were used to define a predictive metabolic performance factor controlling the vector development and maturation in a tropical metropolis. Additionally, the water content into breeding sites is very important for the reproduction of vectors. The complete parametrization will be describe in the following sections, as also the model skill in explaining the Dengue outbreaks.
Table 1. Model parameters in function of environmental variables, associated to the enthomological enzymatic behaviour in function of air temperature. These are coefficients of the parametric performance described by the Sharpe-Schoolfield’s equation (Schoolfield et al., 1981) [51] , applied to ectotherms. The coefficient values were tuned to environmental condi- tions of the Metropolitan Area of Rio de Janeiro-RJ, Brazil. The suffix A indicated the under optimum condition,
References: # This work, e Otero et al. (2006) [23] , * Christophers (1960) [12] . Other consulted reference works are: ! Yang et al. (2009) [45] , Ä Watts et al. (1987) [43] , Å Rueda et al. (1990) [57] , $ Focks et al. (1993) [34] [35] , and % Focks et al. (1995) [36] .
2.3. Available Data
The observational data were employed both to run and to verify the model results. First, atmospheric data observed at surface at the International Airport of Rio de Janeiro (i.e., Tom Jobin airport) are assimilated in the model, providing the necessary meteorological variables (i.e., air temperature, pressure, humidity, wind speed and direction) to the calculation of the terms of the Surface Energy Budget (SEB). Precipitation flux data (i.e., rainfall) are also obtained of local mesonet in MARJ, and assimilated by nudging, for calculations of the Surface Water Balance (SWB). A Newtonian relaxation (i.e., nudging) was used to assimilate all the atmospheric data in the model, considering a sequence of assimilation cycles of 1 hour, along all the integration time. According to Kister (1974) [29] , and Haltiner and Williams (1980) [30] , nudging is a dynamic method to bring the simulated variables close to the observations, without introduces shocks in the model dynamics (i.e., by filtering very short-wave along assimilation cycles). Second, Dengue fever notifications, actually available from the Brazilian public health system, were used in comparison with modelled variables.
The employed data are:
• Notification of Dengue―Used to verify the skill of hte model against observations. The data are obtained directly from the Ministério da Saúde (MS) of Brazil (SVS, 2006) [9] , Secretaria de Vigilância em Saúde (SVS) and Sistema Único de Saúde (SUS, 2006) [31] , and downloaded from Sistema de Informação de Agravos de Notificação (SINAN) at URL http://dtr2004.saude.gov.br/sinanweb/.
• Atmospheric data―The surface meteorological data are assimilated using cycles of 1 hour in the model. The data are obtained from a weather station installed at the International Airport of Rio de Janeiro (i.e., Tom Jobim airport). The station is maintained by the Brazilian Aeronautic Command (COMAER). The original coded data (i.e., METAR) was decode, reformatted and checked statistically (i.e., comparing each variable decoded with its mean ± 2 standard deviation threshold). Additionally, a continuous time coordinates (i.e., decimal year) was computed and added to the data. This continuous coordinates (e.g., 2015.103269290) was employed in the assimilation numerical procedure to control the flux of data in relation the internal integration time (i.e., also computed as a decimal year coordinate). The data preparation was accomplished in a Fortran-90 program created for this task. The model request some atmospheric variables which are not directly available in the observational dataset, such as the density flux of solar radiance (W×m−2) at surface and its components (i.e., direct, diffuse and global). To supply these variables, we have parametrized them following Flores R. et al. (2015) [32] that optimally have fit the Iqbal solar irradiance model (IQC) (Iqbal, 1983) [21] to the observed conditions in MARJ. Indeed, some necessary thermodynamic variables (e.g., specific and relative humidity) are computed following Bolton (1980) [33] .
• Hydrometeorological data-Data of precipitation sampled to each 15 minutes were also assimilated in the model. The data origin is automatic rain-gage mesoscale network (i.e., the AlertaRio system), composed by 32 weather stations dispersed on the Rio de Janeiro’s municipality area, and available from URL http://alertario.rio.rj.gov.br/.
2.4. Dynamic Epidemic Model
Presently, there is a set of Dengue infection dynamics models for human and mosquito population as prognostic variables, or indeed stochastic models with probability of infection as the unknown, written using different levels of complexity. Below we are listing some of them:
Focks et al. (1993, 1995) [34] - [36] proposed a mathematical treatment of the epidemiology of dengue with a view to control based in the concepts of 1) mass action principal, i.e., the course of an epidemic is dependent on the rate of contact between susceptible hosts and infectious vectors, and 2) threshold theory, i.e., the introduction of a few infectious individuals into a community of susceptible individuals will not give rise to an outbreak unless the density of vectors exceeds a certain critical level. These result in two numerical weather-driven models (CIMSiM, the Container-Inhabiting Mosquito Simulation Model, and DENSiM, the Dengue Simulation Model) written in function of the site-specific observed air temperature and precipitation. In accord with Focks and Barrera (2006) [37] , whereas CIMSiM is essentially an accounting program of vector dynamics, DENSiM performes the dynamics of human population and virus transmission between hosts and vectors. Both being weather-driven stochastic models, with a daily time step, that is usually parametrized by the correlations between observed monthly cases and lagged cases, monthly average temperature, monthly rainfall, length of the gonotrophic cycle, in days, and the extrinsic incubation period (EIP), also in days, for the site-specific Dengue [37] .
Otero et al. (2006) [23] described a dry weather model for Dengue dynamics, with temperature-dependent effects, without considering rainfall effects, directly.
Morin et al. (2010) [38] described the Dynamic Mosquito Simulation Model (DMSM), with rainfall and temperature-dependent effects, applied to a Central America tropical city.
Luz et al. (2003) [39] discussed theoretically some uncertainties to the development of Dengue models for Rio de Janeiro-RJ, Brazil, concluding that the two most important entomological parameters to be estimated in the field to compare with a numerical model of Dengue epidemics are mortality rate (of humans) and the extrinsic incubation period.
Sporleder et al. (2009) [40] proposed the Insect Life Cycle Modeling (ILCYM), a software for developing precipitation and temperature-based insect phenology models with applications for regional and global pest risk assessments and mapping, and
Lana et al. (2014) [41] with base in statistic tests with a set of prototype vector models, reccomending that future dengue models should investigate the heterogeneous levels A. aegypit of eggs through the seasons of successive years, as it may affect virus development along the years and also the occurrence of further epidemic outbreaks.
In view of the present state of development of modeling of Dengue epidemics, the following characteristics were chosen for the numerical model described in this work:
• assimilation of both variables, precipitation and air temperature, to compute the entomological parameters. In the same way, other meteorological surface variables such as the incoming solar radiation flux, the air humidity and pressure were assimilated by the Newtonian relaxation method (i.e., nudging), throughout the integration time;
• metabolic factor in function of accumulated thermodynamic variables (i.e., enthalpy, entropy, degree-day index);
• an human reinfection reservoir to implement a positive feedback in the epidemic simulation;
• four virus serotypes reservoirs and associated viremia effecting reinfection parameters and the human mortality rates due to Dengue infection; and
• free software (written in f90) and free distribution.
Consistently in the proposed model, the human mortality rate was estimated from the reinfection rate, so that this last variable can be compared with the notifications of Dengue observed. Also the metabolic factor can be activated by level of the accumulated enthalpy along the months, triggering the reproductive behaviour of the mosquitoes.
A epidemic reinfection model in function of available enthalpy
In this work a model for a infectious disease, based in a system of non-linear differential partial equations, correspondent to the temporal evolution of the dynamics of population during epidemic cycles of Dengue was implemented. The numerical implementation was done in the Fortran-90. Additionally, the assimilation of observed atmospheric data, the role of precipitation, and the effects of feedback associated with reinfections were taken in account.
The atmospheric data (air temperature, precipitation rate, specific humidity, direct and diffuse shortwave radiation flux and air pressure) were prepared and formatted as XYZ.DAT files for a 4D assimilation, imple- mented by Newtonian nudging.
The equations system was divided in three population reservoirs, which in turn were subdivided in boxes. The forecasting variables are relative fractions of the total populations, therefore the unity here represents the pandemic that has spread through the whole population and area.
Dengue virus dynamics equations
The virus population dynamics was based in the theory of exponential growing of Malthus (1798) and also in logistic growing described by Verhulst (1845) [42] . The former reference was mainly applied in population dynamics over effect of different viruses, and the later one, supposes that temporal variation of the number of infected individuals is proportional to the amount of infections, with the variation rate proportional to the fraction of non-infected population, i.e., in accord with a time scale in function of the incubation period.
The model consider four serotypes of Dengue virus, i.e., DENV-1, DENV-2, DENV-3, and DENV-4, indicated by the suffix ()i in the following equation. The time of entry of each serotype also was considered in the model, set up to MARJ, in the years 1986, 1990, 2001, and 2011, respectively. In the model, the dynamics of virus population is controlled by the following proposed equation,

where 



The first term in the r.h.s of Equation (5) represents the logistic development of the virus in the nervous system, intestine and glanders of mosquitoes, associated to the extrinsic incubation period (EIP). The second term was proposed to represent the increase of viremia associated to the infection and re-infection in the intermediate and final hosts; and, finally, the third and forth terms were introduced to represent a small effect associated with random mutation from a serotype into other.
The parameter controlling mutation from serotype j to i that is expressed by 


The air temperature was used to control the rate of incubation of the virus in the mosquitoes. In accord with the laboratory experiments of Watts et al. (1987) [43] the DENV-2 virus can be transmitted to monkeys only by Aedes aegypti was retained at 30˚C or more for 25 days. Indeed, the extrinsic incubation period was 12 days for mosquitoes at 30˚C, and was reduced to 7 days for mosquitoes incubated at 32˚C and 35˚C. Consequently, to represent the temperature-dependence of the extrinsic incubation in the present work, the parameter (

where 
The virus quantification in laboratory involves counting the number of viruses in a specific volume of blood to determine the virus concentration. In accord with Focks and Barrera (2006) [37] , studies comparing the consequences of viral titre (i.e., virus quantification) on the dynamics of endemic dengue suggest that titre, through the agency of probability of dissemination and EIP, does indeed play a role (by hypothesis).
Focks et al. (1995) [36] evaluated virus titres between 105 (i.e., a low value with partial impact on the population) and 106 (i.e., a high value with very broad impact), in relation the median infective dose (
To update of the virus population in the numerical solution, we apply the Euler’s method in finite differences (Mesinger and Arakawa, 1976) [44] , written as

where 
Mosquitoes Population Dynamics Equations
The population dynamics of mosquitoes is described from the differential equations system for the relative population dynamics of the Aedes aegypti in the aquatic and winged phases. This system allows to represent the interrelations between the different phases, in which the metamorphosis stages are related to each other throughout the different phases (i.e., the discriminant compartments of the mathematical model).
The representation in form of differential partial equations system considers different population compart- ments, that represent the successive stages of metamorphosis during the mosquito life cycle.
The equations depend on the entomological parameters, as well as environmental parameters (e.g., Yang et al., 2009 [45] ). In this work, the entomological parameters were established in function of the temperature, as usual, but also in function of the estimated water availability into the breeding sites, from observed rainfall.
In the proposed model, the mosquitoes population dynamics equation are given by

where:
(E) is the relative population of eggs, i.e., the number of eggs divided by the maximum number of eggs supported by the environmental condition.
The dynamic of the eggs population depends of the oviposition rate, 


(L) represents the relative number of larvae, written in function of the eclosion rate


(P) represents the relative population of pupae, which is function of the pupation rate









Additionally, the following parameters are employed.





The larval behavior is controlled in Equation (8) by parameter


The first factor in the r.h.s. of Equation (9) represents the effect of the capacity of the breeding site, considered the minimum necessary volume of water to support larvae development. The variable




where the parameter 
factor in r.h.s. of the BM equation is used to represent the effect of the energy of environment that is favourable to the fertility of the females of Aedes aegypti. The second effect is used to account of the oviposition of the previous year, associated with the intensity of the accumulated DG. When the oviposition was smaller in previous year, the possibility of a Dengue surge in the present year is decreased. The third factor is used to express the accumulation of energy in joules per kg and time step
The development of the larval breeding depends on two parameters: the volume of nutrient water in the breeding and the total number of larvae present. Thus, an appropriate variable to larval development estimated rate is the concentration of larvae per unit volume of water 
In the Equation (9), 





The specific volumes suitable for larvae breeding can be written as


where 




The available water volume and feeding reservoir can constrain the larvae development. The minimal water volume for supporting the maintenance of larvae in the breeding site is approximately
associated with a concentration between 46 to 60 (larvae per litre), as the optimum. The effect of the water volume in simulated breeding sites is the following: if there is too much larva (higher them 46 to 60 larva per litre), the value of 
Epidemic model on human population
The Epidemic model on human population, Equation (13), comprehends five compartments of individuals in different moments of the infection by the Dengue virus (i.e., in a similar way the exemplified models by White et al., 2010). Here, we propose the coexistence of five classe: 




The equations are inter-related and time dependent. The progression of the infection can be controled by the following model parameters:



The dynamic of population under dengue epidemics can be described by

The prognostic model variables for human population, in usual units of (day−1), are:






The parameters of Equation (13), in usual units of day−1, are












The immunization effect after a epidemic is parametrized by

The summation of the equations in the system (13) implies the cancellation of many opposite terms. The obtained equation can be expressed in terms of the total population (T), as follows

This equation states the physical consistency associated to conservation of population. In the other hand, 

Metabolism parametrizations
Yang et al. (2009) [45] he has presented polynomial fit curves of third and sixth order to represent rates of natality, metamorphosis and mortality of Aedes aegypti as a function of the temperature of the breeding site. Unhappily, we cannot use directly these curves for numerical modelling purpose because they diverge from expected values under hypo and hyperthermia, i.e., outside the range of considered observations (»8.5˚C to »35.0˚C). As in the MARJ, the observed maximal air temperature is frequently above 35˚C [46] [47] , due to the Urban Heat Island and the anticiclonic weather condition, the practical alternative is extending the limit range of application of the curves in proper way (i.e., considering the prior technical knowledge on hypothermic and hyper- thermic inactivation effects [12] ), as have been suggested by Morin (2012) [48] and Morin et al. (2013) [49] .
Among others, Otero (2006) [23] has considered the metabolic rates of the mosquitoes in function of enzymatic activity, that is, depending on the poikilothermic enzymatic activity, in units of day−1, following the equation proposed by Sharpe and DeMichele (1977) [50] and Schoolfield et al. (1981) [51] .
The numerical realizations considered in the present work have tested both parametrizations represented by polynomial fits [45] and Sharpe-Schoolfield’s performance equation [50] [51] . The parametrization of poikilo- thermic enzymatic activity seem more appropriate for the simulations since can be really used outside from the optimum range of temperatures, and the model approximates more of the observations.
Sharpe-Schoolfield’s equation
This subsection describes the parametrization used to represent the relative performance of ectotherms in function of the environmental temperature of breeding sites. The temperature of breeding sites is supposed to be a non-linear function of the external air temperature. The breeding sites are considered as a opened cavity to the environment, able to exchange the metabolic gases, thermal energy and water vapor by conduction and convec- tion, and acting as a reservoir for a fraction of the intercepted rainwater. The enzymatic activation/deactivation of maturation and other basal metabolisms can be associated to the relative performance of the ectotherms by equations of reaction kinetics rates (
The basal reactions kinetics rate








The Sharpe-Schoolfield’s equation (Schoolfield et al., 1981) [51] can be rewritten using the formalism of a Bayesian posterior, such as the posterior distribution of the parameters (e.g., as those of kinetic reactions) 




where

Generally, 







It is common in the thermal vicinity 



The enthalpy 


The values of enthalpy and temperatures applied here are shown in Table 1.
Bayesian statistics have been used to build robust framework for parameter estimation and uncertainty analysis in dynamical models for epidemics forecasting (Coelho et al., 2008, 2011) [54] [55] . The quality of Bayesian statistics increases with of number of samples (i.e., observations) used to defined the Likelihood, and, by product with the prior, to achieve the posterior distribution of parameters.
The Sharpe-Schoolfield’s equation [51] can be interpreted in terms of the Bayesian model statistics (i.e., as a theoretical expression of Bayes’s equation). In this case, the prior distribution can indicate the simply fact of metabolic reactions tend to increase with the temperature (e.g., as in Arrenhius’s law). The likelihood informs about the kind of distribution of the model parameters around the thermal optimum. In the Sharpe-Schoolfield’s equation, the likelihood is due to the empirical evidence, the performance have typically a Normal distribution around the optimum. The posterior distribution in function of the temperature is proportional to the product of the prior by the likelihood distribution of the parameter, resulting that Sharpe-Schoolfield’s equation follows an adjunct distribution of the exponential family, associated with a weak informative prior. Consistently, the asymmetry between the low and high temperature of a half deactivation/activation of enzyme reactions, for each site of the optimum, would result in some (positive or negative) asymmetric distribution of performance.
On the other hand, Rall et al. (2012) [56] have suggested that the temperature dependence of functional response parameters is more complex than simples Arrhenius terms, which is basically a expression of tempera- ture dependence. Thus, the biological rates depend not only on temperature, as all chemical reactions, but also on body mass. In Metabolic Theory of Ecology the Arrhenius equation is given by
where 

In the case of interaction between the dengue virus, the insect vector and human host, a minimal virus critical mass seems necessary to trigger an outbreak, since the mass of an isolated virus is extremely small in com- parison to the insect vector masses and the human host. Thus, the insertion capacity and virus proliferation in the human host will likely depend on extrinsic incubation the virus vector, which in turn, is a function of ambient temperature. This effect is implicitly considered in Equation (6).
Mortality rate for Aedes aegypti
In this work, mortality rates for different insect life stages Aedes aegypti were parameterized following the proposition Hosfall (1955), Bar-Zeev (1958) and Rueda et al. (1990). Table 2 shows the mean values of the parameters used in the model to the conditions found in the MARJ.
Open source model
The idea is that the model can receive user community contributions in a dynamic and participatory process of continuous development. Therefore, the model code is proposed as open source, available in the Internet through the Internet site of the Laboratorio de Hidrometeorologia Experimental, located in the Institute of Geosciences of the Federal University of Rio de Janeiro (IGEO-UFRJ).
Basic reproduction number
The basic reproduction number, 
Table 2. Input constants used in the present version of the epidemic model, obtained by trial and error, considering the valid range of values and the increase of the NSE.
at the end of a extrinsic incubation period of the vector, in a large crowded conurbation (Massad et al., 2001 [58] ; Luz et al., 2003 [39] ).
There are some different estimations of 


Interestingly, Luz et al. (2003) [39] considered the risk of dengue transmission in humans proportional to density of infected vectors into the epidemic areas of lower l and high h densities. Hence, (





On the other hand, considering a model of statistical correlations, Luz et al. (2003, 2008) [39] [60] have applied box-plots in comparisons of the simulated parameter performance that lead to prediction of Dengue fever epidemics outbreak (when

In the present work, we estimated 
Breeding sites modeled by linear reservoirs
Christophers (1960) [12] characterizes the cycle of development of the Aedes aegypti mosquito, vector of the yellow fever and of the Dengue, as well as discusses qualitatively the factors of its survival, among them temperature and precipitation. These factors are classified as associated to, first, the daily cumulative develop- ment (CD), which explicitly modify the Aedes aegypti’s metamorphosis in function of the air temperature and surface precipitation, and second, the maintenance factors during the different phases of the insect life. The metamorphosis depends on the presence of water.
In particular, the oviposition and eclosion of the eggs, as well as the survival of the larva, which, after going through the pupation process achieve the stage of maturation, where the metamorphosis into pupa occurs. In all the three stages of metamorphosis mentioned above, it is known that the minimum water may be accumulated from precipitation, irrigation or accumulation for human consumption in the urban reservoirs and must be 10 (mm) or higher in height.
The Surface Energy Balance (SEB) is fundamental to the determination of the temporal evolution of atmospheric variables at surfaces (Oke, 1988) [18] , particularly in cities, where urban surface topography and land cover is able to define different partitions of energy, defining different urban microclimates (e.g., as observed in down- towns with high buildings, green parks, concrete surfaces of parking, roads and even microclimates within urban dwellings). Part of net flux of energy is stored by the urban materials and buildings, providing a 24 hours cycle of hysteresis between temperature and the net flux of radiation (Ferreira et al., 2013) [61] .
According to Piovezan (2009) [62] , the predominant breeding sites for the development of the aquatic phase of the mosquito are presented in three types: dishes and pots for plants, cans, pots and flasks, and other types of removable receptacles. Additionally, it is interesting to include in this list: open water tanks, abandoned pools, big cans, flower pots in cemeteries [23] , refuse dumps etc.
Hypothetically, places considered prone to mosquito aquatic phase development are those subject to recept a partial flux of incoming water during precipitation vents (i.e., a smoothed flux), with thermal conditions around to the most favourable thermal conditions (i.e., close to the optimum), obtained with the Mosquito’s oviposition preference by partially shadowed sites. With that in mind, the breeding sites in the MARJ most propitious to the development of the aquatic phase of Aedes aegypti are those under partial shadowing and with only partial interception of rainfall.
Once the reservoirs of water of the urban breeding sites are essentials to the aquatic phase of the mosquito behavior, the data analysis of precipitation and relative humidity were accomplished in detail. The goal was quantifying the model sensibility in relation to these variables. As result, we observed that a large number of weak to moderate rainfall events, alternated with hot sunny periods, can be most favourable to aquatic develop- ment of larvae than the occurrence of some few strong rainfall events of equivalent height of water. By hypothesis, with rain interspersed with periods of sun the breeding sites can lose water due to evaporation, but not in the potential rate due to the partial shadowing conditions inside them.
A Linear Reservoir Model (LRM) was used to represent the average dynamics of breeding sites. To supply the water for breeding reservoirs the atmospheric precipitation was assimilated by nudging. The lost of water due to evapotranspiration and leaks was also represented in the modelled breeding sites. The loss is parametrized by the sum of the estimated Potential Evapotranspiration (PET) plus a smaller amount reservoir leaking, in the form of a simplified Surface Water Balance (SWB) (Grimmond et al., 2002 [63] ; Karam et al., 2010 [47] ).
The Potential Evapotranspiration (PET) was obtained with the known Penman’s Combination Method (Penman, 1948 [64] ; Thom e Oliver, 1977 [65] , and Monteith and Unsworth, 2007 [66] ). The calculation of the PET depends on the data assimilation of the net irradiance flux (
The LRM used in this work requires a small number of parameters, scale of time of the response time of the reservoir, the ratio of average loss due to leakages, horizontal surface area exposed to rain, and maximum reservoir capacity. A comprehensive introduction about the Surface Energy Budget (SEB) and WSB can be found in Oke (1988) [18] . The specificities of the SEB of different cities have been discussed (e.g., Karam and Pereira Filho (2006) [67] , Lemonsu et al. (2007) [68] and Masson et al. (2014) [69] ). In hydrology, the application of LRM is well known (e.g., Nasch, 1959 [70] ; Beven, 2001 [71] ; and Brutsaert, 2005 [19] ).
In this work, for representing the urban breeding sites we use the LRM and the PET, provided modelled data of the net irradiance flux (Flores Rojas et al., 2015) [32] . In a way similar to doing in simulations of WSB to natural surfaces, for the urban breeding sites the variation of the water volume along the time was given in function of the observed influx and lose of water. The modelled recharge occurs during atmospheric precipi- tation events due to the interception, modelled by a small fraction of the total rainfall, estimated near to 1% for Rio de Janeiro metropolis. Due to the shadowing condition of the breeding sites, it is also considered a fraction of the PET calculated (i.e., equal to 60%) to simulate the evaporative conditions found in the breeding sites.
The idea of using linear reservoirs to simulate the breeding site is well known in the literature. For instance, a application of SWB and SEB for modelling breeding sites for larvae and pupae development, in function of the observed temperature and precipitation, was comprehensively described by Sporleder et al. (2009) [40] . In this case, the researchers obtained the spatial and temporal distributions of the vector population on Australia territory, in a GIS platform. Differently, no rainfall was considered in Otero’s temperature-dependent model for model the summer surges of Dengue fever, for Buenos Aires city, in Argentina, where the climate is subtropical, with cold and rainy weather in winters (Otero et al., 2006) [23] . In the Otero’s model, the oviposition presents hysteresis behaviour to the seasonal variation of the air temperature. That is not the expected case of a tropical city as the Rio de Janeiro’s metropolis, where the diurnal variation of temperature is commonly larger than the seasonal variation (i.e., as typical of a tropical climate city).
Goodness-to-fit statistics
Lana et al. (2014) [41] have applied several goodness-to-fit statistics to verify their model performance, e.g., statistics based on the log-likelihood functions for transition probabilities of fitted Markov chains, e.g., as the Akaike Information Criterion (AIC).
In this work, a set of statistical estimators were applied to verify the model performance and tuning the model parameters. These scalar accuracy measures are the Mean Absolute Error (MAE), the Mean Squared Error (MSE), the Root Mean Squared Error (RMSE), the Coefficient of Determination R2, and the Nash-Sutcliffe Efficiency (NSE), as recommended by Nash and Sutcliffe (1970) [72] , Singh et al., (2005) [73] , Moriasi et al. (2000) [74] , and Wilks (2006) [75] .
3. Results
The analysis of atmospheric observations and Dengue fever notifications were performed, as well as, simula- tions and parameter tuning.
First, a simple statistical analysis was accomplished on dengue notification data from SUS.
The major epidemic events in the analysis period are shown in Figure 1 and Figure 2. Box plots permit to examine the distribution of quantiles associated with the epidemics (Figure 3).
The threshold number for establishing the beginning of epidemics seems to be very small. The variability of notifications (Figure 1) becomes very evident by the use of a logarithmic scale (Figure 2). Therefore, what can be observed is the environmental conditioning, defining not only the surge itself, but also its severity, as can be evidenced by the wide distribution of the number of reports of worsening by dengue fever in the dataset.
The three bigger epidemics of Dengue in the period 2000-2011, occurred in the years of 2002, 2008 and 2011 (Figure 1 and Figure 2).
Based in absolute values of number of Dengue notifications, the month of March is the month with biggest number of cases, followed by February, April and January. Although the month of March presents a larger absolute value in the notified Dengue cases, the month of April shows a larger epidemic volume, occurring a decline in the number of cases from April on.
Dengue shows a seasonal aspect, with a cyclic tendency of the epidemic varying from August to April, suggesting that the monthly distribution of the cases varies in function of the seasons of the year, with a probable chronological delay addressed to the period comprehended between the mosquito life cycle and the appearance of clinical characteristics in human organisms, this delay lasts an average of 40 to 45 days.
The shape of the envelope shown in Figure 1 seems to suggest a nearly periodic cycle of 4 to 6 years.
It is noteworthy the favorable conditions for dengue surge in years 2014 and 2015 in the Brazilian Southeast, associated to a very hot and relatively dry summer in 2014. In association to the recovering of precipitations in summer of 2015 a strong increase of Dengue was verified in State of São Paulo. In the last years, the epidemic character of the Dengue infectious disease seems to be changed to endemic in many areas of Southeast Brazil.
Figure 1. Time evolution of Dengue epidemics in the MARJ between Jan/2000 and Dec/2011. Data source: SUS-Brazil.
Figure 2. Time evolution of Dengue epidemics in the MARJ between Jan/2000 and Dec/2011, plotted with the same data used in Figure 1, but using logarithmic scale for number of occurren- ces. Source of raw data: SINAN-net/SUS.

Figure 3. Box plots of notified cases of Dengue fever reported for the Rio de Janeiro city durante period 2000-2011. Distribution (a) by months and (b) by years. Data source: SINAN-net/SUS.
Summer is the season of the year with the largest number of registered Dengue cases, since the increased temperatures, as well as the distribution and major frequency of accumulated rainfall water, that generally occurs in this period, can favor the development of the mosquito biological cycle and the consequent pro- liferation of the mosquito.
Whereas in summer the egg takes 10 days to reach the adult stage, in the winter this time increases to 30 days, due to the major frequency of cold and dry weather.
A low number of occurrences were notified in the years 2004 and 2005, while, differently, in 2002 and 2008, when a higher number was notified, resulting in a larger accumulated epidemic volume. The increase also occurred in 2011, and also in 2015. In this later year, the epidemics followed a very hot and extremely dry year in part of Southeast Brazil (i.e., during 2014), with particularly severe effects in the hydrologic budget of State of São Paulo.
There is a seasonal tendency of the epidemics for all the administrative subdivisions of MARJ, with the start of the epidemic cycle in the month of September and the ending in March or April. One can observe a signifi- cant gradual decrease of the number of cases during the following months, present along the microclimates of MARJ.
Two fundamental factors for the epidemic seasonality are associated with the annual cycle of weather conditions in MARJ, i.e., hot temperature in the summer and a series of rainfall events to start the aquatic phase of A. aegypti. The temperature presented as a function of MARJ seasons, with a maximum occurrence during Dec/Feb/Mar, frequently.
The results of the simulation is presented ahead. The time step (i.e., time resolution) of the model was 15 minutes. The time integration was accomplished between January-2000 and December-2011.
The model time resolution was set in 15 minutes, considerably greater than the input data resolution (i.e., from dengue notification from SUS, of 30 days). To permit a peer comparison, a simulation output for each 30 days period was also provided (not shown here).
The results for the vector population dynamics are shown in Figure 4.
The simulations generated for the linear hydrological reservoir together with the available precipitable water data were important for the analysis of the model results, because we want to investigate the correlation between Dengue infection data and the distribution of urban rainfall, along the seasons and years.
Figure 4. Simulation of the temporal evolution of the relative population of the Dengue vector. The key of lines are: o = eggs, l = larvae, p = pupae, w1 = non-infected mosquitoes, w2 = infected mosquitoes, non-infectious, w3 = infectious mosquitoes, wtot = total number of mosquitoes.
In the simulation of the virus relative population is presented in Figure 5. The simulation starts in 2000 with the effective coexistence of the DENV-1 and DENV-2 serotypes in MARJ. The introduction of DENV-3 serotype occurred in 2002, and DENV-4, in 2011.
In the simulation, the virus population is dynamically variable, meanwhile the serotypes can maintain a degree of interrelationship, in function of the virus population and incubation temperature.
There is considerable variation in the virus population number (as it appears in the simulation), suggesting that their number can be modulated by the population dynamics of mosquitoes, which in turn is controlled by the enthalpy available as a result of environmental conditions.
A numerical essay was realized to investigate the role of the rainfall intensity. In this essay, the assimilation of only half of observed rainfall is enough for decreasing of the number of re-infected individuals. The results indicated that the distribution of rainfall along the year is also important especially after a long hot spell.
Figure 6 shows the evolution of epidemics in population of humans as simulated by the model.
Figure 5. Simulation of the temporal evolution of the relative population of the Dengue virus. The key are serotypes st1 = DENV-1, st2 = DENV-2, st3 = DENV-3 e st4 = DENV-4.
Figure 6. Simulation of the temporal evolution of the relative population dynamics of humans, in the different infection compartments (s = susceptible, e = exposed, i = infected, ir = reinfected, r = immune, m = dead, tot = total population).
The simulation of the human population dynamics shows two periods in the epidemic cycle, in which the compartment rates shows connections between themselves (in the beginning of 2002 and 2011). Such instants seem to be influenced by the force of the reinfection, as of the introduction of a determined serotype of the virus in the population (i.e., Figure 5).
Associated with the annual cycle of air temperature on RMRJ, the annual variation of enthalpy can be estimated. The available energy in the environment can be used to maintain and control the mosquitoes phy- siology behaviour. The more favorable condition is applied in reproduction. The environmental accumulation of energy was estimated in function of the accumulated enthalpy (i.e., in a similar way, we can consider the DG or entropy variation).
The estimations from observations indicate accumulated DG values up to 
Figure 7 presents the hourly change of DG and, (b) the corresponding accumulated value since late July (i.e., since the basal period). Similar behavior were found for enthalpy and entropy estimations.
It is noticeable that the preceding months of the years of reduced notification (i.e., 2004, 2009 and 2010) show a reduction in the value of accumulated DG (or enthalpy), avoiding or restriting the epidemic develop- ment.
Therefore it is suggested that years with small accumulated DG, due to a long period of negative perturbation of temperature, is able to prevent development of dengue epidemics, at least under similar tropical conditions as found in the Rio de Janeiro city.
Figure 8(a) shows the metabolic factor of the proposed model, which is applied for drive the mosquito population behavior. This factor was estimated in function of the estimated enthalpy variation from observation.
If the enthalpy decreases also decreases the probability of dengue epidemics. This appears have occurred in the years 2001, 2003, 2004 and 2005, when the number of notifications were very small compared to epidemic years.
In the graphic is noticeable the occurrence of high maximum preceding the epidemics of 2002 and 2008, hence it is suggested that the energetic organization driven by enthalpy can be a favourable factor to some epidemic surges (i.e., controlling the gnostrophic cycle of the vector).
The effectiveness of the rainwater catchment by breeding sites was estimated in this model in the form of a parameter (Figure 8(b)) used to control egg eclosion and growing of larvae into the breeding site.
Figure 7. Observed temporal changing of degree-day index (DG).


Figure 8. (a) Time evolution of metabolic factor obtained by parametrization in function of the observed air temperature, assimilated in the model; (b) Time evolution of scale of larvae breeding height.
General discussion
This work started with the investigatory process of the notified cases of hospitalization and death by Dengue, obtained from SINAN-Net and SVS-RJ.
The atmospheric variables were obtained from NOAA-NCDC, referring to observational data of surface meteorological stations in the airports of the RMRJ maintained by the COMAER, and also from the network of mesoscale precipitation observation in the RMRJ, maintained by GEORIO netwrok of rain gauges.
The observational atmospheric data and Dengue notification data were analysed separately and, after that, assimilate in the model for simulations.
The occurrence of correlation between epidemic cycles and atmospheric data was verified.
The simulation allowed a detailed analysis of the population dynamics of living organisms involved in events of the infectious disease Dengue, considering the populations of the virus, mosquito and humans.
The numerical results show the amplitude and phase (lag) in the rates of infection, through the variation of minimums and maximums of the fractions of the population infected (i) and reinfected (ir), during epidemic cycles.
Variables derived from a-biotic observations were also computed for the period of investigation. Among these a-biotic variables are enthalpy, number of rainfall events, water accumulated in reservoirs, etc. Abiotic is not the proper category for the general description of these variables, which are directly related to animal and vegetable physiology, for example, raw primary production and the level hydric stress which plants and animals consider in different environments or moments of their development.
With the introduction of different serotypes in one region, considering the combined effects of reinfections in the population becomes necessary. The viral action of a determined serotype is enlarged by the introduction of other serotype in the previously infected population, as observed in the simulations from the model.
The high temperature is a determining factor in the rise in the number of notified cases of Dengue. The water also contributes to this rise. However the infections are not only modulated by the form of the distribution and intensity of the rains in the Aedes aegypti life cycle, but they were modulated by the accumulation of water in hydrological reservoirs. Thus it is concluded that water is a main factor for the infection, as a maintainer of the minimal quantity for the eggs eclosion, development and survival of the different stages of life of the mosquito.
Regarding the enthalpy and epidemic cycles, it is concluded that energetic biological transformations involv- ing epidemiological cycles follow the laws of thermodynamics and the living organisms involved are thermo- dynamic systems in vivo, therefore demanding constant energy supply; as well as using a large part of this energy in biochemical processes to obtain energy.
It was observed that although the population dynamics of the involved organisms with the Dengue vary concurrently with the temporal-spatial variation of entropy and degree day, being those the determining factors for the biochemical processes of the involved organisms, as the population dynamics presented a good return to available energy in the cycles. The negative rate of accumulated degree days holds high return in the reduction of epidemiological cycles, as well as their maximum amplitudes alongside the epidemic.
Regarding the cycles, it was observed that there is a lag between the simulated and the observed, principally regarding the accumulation of water in the reservoirs of the mosquito breeding sites. This is probably due to the period preceding the infection, as the mosquito eggs can only hold in latency for 450 days.
The prognostic results for reinfection was compared with the observed data of Dengue fever worsening (Figure 9). The model was able to determine the epidemics periods (2002, 2008 and 2011) accurately. However, due to the fact the numerical solution generally smooth the simulated fields, the model can not be proved to be accurate in determining the total number of cases of dengue fever worsening, but underestimates the values for the correctly achieved events of epidemics. Positively, a satisfactory performance clue of the model is that the variables are not directly comparable because not all cases of Dengue are registered or confirmed in posterior time and can be some confusion of symptoms with other tropical infectious diseases. The more subject to epidemic areas in MARJ are also among those where more care infrastructure deficiency. In general, these latter areas present the greatest number of cases. This type of socio-economic effect is not yet described or in the present equations of the model.
The analysis of the temporal evolution of 
Comparison between observation and simulation
The model skill was computed and presented in Figures 9-11. A statistical hypothesis 

Moriasi et al. (2007) [74] proposed three quantitative statistics for model evaluation: Nash-Sutcliffe
Figure 9. Comparison of the observed and simulated epidemic decision variable, in log scale. The time evolutions of the observed notification of dengue fever worsening and predicted reinfections number.
Figure 10. Temporal evolution of (a) Mean Bias Error (MBE) and Root Mean Square Error (RMSE) for the along the period of 12 years of simulation.
efficiency (NSE), percent bias (PBIAS), and ratio of the root mean square error to the standard deviation of measured data (RSR), being that the following ranges are recommended for satisfactory modelling, 

In Table 3 it is showed the higher correlated variables of the model. The reinfection and mortality rate of reinfections are the best correlated in the present model. Other skill scores used in the model verification are: the
Figure 11. The Nash-Sutcliffe efficiency (NSE) of the proposed model. All model results were skilled above the statistical persistence of 63.2%.
Table 3. Correlation between the observed variable (notification) and model variables. Only correlation values above 0.01 are showed.









Baldwin and Kain (2006) [76] have analysed the sensitivity of several performance measures to displacement error, bias, and frequency commonly used in verifications of models performance based in contingency tables for a chosen threshold. In the present work, we consider the level of 75% of normalized logarithmic variables to
build up the contingency table used to obtain the parameters 














quently, the model can be addressed more to determine the change of magnitude order than to discriminate a specific maximum. At least, it can be useful as a skilled tool to update the tendency of epidemic growth. Therefore, the model performance seem to be conditionally acceptable, even considering the many uncertainties and assumed hypothesis.
4. Conclusions
The main conclusions in this research are:
• The accumulation of energy (since July 1st of each year) associated with the degree-day index variation allows us to evaluate the degree of maturation of females of the mosquito Aedes aegypti, thereby determining whether an epidemic period is more or less likely. The accumulated variation of enthalpy or entropy also can be used similarly.
• If the entomological parameters can be parametrized in function of air temperature and accumulation of energy from the environment (through the concepts of degree-day index or the accumulated enthalpy change), a numerical model for the population dynamics under dengue epidemic can be developed considering this relationship.
• The numerical model was developed and the equations were presented in this work. The model was run along 12 years (from Jan. 2000 to Dec. 2012), assimilating continuously some meteorological data available in the area about the Dengue epidemics in the MARJ-Brazil.
• The model design considered the perspective of: a) high portability, based in use of free software and compiler, that is ideal but not absolutely necessary to run the model; b) use of dummy variables in the subroutine, to easy coupling into some advanced atmospheric mesoscale models (a present proposition), c) simply customised, considering preparation of input data, and d) automatized graphical output, accessed by a single line command (job), written in shell script and gnuplot.
• The epidemic model can be used in an externalized way (e.g., as done in this work), or still integrated/ coupled with a atmospheric numerical forecasting model in high resolution. The prediction of Dengue outbreaks is the most suitable for tropical cities characterized by high temperatures and rainfall during the summers. On the other hand, this kind of prediction can also be very useful in the evaluation of advanced risk scenarios for subtropical cities, which are likely to have increased their average temperatures due to climate change over the twenty-first century.
• The model skill was verified with the Student’s t-test and other statistics such as MBE and RMSE, describing the uncertainties of the model along the simulation period. The Nash-Sutcliffe efficiency also was employed to verify the model skill above of the statistical persistence (i.e., daily cycle repetitions).
• The numerical results appear indicating that a greater number of weak and moderate rainfall events, during the year, are more favourable to larvae breeding, than a small number of intense rainfall events. Very intense precipitations are not favourable too due to the washing out effect depleting the egg and larvae population remaining in the breeding.
• The simulated results have supported the existence of correlation between the seasonal variation of degree- day/entropy/enthalpy (as precursor variables) and the outbreaks of epidemic Dengue fever (as a predicted event characterized by the dengue fever worsening notifications).
• According to the simulation results, the seasonal variation of degree day, or the equivalent in terms of entropy, or indeed, in terms of enthalpy, can be associated with the basal metabolism of the insect vector.
• In association and for this reason the amount of eggs deposited in the previous year may constrain (or limit) the epidemic onset in the following summer.
• The oviposition can be established by the state of metabolism and maturation of Aedes aegypti females that are consequence of the net entropy/enthalpy seasonal change, mainly accumulated along the preceding months (i.e., before oviposition and gonostrophic cycle establishment).
• By their turn, the consequence of a reduced oviposition is the decrease in the chance of a epidemic surge, and this is so even though in the months following oviposition; we can observe environmental conditions very favourable to the development of Aedes aegypti, both in their water as aerial phase.
• Furthermore, in the case in what the amount of eggs is not considered a limitation, the net accumulation of enthalpy, entropy or degree-day to above of a threshold of approximately 2 million (J∙kg−1) appears to be a necessary condition for the outbreak of Dengue fever and for the establishment of the epidemic.
• The statistical analysis on model results enlightened the need of a long data series, typically 10 years, in way to tune the parameters and use the epidemic model operationally. This is in accord with the proposition of Coelho et al. (2008, 2011) [54] [55] of obtaining the posterior distribution of parameters with Bayesian frame- work.
• Finally, we must emphasize the importance of reinfection process for the computational modelling of epidemics of acute Dengue fever, without which the dynamics of infected populations cannot be achieved satisfactorily.
• Due to the autocorrelation of hydrometeorological variables through successive years (e.g., Yue et al., 2002) [77] the epidemic period can not be restricted to just a year, specifically. It can be interesting to consider the block of successive years with most favourable conditions. Typically, the low-frequency period observed for the dengue epidemic can be extended by three or four successive years, in a progression that ends at a major epidemic or even can establish the dengue as an endemic disease.
As next steps of the research we can investigate the effect of climate change on the occurrence of outbreaks of dengue fever. To this end, the numerical model described in this paper can be very useful to assimilate atmospheric conditions from different global warming scenarios, which are expected for the next 50 years. For example, a scenario in which the global temperature may be some degrees above the current average, as described by the Intergovernmental Panel on Climate Change (IPCC).
This work was an effort to investigate and to develop prognostic tools able to predict dengue outbreaks months in advance in the metropolitan tropical areas such as the MARJ in Brazil. Hopefully, the biophysical relationships tested there may be useful for predictions Dengue epidemics also in other tropical cities.
Acknowledgements
The first author thanks to Luiz Carlos Ciafrino Neto that kindly read the preliminary version of this work.
Author Contributions
HAK and JCBS proposed the presented numerical model and prepared input dataset. HAK wrote the numerical code in Fortran-90 and performed larger amount of numerics and parameters tuning. HAK and JCBS run the simulations. The analysis of results and discussions received contributions of all authors (HAK, JCBS, AUPF and JLFR). All authors meet the ICMJE criteria for authorship read and met, and agree with the manuscript’s results and conclusions.
Cite this paper
Hugo AbiKaram,Julio Cesar Barreto daSilva,Augusto José PereiraFilho,José Luis FloresRojas, (2016) Dynamic Modelling of Dengue Epidemics in Function of Available Enthalpy and Rainfall. Open Journal of Epidemiology,06,50-79. doi: 10.4236/ojepi.2016.61007
References
- 1. Kyle, J. and Harris, E. (2008) Global Spread and Persistence of Dengue. Annual Review of Microbiology, 62, 71-92.
http://dx.doi.org/10.1146/annurev.micro.62.081307.163005 - 2. Normile, D. (2013) Surprising New Dengue Virus Throws a Spanner in Disease Control Efforts. Science, 342, 415.
http://dx.doi.org/10.1126/science.342.6157.415 - 3. Nogueira, R.M., de Araujo, J. and Schatzmayr, H. (2007) Dengue Viruses in Brazil, 1986-2006. Revista Panamericana de Salud Pública, 22, 358-363.
http://dx.doi.org/10.1590/S1020-49892007001000009 - 4. Estadao (2012) Casos de Dengue 4 aumentam risco de epidemia no RJ.
http://www.estadao.com.br - 5. Terra (2013) Governo admite epidemia de dengue após aumento de 190% no número de casos.
http://noticias.terra.com.br - 6. Frayssinet, F. (2012) Brazil Deploys Junior Firefighters to Snuff out Dengue.
http://www.ipsnews.net/2012/02/ - 7. Braga, I.A. and Valle, D. (2007) Aedes aegypti: Histórico do controle no Brasil. Technical Report 2, Epidemiologia e Servicos de Saúde, Programa Nacional de Controle da Dengue—SVS/MS, Brasília, DF.
- 8. Vynnycky, E. and White, R. (2010) An Introduction to Infectious Disease Modelling. Oxford University Press, Oxford, 400 p.
- 9. Brazil (2005) Guia de Vigilancia Epidemiológica. 6 Edition, Departamento de Vigilancia Epidemiológica, Secretaria de Vigilancia em Saúde-Ministério da Saúde (SVS-MS), Brasília, DF.
- 10. Ferreira, C.P. and Yang, H.M. (2003) Estudo da Transmissao da Dengue entre os Indivíduos em Interacao com a Populacao de Mosquitos Aedes aegypti. TEMA—Tendências em Matemática Aplicada e Computacional, 4, 323-332.
http://dx.doi.org/10.5540/tema.2003.04.03.0323 - 11. Brazil (2012) Séries Estatísticas e Séries Históricas do Instituto Brasileiro de Geografia e Estatística, IBGE.
http://seriesestatisticas.ibge.gov.br/series.asp - 12. Christophers, S.R. (1960) Aedes aegypti (L.), the Yellow Fever Mosquito: Its Life History, Bionomics and Structure. Cambridge University Press, London, 739 p.
- 13. Aguiar, R. (2006) Notícias do IOC.
http://www.ioc.fiocruz.br - 14. FioCruz (2015). Fundacao Oswaldo Cruz.
http://portal.fiocruz.br/ - 15. Brigdman, H.A. and Oliver, J.E. (2006) The Global Climate System Patterns, Processes, and Teleconnections. Cambridge University Press, Cambridge, 205-243.
- 16. Campos, H.R.P. (2009) Estudo da relacao entre variáveis meteorológicas e incidência de dengue utilizando métodos estatísticos e redes neurais artificiais. Master’s Thesis, Universidade Federal de Vicosa, MG, Brazil.
- 17. Rocha, J., Mariano, Z., Aguiar, R. and Lima, A. (2012) Estudo da relacao entre precipitacao e casos de dengue na cidade de jataí, goias. Revista Geonorte, 2, 773-783.
- 18. Oke, T.R. (1988) Boundary Layer Climates. 2nd Edition, Routledge, London, 464 p.
- 19. Brutsaert, W.H. (2005) Hydrology—An Introduction. Cambridge University Press, Cambridge, 618 p.
http://dx.doi.org/10.1017/CBO9780511808470 - 20. Bird, R.E. and Hulstrom, R.L. (1981) A Simplified Clear Sky Model for Direct and Diffuse Insolation on Horizontal Surfaces. Tr-642-761, Solar Energy Research Institute (SERI)—US Department of Energy, Golden, CO.
http://dx.doi.org/10.2172/6510849 - 21. Iqbal, M. (1983) An Introduction to Solar Radiation. Academic Press, Toronto.
- 22. Stull, R.B. (1988) An Introduction to Boundary Layer Meteorology. Springer, Dordrecht, 670 p.
http://dx.doi.org/10.1007/978-94-009-3027-8 - 23. Otero, M., Solari, H.G. and Schweigmann, N. (2006) A Stochastic Population Dynamics Model for Aedes Aegypti: Formulation and Application to a City with Temperate Climate. Bulletin of Mathematical Biology, 68, 1945-1974.
http://dx.doi.org/10.1007/s11538-006-9067-y - 24. Lima-Camara, T.N., Bruno, R.V., Luz, P.M., Castro, M.G., Lourenco-de Oliveira, R., et al. (2011) Dengue Infection Increases the Locomotor Activity of Aedes aegypti Females. PLoS ONE, 6, 15.
http://dx.doi.org/10.1371/journal.pone.0017690 - 25. Atlan, H. (1992) Entre o cristal e a fumaca: Ensaio sobre a organizacao do ser vivo. Jorge Zahar Ed., Rio de Janeiro, 268 p.
- 26. Murphy, M.P. and O’Neill, L.A.J. (1997) O que é vida 50 anos depois. Especulacoes sobre o futuro da Biologia. Fundacao Editora da UNESP, Sao Paulo.
- 27. Brunini, O., Lisbao, R.S., Bernardi, J.B., Fornasier, J.B. and Pedro Júnior, M.J. (1976) Temperatura-base para alface cultivar “White Boston”, em um sistema de unidades térmicas. Bragantia, 35, 213-219.
http://dx.doi.org/10.1590/S0006-87051976000100019 - 28. Descloux, E., Mangeas, M., Menkes, C.E., Lengaigne, M., Leroy, A., et al. (2012) Climate-Based Models for Understanding and Forecasting Dengue Epidemics. PLoS Neglected Tropical Diseases, 6, e1470.
http://dx.doi.org/10.1371/journal.pntd.0001470 - 29. Kister, R.E. (1974) A Study of Data Assimilation Techniques in an Autobarotropic Primitive Equation Channel Model. Master’s Thesis, Department of Meteorology—The Pennsylvania State University, University Park.
- 30. Haltiner, G.J. and Williams, R.T. (1980) Numerical Prediction and Dynamic Meteorology. 2nd Edition, Wiley, New York, 496 p.
- 31. Brazil (2006) Indicadores Demográficos do Brasil. Ministério da Saúde Mato Grosso do Sul—MS, Brazil.
http://tabnet.datasus.gov.br/cgi/idb2006/a03.htm - 32. Flores, R.J.L., Karam, H.A., Marques Filho, E.P. and Pereira Filho, A.J. (2015) Estimation of Atmospheric Turbidity and Surface Radiative Parameters Using Broadband Clear Sky Solar Irradiance Models in Rio de Janeiro, Brazil. Theoretical and Applied Climatology, 1, 1-12.
- 33. Bolton, D. (1980) The Computation of Equivalent Potential Temperature. Monthly Weather Review, 108, 1046-1053.
http://dx.doi.org/10.1175/1520-0493(1980)108<1046:TCOEPT>2.0.CO;2 - 34. Focks, D.A., Haile, D.C., Daniels, E. and Moun, G.A. (1993) Dynamics Life Table Model for Aedes aegypti: Analysis of the Literature and Model Development. Journal of Medical Entomology, 30, 1003-1018.
http://dx.doi.org/10.1093/jmedent/30.6.1003 - 35. Focks, D.A., Haile, D.G., Daniels, E. and Moun, G.A. (1993) Dynamics Life Table Model for Aedes aegypti: Simulations Results. Journal of Medical Entomology, 30, 1019-1029.
- 36. Focks, D.A., Daniels, E., Haile, D.G. and Kessling, J.E. (1995) A Simulation Model of the Epidemiology of Urban Dengue Fever: Literature Analysis, Model Development, Preliminary Validation, and Samples of Simulation Results. The American Journal of Tropical Medicine and Hygiene, 53, 489-506.
- 37. Focks, D.A. and Barrera, R. (2007) Dengue Transmission Dynamics: Assessment and Implications for Control. Technical Report, Scientific Working Group, Report on Dengue, World Health Organization on Behalf of the Special Programme for Research and Training in Tropical Diseases, 1-5 October 2006, Geneva.
- 38. Morin, C.W. and Comrie, A.C. (2010) Modeled Response of the West Nile Virus Vector Culex quinquefasciatus to Changing Climate Using the Dynamic Mosquito Simulation Model. International Journal of Biometerology, 54, 517-529. http://dx.doi.org/10.1007/s00484-010-0349-6
- 39. Luz, P.M., Codeco, C.T., Massad, E. and Struchiner, C.J. (2003) Uncertainties regarding Dengue Modeling in Rio de Janeiro, Brazil. Memórias do Instituto Oswaldo Cruz, 98, 871-878.
http://dx.doi.org/10.1590/S0074-02762003000700002 - 40. Sporleder, M., Chavez, D., Gonzales, J.C., Juarez, H., Simin, R., et al. (2009) ILCYM—Insect Life Cycle Modeling: Software for Developing Temperature-Based Insect Phenology Models with Applications for Regional and Global Pest Risk Assessments and Mapping. Proceedings of the 15th Triennial Symposium of the International Society for Tropical Root Crops (ISTRC), Lima, 2-6 November 2009.
- 41. Lana, R.M., Carneiro, T.G.S., Honório, N.A. and Codeco, C.T. (2014) Seasonal and Nonseasonal Dynamics of Aedes aegypti in Rio de Janeiro, Brazil: Fitting Mathematical Models to Trap Data. Acta Tropica, 129, 25-32.
http://dx.doi.org/10.1016/j.actatropica.2013.07.025 - 42. Verhulst, P.F. (1845) Recherches mathématiques sur la loi d’accroissement de la population. Nouveaux mémoires de l’Académie Royale des Sciences et Belles-lettres de Bruxelles, 18, 1-41.
- 43. Watts, D.M., Burke, D.S., Harrison, B.A., Whitmire, R.E. and Nisalak, A. (1987) Effect of Temperature on the Vector Efficiency of Aedes aegypti for Dengue 2 Virus. American Journal of Tropical Medicine and Hygiene, 36, 143-152.
- 44. Mesinger, F. and Arakawa, A. (1976) Numerical Methods Used in Atmospheric Models, Volume 1. International Council of Scientific Unions—World Meteorological Organization, Geneva.
- 45. Yang, H.M., Macoris, M.L.G., Galvani, K.C., Andriguetti, M.T.M. and Wanderley, D.M.V. (2009) Assessing the Effects of Temperature on the Population of Aedes aegypti, the Vector of Dengue. Epidemiology and Infection, 137, 1188-1202.
http://dx.doi.org/10.1017/S0950268809002040 - 46. Marques Filho, E.P., Sa, L.D.A., Karam, H.A., Miranda, A.G. and Franca, J.R.A. (2009) Rio de Janeiro’s Tropical Urban Climate. Urban Climate News—Quarterly Newsletter of the International Association for Urban Climate (IAUC), 32, 5-9.
- 47. Karam, H.A., Pereira Filho, A.J., Masson, V., Noilhan, J. and Marques Filho, E.P. (2010) Formulation of a Tropical Town Energy Budget (t-TEB) Scheme. Theoretical and Applied Climatology, 101, 109-120.
http://dx.doi.org/10.1007/s00704-009-0206-x - 48. Morin, C.W. (2012) Climate and Environmental Influences on the Ecology of Vectors and Vector-Borne Diseases. PhD Thesis, Doctoral Dissertation, School of Geography and Development—Graduate College, The University of Arizona, Tucson.
- 49. Morin, C.W., Comrie, A.C. and Ernst, K. (2013) Climate and Dengue Transmission: Evidence and Implications. Environmental Health Perspectives, 121, 11-12.
http://dx.doi.org/10.1289/ehp.1306556 - 50. Sharpe, P.J.H. and De Michele, D.W. (1977) Reaction Kinetics of Poikilotherm Development. Journal of Theoretical Biology, 64, 649-670.
http://dx.doi.org/10.1016/0022-5193(77)90265-X - 51. Schoolfield, R.M., Sharpe, P.J.H. and Magnuson, C.E. (1981) Non-Linear Regression of Biological Temperature Dependent Rate Models Based on Absolute Reaction-Rate Theory. Journal of Theoretical Biology, 88, 719-731.
http://dx.doi.org/10.1016/0022-5193(81)90246-0 - 52. Van der Have, T.M. and Jong, G.D. (1996) Adult Size in Ectotherms: Temperature Effects on Growth and Differentiation. Journal of Theoretical Biology, 183, 329-340.
http://dx.doi.org/10.1006/jtbi.1996.0224 - 53. Salom, S.M., Stephen, F.M. and Thompson, L.C. (1987) Development Rates and a Temperature-Dependent Model of Pales Weevil, Hylobius pales (Herbst), Development. Environmental Entomology, 16, 956-962.
http://dx.doi.org/10.1093/ee/16.4.956 - 54. Coelho, F.C., Codeco, C.T. and Struchiner, C.J. (2008) Complete Treatment of Uncertainties in a Model for Dengue R0 Estimation. Cadernos de Saúde Pública, 24, 853-861.
http://dx.doi.org/10.1590/S0102-311X2008000400016 - 55. Coelho, F.C., Codeco, C.T. and Gomes, M.G.M. (2011) A Bayesian Framework for Parameter Estimation in Dynamical Models. PLoS ONE, 6, e19616.
http://dx.doi.org/10.1371/journal.pone.0019616 - 56. Rall, B.C., Brose, U., Hartvig, M., Kalinkat, G., Schwarzmüller, F., et al. (2012) Universal Temperature and Body- Mass Scaling of Feeding Rates. Philosophical Transactions of the Royal Society B, 367, 2923-2934.
http://dx.doi.org/10.1098/rstb.2012.0242 - 57. Rueda, L.M., Patel, K.L., Axtell, R.C. and Stinner, R.E. (1990) Temperature-Dependent Development and Survival Rates of Culex quinquefasciatus and Aedes aegypti (Diptera: Culicidae). Journal of Medical Entomology, 27, 892-898.
http://dx.doi.org/10.1093/jmedent/27.5.892 - 58. Massad, E., Coutinho, F.A., Burattini, M.N. and Lopez, L.F. (2001) The Risk of Yellow Fever in a Dengue Infested Area. Transactions of the Royal Society of Tropical Medicine and Hygiene, 95, 370-374.
http://dx.doi.org/10.1016/S0035-9203(01)90184-1 - 59. Khan, A., Hassan, M. and Imran, M. (2014) Estimating the Basic Reproduction Number for Single-Strain Dengue Fever Epidemics. Infectious Diseases of Poverty, 3, 12.
http://dx.doi.org/10.1186/2049-9957-3-12 - 60. Luz, P.M., Mendes, B.V.M., Codeco, C.T., Struchiner, C.J. and Galvani, A.P. (2008) Time Series Analysis of Dengue Incidence in Rio de Janeiro, Brazil. The American Journal of Tropical Medicine and Hygiene, 79, 933-939.
- 61. Ferreira, M.J., Oliveira, A.P. and Soares, J. (2013) Diurnal Variation in Stored Energy Flux in Sao Paulo City, Brazil. Urban Climate, 5, 36-51.
http://dx.doi.org/10.1016/j.uclim.2013.06.001 - 62. Piovezan, R. (2009) Levantamento de Larvas de Culicidae (Diptera) em diferentes criadouros no Município de Santa Bárbara d’Oeste, SP. Master’s Thesis, Zoology, UNESP, Rio Claro, SP, Brazil.
- 63. Grimmond, C.S.B. and Oke, T.R. (2002) Turbulent Heat Fluxes in Urban Areas: Observations and a Local-Scale Urban Meteorological Parameterization Scheme (LUMPS). Journal of Applied Meteorology, 41, 792-810.
http://dx.doi.org/10.1175/1520-0450(2002)041<0792:THFIUA>2.0.CO;2 - 64. Penman, H.L. (1948) Natural Evaporation from Open Water, Bare Soil and Grass. Royal Society of London, 193, 120- 145.
http://dx.doi.org/10.1098/rspa.1948.0037 - 65. Thom, A.S. and Oliver, H.R. (1977) On Penman’s Equation for Estimating regional Evaporation. Quarterly Journal of the Royal Meteorological Society, 103, 345-357.
http://dx.doi.org/10.1002/qj.49710343610 - 66. Montheith, J. and Unsworth, M. (2007) Principles of Environmental Physics. 3rd Edition, Academic Press, New York, 440 p.
- 67. Karam, H.A. and Pereira Filho, A.J. (2006) Revisao dos métodos de Penman e Penman-Monteith e suaaplicacao a canions urbanos. Revista Brasileira de Meteorologia, 21, 86-106.
- 68. Lemonsu, A., Masson, V. and Berthier, E. (2007) Improvement of the Hydrological Component of an Urban SVAT Model. Hydrological Processes, 21, 2100-2111.
http://dx.doi.org/10.1002/hyp.6373 - 69. Masson, V., Marchadier, C., Adolphe, L., Aguejdad, R., Avner, P., et al. (2014) Adapting Cities to Climate Change: A Systemic Modelling Approach. Urban Climate, 10, 407-429.
http://dx.doi.org/10.1016/j.uclim.2014.03.004 - 70. Nash, J.E. (1959) Systematic Determination of Unit Hydrograph Parameters. Journal of Geophysical Research, 64, 111-115.
http://dx.doi.org/10.1029/JZ064i001p00111 - 71. Beven, K.J. (2001) Rainfall-Runoff Modelling: The Primer. 2nd Edition, Wiley, Chichester.
- 72. Nash, J.E. and Sutcliffe, J.V. (1970) River Flow Forecasting through Conceptual Models. Part I: A Discussion of Principles. Journal of Hydrology, 10, 282-290.
http://dx.doi.org/10.1016/0022-1694(70)90255-6 - 73. Singh, J., Knapp, H.V., Arnold, J.G. and Demissie, M. (2005) Hydrologic Modeling of the Iroquois River Watershed Using HSPF and SWAT. Journal of the American Water Resources Association, 41, 343-360.
http://dx.doi.org/10.1111/j.1752-1688.2005.tb03740.x - 74. Moriasi, D.N., Arnold, J.G., Liew, M.W.V., Bingner, R.L., Harmel, R.D., et al. (2007) Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Transactions of the ASABE, 50, 885-900.
http://dx.doi.org/10.13031/2013.23153 - 75. Wilks, D.S. (2006) Statistical Methods in the Atmospheric Sciences. 2nd Edition, Academic Press, Elsevier, Boston, 627 p.
- 76. Baldwin, M.E. and Kain, J.S. (2006) Sensitivity of Several Performance Measures to Displacement Error, Bias, and Event Frequency. Weather and Forecasting, 21, 236-248.
http://dx.doi.org/10.1175/WAF933.1 - 77. Yue, S., Pilon, P., Phinney, B. and Cavadias, G. (2002) The Influence of Autocorrelation on the Ability to Detect Trend in Hydrological Series. Hydrological Processes, 16, 1807-1829.
http://dx.doi.org/10.1002/hyp.1095
NOTES
*Corresponding author.













