ABSTRACT

Cellular beams are appropriate for large spans with relatively small loads or for conditions in which strain dictates dimensioning. Another important advantage of cellular beams is the possibility of passing utility ducts through the openings, which avoids cutting through the web of the beam or increasing the construction height, which occurs when the ducts pass under the beams. Geo- metrical imperfections result from a lack of straightness during fabrication of rolled profiles. Geometric imperfections are represented numerically by an initial curvature. Additionally, the physical imperfections of rolled profiles result from the appearance of residual stresses. The condition that creates residual stresses in steel is the result of thermal and mechanical industrial pro- cesses. In this study, numerical analyses are performed with cellular beams using Finite Element Method software. During the simulations, through non- linear geometric and physical analyses, geometric imperfections were varied, where lateral torsional buckling in cellular beams was considered as a function of the unrestrained length. In the boundary, conditions were restrained displacements in the axis X, Y, Z and rotation about X-axis, thus simulating the fork support. The beams are submitted to uniform bending and concentrated load. The results from the numerical analyses were compared with the calculation procedures, which verified that the results were significant.

Keywords:

Cellular Beams, Physical Imperfections, Geometrical Imperfections, Lateral Torsional Buckling

1. Introduction

According to Abreu et al. [1] , when the openings are circular, these beams are called cellular beams. Cellular beams are normally made from hot-rolled profiles with cuts that follow patterns (Sonck and Belis [2] ). Each cut consists of continuous modules made up of a semicircle followed by a small, straight section. The two halves are then shifted and welded to each other, as shown in Figure 1.

The result is a beam that has essentially the same amount of steel but has a much higher resistance to bending than that of the original profile due to the greater height of the cross-section (this height increase can be greater than 50%) (Abreu et al. [1] ). Due to their economical use of materials, cellular beams are used for applications in which they are loaded via bending along their axis of greatest inertia (Sonck and Belis [2] ). Further-more, cellular beams are used to cross large spans for small loads (Ward [3] ), such as in roofing.

1.1. Lateral Torsional Buckling (LTB)

When cellular beams reach the ultimate limit state, they are subject to lateral torsional buckling (LTB), which is caused by a bending moment that acts on the axis of the greatest moment of inertia of the cross-section. The primary factors that cause the beams to undergo lateral torsional buckling according to Kochar and Kulkarni [4] are the following: distance between the lateral supports to the compression of the flanges; boundary conditions; loading type and position, section type; material properties; magnitude and distribution of the residual stresses and geometric imperfections. According to Bezerra [5] , the phenomena can be explain due to compressed part of the cross section becomes instable, but being connected continuously through the web to the pulled part, the stabilizing effect of this causes it to cause a lateral translation μ(z) added torsion ø(z), as shown Figure 2.

The phenomenon of buckling can be separated into three intervals, plastic, inelastic and elastic, according to Figure 3, where M_Rk is the resistant critical bending moment; M_pl is the full plastic bending moment and λ_p is the slenderness related to cross-sectional plastification; M_r is the bending moment related to the start of the yielding and λ_r is the slenderness related to the start of the yielding; M_cr is the critical bending moment related to the Lateral Torsional Buckling (LBT).

The plastic phase occurs for beams with short spans, i.e., in the other words, occurs for slenderness (λ) shorter than slenderness related to cross-sectional plastification (λ_p), thus occurring the phenomenon of total yielding of the cross- section occurs. The inelastic phase occurs for intermediate spans, that means, occurs for slenderness (λ) shorter than slenderness related to the start of the yielding (λ_r) in which a portion of the cross-section has already undergone yielding. The elastic phase occurs for large, unrestrained spans.

1.2. Physical and Geometrical Imperfections

Physical imperfections, in this case, the residual stresses, appear in steel structural profiles and plates during the manufacturing process. If no technique is used to alleviate these residual stresses, they unavoidably remain on the profiles or plates. Due to non-uniform cooling, after rolling or welding of the piece, plastic deformations emerge, and residual stresses can, in certain cases, reach the order of magnitude of the yield stress of the material, also cause the premature yielding of material (σ_p). Residual stresses play an important role in the dimensioning of steel columns because they are the primary cause of non-linearity in the stress x strain diagram in the inelastic region as shown Figure 4, according to Alpsten and Tall [6] , because they are stresses that significantly affect the compressive strength.

Residual stresses represent a state of self-equilibrating internal stresses in the steel profiles as a consequence of the industrial production processes. These stresses occur in bodies that undergo non-uniform plastic deformations. If no external forces oppose them, the residual stresses will always be elastic. The

non-homogeneous condition of deformation, which creates the residual stresses in the steel sections, is due to thermal (rolling, welding and torch cutting) and mechanical industrial processes (cold rolling, straightening).

In hot-rolled profiles, the formation of residual stresses requires that the ends of the flanges and the central region of the web are long while the junctions between the web and flange remain tensioned due to slow cooling. For welded profiles with rolled edge plates, the weld between the flanges and the web introduces residual compressive stresses at the ends of the flanges, which increases the region of the residual compressive stresses and adversely affects the strength of metallic structures. In the welded profiles with torch-cut plates, the cut introduces tensile stresses on the edges of the plates due to the heat, which acts favorably on the compressive strength (Bjorhovde et al. [8] and European Convention for Constructional Steelwork (ECCS) [9] ). However, the modified effect of the residual stress on cellular members has still not been investigated and was not considered in the various studies that have investigated the rules for existing projects for lateral torsional buckling strength (Alpsten and Tall [6] ).

Conversely, the presence of geometrical imperfections, such as the initial curvature, in beams transforms the buckling problem into a load-displacement problem, which opposes the problem of bifurcation of the equilibrium. According to Galambos [10] , the real configuration of the initial curvature may be highly variable, which can potentially exhibit simple curvature, double curvature, reverse curvature or even curvatures in both primary directions of the cross-section of the profile (European Convention for Constructional Steelwork (ECCS) [9] ).

1.3. Objective

This paper has as objective to evaluate the ultimate limit state behavior of cellular beam when submitted to different boundary conditions also physical and geometrical imperfections. For this it was used the software ABAQUS 6.12 [11] . Finally, it compares the results of numerical analyses with calculation methods by ABNT NBR 8800:2008 standard [12] and Abreu et al. [1] .

2. Calculation Methods

The ABNT NBR 8800:2008 standard [12] contains a procedure to calculate the nominal bending moment strength to lateral torsional buckling for I-beams with a full web that meets the following conditions: loads applied at the half height of the cross-section, boundary conditions that simulate the fork-like support (free warping and impeded torsional rotation) and constant cross-section through the unrestrained length. The nominal bending moment strength for the ultimate limit state of lateral torsional buckling for I-beams with two axes of symmetry that are bent relative to the axis of the greatest moment of inertia (x-axis) in the elastic regime is described by Equation 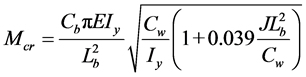(1):

(1)

where

E = Young’s modulus of elasticity.

C_b = Equivalent moment factor for beams which accounts for the effects of moment gradient and end conditions of the beam.

C_W = Warping section constant.

I_Y = Minor axis section moment of area.

J = Torsional constant.

L_b = Unbraced length of the beam.

M_Cr = Critical bending moment.

For a better understanding, the other calculation expressions can be found in ABNT NBR 8800:2008 [12] .

Abreu et al. [1] proposed a procedure to determine the nominal bending moment strength for steel cellular beams to determine the ultimate limit state of lateral torsional buckling for cases in which the beams have a fork-like support (free warping and impeded torsion) at the ends of the unrestrained length and are subjected to cases of uniform moment.

Increasing L_r by 20% yields L_r,cor according to Equation (2). The proposed procedure can be summarized as follows:

・ if L_b > L_r,cor, with:

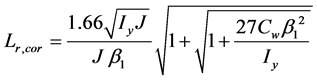(2)

where

L_r,cor = Umbraced length related to the start of the corrected yielding,

with Equation (3):

(3)

where

f_Y = Yield stress,

W_X = Modulus elastic resistant,

β₁ = Ratio of correction for critical slenderness,

yields Equation 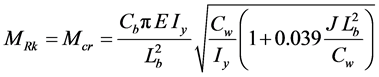(4):

(4)

・ if L_p < L_b < L_r,cor, with Equation 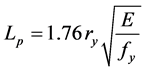(5):

(5)

where

L_p = Unbraced length related to cross-sectional plastification,

r_y = Minor axis section radius of gyration,

yields Equation (6):

(6)

where

M_pl = Full plastic moment;

and Equation (7):

(7)

where

M_r,cor = Bending moment corresponding to start of the yielding.

・ if L_b ≤ L_p, yields Equation (8):

(8)

where

M_Rk = Resistant critical bending moment.

3. Numerical Analyses

3.1. Material

As well as Abreu et al. [1] , in this work it was adopted the stress-strain diagram as shown Figure 5, formed by an elastic zone, which until the yielding resistant (f_y) is reached, by an inelastic zone, consisting for three straight lines, considering a hardening zone, continuing until rupture resistant (f_u), as proposed by Earls [13] .

The steel structure considered was ASTM A572, which Young’s modulus is 200.000 MPa, yielding resistant is equal 345 MPa and rupture resistant is equal 450 MPa. The strains corresponding to the end of each zone were withdrawn according to Salmon and Johnson [14] , in order to ε_y, ε_st, ε_b and ε_u are equal 0, 0,01726, 0,05394 and 0,15719, respectively.

3.2. Boundary Conditions

As per Bezerra [5] , to simulate the fork-like support in cellular beams, the displacements in the y-direction were restricted along the entire web, the displacement in the z-direction was restricted only in the node situated at the half height of the web at one end of the beam, and the displacement in the x-direction was restricted in all of the nodes at the ends of the beam. Rotation around the z-axis was also impeded in all of the nodes at both ends, and thus, torsion is not allowed, leaving the beam free to warp. According thus, a fork support is defined, as shown Figure 6.

3.3. Loads

The beams were submitted to two different loads cases: uniform bending and concentrated load. To validate the numerical model was applied uniform bending and in the simulation nonlinear physical and geometric analysis was applied a concentrated loading, as shown in Figure 7.

3.4. Analyses

First, analyses of elastic buckling were performed using the Buckle calculation model available in ABAQUS 6.12 [11] , which is a procedure of linear perturbation of eigenvalues and eigenvectors, where the first eigenvalue represents the loading factor of elastic buckling and its respective eigenvector represents the deformation. In the post-buckling analysis, to apply physical and geometrical imperfections, the Static Riks calculation method was used, which is generally used to predict the collapse of a structure and is often used in non-linear physical and geometrical analyses. The eigenvalue from the Buckle analysis provides complete information regarding the collapse of the structure and is used to increase the convergence velocity of the method for cases of instability.

Specifically in relation to residual stresses, the physical imperfections were applied only to the flanges of the profiles, as shown in Figure 8, which considered the yield stress of the steel (f_y) to be 345 MPa. To applied residual stress, was used the command **INITIAL CONDITIONS, TYPE = STRESS, in the input file. For applying the geometrical imperfections, the curvature was varied from L/1000, L/2000, L/2500, L/5000, L/10000, L/15000 and L/20000 for each analysis according to the slenderness of the beam, using the command **IMPERFECTION in the input file.

4. Results

4.1. Validation of Numerical Model

To validate the numerical model, the W320 × 32.7 profile was used, as shown in

Figure 9. With this profile, simulation analyses were performed for different spans and subjected to a constant moment, and the obtained results were compared with the calculation procedure of ABNT NBR 8800:2008 [12] to validate the numerical model.

The results are shown in Figure 10.

An analysis of the relative errors was performed, i.e., an analysis of the differences between the results obtained in the numerical simulation and the ABNT NBR 8800:2008 standard [12] . As observed in the analyses, the results were good because the maximum difference between the numerical analyses and the analytical procedure of ABNT NBR 8800:2008 [12] was 12% in the plastic phase. Thus, the numerical model was validated.

4.2. Non-Linear Geometrical and Physical Analyses

Similar to Abreu et al. [1] , in this study, the model of cellular beams was generated by adopting the W310 × 32.7 rolled profile as the original profile made in Brazil by GERDAU AÇOMINAS. The total height of the cellular beams was set equal to approximately 1.5 times the height of the original profile, the spacing between the centers of the openings was equal to 1.5 times the diameter of the openings, and the diameter of the openings was equal to 0.7 times the total height of the corresponding cellular beams, as shown Figure 11.

Firstly, through a linear perturbation analysis (Buckle), the elastic buckling load is obtained by multiplying the first positive eigenvalue by the applied load value. In all the jobs were applied 1000 N. So as result the first eigenvalue multiplied by 1000, as shown Figure 12.

The second step was non-linear geometrical and physical analyses, which initialize with application of elastic buckling load in Static Riks method. In this step, the buckling load is estimated by multiplying the load applied by the load proportional factor (LPF), as shown Figure 13.

With the values obtained in the numerical analysis of the cellular beams from ABAQUS 6.12 [11] , as shown in Table 1, curves of the nominal bending moment strength were traced for the elastic state of lateral torsional buckling, M_Rk, as a function of the unrestrained length L_b.

These curves were compared with those obtained using the prescriptions of the ABNT NBR 8800:2008 [12] and the procedure proposed by Abreu et al. [1] . In Figure 14, the results from the analyses with a concentrated applied load at the half height of the beam are shown.

In fact, as can be observed in Figure 14, the effects of the physical and geometrical imperfections exert a large influence on the ultimate strength of the cellular beams when LTB is considered, as shown in Figure 15.

It can also be observed in Figure 14 that the smaller the initial curvature (geometric imperfection) is, the greater the resisting moment. For the analyses performed, the geometric imperfection that showed the smallest error was L/ 20000 relative to the calculation proposed by Abreu et al. [1] , as shown in Figure 16.

In addition to the comparisons with the calculation models, analyses of the lateral displacement in the upper flange at a point in the middle of the cellular beam were also performed. Load × displacement curves were traced, as shown in Figure 17.

It was observed that the smaller the applied geometric imperfection was, the greater the critical buckling load for a smaller lateral displacement.

5. Conclusions

According to the analyses performed with the variation of geometrical imperfections, a large variation was observed in the resisting bending moment for spans

between 2 and 4 meters. Furthermore, the comparison of the results with the calculation from ABNT NBR 8800:2008 [12] also showed a large difference, approximately 30% to 40%. This variation demonstrates that the calculation for the resisting moment from ABNT NBR 8800:2008 [12] is extremely important for full web rolled profiles (original web rolled profiles), which makes the procedure more conservative.

However, the procedure proposed by Abreu et al. [1] showed only a slight variation for values compared with the analyses on the elastic buckling interval. In the inelastic phase, the procedure proposed by Abreu et al. [1] showed large differences compared with the numerical analysis, which thus indicates that the procedure is unsatisfactory for short spans. It was also observed that the smaller the initial curvature, the more the resisting moment approaches the proposed procedure.

Thus the procedure proposed by Abreu et al. [1] is easy to formulate and suitable for calculations of resisting moments for cellular beams with spans in the elastic phase using the properties of the cross-section in the center of the openings, increasing the value of the unrestrained length by 20%, which corresponds to the beginning of yielding, and assuming the maximum resisting moment to be 90% of the moment of yielding.

Cite this paper

Martins, C.H., Fer- reira, F.P.V., Rossi, A. and Trentini, E.V.W. (2017) Numerical Analysis of Physical and Geometrical Imperfections in Cellular Beams. Open Journal of Civil Engineering, 7, 116- 129. https://doi.org/10.4236/ojce.2017.71007

References