Open Journal of Civil Engineering
Vol.2 No.3(2012), Article ID:22992,13 pages DOI:10.4236/ojce.2012.23020
Dynamic and Static Behaviors of Shear Wall with Openings Composed of LVL and Fiber Cement Board Sheathing
Laboratory of Structural Function, Research Institute for Sustainable Humanosphere (RISH), Kyoto University, Kyoto, Japan
Email: maryokohadi@gmail.com
Received May 26, 2012; revised June 25, 2012; accepted July 10, 2012
Keywords: Earthquake-Resistant; Shear Wall with Opening; LVL; FCB
ABSTRACT
The shear wall with and without openings that served as a structural element or/and partition wall was utilized in a low-cost housing for the low-income people in Indonesia. The houses, however, should be with stood from earthquake inertial force, so there must be no casualties when disaster struck. The alternative types of composite structure made of wood and cement based building materials needed to meet with the high ddemand for earthquake-resistant houses in Indonesia. In order to understand the mechanism of earthquake resisting performance of shear wall, we needs to investigate behavior of shear walls not only for cyclic static but also for dynamic loading. In this study, the series of full-scale experiment on timber frame shear walls with and without openings, compose of Laminated Veneer Lumber (LVL) engineered wood (Paraserianthes falcataria and Hevea brasiliensis) and sheathed by Fiber Cement Board (FCB), was carried out. By analyzing testing result using theoretical approaches, we intended to predict static initial stiffness and yielding strength as well as basic dynamic properties shear walls. For static behavior, good agreements were obtain from comparison between experiment and theoretical prediction based on mechanical model. While, for dynamic behavior, agreement was not sufficient due to the effect of bending and rocking of actual test specimens. The information obtain by this study will be useful for practical engineers or structural designers to design the high performance earthquake resisting timber houses with a low construction cost.
1. Introduction
In Indonesia, housing privation for low-income peoples increases year by year, so that house design by taking requirements of its withstand to the earthquake, healthy, simple and instantaneous in the construction process with a low cost of construction is required. For these ends, the authors have been carried out experimental and analyticcal researches on shear walls composed of LVL and fiber cement board (denotes as FCB hereafter) sheathing with no openings for applying them to structural components of low-cost earthquake-resisting houses. While in actual design situations, it is necessary to design various types of shear walls having windows or/and door-type openings. Therefore, in this study, we extended our focus on such shear walls having openings.
Studies on wooden house that was structurally designed by utilizing shear walls with and without openings made of wooden frame and various sheathing materials has been done in past by many researchers [1-8]. In this study, not only static properties but also basic dynamic properties such as natural frequency and damping coefficient are estimated for understanding the effect of openings on the fundamental mechanical properties of nailedon sheathed shear walls to be installed in wooden residential houses.
2. Experimental Study
To predict thetangible behavior of shear walls with openings made of LVL and FCB by applying rigorous theoretical design equations, some material testswere done.
2.1. Materials
2.1.1. Framing Materials
LVL made of falcataria and rubber wood (Paraserianthes falcataria and Hevea braziliensis) of 45 × 90 × 3000 mm was used for framing material as shown in Figure 1, whose mechanical and physical properties are shown in Table 1. The LVL beam of 45 × 90 mm cross-sections was attached on top of shear wall for loading girder.
2.1.2. Sheathing Materials [10]
The Sheathing material is Fiber Cement Board (FCB), in which Silica (35% by weight), calcium (35% by weight), pulp and wooden fiber (15% by weight) and others (15% by weight) produced by a Japanese commercial company in a size of 1800 × 900 × 12 mm as shown in Figure 2. The material properties of FCB are given in Table 2.
2.1.3. Fasteners
The steel nails were used as fastener of all shear wall component connection and there were two kinds of nails

Table 1. Mechanical and physical property of LVL [9].

Figure 1. LVL wood used as shear wall frames member.

Figure 2. FCB used as frame specimen sheathed.
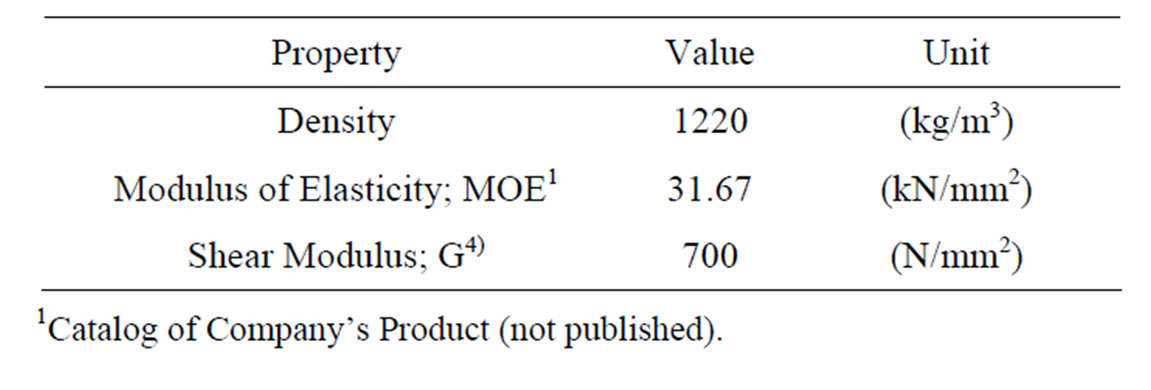
Table 2. Mechanical and physical property of FCB.
were used and their specification is shown in Table 3.
The N100 nails were use for fastening frame members and double heads nails that are equivalent to the normal N75-nail shown in Figure 3 were used as fastener for connecting FCB sheathing to the frame member due to convenience of dismantle of tested specimens.
2.2. Specimens
2.2.1. Single-Nail Shear Test between Sheathing and Frame Member
The single-nail shear test between LVL and FCB sheathing material was carried out, to obtain load-slip relationship, which dominates non-linear behavior of shear wall. The size of LVLwas 45 × 90 × 300 mmand 12 mm thick of FCB was connected byusing double heads N75 nails as shown in Figures 4. Test speed was 1 mm per minute on Universal Testing Machine (UTM).
2.2.2. Shear Wall Specimens
Three different types of shear wall specimens were prepared. These were composed of LVL of 45 × 90 cross section as framing members assembled with each other by N100 nails and FCB as sheathing members of 910 × 2730 mm size nailed on the framing members by double heads N70 nails. The nailing pitch in all types of shear walls was 150 mm. The shear wall specimens without openings were named as SWS (Figure 5).
Shear walls with window opening was named as SWWOS, where the size of openings was 910 × 878 mm (Figure 6). And shear wall with door-type opening was named as SWDOS; the size of openings was910 × 1777 mm (Figure 7).
All specimens composed of three sizes of panel, the individual panel-A, panel-B and panel-C has different nailing pattern as shown in Figure 8. Based on those three panels, the mechanical models were constituted for predicting static and dynamic performance of three different shear walls.

Table 3. Nail specification.

Figure 3. The steel nail used as fastener between sheathing and frame member.


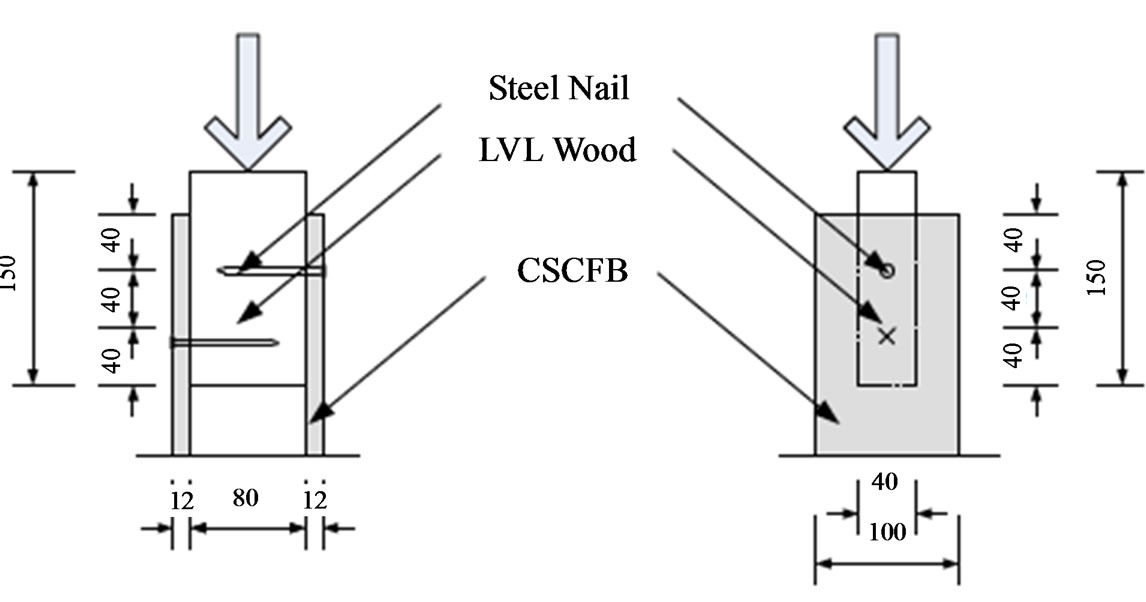
Figure 4. Single-nail shear test specimen of LVL and FCB fastened by double heads N75 nails in parallel (left-hand side) and perpendicular to the grain (right-hand side) under test machine.
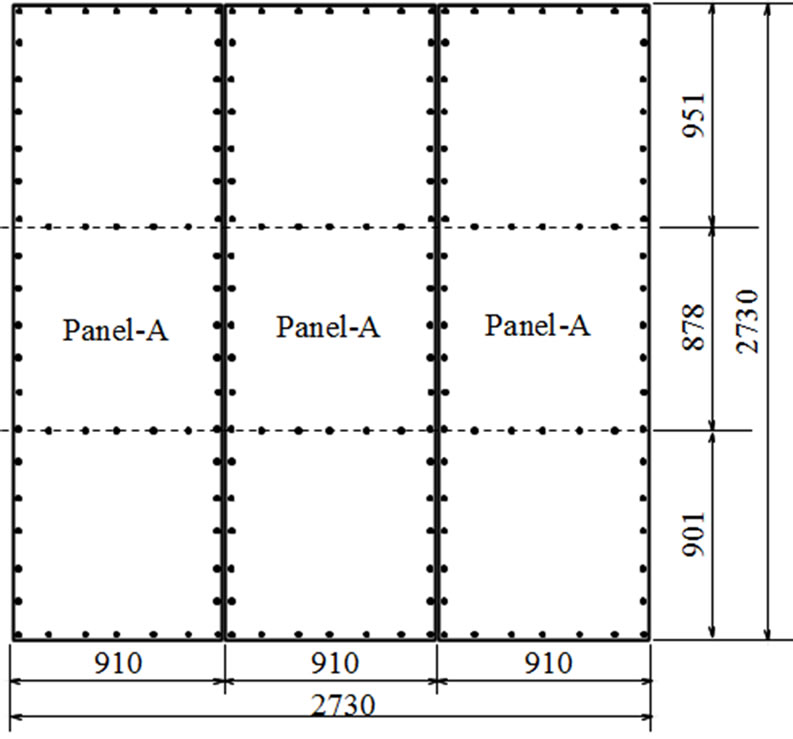
Figure 5. Wall type test specimen (SWS).

Figure 6. Window-typetest specimen (SWWOS).
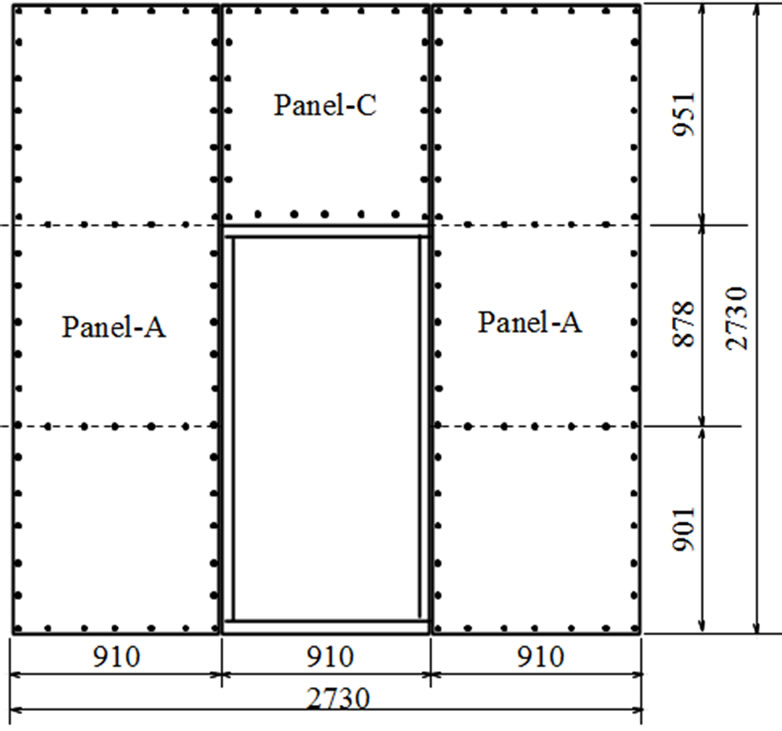
Figure 7. Door-typetest specimen (SWDOS).
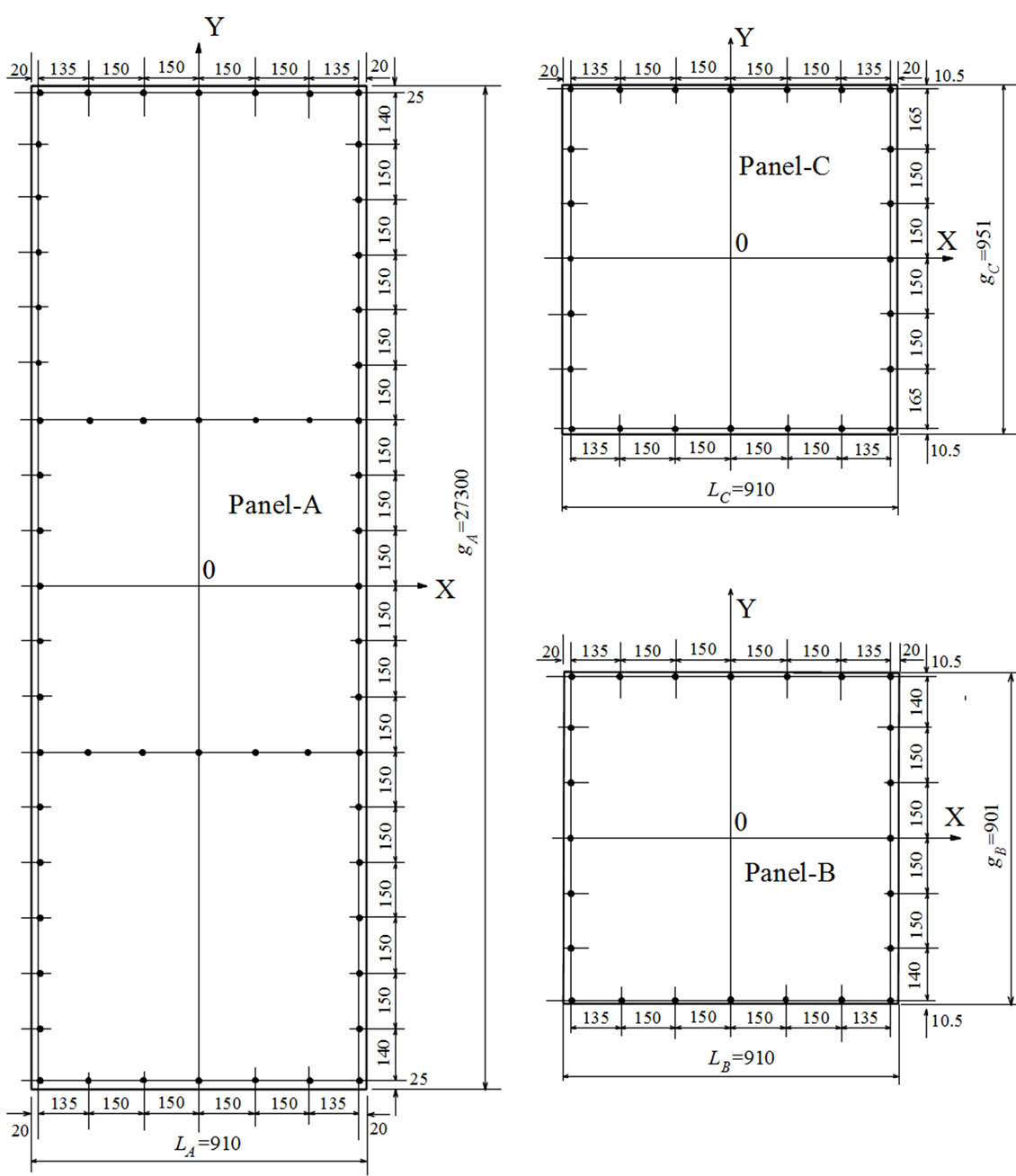
Figure 8. Nailing pattern in panel-A, panel-B and panel-C.
2.3. Testing Methods
Experimental studies in laboratory commenced with the test of connection between the LVL with FCB fastened by steel nails, then dynamic test was done by using a portable shake excitation machine (Figure 9) which can generate harmonic horizontal vibration. After dynamic tests, static push-pull cyclic loading tests were carried out on the same specimens.
2.3.1. Dynamic Test Method Using Portable Shake Excitation Machine
Dynamic test was done to obtain the values of natural frequency and dumping factors on each test specimen. The test were performed by fixing the specimen on a steel reaction portal frame apparatus by using 4 anchor bolts on sill members and hold-down connectors on both side-studs so that it was assumed that the specimens were fixed rigidly on the steel base. The vibration generator mounted on the top of the specimen, while the specimen is free to move in the direction of horizontal vibration.
Portable Shake Excitation Machine A portable shake excitation machine (DTH-500-30, Asahi-factory Corp.) shown in Figure 10 was used for measuring such dynamic properties of test specimens as the natural frequency and damping factor. Nominal excitation force of the machine was 490 N, nominal maximum acceleration without dead load was 7.3 m/s2 and the weight of movable part of the machine was 27 kg (machine) + 40 kg (additional weight) = 67 kg.
2.3.2. Static Push-Pull Cyclic Testing Methods
Figure 9, 11, 12 shows testing set-up and location of measuring devices. Loading protocol used in this study

Figure 9. Test set-up for shear wall with out opening ([k1] SW).

Figure 10. The portable shake excitation machine.
was tentatively determined in accordance with usual shear wall testing method in Laboratory of Structural Function, Kyoto University. Therefore, only one cyclic loading in each target deformation angle loop was used, as shown in below.
First loop: 0 ® +1/300 rad ® –1/300 rad ® 0 Second loop:0 ® +1/200 rad ® –1/200 rad ® 0 Third loop: 0 ® +1/150 rad ® –1/150 rad ® 0 Fourth loop: 0 ® +1/100 rad ® –1/100 rad ® 0 Fifth loop: 0 ® +1/75 rad ® –1/75 rad ® 0 Sixth loop: 0 ® +1/60 rad ® –1/60 rad ® 0 Seventh loop: 0 ® +1/30 rad ® –1/30 rad ® 0 Eighth loop: 0 ® +1/15 rad ® –1/15 rad ® 0 Final loading: 0 ® +Pmax ® –Pmax ® 0 The horizontal push-pull static cyclic load was applied using an oil jack of 500 kN capacity and 500 mm strokes for simulating earthquake load.
3. Theories and Analytical Study
Mechanical models of each shear wall were established

Figure 11. Test set-up for shear wall with windows opening ([k1] SWWO).

Figure 12. Test set-up for shear wall with door opening ([k1] SWDO).
by taking the openings into considerations for predicting fundamental performance of each shear walls. In order to let calculation process be simple, individual panels are assumed to share the same shear deformation angle with each other at least up to commence of yielding level.
3.1. Wall-Type: (SWS) Mechanical Model
In the type of shear walls without openings, the force distribution mechanism and its response are assumed that three same panels share with same shear deformations as shown in Figure 13. From equilibrium condition of external moment and internal ones,
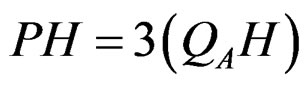 (1)
(1)
From compatibility condition that all panels should share the same deformation angle,
 (2)
(2)
Shear stiffness of panel-A is expressed in equations (3) and (4) in accordance with the suggestion made by Murakami and Inayama [4].
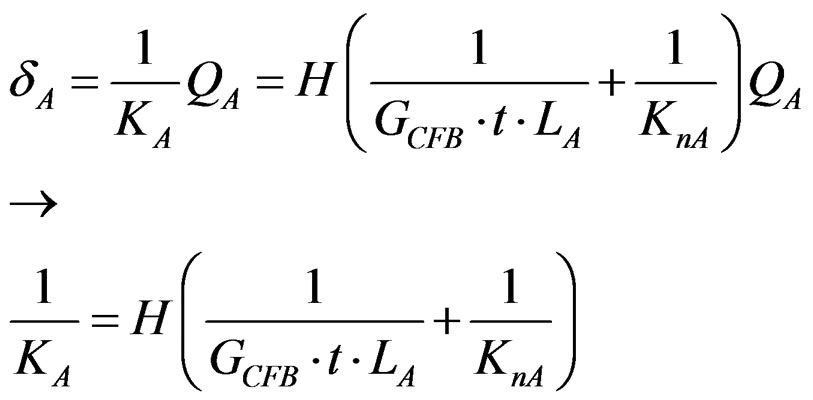 (3)
(3)
 (4)
(4)
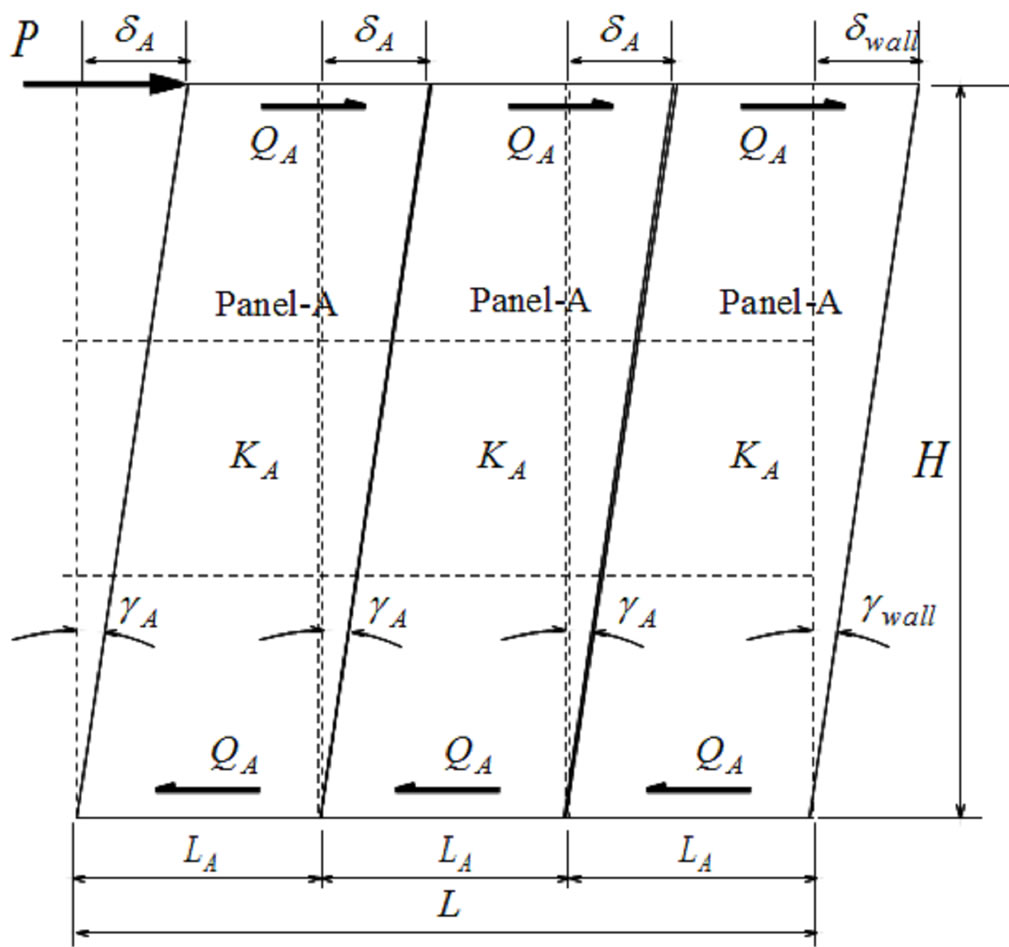
Figure 13. Mechanical models of Wall-Type (SWS) composed of three panel-A.

where,
 : Shear rigidity of CFB (N/mm2),
: Shear rigidity of CFB (N/mm2),
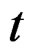 : Thickness of CFB (mm),
: Thickness of CFB (mm),
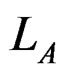 : Length of Panel-A (mm),
: Length of Panel-A (mm),
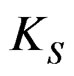 : Slip modulus of nailed-on CFB with LVL frame (N/mm),
: Slip modulus of nailed-on CFB with LVL frame (N/mm),
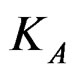 : Total shear stiffness of panel-A (N/mm),
: Total shear stiffness of panel-A (N/mm),
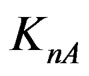 : Partial shear stiffness of panel-A due to nail slip (N/mm),
: Partial shear stiffness of panel-A due to nail slip (N/mm),
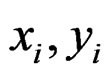 : x,y coordinate of i-th nail in Panel-A (See Figure 8),
: x,y coordinate of i-th nail in Panel-A (See Figure 8),
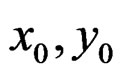 : Rotational center of Panel-A (See Figure 8)Finally, relationship between external shear force
: Rotational center of Panel-A (See Figure 8)Finally, relationship between external shear force 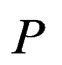 and wall rotational angle
and wall rotational angle 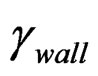 is obtained as,
is obtained as,
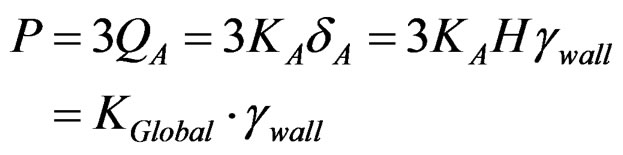 (5)
(5)
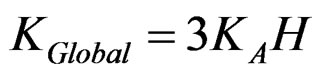 . (6)
. (6)
Force acting on i-th nail in x-direction is expressed in Equation (7) by assuming each slip modulus has the same value of Ks;
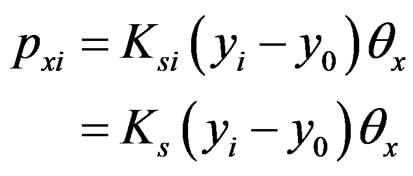 (7)
(7)
x-directional rotational angle is expressed in equation (8);
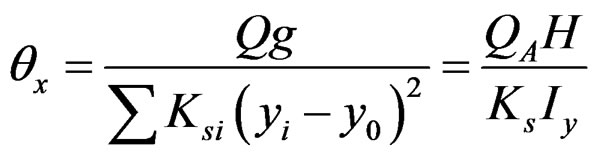 (8)
(8)
Combining Equations (7) and (8), we get;
 (9)
(9)
In the same way, y-directional force pyi on i-th nail and rotational angle qy is expressed as Equations (10) and (11);
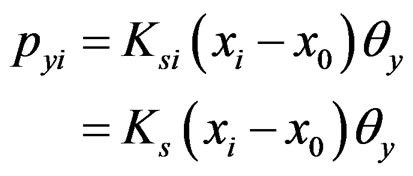 (10)
(10)
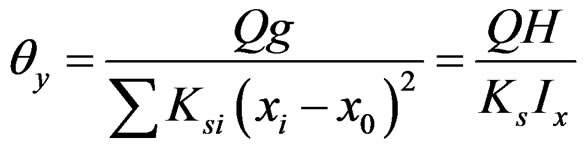 (11)
(11)
Combining Equations (10) and (11), we get;
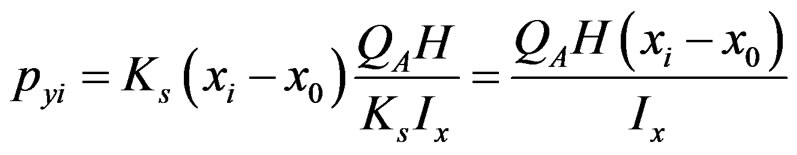 (12)
(12)
The resultant force at each corner of the Panel-A, which might give the yielding of nailed-on-sheathing panel, is calculated as Equation (13);
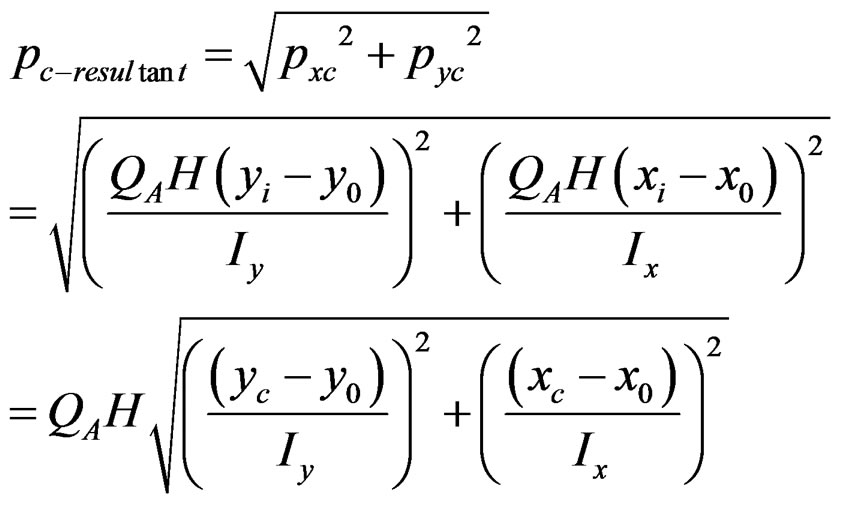 (13)
(13)
On the other hand, the relationship between shear force on Panel-A and external force is;
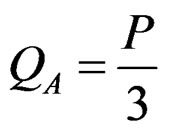 (14)
(14)
Therefore, the yielding load of wall-type specimen will be predicted by Equation (15).
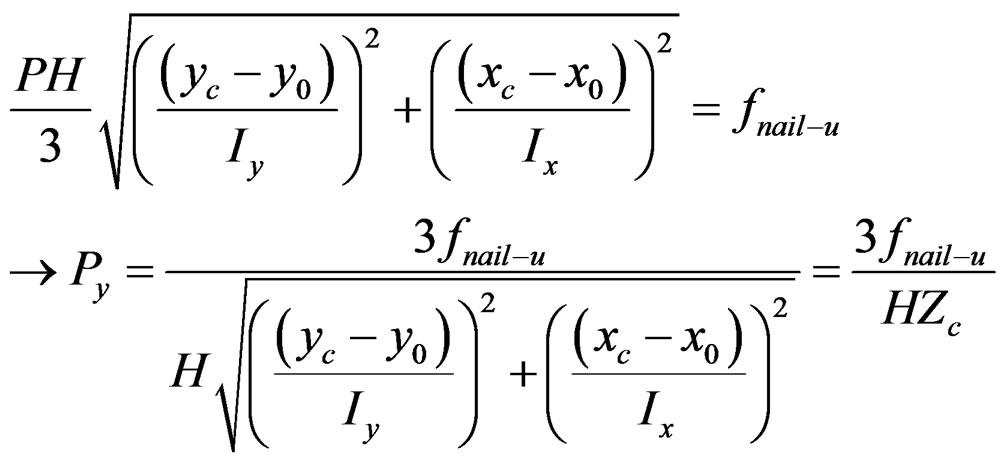 (15)
(15)
where,
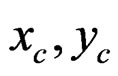 : x,y coordinate of corner nail in Panel-A (mm)
: x,y coordinate of corner nail in Panel-A (mm)
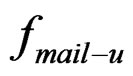 : Ultimate strength of nailed CFB on LVL frame and this value should be determined by nailed single shear joint test (N).
: Ultimate strength of nailed CFB on LVL frame and this value should be determined by nailed single shear joint test (N).
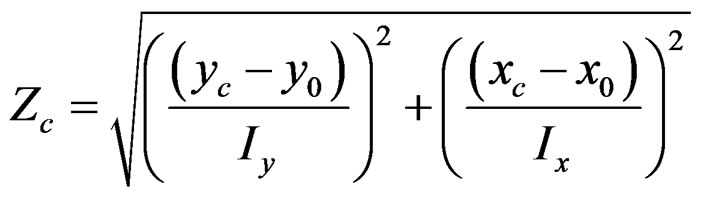
3.2. Window-Type SWWOS Mechanical Model
The mechanical model of shear walls with window openings composed of panel-A, B and C is shown in Figure 14.
Moment equilibrium gives,
 (16)
(16)
Compatibility conditions give,
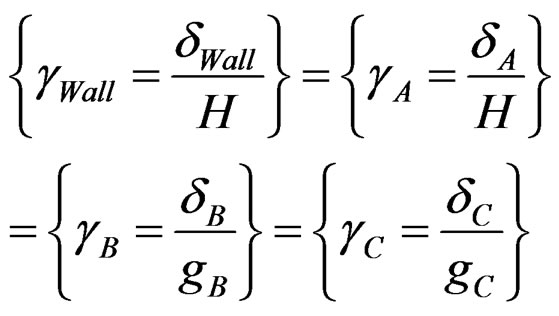 (17)
(17)
Shear stiffnesses of each panel are,
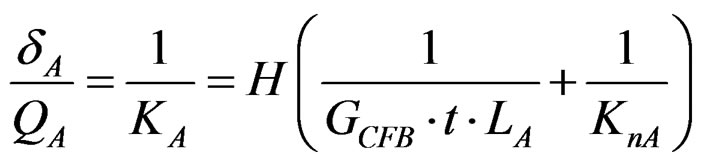 (18)
(18)

Figure 14. Mechanical models of Window-Type (SWWOS) composed of panel-A, panel-B and panel-C.
 (19)
(19)
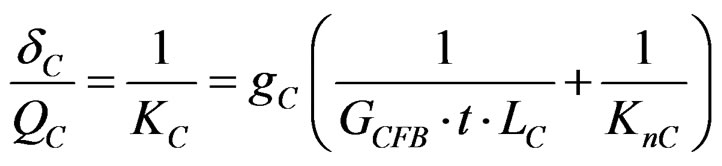 .(20)
.(20)
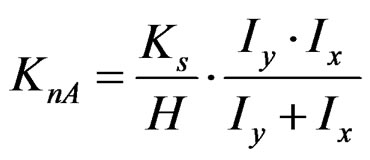 (21)
(21)
 (22)
(22)
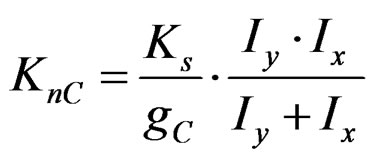 (23)
(23)
From Equations (16) to (20), total shear external force P can be expressed as a function of each panel’s stiffness and dimensions as,
 (24)
(24)
At the same time, individual shear force on each panel can be expressed using global stiffness of total shear wall as follows;
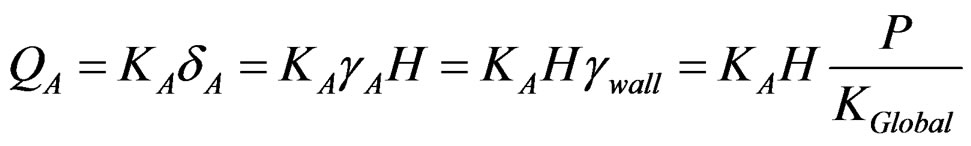 (25)
(25)
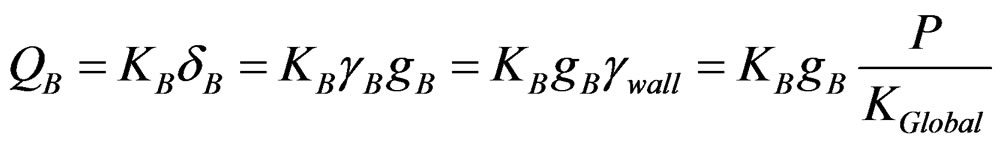 (26)
(26)
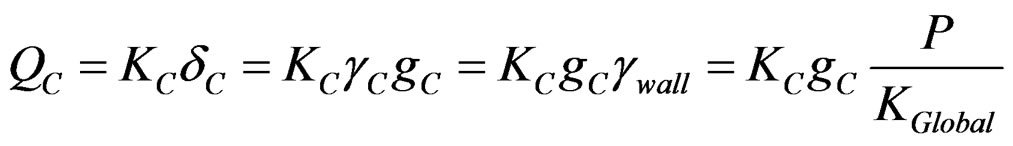 (27)
(27)
Rewriting Equation (13),
 (13)
(13)
Equations for predicting yielding of each panel, which might be caused by the corner nail’s ultimate situation, are obtained asFor Panel-A:
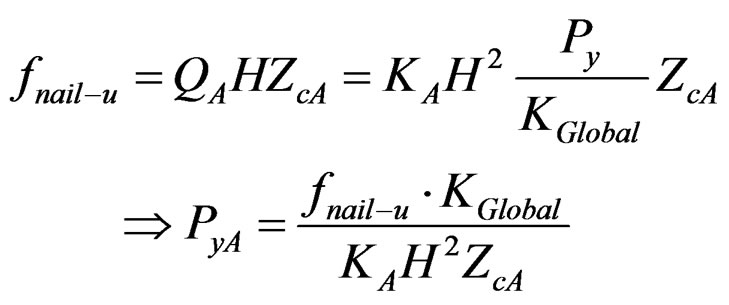 (28)
(28)
For Panel-B:
 (29)
(29)
For Panel-C:
 (30[k1])
(30[k1])
Thus, yielding of window-type shear wall will be predicted as the minimum value of equations (28) to (30).
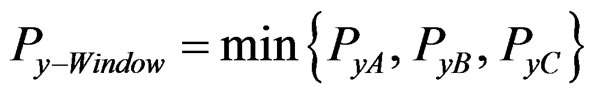 (31)
(31)
3.3. Door-Type SWDOS
For the type of shear walls with door openings, which is composed of two panels A, and one panel C, is shown in Figure 15.
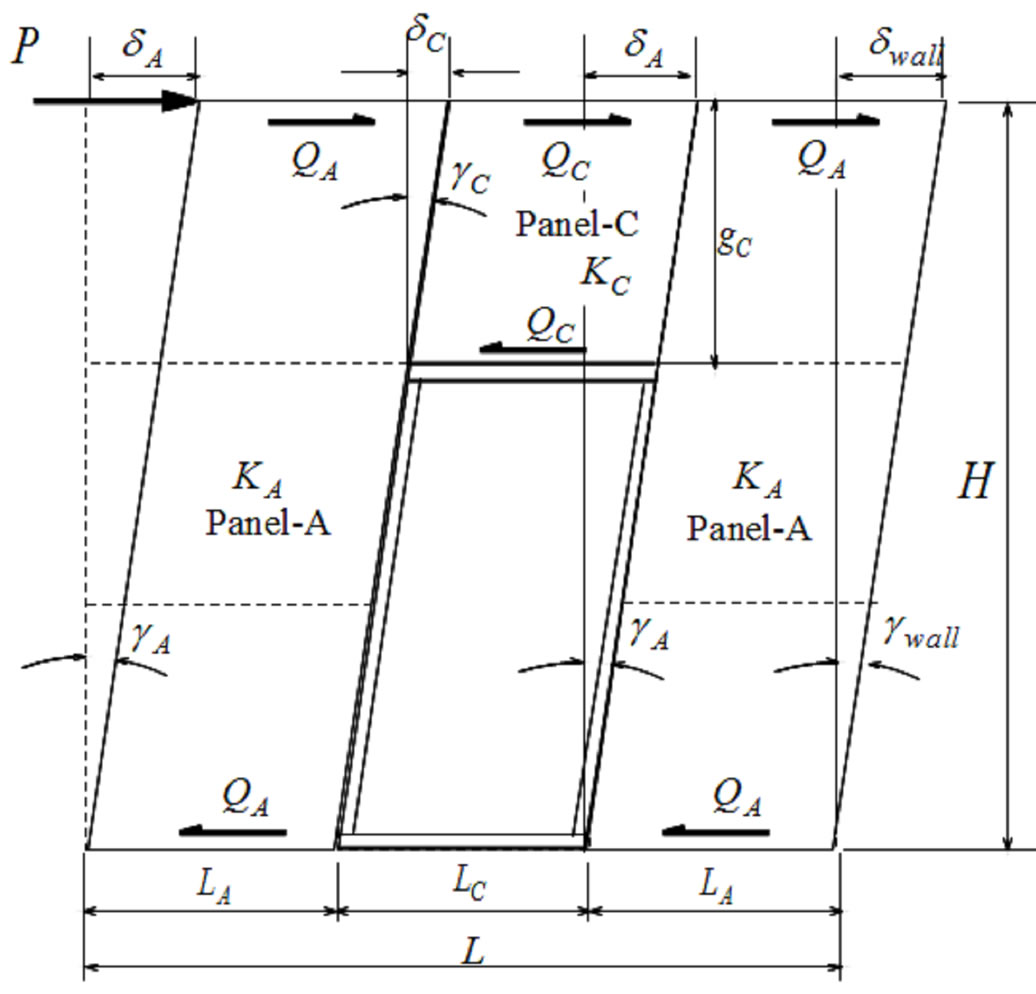
Figure 15. Mechanical models of Door-Type (SWDOS) composed of panel-A and panel-C.
Moment equilibrium gives,
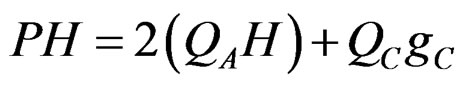 (32)
(32)
Compatibility conditions give,
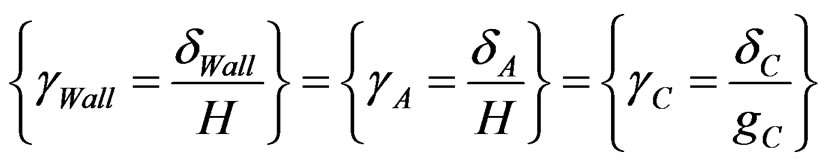 (33)
(33)
Shear stiffnesses of each panel are,
 (34)
(34)
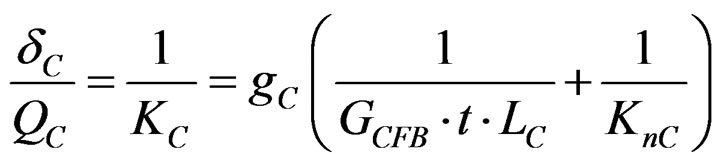 (35)
(35)
 (36)
(36)
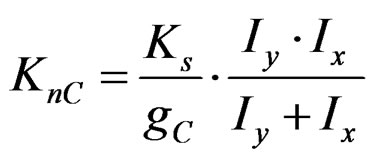 (37)
(37)From Equations (32) to (35), total shear external force P can be expressed as a function of each panel’s stiffness and dimensions as,
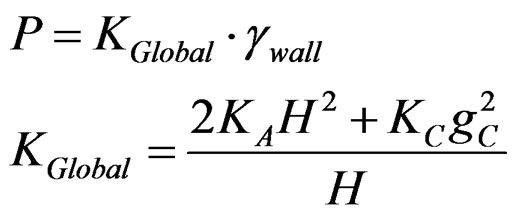 (38)
(38)
At the same time, individual shear force on each panel can be expressed using global stiffness of total shear wall as follows;
 (39)
(39)
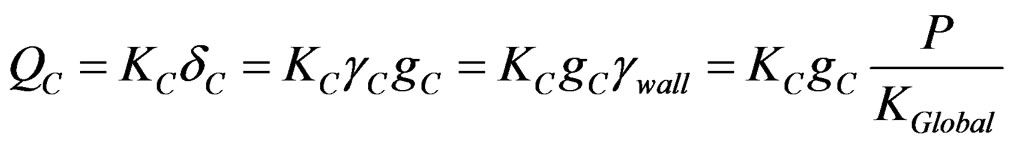 (40)
(40)
Equations for predicting yielding of each panel, which might be caused by the corner nail’s ultimate situation, are obtained asFor Panel-A:
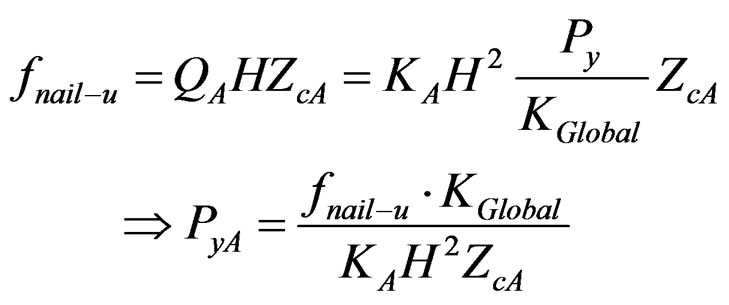 (41)
(41)
For Panel-C:
 (42)
(42)
Thus, yielding of door-type shear wall will be predicted as the minimum value of Equations (41) and (42).
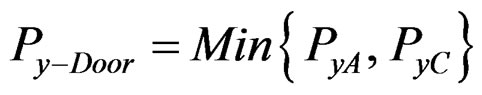 (43)
(43)
4. Results and Discussions
4.1. Nailed Joint Test
Slip modulus and ultimate strength of single shear nailed joint on LVL sheathed with CFB were evaluated in accordance with a standard method based on the equivalent energy approximation principle using perfect bilinear relationship [11] as shown in Figure 16 and 17.
For the stiffness calculation of test specimens, mean value of initial stiffness estimated from both test results on parallel and perpendicular cases was used as a slip modulus, while for the prediction of the yielding load of whole shear wall specimens, lower ultimate nail strength value obtained from perpendicular case was used. These wereKs = 1.04 kN/mm, fnail-u = 1.03 kN
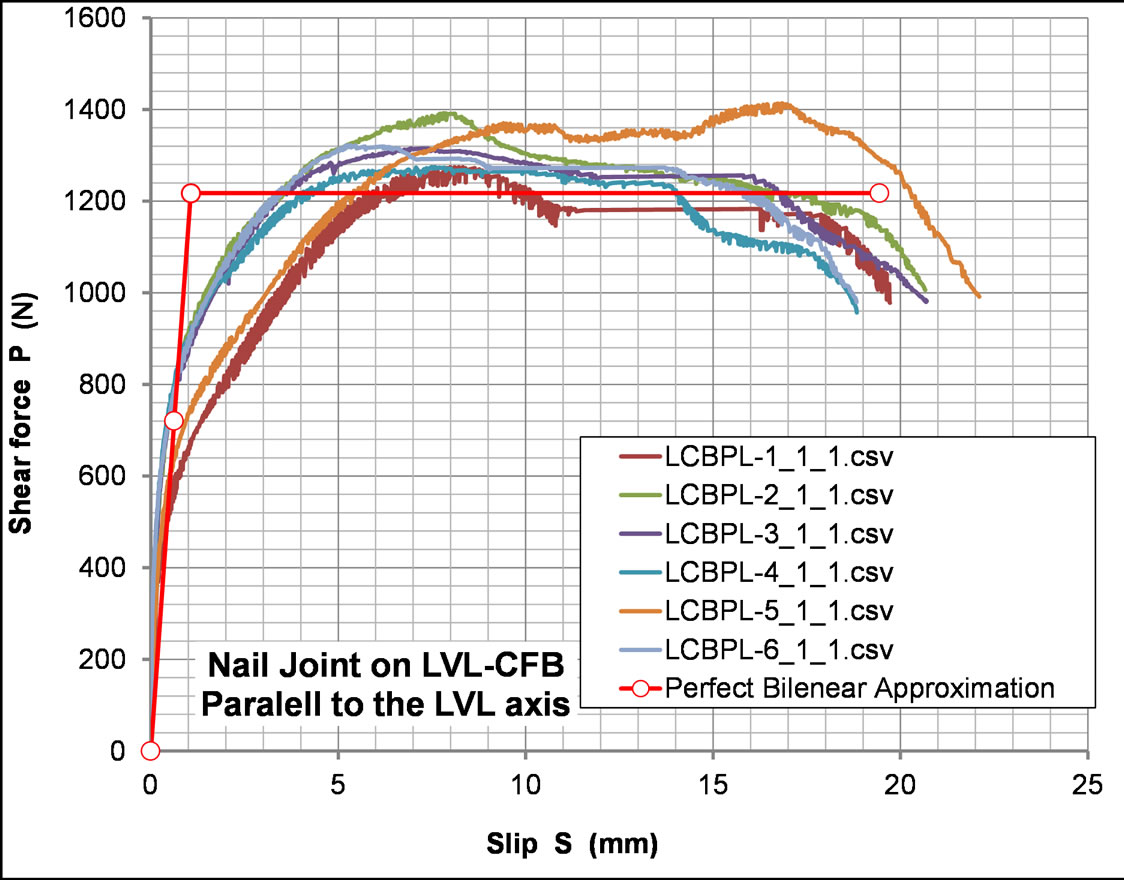
Figure 16. Nail joint on LVL-CFB parallel to the LVL axis.
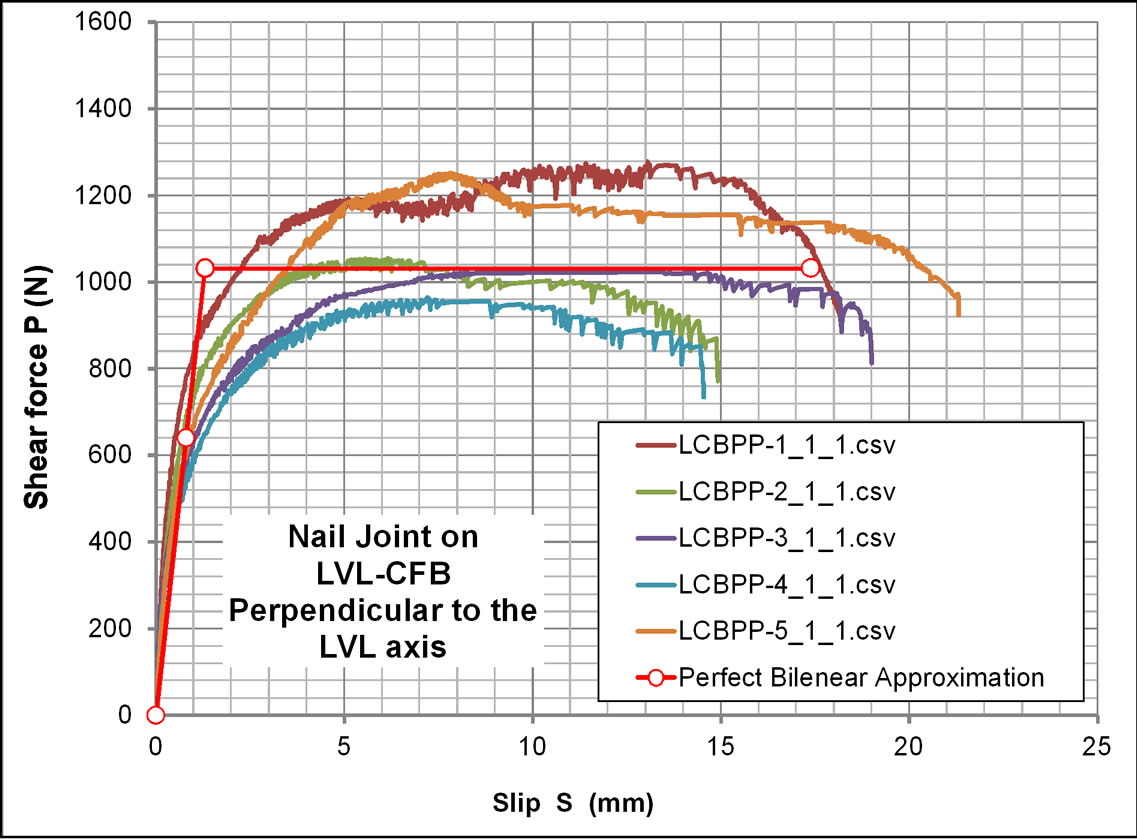
Figure 17. Nail joint on LVL-CFB perpendicular to the LVL axis.
4.2. Comparisons Between Static Test Result and Predicted Result
The typical damage that occurs in all three specimens showed similarities, namely first failure occurred at corner nail by tearing off of sheathing member from the LVL member. Shown in Figures 18, 19, 21, 22, 24, 25.
Figures 20, 23 and 26 shows comparisons between observed load (P)-pure shear deformation angle (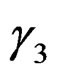 ) relationship and predicted results using, Equations (5) and (15) for wall-type (SWS) specimen, Equations (24) and (31) for window-type (SWWOS) specimen and Equation
) relationship and predicted results using, Equations (5) and (15) for wall-type (SWS) specimen, Equations (24) and (31) for window-type (SWWOS) specimen and Equation

Figure 18. Final condition of shear wall type (SWS).

Figure 19. Tear off of CFB member from LVL frame.
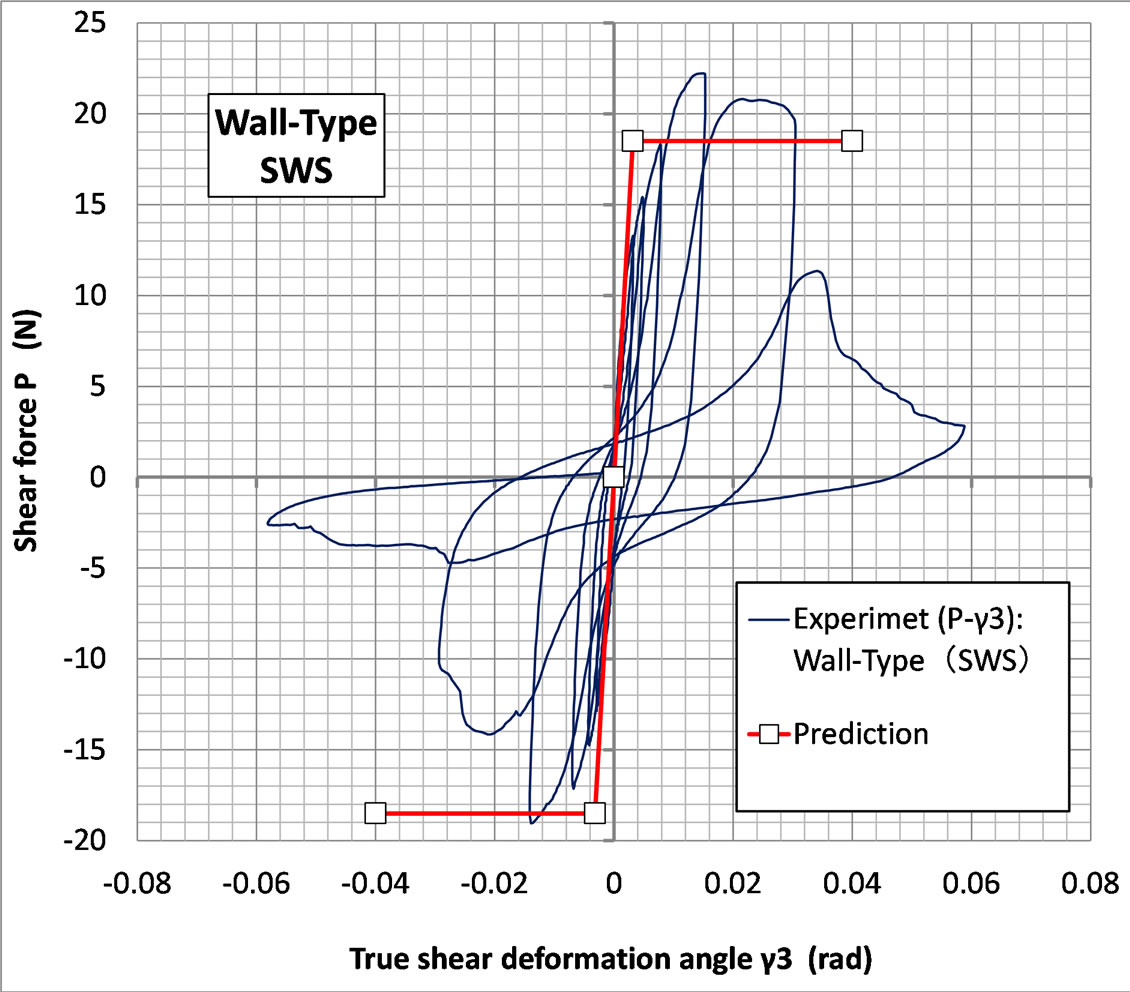
Figure 20. Comparison between calculation and observation on wall-type (SWS) specimen.

Figure 21. Final condition of shear wall with window type opening (SWWOS).

Figure 22. Falling down of Panel-B from LVL frame. opening (SWWOS).
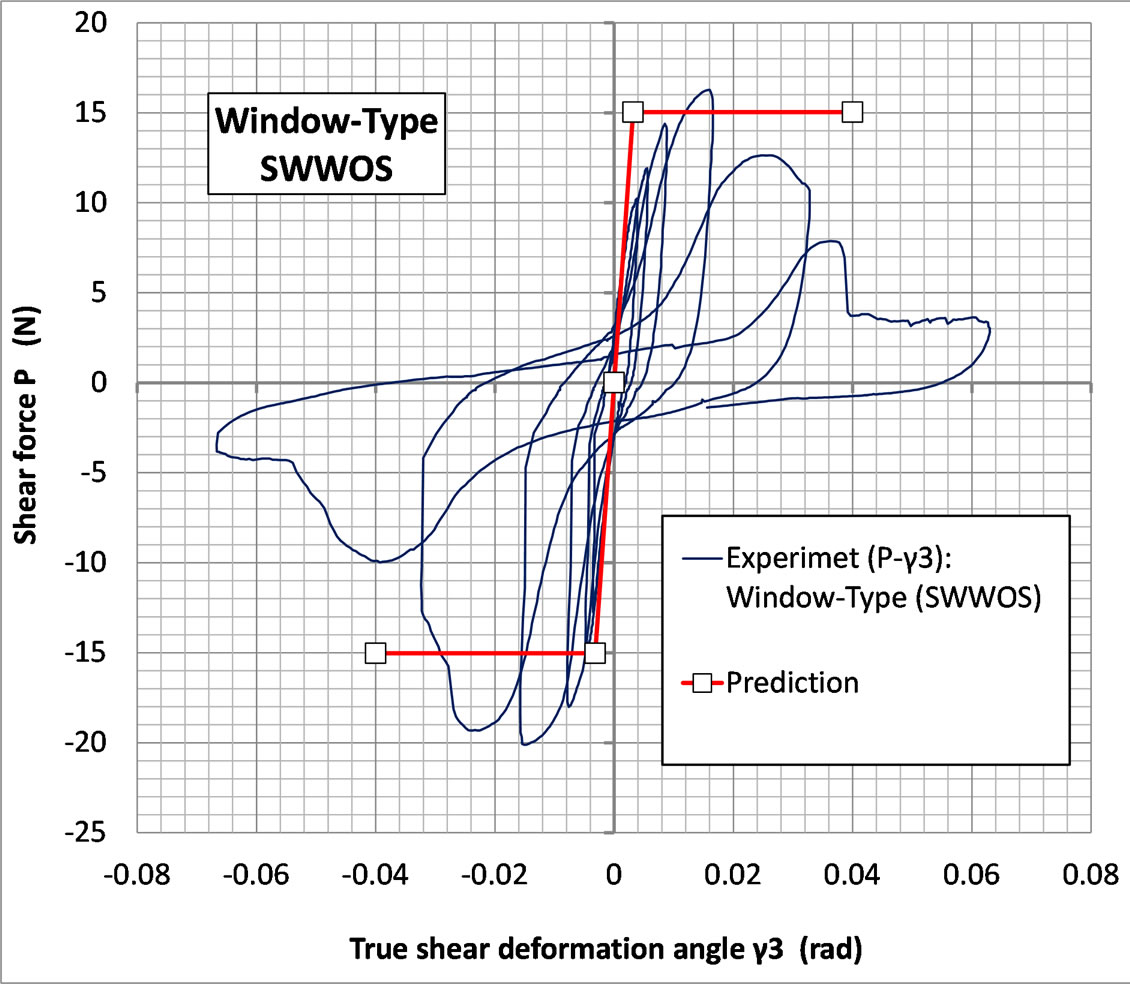
Figure 23. Comparison between calculation and observation on window-type (SWWOS) specimen.

Figure 24. Final condition of shear wall with window type opening (SWWOS).opening (SWWOS).

Figure 25. Apart of Panel-B from LVL frame opening (SWWOS). opening (SWWOS).
(38) and (43) for door-type (SWDOS) specimen, respectively.
4.3. Dynamic Test Result
Figure 27, 28 and 29 show the spectrum diagrams of test specimens for wall-type (SWD), window-type (SWWOD) and door-type (SWDOD), respectively. The natural frequency of wall-type specimens was 4.31 Hz and it was the highest among three specimen as expected. The natural frequency of window-type was 3.86 Hz and it was middle among three and that of door-type was 3.14 Hz and it was the lowest as expected.
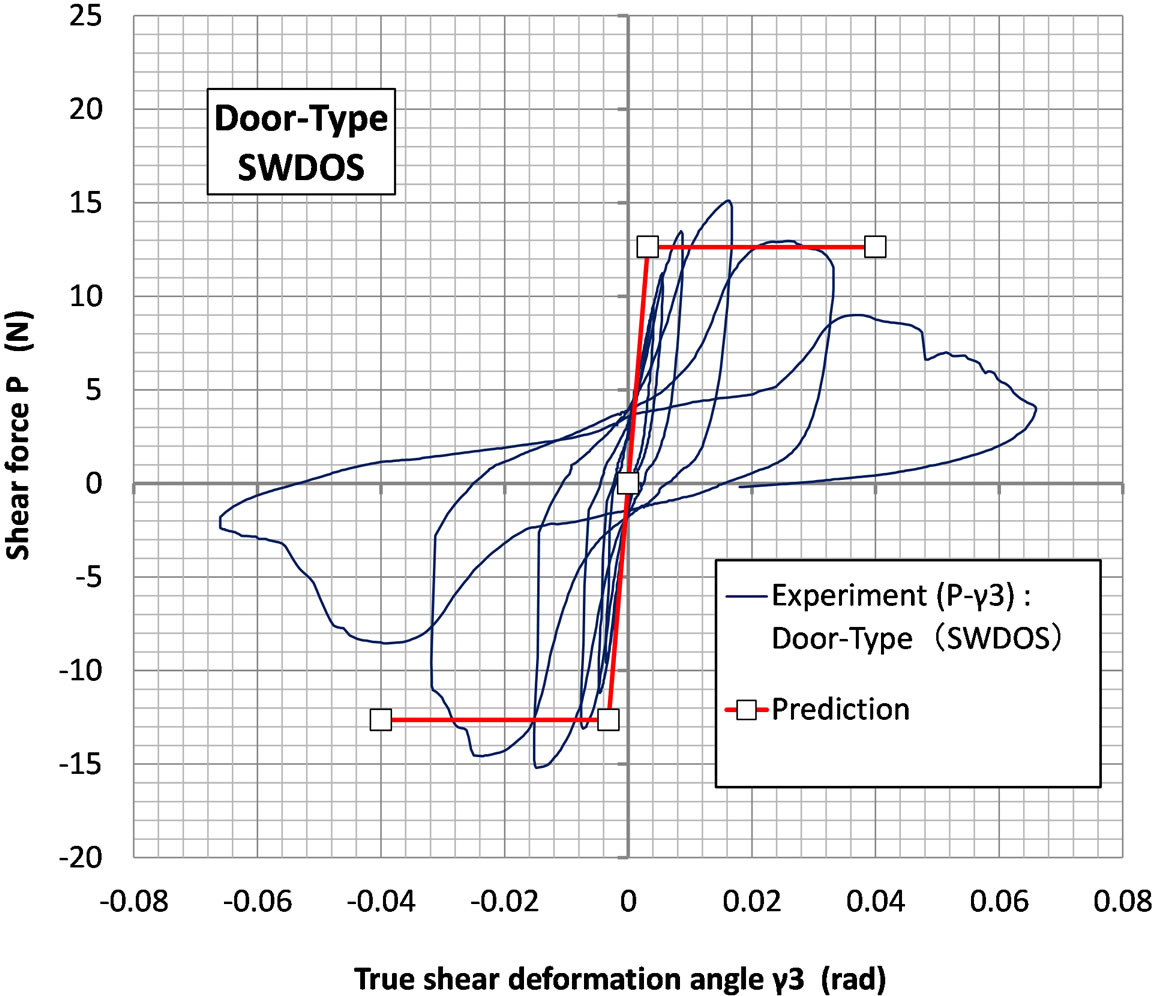
Figure 26.Comparison between calculation and observation on door-type (SWDOS) specimen.

Figure 27. Spectrum diagrams of Wall-Type(SWD) of shear walls.
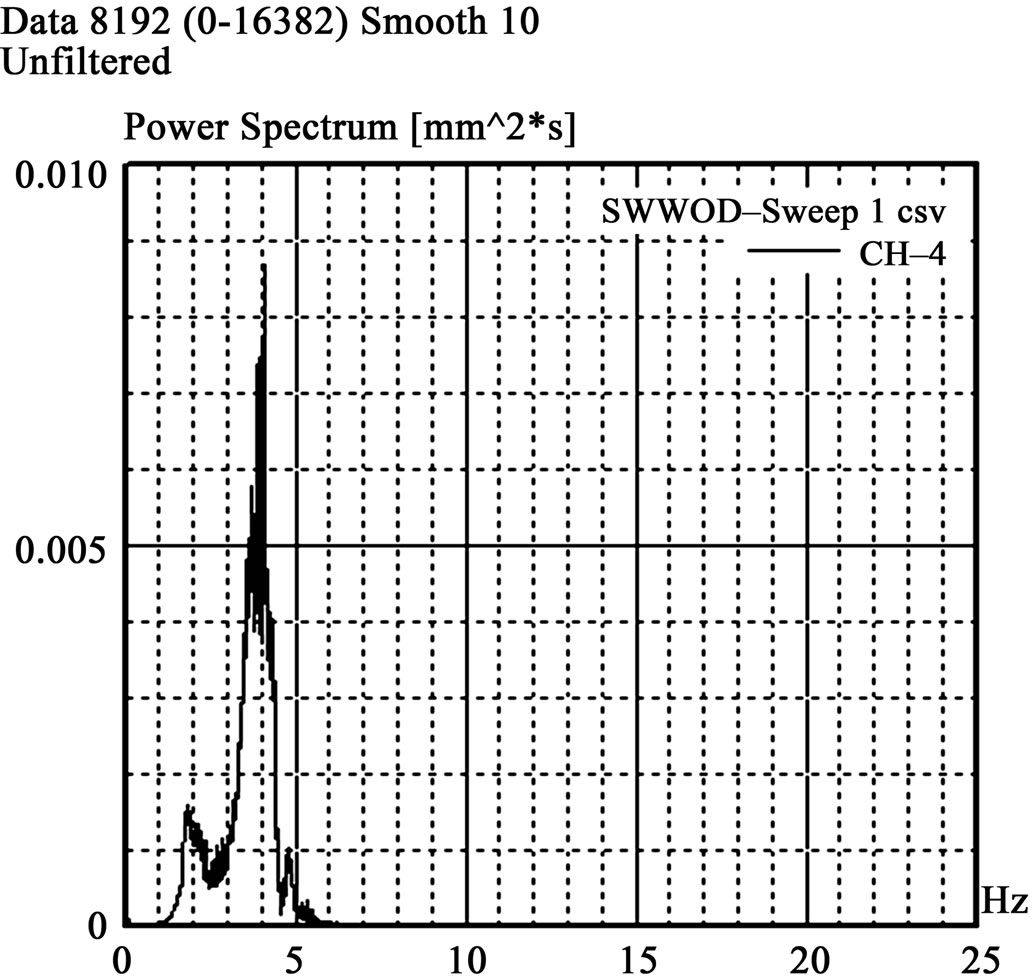
Figure 28. Spectrum diagrams of Window Opening-Type (SWWOD) of shear walls.

Figure 29. Spectrum diagrams of Door Opening-Type (SWDOD) of shear walls.
According to a theory [12], natural frequency f of structure might be calculated using Equation (44)
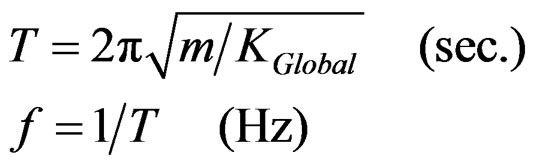 (44)
(44)
where,
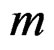 : Mass of test specimen with machine weight (
: Mass of test specimen with machine weight ( )
)
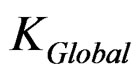 : Global pure shear stiffness of test specimen derived from previous section in which effects of base rotation and bending were not involved (N/m).
: Global pure shear stiffness of test specimen derived from previous section in which effects of base rotation and bending were not involved (N/m).
The comparisons between calculated natural frequency and that of observed shows on Table 4.
There were some amounts of discrepancies in 32% to 52% between calculated natural frequency and that of measured. A few reasons for these discrepancies might be explain due to the effect of bending and rocking of actual test specimens which were involved in measured values, while calculated frequency was estimated by using only pure shear stiffness derived on each specimen.
Figures 30, 31 and 32 show free vibration phenomena obtained after forced vibration test with a constant frequency of corresponding natural frequency then stopping portable shake excitation machine suddenly to estimate the damping coefficient. Damping coefficient estimated for each specimen were 3.7%, 3.3% and 3.6%, respectively.
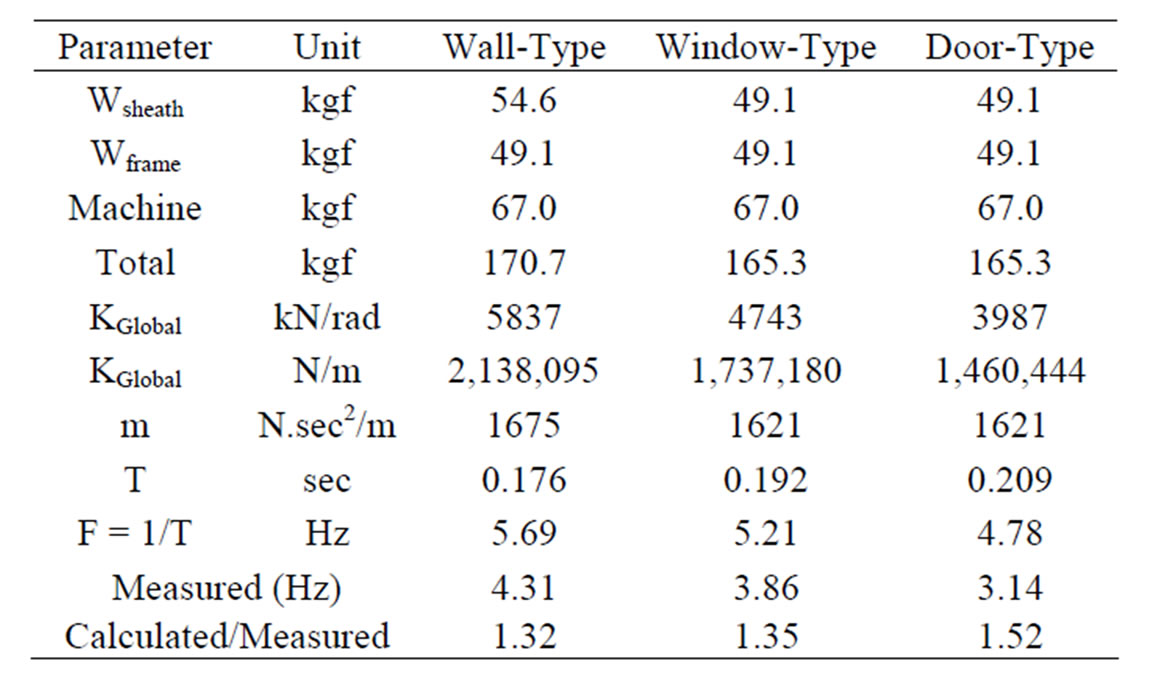
Table 4. Comparisons between calculated natural frequency and that of observed.
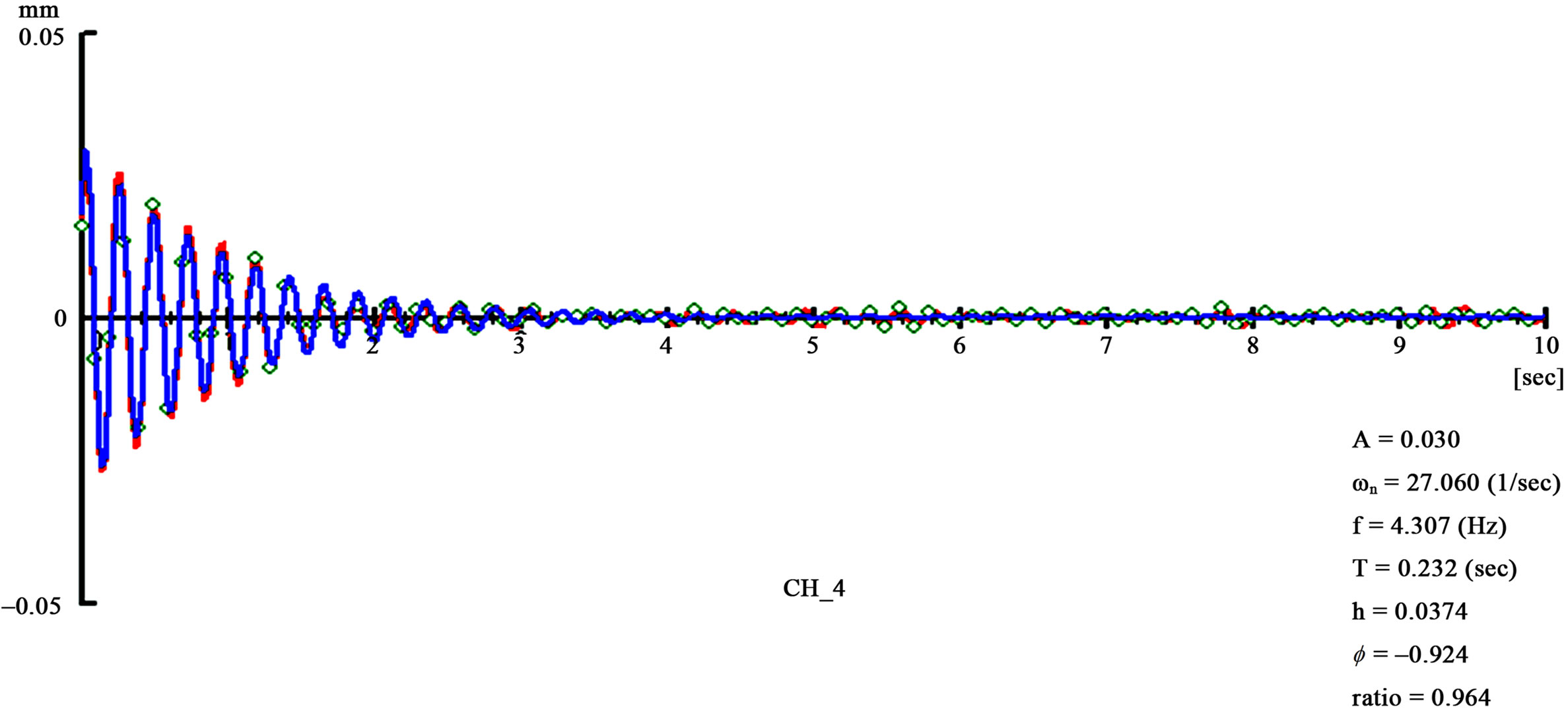
Figure 30. Free vibration curve Wall-Type(SWD) of shear walls.
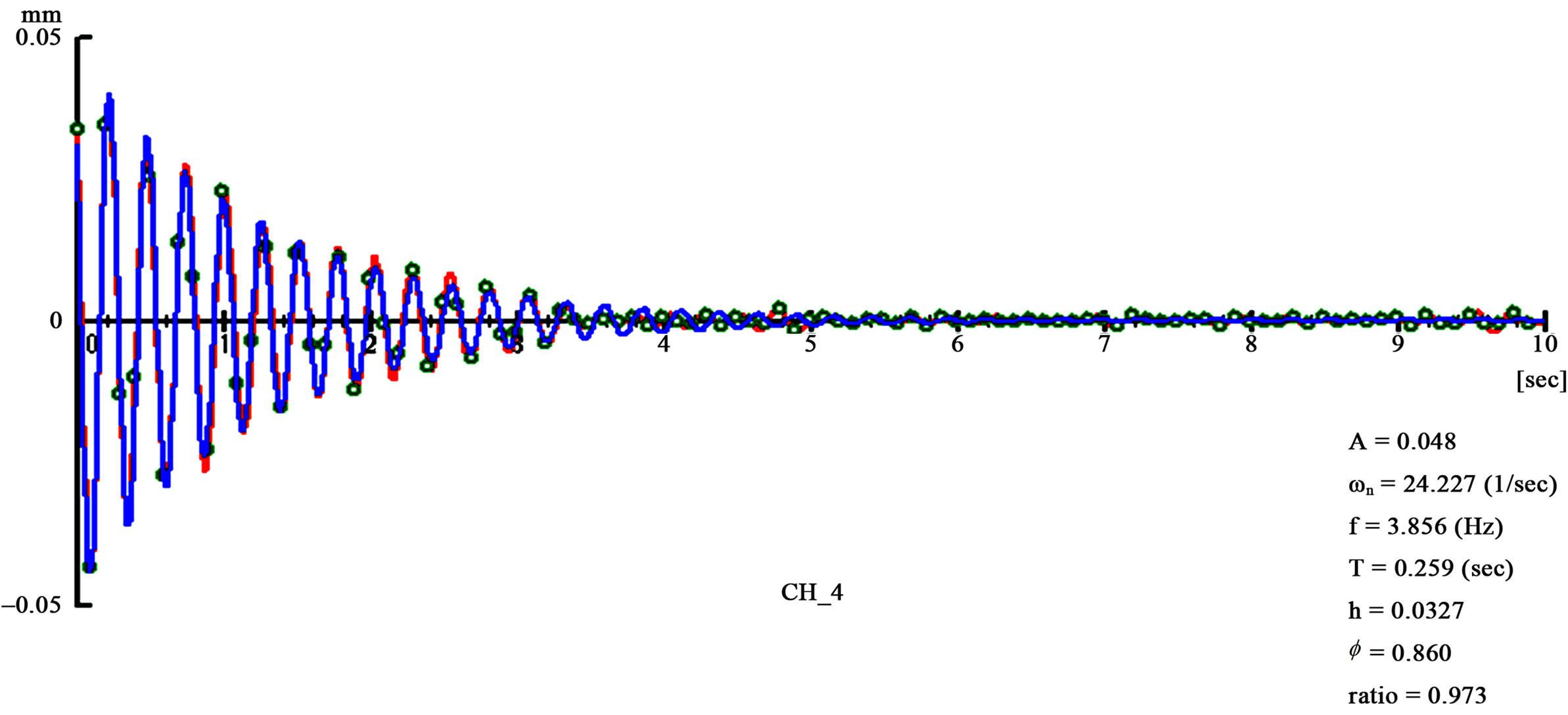
Figure 31. Free vibration curve of Window-Type(SWWOD) of shear walls.
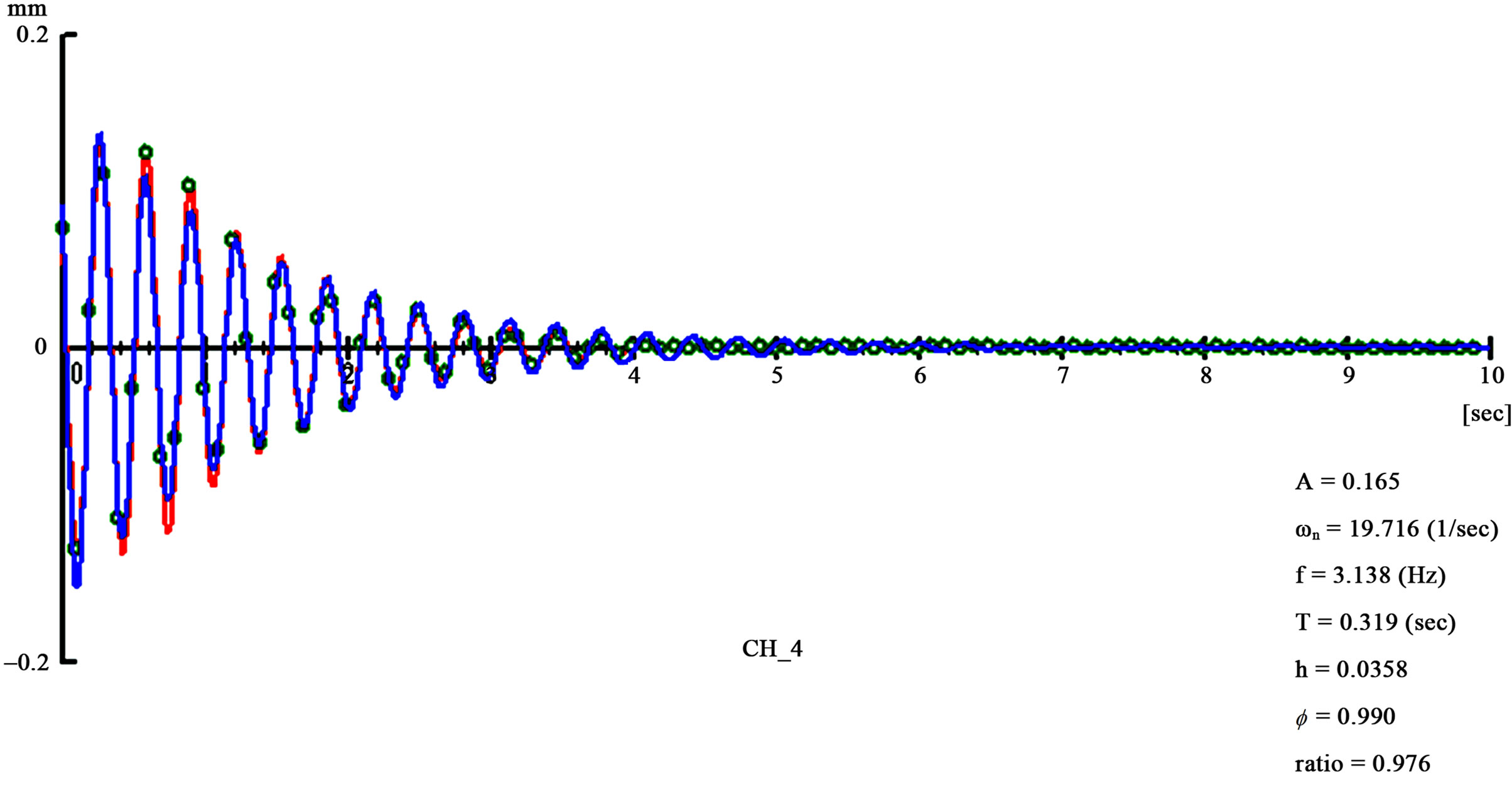
Figure 32. Free vibration curve of Door-Type (SWDOD) of shear walls.
5. Conclusion
The mechanical models proposed in this study could predict the behavior of shear walls subjected to horizontal push-pull static cyclic load. While in the case of dynamic loading case, agreements between experiments and prediction due to theory was not always sufficient because theoretical calculation could only predict pure shear stiffness of shear wall, while experimentally observed value was thought to involve another effects.
6. Acknowledgements
We would like to express our sincere thanks to JSPS for Ronpaku program, Laboratory of Structural Function, RISH, Kyoto University, Japan, and RIHS, Ministry of Public Works of Indonesia for all research activity.
REFERENCES
- J. W. van de Lindt, “Evolution of Wood Shear Wall Testing, Modeling, and Realibility Analysis, Bibliography,” Practice Periodical on Structural Design and Construction, Vol. 9, No. 1, 2004, pp. 44-53. HUdoi:10.1061/(ASCE)1084-0680(2004)9:1(44)UH
- C. K. Cheung, R. Y. Itani and A. Polensek, “Characteristics of Wood Diaphragms: Experimental and Parametric Studies,” Wood Fiber Science, Vol. 20, No. 4, 1988, pp. 438-456.
- R.Y. Itani, R. L. Tuomi and W. J. McCutcheon, “Methodology to Evaluate Racking Resistance of Nailed Walls,” Forest Products Journal, Vol. 32, No. 1, 1982, pp. 30-36.
- M. Murakami and M. Inayama, “Formulae to Predict the Elastic and Plastic Behaviour of Shearwall with Any Nailing Arrangement Pattern,” Journal of Structural and Construction Engineering, Vol. 519, 1999, pp. 87-93.
- M. Hadi, S. Murakami, A. Kitamori, W.-S. Chang and K. Komatsu, “Performance of Shear Wall Composed of LVL and Cement Fiber Board Sheathing,” Journal of Asian Architecture and Building Engineering, Vol. 9, No. 2, 2010, pp. 463-469. HUdoi:10.3130/jaabe.9.463U
- H. Sugiyama and T. Matsumoto, “A Simplified Method of Calculating the Shear Strength of a Plywood-Sheathed Shear Wall with Opening I. Evaluation of the Racking Load of a Shear Wall with Openings,” Journal of the Japan Wood Research Society, Vol. 39, No. 1, 1993, pp. 75-79.
- H. Sugiyama and T. Matsumoto, “A Simplified Method of Calculating the Shear Strength of a Plywood-Sheathed Shear Wall with Opening II. Analysis of the Shear Resistance and Deformation of a Shear Wall with Openings,” Journal of the Japan Wood Research Society, Vol. 39, No. 8, 1993, pp. 924-929.
- H. Sugiyama and T. Matsumoto, “A Simplified Method of Calculating the Shear Strength of a Plywood-Sheathed Shear Wall with Openings III. Analyses of the Shear Resistance of a Wall and of the Strength Behavior of Panel Elements,” Journal of the Japan Wood Research Society, Vol. 40, No. 3, 1994, pp. 280-286.
- Y. A. Tjondro and M. Hadi, “Mechanical Properties and Behavior of Falcataria-Rubber Wood LVL,” Proceeding of 19th Australasian, Conference on the Mechanics of Structures and Materials, Chrischurch, New Zealand, 2006.
- M. Hadi, S. Murakami and K. Komatsu, “Prediction of Nonlinear Cyclic Behaviors of Shear Wall Composed of Acacia Mangium Framing and Fiber Cement Board Sheathing,” Open Journal of Civil Engineering, Vol. 2, No. 1, 2012, pp. 1-9.
- Allowable Design Method for Conventional Wooden Post & Beam Construction HOWTEC, 2008.
- M. Paz and W. Leigh, “Structural Dynamics,” 5th Edition, Springer, 2008.
- [k1]Try to express these equation into single line for deducing page numbers into 8

