Modern Mechanical Engineering
Vol.3 No.1(2013), Article ID:28260,5 pages DOI:10.4236/mme.2013.31007
Location Results for Brace Spacing in Gap Tubular “K” Joints Using FEM
Civil Engineering Department, University of Agriculture, Makurdi, Nigeria
Email: peterjiki@yahoo.com
Received November 22, 2012; revised December 27, 2012; accepted January 8, 2013
Keywords: Tubular Joint; Finite Element; Computer Simulation; Structural Joints; Effect of Bracing; Stress Concentration; Stress Distribution
ABSTRACT
The 8-node iso-parametric thin shell element was employed in the study of stress concentrations in the welded tubular “K” joint. Element equilibrium equations were derived using isoparametric formulation based on thin shell theory. After assembly, the resulting system equations were solved using existing fortran programs. Numerical experiments were conducted to isolate and locate ideal gap (positions) for the two braces of the “K” joint. The nominal stresses were calculated from which stress concentration factors were obtained. The resulting stress concentration factors were presented both as tables and as figures. A good agreement between our solutions and those for model joints in the literature is good and acceptable. It was found that the wider apart the brace spacing is, the weaker the strength of the joint. It was also found that the best location for the braces occurs when the stress level changes sign either from positive to negative or vice versa at a critical sampling point.
1. Introduction
Lapped joints generally, and lapped tubular joints in particular are known to be stronger than gapped joints following a heuristic reasoning. However, for the purpose of bracing, it is not always feasible or even possible to brace a structural system with lapped joint throughout. Hence a strong case arises from using gapped tubular joints which are in many cases welded on site due to ease of construction and transportation. As usual, one of the problems with welded steel construction is the development of stress concentration or ‘hot spot’ stresses. The hot spots affect the strength of both lapped and gapped joints.
The problem of hot spot stresses or stress concentrations has been investigated by Kuang et al. [1] in their work on stress concentrations in tubular joints. Potuin et al. [2] also investigated stress concentrations in tubular joints. Gibstein [3] used a parametric study to investigate stress concentrations in T joints. Wordsworth and Smedly [4] investigated stress concentrations in offshore tubular joints without stiffners. However, joints of hollow square, rectangular and tubular sections are very often used in very important constructions such as large space roofs, offshore platforms [4] and trussed bridges [5,6] instead of their solid counterparts to reduce dead loads due to self weights. However, failure of these systems due to joint failures still pose engineering challenges. In order to understand why these joints still fail, So and So [7] carried out a study of “hot spot” stresses in a tubular “K” joint with combined in-plane and out-of-plane loadings. May be due to combined in-plane and out-of-plane loading, very high “hot spot” stresses were obtained from their model. Although they studied the effect of load variation, they did not study the effect of varying the gap between braces, on the strength of joint they studied. In order to understand the behaviour of these joints further, more studies were initiated by Paul et al. [8] to study the ultimate resistance of un-stiffened multi-planar tubular “T” and “K-K” joints. Parker [9] proposed the use of concrete filled hollow square section (“HSS”) joints to improve the strength of such joints. The results of the finite element study on square hollow “K” joints by Jiki [10] seem to represent more realistically the behaviour of the joints but it was realised that the sharp corner edges of the section increased stress concentrations. This effect of geometry was also observed by Jiki [11] in the study of a rectangular hollow (RH) “K” joints. For the purpose of comparison using the finite element method to study the effect of section geometry on the distribution of stress concentrations in hollow joints, the same 8-node isoparametric thin shell element is used to model these sections with different geometries. In all joints modelled by the finite element method, welded joint construction and the 8 node iso-parametric shell element were used through out to facilitate room for comparison.
It can be seen from the above review that the effect of stress concentrations on strength of tubular joints has been found to be a problem generally [5,6].
However, the particular problem of stress concentrations in lapped and gapped tubular joints with respect to effective location of the spacing of the braces has not hitherto been properly addressed.
The purpose of this study is to investigate the effect of effective location of braces (brace spacing) on the strength of the gapped tubular “K” joints. The effect of section geometry on the distribution of stress concentration factors in hollow section (HS) or tubular joints is also investigated. The finite element method of analysis was used in the investigation of the static stress concentrations.
2. Equilibrium Equations
The usual curved thin shell iso-parametric element was used for the present investigation (e.g. see Hinton and Owen [12]. The shape of the element is shown in Figure 1. Using potential energy formulation and the RayleighRitz process, the equilibrium equations were derived as follows:
The element total potential energy functional is given as :
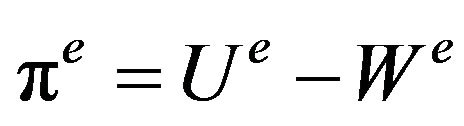 (15)
(15)
where 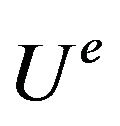 is the strain energy of the element
is the strain energy of the element 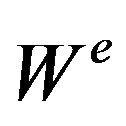 is the external work done by the element during deformation.
is the external work done by the element during deformation.
In a compact formulation Equation (15) can be written as:
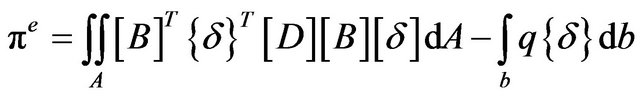 (16)
(16)
 (17)
(17)
In which  is the element stiffness matrix
is the element stiffness matrix  is the element boundary loads, such that:
is the element boundary loads, such that:
 (18)
(18)

Figure 1. An 8-node isoparametric element.
 (19)
(19)
After assembly we solve the system equations of Equation (20) for displacements.
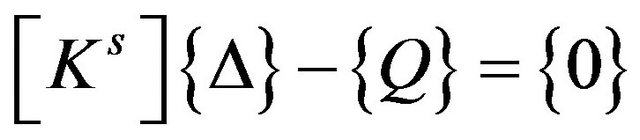 (20)
(20)
The finite element stresses are calculated from
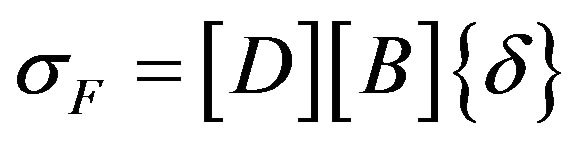 (21)
(21)
in which
 (22)
(22)
3. Solution of System Equilibrium Equations
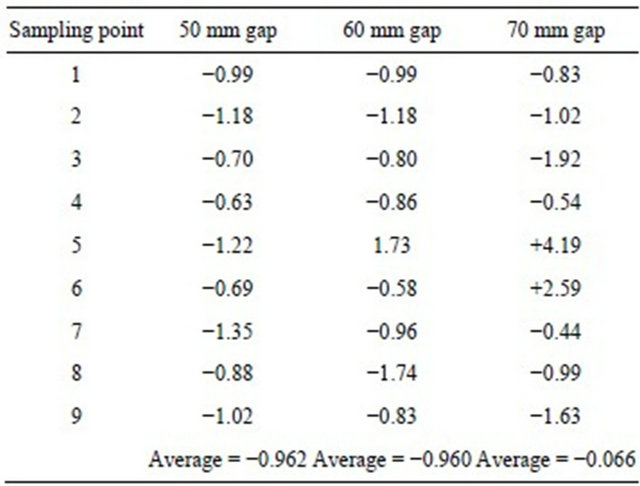
The system equilibrium equations for the present problem were solved after application of boundary conditions using the frontal solution algorithm and code developed by Hinton and Owen [12]. To check the validity of the program used we compare our results with those of So and So [7] for the case of in-plane loads as shown in Table 1 herein. As we can see from that table our results or findings closely agree with theirs and is therefore acceptable. We have also investigated the effect of increasing the gap between braces on the stress concentration factors and our findings in this regard are shown in Tables 2 and 3. Having been satisfied with the performance of our program as a tool for the analysis, we have now studied the effect of variable brace spacing or gap on the strength of gap tubular “K” joints in details as presented in the tables and figures in this work.
4. Investigation of Stress Concentrations
The finite element discretization and loading of the joint for purpose of stress analysis is shown in Figure 2. Due to symmetry only half of the “K” joint used for the present study. After assembly we solve Equation (20) for nodal displacements and use Equation (21) to calculate stresses using Fortran code developed by Hinton and Owen [12]. After the finite element stresses were calculated, we also calculated nominal stresses using the usual expression for combined bending and axial effect as:
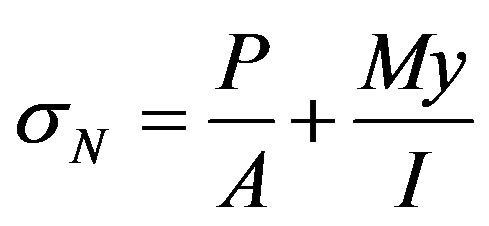 (24)
(24)
and the nominal shear stresses are calculated from:
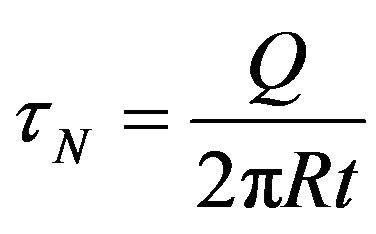 (25)
(25)
Table 1. Comparison of SCFs for “K” tubular joints subjected to inplane loads.

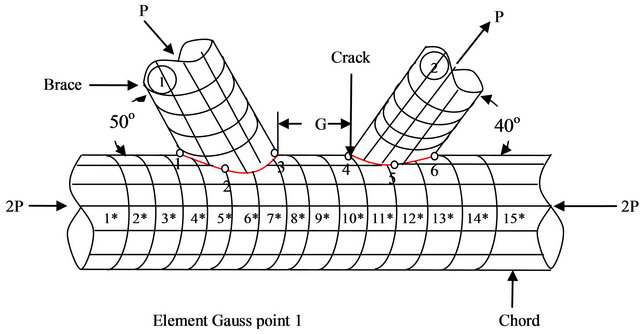
Figure 2. A finite element mesh for the K joint.
Table 2. Effect of increasing brace spacing (gap) on SCF at corner of top chord (Brace angles = 50/40 deg).
in which Q is applied shear force, R is shell radius and t is shell thickness. The gap between the two braces in the first case was kept constant at 50 mm and stress concentration factor 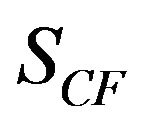 was obtained as
was obtained as
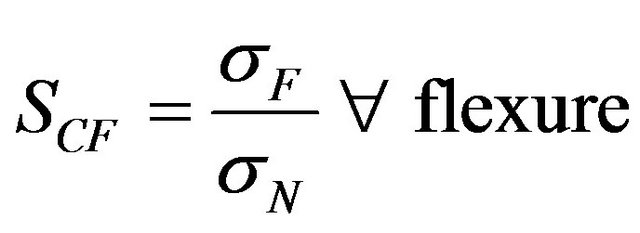 (26)
(26)
or
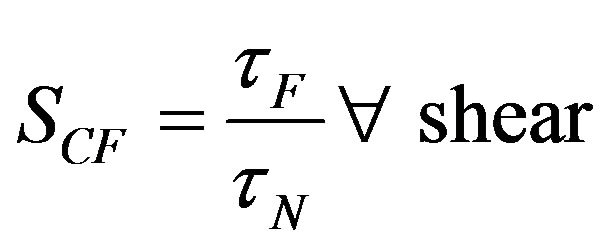 (27)
(27)
where 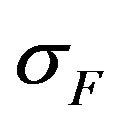 is finite element stress in the longitudinal axis of the chord
is finite element stress in the longitudinal axis of the chord 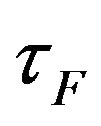 is shear stress in the chord.
is shear stress in the chord. 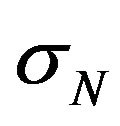 is
is
Table 3. Effect of increasing brace spacing (gap) on SCF at corner of top chord (Brace angles = 50/50 deg).

nominal stress given as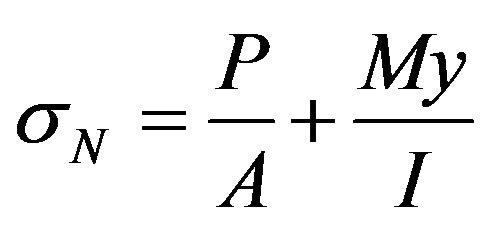 .
.
5. Applications
Geometric parameters for the “K” joint.
Example 1.
For the purpose of comparison with our solution the dimensions of the “K” joint studied by So and So [7] are used here:
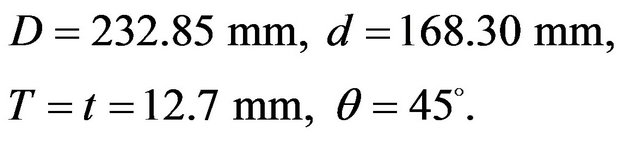
We have also:
t/T = Brace of chord thickness ratio = 1.0D/T = Chord diameter to thickness ratio = 25.50d/D = Brace of chord diameter ratio = 0.52L/D = Chord length to diameter ratio = 6.18g/D = Brace separation to chord diameter ratio = 0.015 From g/D = ratio of 0.015, we calculate g to be , say =5 mm.
, say =5 mm.
And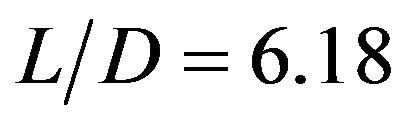 , we calculate L used by So and So [7]:
, we calculate L used by So and So [7]: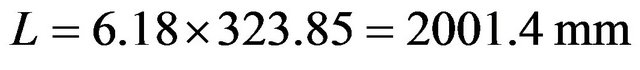 , say 2000 mm.
, say 2000 mm.
We next subject the joint with the above details to in-plane loading for the purpose of bending stress analysis. The result of analysis from our finite element code is compared with those of So and So [7] and Efthymiou and Durkin.
Our result for the chord is 0.53% lower than that of Efthymiou and Durkin and 4.37% higher than that of So and So [7], while for the chord; it is 2.37% lower that of Efthymiou and Durkin and 0.98% higher than that So and So [7]. In this case, we conclude that the comparison between our solution and that of the two published authors is overall less than 5% difference and is good and acceptable.
Example 2.
In this example we investigate the effect of damage and brace spacing/ separation on the strength of the “K” tubular joint. The geometric details of the joint is as follows:
Chord:
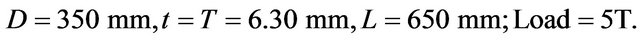
Brace:
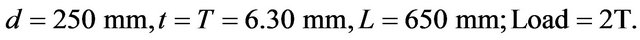
The result of the peak (adverse) stress concentrations obtained mainly from top chord of the “K” joint are presented here in Tables 2 and 3.
6. Discussion of Results
Bracings in structural systems provide strength to the systems. However, there is no universal method of selecting locations for a selected bracing system. Usually the designer selects brace separations or gaps based on previous experience or heuristic reasoning. In this work we have used the finite element method as a tool to carry out some numerical experiments on locations of effective brace separations or spacings rather than use usual rule of thumb to select the desired spacings or gap between braces. By varying the gap between two braces and making computer runs produce a set of results. A close look at the results produced shows a trend in degradation of stresses as the gap is increased. This can give the analyst or the designer some idea of which brace separation to choose in the design.
In Tables 2 and 3 we have presented the results of our study for three brace separations e.g. 50 mm, 60 mm and 70 mm respectively. We see in the tables that from 50 mm to 60 mm spacing/separation there is no alternating stress concentration factors SCFs i.e. from positive to negative; that is, we have monotonic stress pattern and there is no stress reversal. However, as we increase the separation gap to 70 mm, we see the alternating pattern of stress concentration factors. This marks the limit of brace separation for the joint details above.
7. Conclusions
From our study of gapped tubular “K” joints we conclude as follows:
1) Brace separation distance for “K” tubular joint should be carefully selected so as to reduce over stress concentrations.
2) For best result, the joint should be lapped.
3) However, if the joint must be spaced, then based on our findings in Tables 2 and 3 and Figures 3 and 4, 50 mm gap should be the limit of the spacing or gap. This is because after the 50 mm brace spacing or gap, adverse stress concentrations are observed when the spacing is increased beyond the 50 mm mark. In any case, the geometric parameters of the joint should be considered in order to avoid joint over stress.
4) We recommend or propose here that the finite element method be used as an ideal tool for the location of best brace spacing or gap (g).
5) Using our example joint studied here, we propose as a guide in the location result, that the ratio of the spacing
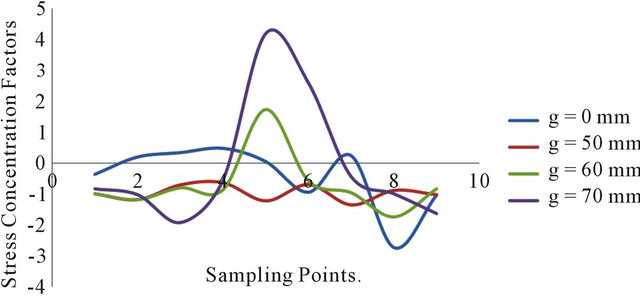
Figure 3. Effect of gap (g) on SCF of top chord (centre).
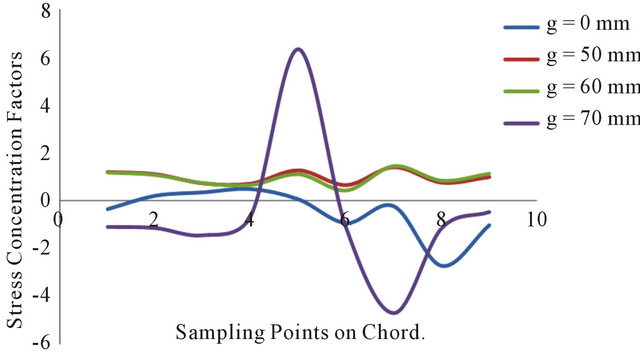
Figure 4. Effect of gap (g) on SCF of top Chord (edge).
or gap g to the chord diameter D should not be greater than 1, that is, g/D ≤ 1.
REFERENCES
- J. G. Kuang, A. B. Potuin and R. D. Leick, “Stress Concentration in Tubular Joints,” Offshore Technol Conference, Houston, 4 May 1972, pp. 6-15.
- A. B. Potuin, J. G. Kuang, R. D. Leick and J. L. Kahlich, “Stress Concentration in Tubular Joints,” SPE Journal, Vol. 17, No. 4, 1977, pp. 287-299.
- M. S. Gibstein, “Parametric Stress Analysis of T-Joints,” Offshore Steel Seminar, Cambridge, 1978, pp. 3-26.
- A. C. Wordsworth and G. P. Smedley, “Stress Concentrations at Unstiffened Tubular Joints,” Offshore Steel Seminar, Cambridge, 1978.
- S. Walbridge and A. Nussbaumer, “Probablistic Fatigue Analysis of Shop and Field Treated Tubular Truss Bridges,” Journal of Construction Steel Research, Vol. 64, No. 2, 2008, pp. 156-166. doi:10.1016/j.jcsr.2007.06.001
- A. Schumacher, and A. Nussbaumer, “Experimental Study on the Fatigue Behaviour of Welded Tubular K Joints for Bridges,” Journal of Engineering Structures, Vol. 28, No. 5, 2006, pp. 745-755. doi:10.1016/j.engstruct.2005.10.003
- A. K. Soh and C. K. Soh, “Hot-Spot Stresses of Tubular K Joints Subjected to Combined Loading,” Journal of Construction Steel Research, Vol. 26, No. 2-3, 1993, pp. 125-140. doi:10.1016/0143-974X(93)90032-N
- J. C. Paul, Y. Makins and Y. Kurobane, “Ultimate Resistance of Unstiffened Multi Planar Tubular T T and K K Joints,” Journal of Structural Engineering, ASCE, Vol. 120, No. 10, 1994, pp. 2853-2870. doi:10.1061/(ASCE)0733-9445(1994)120:10(2853)
- J. A. Parker, “Concrete Filled HSS Connections,” J. of Structural Engineering, ASCE, Vol. 120, No. 3, 1995, pp. 458-467.
- P. N. Jiki, “Prediction of Stress Concentration Factors in Un-lapped Square Hollow ‘K’ Joints by the Finite Element Method,” Nigerian Journal of Technology, Vol. 25, No. 1, 2006, pp. 5-14.
- P. N. Jiki, “Stress Analysis of Un-lapped Rectangular Hollow ‘K’ Joints by the Finite Element Method,” Botswana Journal of Technology, Vol. 17, No. 2, 2009, pp. 46-53. (Botswana)
- E. Hinton and D. R. J. Owen, “Finite Element Programming,” Academic Press, London, 1977, pp. 95-110.

