Open Journal of Composite Materials
Vol.3 No.2A(2013), Article ID:30863,7 pages DOI:10.4236/ojcm.2013.32A007
Crossover to Quantized Thermal Conductance in Nanotubes and Nanowires
![]()
1Institute of Applied Physics and Tsukuba Research Center for Interdisciplinary Materials Science, University of Tsukuba, Tsukuba, Japan; 2Green Innovation Research Laboratory, NEC Corporation, Tsukuba, Japan.
Email: *nkoba@bk.tsukuba.ac.jp
Copyright © 2013 Kohei Yamamoto et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 28th, 2013; revised March 28th, 2013; accepted April 18th, 2013
Keywords: Carbon Nanotube; Nanowire; Thermal Transport; Quantum Conductance; Non-Equilibrium Green’s Function
ABSTRACT
Using the non-equilibrium Green’s function techniques with interatomic potentials, we study the temperature dependence and the crossover of thermal conductance from the usual behavior proportional to the cross-sectional area at room temperature to the universal quantized behavior at low temperature for carbon nanotubes, silicon nanowires, and diamond nanowires. We find that this crossover of thermal conductance occurs smoothly for the quasi-one-dimensional materials and its universal behavior is well reproduced by the simplified model characterized by two parameters.
1. Introduction
Recently, phonon thermal transport properties of quasione-dimensional materials, such as carbon nanotubes (CNTs) and silicon nanowires (SiNWs), have attracted much attention in the fields of nanometer-scale electron devices and thermoelectric devices. The high thermal conductance opens the way to reduce the heating problems in nanometer-scale electron devices, while low thermal conductance leads to high efficiency of thermoelectric devices [1]. Consequently, it is very important to know how the quasi-one-dimensional materials conduct heat. It is predicted that thermal conductance is quantized as  at low temperature and this quantization dose not depend on kinds of materials and carriers [2]. Indeed, this
at low temperature and this quantization dose not depend on kinds of materials and carriers [2]. Indeed, this 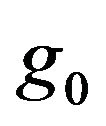 is experimentally measured for phonons [3], electrons [4], and even photons [5]. However, it is known that this quantization breaks at high temperature. Moreover, in macroscopic, the conductance should be proportional to the cross-sectional area of wires [6]. We investigate this region between quantized and macroscopic thermal conduction. For such studies, including quantized thermal conductance, we need the computational approach taking the quantum effects explicitly into account. The Landauer formula [7] or the non-equilibrium Green’s function (NEGF) technique [8] has been widely studied. In addition to electron transport [9,10], these methods have recently been applied to the thermal transport [11] and the thermal conductance is calculated for SiNWs [12] and CNTs [13]. Recently using the NEGF technique, the quantized thermal conductance has been analyzed for SiNWs [14]. According to the calculation, thermal conductance is quantized not proportional to diameter at all at low temperature and has a diameter dependence gradually as the temperature increases. Over the temperature 100 K, the thermal conductance becomes proportional to cross-sectional area of nanowires.
is experimentally measured for phonons [3], electrons [4], and even photons [5]. However, it is known that this quantization breaks at high temperature. Moreover, in macroscopic, the conductance should be proportional to the cross-sectional area of wires [6]. We investigate this region between quantized and macroscopic thermal conduction. For such studies, including quantized thermal conductance, we need the computational approach taking the quantum effects explicitly into account. The Landauer formula [7] or the non-equilibrium Green’s function (NEGF) technique [8] has been widely studied. In addition to electron transport [9,10], these methods have recently been applied to the thermal transport [11] and the thermal conductance is calculated for SiNWs [12] and CNTs [13]. Recently using the NEGF technique, the quantized thermal conductance has been analyzed for SiNWs [14]. According to the calculation, thermal conductance is quantized not proportional to diameter at all at low temperature and has a diameter dependence gradually as the temperature increases. Over the temperature 100 K, the thermal conductance becomes proportional to cross-sectional area of nanowires.
Here, we report the thermal conductance of the quasione-dimensional systems, in particular, diameter dependence for materials such as CNTs, SiNWs, and diamond nanowires (DNWs) at various temperatures. Using a simplified model based on the assumption for the phonon dispersion relations, we first show the general behaviors of the crossover to quantized thermal conductance from the usual behavior, proportional to the cross-sectional area, to the unusual “quantum-type”, not dependent on the cross-sectional area or the diameter with decreasing temperature. Especially, we consider the following model. Since the quasi-one-dimensional materials have four acoustic phonon modes; one longitudinal mode, two flexural modes, and one torsional mode, we propose the model that these modes are well separated in the phonon dispersion relation from the other optical modes, the number of which is proportional to the number of atoms in cross-section of materials. We can obtain the universal thermal conductance behavior with only two parameters to describe the present simplified model. Then, we present the elaborate atomistic calculations for the thermal conductance of various realistic systems using the NEGF technique. We explain the difference of the temperature dependence of thermal conductance by comparing with those for the simplified model and clarify the important two parameters to account for the crossover to the quantized thermal conductance.
2. Simplified Model
First, we introduce a simplified model to discuss the temperature dependence of thermal conductance of quasi-one-dimensional systems. In particular, we try to analyze qualitatively the crossover to quantized thermal conductance from the usual conductance, which is proportional to its cross-sectional area. Here we note that in the Debye approximation where the phonon dispersion relation for the quasi-one-dimensional model composed of mono-atomic chain is approximated by the simple linear dispersion as shown in Figure 1(a), there apparently shows no crossover of thermal conductance since the transmission coefficient exists only for that phonon

Figure 1. (a) Phonon dispersion relation of a quasi-onedimensional mono-atomic model for the acoustic mode in the debye approximation; (b) Schematic picture of phonon dispersion relation in the present simplified model, which is composed of four acoustic phonon modes for 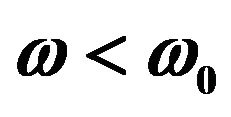 and the other uniform phonon modes for
and the other uniform phonon modes for ; (c) Typical transmission coefficient
; (c) Typical transmission coefficient 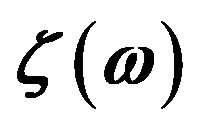 as a function of phonon frequency
as a function of phonon frequency ![]() for the one-dimensional monoatomic model in (a); (d) Transmission coefficient
for the one-dimensional monoatomic model in (a); (d) Transmission coefficient 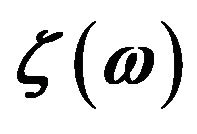 in the simplified model.
in the simplified model. 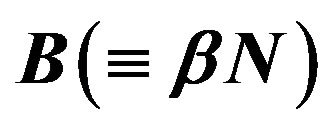 is the number of phonon modes at
is the number of phonon modes at![]() , where we assume
, where we assume  is proportional to the number of atoms
is proportional to the number of atoms  in the cross-sectional area.
in the cross-sectional area.
mode (Figure 1(c)).
Instead, we consider a system for the phonon thermal transport which is described by two dimensionless parameters  and
and . Here
. Here  indicates the ratio of
indicates the ratio of , where
, where 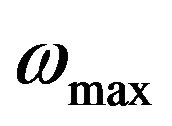 is the maximum phonon frequency for all the phonon modes and
is the maximum phonon frequency for all the phonon modes and 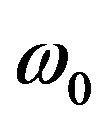 is the phonon frequency under which only four acoustic phonon modes exist. It should be noted that the torsional mode appears in the quasi-one-dimensional systems in addition to the one longitudinal mode present typically in one-dimensional system as in Figure 1(a) and two flexural modes present for bulk system. Important point is that we consider these four modes are well separated from the other phonon modes which exist in the higher energies and play the important role for the quantized thermal conductance at low temperature. As the temperature increases, various phonon modes are excited beyond these acoustic modes. In general, the degrees of the freedom increase linearly with the number of the atoms and the number of the phonon bands increases correspondingly.
is the phonon frequency under which only four acoustic phonon modes exist. It should be noted that the torsional mode appears in the quasi-one-dimensional systems in addition to the one longitudinal mode present typically in one-dimensional system as in Figure 1(a) and two flexural modes present for bulk system. Important point is that we consider these four modes are well separated from the other phonon modes which exist in the higher energies and play the important role for the quantized thermal conductance at low temperature. As the temperature increases, various phonon modes are excited beyond these acoustic modes. In general, the degrees of the freedom increase linearly with the number of the atoms and the number of the phonon bands increases correspondingly.
In the region of frequencies between 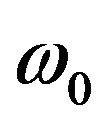 and
and , we assume for simplicity that the number of the phonon modes becomes uniform and is proportional to the number of atoms
, we assume for simplicity that the number of the phonon modes becomes uniform and is proportional to the number of atoms  in the cross-sectional area. Since the transmission coefficient
in the cross-sectional area. Since the transmission coefficient 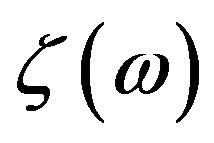 corresponds to the number of phonon modes for ballistic transport, we obtain
corresponds to the number of phonon modes for ballistic transport, we obtain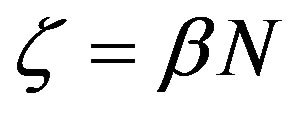 , where we introduce the parameter
, where we introduce the parameter  as the proportional constant. As an example of the simplified model, we show a schematic phonon dispersion relation and the corresponding transmission function
as the proportional constant. As an example of the simplified model, we show a schematic phonon dispersion relation and the corresponding transmission function 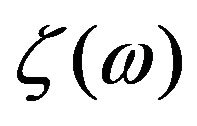 in Figures 1(b) and (d), respectively.
in Figures 1(b) and (d), respectively.
The thermal current  for the system is expressed in the Landauer’s type as follows, [2]
for the system is expressed in the Landauer’s type as follows, [2]
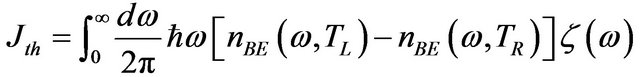 , (1)
, (1)
where 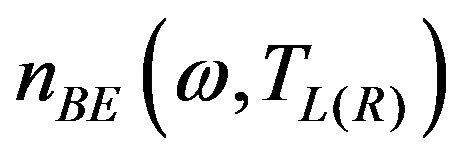 is the Bose-Einstein distribution function of equilibrium phonons with an energy of
is the Bose-Einstein distribution function of equilibrium phonons with an energy of 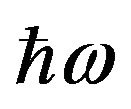 in the left (right) lead at temperature
in the left (right) lead at temperature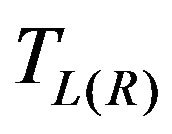 . For adiabatic contact between the wire and the leads,
. For adiabatic contact between the wire and the leads, 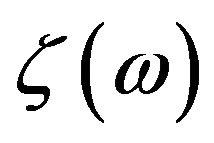 is expressed in the present model as follows,
is expressed in the present model as follows,
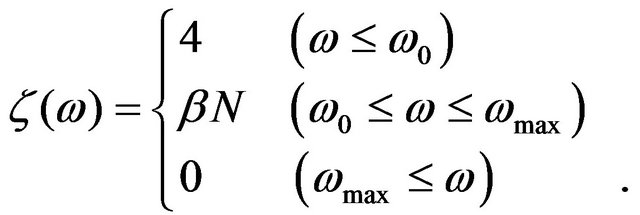 (2)
(2)
In the limit of small temperature difference between the left and right leads, the temperature dependence of thermal conductance 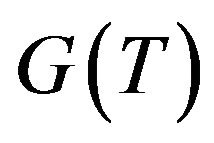 is given by
is given by
 (3)
(3)
The thermal conductance 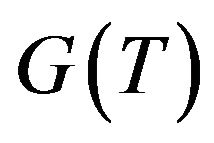 shows explicitly the size dependence for
shows explicitly the size dependence for  in addition to the temperature dependence. At low temperature the first term dominates the thermal conductance and
in addition to the temperature dependence. At low temperature the first term dominates the thermal conductance and  shows the quantized thermal conductance, without any dependence of
shows the quantized thermal conductance, without any dependence of , a universal features as
, a universal features as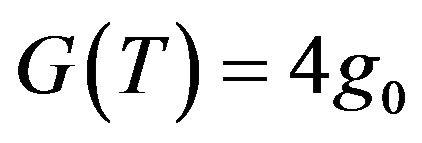 . As the temperature increases, the contribution from the second term having the size dependence plays a dominant role. Since this term is proportional to
. As the temperature increases, the contribution from the second term having the size dependence plays a dominant role. Since this term is proportional to , that is, its cross-sectional area, it represents the usual thermal conductance. With use of these expressions, we calculate the temperature dependence of the thermal conductance to discuss the crossover region between the quantized conductance and the usual conductance.
, that is, its cross-sectional area, it represents the usual thermal conductance. With use of these expressions, we calculate the temperature dependence of the thermal conductance to discuss the crossover region between the quantized conductance and the usual conductance.
In order to express the characteristic feature on the temperature dependence of thermal conductance explicitly, let us extrapolate the thermal conductance by the power-law as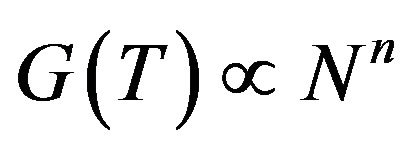 . This enables us to discuss the crossover from
. This enables us to discuss the crossover from 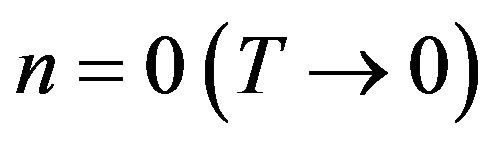 to
to 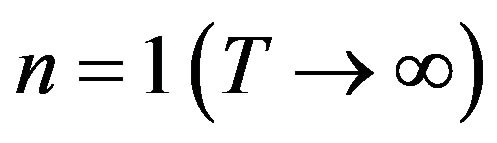 for various temperatures. Figure 2 shows the exponent
for various temperatures. Figure 2 shows the exponent ![]() as a function of the temperature. The temperature is measured in units of
as a function of the temperature. The temperature is measured in units of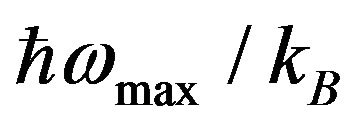 . The horizontal axis cor-
. The horizontal axis cor-
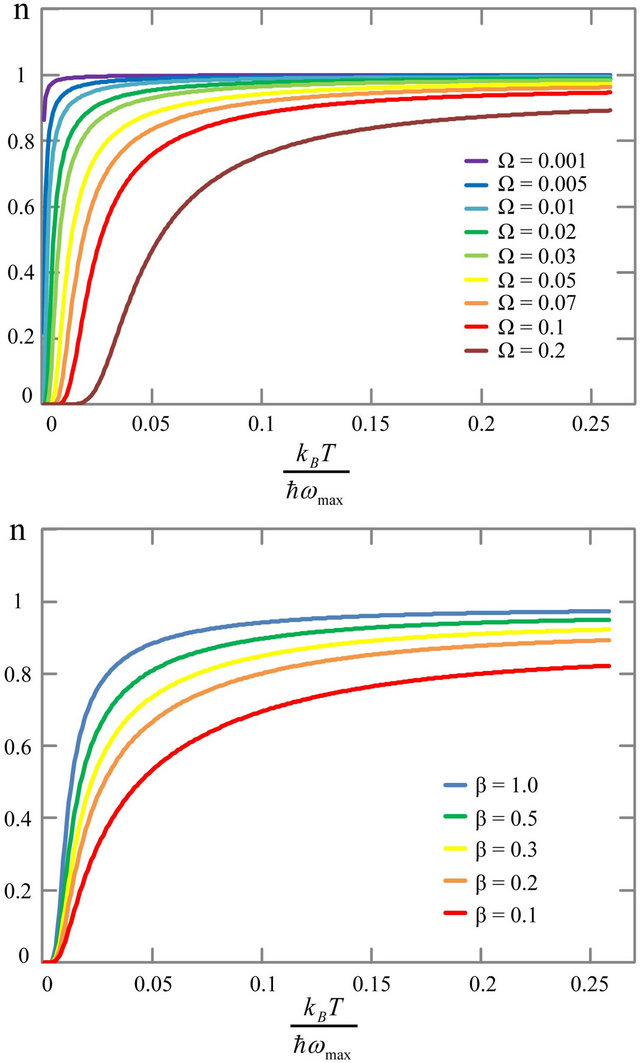
Figure 2. (Top) Exponent ![]() of thermal conductance
of thermal conductance  as a function of temperature
as a function of temperature  for various parameters of
for various parameters of 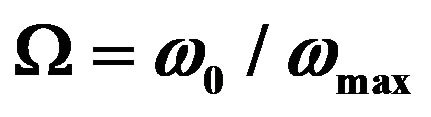 with
with ; (Bottom) Exponent
; (Bottom) Exponent ![]() as a function of
as a function of  for various parameters of
for various parameters of  with
with .
.
responds to the temperatures from 0 to 300 K for the maximum phonon energy of typical parameter of 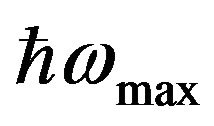 of 100 meV. We note that this parameter value would be different from material to material in the realistic systems. It is observed that smooth transition curves from the quantized conductance regime
of 100 meV. We note that this parameter value would be different from material to material in the realistic systems. It is observed that smooth transition curves from the quantized conductance regime  to the usual thermal conductance regime
to the usual thermal conductance regime  are obtained. The upper panel shows the exponent
are obtained. The upper panel shows the exponent ![]() for various
for various  with
with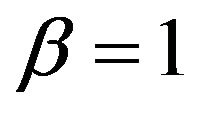 . The onset temperature is determined by
. The onset temperature is determined by  because only four phonon modes exist under the frequency
because only four phonon modes exist under the frequency  leading to the quantized conductance. With an increase of temperature, the second term dependent on
leading to the quantized conductance. With an increase of temperature, the second term dependent on  in Equation (3) enhances and
in Equation (3) enhances and ![]() approaches to one. The lower panel shows the exponent for various
approaches to one. The lower panel shows the exponent for various  with
with . As the parameter
. As the parameter  becomes smaller or
becomes smaller or  becomes larger, the asymptotic behavior of the exponent
becomes larger, the asymptotic behavior of the exponent ![]() to approach the value of
to approach the value of 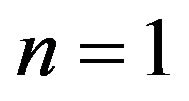 becomes slower. This is because the first term which is independent of
becomes slower. This is because the first term which is independent of  in Equation (3) becomes not negligible in this case.
in Equation (3) becomes not negligible in this case.
These calculations suggest that qualitative general behaviors might be elucidated using a simplified model based on the assumption of simple phonon dispersion relation. We note that these characteristic features are represented by only two critical parameters,  and
and . Realistic materials have more complex phonon dispersions. In the next section, we perform more elaborate atomistic calculations for the phonon dispersion and the thermal transport to investigate the details of crossover to the quantized thermal conductance and study the validity of the present simplified model.
. Realistic materials have more complex phonon dispersions. In the next section, we perform more elaborate atomistic calculations for the phonon dispersion and the thermal transport to investigate the details of crossover to the quantized thermal conductance and study the validity of the present simplified model.
3. Realistic Atomistic Calculations
Next, we consider the temperature dependence of thermal conductances of realistic quasi-one-dimensional materials. As typical examples, we take SiNWs, DNWs, and CNTs, and analyze the phonon transport properties from an atomistic viewpoint. The Hamiltonian  for the present phonon transport is expressed as follows:
for the present phonon transport is expressed as follows:
 (4)
(4)
Here 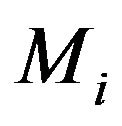 is a mass of
is a mass of  -th atom and
-th atom and  is an operator for displacement of
is an operator for displacement of  -th atom along
-th atom along ![]() direction from equilibrium position, respectively. We split the total Hamiltonian into four pieces:
direction from equilibrium position, respectively. We split the total Hamiltonian into four pieces:
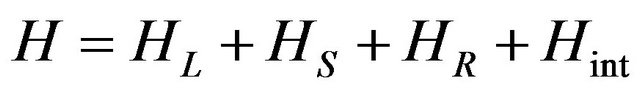 where
where 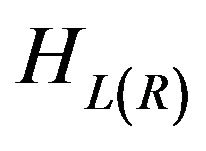 is the Hamiltonian for the left (right) lead,
is the Hamiltonian for the left (right) lead,  is for the scattering region, and
is for the scattering region, and  is for the interaction between the scattering region and the left (right) lead. Using the NEGF technique [11], the thermal current
is for the interaction between the scattering region and the left (right) lead. Using the NEGF technique [11], the thermal current  and the thermal conductance
and the thermal conductance  from the left lead to the scattering region can be expressed in the similar form as Equations (1) and (3) such as
from the left lead to the scattering region can be expressed in the similar form as Equations (1) and (3) such as
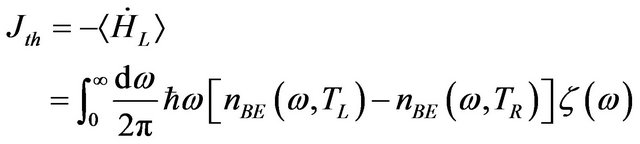
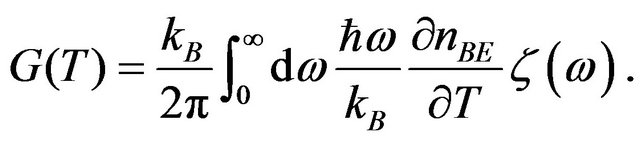 (5)
(5)
Here the bracket ![]() denotes the non-equilibrium statistical average of the physical observable and
denotes the non-equilibrium statistical average of the physical observable and 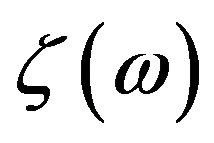 is the transmission coefficient for the phonon transport through the scattering region given by
is the transmission coefficient for the phonon transport through the scattering region given by
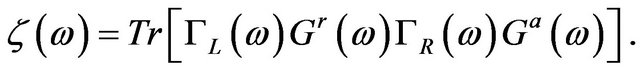 (6)
(6)
Here, 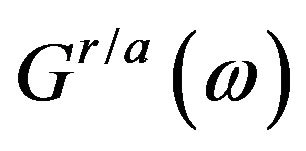 is the retarded/advanced Green’s function for the scattering region and
is the retarded/advanced Green’s function for the scattering region and  is the coupling constant. For the ideal ballistic limit without any scatterings,
is the coupling constant. For the ideal ballistic limit without any scatterings,  is equal to the number of phonon subbands at frequency
is equal to the number of phonon subbands at frequency![]() .
.
The retarded/advanced Green’s function for the scattering region is given by
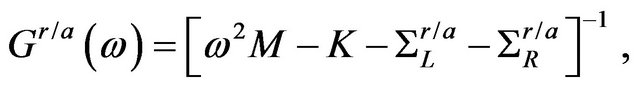 (7)
(7)
where  is the diagonal matrix whose element is a mass of a silicon or a carbon atom and
is the diagonal matrix whose element is a mass of a silicon or a carbon atom and  is the retarded/advanced self-energy due to the coupling to the left/right semi-infinite lead with the scattering region, which is obtained independently from the atomistic structure of the lead. We use a quick iterative scheme with the surface Green’s function technique [15] to calculate the self-energy for complex atomic structures of nanowires. The coupling constant
is the retarded/advanced self-energy due to the coupling to the left/right semi-infinite lead with the scattering region, which is obtained independently from the atomistic structure of the lead. We use a quick iterative scheme with the surface Green’s function technique [15] to calculate the self-energy for complex atomic structures of nanowires. The coupling constant 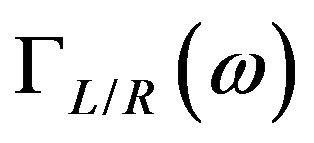 in Equation (6) is then obtained from
in Equation (6) is then obtained from
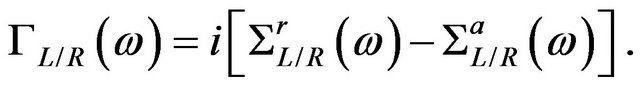 (8)
(8)
The dynamical matrix  which is contained in the total Hamiltonian is constructed from the force constants between the atoms. The matrix elements of
which is contained in the total Hamiltonian is constructed from the force constants between the atoms. The matrix elements of  are calculated by finite difference of the force
are calculated by finite difference of the force 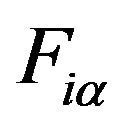 with respect to
with respect to 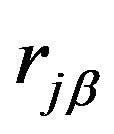 as
as
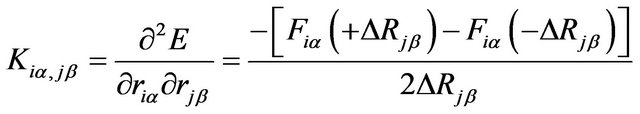 (9)
(9)
The force 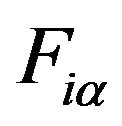 is obtained from the derivative of
is obtained from the derivative of ![]() with respect to
with respect to , where
, where 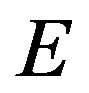 is the total energy of the system and
is the total energy of the system and 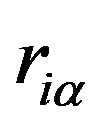 is the atomic coordinate of the
is the atomic coordinate of the 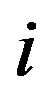 -th atom along the
-th atom along the ![]() direction. Therefore
direction. Therefore  indicates the force of the
indicates the force of the  -th atom along the
-th atom along the ![]() direction generated by the
direction generated by the  -th atom along the
-th atom along the  direction with a displacement of
direction with a displacement of 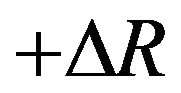 from the pristine wire’s equilibrium positions. Here
from the pristine wire’s equilibrium positions. Here 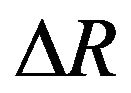 is a displacement, for which we take
is a displacement, for which we take 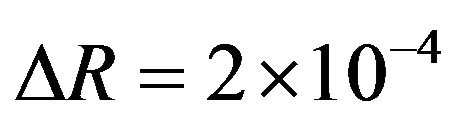 Å in the present work. As for the total energy formula
Å in the present work. As for the total energy formula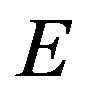 , we use the interatomic Tersoff potential [16] for silicon systems and Brenner potential [17] for carbon systems. These potentials describe the interatomic potentials with only elementary functions of atomic coordinates. The Tersoff (Brenner) potential describes total energy as follows:
, we use the interatomic Tersoff potential [16] for silicon systems and Brenner potential [17] for carbon systems. These potentials describe the interatomic potentials with only elementary functions of atomic coordinates. The Tersoff (Brenner) potential describes total energy as follows:
 (10)
(10)
 (11)
(11)
Here,  ,
, 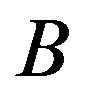 ,
, 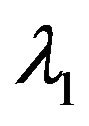 and
and  are constants,
are constants, ![]() is a distance between the
is a distance between the 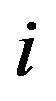 -th and
-th and  -th atoms and
-th atoms and 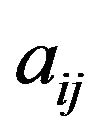 and
and  are determined by only atomic coordinates.
are determined by only atomic coordinates.
Figures 3(a)-(c) show the phonon dispersion relations
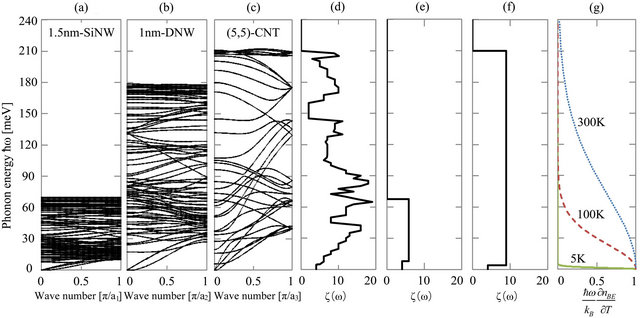
Figure 3. Phonon dispersion relations of (a)  -SiNW with 1.5 nm in diameter; (b)
-SiNW with 1.5 nm in diameter; (b)  -DNW with 1 nm in diameter; and (c) (5,5)-CNT. Here,
-DNW with 1 nm in diameter; and (c) (5,5)-CNT. Here, ![]() =5.362 Å,
=5.362 Å, 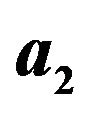 =3.567 Å, and
=3.567 Å, and 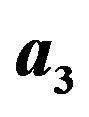 =2.49 Å are unit vectors of the SiNW, DNW, and CNT, respectively; (d) Transmission function
=2.49 Å are unit vectors of the SiNW, DNW, and CNT, respectively; (d) Transmission function 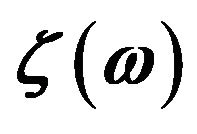 for the phonon dispersion relation of (5,5)-CNT; (e)
for the phonon dispersion relation of (5,5)-CNT; (e) 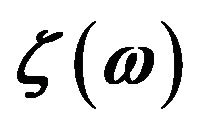 corresponding to the simplified model for the
corresponding to the simplified model for the  -SiNW; (f)
-SiNW; (f) 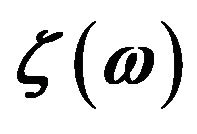 corresponding to the simplified model for the (5,5)-CNT; (g) Differentials of the distribution functions
corresponding to the simplified model for the (5,5)-CNT; (g) Differentials of the distribution functions 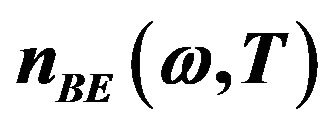 with respect to
with respect to ![]() for 5 K (green solid line), 100 K (red dashed line), and 300 K (blue dotted line). Note that the integral of its product with
for 5 K (green solid line), 100 K (red dashed line), and 300 K (blue dotted line). Note that the integral of its product with  corresponds to
corresponds to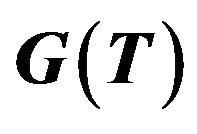 .
.
of a 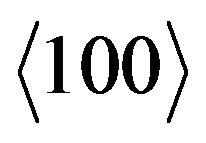 -SiNW with a diameter of 1.5 nm, a
-SiNW with a diameter of 1.5 nm, a  -DNW with a diameter of 1.0 nm, and a (5,5)-CNT respectively. Since the SiNW and the DNW have the same atomic configurations with the same numbers of atoms in cross-sectional areas, these two phonon bands have similar structures with a difference of the phonon energy range, for which DNW has a larger value due to the stronger interatomic force acting between carbon atoms. On the other hand, the CNT has a cylindrical shape and each band of the CNT tends to have dispersions with a wide energy range, which induces large thermal conductance. Figures 3(d) and (g) show the transmission function
-DNW with a diameter of 1.0 nm, and a (5,5)-CNT respectively. Since the SiNW and the DNW have the same atomic configurations with the same numbers of atoms in cross-sectional areas, these two phonon bands have similar structures with a difference of the phonon energy range, for which DNW has a larger value due to the stronger interatomic force acting between carbon atoms. On the other hand, the CNT has a cylindrical shape and each band of the CNT tends to have dispersions with a wide energy range, which induces large thermal conductance. Figures 3(d) and (g) show the transmission function 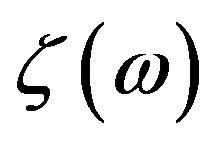 for the CNT and the differentials of the distribution functions
for the CNT and the differentials of the distribution functions  as a function of the phonon energy. The integral of these products corresponds to the thermal conductance
as a function of the phonon energy. The integral of these products corresponds to the thermal conductance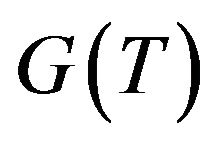 .
.
At small phonon energy regime, we see that all quasione-dimensional structures have four acoustic modes, one longitudinal, two flexural, and one torsional modes, which do not depend on the detailed structures of nanowires. When only these four modes conduct heat, thermal conductance shows a universal feature for any material or diameter. This accounts for the quantized thermal conductance at low temperature regime [2]. As the temperature increases, various phonon modes begin to contribute to the thermal transport.
Here, we compare the behaviors of thermal conductance for SiNWs and CNTs, which have completely different atomic configurations as nanowires. The bottom panels of Figure 4 show the temperature dependences of
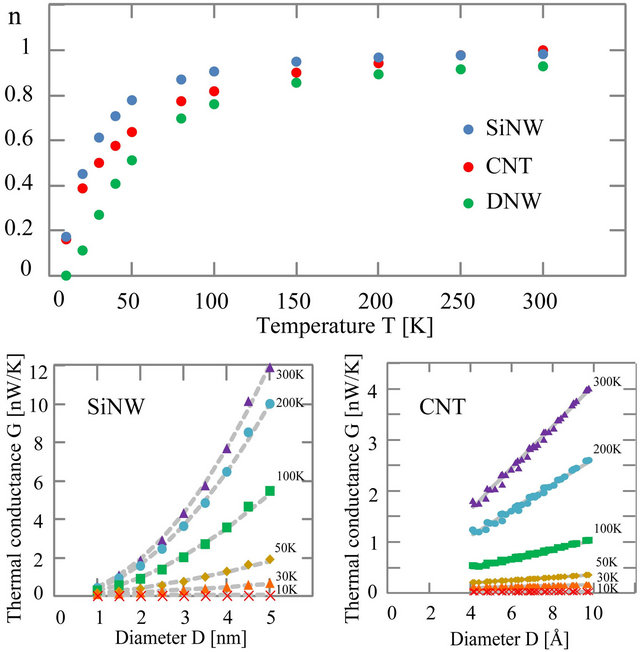
Figure 4. (Top) Exponent ![]() for several temperatures extrapolated from the thermal conductance as described by
for several temperatures extrapolated from the thermal conductance as described by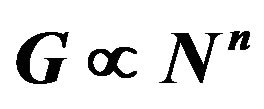 , where
, where  is the number of atoms in the crosssection area. (Bottom) Thermal conductance as a function of the diameter
is the number of atoms in the crosssection area. (Bottom) Thermal conductance as a function of the diameter  for several temperatures in cases of the SiNW (left) and the CNT (right).
for several temperatures in cases of the SiNW (left) and the CNT (right).
the calculated thermal conductances as a function of the diameter  for the SiNW (left) and the CNT (right). At 300K the thermal conductances are proportional to the square of the diameter
for the SiNW (left) and the CNT (right). At 300K the thermal conductances are proportional to the square of the diameter 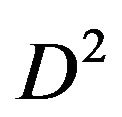 for SiNWs (left) and to the diameter
for SiNWs (left) and to the diameter  for CNTs (right). Since the SiNWs have columnar shapes and the CNTs have cylindrical shapes,
for CNTs (right). Since the SiNWs have columnar shapes and the CNTs have cylindrical shapes, 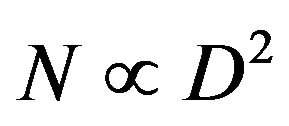 for the SiNWs and
for the SiNWs and 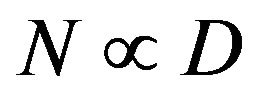 for the CNTs. This indicates that the thermal conductance is proportional to the cross-sectional area at high temperature. As the temperature decreases from 300 K, the behaviors of thermal conductances to the diameter dependence are seen to change gradually. At enough low temperature, we see no dependence on a diameter
for the CNTs. This indicates that the thermal conductance is proportional to the cross-sectional area at high temperature. As the temperature decreases from 300 K, the behaviors of thermal conductances to the diameter dependence are seen to change gradually. At enough low temperature, we see no dependence on a diameter  for the thermal conductance
for the thermal conductance 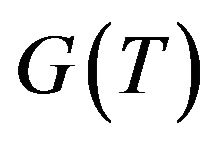 for both cases.
for both cases.
To analyze the temperature dependence of the thermal conductance, as we did in the previous section, we extrapolate the exponents ![]() for the thermal conductance
for the thermal conductance 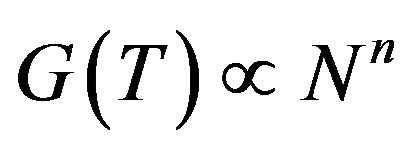 for the SiNWs, DNWs and CNTs, which are shown in the top panel of Figure 4. At 300 K, the exponents of wires are nearly equal to 1 which correspond to usual thermal conductance and the exponents approach to 0 which correspond to “quantum-type” thermal conductance as the temperature decreases. We see that the crossover to
for the SiNWs, DNWs and CNTs, which are shown in the top panel of Figure 4. At 300 K, the exponents of wires are nearly equal to 1 which correspond to usual thermal conductance and the exponents approach to 0 which correspond to “quantum-type” thermal conductance as the temperature decreases. We see that the crossover to  from
from  differs slightly according to the kinds of materials. The rapid decrease of the exponent
differs slightly according to the kinds of materials. The rapid decrease of the exponent ![]() from the saturation appears at the lowest temperature for SiNWs. This can be understood from the scaling of the temperature by
from the saturation appears at the lowest temperature for SiNWs. This can be understood from the scaling of the temperature by  as shown in Figures 3(e) and (f), where
as shown in Figures 3(e) and (f), where 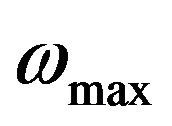 are 70 meV for SiNWs, 180 meV for DNWs, and 210 meV for CNTs. Among these materials the normalized temperature of SiNWs is the lowest, which is also related to the Debye temperature in the specific heat. To compare the behaviors of thermal conductance between DNWs and CNTs which have similar
are 70 meV for SiNWs, 180 meV for DNWs, and 210 meV for CNTs. Among these materials the normalized temperature of SiNWs is the lowest, which is also related to the Debye temperature in the specific heat. To compare the behaviors of thermal conductance between DNWs and CNTs which have similar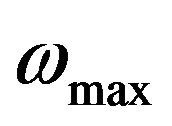 , we see that the onset temperature of CNTs is lower. This can be understood because
, we see that the onset temperature of CNTs is lower. This can be understood because 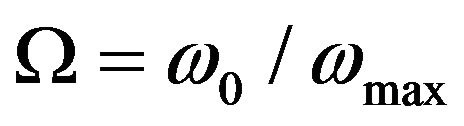 is smaller for CNTs than DNWs. We note that another parameter of the proportional constant
is smaller for CNTs than DNWs. We note that another parameter of the proportional constant  is determined so that
is determined so that 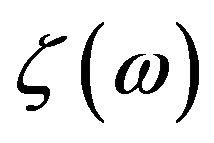 in the simplified model has the same area as that in the realistic atomic system.
in the simplified model has the same area as that in the realistic atomic system.
These data show that the simplified model as introduced in the previous section is effective to understand the behaviors of crossover to quantized thermal conductance, even if it is expressed with two parameters by the abbreviation of the precise transmission coefficients 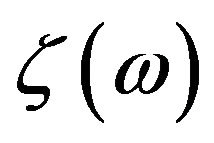 to the simplified ones as shown in Figures 3(e) and (f). Here we note that, in the present theoretical scheme, thermal conductance should not necessarily be proportional to the cross-sectional area in the high temperature limit, since the contribution to the transport from each phonon band depends on the width of the band dispersion, while the number of total phonon modes is proportional to the number of atoms in a unit cell.
to the simplified ones as shown in Figures 3(e) and (f). Here we note that, in the present theoretical scheme, thermal conductance should not necessarily be proportional to the cross-sectional area in the high temperature limit, since the contribution to the transport from each phonon band depends on the width of the band dispersion, while the number of total phonon modes is proportional to the number of atoms in a unit cell.
Phonon-phonon scattering effect is not taken into account here. Experimentally it has been observed that for nanowires less than 37 nm thick, the effect of anharmonicity on the thermal conductivity is not significant up to room temperature. Instead, the phonon boundary scattering due to surface roughness becomes important for the nanowires [18]. The effect is also discussed theoretically [12]. It is shown that anharmonicity is suppressed for nanowires shorter than tens of nanometers. We consider the clean wire case, where no edge or internal scatterings are present simply. However, note that such scatterings have the effects on the thermal conductance in the length direction![]() . We have checked the effects of the boundary scattering due to surface roughness in the SiNW on the exponent
. We have checked the effects of the boundary scattering due to surface roughness in the SiNW on the exponent![]() . We remove 5% atoms from the surface randomly with 10 different configurations and treat the results statistically. As a result, we find that the trend of the exponential behavior of the conductance from
. We remove 5% atoms from the surface randomly with 10 different configurations and treat the results statistically. As a result, we find that the trend of the exponential behavior of the conductance from 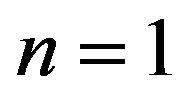 to 0 remains for the boundary scattering although the conductance reduces.
to 0 remains for the boundary scattering although the conductance reduces.
4. Conclusion
We have proposed a simplified model to discuss the crossover to universal quantized thermal conductance of the quasi-one-dimensional systems. From the calculations of the temperature dependence of thermal conductance for the realistic atomistic systems of CNTs, SiNWs, and DNWs, for which the crossover from the usual behavior at room temperature to the universal “quantum-type” behavior at low temperature is obtained by using the non-equilibrium Green’s function techniques with interatomic potentials, we find that this crossover occurs smoothly for the quasi-one-dimensional materials and its universal behavior is well reproduced by the simplified model characterized by two parameters.
5. Acknowledgements
This work is supported in part by a Grant-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science and Technology of Japan.
REFERENCES
- A. I. Boukai, Y. Bunimovich, J. T. Kheli, J.-K. Yu, W. A. Goddard III and J. R. Heath, “Silicon Nanowires as Efficient Thermoelectric Materials,” Nature, Vol. 451, 2008, pp. 168-171. doi:10.1038/nature06458
- L. G. C. Rego and G. Kirczenow, “Fractional Exclusion Statistics and the Universal Quantum of Thermal Conductance: A Unifying Approach,” Physical Review B, Vol. 59, No. 20, 1999, pp. 13080-13086. doi:10.1103/PhysRevB.59.13080
- K. Schwab, E. A. Henriksen, J. M. Worlock and L. Roukes, “Measurement of the Quantum of Thermal Conductance,” Nature, Vol. 404, 2000, pp. 974-977. doi:10.1038/35010065
- O. Chiatti, J. T. Nicholls, Y. Y. Proskuryakov, N. Lumpkin, I. Farrer and D. A. Ritchie, “Quantum Thermal Conductance of Electrons in a One-Dimensional Wire,” Physical Review Letters, Vol. 97, 2006, Article ID: 056601. doi:10.1103/PhysRevLett.97.056601
- M. Meschke, W. Guichard and J. P. Pekola, “Single-Mode Heat Conduction by Photons,” Nature, Vol. 444, 2006, pp. 187-190. doi:10.1038/nature05276
- Y. Dubi and M. Di Ventra, “Colloquium: Heat Flow and Thermoelectricity in Atomic and Molecular Junctions,” Reviews of Modern Physics, Vol. 83, No. 1, 2011, pp. 131-156.
- M. Büttiker, Y. Imry, R. Landauer and S. Pinhas, “Generalized Many-Channel Conductance Formula with Application to Small Rings,” Physical Review B, Vol. 31, 1985, pp. 6207-6215. doi:10.1103/PhysRevB.31.6207
- L. V. Keldysh, “Diagram Technique for Nonequilibrium Processes,” Soviet Physics—JETP, Vol. 20, No. 4, 1965, pp. 1018-1026.
- C. Caroli, R. Combescot, P. Nozieres and D. Saint-James, “Direct Calculation of the Tunneling Current,” Journal of Physics C: Solid State Physics, Vol. 4, No. 8, 1971, p. 916. doi:10.1088/0022-3719/4/8/018
- Y. Meir and N. S. Wingreen, “Landauer Formula for the Current through an Interacting Electron Region,” Physical Review Letters, Vol. 68, No. 16, 1992, pp. 2512-2515. doi:10.1103/PhysRevLett.68.2512
- A. Ozpineci and S. Ciraci, “Quantum Effects of Thermal Conductance through Atomic Chains,” Physical Review B, Vol. 63, No. 12, 2001, Article ID: 125415. doi:10.1103/PhysRevB.63.125415
- N. Mingo and L. Yang, “Phonon Transport in Nanowires Coated with an Amorphous Material: An Atomistic Green’s Function Approach,” Physical Review B, Vol. 68, No. 24, 2003, Article ID: 245406. doi:10.1103/PhysRevB.68.245406
- T. Yamamoto and K. Watanabe, “Nonequilibrium Green’s Function Approach to Phonon Transport in Defective Carbon Nanotubes,” Physical Review Letters, Vol. 96, No. 25, 2006, Article ID: 255503. doi:10.1103/PhysRevLett.96.255503
- K. Yamamoto, H. Ishii, N. Kobayashi and K. Hirose, “Effects of Vacancy Defects on Thermal Conduction of Silicon Nanowire: Nonequilibrium Green’s Function Approach,” Applied Physics Express, Vol. 4, 2011, Article ID: 085001. doi:10.1143/APEX.4.085001
- M. P. Lopez-Sancho, J. M. Lopez-Sancho and J. Rubio, “Quick Iterative Scheme for the Calculation of Transfer Matrices: Application to Mo (100),” Journal of Physics F: Metal Physics, Vol. 14, No. 5, 1984, p. 1205. doi:10.1088/0305-4608/14/5/016
- J. Tersoff, “Empirical Interatomic Potential for Silicon with Improved Elastic Properties,” Physical Review B, Vol. 38, No. 14, 1988, pp. 9902-9905. doi:10.1103/PhysRevB.38.9902
- D. W. Brenner, “Empirical Potential for Hydrocarbons for Use in Simulating the Chemical Vapor Deposition of Diamond Films,” Physical Review B, Vol. 42, No. 15, 1990, pp. 9458-9471. doi:10.1103/PhysRevB.42.9458
- D. Li, Y. Wu, P. Kim, L. Shi, P. Yang and A. Majumdar, “Thermal Conductivity of Individual Silicon Nanowires,” Applied Physics Letters, Vol. 83, No. 14, 2003, p. 2934.
NOTES
*Corresponding author.

