Received 13 July 2015; accepted 8 August 2015; published 11 August 2015

ABSTRACT

This paper presents a similitude and computational analysis of the performance of a scaled-down model of a paddle wheel style hydrokinetic generator device used for generating power from the flow of a river. The paddle wheel dimensions used in this work are one-thirtieth scale of the full- size paddle wheel. The reason for simulating the scaled-down model was to prepare for the testing of a scaled-down physical prototype. Computational Fluid Dynamics using ANSYS Fluent 14.0 software was used for the computational analysis. The scaled-down dimensions were used in the simulations to predict the power that can be generated from the scaled size model of the paddle wheel, having carried out similitude analysis between the scaled down size and its full-size. The dimensionless parameters employed in achieving similitude are the Strouhal number, power coefficient, and pressure coefficient. The power estimation of the full-size was predicted from the scaled size of the paddle wheel based on the similitude analysis.

Keywords:

Similitude, Paddle Wheel, CFD, Power Generation, Hydrokinetics

1. Introduction

The demand for energy coupled with maintaining its affordability and decreasing its pollution makes it imperative to look into ways in which affordable, clean and readily available energy sources can be harnessed.

Hydropower is an energy form obtainable from water and it is a clean form of energy source which is also renewable. Different forms of hydroelectric power generation have previously been developed, the most important forms being (a) Conventional hydroelectric dam, (b) Tidal power and (c) Ocean wave energy [1] .

The above mentioned forms of hydroelectric power generation use either the pressure-head of water (dams) or oscillatory motion of the water (ocean waves and tides) for electricity generation, though some [2] [3] have actually looked into the run-off of rivers as a power generation means.

The paddle wheel is a hydrokinetic power generating device that uses the flow of a river (low-head) for its energy. The paddle wheel in this paper is designed such that the rotational effect created on it by the water current is transferred from the paddles onto a shaft in its midsection, and this shaft drives a generator in order to produce electric power.

Previous research work on the generation of electricity from a paddle-wheel was carried out using analytical and computational analysis on a full-size (pilot) paddle wheel [4] . Computational Fluid Dynamics (CFD) using ANSYS FLUENT13.0 version software was employed for the computational analysis in the previous work.

The aim of this paper is to generate a computational analysis result for a scaled down version of the paddle wheel, in order to have a comparison to results that will be generated in a laboratory test of the scaled size model, ensure similitude between the full-size and the scaled-down model, and also develop a mathematical relationship that can predict the power generation capacity of a full scale-sized paddle wheel from a scaled-down size of the paddle wheel.

2. Problem Statement

Over the last 22 years, global electricity production has doubled and electricity demand is rising rapidly around the world as economic development spreads to emerging economies [5] . Not only has electricity demand increased significantly, it is the fastest growing end-use of energy [6] . According to the International Energy Agency, the world needs to invest $48 trillion between now and 2035 to meet global energy demands [7] . The bulk of this will be used in offsetting the declining base oil and gas production, replace aging power plants and fund projects to meet the growing needs of emerging economies.

Energy Overview

There are two main sources from which energy is generated. These are renewable and non-renewable energy sources.

Renewable energy: It is generally defined as the energy that comes from resources which are replenished over time. Renewable energy sources are much sought after due to their low carbon dioxide emission [8] , thus providing eco-efficient solution for developed and developing countries. The European Union is said to be generating 71% of its electricity from renewable energy sources [9] .

The different forms of renewable energy sources include; solar energy, wind power, hydropower, biomass, and geothermal energy. This study looks into a means of generating energy from hydropower.

3. Hydropower

Hydropower can simply be referred to as the power captured from water as it flows. This movement could be from potential to kinetic energy, the process of which is achieved by gravity [10] . Hydropower is at present; the primary large-scale renewable alternative to fossil fuel and nuclear in the generation of electricity. It provides approximately 19% of the electricity produced worldwide [11] . Studies show that a total of 66 countries obtain at least half of their electricity from hydropower, with large economies like Brazil, Canada, and Norway having 97%, 62%, and 99% of national electricity production, respectively [12] . Worldwide, only about a third of the economically feasible potential of hydropower has been developed.

Unlike other renewable energy technologies, the multiplicity of wave, tidal, and hydrokinetic power devices show that the power generation potential from world’s ocean and rivers is considerable [13] . Many devices are currently being explored and tested in order to harness the kinetic energy in the ocean and rivers. Examples of some hydrokinetic energy devices are point absorbers, hydrokinetic turbines, and paddle wheels.

3.1. Point Absorber

One form of Wave Energy Converter (WEC), developed in 2011, is used when the horizontal size of the device is much smaller than the typical wavelength [14] . The point absorber, either floating or submerged, transforms the vertical motion of the ocean waves into rotational or linear motion, which is then used to drive an electrical generator by means of a power take off (PTO) system.

Initially, high speed rotary machines, such as hydraulic turbines, were being used by point absorbers to extract energy from ocean waves, but in recent years, linear generators have been proposed in several marine applications as a well-suited technology [15] [16] .

Disadvantages of the point absorber approach include: the complexity of the drive mechanism, difficulty of mooring in an offshore environment, and its low efficiency when not in resonance with the incident wave regime.

3.2. Hydrokinetic Turbines

These types of turbines are fully submerged in water and make use of the kinetic flow of the water in driving the turbine blades and hence generate electricity. The power generation capacity of hydrokinetic turbines is in the range of 30 - 50 kW for a water speed of 3 - 4 m/s [17] . A major disadvantage of these turbines is the damage to the blades of the turbines as a result of debris that may be in the water flow path which consequently stops the power production of the turbine [18] . Typical examples of the hydrokinetic turbine are the submerged windmill turbine [19] and transverse horizontal axis turbine [17] [20] .

3.3. Paddle Wheel

The paddle wheel has been used for many years on ships or vessels to produce thrust, when powered by an engine. However, the paddle wheel took a cue from the water wheel in the generation of power. The water wheel, initially used to lift water and irrigate fields and later a means to generate mechanical power for milling, attracted scientific interest as an important energy generating device. The water wheel was utilized well into the last century where about 7554 wheels were in operation 1927 in Germany [21] , and in Switzerland about 7000 small scale hydropower stations were in operation till 1924 [22] . Despite the variety of designs of paddle wheels proposed by Watkins [23] , Rogers [24] , and Winus [25] , very few modern researchers have looked into paddle wheel as a power generation device.

Recent development of hydrokinetic devices have created renewed interest in the use of these devices for power generation and paddle wheels are more advantageous in that they may be more resistive to debris that may be in the water flow [18] .

This study is a furtherance of a research on paddle wheel as a device for power generation. Liu and Penyanmi [4] carried out empirical and computational analysis on a paddle wheel making use of the full-size design in the analysis. This device is required to be tested in a laboratory in order to validate the empirical and computational results obtained. In order to achieve this feat, a scaled-down size of the paddle wheel is required, since it would be expensive, time consuming, and unwise to carry out experiment on a full-size prototype.

The aim of this study is to carry out CFD analysis on the scaled-down model. The behavior of the full-size prototype must be similar to that of the scaled-down model; hence similitude must be achieved between these two sizes, and the power generation capacity of the full-size should be approximately predicted from the performance of the scaled-down model.

4. Similitude

Similitude is used to describe model tests and is used to transfer model test results to the real application. It makes use of the laws of similarity. The most important thing in scaling is to achieve similarity between the scaled model and its test conditions to that of the real application and its test conditions.

There are three basic types of similitude in hydraulic problems namely: geometric similarity (similarity of shape), kinematic similarity (similarity of motion), and dynamic similarity (similarity of forces). These similarities should be fulfilled to ensure hydrodynamic similarity between a scaled model and its full-size.

Dynamic similarity is often used as a catch-all, because it implies that geometric and kinematic similitudes have already been met. Dimensionless numbers play an important role in establishing dynamic similarity, and these numbers are obtained from ratios of relevant forces that act in fluid dynamics. The dimensionless numbers often come across in fluid dynamics are [26] : Reynolds number, Froude number, Euler number, Cauchy number, Weber number, and Strouhal number.

4.1. Similitude for Turbomachinery

Dimensionless analysis plays an important role in the development and utilization of turbomachinery, as it has enabled the test of relatively small turbomachines. Dimensionless coefficients can be obtained through various parameters involved in the application of turbomachinery, and the coefficients form the basis of similitude in turbomachinery.

Parameters of significant consideration in turbomachines include: Power, rotational speed, flow rate, pressure change across the blade, density of fluid, viscosity of fluid, and the outer diameter of the machine [26] . Using these parameters, various dimensionless groupings can be obtained.

4.2. Scale Effects

Scale effects result from distortions introduced by a non-dominant force in a hydrodynamic analysis [27] . They occur when one or more dimensionless parameters differ between a model and its real world prototype. Scale effects are often small, but not always negligible altogether. Some forces become more dominant in the model than in the full size prototype, and this distorts the results [28] .

5. Analysis of the Scaled Model of Paddle Wheel

For the paddle wheel in a river scenario, the parameters of significant consideration are: Power (Ẇ), velocity of fluid (V), rotational speed of paddles (ω), pressure change across paddle blades (∆P), gravitational acceleration (g), density of fluid (ρ), viscosity of fluid (μ), and characteristic length of paddle wheel (wetted depth) (l).

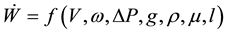
Using ρ, v and l as the repeating variables, a set of dimensionless groupings obtained are:

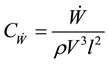
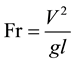
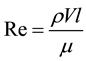
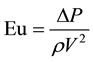
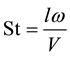
The Euler number is shown to be a function of the Froude and Reynolds number in most practical hydraulic model tests [27] , thus satisfying the Euler number approximately satisfies the Froude and Reynolds numbers. Hence the dimensionless grouping for the paddle wheel model reduces to:

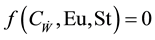
Making these numbers constant for both the model and its real application ensures similitude of the paddle wheel.

The Euler number 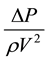can be written in force form as and this has to be constant for both full scale prototype (shown with the subscript f) and model (shown with the subscript m),

(1)

And if the scaling factor, λ, is defined as the characteristic length of the full-size prototype (l_f) over the characteristic length of the model (l_m), we get the equations shown in (2) below.

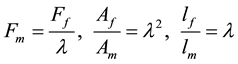(2)

If ρ is constant,

(3)

If ρ is not constant,

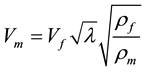(4)

From the Strouhal number, St:

(5)

From the power coefficient, C_Ẇ:

If ρ is constant,

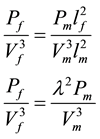(6)

The Euler number is also a form of the pressure coefficient, given as:

If ρ is constant,

(7)

If the paddle wheel parameters satisfy these coefficients, the model and full scale of the paddle wheel are in mechanical similitude.

Based on the above analysis of the model of the paddle wheel’s water velocity and angular velocity, and assuming that density is a constant; the empirical analysis of the model of the paddle wheel was evaluated using the equations from the analysis of the full scale size [4] , and the result is as shown in Figure 1.

5.1. Computational Model

Computational analysis was used to estimate the power generation capacity of the paddle wheel, and the soft ware package ANSYS FLUENT [29] was used in modeling, analyzing, and simulating the paddle wheel in water scenario. The input variables to the computational analysis were based on the results obtained from the similitude analysis.

5.1.1. Geometry

The geometry of the paddle wheel and the associated moving water was designed in the Design-Modeler, 3D Computer Aided Design (CAD) software available in the ANSYS workbench. In the computational environment, the physical domain is considered to be only fluid as there is no heat or mass transfer between the paddle wheel and water [4] . The air above the water line was not considered in the simulation as this area was taken as a pressure outlet. The geometry of the paddle wheel under water is shown in Figure 2(a).

5.1.2. Meshing

Mesh generation is one of the most important steps during the pre-processing stage after the definition of the domain geometry. CFD requires the subdivision of the domain into smaller, non-overlapping subdomains in order to solve the flow physics within the domain geometry that has been created. This results in the generation of a grid of cells (elements or control volumes) overlaying the whole domain geometry [30] . The meshing for the entire body of the model was carried out using automatic (quadrilateral dominant) mesh method. The mesh of the paddle wheel is shown in Figure 2(b) having a number of cells of 4668.

5.1.3. CFD Analysis

Water velocities for the scaled-down model of 22, 27, 33, 44, and 55 mph were used. These velocities were obtained from the similitude analysis based on 4, 5, 6, 8, and 10 mph applied to the full-size model. Thus the scaled-up velocities were used for the CFD analysis to find the power generation capacity of the scaled-down model. At each velocity, six angular velocities (resulting from the Strouhal number analysis) from 0 to a maximum angular velocity (where the maximum angular velocity was defined as being when the net generated torque on the wheel becomes zero), were applied to the paddle wheel for the simulation. In carrying out the analysis, some important algorithms, theoretical models, and other settings were used as shown in Table 1.

5.2. Power Prediction from Scaled Model

The essence of building a model is to be able to save cost in experimenting, and also predict the performance of the full-scale device from the results obtained from the model, by scaling up these results. Hence, the power and torque obtained from the simulation of the model of the paddle wheel was scaled up using the power coefficient as given in Equation (6).

,

From (3)

(8)

Similarly

From (7),

But from (4)

Therefore

(9)

6. Results

From the analysis of similitude in (3), the velocities to be applied on the scaled down size of the paddle wheel for laboratory test and simulation are given in Table 2.

6.1. Power Generated from Paddle Wheel

The power generation capacity of the scaled model of the paddle wheel was estimated from simulations at the evaluated water velocities and corresponding angular velocities, and the results obtained are shown in Figure 3.

6.2. Similarity Law

To ensure similitude between the full-scale size and the scaled-model of the paddle wheel, dimensionless

groupings power coefficient, and pressure-coefficient, = constant should be the same for

both scale. This was evaluated, using the results shown above, and assuming the same fluid was used in the full- size analysis and the scaled model analysis i.e. density is constant, and is shown in Table 3. The results in Table 3 show that the Power Coefficient and the Pressure Coefficient are very similar, leading to the conclusion that similitude was achieved to a large extent during the analysis.

6.3. Prediction Capacity of Scaled Model of Paddle Wheel

Another essence of similitude, other than dimensionless groupings being constant for both full-sizes and scaled models, is to predict the result of the variable of interest for the full size from scaling up the results obtained from the analysis of the scaled model. Equation 8 was used for the prediction analysis of the power estimate of the full-size prototype, and the result obtained was compared to that obtained from the analysis carried out by Liu and Penyanmi [4] on the full-size model. The full-size of the paddle wheel was scaled down to a one-thirtieth of its dimension to make the scaling factor λ = 30. The predicted power from the scaled model is shown in Table 4.

7. Discussion

Similitude analysis was used to obtain the velocities that would be required to be applied on the scaled-down size of the paddle wheel as seen in Table 2, from which the corresponding angular velocities used for the simulation were obtained. The velocities obtained were based on the premise that the working fluid for both the full- size and scaled down size of the paddle wheel is water, hence the density is constant.

Figure 4 shows the pressure and velocity distributions of water around the paddle wheel and it was observed that the four blades to the left of the wheel contribute significantly to the power generation, while the remaining three blades merely assist in the continuous rotation of the wheel. Further work could be done to optimize the number of blades used.

For similitude to be justified, an evaluation of the power-coefficient and the pressure-coefficient was carried out on the full-size and the scaled model of the paddle wheel and the result as seen in Table 3 shows that these coefficients are close. The resulting disparities are as a result of scaled effects which occur when non-dominant forces on the full-size become dominant in the scaled model. In this instance, the gravitational force on the model is reduced which was dominant in the full size while turbulence is increased which was less dominant, and thus brings about an increase in the power coefficient in the model compared to that in the full size.

To further justify similitude, the result of power estimated from the simulation of the scaled model of the paddle wheel was scaled up based on the equation relating the model to the full-size for power prediction, it can be observed that the model sufficiently predicts the power that can be obtained from the full-size prototype, as Table 4 clearly depicts.

In reality, the velocities and angular velocities (up to 55 mph and 988 rpm) used in the simulation of the model of the paddle wheel will be highly difficult to achieve in the laboratory test of the wheel. It is recommended that a different, higher density, fluid be used for the laboratory test of the model. Based on the similitude analysis, the density of the fluid to be used for the model needs to be denser than water, as this will help reduce the operating velocity and make the laboratory test practicable.

8. Conclusion

The present work carried out CFD analysis on the scaled-down model of the paddle wheel. It demonstrated how similitude can be applied to a paddle wheel for the relevance of laboratory test or experimentation. It shows the relevant dimensionless groupings to the paddle wheel application and gives equations for predicting power and torque for hydrodynamic problems related to the paddle wheel. The velocity of water applied to the scaled model of the paddle wheel is very high, and this velocity is highly impractical to be achieved for the laboratory test of an actual scaled down prototype of the paddle wheel. The results obtained from this analysis will be compared to the laboratory test that will be carried out on the scaled down size of the paddle wheel at a future date.

9. Future Work

It is proposed that a liquid of higher density than water be used for the laboratory test in order to reduce the velocity of liquid that will be applied on the scaled model of paddle wheel for the laboratory test. This velocity can be obtained by the application of (4).

The paddle wheel in this study can be redesigned such that the blades do not run solidly from the axle edge, as this causes a wake zone behind each blade hence increasing the drag force that limits the rotation of the wheel and hence the power production capacity. The proposed design will have a section of the blade near the tip of the wheel and an open space between the axle and the blade. This will help eliminate wake zones behind the blades and improve power generation.

The power generation capacity can also be improved by adding a plate (bottom-fin) to the design of the wheel. This plate is placed beneath the paddle wheel at an inclined angle, and it directs water towards blades that the flow may not come in contact with. This helps to increase the number of blades that contribute to power generation.

Cite this paper

Oladapo S.Akinyemi,Terrence L.Chambers,YuchengLiu, (2015) Evaluation of the Power Generation Capacity of Hydrokinetic Generator Device Using Computational Analysis and Hydrodynamic Similitude. Journal of Power and Energy Engineering,03,71-82. doi: 10.4236/jpee.2015.38007

References