Journal of Materials Science and Chemical Engineering
Vol.03 No.07(2015), Article ID:57486,15 pages
10.4236/msce.2015.37007
The Reconstruction Technique of Multi-Product Production and MINLP Mathematical Modelling
Jernej Hosnar*, Anita Kovač-Kralj
Faculty of Chemistry and Chemical Engineering, University of Maribor, Maribor, Slovenia
Email: *jernej.hosnar@um.si
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 May 2015; accepted 26 June 2015; published 29 June 2015
ABSTRACT
Low efficiency, negative impacts on the environment and non-profitable operations are the main shortcomings of out-dated industrial processes. Such systems can be reconstructed and improved in the direction of multi-product operations. The study of this article focuses on the development of a method for multi-product operations by reconstructing out-dated industrial processes. This article contains the theory of a developed method that enables the updating of existing process units and integrated systems on the basis of reconstruction scenarios and pathways. The goals of the set out method are: 1) to maintain the existing process units and chemical plants to a greater extent, 2) to enable the potential for finding new process alternatives and technological solutions, 3) to provide a streamlined operation for all subsystems and total systems, 4) to promote environmental and social responsibilities, and 5) to apply the concept of the presented reconstruction method to non-profitable industrial processes. In regard to multi-product operations, a conceptual model is a suitable tool for the reconstruction of industrial processes. It connects several software tools and so enables quick decision-making between process alternatives. A reconstruction method provides foresight into the possible improvements to existing industrial processes. In comparison with the indirect synthesis of DME (simple reconstruction pathway), the lower operating costs from the direct synthesis of DME (complex reconstruction pathway) were confirmed.
Keywords:
Reconstruction of Industrial Processes, Multi-Product Production, Complex and Simple Reconstruction Pathways, MINLP Mathematical Modelling

1. Introduction
Low efficiency, negative effects on the environment and non-profitable operations are the main shortcomings of outdated industrial processes [1] . They can be remedied to a lesser extent by retrofits of individual process units or by saving energy or utility consumption (UC). Existing chemical plants can be adequately reconstructed in more suitable forms. A number of techniques, approaches and mathematical models have been developed for these purposes [2] - [5] . Models for approaches to the reconstructions of already existing and non-profitable chemical plants were obtained by authors [6] . In order to ensure flexible production and optimum operation it is insufficient just to look for savings in UC but it does make sense to adapt processes towards the direction of multi-feed/multi-product (MFMP) operations. MFMP systems have a positive impact on energy savings, cleaner production, and economic benefits. In recent times a significant amount of scientific research has been carried out in the field of synthesizing alternative and environmentally-friendly fuels. A promising alternative fuel is dimethyl-ether (DME). Scientists and technical experts describe it as having excellent chemical, physical and eco-friendly properties [7] . Fuel can be synthesized from a variety of raw materials containing high contents of carbon (C), oxygen (O) and hydrogen (H). Fuel production runs from: fossil fuels such as natural gas (NG) [8] and black coal [8] - [10] , bio-gas (BG) [11] , bio-mass [12] - [16] , waste-products with high contents of C and H, corn [17] , and the traditional technique of dehydrating MeOH [18] [19] . Two synthetic approaches are in use when processing the formation of DME. The first or commercially better-known indirect (two-step) [20] and the second direct (single-step) synthesizing process [21] . The latter is more efficient, more environmentally-friendly and its molar yield of reactants exceed 90% thanks to modern technologies. Different catalysts for the direct synthesis of DME provide satisfactory molar yield and are considered by the authors [22] - [24] . The production design of industrial processes in the direction of synthesizing alternative fuels provides additional reasons if the existing chemical plants can technologically, economically and environmentally no longer be justified. Such systems can be reconstructed along the path of multi-product production with a basic simultaneously solvable MINLP (mixed-integer nonlinear programming) mathematical model of continuous and discrete variables and it was firstly used by the authors [25] .
The examined study of this article focuses on the development of a method of multi-product production for reconstructing out-dated industrial processes. This article contains the theory of the developed method that enables the updating of existing process units and integrated systems on the basis of reconstruction scenarios and pathways. The reconstruction pathway covers analysis of the current state of a chemical plant, the search for alternatives regarding multi-product production, simulation of process alternatives using computer-aided software, the search for mathematical connections between chemical and physical quantities, mathematical modelling of a super-structure, and quantitative evaluation of the results from the reconstruction method. This can be implemented after case study of an existing MeOH plant as to whether the plant is non-profitable. MINLP mathematical model is based on simple and complex reconstruction scenarios that can be examined in more de- tail during case-studies regarding indirect and direct syntheses of DME from MeOH or direct from natural gas (NG).
The goals of the presented set method are: 1) to maintain the existing process units and chemical processes to a greater extent, 2) to enable the potential for finding new process alternatives and technological solutions, 3) to provide a streamlined operation of all subsystems and systems, 4) to promote environmental and social responsibilities, and 5) to use mentioned method of multi-product operational processes on related industrial processes.
2. Reconstruction Method of a Multi-Product Operation
The chapter presents: the basic theory of a multi-product operation, the method of reconstructing pathways and scenarios, MINLP mathematical modelling of simple and complex reconstructive pathways within a super- structure model, the connection of computer-aided software for data capture, the creation of mathematical connections between physical and chemical quantities, and process of optimization.
2.1. Multi-Product Operation
The Multi-product operation basic function represents the inlet of raw materials, formed chemical products and produced fuels. More synthesis fuels (for example, DME, H2, olefins, gasoline, etc.) and produced energy can be generated within a chemical process from fossil fuels, water and air. Such systems are multi-feed/ multi-product (MFMP). The Multi-product operation includes single-feed/multi-product (SFMP) and/or MFMP operations.
The reconstruction method of multi-product production for an industrial process is displayed in Figure 1. Into the process enters
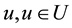 different raw materials and exits
different raw materials and exits
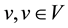 of pure chemical products and produced energy.
of pure chemical products and produced energy.
When reconstructing existing plants, multi-product production is based on the basic principle of flexibility. So fossil fuels, such as NG and coal, as well as bio-mass, bio-gas, corn, etc. can be used during the gasification process. When in taking one or more raw materials it is possible to simultaneously produce a number of chemical products. Their productivity depends on the chemical potential and demands in the market. When feeding into the process it is possible to choose between alternative raw materials that are economically appropriate or accessible.
The objective function of a reconstructed industrial process in the direction of multi-product operation is based on the maximized annual profit from individual process alternative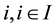 . The basic formulation of the optimization problem is represented by economic connection (Equation (1)), at basic mass balances (Equation (1a), Equation (1b), Equation (1c)), and other logical conditions (Equation (1d)) and (Equation (1e)).
. The basic formulation of the optimization problem is represented by economic connection (Equation (1)), at basic mass balances (Equation (1a), Equation (1b), Equation (1c)), and other logical conditions (Equation (1d)) and (Equation (1e)).
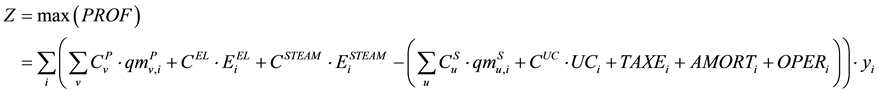 (1)
(1)
At conditions:
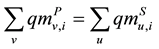 (1a)
(1a)
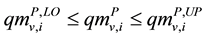 (1b)
(1b)
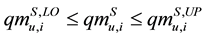 (1c)
(1c)
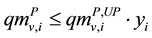 (1d)
(1d)
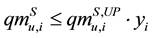 (1e)
(1e)
and:
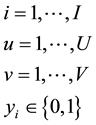
Incomes present:
sales of all generated products
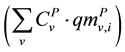 according to market value, and
according to market value, and
Figure 1. Multi-product production of an industrial process.
sales of fuels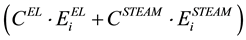 ; produced electricity and low pressure steam (LPS), medium pressure steam (MPS) or high pressure steam (HPS).
; produced electricity and low pressure steam (LPS), medium pressure steam (MPS) or high pressure steam (HPS).
Expenses on an annual basis represent:
the cost of all raw materials used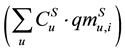 ,
,
the cost of utility consumption used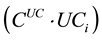 ,
,
exhaust emission taxes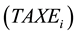 ,
,
amortization of additional process units

additional operating costs during the process
Equation (1a) represents the total mass balance of raw materials on the feed into the process and is equal to the mass out-feed of products from the process. Inequalities Equation (1b) and Equation (1c) represent a possible consumption of raw materials on the feed into the i-th alternative or produced mass capacity of an individual product according to market demand. Inequalities Equation (1d) and Equation (1e) represents the activation or deactivation of individual raw material/product of i-th process alternative.
2.2. The Methods of Simple and Complex Reconstruction Pathways
Reconstructions of existing chemical processes are carried out in three main directions: 1) change of productivity (new products and more products), 2) change in the method of obtaining the product/-s (new processes and technologies) and 3) modification on the side of raw materials (different input raw materials). The method of reconstruction pathways is based on: a situation analysis of the existing plant, a search for process alternatives and technologies, and on computer simulation of selected process schemes. Figure 2 presents the current state of the existing industrial process (point A), reconstructive pathways based on required restrictions and the desired state (point B). The reconstruction process is further limited in practice with: technological, environmental, economic, security and social requirements.
Based on the state of the industrial process, the following questions are raised:
1) How to choose a potential process alternative for transforming the inlet of raw materials into multi-product production?
2) Which reconstruction pathway to choose in order to achieve a new desired state (B) of the existing plant?
3) Can reconstruction be carried out with the help of mathematical modelling?
4) Is it possible to confirm the usefulness of the analysed method on the existing process?
Figure 2. The existing industrial process (A), and based reconstruction pathways.
Existing chemical plants are satisfactorily optimized according to the assumption, but nevertheless do not bring economic profit. In order to improve this, simple and complex reconstructive pathways are at our disposal. From a technical point of view simple reconstruction pathways represent easy but less efficient improvements. These improvements are: replacement of the existing raw materials with new ones, a combination of inlet fossil and renewable fuels, changes in the process parameters and the production of new products. Alternatively the upgrading of existing processes, where products from the raw materials within a new part of the process are currently being produced. A more complex type of reconstruction concerns topological changes to the existing process units, replacements of reactors with new ones.
2.3. Mathematical Modelling
The examined mathematical model includes the results of various software tools (ASPEN PLUS, SYNHEAT and Excel), thus enabling quick decision-making between potential process alternatives. As far as heat analysis is concerned, Duran and Grossmann [26] showed that the simultaneous optimization and heat integration (HI) of process flows enables high energy and cost savings in industrial processes.
The mathematical model of the process’ super-structure (Figure 1) chooses between

















The big-M formulation [28] -[31] provides an appropriate size for the permitted optimization space and is applicable for all size variables of the process units. It is described by inequalities (Equation (26))-(Equation (30)). The investment in additional process equipment is calculated using mathematical equations (Equation (31)- Equation (33)). The total investment in the heat exchanger, heater and cooler is calculated according to equation (Equation (31)), the investment of the tubular reactor with studied layer of catalyst according to equation (Equation (32)) and the investment in the purchase of a compressor according to equation (Equation (33)). The cost of process equipment is valued as a steady annual amortization over a 10-year period. Amortization of basic units’ purchases is determined by connection (Equation (34)). The investment in distillation columns is excluded from amongst the amortization costs. Distillation columns were already available in the analyzed plant and their dimensions and characteristics coincided with the planned ones. The objective function―annual profit (Equation (35)) that represents the difference between all incomes and all expenses on an annual basis, was chosen as the optimization criterion. It is formed under conditions of continuous and discrete variables by equations (Equation (36))-(Equation (40)). Equation (Equation (36)) represents the total income of process alternative i that is the sum of the sales of the produced products and fuels. Equation (Equation (37)) represents the expenses that are presented as the cost of raw materials, UC, emission fees, amortization costs and additional operating costs. Inequalities (Equation (38))-(Equation (40)) represent the basic big-M formulation.
3. The Existing Chemical Plant, and the Technological Alternatives
An analysis of the existing chemical synthesis process of MeOH was conducted and an overview of simple and complex reconstruction pathways was designed by using the reconstructive method of multi-product production. These reconstruction pathways represent the indirect (simple) or direct (complex) pathways.
3.1. The Existing MeOH Plant
The existing chemical plant for the synthesis of MeOH from NG had a capacity of 150,000 tons per year, and has been further analysed by the authors Kovač and Bencik [19] . The process is shown in Figure 3. In the process of the synthesis of MeOH enter: a) NG at a temperature of 0˚C, at a pressure of 24.5 bar and with a capacity of 10,500 kg/h, and b) MP steam at a temperature of 427˚C, at a pressure of 22.2 bar and with a capacity of 33,000 kg/h.
3.2. Indirect Synthesis of DME and a Review of Process Alternatives
DME synthesizes from NG over 3-stages along an indirect pathway of the synthesis. The basic process operations of DME formation are: 1) preheating of raw MeOH, 2) reaction of dehydration until DME, 3) separation and purification of the products and 4) the recycling of non-reactive reactants back to the reactor.
The conceptual alternative process schemes were considered on the basis of the listed literature, and upgraded for the existing industrial process shown in the case study.
The alternative process scheme A (Appendix II) represents a low-pressure synthesis process for the production of DME from raw MeOH. This process scheme was further examined by the authors [30] . The process scheme B (Appendix III) represents a high-pressure synthesis process regarding the production of DME from raw MeOH. The alternative process scheme C (Appendix IV) represents a high-pressure synthesis process. Men- tioned process scheme was further examined by the authors [32] . The alternative process scheme D (Appendix V) represents the medium-pressure synthesis process of the high temperature production of DME from raw MeOH. This process scheme was further examined by the authors [33] .
3.3. Direct Synthesis of DME and a Review of the Process Alternatives
In the direct pathway regarding synthesis, DME is formed directly from SNG by a catalysed dehydration reaction. A bi-functional catalyst with 2-active places within a single reactor enables simultaneous formation and dehydration of MeOH until the formed product. Formation of the product from SNG is represented by reactions (R1)-(R4).




The conceptual alternative process schemes were considered on the basis of the listed literature, and upgraded for the existing industrial process shown in the case study.
The alternative process scheme E (Appendix VI) represents a direct synthesis process for the production of

Figure 3. The existing MeOH plant.
DME from NG at HP. This process scheme was further examined by the authors [34] . The alternative process scheme F (Appendix VII) represents a synthesis process a pressure of 50 bar and a temperature of 270˚C. Mentioned process scheme was further examined by the authors [35] .
4. Case Study
The presented method of reconstruction pathways regarding multi-product production was tested on an existing MeOH process. An analysis of the prior state of the chemical process was made, and simple and complex reconstruction scenarios were predicted. Simulations of potential process alternatives were conducted by ASPEN PLUS computer-aided software [36] . Mathematical connections between the chemical and physical quantities were searched and generated with an MINLP mathematical super-structure model. This model represented the connection of software tools for quick decision-making between simple and complex process alternatives. The results of the developed reconstruction method were quantitatively evaluated.
4.1. Comprehensive Description of the Super-Structure
Figure 4 shows the mathematical model of the super-structure of the reconstructed MeOH process in regard to multi-product production. The NG and MP steam inflow the feed into the process. 2 chemical products (pure DME and MeOH) and produced MPS are created during the process.
An MINLP mathematical model enables selection between simple or complex reconstruction pathways on the basis of included process alternatives. A simple reconstruction pathway is based on an indirect synthesis of DME from MeOH. The alternatives are presented using four process alternatives: from A to D. The second reconstruction pathway is a complex one and is based on a direct synthesis of DME that is presented using two alternatives: E and F.
4.2. MINLP Mathematical Modelling of a 2-Product Production
A general mathematical model (Appendix I) was built within the GAMS language on the basis of reviewing the reconstruction scenarios and the simulations of individual process alternatives. It is formulated with total mass balances, heat balances, temperatures, and flow pressures. The main chemical components (DME, MeOH, H2O, CO and CO2) are included within the system. The examined study describes such basic mathematical connections as mentioned in the theory regarding specific mathematical connections, applicable only to the analysed plant. The general mass balance of the reactor is adjusted to the synthesis of DME and pure MeOH, where mathematical connections (Equation (41)-Equation (43)) are applicable. In the mathematical model, the incomes from the sale of both products (DME and MeOH) of individual process alternative are presented by equation (Equation (44)). The income from the sale of MPS is the result of utilizing the exothermic reaction. The equation in the model is shown by mathematical connection (Equation (45)). This study included only CO2 emissions. Emission fees are the result of releasing greenhouse gases into the environment and are presented by equation (Equation (46)). The additional operating costs of complex reconstruction pathways are not the main focus of this study and are therefore assessed as a fixed operating cost of the modified plant.
4.3. Input Data of the Mathematical Model
The inputted physical and chemical data were taken from the process simulator ASPEN PLUS. All the inputted data of the reconstruction method regarding the 2-product production are summarized in Table 1 and Table 2.
Figure 4. Super-structure mathematical model of a 2-product production of a reconstructed MeOH plant.
Table 1. Inputted physical and chemical quantities of the mathematical model.
Table 2. Other input data of the mathematical model.
4.4. Computer Software
The study was based on data obtained from the existing MeOH plant. The remaining data were taken from the literature and computer simulations (Aspen Plus). Data processing was conducted using the following computer programs: Excel (collecting of inputted data and results processing), ASPEN PLUS [36] (simulation of process alternatives), SYNHEAT [37] and GAMS [38] (heat integration of process flows, modelling, optimization and search for satisfactory reconstruction solutions).
5. Results
This work covered two sets of results. The first part of the results covered the quantitative calculations of the minimal UC of individual process alternatives and economic evaluation of the optimal scenario at the required limits of simple and complex reconstruction pathways. The second part examined the suitability of the reconstruction method regarding multi-product production and economically evaluated the optimal alternative.
5.1. Values of the Objective Function and UC Consumption
Minimal UC was calculated using the SYNHEAT program in the GAMS [37] . The maximum value of the objective function regarding simple reconstruction pathways was achieved by the alternative D (800 kEUR/a)―from amongst all the indirect pathways of the DME synthesis. The maximum value for the objective function regarding complex reconstruction pathways was achieved by the alternative E (9,900 kEUR/a)―between both direct methods of the product synthesis. The most favourable of all reconstruction pathways was the complex reconstruction pathway, the alternative E at restrictions. The values of the objective function Z and UC of individual process alternatives for a 2-product operation are shown in Table 3.
5.2. The Optimal Alternative Process Scheme
The optimal alternative process scheme E represents a direct synthesis process for the production of DME from NG at high pressure, as in Appendix VI. Pre-formed SNG from the reformer is first cooled to 102˚C and then compressed over 3-stages within the compressors (COMP-1E, COMP-2E and COMP-3E) at 68.0 bars. Cooling of the mixture is necessary due to discharge of the H2O present. The feed into the DME reactor (slurry/liquid phase) (REAC-DME-E) is preheated to 190˚C. The equilibrium chemical reaction of forming DME is conducted over 3 stages (R1-R4). The produced products from the reactor are cooled in a refrigerator (COOL-1E) to 65˚C, and their pressure potentials are exploited with the usage of a gas turbine. Separation of the gas products is carried out in an absorption column (SEP-CO2) at −45.0˚C, where removal is conducted of the CO2 present. Further separation of the liquid mixture is carried out over a series of two distillation columns (DEST-1E and DEST-2E). DME is produced in the first column and the remainder enriched with MeOH, and H2O is separated in the second rectification column. In the latter MeOH arises at the top and H2O at the bottom of the column.
5.3. Economic Analysis of the Results Regarding the Selected Alternative
Table 4 presents the results of a mathematical model for the optimal process alternative E, which is one of the reconstruction methods of multi-product production.
The results listed in Table 4 represent the amount of UC. The consumption amounted to 9,300 kW after extreme cooling and 5,900 kW after additional heating. The amortization assets of the additional process units (which amounted to an additional 3,000 kEUR/a) are shown by the results. The cost of DME reactor (V ≈ 22.0
Table 3. Values of the objective functions of Z and utility consumptions (UC).
m3) with catalyst filler represented the majority of the amortization. The distillation columns were excluded from the amortization. There was no need to purchase an additional heater or cooler within the planned process; it was only necessary to purchase an additional heat exchanger (A ≈ 54.0 m2). Modification of the reformer and operation at high temperatures were additional operating costs, which were estimated to be approximately 7,200 kEUR/a. The total annual profit from the alternatives amounted to more than 9,900 kEUR.
Figure 5 shows the economic analysis of the process alternative E. The diagram shows that income from the sale of DME represented 90.0%, the income from the sale of pure MeOH almost 9.0%, and the income from the MP steam produced within the DME reactor to a little more than 1.0% of the total incomes. The cost of raw material (NG) exceeded 83.1% of all expenses generated on the expenditure side. The additional costs were represented by: modifications and operations of the reformer at a higher temperature (10.2%), amortization of additional process units, purchase of the DME reactor (it amounted to 5.4% of the total expenses on an annual basis with 10-year amortization), and the UC and CO2 emission fees (together they did not exceed 1.5% of the total expenses).
Table 4. The results of a mathematical model of the optimal process alternative E.
(*) 5th is the optimal process alternative with name E.
Figure 5. Economic analysis of a 2-product production regarding the process alternative E.
5.4. Suitability of the Reconstruction Method
The reconstruction method of multi-product production and flexible operation has confirmed the foresight on the possible improvements to existing non-profitable industrial process. The suitability of the method, which can transform MeOH process into a technologically, environmentally, and above all economically more favourable process, was confirmed regarding the examined case.
6. Conclusions and Suggestions
This article conceptually presented the reconstruction method in regard to the direction of multi-product production regarding industrial processes. The reconstruction technique can be expected to cover: 1) change of productivity, 2) change in the method of obtaining the product/-s and 3) modification on the side of input raw materials. The reconstruction pathway represented: an analysis of the state of chemical plant, the search for simple and complex alternatives regarding multi-product production, simulations of potential process alternatives with an integrated computer-aided software, the search for mathematical connections between chemical and physical quantities, mathematical modelling of a super-structure, and quantitative evaluation of the method’s results. The purpose of mathematical modelling and optimization regarding reconstruction in the direction of multi-product production is the establishment of appropriate formulation. This formulation enables easier decision-making and searching for appropriate solutions between potential reconstructive pathways. Mathematical formulation pre- sents a set of equations and inequality conditions representing mass and energy balances, connections for the size of process equipment, specifications of the temperatures and pressures of individual process units, and restrictive requirements. Mentioned program chooses between simple and complex pathways and process alternatives. Complex reconstruction pathways are more demanding in comparison with simple ones as they represent interference with the already constructed structure of an industrial process. They also represent higher costs, are more effective in most cases and their solutions help to improve the states of the existing plants. Computer-aided software that enables systematic data collection and processing plays an important role during the modelling and optimization.
The prices of raw materials and the prices of market products play important roles in the process of transforming one fuel (for example NG to DME, MeOH, etc.), which are physically, technologically, environmentally and economically more favourable. In comparison with the indirect synthesis of DME (simple reconstruction pathway), the lower operating costs of direct synthesis regarding DME (complex reconstruction pathway) were confirmed. Alternatives to the indirect pathways of the synthesis are cheaper from the point of view of investment contribution during reconstruction but their performances deteriorate. The efficiency of single-step DME from SNG is significantly higher, which justifies the functionality of chemical process planning in this direction.
In the future it will be reasonable to develop reconstruction methods for industrial processes. These reconstruction methods would have to be based on a more efficient yield of reactants (new catalysts), on the production of new products, and on a new process synthesis.
Acknowledgements
This research work was funded by the Public Agency for the Development of the Republic of Slovenia (ADRS), the Ministry of Education, Science, Culture and Sport, for which we sincerely thank them.
References
- Lee, S., Oh, S. and Choi, Y. (2009) Performance and Emission Characteristics of an SI Engine Operated with DME Blended LPG Fuel. Fuel, 88, 1009-1015. http://dx.doi.org/10.1016/j.fuel.2008.12.016
- Papalexandri, K. and Pistikopoulos, E.N. (1993) A Retrofit Design Model for Improving the Operability of Heat Exchanger Networks. In: Pilavachi, P.A., Ed., Energy Efficiency in Process Technology, Springer, Netherlands, 915-928. http://dx.doi.org/10.1007/978-94-011-1454-7_81
- Papalexandri, K. and Pistikopoulos, E.N. (1993) A MINLP Retrofit Approach for Improving the Flexibility of Heat Exchanger Networks. Annals of Operations Research, 42, 119-168. http://dx.doi.org/10.1007/BF02023174
- Soršak, A. and Kravanja, Z. (2004) MINLP Retrofit of Heat Exchanger Networks Comprising Different Exchanger Types. Computers & Chemical Engineering, 28, 235-251. http://dx.doi.org/10.1016/S0098-1354(03)00167-4
- Kovac-Kralj, A. and Glavič, P. (2000) Simultaneous Retrofit of Complex and Energy Intensive Processes―III. Computers Chemical Engineering, 24, 1229. http://dx.doi.org/10.1016/S0098-1354(00)00361-6
- Novak-Pintaric, Z. and Kravanja, Z. (2007) Multiperiod Investment Models for the Gradual Reconstruction of Chemical Processes. Chemical Engineering & Technology, 30, 1622-1632. http://dx.doi.org/10.1002/ceat.200700334
- Arcoumanis, C., Choongsik, B., Crookes, R. and Eiji, K. (2008) The Potential of Dimethyl Ether (DME) as an Alternative Fuel for Compression-Ignition Engines: A Review. Fuel, 87, 1014-1030. http://dx.doi.org/10.1016/j.fuel.2007.06.007
- Zhou, L., Hu, S., Li, Y. and Zhou, Q. (2008) Study on Co-Feed and Co-Production System Based on Coal and Natural Gas for Producing DME and Electricity. Chemical Engineering Journal, 136, 31-40. http://dx.doi.org/10.1016/j.cej.2007.03.025
- Larson, E.D. and Yang, H. (2004) Dimethyl Ether (DME) from Coal as a Household Cooking Fuel in China. Energy for Sustainable Development, 8, 115-126. http://dx.doi.org/10.1016/S0973-0826(08)60473-1
- Gangadharan, P., Zanwar, A., Zheng, K., Gossage, J.L. and Helen, H. (2012) Sustainability Assessment of Polygeneration Processes Based on Syngas Derived from Coal and Natural Gas. Computers & Chemical Engineering, 39, 105- 117. http://dx.doi.org/10.1016/j.compchemeng.2011.10.006
- Kovač-Kralj, A. and Bencik, D. (2012) Replacing the Existing Methanol Production within DME Production by Using Biogas. Chemical Engineering Transactions, 27, 25-30.
- Kabir, K.B., Hein, K. and Bhattacharya, S. (2013) Process Modelling of Dimethyl Ether Production from Victorian Brown Coal―Integrating Coal Drying, Gasification and Synthesis Processes. Computers & Chemical Engineering, 48, 96-104. http://dx.doi.org/10.1016/j.compchemeng.2012.08.008
- Srirangan, K., Akawi, L., Moo-Young, M. and Chou, C.P. (2012) Towards Sustainable Production of Clean Energy Carriers from Biomass Resources. Applied Energy, 100, 172-186. http://dx.doi.org/10.1016/j.apenergy.2012.05.012
- Swain, P.K., Das, L.M. and Naik, S.N. (2011) Biomass to Liquid: A Prospective Challenge to Research and Development in 21st Century. Renewable and Sustainable Energy Reviews, 15, 4917-4933. http://dx.doi.org/10.1016/j.rser.2011.07.061
- Ju, F., Chen, H., Ding, X., Yang, H., Wang, X., Zhang, S. and Dai, Z. (2009) Process Simulation of Single-Step Dimethyl Ether Production via Biomass Gasification. Biotechnology Advances, 27, 599-605. http://dx.doi.org/10.1016/j.biotechadv.2009.04.015
- Trippe, F., Fröhling, M., Schultmann, F., Stahl, R., Henrich, E. and Dalai, A. (2013) Comprehensive Techno-Economic Assessment of Dimethyl Ether (DME) Synthesis and Fischer-Tropsch Synthesis as Alternative Process Steps within Biomass-to-Liquid Production. Fuel Processing Technology, 106, 577-586. http://dx.doi.org/10.1016/j.fuproc.2012.09.029
- Li, Y.P., Wang, T.J., Yin, X.L., Wu, C.Z., Ma, L.L., Li, H.B., et al. (2010) 100 t/a-Scale Demonstration of Direct Dimethyl Ether Synthesis from Corncob-Derived Syngas. Renewable Energy, 35, 583-587. http://dx.doi.org/10.1016/j.renene.2009.08.002
- Li, Z., Liu, P., He, F., Wang, M. and Pistikopoulos, E.N. (2011) Simulation and Exergoeconomic Analysis of a Dual- Gas Sourced Polygeneration Process with Integrated Methanol/DME/DMC Catalytic Synthesis. Computers & Chemical Engineering, 35, 1857-1862. http://dx.doi.org/10.1016/j.compchemeng.2011.01.015
- Kovac-Kralj, A. and Bencik, D. (2011) Replacing an Existing Product’s Production within a Similar Product Production by Using a Replacement Technique. Energy Science & Technology, 2, 79-84.
- Nasehi, S.M., Eslamlueyan, R. and Jahanmiri, A. (2006) Simulation of DME Reactor from Methanol. Proceedings of the 11th Chemical Engineering Conference, Kish Island, 28-30 November 2006.
- Sai Prasad, P.S., Bae, J.W., Kang, S.H., Lee, Y.J. and Jun, K.W. (2008) Single-Step Synthesis of DME from Syngas on Cu-ZnO-Al2O3/Zeolite Bifunctional Catalysts: The Superiority of Ferrierite over the Other Zeolites. Fuel Processing Technology, 89, 1281-1286. http://dx.doi.org/10.1016/j.fuproc.2008.07.014
- García-Trenco, A. and Martínez, A. (2014) The Influence of Zeolite Surface-Aluminum Species on the Deactivation of CuZnAl/Zeolite Hybrid Catalysts for the Direct DME Synthesis. Catalysis Today, 227, 144-153.
- García-Trenco, A., Valencia, S. and Martínez, A. (2013) The Impact of Zeolite Pore Structure on the Catalytic Behavior of CuZnAl/Zeolite Hybrid Catalysts for the Direct DME Synthesis. Applied Catalysis A: General, 468, 102-111. http://dx.doi.org/10.1016/j.apcata.2013.08.038
- Zhang, M.H., Liu, Z.M., Lin, G.D. and Zhang, H.B. (2013) Pd/CNT-Promoted CuZrO2/HZSM-5 Hybrid Catalysts for Direct Synthesis of DME from CO2/H2. Applied Catalysis A: General, 451, 28-35. http://dx.doi.org/10.1016/j.apcata.2012.10.038
- Biegler, L.T., Grossmann, I.E. and Westerberg, A.W. (1997) Systematic Methods of Chemical Process Design. Prentice Hall PTR, Upper Saddle River.
- Duran, M.A. and Grossmann, I.E. (1986) Simultaneous Optimization and Heat Integration of Chemical Processes. AIChE Journal, 32, 123-138.
- Kravanja, Z. and Novak-Pintaric, Z. (2006) Optimiranje procesov: Zbrano gradivo. Fakulteta za kemijo in kemijsko tehnologijo, Univerza v Mariboru, Maribor.
- Ropotar, M. and Kravanja, Z. (2006) Implementation of Efficient Logic-Based Techniques in the MINLP Process Synthesizer MIPSYN. In: Marquardt, W. and Pantelides, C., Eds., Computer Aided Chemical Engineering, Elsevier, Amsterdam, 233-238.
- Jackson, J.R. and Grossmann, I.E. (2002) High Level Optimization Model for the Retrofit Planning of Process Networks. Industrial Engineering Chemistry Research, 41, 3762-3770.
- Turton, R., Bailie, R.C., Whiting, W.B. and Shaeiwitz, J.A. (2009) Analysis, Synthesis, and Design of Chemical Processes. Prentice Hall, Upper Saddle River.
- Towarmalani, M. and Sahinidis, N.V. (2005) A Polyhedral Branch-and-Cut Approach to Global Optimization. Mathematical Programming, 103, 225-249. http://dx.doi.org/10.1007/s10107-005-0581-8
- Yomamoto, Y.S. (1995) Ulmann’s Encyclopedie of Industrial Chemistry. Completely Revised Edition, Vol. A24, VCH, New York, 540-543.
- Aktas, B. (2012) Production of Dimethyl Ether: Feasibility Study. Free Docs., 1-7.
- Clausen, L.R., Elmegaard, B., Ahrenfeldt, J. and Henriksen, U. (2011) Thermodynamic Analysis of Small-Scale Dimethyl Ether (DME) and Methanol Plants Based on the Efficient Two-Stage Gasifier. Energy, 36, 5805-5814. http://dx.doi.org/10.1016/j.energy.2011.08.047
- Zheng, D. and Cao, W. (2007) Retrofitting for DME Process by Energy-Flow Framework Diagram. Chemical Engineering and Processing: Process Intensification, 46, 2-9. http://dx.doi.org/10.1016/j.cep.2006.03.018
- ASPEN PLUS (2002) User Manual Release 11.1. Aspen Technology Inc., Cambridge.
- Yee, T.F. and Grossmann, I.E. (1990) Simultaneous Optimization Models for Heat Integration―II. Heat Exchanger Networks Synthesis. Computers & Chemical Engineering, 14, 1165-1184.
- GAMS (2007) Beta 22.4: The Solver Manuals. GAMS Development Corporation, Washington DC.
Nomenclatures
NOTES
*Corresponding author.







