Journal of Applied Mathematics and Physics
Vol.07 No.01(2019), Article ID:89888,21 pages
10.4236/jamp.2019.71007
Dimension-Reduced Model for Deep-Water Waves
Michael Bestehorn1, Peder A. Tyvand2, Thomas Michelitsch3
1Department of Physics, Brandenburg University of Technology, Cottbus, Germany
2Department of Mathematical Sciences and Technology, Norwegian University of Life Sciences, Ås, Norway
3CNRS, Institut Jean le Rond d’Alembert, Sorbonne Université, Paris, France

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 12, 2018; Accepted: January 12, 2019; Published: January 15, 2019
ABSTRACT
Starting from the 2D Euler equations for an incompressible potential flow, a dimension-reduced model describing deep-water surface waves is derived. Similar to the Shallow-Water case, the z-dependence of the dependent variables is found explicitly from the Laplace equation and a set of two one-dimensional equations in x for the surface velocity and the surface elevation remains. The model is nonlocal and can be formulated in conservative form, describing waves over an infinitely deep layer. Finally, numerical solutions are presented for several initial conditions. The side-band instability of Stokes waves and stable envelope solitons are obtained in agreement with other work. The conservation of the total energy is checked.
Keywords:
Hydrodynamics, Ocean Waves, Deep-Water Waves, Numerical Solutions, Fractal Derivatives

1. Introduction
The procedure for deriving reduced equations by expressing the dependence of the dependent variables on a certain, geometrically distinguished spatial coordinate analytically is widespread in nonlinear pattern formation and wave dynamics. As a first attempt, one can consider the Shallow-Water or Saint-Venant equations [1] , which are systematically derived from the hydrodynamic basic equations for an inviscid potential flow by solving iteratively the Laplace equation for the velocity potential function. Thereby, all expansions are controlled by a geometry parameter
(1)
where d is the layer’s depth and a typical lateral length scale (e.g. wave length). A similar expansion can be done for highly viscous problems and the so-called Thin-Film equation is obtained which describes the dynamical behavior of the shape of the film’s surface [2] [3] [4] . For convection problems, a projection onto certain z-dependent modes allows for the reduction to 2D systems where only the horizontal coordinates occur. Standard equations in normalized form like the Allen-Cahn, the (complex) Ginzburg-Landau or the Swift-Hohenberg equations can be derived, partially by heuristic arguments concerning at least their nonlinear parts [5] .
Stokes [6] initiated the theory of nonlinear deep-water waves. Three branches of development for strongly nonlinear theory have grown from seminal papers. 1) The highest Stokes wave [7] . 2) The instability of Stokes waves [8] . 3) Breaking of deep-water waves [9] .
The early nonlinear theories in 2D have now grown into full 3D theories. However, a long-standing problem is that of dimensional reduction of the nonlinear 3D problem to a 2D analysis, as it can be done straightforwardly for the case of shallow water. For deep water waves, the Hamiltonian formulation [10] [11] provides a nonlinear system for two two-dimensional field variables, namely surface elevation and potential at the surface. To compute the velocity normal to the surface, the solution of the underlying 3D-Laplace equation is achieved by an expansion with respect to powers of the surface elevation into spectral function. These algorithms have been named ‘higher order spectral methods’ (HOSM) and go back to the work of West et al. [12] and Dommermuth and Yue [13] . Another attempt is the systematic derivation of an equation describing the slowly varying envelope of a given monochromatic wave train. This equation has the form of a nonlinear cubic Schrödinger equation [10] [14] and reflects the side-band instability of Stokes waves as well as envelope solitons as localized stable solutions.
Contrary to the Shallow-Water or Thin-Film equations, no intrinsic length scale exists for the deep-water case. The only available scales are given by the solutions sought for, namely the wave length (if the waves are nearly coherent) and the amplitude A of those waves. In deep-water waves, the ratio of amplitude to wave length is normally rather small. Thus, using the wave steepness
(2)
with for expanding the nonlinearities seems to be quite natural.
The present paper offers a consistent scheme of reducing the spatial dimension of nonlinear deep-water wave theory by introducing the concept of fractional derivatives along the free surface. Starting from the 2D Euler equations for an incompressible potential flow, a one-dimensional model describing deep-water surface waves is derived. Similar to the Shallow-Water case, the z-dependence of the dependent variables is determined from the Laplace equation and a set of two nonlinear equations for the surface velocity and the surface elevation remains. The system is nonlocal and can be formulated in conservative form, describing waves over an infinitely deep layer. It contains nonlinearities of the lowest (quadratic) order in velocity and surface elevation but can be systematically extended to higher orders. Numerical solutions are presented for different initial conditions. Coherent wave trains prove to be unstable due to the Benjamin-Feir instability [8] and localized solutions in form of envelope solitons are obtained. Finally, a spatially localized and temporally oscillating surface pressure variation is used to act as a wave-maker. The propagation of different wave ensembles is studied and linear and nonlinear results are compared to show the importance of the nonlinear terms.
The conservation of the total energy can be considered as a quality test for both the derived system and the numerical method applied for its solutions. We show that the energy is conserved within a few percents which give us confidence in our derivation and results.
The model can be extended to the case of a 3D potential flow, resulting in a set of three two-dimensional evolution equations.
2. The Model
2.1. Potential Flow
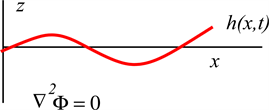
For the sake of simplicity we restrict the treatment first to two dimensions, . We are looking for solutions of the non-dimensional Euler eqs. for an incompressible fluid in the half space , see Figure 1:
(3)
(4)
(5)
where time is scaled by
(6)
and lengths with an arbitrary which will be identified later (sect. 3.2) with the characteristic wave length of the initial condition. We assume that the flow field can be derived from a potential
(7)
which then, due to (5) must be a solution of the Laplace eq.
(8)
Figure 1. Sketch of the system (2D). A potential flow is considered in the half space .
which also implies
(9)
Let
(10)
be the horizontal velocity component at the free surface located at .
From (3) we derive
(11)
Equation (11) serves as a boundary condition (b.c.) for (9) at . The surface function h is determined by the kinematic b.c.
(12)
For the following treatment, it is of advantage to formulate (12) also in conservative form
(13)
with the flux
(14)
For an infinitely deep layer, the asymptotic b.c.
(15)
must hold. Hence the general solution of (9) reads
(16)
with c.c. as the complex conjugate.
2.2. Nonlocal Expansion
Considering (11) and (13) as evolution Equations, the original 3D (here 2D) problem is reduced to a 2D (here 1D) system in the horizontal coordinates x,y (here x) only. However, to evaluate the flux (14) one needs to know . Taking (16), Equation (14) reads
(17)
To determine the amplitudes from , we evaluate (16) at and expand the exponential function up to a given order :
(18)
Next we introduce the fractional differential operator of order :
(19)
with the nonlocal operator defined as
(20)
for every function via its Fourier transform . We note that (20) is one of the definitions of the fractal Laplacian, here in 1D [15] . Now Equation (18) can be written as
(21)
(in the 3D case, must be replaced by the horizontal Laplacian ).
Using the same technique, S from (17) can be expressed as
(22)
leading finally to
(23)
where is the operator inverse to and is computed from
(24)
Thus, the equations (11) and (13) are closed by the relation (23). Note that is a nonlocal operator only for odd n. For n even it can be expressed by spatial derivatives of order n in position space. Moreover, assuming periodic lateral boundary conditions, it is self-adjoint for all n.
2.3. Second Order Model
In the following we shall restrict ourselves to , resulting in a model of second order in the dependent variables . With
(25)
its inverse
(26)
and the self-adjoint operator
(27)
Equation (23) turns into
(28)
where only terms up to the second order in are included.
In (11), the pressure gradient evaluated at turns into
(29)
where is the pressure along the free surface and assumed to be constant (external pressure). To find we evaluate (4) at the surface and include only linear terms in , leading to
(30)
with the vertical velocity component
(31)
along the surface. is related to by (5) according to
(32)
where again only linear terms are considered. Finally, we have
(33)
where the first term on the right-hand side corresponds to the hydrostatic pressure, the second one to the dynamic part. Using (33), Equation (11) can be cast into the form
(34)
2.3.1. Model
After inversion of the operator on the left-hand side of (34), the complete system up to the second order reads
(35)
(36)
with from (28).
2.3.2. Linear Waves
Taking only linear terms into account one finds from ((35), (36))
(37)
or, eliminating , the linear wave equation
(38)
where we have used the identity . Equation (38) possesses the well-known short-wave dispersion relation
(39)
2.3.3. Two Horizontal Dimensions
If we add the second horizontal dimension we are able to describe a 3D flow which, however, is still potential. Extending the surface velocity to a 2D vector
(40)
the derivation of the reduced system is straightforward and it reads
(41)
(42)
(43)
(44)
with the 2D nabla operator .
2.4. Similarities and Differences with HOSM
Contrary to the higher-order spectral methods (HOSM) presented in [12] [13] , we use the surface elevation and the surface velocity instead of the surface potential. With the kinematic b.c. (36) formulated by the help of the flux S, this results in model equations that can be written in conservative form. Due to the self-adjointness of it can be easily seen that are conserved in time, also for the numerical scheme, if the derivatives with respect to x are expressed by simple central differences (see sect. 3.1 below). On the other hand, our method can be formulated in a closed form in position space and is, at least up to second order, faster and easier to implement numerically, allowing for larger aspect ratios and an effective numerical realization in two horizontal dimensions. Eventually, Equations ((35), (36)) can be considered as a systematic expansion with respect to the wave steepness . With the self-consistent assumption , our model includes all terms up to the order . Hence it should deliver accurate results up to second-order stokes waves, which corresponds to [16] , about 36 percents of the steepest possible Stokes wave with . Then the maximal wave amplitude of a wave with (wave length ) should not be much higher than .
3. Numerical Method and Results
3.1. Numerical Method
We concentrate on the 2nd order model ((35), (36)) with x in the domain and periodic lateral b. c. . To evaluate (28), the expressions
(45)
must be computed. The operator introduced in (20) thus reads . It is nonlocal for odd n and (45) can be written as
(46)
with the Green’s function
(47)
and . Taking a finite difference scheme for the numerical integration of the system, the variable x is discretized as
where N is the number of mesh points and with . The discrete form of (46) thus reads
(48)
with
(49)
which would result in time-consuming computations of convolutions when evaluating (28). Hence it is much more effective to compute (48) in Fourier space where it simply reads
(50)
where is the discrete Fourier transform of that can be obtained numerically by any standard Fast-Fourier transform (FFT) [17] .
To evaluate S according to (28) it is therefore necessary to compute and in Fourier space, then perform the products and in real space and finally compute in Fourier space again. In addition for (35), has to be determined in Fourier space. Thus, seven FFTs (three forward and four backward) have to be performed at each time step.
The derivatives with respect to x occurring in ((35), (36)) are approximated with centered differences
(51)
what ensures the conservation of .
Finally, time integration is achieved by an explicit 4th-order Runge-Kutta algorithm [18] .
3.2. Results
3.2.1. Benjamin-Feir Instability of Slightly Disturbed Coherent Wave Trains
The initial conditions are based on surface elevations in form of a traveling wave with given amplitude and wave number . If for the spatial scaling introduced in (6) the wave length is chosen, we can put . The x-dimension is discretized with mesh points, the step sizes used are , , resulting in a side length of and allowing for 60 initial wave lengths. Each wave length is resolved with about 33 mesh points.
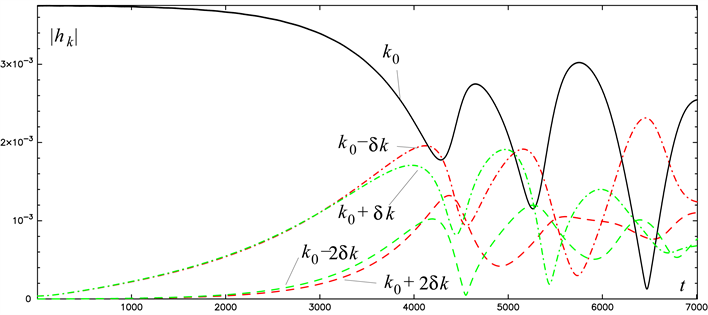
As first shown in [8] , coherent Stokes waves with a single frequency and wave length are unstable with respect to the side-band instability. The time series in Figure 2 presents the evolution of a 2nd-order Stokes wave [19] traveling to the right side as initial condition:
(52)
Figure 2. Snapshots of a BF unstable wave train. Numerical solution of the 1D model ((35), (36)).
with
To trigger the side band (Benjamin-Feir, BF) instability [20] , weak disturbances of the form
(53)
with and have been added. The speed and wave length of the (undisturbed) traveling wave follows as
(54)
what yields a Courant number of
The disturbances (39) belong to neighbored waves of in Fourier space. The absolute values of the Fourier amplitudes over time for the carrier wave ( ) as well as for its five neighbors ( ) are shown in Figure 3. In the beginning, the side bands grow exponentially, taking the energy from the carrier wave that decreases.
3.2.2. Envelope Solitons
If a coherent wave is enveloped by a slowly varying function according to
(55)
Zakharov [10] showed that for small but finite amplitudes an equation for the complex valued can be derived, having the form of the nonlinear Schrödinger equation (NLS):
(56)
with and
(57)
Figure 3. Absolute values of the Fourier amplitudes over time for the run shown in Figure 2. Solid: carrier wave , dashed-dotted: side bands , dashed: side bands .
The nonlinear coefficient depends on the ratio of the water depth to the wave length of the carrier wave [11] and reads for infinite depth
(58)
Equation (56) has the well-known localized hyperbolic secant solutions
(59)
with the relation between reciprocal width and amplitude
(60)
and .
To see how envelope solitons behave in our model, we take as initial condition
(61)
Figure 4 shows snapshots from the evolution for
with and . The envelope soliton travels thereby with the group speed as given in (57) which is half of the phase speed of the carrier wave.
To confirm the agreement of our model and its numerical solutions with the results of the weakly nonlinear NLS, we also studied an initial condition as (61), but with an amplitude and width of the envelope that does not satisfy the relation (60). Taking the same but , the package flows apart and finally extends over the whole domain, Figure 5.
Finally we show in Figure 6 the interaction of two colliding envelope solitons, generated by the initial condition
(62)
with
The solitons travel in opposite direction and interact without changing their shapes strongly. Due to the periodic b.c. these interactions repeat after equidistant time intervals of .
3.2.3. Conservation of Energy
It is interesting to check the temporal variation of the energy during the runs. For an inviscid fluid, the total energy
Figure 4. Envelope soliton for an initial condition (61) fulfilling the relation (60).
(63)
with the potential energy
(64)
and the kinetic energy
(65)
must be conserved. For the latter one, one finds up to quadratic order the expression
Figure 5. Evolution of a localized initial condition (61) which does not fulfill the relation (60) for envelope solitons.
Figure 6. Two envelope solitons with different amplitudes traveling in opposite directions.
(66)
The conservation of (63) can serve as a quality feature for the numerical solutions as well as for the accuracy of the derived system itself.
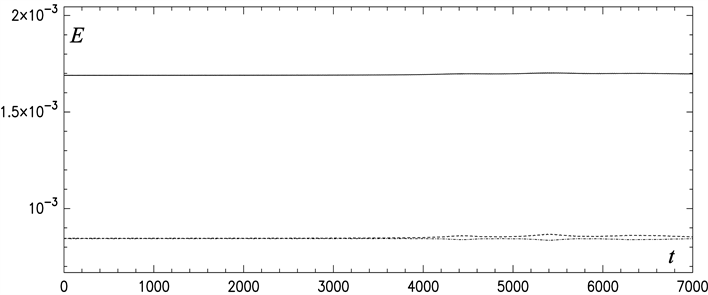
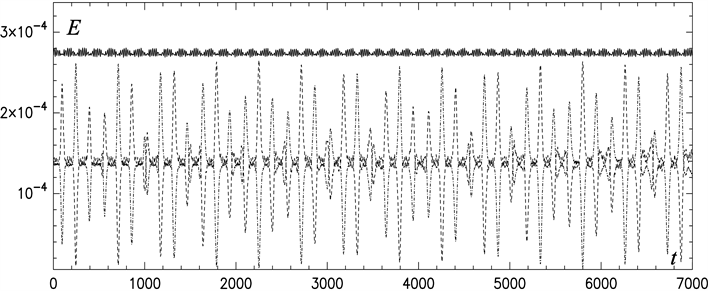
Figure 7, Figure 8 show the three energies (63)-(65) over time for the series depicted in Figure 2 and Figure 6, respectively. In Figure 8, potential as well as kinetic energy varies strongly during the collision phases but the sum (63) remains fairly constant. Table 1 shows the standard deviations normalized with the square mean defined as
(67)
Figure 7. Energies plotted over time of the evolution shown in Figure 2. solid: total, dashed: kinetic, dashed-dotted: potential.
Figure 8. Energies of the evolution shown in Figure 6. solid: total, dashed: kinetic, dashed-dotted: potential.
Table 1. Standard deviations of the energies shown in Figure 7, Figure 8.
with the mean
(68)
and f as one of the three energy functions.
Note that all computations are only up to second order which then applies also for the energy conservation so that
(69)
where stands for h, and combinations.
3.2.4. High Waves Caused by Dispersive Focusing of an Unstable Stokes Wave
Waves on deep water are generated by wind and have a broad spectrum of wave lengths. Since their phase and group speed is proportional to , longer waves are faster than shorter ones and, if they propagate in the same direction, may catch up and enhance the total amplitude. This is already a linear effect but can be amplified by nonlinearities what then leads to even higher wave heights . In this way, very large heights can be obtained, which is one of the mechanisms responsible for the occurrence of freak or rogue waves [14] and named “dispersive focusing” or “dispersive enhancement”.
To classify waves with respect to their height, the “abnormality index” AI
(70)
is introduced, where is the height of the wave and the significant wave height. The significant wave height is defined as the average height of the upper third of the wave height distribution (over time or space). Another way to compute is to use the root of the zeroth order moment of the spectrum
(71)
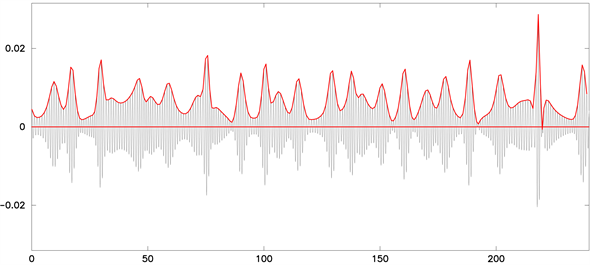
Then, a freak wave can be defined by AI > 2. The probability for freak waves depends strongly on the initial wave pattern and on the dimensionality of the system. In 2D, only two propagation directions are possible and freak waves should occur quite often. Figure 9 shows the evolution of an unstable Stokes wave as (52), but for a larger aspect ratio and a higher grid resolution at . A freak wave shows up with AI ≈ 2.8. In Figure 10 we plot AI over time, the circle marks the situation shown in Figure 9.
Figure 11 shows the the absolute values of the Fourier amplitudes of depicted in Figure 9. A scaling law according to
(72)
with can be seen over wide regions, in agreement with the findings of Zakharov et al. [21] .
3.2.5. Waves Generated by Localized Pressure Forcing
In this section we consider an initially quiescent flat layer with at
Figure 9. A large wave with AI ≈ 2.8 is formed after from the initial condition (52). Here, and , resulting in a spatial resolution of almost 70 mesh points per carrier wave length.
Figure 10. Abnormality index over time for the run leading to Figure 9, computed along (70) with (71). Two singular events are evident, the other one around .
Figure 11. Absolute values of the Fourier amplitudes of shown in Figure 9.
on which waves are generated by a spatially localized surface pressure of the form
(73)
Inclusion of (73) modifies (35) to
(74)
If the amplitude varies harmonically, (73) acts as a wave maker and produces waves with wave length , traveling symmetrically to both sides. To simulate the situation where waves with shorter wave lengths are followed by longer (faster) waves, we perform a run with and . Frequency and amplitude of the pressure are decreasing linearly in time, according to
(75)
with . Two runs have been performed, one with the nonlinear model ((74), (36)), the other with the same system but only keeping linear terms in . From Figure 12 it is evident that the nonlinearities amplify the amplitudes and provide significantly higher waves. Maximal focusing is obtained after at , see Figure 13.
4. Conclusions
We presented the derivation and numerical solutions of dimension-reduced deep-water equations. The system can be considered as a systematic expansion
Figure 12. Abnormality index of the wave field over time for waves generated by a local pressure variation (73) with frequency and amplitude variation according to (75). Black: nonlinear model (2nd order), blue: linear equations. Amplitudes are significantly enhanced by nonlinear coupling. Maximal focusing takes place after at .
Figure 13. Snapshots before, while and after maximal focusing. mesh points are used for , but only half of the layer is shown.
of the basic hydrodynamic equations with respect to powers of the wave steepness. We discussed the model in the lowest nonlinear order and showed numerical 1D-solutions where the Benjamin-Feir instability of coherent waves turned out and the behavior of envelope solitons has been studied. All results are in good agreement with previous work. The envelope solitons coincide well with solutions of the nonlinear Schrödinger equation both in amplitude and width. Our model is not based on a certain carrier wave and no spatial direction along the surface is distinguished. The formulation is rotationally invariant in the horizontal dimension(s) and allows therefore also for the study of colliding wave trains.
From the numerical side, the great advantage of the present model is its relatively straightforward and effective numerical realization. Due to the dimension reduction, CPU-times of the runs shown are in the range of hours on normal PCs or Laptops. Our system can be extended both to higher order nonlinearities as well as to three-dimensional potential flows, resulting in a reduced 2D set. Thus, the numerical examination of 2D envelope solitons occurring on the surface of a 3D potential flow should become feasible. This work is currently in progress and will be presented in a following paper.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Bestehorn, M., Tyvand, P.A. and Michelitsch, T. (2019) Dimension-Reduced Model for Deep-Water Waves. Journal of Applied Mathematics and Physics, 7, 72-92. https://doi.org/10.4236/jamp.2019.71007
References
- 1. Saint-Venant, A.J.C. (1871) Théorie du mouvement non permanent des eaux, avec application aux crues des rivières et a l’introduction de marées dans leurs lits. Comptes Rendus des Séances de Académie des Sciences, 73, 147, 237.
- 2. Vrij, A. (1966) Possible Mechanism for the Spontaneous Rupture of Thin, Free Liquid Films. Discussions of the Faraday Society, 42, 23. https://doi.org/10.1039/df9664200023
- 3. Oron, A., Davis, S.H. and Bankoff, S.G. (1997) Long-Scale Evolution of Thin Liquid Films. Reviews of Modern Physics, 69, 931. https://doi.org/10.1103/RevModPhys.69.931
- 4. Bestehorn, M. (2013) Laterally Extended Thin Liquid Films with Inertia under External Vibrations. Physics of Fluids, 25, 114106. https://doi.org/10.1063/1.4830255
- 5. Bestehorn, M. (2009) Fluid Dynamics and Pattern Formation. In: Meyers, R.A., Ed., Contribution to Encyclopedia of Complexity and System Science, 4, Springer, Berlin, 3611. https://doi.org/10.1007/978-0-387-30440-3_214
- 6. Stokes, G.G. (1847) On the Theory of Oscillatory Waves. Trans. Camb. Phil. Soc., 8, 441.
- 7. Dean, R.G. (1965) Stream Function Representation of Non-Linear Ocean Waves. Journal of Geophysical Research, 70, 4561. https://doi.org/10.1029/JZ070i018p04561
- 8. Benjamin, T.B. and Feir, J.E. (1967) The Disintegration of Wave Trains on Deep Water. Journal of Fluid Mechanics, 27, 417. https://doi.org/10.1017/S002211206700045X
- 9. Longuet-Higgins, M.S. and Cokelet, E.D. (1976) The Deformation of Steep Surface Waves on Water. I. A Numerical Method of Computation. Proceedings of the Royal Society of London, A350, 1. https://doi.org/10.1098/rspa.1976.0092
- 10. Zakharov, V.E. (1968) Stability of Periodic Waves of Finite Amplitude on the Surface of a Deep Fluid. Journal of Applied Mechanics and Technical Physics, 9, 190. https://doi.org/10.1007/BF00913182
- 11. Newell, A.C. (1985) Solitons in Mathematics and Physics. CBMS-NSF Regional Conference Series, 48.
- 12. West, B.J., Brueckner, K.A., Janda, R.S., Milder, D.M. and Milton, R.L. (1987) A New Numerical Method for Surface Hydrodynamics. Journal of Geophysical Research, 92, 11803. https://doi.org/10.1029/JC092iC11p11803
- 13. Dommermuth, D.G. and Yue, D. (1987) A High-Order Spectral Method for the Study of Nonlinear Gravity Waves. Journal of Fluid Mechanics, 184, 267. https://doi.org/10.1017/S002211208700288X
- 14. Kharif, C., Pelinovsky, E. and Slunyaev, A. (2009) Rogue Waves in the Ocean. Springer.
- 15. Kwasnicki, M. (2017) Ten Definitions of the Fractional Laplacian Operator. Fractional Calculus and Applied Analysis, 20, 7. https://doi.org/10.1515/fca-2017-0002
- 16. Le Méhauté, B. (1976) An Introduction to Hydrodynamics and Water Waves. Springer, Berlin. https://doi.org/10.1007/978-3-642-85567-2
- 17. Swarztrauber, P.N. (1982) Vectorizing the Fast Fourier Transforms. Academic Press, Cambridge.
- 18. Bestehorn, M. (2018) Computational Physics, with Worked out Examples in FORTRAN and MATLAB, De Gruyter. https://doi.org/10.1515/9783110515145
- 19. Kundu, P.K. and Cohen, I.M. (2004) Fluid Mechanics. Elsevier Academic Press, Cambridge.
- 20. Witham, G.B. (1974) Linear and Nonlinear Waves. John Wiley, Hoboken.
- 21. Zakharov, V.E., Dyachenko, A.I. and Prokofiev, A.O. (2006) Freak Waves as Nonlinear Stage of the Stokes Wave Modulation Instability. European Journal of Mechanics, 25, 677. https://doi.org/10.1016/j.euromechflu.2006.03.004