Journal of Applied Mathematics and Physics
Vol.05 No.10(2017), Article ID:79866,47 pages
10.4236/jamp.2017.510169
Propagation of Acoustic Waves Caused by the Accelerations of Vibrating Hand-Held Tools in Viscoelastic Soft Tissues of Human Hands and a Mechanobiological Picture for the Related Injuries
Eugen Mamontov1*, Viktor Berbyuk2
1Versati AB, Askim, Sweden
2Department of Mechanics and Maritime Sciences, Chalmers University of Technology, Gothenburg, Sweden
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 7, 2017; Accepted: October 23, 2017; Published: October 26, 2017
ABSTRACT
As is well known, hand-arm vibration syndrome (HAVS), or vibration-induced white finger (VWF), which is a secondary form of Raynaud’s syndrome, is an industrial injury triggered by regular use of vibrating hand-held tools. According to the related biopsy tests, the main vibration-caused lesion is an increase in the thickness of the artery walls of the small arteries and arterioles resulted from enlarged vascular smooth muscle cells (VSMCs) in the wall layer known as tunica media. The present work develops a mechanobiological picture for the cell enlargement. The work deals with acoustic variables in solid materials, i.e., the non-equilibrium components of mechanical variables in the materials in the case where these components are weakly non-equilibrium. The work derives an explicit expression for the infinite-time cell-volume relative enlargement. This enlargement is directly affected by the acoustic pressure in the soft living tissue (SLT). In order to reduce the enlargement, one can reduce either the ratio of the acoustic pressure in the SLT to the cell bulk modulus or the relaxation time induced by the cell osmosis, or both the characteristics. Also, a mechanoprotective role of the above relaxation time in the cell-volume maintenance is noted. The above mechanobiological picture focuses attention on the pressure in an SLT and, thus, modeling of propagation of acoustic waves caused by the acceleration of a vibrating hand-held tool. The present work analyzes the propagation along the thickness of an infinite planar layer of an SLT. The work considers acoustic modeling. As a general viscoelastic acoustic model, the work suggests linear non-stationary partial integro-differential equation (PIDE) for the weakly non-equilibrium component of the average normal stress (ANS) or, briefly, the acoustic ANS. The PIDE is, in the exponential approximation for the normalized stress-relaxation function (NSRF) reduced to the third-order linear non-stationary partial differential equation (PDE), which is of the Zener type. The unique advantage of the PIDE is that it presents a compact model for the acoustic ANS in an SLT, which explicitly includes the NSRF, thereby enabling a consistent description of the lossy-propagation effects inherent in SLTs. The one-spatial-coordinate version of this PDE in the planar SLT layer with the corresponding boundary conditions is considered. The relevance of these settings is motivated by a conclusion of other authors, which is based on the results of the frequency-domain simulation in three spatial coordinates. The boundary-value problem at arbitrary value of the stress-relaxation time (SRT) and arbitrary but sufficiently regular shape of the external acceleration is analytically solved by means of the Fourier method. The obtained solution is the steady-state acoustic ANS and allows calculation of the corresponding steady-state acoustic pressure as well. The derived analytical representations are computationally implemented. Propagation of the pressure waves in the SLT layer at zero and different nonzero values of the SRT, and the single-pulse external acceleration is presented. They complement the zero-SRT and zero-SRT-asymptote results with the results for various values of the SRT. The obtained pressure values are, at all of the space-time points under consideration, meeting the condition for the adequateness of the linear model. In the case where the SRT is zero, the results well agree with the ones obtained by using the simulation software package LS-DYNA. The dependence of the damping of acoustic variables in an SLT on the SRT in the present third-order case significantly generalizes the one in the second-order linear systems. The related resonance effect in the waves of the acoustic pressure propagating in an SLT is also discussed. The effects of the NSRF-originated memory function provided by the present third-order PDE model are necessary for proper simulation of the pressure, which is of special importance in the aforementioned mechanoboiological picture. The results obtained in the work present a viscoelastic acoustic framework for SLTs. These results open a way to quantitatively specific evaluation of technological strategies for reduction of the vibration-caused injuries or, loosely speaking, achieving “zero’’ injury.
Keywords:
Mechanobiology, Viscoelastic Soft Living Tissue, Acoustic Wave, Stress-Relaxation Time, Third-Order Partial Differential Equation

1. Introduction
As is well known (e.g., [1] ), vibration and compressive loads are mechanical stimuli that have a powerful influence on living tissues. Recent studies in the animal models demonstrate that certain types of mechanical loads regulate various tissues. However, “over exposure’’ to mechanical stimuli is damaging for the tissues. It can cause symptoms, syndromes, and even diseases (e.g., see Refs. 7 - 9 in [1] and the papers in [2] ). One of the most well-known negative implications is hand-arm vibration syndrome (HAVS), or vibration-induced white finger (VWF). It is a secondary form of Raynaud’s syndrome, an industrial injury triggered by regular use of vibrating hand-held tools.
The vibrating tools generate the accelerations acting on, and perpendicular to the surface of human fingers and neighboring regions of palms. These accelerations create acoustic waves propagating in the human soft tissues and causing injuries. An acoustic variable in a solid material is the non-equilibrium component of a mechanical variable in the material in the case where this component is weakly non-equilibrium.
The Appendix develops a mechanobiological picture for the main vibration injuries. It indicates that there are two characteristics that directly affect the cell volume. One of them is the mechanical variable, which is the acoustic pressure in a SLT, whereas the other is the biophysical variable, which is the relaxation time induced by the cell osmosis. The main text of the present work focuses on modeling of the mentioned pressure. The purpose of the work is formulated in Subsection 1.2 on the basis of the discussion of the state of the art in the area in Subsection 1.1. Subsection 1.3 specifies the topics of the other sections and outlines the approach of the work.
1.1. State of the Art in Propagation of Acoustic Waves in Soft Solids
Propagation of acoustic waves in solids in the cases where the solids are elastic, i.e., inviscid, or, equivalently, conservative systems, is the well-studied topic. There is a vast literature on it (e.g., [3] and the references therein) and a lot of corresponding software packages, commercial or research. Moreover, the topic is described and analyzed in many text-books. To mention a few, we note [4] [5] and [6] . These materials enable one to solve virtually any elastic-solid acoustic problem. This is equally true with respect to soft solids as is explained in the remark below.
Remark 1.1. The expressions for the elastic components of the entries of the Cauchy stress matrix in a solid material (e.g., [5] , (1.3), (1.2)) in terms of the strains are known as the Hooke law (e.g., [5] , (1.43)). These expressions are linear in the strains with the coefficients, which present the bulk and shear moduli of the material, and . The latter one is also known as the modulus of rigidity. These moduli are coupled with the Young modulus and the Poisson coefficient as follows
, (1.1)
and determine the volume and shear viscosities and ,
(1.2)
where is the stress-relaxation time (SRT).
As follows from the experimental data in Table 1, shear moduli of SLTs are usually a few orders less than the corresponding bulk moduli. Table 1 specifies this feature in the case of SLTs in Column 3. Note that elastic properties and parameters of SLTs are discussed in considerable detail in the review work [9] (see also the references therein).
The mentioned feature enables one to neglect the shear-modulus-related terms in the aforementioned expressions for the elastic components of the entries of the Cauchy stress matrix, thereby reducing the stress matrix to the scalar matrix. The scalar in this matrix is where is the acoustic average normal stress (ANS).
Term presents the sum of its elastic and viscous components. The elastic one is known as the acoustic pressure, . Consequently, coincides with if and only if the material is inviscid, i.e., (see (1.2)), at . Thus, is the viscous components of . ,
The above discussion shows that acoustic problems in soft elastic solids can adequately be solved in terms of the well-established elastic-solid models (e.g., [3] and [9] , and the references therein). This means that new research and development in acoustics of soft solids are associated with other, less studied problems. One of them is soft viscoelastic solids. An important example of viscoelastic solids is living tissues (e.g., p. R3 of [9] , pp. 194 and 196 of [3] ), both SLTs and bones (e.g., [10] ).
In the case of soft viscoelastic solids, the reduction to the shearless version (see Remark 1.1) is also applicable. However, key difficulties here are associated with allowing for non-nonzero values of bulk (or volume) viscosity or, equivalently (see (1.2)), SRT .
The spatially heterogeneous viscoelastic model for solids, which is known since long ago, is the corresponding generalization (e.g., [5] , (6.15), [11] , Chapter 3 and Epilogue, [12] , §34) of the spatially homogeneous Kelvin-Voigt (KV) model (e.g., [5] , (6.8) or (6.9)). This generalization presents the system of linear nonstationary (LNS) partial differential equations (PDEs) for the entries of the three-dimensional displacement vector in a solid, and includes not only
Table 1. Experimental data on the bulk and shear moduli of soft tissues [7] . For comparison, one can obtain value for natural rubber from the Poisson coefficient reported in Table 1 in [8] and the first equality in (1.1).
elastic moduli (1.1) but also viscosities (1.2). In particular, a version of this model is used as the linearized core ( [3] , (5) or (6)) of the non-linear model in one spatial coordinate considered in [3] . (Note that the equation of the form ( [3] , (5)) was published by G.G. Stokes [13] , and further analyzed in ( [11] , Chapter 3 and Epilogue) and [14] long before work [3] was submitted.)
Remark 1.2. According to theoretical physics (e.g., [15] , Section 6 of Chapter II, [16] , (8.6); see also the discussion in [17] , Appendix), the acoustic stress in any viscoelastic solid is the sum of its elastic and viscous components where the viscous component is presented with the Boltzmann superposition integral. The integrand in this integral includes the normalized stress-relaxation function (NSRF). It is a function of the non-negative time separation. The integral of the NSRF in the time separation over the interval from zero to infinity is known as the SRT, . (The above term “normalized’’ means that the NSRF at zero time separation is unit.)
As one can show, the Boltzmann superposition integral, in the asymptotic limit case as , is the product of and the time-derivative of the elastic component of the acoustic stress. This product presents the zero-SRT asymptote. Also, in the mentioned limit case, the expression for the total acoustic stress in a solid presents the KV model. ,
One should note that the models based on the KV representation are, as models for the stress rather than the strain, applicable in the asymptotic limit indicated in Remark 1.2 only. The aforementioned work [3] on the brain tissue indicates value 232 ps of the SRT ( [3] , p. 196). It is apparently within the applicability of the zero-SRT asymptote and is only 166 times greater than the extremely low value of the SRT for liquid water (see Remark 2.1 below).
Along with this, the SRT values for the SLTs of the VWF-patient fingers and palms need not be that low. (These SLTs include the dermis, epidermis, subcutaneous tissue, and muscle tissue mentioned in Appendix.) For this very reason, the zero-SRT asymptote or the KV treatments are generally not suitable for the VWF problems.
However, to our knowledge, there is no any consistent acoustic model, which takes into account the NSRF at arbitrary values of the SRT rather than in the particular case of the zero-SRT asymptote only.
1.2. Beyond the State of the Art. Purpose of the Work
In order to fill the gap indicated in the last sentence of the previous subsection, paper [17] derives the general LNS partial integro-differential equation (PIDE) in the three spatial coordinates for the acoustic ANS (see [17] , (2.10)). This equation takes into account the NSRF strictly in the way summarized in Remark 1.2. Moreover, in the NSRF exponential approximation determined by a single parameter, SRT, the derived equation is reduced to the third-order LNS PDE (see [17] , (2.11)), which appears to be of the Zener type.
There are more complex approximations for the NSRF, for instance, the Prony series (e.g., [18] ) and a number of other empirical and semi-empirical models (e.g., [19] ). However, parameters of these models are determined from the NSRF measured values, which are difficult (if possible at all) to obtain by means of the patient-specific in vivo or ex vivo tests. In contrast to that, the single parameter of the exponential NSRF model, SRT , can be obtained from the measured values of one of the viscosities and the corresponding elastic modulus (see (1.2)). Another advantage of the exponential approximation is that it not only includes the basic parameter, SRT, but also allows to keep the number of the input parameters for the modeling at the minimum level. Also note that a consistent theoretical-physics model for the NSRF and the list of its parameters remains unknown.
The following four facts should also be noted.
Firstly, in a number of cases (e.g., [20] , Figure 3), the accelerations generated by vibrating hand-held tools, can be outlined the following way. The acceleration is in the form of, loosely speaking, large periodic pulses (e.g., with the periods of 0.03 - 0.02 s [20] ). The pulse-peak values of these accelerations may reach ±105 m/s2. The corresponding displacements are, however, extremely small. All of the pulses are very similar to each other, roughly, the same. The shape of a pulse tends to zero as the time tends to infinity. The settling-to-zero time is usually noticeably less than the period. The corresponding acoustic signals in SLTs also well settle to zero within the period between the pulses. Consequently, it is usually sufficient to analyze the acoustic response to a single pulse only.
Secondly, works related to the areas described in Subsection 1.1 (e.g., [3] and [9] and the references therein) include numerous illustrations of computer-simulation results on propagation of acoustic waves in SLTs. They facilitate understanding of the acoustic phenomena.
Thirdly, a finger and a palm of the hand, which holds the handle of a vibrating tool, presents a complex geometrical system. Within a bounded area of the finger/palm-handle contact, the contact surface can be regarded as planar and the tool acceleration acting on the surface can be regarded as acting perpendicularly to the planar surface. These settings are adopted, for example, in paper [21] (where the planar contact region of the finger is termed the finger pad). The acoustic computer simulation of a finger model in three spatial dimensions presented in [21] , which was preceded by the simulation in two spatial dimensions [22] , comes to the following conclusion. The region of the soft tissue, which is the most prone to formation of vibration-induced injuries, is the tissue domain neighboring the contact, and this domain is the location of the greatest variations of acoustic variables (e.g., strains) during vibration exposure. Consequently, analysis of the dominating acoustic phenomena in the finger or palm soft tissue can focus on a planar layer of the tissue between the contact plane and the finger/palm bones in the direction of the spatial coordinate perpendicular to the plane, i.e., along the thickness of the layer. One can add that, for simplicity, the planar layer can be regarded as infinite.
Fourthly, the computer simulations in the aforementioned papers [21] and [22] are based on nonlinear frequency-domain methods, which provide nonlinear response functions, and only deal with harmonic external time-varying signals. In contrast to that, the approach developed in the present work is intended to deal not only with smooth signals (such as linear combinations of harmonics) but also the measured, highly irregular external time-varying signals. For this reason, it considers the time-domain models and methods only.
Taking into account the above four facts and the fact that the aforementioned third-order PDE open a way to consistent computer simulation of SLTs, the purpose of the present work is three-fold:
1) derivation of the answers to the three questions formulated in Appendix;
2) development of the Fourier-method steady-state solutions of the boundary-value problem for the third-order LNS PDE of the Zener type in an infinite planar layer of an SLT under the action of the acceleration produced by the vibrating hand-held tools;
3) simulation of propagation of the pressure waves in the SLT layer, which are caused by the single-pulse accelerations, at zero and different nonzero values of the SRT, and different settings for the acceleration pulse; the simulation is supposed to be implemented in two different ways: by means of the one- dimensional version of the model in Point (1) and, at zero relaxation time, by means of LS-DYNA, the well-known purely numerical, finite-element simulator (e.g., [23] ).
Achieving the above purpose will complement the aforementioned, zero-SRT and zero-SRT-asymptote results with the results for arbitrary values of the SRT. Task (1) is solved in Appendix. Tasks (2) and (3) are solved in the way described in the next subsection.
1.3. Topics of the Subsequent Sections and an Outline of the Present Approach
The work presents and discusses the aforementioned third-order PDE for the acoustic ANS in an SLT (Section 2). The corresponding boundary-value problem is formulated in the case of an infinite planar layer of an SLT (Sections 3 and 4). This formulation includes the external acceleration of a vibrating hand-held tool. The exact analytical expression for the acoustic ANS in the general case of the arbitrary but sufficiently regular shape of the acceleration is derived in the form of the Fourier-method series (Sections 5 and 6).
The above results are summarized in Section 7. The analytical representation for the acoustic pressure in an SLT and the convergence of the series are considered in Section 8.
The developed analytical representations are computationally implemented in computer simulation. The corresponding simulation results along the thickness of the muscle-tissue layer of a palm are exemplified in Section 9. Section 10 concludes the work. It can also serve as an executive summary. The role of Appendix is mentioned in Subsection 1.2 and specified at the beginning and in the first bullet of Section 10.
In general, exact analytical expressions for solutions of models provide the most transparent views of the structure of the solutions. These forms include the explicit dependences of the solutions on the parameters and other input variables of the models. This is an advantage of analytical solutions.
Another advantage is that analytical solutions can provide the modeling terms, which are inaccessible in purely numerical approaches. For instance, the latter do not allow to determine the natural angular frequencies, which, in particular, can play a noticeable role in interpretation of the features of the related computational results (see (6.7) in connection with the text in Table 3).
The present work only considers the steady-state solutions of the aforementioned boundary-value problem. Loosely speaking, these are the ones independent of the initial values (e.g., see [24] for further details). Due to this feature, the steady-state solutions present the core behaviors of the systems, i.e., the behaviors, which are not affected by specific initial values or initial time points.
Also note that all of the physical-quantity values specified below, with the exception of the ones in Figures 1-12 are presented in the SI.
2. Acoustic Equation for the Scalar Stress in Soft Living Tissues
The model described below assumes that SLTs are isotropic, isothermal, spatially homogeneous at equilibrium, and, according to the SLT data in Table 1, shearless. In this case, one can use the LNS PIDE for acoustic ANS of the following form (see (2.10) in work [17] )
, (2.1)
where is the speed of the bulk acoustic waves, is the Laplace
Figure 1. Propagation of the pressure waves in the 10-mm layer of the muscle tissue in the case of Example 1 at zero value of SRT θ. The pressure unit is MPa. The data were obtained with the help of the LS-DYNA software package [33] .
Figure 2. Propagation of the pressure waves in the 10-mm layer of the muscle tissue in the case of Example 1 at zero value of SRT θ. The data were obtained in the present treatment.
Figure 3. Propagation of the pressure wave in the 10-mm layer of the muscle tissue in the case of Example 1 at value 0.001 × θ* = 0.95 × 10−7 of SRT θ (see (9.1) for θ*). The data were obtained in the present treatment.
Figure 4. Propagation of the pressure waves in the 10-mm layer of the muscle tissue in the case of Example 1 at value 0.003 × θ* = 0.285 × 10−6 of SRT θ (see (9.1) for θ*). The data were obtained in the present treatment.
Figure 5. Propagation of the pressure waves in the 10-mm layer of the muscle tissue in the case of Example 1 at value 0.010 × θ* = 0.95 × 10−6 of SRT θ (see (9.1) for θ*). The data were obtained in the present treatment.
Figure 6. Propagation of the pressure waves in the 10-mm layer of the muscle tissue in the case of Example 1 at value 0.030 × θ* = 0.285 × 10−5 of SRT θ (see (9.1) for θ*). The data were obtained in the present treatment.
Figure 7. Propagation of the pressure waves in the 10-mm layer of the muscle tissue in the case of Example 1 at value 0.100 × θ* = 0.95 × 10−5 of SRT theta (see (9.1) for θ*). The data were obtained in the present treatment.
Figure 8. Propagation of the pressure waves in the 10-mm layer of the muscle tissue in the case of Example 1 at value 0.300 × θ* = 0.285 × 10−4 of SRT θ (see (9.1) for θ*). The data were obtained in the present treatment.
Figure 9. Propagation of the pressure waves in the 10-mm layer of the muscle tissue in the case of Example 1 at value 1.000 × θ* = 0.95 × 10−4 of SRT theta (see (9.1) for θ*). The data were obtained in the present treatment.
Figure 10. Propagation of the pressure waves in the 10-mm layer of the muscle tissue in the case of Example 2 at value 0.030 × θ* = 0.285 × 10−5 of SRT theta (see (9.1) for θ*). The data were obtained in the present treatment.
Figure 11. Propagation of the pressure waves in the 10-mm layer of the muscle tissue in the case of Example 3 at zero value of SRT θ. The pressure unit is kPa. The data were obtained with the help of the LS-DYNA software package [33] .
Figure 12. Propagation of the pressure waves in the 10-mm layer of the muscle tissue in the case of Example 3 at zero value of SRT θ. The data were obtained in the present treatment.
differential expression with respect to the three spatial coordinates, is the time separation, and is the NSRF. The term “normalized’’ denoted with the letter “N’’ in the abbreviation “NSRF’’ (introduced in Subsection 1.2) means that .
The first and second terms in the brackets in (2.1) correspond to the elastic and viscous stresses in the way discussed in Section 2 and Appendix of work [17] . Parameters s and K are coupled by means of relation (e.g., [17] , (2.2))
(2.2)
where is the volumetric mass density of an SLT. The integral in (2.1) is known as the Boltzmann superposition integral. Due to the presence of this integral in Equation (2.1), the equation is suitable for viscoelastic rather than elastic-only materials.
The basic parameter of NSRF is SRT (already mentioned in Remark 1.1), which is determined with the well-known relation (e.g., [17] , (A.6))
(2.3)
Parameter is included in (1.2). Any of the relations (1.2) can be used for evaluation of . Two of many examples are indicated in the remarks below.
Remark 2.1. In the case of liquid water, and (e.g., [25] and [26] , respectively). Application of these values to the first equality in (1.2) results in estimation for liquid water. ,
A number of works on non-invasive measurements in SLTs available in the literature indicate that in various SLTs, . As follows from Column 2 of Table 1, the related values of G are 8 - 340 ´ 103. Application of the values of and G to the second equality in (1.2) results in the range of the values of SRT , which appear to be typical for SLTs, namely between and .
Equation (2.1) was derived under the condition that (e.g., [27] , (A.1.13))
(2.4)
(see Remark 1.1 for ). Condition (2.4) assures that the SLT under consideration can be regarded as a linear material.
Remark 2.2. As follows from equations (A.1.14) and (B.8) in [27] , that
(2.5)
where is the strain matrix, is the identity matrix, and is the trace of a matrix. Equality (2.5) enables one to formulate condition (2.4) in terms of the strain matrix.
If one prefers the frequency-domain paradigm rather than the time-domain one, one can use a consistently derived frequency-domain counterpart of relation (2.5) in order to check condition (2.4). ,
In the simplest, exponential approximation for NSRF , i.e., under the assumption that at all , Equation (2.1) is specified to (see (2.12) in [17] )
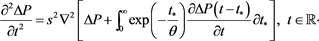 (2.6)
(2.6)
Paper [17] shows that PIDE (2.6) expresses the steady-state solution of LNS PDE (see [17] , (2.11))
(2.7)
regarded as an ordinary differential equation (ODE) of the first order for variable . Equation (2.7) is formally a PDE of the Zener type ( [5] , (6.40)) but, with respect to the origin and meaning, differs from the Zener PDEs noticeably (see the corresponding discussion in [17] ). The fact that PIDE (2.6) is nothing but the aforementioned steady-state case of PDE (2.7) indicates that (2.7) is a more general description than (2.6).
Each of the PIDEs (2.1) and (2.6), and, thus, PDE (2.7) is valid only if condition (2.4) holds. In order to verify it, should be available. Work [17] also derives the explicit expressions for in terms of solutions of PDE (2.7). The simplest of them is expression ( [17] , (2.8))
(2.8)
As is noted on p. 512 in [17] , ODE (2.8) is the ANS-member of the family of spatially homogeneous versions of the Zener acoustic models (e.g., [5] , (6.25)), which corresponds to the exponential approximation for the NSRF. Notably, this family is also used for experimental determination of SRTs in SLTs. For example, work [28] proposes a framework of quantitative assessment of SLTs that can be used in clinical diagnostics. The work applies the Zener models "(e.g., see (1) in [28] ) and determines the tissue SRT in terms of the Young modulus and the corresponding viscosity (see [28] , the right column on p. 154). Since the Young modulus E is coupled with both bulk and shear moduli K and G with the well-known linear relations (see the first relation in (1.1)), the SRT determined in the above way can be used in the capacity of SRT regarded in the present work (in particular, in expressions (1.2) for the corresponding viscosities).
Remark 2.3. In view of (2.3), the asymptotic representation of PIDE (2.1) in the limit case as is PDE (2.1) in [17] ,
(2.9)
that, at , is reduced to
(2.10)
Both (2.9) and (2.10) do not include the integral indicated in (2.1). This integral where the kernel function is the NSRF is often termed the memory function. It provides the integral influence of the values of a solution of (2.1) at all upon the value at t. In this sense, the value at t “remembers’’ the values at all . This effect significantly complicates the behaviors of the solutions. The NSRF-originated memory function corresponds to the friction distributed in time.
Equation (2.9) was derived in [27] . It presents the zero-SRT asymptote of (2.1). In the case where the solution variable is the velocity potential of a fluid, the version of (2.9) was derived by G.G. Stokes [13] (see the discussion in [27] , p. 964).
Equation (2.10) presents the zero-SRT case of (2.1) and corresponds to a purely elastic (or inviscid) material.
Comparison of particular version (2.6) of Equation (2.1) with Equation (2.7) shows that, in the latter equation, the terms, which include SRT , originate from the exponential-NSRF-originated memory function in (2.6). ,
The advantage of PIDE (2.1) and its particular cases (2.6) or (2.7) is that any of them eliminates the zero-SRT asymptote limitation of the Stokes-type equation indicated in Remark 2.3.
Remark 2.4. The input data for PDE (2.7) are the following three parameters: , , and . Number used in (2.7) is determined in terms of and by means of (2.2).
The output data of LNS-PDE (2.7) include (but need not be limited to) the following two space-time-dependent variables of an SLT, acoustic ANS and acoustic pressure (see (2.8)). ,
Expression (2.8) not only describes pressure in terms of the but also enables one to answer the question on if the results of the above linear models are acceptable. For example, any solution of PDE (2.7), which, by means of (2.8), provides the values of such that (2.4) holds, presents an adequate result. This, so to say, self-testing allows to avoid a use of much more complex, nonlinear models (e.g., [3] ) in the cases where linear models suffice.
3. Boundary Conditions for the Stress in the Case of an Infinite Planar Layer of a Soft Living Tissue
The present section considers the geometrically simplest case of the configuration of an SLT, namely where the SLT is an infinite planar layer. Without a loss of generality, one can assume that the coordinate axis perpendicular to the layer is the x-axis and the two planar surfaces of the layer correspond to two different values of coordinate x, say, and where is the thickness of the layer. Consequently, PDE (2.7) is reduced to
. (3.1)
One of the basic settings for this equation presumes that the external acceleration acting on the SLT layer is present at plane , whereas the other plane, the one at , contacts air. The corresponding boundary conditions are
(3.2)
where is the acceleration and
. (3.3)
Note that term presents the volumetric density of the force acting at space-time point .
Remark 3.1. The input data for boundary-value problem (3.1)-(3.3) are the three parameters indicated in Remark 2.4, as well as parameter h and function .
The output data of the mentioned problem are the versions of the two space- time-dependent variables indicated in Remark 2.4 in one spatial coordinate, x.,
Remark 3.2. The above single-layer system can be generalized to a multi-layer system. In this case, one should include the boundary conditions at the inter-layer surfaces. Each of these conditions presents the equality of the acoustic ANS and the equality of the accelerations in the neighboring layers.
Multi-layer systems can substantially extend the scope of the present approach. For example, in a three-layer system, one of the layers can be the muscle tissue of a palm, whereas the other two layers can be the skin and a layer of a protective material intended for a reduction of the amplitude or altering the frequency content of the acoustic waves penetrating into the soft tissues. Another example is a three-layer system where the layers represent the stratum corneum, epidermis, dermis, and subcutaneous tissue of a finger. The list of the related examples can easily be continued. ,
Individual solutions of boundary-value problem (3.1)-(3.3) are specified with the initial conditions and can be obtained by the Fourier method.
4. Transformation of the Boundary-Value Problem for the Stress to the One with Homogeneous Boundary Conditions
As is well known, the Fourier method is applicable to boundary-value problems if the boundary conditions are homogeneous. Problem (3.1)-(3.3) can be transformed into this form in the following way (e.g., [4] , Section 4 in Chapter IX).
One introduces the change of variable
(4.1)
where the physical dimension of variable is the squared velocity. This change allows to substitute (4.1) into (3.1)-(3.3) and thereby obtain the PDE and homogeneous boundary conditions for ,
(4.2)
(4.3)
(4.4)
where
(4.5)
The last term on the right-hand side of (4.2) presents the source term. It results from change of variable (4.1). In connection with the source terms, we accept the following.
Assumption 4.1. Function and, thus (see (4.5)), function are piecewise differentiable in the entire time axis. ,
Assumption 4.1 is used in the consideration below.
5. Exact Analytical Expression for the Steady-State Stress
The present section considers solution of boundary-value problem (4.2)-(4.4) by means of the Fourier method (e.g., [4] , Chapters VIII and IX). It is applicable to the PDEs, which are based on the Laplace differential operators. The Fourier method provides expansions of solutions of these PDEs in the space-dependent operator eigenfunctions with time-dependent coefficients (e.g., [29] , Chapter V) and formulates the ODE systems for these coefficients. The main advantages of the Fourier method are the following.
・ The above expansions enable the exact analytical solutions.
・ The exact analytical expressions provide an explicit insight in the structure of the solution in the terms, which are also meaningful physically.
・ The method allows a variety of approximations of different accuracy and complexity.
The consideration in this section down (5.5) is based on the well-known ideas (e.g., [4] , Ch. IX, Sections 1 and 4 in Chapter IX). According to the Fourier method, solutions w of boundary-value problem (4.2)-(4.4) are representable in the form of function series
(5.1)
where are the orthonormed eigenfunctions of the Laplace operator in PDE (4.2). This operator is differential expression endowed with boundary conditions (4.3) and (4.4). As one can easily check, the eigenvalues and eigenfunctions of the operator are numbers , where
(5.2)
and
(5.3)
Since the source term in PDE (4.2) includes linear function , it is necessary to involve the corresponding expansion for this function. By using (5.2), (5.3), and the well-known results (e.g., [29] , Sections 21.4 and 22.3 of Chapter V, [30] , 440.11), one can show that the expansion is
(5.4)
Application of (5.1) and (5.4) to PDE (4.2) results in
(5.5)
Relations (5.5) present the countably infinite set of linear non-autonomous ODEs of the third order for time-dependent coefficients in the Fourier expansion (5.1). The forms of these ODEs show that they can be mutually independent.
The third-order ODEs (5.5) can be represented in the form of the first-order ODE systems
(5.6)
where vectors and , and matrixes are described with the following expressions
(5.7)
(5.8)
(5.9)
As is well known in theory of systems of linear ODEs, if systems (5.6) are asymptotically stable, then:
・ the steady-state solutions of these systems (under Assumption 4.1) are described as
(5.10)
where
(5.11)
are the Cauchy matrixes of the systems
・ and all entries of these matrixes exponentially tend to zero as .
Note that column-vectors , , and of matrixes (5.11) are the solutions of homogeneous version
(5.12)
of the ODE system (5.6), which are such that (see (5.11)) , where is the identity -matrix, or, equivalently,
(5.13)
where is the l th column of matrix . Due to (5.8), relations (5.10) are reduced to expressions
(5.14)
which do not include matrixes (5.11) and emphasize a special role of their third columns . In view of the structure of vectors (5.7), it is sufficient to consider the first entries of vectors (5.14) only. The versions of (5.14) for these entries are
(5.15)
where is the first entry of vector . Thus, the analytical expressions for the time-dependent coefficients in expansion (5.1) are (5.15). Note that the physical dimension of is the squared time.
Assumption 5.1. Each of the functions and , and, thus (see (4.5)), function is uniformly bounded in the entire time axis. ,
Taking into account the exponential tendency to zero noted in the text on (5.12) as well as Assumptions 4.1 and 5.1, one can show that all of the coefficients (5.1) are uniformly bounded in the entire time axis.
Combination of (4.1), (5.1), (5.3), and (5.15) results in
(5.16)
Remark 5.1. The exact analytical expression for the steady-state solution of boundary-value problem (3.1)-(3.3) is described with expression (5.16) (see also (4.5) and (5.2)) in terms of entries of the Cauchy matrixes (5.11) of ODE systems (5.6) under Assumptions 4.1 and 5.1, as well as the assumption that all of the ODE systems (5.6) are asymptotically stable. ,
The next section establishes asymptotic stability of systems (5.6) and derives the exact analytical expressions for the entries mentioned in Remark 5.1.
6. Expression for the Stress in Terms of the Input Data Only
The present section establishes asymptotic stability of the ODE systems for the time-coefficients in the Fourier representation for the scalar stress and derives expressions for the entries of the Cauchy matrixes of these systems. On the basis of this, the section obtains the exact analytical representation for the steady-state stress in terms of the input data.
In order to investigate the asymptotic stability of ODE systems (5.6), one needs to consider the real parts of the eigenvalues of matrixes (5.9) in (5.6). Due to the connection of the first-order systems (5.6) to the third-order scalar Equation (5.5), these eigenvalues are the roots of equations
(6.1)
which are the characteristic equations for homogeneous versions
(6.2)
of ODEs (5.5). Note that in (6.1) are determined with (5.2). In view of the results developed in Theorem 2.1 of [17] on characteristic Equation (2.13), the following statements are valid.
(i) Each of the characteristic Equation (6.1) has one real root, , and a pair of the complex conjugate roots , where is the imaginary unit, i.e., .
(ii) .
(iii) , , and strictly monotonically increases as increases from zero to infinity.
(iv) Asymptotic representation for in the limit case as is .
(v) .
(vi) Asymptotic representations for in the limit cases as and are and , respectively.
(vii) Each of ODEs (5.5) is asymptotically stable.
Statement (vii) implies that each of the ODE systems (5.6) is asymptotically stable and, thus, the analysis presented in Section 5 below (5.9) is relevant. As follows from statements (ii) and (v), the parameters and of the complex conjugate root in statement (i) are functions of not only SRT and angular frequencies , which directly follow from the input data (see Remark 3.1, (2.2), and (5.2)), but also , which is not quantified above.
As is indicated in statement (i), is the only real root of cubic Equation (6.1). It can be determined with the help of the well-known method of S. del Ferro and N. F. Tartaglia for solving cubic equations. Nowadays, it is known as the Cardano solution (e.g., [31] , 1.8-3). One can show that, according to it, the mentioned root is determined as follows
(6.3)
where
(6.4)
and
(6.5)
Continuous variable in (6.4) and (6.5) generalizes discrete variable in (6.3). Numerical values of function (6.4) are exemplified in Table 2.
In view of (6.3), the equality in statement (ii) is equivalent to
(6.6)
which, in turn, transforms the expression in statement (v) into
(6.7)
Remark 6.1. As follows from statements (iii) and (iv), as well as expressions
Table 2. Examples of the numerical values of function (see (6.4)).
(6.3) and (6.6), the properties below hold.
・
・
・ Function strictly monotonically increases as increases from zero to infinity.
・ The asymptotic representation for in the limit case as is . ,
Remark 6.2. As follows from the fist two bullets in Remark 6.1 and expression (6.7), relations
hold. ,
Remark 6.3. The above consideration enables one to express three sequences , , and of the parameters of the real root and complex conjugate roots in statement (i) in terms of parameter , physically dimensionless function , and physically dimensionless sequence where and are determined with (2.2) and (5.2) by means of (6.3), (6.6), and (6.7). ,
According to theory of linear ODEs with time-independent coefficients, the roots of Equation (6.1), which are indicated in Remark 6.2, enable one to specify the general solutions of the third-order scalar ODEs (6.2) at the initial time point, , which was already used in expressions (5.11). These solutions are
(6.8)
where , , and are the arbitrary parameters independent of time. This, in particular, means that
(6.9)
The forms of the corresponding solutions of the first-order ODE systems (5.12) are
(6.10)
These vector-functions describe all of the solutions of the systems specifying them with individual values of parameters , , and . In particular, vectors (6.10) describe the three columns of each of the Cauchy matrixes (5.11) by means of conditions (5.13) with expressions . Consequently, the third columns, which include entries used in (5.16), are determined as , or, in more detail,
(6.11)
In order to carry out the calculations presumed by (6.11), one needs to evaluate the first and second time derivatives of function . As follows from (6.8),
(6.12)
(6.13)
Entries are specified with the condition indicated on the right-hand side of (6.11). On the strength of (6.8), (6.12), and (6.13), this condition is equivalent to three equalities, which are the second ones in the following three relations
These systems are the ones for determination of parameters , , and . One can readily check that the corresponding solutions are
or, in view of (6.3) and (6.6),
(6.14)
(6.15)
where
(6.16)
(6.17)
Note that parameters (6.16) and (6.17) are physically dimensionless. The remark below is similar to Remark 6.2.
Remark 6.4. As follows from the fist two bullets in Remark 6.1, Remark 6.2, and express- ions (6.15)-(6.17), relations
hold. ,
Remark 6.5. Three sequences , , and are expressed in terms of SRT , physically dimensionless function (see (6.4)), and physically dimensionless sequence by means of (6.7) and (6.14)-(6.17). ,
We also not the following feature.
Remark 6.6. As follows from (6.16), (6.2), the properties of function in Remark 6.1, and statement (vi), the asymptotic representation for in the limit case as is . ,
As is well known (e.g., [30] , (401.02), (401.04))
Substituting these expressions into (6.8) and taking into account the first entries of vectors (6.11), one obtains
which, after application of (6.14)-(6.17), become
These expressions enable one to calculate the integrals in (5.16) as
(6.18)
where
(6.19)
(6.20)
(6.21)
In view of (4.5), the physical dimension of each of the coefficients (6.19)-(6.21) is acceleration. Relation (6.18) transforms (5.16) into
(6.22)
The derived analytical expression (6.22) explicitly shows the wave nature of the scalar stress propagating in layers of SLTs. The scalar stress presents the superposition of the space- or time-dependent sine and cosine waves with coefficients (6.19)-(6.21), which depend on time and the external-acceleration function with coefficients.
A special advantage of expressions (6.22) and (6.19)-(6.21) is that they deal with the general case of the involved variables and parameters rather than selected particular examples. The general case enables any number of particular examples, which can present individual settings and be quantified by computing, thereby providing the input data for the corresponding visualization for illustrative purposes. Other related output acoustic variables (such as the pressure) have similar properties. The expression for the pressure based on solution (6.22) is discussed in Section 8, which also explains the convergences of the series in (6.22).
Remark 6.7. The numerator in each of the ratios in (6.22) comprises three additive terms. Expressions (6.19)-(6.21), as well as (6.3), (6.6), and (6.17) show the following.
The sum of the second and third of the three terms presents the harmonic-type oscillations with frequency , time-dependent amplitude
,
and a time-dependent phase around zero. These oscillations are present, no matter if SRT is positive (damped oscillations) or zero (undamped oscillations described with (2.10)).
In contrast to that, the first of the three terms, namely (6.19), is present only if SRT is positive. If the latter is zero, the term is also zero. This means that the first term is present if and only if the exponential-NSRF-originated memory function noted in Remark 2.3 is not neglected as, for instance, in the zero-SRT and zero-SRT-asymptote cases also noted in Remark 2.3. Notably, expression (6.19) indicates that this term is, in contrast to the above harmonic, of the non-oscillatory form. As follows from its role in the aforementioned numerator, it creates a time-dependent shift of the above harmonic along the -axis, thereby producing the behavior and values of unavailable in the harmonic-type oscillations. ,
The effect of the exponential-NSRF-originated memory-function terms discussed in Remark 6.7 is quantitatively illustrated with computer-simulation results in Section 9.
Section 7 summarizes the exact analytical solution derived in the present section.
7. Summary of the Expression for the Stress
Boundary-value problem (3.1)-(3.3) describes the acoustic ANS propagating in an SLT layer due to the external time-dependent acceleration. The input data for this problem are listed in Remark 3.1.
The exact analytical expression for the steady-state solution of the problem is, according to Remark 5.1, expression (6.22) (see also (4.5), (5.2), (6.16), and (6.17)) under Assumptions 4.1 and 5.1, and with coefficients (6.19)-(6.21). Parameters , , , , and are determined with (2.2), (5.2), (6.3), (6.6), and (6.7), respectively, in terms of the input parameters , , , and .
As follows from (6.22), the derived solution presents the superposition of the space- and time-dependent sine and cosine waves with the coefficients, which depend on the time and the external-acceleration function. Expression (6.22) is similar to the ones, which are well known in analysis of wave equations in acoustics (e.g., [4] , Section 4 of Chapter IX). Thus, solution (6.22) explicitly shows the wave nature of the signals propagating in SLTs.
The above analytical expression provides the explicit dependences of the solution not only on the space-time point but also on each of the input parameters and the external-acceleration function.
8. Expressions for the Steady-State Pressure. Convergences of the Corresponding Series
As follows from Remark 3.1, in addition to solution (6.22), there is one more space-time-dependent output variable: the acoustic pressure. The corresponding expressions are derived in this section.
Expression (6.22) presents the steady-state acoustic ANS. The related acoustic pressure can be obtained as the steady-state solution of ODE (2.8) regarded as the equation for .
The steady-state solution of ODE (2.8) is
(8.1)
We accept the following assumption.
Assumption 8.1. Function , as a function of t at every fixed , is uni- formly bounded in the entire t-axis. ,
Integrating the second integral by parts and taking into account Assumption 8.1, one obtains that
(8.2)
Substitution of (8.2) into (8.1) leads to
(8.3)
In the limit case as , the integral in (8.3) tends to .
Term in (8.3) is determined with (6.22) (see also (6.19)-(6.21)). Regarding the convergence of the series in (6.22), one can note the following.
Remark 8.1. One can readily check that each of the coefficients (6.19)-(6.21) of the series in (6.22) is uniformly bounded in and . Moreover, the i th term, , of the series in the limit case as , is proportional to or, equivalently (see (5.2)), to . This follows from the denominator in (6.22), expression (6.16) and (6.17), the form of sine and cosine coefficients (6.20) and (6.21), statement (vi) in Section 6, and Remark 6.6. Since series converges (e.g., [30] , 48.004), the series in (6.22) converges uniformly and absolutely in and . ,
Remark 8.1 shows that representation (6.22) is properly defined.
9. Examples of the Computer Simulation Results along the Thickness of an Infinite Planar Layer of the Muscle Tissue of a Palm
This section reports examples of computer simulation results obtained by means of computational implementation of the present modeling. The examples are based on the following values of the input parameters (see Remark 3.1) , , , and : , , , and where
(9.1)
The value of is determined as described below.
As follows from the discussion on pp. 1961 and 1966 in [7] , the tissues indicated in Table 1 are generally anisotropic materials and the ranges of the values in this table can be due to this feature. Since the heart tissues are muscle tissues, the lowest value of for heart in Table 1, i.e., , can be regarded as the one corresponding to the direction across the muscle fibers. The measured value of the shear viscosity of the in vivo bovine muscle fibers is (e.g., see p. 59 in [32] ). These values of and , in view of the second equality in (1.2), result in value (9.1) of .
The present work considers the three examples. They are based on the above values of , , and at different values of indicated in the captions for Figures 1-12. The examples also differ with different external-acceleration functions of the following two forms
(9.2)
(9.3)
where is the parameter of function . More specifically, function is: (9.2) at in Example 1, (9.3) at in Example 2, and (9.2) at in Example 3. In all of the examples, the pressures in Figures 2-10 and Figure 12 are calculated according to (8.3) where term is determined with (6.22). The countably infinite sum in (6.22) is replaced with the finite sum where the number of the terms is on the order of a few tens or hundreds, depending on specific example.
For comparison of the quantitative results of the present modeling, the simulation with the multi-physics LS-DYNA software package is also carried out. According to [33] , the corresponding settings are the following.
The prediction of wave propagation in the SLT material is modeled with a two-dimensional plane strain finite-element model. The central-difference method is adopted. The numerical simulation model consists of a rectangular plate of the material with a height of 10−2, discretized with two-dimensional plane strain continuum elements. In order to make the simulation model comparable to the above one-dimensional simulation, a lateral displacement boundary condition is introduced, which reduces the model to a one-dimensional problem. In addition, a non-reflecting boundary condition is used at the lateral boundaries of the simulation model in order to prevent stress wave reflections, which otherwise would be generated at these boundaries. At the upper boundary, no boundary condition is applied, so that approaching pressure waves are completely reflected. The material-layer response is time and history dependent and is usually described by viscoelastic constitutive models, based on, in the simplest case, exponential stress relaxation functions. In the present one-dimensional version, shear relaxation phenomena are not present and such physical phenomena as strain rate dependence and bulk viscosity are not taken into account. Therefore, the material is described with a linear elastic isotropic material model with the aforementioned values of and (see the text above (9.1)). The tissue layer is accelerated at the bottom boundary with a single sinusoidal pulse (9.1). The pressure is evaluated at five discrete spatial points throughout along the height of the tissue layer to capture the transient propagation and subsequent reflection of the pressure wave at the top and bottom.
Analysis of Figures 1-12 enables one to indicate a few features.
1) Comparison of Figure 1 and Figure 2, as well as Figure 11 and Figure 12 shows that, in the cases of Examples 1 and 3 and at zero SRT, the computational results of the present work well agree with the purely numerical results obtained with the help of the LS-DYNA simulation package.
2) The influence of different values of the SRT scaled with respect to value (9.1) is exemplified with the present results in Figures 3-10.
Comparison of Figure 3 and Figure 4 indicate that the SRT value is that small that the pressure is very weakly affected by the SRT.
The influence of the SRT upon the pressure is more pronounced in Figure 4, which corresponds to .
Figures 5-9 corresponding to the SRT values , , , , and , respectively, show that these values indicate that the pressures well “feel’’ them. In Figures 5-7, one can even see how the pressures settle to zero. However, this settling cannot be seen in Figure 8 and Figure 9 because it takes place at the time values beyond the interval shown in the figures due to rather high SRTs, and .
Figures 3-9 show that the damping of the pressure waves in an SLT is inversely proportional to SRT at not very small but is directly proportional to if is sufficiently small (cp., Figure 2 and Figure 3), and is not present at all if (see Figure 2). This picture is physically sound and remains valid not only for the pressure but also for other acoustic variables because it reflects the properties of the eigenvalues of matrixes (5.9) in (5.6) (see (6.6) and Remark 6.1). The mentioned dependence of the damping on SRT means that this dependence is nonlinear.
3) Concerning the high maximums of the pressures in Figures 2-9, one can note the following.
In the case of Figures 1-9, the external acceleration is (9.2) at , i.e., with the angular frequency
(9.4)
As is well known (e.g., [4] , (66) in Chapter IX), in the case where or, equivalently, PDE (2.7) is of the second rather than third order (e.g., see Figure 1), the Fourier series for the solution includes the resonance terms proportional to where is the angular frequency of the external signal (cp., (9.4)) and , are the natural angular frequencies of the system (cp., (6.7)). If there is such that , then the resonance occurs and the solution is infinite. None of these equalities takes place in the case corresponding to Figure 1, according to the present computational results. However, there are two natural angular frequencies, which are rather close to (see Row 1 of Table 3). Consequently, the corresponding versions of contribute to the resonance-related increase in the amplitude of the solution.
Note that, in the case of Example 3 in Figure 11 or Figure 12, the external- acceleration angular frequency is an order higher than the one in the case of Example 1 in Figure 1 or Figure 2. Consequently, the frequency in Example 3 is an order away from the principal frequency and the one closest to it in Row 1 of Table 3. This feature contributes to the fact that the pressure amplitude in Example 3 (see Figure 11 or Figure 12) is significantly lower than the one in Example 2 (see Figure 1 or Figure 2) due to the reduced resonance effect.
In the cases of Figures 2-9, SRT is positive rather than zero and, thus, PDE (2.7) is of the third order. In each of these cases, there are also two natural angular frequencies, which are rather close to (see Rows 2-8 of Table 3). However, the non-zero SRT values preclude the solution to become infinite, and the third order of the equation makes the resonance-effect dependences more complex. When the pressure weakly “feels’’ the SRT value, as is the cases of the behaviors in Figure 3 and Figure 4, the increase in the pressure amplitude is fairly small. When the pressure “feels’’ the SRT value well, as is the cases of the behaviors in Figures 5-9, the increase in the pressure amplitude is quite pro- nounced.
Moreover, the fact that PDE (2.7) at positive SRT ( ) is of the third rather than second order creates the time behaviors, which do not exist in the second-order, i.e., zero-SRT ( ) case. Indeed, Remark 6.7 emphasizes the new components of the solution, which are due to the exponential-NSRF- originated memory function in (2.6) and time-dependently shift the oscillations along the -axis. These shifts, in view of (8.3), provide the time-dependent shifts along the -axis as well. Since the single pulse in Example 1 (see (9.2)) and each pulse in the pulse sequence in Example 2 is positive, the shifts are in the positive direction of the -axis (e.g., they, in particular, increase positive
Table 3. The pairs of the angular natural frequencies of the solution of the model in the case of Example 1, which are closest to the external-acceleration angular frequency (9.4). The values of the SRT correspond to the ones for Figures 1-12. These values present the fractions of the SRT value (see (9.1)), which is discussed at the beginning of Section 9. The fractions are indicated in the left column. The data in the middle and right columns are obtained in the present approach.
amplitudes). These effects are especially clearly seen in Figures 5-9. The presented behaviors and values of unavailable with common wave PDE (2.10) or the Stokes-type PDE (2.9).
One should also note that the compressions and rarefactions in an SLT, which are associated with an oscillatory pressure, can cause lesions in it. The above shifts in the pressure oscillations lead to the pressure values that cannot be described in terms of familiar wave equations. Thus, the effects of the NSRF-originated memory function provided by the present, third-order PDE model are of importance for proper evaluation of the risks of formation of lesions in SLTs.
4) The aforementioned figures illustrate how the pressure damps to zero if the external acceleration damps to zero (see (9.2)). If the acceleration does not damp to zero, for example, is periodic at positive values of the time (see (9.3)), the pressure does not damp to zero either, and the shape of its damping is more complex.
Figure 10 corresponds to the SRT value of , i.e., the same one related to Figure 6. Figure 10 shows that the pressure damps to periodic oscillations rather than zero, as is the case in the behavior in Figure 6. The time-dependent shifts along the -axis in its positive direction are already commented in the next to last paragraph of the above Point 3. Comparison of Figure 10 and Figure 6 illustrates that the shape of the acceleration, even at the same key parameters (such as the amplitude and frequency), in general affects the outcome of the pressure damping.
5) The above results are obtained in the exponential approximation for NSRF (see the text above (2.6)). The exponential dependence qualitatively correctly represents the behaviors of the NSRF of more complex shapes. Consequently, the qualitative aspects of the obtained results remain valid in the general case where the NSRF need not be exponential. Also, since NSRF enters the general PIDE (2.1) under the sign of integral, the errors of one or another approximation for the NSRF affect the quantitative behaviors of the acoustic ANS and, thus (see (8.3)), the acoustic pressure not very significantly. We also note the following.
Remark 9.1. In view of the value (see above) and relation (2.4), the pressure values in Figures 1-12 meet requirement (2.4). This shows that, in all of the mentioned cases, the linearity of the present model is adequate. ,
Remark 9.2. The present work assumes that the soft tissue under consideration is linearly viscoelastic. The work emphasizes condition (2.4) for the linear-model adequacy and check it with the obtained results. It appears that the linear-model results are adequate.
In contrast to that, work [22] assumes that the viscoelastic soft tissues, which are under consideration in it, are non-linearly elastic. The work calculates all of the entries of the strain matrix in the frequency domain. This matrix is used in the frequency-domain version of relation (2.5). However, work [22] does not check, e.g., in the way specified in Remark 2.2, if the results of [22] violate condition (2.4) for the linear-model adequacy at least at a single space-time point. This leaves the need in the elastic model of work [22] to be nonlinear beyond the scope. Consequently, the purpose of the nonlinear model underlying [22] remains elusive. As is well known, nonlinearity of models significantly complicates not only both qualitative and quantitative analyses but also a meaningful interpretation of their results. ,
Remark 9.3. Work [22] dealing with a nonlinear acoustic model in the frequency domain notes a few peaks of the displacement in the finger soft tissue and interprets them as the resonance ones. However, the work does not include analysis sufficient for this interpretation.
Indeed, the nature of nonlinear systems is much more complex than the one of linear systems. In general, a peak in the frequency behavior of a scalar variable of a non-linear system need not be a manifestation of resonance. From the point of view of physics, resonances in both linear and nonlinear systems are defined by whether or not the external-signal frequency coincides with, or close to, one of the (generalized) natural frequencies of the system (e.g., [34] , Section 29, [35] ). However, work [22] does not show that the above peaks result from the coincidence (or proximity) of the external-signal frequency and one of the generalized natural frequencies. In other words, no natural frequency is derived or at least approximately estimated. This is in a striking contrast with what is discussed in the above Point 3 in connection with the natural frequencies listed in Table 3. Thus, the resonance reading in [22] needs a substantial extra development. ,
One can also note that paper [22] formulates other conclusions, which are in fact at the hypothesis level. For example, this paper, by means of computer simulation, studies the behavior of the finger-tissue strain in the frequency interval (that does not contain values 105 and 106 used in the above Examples 1 - 3). The conclusion of [22] is that the strain is concentrated in the skin tissue (at the soft-tissue depth less than 10−3) at all frequencies in the range (see [22] , p. 726). The reason why this interval includes not only interval , which is a part of the above range , but also interval , which is not considered in [22] at all, is unknown.
The results of the present works are summarized in the next section.
10. Conclusion
As is well known, hand-arm vibration syndrome (HAVS), or vibration-induced white finger (VWF), which is a secondary form of Raynaud’s syndrome, is an industrial injury triggered by regular use of vibrating hand-held tools. According to the related biopsy tests (see the corresponding references in Appendix), the main vibration-caused lesion is an increase in the thickness of the artery walls of the small arteries and arterioles resulted from enlarged vascular smooth muscle cells (VSMCs) in the wall layer known as tunica media. The threefold purpose of the work formulated in Points (1)-(3) in Section 1.2 is achieved. More specifically, the outcomes of the work include the following key components.
・ The present work develops a mechanobiological picture for the cell enlargement. The work deals with acoustic variables in solid materials, i.e., the non-equilibrium components of mechanical variables in the materials in the case where these components are weakly non-equilibrium. The work derives an explicit expression for the infinite-time cell-volume relative enlargement. This enlargement is directly affected by the acoustic pressure in the SLT. In order to reduce the enlargement, one can reduce either the ratio of the acoustic pressure in the SLT to the cell bulk modulus or the relaxation time induced by the cell osmosis, or both the characteristics. Also, the mechanobiological picture shows a mechanoprotective role of the above relaxation time in the cell-volume maintenance.
The mentioned results focus attention on the acoustic pressure and, thus, modeling of propagation of acoustic waves caused by the acceleration of a vibrating hand-held tool. This topic is addressed by the results listed below.
・ The present work analyzes the propagation along the thickness of an infinite planar layer of an SLT. The work considers the modeling in the time domain (rather than the frequency domain) only. As a general viscoelastic acoustic model, the work suggests linear non-stationary partial integro-differential equation (PIDE) (2.1) for the weakly non-equilibrium component of the average normal stress (ANS) or, briefly, the acoustic ANS that was derived in [17] . This equation explicitly includes the normalized stress-relaxation function (NSRF).
The unique advantage of Equation (2.1) is that it presents a compact model for the acoustic ANS in an SLT, which explicitly includes the NSRF, thereby enabling a consistent description of the lossy-propagation effects inherent in SLTs. A more simple equation, the third-order linear non-stationary partial differential equation (PDE) (2.7) of the Zener type, has the same advantage, however, only in the case where the NSRF is of the exponential type.
・ The one-spatial-coordinate version (3.1) of PDE (2.7) in the SLT layer with boundary conditions (3.2) and (3.3) is considered. The relevance of these settings is motivated by a conclusion of other authors on the results of the frequency-domain simulation in three spatial coordinates. The boundary-value problem (3.1)-(3.3) at arbitrary value of SRT and arbitrary but sufficiently regular shape of the external acceleration is analytically solved by means of the Fourier method. The obtained solution is the steady-state acoustic ANS. It allows calculation of the corresponding steady-state acoustic pressure with (8.3).
・ The derived analytical representations are computationally implemented in simulation software. Propagation of the pressure waves in the SLT layer at zero and different nonzero values of the SRT and the single-pulse external acceleration is illustrated by the corresponding simulation results. They complement the zero-SRT and zero-SRT-asymptote results with the results for various values of the SRT.
・ The obtained pressure values are, at all of the space-time points under consideration, meeting the condition for the adequateness of the linearity of the applied model.
・ It is shown that, in the case where , the obtained quantitative results well agree with the ones obtained by numerical simulation with the help of the LS-DYNA software package.
・ The influence of values of SRT is discussed in terms of the obtained quantitative results and graphic illustrations. It is shown that dependence of the damping of acoustic variables in an SLT on in the present, third-order case significantly generalizes the one in the second-order linear systems. This picture is consistent and physically sound. Also, the related resonance effect in the waves of the acoustic pressure propagating in an SLT is discussed. It is explained in terms of the angular frequency of the external acceleration and specific values of the angular natural frequencies. The latter are computed in the present approach but are difficult to be determined within the frame of purely numerical simulation software.
・ There are the solution components, which are new with respect to the zero-SRT and zero-SRT-asymptote cases and are due to the effects of the NSRF-originated memory-function. The role of the new components is discussed in connection with the shifts of the pressure plots along the pressure axis. The memory-function effects provided by the present, third-order PDE model are of importance for proper evaluation of acoustic variables in SLTs.
・ It is found that, in general, a combination of the resonance effects and the effects of the above damping-only components complicate the space-time behaviors of the acoustic ANS and acoustic pressure.
The results mentioned in the above bullets, with the exception of the first one, are obtained in the exponential approximation for the NSRF. More general cases where the NSRF shape need not be exponential can also be targeted. However, it is explained that the results based on the exponential approximation are correct qualitatively and can be acceptable quantitatively.
The outcomes of the main part of the work, in conjunction with the mechanobiological picture developed in Appendix, present a viscoelastic acoustic framework for SLTs. This framework opens a way to quantitatively specific evaluation of technological strategies for reduction of the vibration-caused injuries or, loosely speaking, for achieving “zero’’ injury. This evaluation is suggested as the topic for the nearest future research.
Acknowledgements
The authors are grateful to Vinnova, Sweden’s Innovation Agency, for a partial support of the present work from the project 2015-00352 “Zero Vibration Injuries, Phase 2’’. The authors thank Hans Lindell, Swerea IVF AB, Mölndal, Sweden, for valuable information on hand-held impact machines design and performance, numerous discussions, and reading the manuscript. The authors also thank Dr. Henrik Enquist, Medical Services, Laboratory Medicine, Region Skåne, Lund, Sweden, for drawing their attention to reference [7] .
Cite this paper
Mamontov, E. and Berbyuk, V. (2017) Propagation of Acoustic Waves Caused by the Accelerations of Vibrating Hand-Held Tools in Viscoelastic Soft Tissues of Human Hands and a Mechanobiological Picture for the Related Injuries. Journal of Applied Mathematics and Physics, 5, 1997-2043. https://doi.org/10.4236/jamp.2017.510169
References
- 1. McHenry, C.L. et al. (2014) Potential Regenerative Rehabilitation Technology: Implications of Mechanical Stimuli to Tissue Health. BMC Research Notes, 7, 334/1-334/11.
- 2. Krajnak, K., et al. (2012) Frequency-Dependent Effects of Vibration on Physiological Systems: Experiments with Animals and Other Human Surrogates. Industrial Health, 50, 343-353.
- 3. Valdez, M. and Balachandran, B. (2013) Longitudinal Nonlinear Wave Propagation through Soft Tissue. Journal of the Mechanical Behavior of Biomedical Materials, 20, 192-208. https://doi.org/10.1016/j.jmbbm.2013.01.002
- 4. Koshlyakov, N.S., Smirnov, M.M. and Gliner, E.B. (1964) Differential Equations of Mathematical Physics. North-Holland Publishing, Amsterdam.
- 5. Pollard, H.F. (1977) Sound Waves in Solids. Pion, London.
- 6. Rose, J.L. (1999) Ultrasonic Waves in Solid Media. Cambridge University Press, Cambridge.
- 7. Saraf, H., Ramesh, K.T., Lennon, A.M., Merkle, A.C. and Roberts, J.C. (2007) Mechanical Properties of Soft Human Tissues under Dynamic Loading. Journal of Biomechanics, 40, 1960-1967. https://doi.org/10.1016/j.jbiomech.2006.09.021
- 8. Mott, P.H. and Roland, C.M. (2009) Limits to Poisson’s Ratio in Isotropic Materials. Physical Review B, 80, 132104/1-132104/4. https://doi.org/10.1103/PhysRevB.80.132104
- 9. Parker, K.J., Doyley, M.M. and Rubens, D.J. (2011) Imaging the Elastic Properties of Tissue: The 20 Year Perspective. Physics in Medicine and Biology, 56, R1-R29. https://doi.org/10.1088/0031-9155/56/1/R01
- 10. Kim D.-G., et al. (2010) Relationships of Viscosity with Contact Hardness and Modulus of Bone Matrix Measured by Nanoindentation. Journal of Biomechanical Engineering, 132, 024502/1-024502/5.
- 11. Ricker, N.H. (1977) Transient Waves in Visco-Elastic Media. Elsevier, Amsterdam.
- 12. Landau, L.D. and Lifshitz, E.M. (1986) Theory of Elasticity. Pergamon Press, Oxford.
- 13. Stokes, G.G. (1845) On the Theories of the Internal Friction of Fluids in Motion and of the Equilibrium and Motion of Elastic Solids. Transactions of the Cambridge Philosophical Society, 8, 287-319.
- 14. Longman, I.M. (1980) Wave Propagation in a Viscoelastic Solid. Journal of Computational Physics, 37, 171-182. https://doi.org/10.1016/0021-9991(80)90019-4
- 15. Gross, B. (1953) Mathematical Structure of the Theories of Viscoelasticity. Hermann & Cie, Paris.
- 16. Gibson, R.F. (2012) Principles of Composite Material Mechanics. CRC Press, Boca Raton.
- 17. Mamontov, E. and Berbyuk, V. (2015) Identification of Material Parameters of Thin Curvilinear Viscoelastic Solid Layers in Ships and Ocean Structures by Sensing the Bulk Acoustic Signals, In: Salvatore, F., Broglia, R. and Muscari, R., Eds., VI International Conference on Computational Methods in Marine Engineering, MARINE, Rome, 15-17 June 2015, 502-513.
- 18. https://en.wikipedia.org/wiki/Viscoelasticity#Prony_series
- 19. Junisbekov, T.M., Kestelman, V.N. and Malinin, N.I. (2003) Stress Relaxation in Viscoelastic Materials. Science Publishers, Enfield, NH, USA.
- 20. Lindell, H., Lönnroth, I. and Ottertun, H. (1998) Transient Vibration from Impact Wrenches: Vibration, Negative Effect on Blood Cells and Standards for Measurement. 8th International Conference on Hand-Arm Vibration Umeå, Sweden, June 9-12, 113-117.
- 21. Wu, J.Z., Krajnak, K., Welcome, D.E. and Dong, R.G. (2008) Three-Dimensional Finite Element Simulations of the Dynamic Response of a Finger-Tip to Vibration. Journal of Biomechanical Engineering, 130, 054501/1-054501/8.
- 22. Wu, J.Z., Krajnak, K., Welcome, D.E. and Dong, R.G. (2007) Finite Element Analysis of the Penetrations of Shear and Normal Vibrations into the Soft Tissues in a Fingertip. Medical Engineering and Physics, 29, 718-727.https://doi.org/10.1016/j.medengphy.2006.07.005
- 23. https://en.wikipedia.org/wiki/LS-DYNA
- 24. Mamontov, E. (2008) Dynamic-Equilibrium Solutions of Ordinary Differential Equations and Their Role in Applied Problems. Applied Mathematics Letters, 21, 320-325. https://doi.org/10.1016/j.aml.2007.02.031
- 25. https://en.wikipedia.org/wiki/Volume_viscosity
- 26. https://en.wikipedia.org/wiki/Bulk_modulus
- 27. Mamontov, E. and Berbyuk, V. (2014) A Scalar Acoustic Equation for Gases, Liquids, and Solids, incLuding Viscoelastic Media. Journal of Applied Mathematics and Physics, 2, 960-970. https://doi.org/10.4236/jamp.2014.210109
- 28. Palacio-Torralba, J., et al. (2015) Quantitative Diagnostics of Soft Tissue through Viscoelastic Characterization Using Time-Based Instrumented Palpation. Journal of the Mechanical Behavior of Biomedical Materials, 41, 149-160. https://doi.org/10.1016/j.jmbbm.2014.09.027
- 29. Vladimirov, V.S. (1984) Equations of Mathematical Physics. Mir, Moscow.
- 30. Dwight, H.B. (1961) Tables of Integrals and Other Mathematical Data. McMillan, New York.
- 31. Korn, G.A. and Korn, T.M. (1961) Mathematical Handbook for Scientists and Engineers. Definitions, Theorems and Formulas for Reference and Review. McGraw-Hill, New York.
- 32. Chen, S., et al. (2009) Shearwave Dispersion Ultrasound Vibrometry (SDUV) for Measuring Tissue Elasticity and Viscosity. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 56, 55-62. https://doi.org/10.1109/TUFFC.2009.1005
- 33. Lindell, H. and Machens, M. (2017) Private Communication. (Unpublished)
- 34. Landau, L.D. and Lifshitz, E.M. (1976) Mechanics. Butterworth-Heinemann, Oxford.
- 35. Kartashova, E. (2010) Nonlinear Resonance Analysis. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511779046
- 36. Takeuchi, T. et al. (1986) Pathological Changes Observed in the Finger Biopsy of Patients with Vibration-Induced White Finger. Scandinavian Journal of Work, Environment & Health, 12, 280-283. https://doi.org/10.5271/sjweh.2140
- 37. Rizzoni, D., et al. (2000) Cellular Hypertrophy in Subcutaneous Small Arteries of Patients with Renovascular Hypertension. Hypertension, 35, 931-935. https://doi.org/10.1161/01.HYP.35.4.931
- 38. Mamontov, E., Koptioug, A.V. and Psiuk-Maksymowicz, K. (2006) The Minimal, Phase-Transition Model for the Cell-Number Maintenance by the Hyperplasia-Extended Homeorhesis, Acta Biotheoretica, 54, 61-101. https://doi.org/10.1007/s10441-006-8263-3
- 39. Terada, K., et al. (2007) Laser Doppler Imaging of Skin Blood Flow for Assessing Peripheral Vascular Impairment in Hand-Arm Vibration Syndrome. Industrial Health, 45, 309-317. https://doi.org/10.2486/indhealth.45.309
- 40. Vajda, K., et al. (1982) Ultrastructural Investigations of Finger Pulp Biopsies: A Study of 31 Patients with Raynaud’s Syndrome. Ultrastructural Pathology, 3, 175-186. https://doi.org/10.3109/01913128209016642
- 41. Sedov, L.I. (1971) A Course in Continuum Mechanics. Vol. 1, Wolters-Noordhoff, Groningen.
- 42. Fournier, R.L. (2007) Basic Transport Phenomena in Biomedical Engineering. Taylor & Francis, New York.
- 43. https://en.wikipedia.org/wiki/Starling_equation#Reflection_coefficient
- 44. Mathura, R.A., Russell-Puleri, S., Cancel, L.M. and Tarbell, J.M. (2016) Hydraulic Conductivity of Smooth Muscle Cell-Initiated Arterial Cocultures. Annals of Biomedical Engineering, 44, 1721-1733. https://doi.org/10.1007/s10439-015-1421-5
- 45. https://en.wikipedia.org/wiki/Centimetre_of_water
- 46. https://en.wikipedia.org/wiki/Artery#/media/File:Blausen_0055_ArteryWallStructure.png
Appendix. Main Vibration Injuries in an SLT, the Corresponding Mechanobiological Picture, and the Role of a Time-Varying Acoustic Pressure
The VWF injuries or, in a more professional language, lesions in human fingers are well known. They are described in work [36] in terms of the data obtained by means of biopsy tests. This work notes ( [36] , p. 280) that the main lesion is an increase in the thickness of the artery walls of the small arteries and arterioles resulted from muscular hypertrophy. As is shown in Figure 13, the muscular content of the artery wall is the wall layer known as tunica media and formed by vascular smooth muscle cells (VSMCs). More specifically ( [36] , pp. 280-281), the thickening of the tunica media is identified by the presence of hypertrophied nuclei and an increased cytoplasmic bulk of the cells, i.e., enlargement of VSMCs.
Paper [37] , which is also based on the biopsy-test data, studies the enlargement of VSMCs in the small arteries as well. It deals with the arteries in the inner layer of the skin, i.e., the layer of subcutaneous fat. As follows from the measurement data in ( [37] , Table 2), the enlarged VSMC presents a significant lesion when the volume of an enlarged cell 1.5 times greater than the volume of a normal cell.
The mentioned results of biopsy tests mean that populations of the enlarged VSMCs present long-lasting lesions. To the best of our knowledge, the literature does not provide facts on that these lesions, in the course of time, return to normal states (i.e., the enlarged-cell volumes return to their normal values). In
Figure 13. The structure of an artery wall [46] .
this respect, the mentioned populations are similar to other long-lasting lesions such as scars or other infiltrates in chronic inflammation, and lesions caused by homeorhetic dysfunctions. The infiltrates and the notion of a homeorhetic dysfunction are discussed, for example, in [38] and a number of the references therein.
The skin of the VWF patients also contains lesions. The experimental studies of [39] show a significantly reduced skin blood perfusion. In the light of works [36] and [37] , the reduced perfusion can be explained with the aforementioned artery-wall thickening caused by an increase in the volumes of VSMCs. Other lesions in the VWF skin are described in [40] .
As is well known, fingers, in contrast to palms, do not contain muscles (other than arrector pili). The soft tissues of a finger comprise the epidermis, dermis, and subcutaneous tissue. The soft tissues of a palm include the muscle tissue as well. The lesions in fingers of the VWF patients are also present in palms, first of all, in the palm regions neighboring the fingers (e.g., [39] ).
Thus, the vibration injuries to be prevented are VSMCs with noticeably increased volumes or, briefly, enlarged VSMCs. Enlargement of a cell is literally a geometric effect. It has a number of mechanical implications. However, the fact that, as is noted above, enlargement of the cells was emphasized by histopathologists (e.g., [36] [37] ) endows this phenomenon with a critical biomedical content. It indicates the mechnobiological nature of HAVS/VWF.
In order to provide the aforementioned prevention, it is necessary to develop a quantitative acoustic model that would include the influence of the acceleration of the vibrating hand-held tool upon the volumes of VSMCs. The questions to be answered on the way to this model are the following.
1) What characteristics of an SLT directly influence upon enlargements of the cells in the SLT?
2) How specifically is the mentioned influence implemented?
3) How can one reduce the resulting enlargements of the cells?
The answers to all of these questions are suggested in the present section. It deals with a cell, which is located at fixed spatial point x in an SLT, and acoustic pressure in the SLT (see (8.3)). In what follows, we, for brevity, do not explicitly indicate the dependences on x but acknowledge their presence by denoting the time differential as the partial differential .
Let and be the volume and bulk modulus of the cell, respectively. We also consider the pressures and in the cell and the interstitial fluid (IF) surrounding the cell in the SLT. The equilibrium versions of these pressures are denoted with and . Then the corresponding acoustic pressures are expressed as
(A.1)
where the sign “overline’’ denotes the equilibrium version of the corresponding quantity. This convention is used down to the end of the present section.
As is assumed above (see (2.4)), the SLT is a linear solid. Similarly, we regard the cell as a solid body and assume that it is also a linear solid, i.e.,
(A.2)
Note that the property (A.2) also means (e.g., [5] , (1.13), (1.38)) that
(A.3)
where
(A.4)
is the relative change of the cell volume.
Taking into account the linearity and the well-known continuum-mechanics result ( [41] , (2.8.22)), one can check that
(A.5)
where is the cell-volume rate due to the phenomena that are not represented with the terms on the left-hand side. This rate is expressed with the well-known Starling equation (e.g., [42] , (3.4); see also (3.2))
(A.6)
where is the hydraulic conductance of the semi-permeable membrane of the cell, is the area of the cell-membrane surface, is the reflection coefficient of the cell membrane (e.g., [42] , Section 3.4.3, [43] ), which is dimensionless and is such that , is the Boltzmann constant, is the absolute temperature of the tissue, is the total concentration of the solutes in the intracellular fluid (ICF) of the cell, and is the total concentration of the solutes in the IF. A discussion on the solutes in the IF and ICF can be found in [42] (see also [42] , Table 3.2). The term in the parentheses in (A.6) corresponds to the difference of the osmotic pressures in the cell and IF.
Note that the sign “minus’’ in front of the term (A.6) in equation (A.5) is due to the well-known facts (e.g., [42] , p. 100).
If the term in the brackets in (A.6) is positive, there is a flow of fluid from the ICF into the IF. This flow decreases the cell volume.
If the term in the brackets in (A.6) is negative, there is a flow of fluid from the IF into the ICF. This flow increases the cell volume.
At equilibrium, the term in the brackets in (A.6) is zero, i.e., . Rewriting (A.6) in terms of (A.1) and allowing for the latter equality, one obtains
(A.7)
We assume that concentration remains unchanged, i.e.,
(A.8)
and the number of the solute molecules in the ICF, , remains unchanged as well that results in
(A.9)
Combination of (A.7)-(A.9) enables one to present Equation (A.5) as follows
(A.10)
This equation includes three acoustic pressures: , which is modeled in the main text of the present work, as well as and , which are not modeled in the work. In order to simplify Equation (A.10) to the form where the available pressure is the only one, which is used, we assume that and . These relations transform (A.10) into
(A.11)
The cell enlargement develops approximately at the same proportion along each of the three spatial axes (e.g., see the experimental data on the VSMC enlargement in ( [37] , Table 2)). This means that or, in terms of (A.4),
(A.12)
Substituting (A.4) into (A.11) and (A.12), one obtains
or, equivalently,
(A.13)
where
(A.14)
is the relaxation time induced by the cell osmosis. We consider ODE (A.13) in a semi-infinite time interval under the initial condition that the cell volume is at equilibrium at point , i.e. (see (A.4)),
(A.15)
Example A.1. According to experimental study in [37] , VSMCs have the shapes that can approximately be described as elongated cylinders (e.g., see [37] , Table 2). In the case of a normal VSMC, the cylinder cell volume is , and the cell has the length of and the radius of about . The corresponding cell-surface area is estimated as . Consequently, value (A.14) is
. (A.16)
Next, at normal human temperature of about 37˚C, . This results in that transforms (A.16) into
(A.17)
Parameter , the hydraulic conductance of the VSMC membrane, can be taken from [44] . Indeed, according to Fig. 2(b) in [44] on the basal-cell case, , i.e. (e.g., [45] ), . Substituting this value into (A.17), one obtains
(A.18)
We assume that the well-known typical value of for an intracellular fluid (e.g., [42] , the last column in Table 3 and Section 3.4.3) is applicable to the case of a VSMC. This value is or, in terms of the volumetric number density, , that specifies (A.18) to , i.e., . This value can be used as a preliminary estimation. ,
Remark A.1. Multiplying Equation (A.13) considered in interval by to and passing in the resulting equation to the limit as , one obtains that at all . This result and (A.15) lead to property
(A.19)
It indicates that the cell osmosis plays a mechanoprotective role in the cell-volume maintenance. ,
We note note a few features of the problem under consideration.
Vibrating hand-held tools (e.g., impact wrenches outlined in Section 1) are usually used in such a way that the periods when the tool is active (continuously functions) alternate with the periods when the tool is inactive (does not function). Any of the activity periods is bounded and the total number of them is finite. In each of the inactivity periods, acceleration in (6.22) is a function with bounded support, and thus , and, in view of (8.3), exponentially tend to zero (cp., (6.19)-(6.22)). In view of these features and the fact that , as function of time, is uniformly bounded (e.g., see (A.2)), property
exists and is finite, (A.20)
holds. It in particular implies that
(A.21)
Vibrations, which are produced by the handles of active hand-held tools on the fingers of the users, present series of more or less regular pulses of the acoustic pressure in the finger SLT , which are compressive, i.e.,
values of at all are predominantly positive; this feature is illustrated with any of Figures 3-10. (A.22)
As is noted in the second paragraph of the present section, an enlarged cell is a significant lesion if its volume is about 1.5 greater than the volume of a normal cell. This figure corresponds to . However, such lesions become measurable only after a sufficiently long time of use of the vibrating tools. More specifically, the cell enlargement is an additive effect of a large number of the activity periods, i.e., a significant relative enlargement is achieved as the result of a long series of enlargements for small amounts. This means that it is sufficient to consider ODE (A.13) at small values of prescribed by (A.3) in any period of the tool activity. This leads to reduction (A.13) to equation
(A.23)
which is a linear ODE.
The solution on the initial-value problem (A.23), (A.15) are studied in the following theorem.
Theorem A.1. Let be the range of function in interval , i.e.,
, (A.24)
where
(A.25)
It is assumed that
(A.26)
We also accept notation
(A.27)
Then the following assertions are valid.
(i) The solution of initial-value problem (A.23), (A.15) is
(A.28)
(ii) Inequalities
(A.29)
(A.30)
hold.
(iii) Linear ODE (A.23) is applicable.
(iv) Relation
(A.31)
is valid.
Proof. According to theory of non-autonomous linear ODEs, the solution of initial-value problem (A.23), (A.15) is
or, equivalently,
(A.32)
Calculating the integral, which is the second multiplier in (A.32), by parts, one obtains
that is
(A.33)
Substitution of (A.33) into (A.32) results in (A.28). This proves assertion (i).
Inequalities (A.29) follow from the from of the right-hand side of (A.28) and notations (A.25), (A.24). Inequalities (A.30) follow from (A.29) and also notations (A.25), (A.24). This proves assertion (ii).
In order to prove assertion (iii), it is sufficient to note that application of assumption (A.26) to inequalities (A.30) assures relation (A.3), which, as is explained in the text above equation (A.23), makes this equation valid.
Passing to the limit as t tends to infinity in (A.28) and taking into assumption (A.26), notations (A.24), (A.25), and limit relation account (A.21), one obtains (A.31). This completes both the proofs of assertion (iv) and the theorem. ,
In view of (A.27), the infinite-time value (see (A.31)) presents the infinite-time residual value of the cell volume. In view of (A.22), one should expect that the limit in (A.31) is greater than unit and, thus,
(A.34)
i.e., the above residual value corresponds to the relative enlargement of a cell.
Remark A.2. The main result of the present section is the explicit expression (A.31) (see also (A.34)) for the infinite-time value of the cell-volume relative enlargement in terms of:
・ , the relaxation time induced by the cell osmosis and described with (A.14);
・ , the bulk modulus of the cell;
・ , the acoustic pressure (see (8.3)) in the SLT, which includes the cell under consideration.
Parameter and the parameters underlying are mechanical. Concerning , one can note that definition (A.14) of this parameter also includes mechanical parameters, namely , , , and . However, the three other parameters in (A.14), namely
・ , the hydraulic conductance of the semi-permeable membrane of the cell;
・ , the reflection coefficient of the cell membrane;
・ , the equilibrium value the total concentration of the solutes in the ICF of the cell;
are biological. Thus, expression (A.31) provides an explicit picture of the combined, mechanobiological effect on the infinite-time value of the cell-volume relative enlargement. This picture indicates that is directly proportional to both the ratio (see (A.26) and (cp., Remark A.1).
The developed mechnobiological picture for the cell enlargement can be summarized in terms of the answers to questions (1)-(3) formulated in the text above (A.1) as follows.
According to (A.31), an acoustic variable in an SLT that directly affects the cell enlargement is acoustic pressure in the SLT. This is the answer to quation (1).
Expression (A.31) also provides the answer to question (2). Indeed, the role of is specified with (A.31).
The corresponding answer to question (3) is the following. In order to reduce the cell enlargement, one can reduce either the ratio of the acoustic pressure in the SLT to the cell bulk modulus or the relaxation time induced by the cell osmosis, or both the characteristics.
Also, the mechanobiological picture shows a mechanoprotective role of the above relaxation time in the cell-volume maintenance. In particular, in the idealized case as this relaxation time tends to zero, the cell volume remains unchanged (see Remark A.1). ,
Design of future vibtrating hand-held tools often focuses on improvement of the vibration characteristics, for example, on reduction of . However, these activities cannot be regarded successful until the effect of the improvement is estimated from either biopsy tests of the fingers of the persons who used the advanced tools (which is highly resource and time consuming) or, at least, from quantitative simulation in accordance with the summary formulated in Remark A.2 (which is much more affordable). ,
Abbreviations
ANS average normal stress
HAVS hand-arm vibration syndrome
KV Kelvin-Voigt
LNS linear nonstationary
NSRF normalized stress-relaxation function
ODE ordinary differential equation
PDE partial differential equation
PIDE partial integro-differential equation
SLT soft living tissue
SRT stress-relaxation time
VWF vibration-induced white finger















