ABSTRACT

In this paper, we study the non-definite Sturm-Liouville problem comprising of a regular Sturm-Liouville equation and Dirichlet boundary conditions on a closed interval. We consider the case in which the weight function changes sign twice in the given interval of definition. We give detailed numerical results on the spectrum of the problem, from which we verify various results on general non definite Sturm- Liouville problems. We also present some theoretical results which support the numerical results. Some numerical results seem to be in contrast with the results that are so far obtained in the case where the weight function changes sign once. This leads to more open questions for future studies in this particular area.

Keywords:

Eigenvalue, Eigenfunction, Non-Definite, Turning Point, Richardson Number, Richardson Index, Haupt Index, Oscillation Number, Right-Definite, Left-Definite

1. Introduction

The regular Sturm-Liouville problem involves finding the values of a parameter 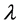(generally complex) for which the equation

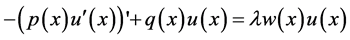(1)

has a solution u (non-identically zero) in 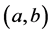satisfying the boundary conditions (2)-(3) below.

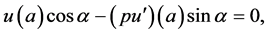(2)

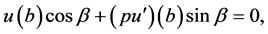(3)

The parameter is called an eigenvalue and the corresponding function u is called an eigenfunction. The set consisting of all the eigenvalues of the problem consisting of (1) and the boundary conditions (2)-(3) is called the spectrum. The coefficient functions are such that

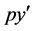
is absolutely continuous in 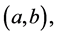and 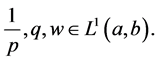In what follows (,) denotes

the inner product of the Hilbert space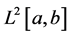. A point at which the weight function 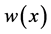changes sign is called a turning point. The number of zeros that an eigen- function has within the open interval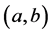, is called the oscillation number of the corresponding eigenvalue. In this paper, the setting is that 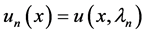has exactly n zeros in 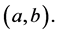That is, 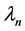has oscillation number n.

Definition 1. Suppose that the eigenfunctions of a Sturm-Liouville problem are ordered according to increasing eigenvalues of the problem, the eigenfunctions are said to have the interlacing property, if between two zeros of the eigenfunction 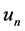lies exactly one zero of the eigenfunction.

Definition 2. A homogeneous linear differential equation

of order n is called disconjugate on an interval I if no non-trivial solution has n zeros on I, multiple zeros being counted according to their multiplicity.

We pronounce that the strong interest of this field during all these years is that this theory is important in Applied Mathematics, where SL problems occur very commonly. The differential equations considered here arise directly as mathematical models of motion according to Newton’s law, but more often as a result of using the method of separation of variables to solve the classical partial differential equations of physics, such as Laplace’s equation, the heat equation, and the wave equation, (see e.g [1] ). Let (1) be written as

(4)

Then, the problem consisting of (4) and the boundary conditions (2)-(3) is called right-definite if the form

(5)

is definite. In this case there is a sequence of real eigenvalues such that

and as with a finite number of negative eigenvalues (see e.g, [2] [3] ). If the form

(6)

is definite for each, the problem is called left-definite. In this case the problem consists of two sequences of eigenvalues such that as If we let to be a real eigenvalue with smallest absolute value, then in the left- and right- definite case, the corresponding eigenfunction has no zero in When neither nor is definite, then the problem is called non-definite (indefinite). In this paper our focus is on a non-definite Sturm-Liouville problem in which the weight function has two turning points in the interval of definition.

The Non-Definite (or Indefinite) Case

Here we give a summary on the non-definite case, detailed literature can be found in the papers [3] - [9] , etc, and the references there in. In the non-definite case the spectrum is discrete, always consists of a doubly infinite sequence of real eigenvalues, and has at most a finite and even number of non-real eigenvalues (necessarily occurring in complex conjugate pairs).

Remark 1. If the problem consisting of the equation

(7)

and the boundary conditions (2)-(3) has N distinct negative eigenvalues, then the number of distinct pairs of non-real eigenvalues of the problem (1)-(3) cannot exceed N.

For more details on remark 1, we refer the interested reader to the papers [2] (Theorem 4.2.1), [3] (Theorem 2), [10] (Corollary 1.7), and the references there. In the non-definite case, as Richardson [4] puts it, the march of the zeros is not monotone with (in contrast with the left- and right-definite cases). In fact there may be a range of values of such that as increases, the number of zeros first decreases, then increases, then decreases and finally increases, the minimum number being a positive integer. As a result the eigenfunction corresponding to the eigenvalue can have any number of zeros in in contrast with the definite case, that is to say, a non-definite Sturm-Liouville problem will tend not to have a real ground state (positive eigenfunction). In relation to this behaviour of the real spectrum of the non-definite Sturm-Liouville problem, Mingarelli [6] defines two types of indexes which are due to Richardson [4] and Haupt [11] .

Theorem 1. ( [6] Haupt-Richardson Oscillation Theorem)

In the non-definite case of (1)-(3), there exists an integer such that for each there are at least two real solutions of (1)-(3) having exactly n zeros in while for there are no real solutions having n zeros in Furthermore there exists a possibly different integer such that for each there are precisely two solutions having exactly n zeros in

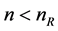
Mingarelli [6] calls and the Richardson Index and Haupt Index, respec- tively. If we consider positive eigenvalues separately, we can define for all an integer, such that for each, there is at least one real solution of the problem (1)-(3) having n zeros in, while for there are no real solutions having n zeros. Also, there is an integer such that for each, there is exactly one real solution having precisely n zeros in, while for there are no solutions having n zeros in. Analogue for defines and.

Furthermore, for real there exist two numbers and called the Richardson numbers defined as

We note that. We can interpret as the smallest number such that the real eigenvalues greater than behave as in a “typical” Sturm-Liouville problem, that is, an eigenvalue is uniquely associated with its oscillation number, and is interpreted similarly [7] . We note that in the right-definite case, while in the left-definite case, As Jabon and Atkinson [7] rightly put it, in the non-definite case, the determination of these numbers is a very significant problem.

Theorem 2. ( [3] Theorem 3)

Let and be a non-real eigenvalue and associated non-real eigenfunction of problems (1)-(3). If has precisely n turning points in then may vanish at most -times in

Corollary 1. (Corollary 1 [3] )

Let and be a non-real eigenvalue and associated non-real eigenfunction of problems (1)-(3). If has exactly one turning point in then in

In relation to corollary 1, we state the following theorem which is due to Richardson [4] , see also the papers [3] [6] .

Theorem 3. (Richardson’s Oscillation theorem)

Let w be continuous and not vanish identically in any right neighborhood of If changes its sign precisely once in then the roots of the real and imaginary parts and of any non-real eigenfunction corresponding to a non-real eigenvalue, separate one another (or interlace).

Below are some of the many open questions that Mingarelli in [3] [6] raises on non-definite or indefinite Sturm-Liouville problems.

1) Estimate the oscillation numbers and in terms of the given data etc.

2)Estimate the eigenvalues and in terms of the given data.

3) Give sufficient conditions for the existence of at least one non-real eigenvalue.

4) Estimate the real and imaginary parts of non-real eigenvalues.

5) Is Richardson’s oscillation theorem for non-real eigenfunctions true in general?

6) To what extent is Richardson’s theorem for non-real eigenfunctions true?

The following is a brief list of part of the work done towards answering some of the questions raised above.

1) In the one-turning point case for w, Atkinson and Jabon, [7] obtain upper bound for and lower bound for.

2) In the two-turning point case for w, Kikonko and Mingarelli [8] obtain upper bound on.

3) On sufficient conditions for the existence of at least one non-real eigenvalue, Allegretto and Mingarelli [5] cover the case and; Also Behrndt, Katatbeh, and Trunk [12] in a singular case with the same weight; [2] [3] , [10] , etc.

4) On estimating the real and imaginary parts of non-real eigenvalues, Mingarelli [13] uses Green’s function arguments; a good number of recent papers, e.g Qi and Chen [9] ; Qi, Xie and Chen [14] ; Behrndt, Chen, Philip, and Qi [15] ; Xie and Qi [16] ; Behrndt, Philip and Trunk [17] ; etc, use L²-estimates coupled with quadratic form arguments and theory of Krein spaces.

5) On Richardson’s Oscillation theorem, numerical results in the conference paper [18] indicated that the interlacing property fails in the two-turning point case and no non-real eigenfunction vanished inside the given interval of definition at least for the values of that were considered then.

The main motivation for this paper is the results obtained from the important paper [7] in which the Authors considered a special indefinite (non-definite) problem in which the weight function has one turning point in the interval. Pre- sented in that paper were results of numerical calculations of the spectrum of the problem

In the next section we extend their study to the case in which the weight function changes sign twice (has two turning points) on the interval. In particular, we wish to verify whether or not, theorem 3 holds in the two-turning point case. Further- more, theorem 2 implies that in the two-turning point case, if a non-real eigenfunction vanishes in it can only do so once, which is worthy verifying too. We carried out numerical calculations on the spectrum of our problem using the Maple^Ó package RootFinding[Analytic]. This package attempts to find all complex zeros of an analytic function, within the rectangular region in the complex plane. From the numerical results in this paper we pronounce the following results.

1) The interlacing property which holds in the one-turning point case does not hold in the two turning-point case in general.

2) The real and imaginary parts of any non-real eigenfunction corresponding to a non-real eigenvalue either have the same number of zeros in the interval or the numbers of zeros differ by two.

3) For some values of considered in this paper, some non-real eigenfunctions seem to vanish inside the interval

The result 2) is partly surprising and leads us into raising yet more open questions in the field.

2. Main Results

Here we consider the Dirichlet problem

(8)

(9)

Here, for all, the weight is a piecewise constant step-function described by the relations

where we assume, without loss of generality, that. We note that (8) is in Sturm-Liouville form (1) with and replaced by. In this case, the forms (5) and (6) respectively simplify to

(10)

and

(11)

It was shown in [18] and [8] that the two forms are sign indefinite for values of x for which, hence we have the non-definite case with two turning points since the weight function changes its sign twice inside the interval of definition. The solution of the problem (8)-(9) in this case is given by

where

and. The solution is found by piecing together the various solutions on the intervals [−1,0], (0,1] and (1,2] so as to obtain a con- tinuously differentiable function on [−1,2]. By solving the dispersion relation

(12)

and fixing the values of A, B and C to be, , and, we calculated eigenvalues lying within the rectangle

using the Maple^Ó package Root Finding [Analytic]. Since changes sign in the interval we need to pick values of carefully so that the spectrum can have non-real eigenvalues. Note that if we set in Equation (8) and solve the equation subject to boundary conditions in (9) with the assumption that we see that the eigenvalues of this new problem (which we shall call the corresponding right-definite problem (RDP)) are given by

From this we see that if for all n the new problem can not have any negative eigenvalues and when for all n we expect to have at least one negative eigenvalue of the problem and by remark 1 the problem (8)-(9) may have at least one pair of non-real eigenvalues for such. Hence we are assured of non-real eigenvalues for problem (8)-(9) for

Therefore we calculated eigenvalues in the cases and in the rectangle E using the Maple package Root Finding [Analytic]. We note that this is an extension of the work covered in [18] , where we only considered values of less than or equal to in a smaller rectangle. In Figure 2, we show graphs of eigenfunctions corresponding to positive eigenvalues of the problem (8)-(9) when and from this figure, we estimate the upper bound of the Richardson number, and the integers and. We also show a typical behaviour of the real and imaginary parts of the non-real eigenfunctions corresponding to non-real eigenvalues of the problem (8)-(9) in Figure 1.

The summary of the results are shown in Table 1 and Table 2. Table 1 brings out the difference between the number of zeros of real and imaginary parts of the non-real eigenfunctions corresponding to non-real eigenvalues of the problem (8)-(9). The results in this table are complemented by the results shown in Figure 1 which shows that the number of zeros of the real and imaginary parts of the non-real eigenfunctions are either equal or differ by two. Figure 1 also shows that the interlacing property of

the real and imaginary parts of non-real eigenfunctions fails in the two-turning point case. Table 2 shows that the smallest number of zeros of the eigenfunctions corre- sponding to positive eigenvalues for each value of the parameter considered, is two and so problem (8)-(9) has no real ground state (positive eigenfunction). The table also compares the number of distinct negative eigenvalues of the corresponding right- definite problem with the number of pairs of distinct non-real eigenvalues of the

problem (8)-(9).

A closer look at Figure 2 shows that the smallest positive eigenvalue for this case is with corresponding eigenfunction oscillating twelve times in the interval. Furthermore, and corresponding eigenfunction oscillating eleven times in The oscillation numbers decrease by one as the value of increases until the fifth eigenvalue. From the sixth eigenvalue onwards the oscillation numbers increase by one as the value of increases and from the eleventh eigenvalue (i.e.,) onwards, each eigenfunction has a unique oscillation number. Since has corresponding eigenfunction oscillating thirteen times in we can say that for each there is precisely one eigenfunction with n zeros in and so. Hence the correct notation is that and thus the Richardson number satisfies. Another observation is that there is no positive eigenvalue with corresponding eigenfunction having less than eight zeros in while for each, there is at least one eigenfunction having n zeros in, hence we have that

Figure 3 gives the spectrum for larger values of 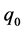in the rectangle E. We see that in each of the cases, the spectrum consists of a finite number of non-real eigenvalues and two infinite sequences of positive and negative eigenvalues.

3. Discussion and Conclusions

3.1. Discussion

From Figure 3, we see that the spectrum is made up of an infinite number of real eigenvalues and a finite number of non-real eigenvalues for each value of con- sidered. That the number of non-real eigenvalues of problem (8)-(9) is finite, is not a surprise because this is expected, by remark 1. It can be seen from the graphs of the eigenfunctions that generally oscillation numbers decrease as the parameter value increases, but then oscillations will stabilize and the usual oscillation theorem event- ually holds. This leads to the estimation of, , and. We also observe

disconjugacy in the first and last intervals and many oscillations in the middle interval since for all because in the interval. However, for some values of a few oscillations are expected in the first and last intervals. This is so because in some cases, can be so large that For example in Figure 2, eigenfunctions corresponding to the first three positive eigenvalues have at least one zero in the first and third intervals.

Generally speaking, the number of non-real eigenvalues seems to increase with increasing. The number of pairs of distinct non-real eigenvalues of the problem does not exceed the number of negative eigenvalues of the corresponding right-definite problem. For all values of considered (cases where there are non-real eigenvalues), the smallest oscillation number is 2 and so the problem does not have a positive eigenfunction in (−1,2). Furthermore, the real and imaginary parts of the non-real eigenfunctions do not interlace which is different from the results in the one turning point case considered by Richardson [4] . For larger values of, some non-real eigen- functions vanish once in since the the real and imaginary parts of such functions are both zero at (see for example, Figure 1(b), Figure 1(d), and Figure 1(f)). This was not one of the observation in the paper [18] in which we only considered generally smaller values of.

3.2. Conclusions

In this paper, we undertook a numerical study of the non-real eigenfunctions and eigenvalues of a non-definite Sturm-Liouville problem with two turning points, paral- leling the study in [7] in the case of one turning point. Our ultimate goal was to examine the behavior of the eigenfunctions, both real and non-real, of this non-definite Sturm-Liouville problem.

One of the interesting observations was that the zeros of the real and imaginary parts of a non-real eigenfunction interlace in some subintervals of and not on the whole interval, contrary to the results on the one turning point case covered in theorem 3. Whether this is an accident or a result of a more general yet unproven theorem, is unknown, but we conjecture that it is so and pose this as an open question for future research.

It is further observed that the complex eigenfunctions (corresponding to non-real eigenvalues) do not vanish in, at least for smaller values of considered in this paper, while for some larger values of, there are cases in which the non-real eigenfunctions vanish once in. We note that this result seems to verify theorem 2 which indicates that if an eigenfunction of problem (8)-(9) has to vanish, it may do so at most once in the interval, since in this case. However, there is need to establish sufficient conditions for a non-real eigenfunction to vanish in an interval, say. Thus, we have our second open question.

Furthermore, the number of zeros of the real part of each of the non-real eigen- functions considered is greater (by two) than the number of zeros of the imaginary part in some cases, while in other cases, the number of zeros of the real part is equal to that of the imaginary part of a non-real eigenfunction corresponding to a non-real eigen- value. Also this may be a consequence of a more general theorem which we don’t know, so then, we have a third interesting open question for future research.

Summing up, we mean that the research initiated in [18] and presented in detail in this paper has implied a number of new interesting open questions of both theoretical and practical importance.

Acknowledgements

The author wishes to thank Prof. Angelo B. Mingarelli (Carleton University, Ottawa, Canada), and Prof. Lars-Erik Persson (Luleå University of Technology) for reading through the manuscript and giving valuable suggestions and comments.

We also wish to thank the International Science Programme in mathematical sci- ences, Uppsala University, Sweden, and Luleå University of Technology, Sweden, for financial support which made this research possible.

Furthermore, we thank the careful referee for good suggestions and questions that improved the final version of this paper.

Cite this paper

Kikonko, M. (2016) On a Non-Definite Sturm-Liouville Problem in the Two-Turning Point Case―Analysis and Numerical Results. Journal of Applied Mathematics and Physics, 4, 1787- 1810. http://dx.doi.org/10.4236/jamp.2016.49184

References