Received 1 February 2016; accepted 27 March 2016; published 30 March 2016

ABSTRACT

The Riemann hypothesis is part of Hilbert’s eighth problem in David Hilbert’s list of 23 unsolved problems. It is also one of the Clay Mathematics Institute’s Millennium Prize Problems. Some mathematicians consider it the most important unresolved problem in pure mathematics. Many mathematicians made a lot of efforts; they don’t have to prove the Riemann hypothesis. In this paper, I use the analytic methods to deny the Riemann Hypothesis; if there’s something wrong, please criticize and correct me.

Keywords:

Riemann Hypothesis, Disavowal

1. Introduction

Riemann Hypothesis was posed by Riemann in early 50’s of the 19th century in his thesis titled “The Number of Primes Less than a Given Number”. It is one of the unsolved “super” problems of mathematics. The Riemann Hypothesis is closely related to the well-known Prime Number Theorem. The Riemann Hypothesis states

that all the nontrivial zeros of the zeta-function lie on the “critical line”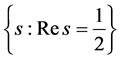. In this paper, we use the

analytical methods, and refute the Riemann Hypothesis. For convenience, we will abbreviate the Riemann Hypothesis as RH.

2. Some Theorems in the Classic Theory

In this paper, 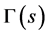is the Euler gamma function, 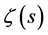is the Riemann zeta function.

Lemma 2.1. If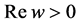, then

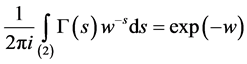
where Re w is the real part of complex number w.

Let 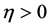be given, when and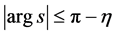, then

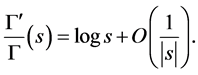
If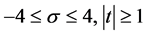, then

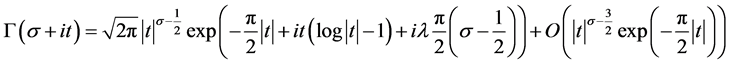
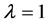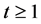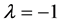where if, if.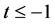

See [1] page 523, page 525.

Lemma 2.2. If, then

where is the Mangoldt function.

Let s is any complex number, we have

where be the nontrivial zeros of, be the positive constant.

We write If then

where Im s is the imaginary part of complex number s.

See [2] page 4, page 31, page 218.

Lemma 2.3. Let is the number of zeros of in the rectangle then

where

See [3] page 98.

Lemma 2.4. Assume that RH, If, then

where.

See [3] page 113.

3. Some Preparation Work

Lemma 3.1. Assume that RH, and, then

where is the ordinate of nontrivial first zero of,

Proof. By Lemma 2.2 and RH, we have

because

and

therefore

And because

therefore

Similarly, we have

This completes the proof of Lemma 3.1.

Throughout the paper, we write

It is easy to see that

Lemma 3.2. We calculate the three complex numbers.

Because

therefore when t is the real number, we have

the three complex numbers required below.

Lemma 3.3.

Proof. By Lemma 2.1 and Lemma 3.2, we have

This completes the proof of Lemma 3.3.

Lemma 3.4.

Proof. By Lemma 2.1 and Lemma 3.2, we have

we write

This completes the proof of Lemma 3.4.

Lemma 3.5.

Proof. When, by Lemma 2.1, we have

By Lemma 2.1 and Lemma 3.2, we have

This completes the proof of Lemma 3.5.

Lemma 3.6. Assume that RH, then

where

Proof. By Lemma 3.2, it is easy to see that

We write

It is easy to see that

Assume that RH and, by the contour integration method, we have

By Lemma 2.1 and Lemma 3.2,

By Lemma 2.1, Lemma 3.1 and Lemma 3.2, we have

When, we have

Similarly,

Assume that RH and, by the contour integration method, we have

same as above

When, we have

Similarly,

Synthesize the above conclusion, we have

therefore

Similarly,

therefore

Similarly,

Therefore

We use the same process, we can get

This completes the proof of Lemma 3.6.

Lemma 3.7. Assume that RH, we have

where be the ordinates of the nontrivial zeros of.

Proof.

by Lemma 2.3, the above formula

By Lemma 3.4, the above formula

by Lemma 3.5 and Lemma 3.6, above formulas.

By Lemma 2.1 and Lemma 3.2, we have

This completes the proof of Lemma 3.7.

Lemma 3.8. Assume that RH, if, then

Proof. By Lemma 2.4, we have

This completes the proof of Lemma 3.8.

4. Conclusions

When, n is the positive integer; by Lemma 2.1, we have

By Lemma 2.2, we have

By Lemma 2.2 and RH, the above formula is

By Lemma 3.3 and Lemma 3.7, the above formula is

By Lemma 3.8, we get a contradiction; therefore the RH is incorrect.

Cite this paper

Jinhua Fei, (2016) About the Riemann Hypothesis. Journal of Applied Mathematics and Physics,04,561-570. doi: 10.4236/jamp.2016.43061

References