Journal of Applied Mathematics and Physics
Vol.04 No.02(2016), Article ID:63772,8 pages
10.4236/jamp.2016.42036
The Confidence Distribution Method to the Behrens-Fisher Problem
Wenyong Tao, Wanzhou Ye
School of Science, Shanghai University, Shanghai, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 January 2016; accepted 22 February 2016; published 25 February 2016
ABSTRACT
We use the methods of “The Welch-Satterthwaite test”, “The Cochran-Cox test”, “The Generalized p-value test”, “Computational Approach test” to structure different Confidence Distributions, and use the Confidence Distributions to give an new solution the confidence interval of the difference between two population means where the populations are assumed to be normal with unknown and unequal variances. Finally, we find the most effective solution through the numerical simulation.
Keywords:
Behrens-Fisher Problem, Confidence Distribution, Interval Estimation Component

1. Introduction
1.1. Behrens-Fisher Problem
Let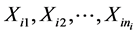 , i = 1, 2, be i.i.d. samples from two normal populations
, i = 1, 2, be i.i.d. samples from two normal populations , i = 1, 2. Four parameters
, i = 1, 2. Four parameters 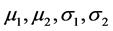 are assumed to be unknown and not necessarily equal. Behrens-Fisher problem is to give the interval estimation of the parameter
are assumed to be unknown and not necessarily equal. Behrens-Fisher problem is to give the interval estimation of the parameter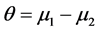 .
.
In the case of 1) 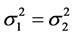 but unknown; 2)
but unknown; 2)  and
and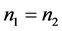 , we can use frequentist approach to solve Behrens-Fisher problem. In general case, we usually use large sample theory to find the approximate confidence interval [1] .
, we can use frequentist approach to solve Behrens-Fisher problem. In general case, we usually use large sample theory to find the approximate confidence interval [1] .
1.2. Confidence Distribution
In Bayesian inference, researchers typically rely on a posterior distribution to make inference on a parameter of interest, where the posterior is often viewed as a “distribution estimator” [2] for the parameter. A nice aspect of using a distribution estimator is that it contains a wealth of information for almost all types of inference. In frequentist inference, however, we often use a single point or an interval to estimate a parameter of interest. A simple question is: Can we also use a distribution function, or a “distribution estimator”, to estimate a parameter of interest in frequentist inference in the style of a Bayesian posterior?
Confidence Distribution is one such a “distribution estimator” that can be defined and interpreted in a frequentist framework, in which the parameter is a fixed and non-random quantity. The concept of confidence distribution has a long history, especially with its early interpretation associated with fiducial reasoning. Historically, it has been long misconstrued as a fiducial concept, and has not been fully developed under the frequentist framework. One nice aspect of treating a confidence distribution as a purely frequentist concept is that the confidence distribution is now a clean and coherent frequentist concept. Recently as the development of Confidence Distribution’s applications (such as Monte Carlo simulation based on Confidence Distribution), this approach has again aroused general concern.
To put it simply, Confidence Distribution is a distribution of the parameter, we can know almost all of the information of the parameter. But methods to the construction of the Confidence Distribution are not unique, so we can get different Confidence Distributions and then find the optimal one.
The main work of this article is using the Confidence Distribution method to solve the Behrens-Fisher problem. Firstly, we define the Confidence Distribution; then, we construct Confidence Distribution through some test method and prove these distributions to meet the definition; finally we find the optimal solution Confidence Distribution through numerical simulation.
2. Definition
The concept of “confidence” was first introduced by Neyman (1934, 1937) in his seminal papers on confidence intervals, where frequentist repetition properties for confidence were clarified. The earliest use of the terminology “confidence distribution” that we can find so far in a formal publication is Cox (1958). But for a long time nobody gives a complete and specific definition for Confidence Distribution.
The following definition is proposed and utilized in Schweder & Hjort (2002) [3] and Singh et al. (2005, 2007) [4] [5] .
Definition 2.1: Given:  is the parameter space of the unknown parameter of interest
is the parameter space of the unknown parameter of interest ; X is the sample space corresponding to sample data
; X is the sample space corresponding to sample data . We called the function
. We called the function 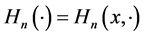 a confidence distribution (CD) for a parameter
a confidence distribution (CD) for a parameter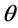 , if
, if
1) For each given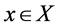 ,
,  is a cumulative distribution functionon
is a cumulative distribution functionon ;
;
2) At the true parameter value

Also, the function 
Theorem 2.1: If for each given




Proof: The cumulative distribution function 




At
Thus, 
3. Structure and Proof
There is no fixed method to structure Confidence Distribution, we only need to construct to meet the definition of confidence distribution. Here we use some test method of Behrens-Fisher problem to structure Confidence Distribution.
3.1. WS Distribution
Firstly, we use one of the most widely used method―“Welch?Satterthwaite test” (WST) [6] [7] to structure Confidence Distribution. The known conclusion is:
where

is the 
On the basis of the conclusion above, we can easily get a probability distribution function (PDF) of
Theorem 3.1:


Proof: According to the probability distribution function (PDF) of the Student’s t distribution:
where k is the degree of freedom, 





3.2. CC Distribution
The most prominent test after the WST is the one proposed by Cochran and Cox (1950) [8] . The known conclusion is:
where

is the 

On the basis of the conclusion above, we can easily get a probability distribution function (PDF) of
Theorem 3.2:


Proof: 



3.3. GP Distribution
Taking advantage of the computational resources that are available today, the generalized p-value test (GPT) [9] uses a suitable pivot to come up with a simple test procedure. The known conclusion is:
where 


On the basis of the conclusion above, we can easily get a probability distribution function (PDF) of
1) The probability distribution function (PDF) of
2) The probability distribution function (PDF) of
3) The probability distribution function (PDF) of
4) The probability distribution function (PDF) of
Theorem 3.3:


Proof: 



3.4. CA Distribution
According to the classical Likelihood Ratio Tests and parameters bootstrap method, Chang and Pal (2008) [10] proposed Computational Approach Test (CAT). The known conclusion is:
where 


On the basis of the conclusion above, we can easily get a probability distribution function (PDF) of
Theorem 3.4:


Proof: 





In this section, we construct four different Confidence Distributions to solve the Behrens-Fisher problem. Through this method, we the Confidence Distribution method, we can get almost all of the information of the parameter
4. Numerical Simulation
4.1. Effectiveness
First of all, we need to consider the effectiveness of the Confidence Distribution in Behrens-Fisher problem. Here, we define the effectiveness of the Confidence Distribution:
In this problem, we have a very small sample. In the numerical simulation, we define:
where, I is a indicative function. The more 

After the text edit has been completed, the paper is ready for the template. Duplicate the template file by using the save as command, and use the naming convention prescribed by your journal for the name of your paper. In this newly created file, highlight all of the contents and import your prepared text file. You are now ready to style your paper.
4.2. Optimality
Both 







4.3. Numerical Simulation
In the case of similar effectiveness, we consider the length of the confidence interval, the shorter length of the confidence interval corresponding Confidence Distribution is optimum (Table 1).
According to the result of numerical simulation, we can see:
1) With the increase of sample size, the effectiveness of each Confidence Distribution increase;
2) In the small sample size, the effectiveness of ws and ca is relatively high;
3) In the relatively big sample size, cc, ws, ca are relatively stable and highly effective.
5. Conclusion
We construct four different Confidence Distributions. Through the numerical simulation we can find the optimal Confidence Distribution. In small sample size and relatively big sample size, the effectiveness of ws care rela-
Table 1. Under the condition of

tively close, so we can compare the length of the confidence interval. Due tows come from the Student’s t distribution, ca comes from the standard normal distribution and the Student’s t distribution is a fat tail distribution, so ca is better than cc and ws. Therefore, this paper argues that the ca distribution is the optimal Confidence Distribution to solve the Behrens-Fisher problem.
Cite this paper
WenyongTao,WanzhouYe, (2016) The Confidence Distribution Method to the Behrens-Fisher Problem. Journal of Applied Mathematics and Physics,04,286-293. doi: 10.4236/jamp.2016.42036
References
- 1. Xu, J.Q. (2011) The Generalized Confidence Interval of the Behrens-Fisher Problem. Statistics and Decision, 2, 29-30.
- 2. Xie, M.G. and Singh, K. (2013) Confidence Distribution, the Frequentist Distribution Estimator of a Parameter: A Review. International Statistical Review, 81, 3-39.
- 3. Schweder, T. and Hjort, N.L. (2002) Confidence and Likelihood. Scandinavian Journal of Statistics, 29, 309-332.
http://dx.doi.org/10.1111/1467-9469.00285 - 4. Singh, K., Xie, M. and Strawderman, W.E. (2005) Combining Information from Independent Sources through Confidence Distributions. Annals of Statistics, 33, 159-183.
http://dx.doi.org/10.1214/009053604000001084 - 5. Singh, K., Xie, M. and Strawderman, W.E. (2007) Confidence Distribution (CD)—Distribution Estimator of a Parameter. Complex Datasets and Inverse Problems, 54, 132-150.
http://dx.doi.org/10.1214/074921707000000102 - 6. Welch, B.L. (1949) Further Notes on Mrs. Aspin’s Tables. Biometrika, 36, 293-296.
- 7. Satterthwaite, F.E. (1946) An Approximate Distribution of Estimates of Variance Components. Biometrics Bulletin, 2, 110-114.
http://dx.doi.org/10.2307/3002019 - 8. Cochran, W.G. and Cox, G.M. (1950) Experimental Designs. John Wiley and Sons, New York.
- 9. Weerahandi, S. (1994) Exact Statistical Methods for Data Analysis (174-181). Springer Series in Statistics, Springer-Verlag, New York.
- 10. Chang, C.H. and Pal, N. (2008) A Revisit to the Behrens-Fisher Problem: Comparison of Five Test Methods. Communications in Statistics—Simulationand Computation, 37, 1064-1085.
- 11. Singh, K., Xie, M. and Strawderman, W. (2001) Confidence Distributions—Concept, Theory and Applications. Technical Report, Dept. of Statistics, Rutgers University, New Jersey, USA.






















