Journal of Applied Mathematics and Physics
Vol.04 No.01(2016), Article ID:62995,14 pages
10.4236/jamp.2016.41013
Flow over a Darcy Porous Layer of Variable Permeability
M. S. Abu Zaytoon, T. L. Alderson, M. H. Hamdan
Department of Mathematical Sciences, University of New Brunswick, Saint John, Canada

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 December 2015; accepted 22 January 2016; published 25 January 2016
ABSTRACT
In this work we consider coupled-parallel flow through a finite channel bounded below by a porous layer that is either finite or infinite in depth. The porous layer is one in which Darcy’s equation is valid under the assumption of variable permeability. A suitable permeability stratification function is derived in this work and the resulting variable velocity profile is analyzed. It will be shown that when an infinite porous layer is implemented, Darcy’s equation must be used with a constant permeability.
Keywords:
Coupled-Parallel Flow, Darcy Equation, Variable Permeability

1. Introduction
Flow through and over porous layers is encountered in natural and industrial settings. These include the natural flow of ground water and flow oil through the porous bedrock, the flow of nutrients into plants and blood flow in animal tissues [1] -[3] . Flow over porous layers, and over porous plates and surfaces is also driven by various industrial applications including lubrication mechanisms involving porous plates and linings, design of heating and cooling systems, engine cooling systems, and the design of porous surfaces (such as aircraft wings with porous cavities) to reduce drag. In addition, studies of fuel cells heavily depend on analysis of flow through and over porous layers.
The above and many other applications, together with a literature review of what has been accomplished in this field, have been discussed in greater details by Vafai and Thiagarajah [4] , who presented a classification of three fundamental problems and interface zones, involving interfacial interactions in saturated porous media.
Vafai and Thiagarajah [4] contend that most attention in the literature has been devoted to the problem of the interface region between a porous medium and a fluid. This problem involves coupled parallel flow through a free-space channel underlain by a porous layer of either finite or infinite depth. Flow through free-space is governed by Navier-Stokes equations and in the porous sediment by an appropriate model [5] . The use of Darcy’s law in the porous sediment has been predominant. This has received the most attention in order to determine the most appropriate model to use in the porous layer (that is, a Darcy or a non-Darcy model) and the most appropriate matching condition at the interface between the fluid layer and the porous medium. A survey of the various models employed in the porous layer, and the matching conditions at the interface, have been provided in an elegant article by Alazmi and Vafai [5] . Models of Darcy, Brinkman, and Forchheimer have been used, without consensus, by various authors to govern the flow in the porous layer, and matching conditions have ranged from Beavers and Joseph’s slip hypothesis [6] to the jump stress condition of Ochoa and Whitaker [7] , and continuity of velocity and shear stress at the interface (as suggested by Neale and Nader [8] ). Other theoretical and experimental conditions have been reviewed and discussed by Ehrhardt [9] .
Coupled parallel flow gained interest following the experiments of Beavers and Joseph [6] , approximately five decades ago, to determine the matching conditions at the interface between a porous medium and free-space. Prior to the pioneering work of Beavers and Joseph [6] , the use of a no-slip velocity condition along a porous interface between free-space and a porous medium was wide-spread in lubrication problems [10] . With their experimental observation that the mass flux through free-space channel is larger than that predicted by the Poiseuille flow when a no-slip condition is imposed, Beavers and Joseph [6] , provided an explanation in terms of a slip flow hypothesis at the interface and proposed the following empirical slip-flow condition that agreed well with their experiments:
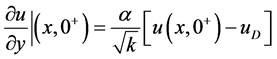 (1)
(1)
where 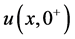 is the tangential velocity in the free-space channel,
is the tangential velocity in the free-space channel, 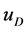 is the uniform Darcy velocity in the porous layer, k is the constant permeability, and
is the uniform Darcy velocity in the porous layer, k is the constant permeability, and 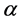 is a slip coefficient that depends on the porous medium properties.
is a slip coefficient that depends on the porous medium properties.
Saffman [11] , provided analysis based on Brinkman’s equation and suggested the following modification of Beavers and Joseph’s condition:
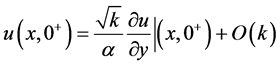 (2)
(2)
It is worth noting that Saffman’s modification (Equation (2)) decouples the tangential velocity in the channel from both the slip velocity and Darcy’s filtration velocity, but retains its dependence on the permeability and slip parameter. Ehrhardt [9] , provided an excellent review of the available interfacial conditions, and reported that due to the decoupling in equation (2), if the slip velocity is smaller than the maximal filtration velocity then setting the tangential velocity to zero is a reasonable approximation.
Based on their volume averaging analysis, Ochoa-Tapia and Whitaker [7] , showed that while matching Navier-Stokes equation with Brinkman’s equation maintains velocity continuity, a jump in the shear stress is induced. This was remedied by introducing the following jump condition that takes into account momentum transfer at the interface with the porous layer:
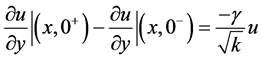 (3)
(3)
where 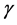 is an adjustable jump coefficient.
is an adjustable jump coefficient.
Detailed analysis of boundary conditions at the interface and the jump stress conditions have been provided by Chandesris and Jamet [12] , who bolstered the importance of the stress condition and its wide applicability in the study of flow over porous layers, and other contributors (cf. [3] [13] - [15] and the references therein).
Neale and Nader [8] discussed the significance of Brinkman’s equation and suggested the use of Brinkman’s equation in coupled parallel flow instead of Darcy’s law, due to the low differential order of Darcy’s law and its incompatibility with the Navier-Stokes differential order. They [8] , suggested conditions of velocity and shear
stress continuity at the interface, and obtained Beavers and Joseph’s results by using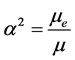 , where
, where 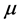 is the
is the
viscosity of the fluid and 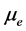 is the effective viscosity, that is, the viscosity of the fluid saturating the porous medium.
is the effective viscosity, that is, the viscosity of the fluid saturating the porous medium.
In addition to the work of Neale and Nader [8] , many other investigations point to a general agreement that conditions at the interface must emphasize velocity continuity and shear stress continuity in order to facilitate the matching of flow in the channel with the flow through the porous medium. These conditions have been successfully implemented in the analytical and numerical solutions of flow over porous layers (cf. [3] , and the references therein). Furthermore, many investigations point to the need for a non-Darcy model to govern flow through the porous layer. In particular, there had been increasing interest in the use of Brinkman’s equation [1] [2] , as a viable and more appropriate model to govern the flow in the porous layer due to a number of short- comings of Darcy’s. Of particular importance is the work of Rudraiah [3] , who concluded that Brinkman’s equation is a more appropriate model when the porous layer is of finite depth, and the work of Nield and Koznetsov [1] , who employed Brinkman’s equation in their pioneering work on transition layers between free space and Darcy’s layers.
In the above investigations, permeability has, in general, been considered constant (although in some of the models reported in Alazmi and Vafai [5] , permeability was defined in terms of the medium porosity or given as a function of porosity). In reality, however, it can be argued that naturally occurring porous layers (such as soil sediments) possess a layered structure with variable permeability. This is not a new idea. In fact, many investigations have dealt with flow through porous media with variable permeability, (cf. [16] [17] and the references therein), and flow through layers with permeability stratification, and the use of variable permeability in Brinkman’s equation, as it has been used by Nield and Kuznetsov [1] to serve as a transition layer between Darcy’s layer and a free-space channel.
Hamdan and Kamel [18] , considered idealization of Brinkman porous layer with permeability stratification, while Cheng [16] , considered flow through inhomogeneous porous media as governed by Darcy’s law with variable permeability that follows polynomial distribution. This concept of flow through and over porous layers with variable permeability motivates this work in which we consider, for the first time, flow through a channel bounded by a Darcy porous layer of variable permeability. This work is undertaken to demonstrate correctness of the imposed continuity conditions at the interface and to illustrate the behavior of the flow in a variable permeability environment. Furthermore, the type of modelling involved does away with the concept of a slip-velocity, as proposed by Beavers and Joseph [6] , for a judicious choice of permeability function that reaches its maximum at the interface between the channel and the medium. Furthermore, when permeability is taken as a variable function, Darcy’s law implies the velocity in the porous layer will be a non-constant, which in turn affords Darcy’s law compatibility of the Navier-Stokes equations in the chosen configuration. The two cases of finite and infinite porous layers are considered to illustrate characteristics of the flow, and to emphasize the conclusion that when an infinite Darcy layer is used then the permeability is essentially constant.
2. Problem Formulation and Solution
2.1. Problem Formulation: Finite Layer
Consider the flow of a viscous fluid through a straight channel of depth D bounded by a porous layer of thickness D, as shown in Figure 1.
Figure 1. Channel bounded by a porous layer.
The channel is bounded above by a solid wall at y = D, and the porous layer is terminated from below by a macroscopic boundary (solid wall) at y = −D. Flow through the configuration is driven by the same constant pressure gradient. Flow in the channel is governed by the Navier-Stokes equations, which take the form for the unidirectional flow at hand:
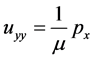 (4)
(4)
where 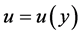 is the velocity in the channel,
is the velocity in the channel, 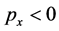 is the constant pressure gradient, and
is the constant pressure gradient, and 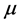 is the viscosity coefficient. Flow through the porous layer is governed by the following form of Darcy’s equation, written here for a variable permeability porous layer:
is the viscosity coefficient. Flow through the porous layer is governed by the following form of Darcy’s equation, written here for a variable permeability porous layer:

where 

For inhomogeneous soil layers the following form of variable permeability has been used [16] [17] :

where



It is thus required to solve Equations (4) and (5) subject to the following conditions.
No-slip on solid boundaries:


No penetration (zero permeability) on solid boundaries:

Maximum penetrability at the interface:

Velocity continuity at the interface:

Shear stress continuity at the interface:

2.2. Problem Solution
Equation (4) admits the solution

where 

Using (11) in (13) yields

while using (7) and (14) in (13) yields

Solution (13) thus takes the form:

An expression for the shear stress is obtained from (16) as:

At y = 0, Equation (17) reduces to:

Equation (5) gives the following expression at y = 0:

which, together with (11), gives the following expression for velocity at the interface:

From (5) we also obtain

and

Condition (12), together with (18) and (22) yield

and upon using (20) in (23), we obtain

or

Equation (25) provides an expression for the slope of the permeability function at the interface.
Velocity profile in the channel takes the following form, obtained by using (20) in (16):

Using (10) and (25) in (26) yields the following expression, equivalent to (16), for the velocity profile in the channel:

In order to determine a permeability profile, we rely on Equation (25) which 


Solution to (28) is obtained via separation of variables as:

In order to find the arbitrary constant 


Permeability profile (29) thus takes the form

The value of 

while the velocity at the interface, 

Velocity profile in the channel, Equation (26), thus takes the following form, in light of (32)

while the velocity profile in the porous layer is obtained from (5) and (31) as

Shear stress in the channel and in the porous layer are given, respectively, by


Shear stress at the interface, y = 0, is obtained from (36) or (37) as

2.3. Dimensionless Form of Solution
Solution presented by Equations (31) through (38) is expressed in dimensional form in order to illustrate the effects of viscosity, pressure gradient and channel depth on the flow variables. It is also important to express the solution in dimensionless form to better understand the role of dimensionless numbers (such as Reynolds number and dimensionless pressure gradient). To this end we present two forms of dimensionless results: one with respect to channel depth and one with respect to channel depth and a characteristic velocity.
The dimensionless form of the solution with respect to channel depth is obtained by defining the following dimensionless variables, where quantities with asterisks (*) are dimensionless,

Equation (31) through (38) take the following dimensionless forms, respectively, which do not involve a Reynolds number of the flow or a dimensionless pressure gradient:








The dimensionless form of the solution with respect to channel depth and characteristic velocity is obtained by defining the following dimensionless variables with respect to channel depth, D, and characteristic velocity, 

Equation (31) through (38) take the following dimensionless forms, respectively, which involve a Reynolds number of the flow and a dimensionless pressure gradient:








Both dimensionless forms are equivalent as they produce the same permeability, however, the velocities and shear stresses are scaled differently. Results based on both dimensionless forms are discussed in the Results and Discussion section, below.
2.4. Problem Formulation: Infinite Depth Layer
If in Figure 1 the bounding porous layer is of infinite depth, then we are required to solve Equation (4) On



Now, from Equations (5) and (58), we obtain

From (29) and condition (58) we obtain

Equation (60) implies that 

Observation 1:
In the study of coupled parallel flow through a channel over a porous layer of infinite depth, the flow through which is governed by Darcy’s law with an assumed exponential permeability, the only allowable permeability is essentially constant.
2.5. Volumetric Flow Rates
The Darcian volumetric flow rate through the porous layer is denoted here by

Using the velocity 

and an average Darcian velocity in the porous layer of

The Navier-Stokes volumetric flow rate through the channel is denoted here by

Using the velocity 

Under Poiseuille conditions, Navier-Stokes flow through a channel bounded by solid walls at y = 0 and y = D, on which no-slip conditions are imposed, has the velocity profile

and a volumetric flow rate of

The ratio of the volumetric flow rates, Equations (65) to (67), is given by

This ratio is greater than unity, thus indicating a reduction in the flow rate due to the introduction of a porous matrix in the flow domain.
2.6. Results and Discussion
2.6.1. Permeability Distribution
The dimensional permeability function has been determined as the smoothly varying function given by Equation (31). Dependence of the dimensional permeability function on the porous layer depth is illustrated in Figure 2, which demonstrates that the permeability is zero at the solid wall (y = −D) and increases until it reaches its maximum, 

Equations (40) and (49) render the same dimensionless permeability function, whose graph in Figure 2 coincides with the graph of the dimensional permeability when D = 1. The resulting dimensionless



Figure 2. Permeability distribution for D = 0:5; D = 1, and D = 2.
2.6.2. Velocity Distribution
The dimensional velocity profiles in the channel (Equation (34)) and in the porous layer (Equation (35)) are illus trated graphically in Figures 3-5 for different values of D and different ratios


Figure 3. Velocity profiles u(y) and v(y) for D = 0.5 and different values of
Figure 4. Velocity profiles u(y) and v(y) for D = 1 and different values of
Figure 5. Velocity profiles u(y) and v(y) for D = 2 and different values of
valently higher values of the driving pressure gradient for a fixed viscosity, results in increasing the velocity in both the porous layer and the channel, as well as increasing the velocity at the interface. It is worth noting that the chosen permeability distribution results in a smoothly varying velocity profiles for all values of pressure gradients, without the occurrence of a velocity slip at the interface.
As is well-known, a Navier-Stokes Poiseuille flow in a channel in the absence of a porous layer results in a parabolic velocity profile that is symmetric about mid-channel. In other words, the maximum value of velocity in the profile occurs at mid-channel. The introduction of a porous layer with a non-zero velocity at the interface results in a loss of symmetry of the parabolic velocity profile in the channel, and the attainment of a maximum velocity in the channel at a point lower than mid-channel. In fact, the location of maximum velocity in the
channel is independent of the ratio 



Each of Figures 3-5, shows the increase in the velocity at the interface, 


Figure 4 also corresponds to the dimensionless velocity profiles given by Equations (52) and (53) for different values of the product 



Figure 6. Dimensionless velocity profiles for 
Figure 7. Dimensionless velocity profiles for Re = 1and different values of
2.6.3. Interfacial Velocity and Shear Stress
Values of dimensional velocity, 




Values of dimensionless velocity, 






Table 1. Values of dimensional velocity and shear stress at the interface for different values of D and 
Table 2. Values of dimensionless velocity and shear stress at the interface for different values of Re and
3. Conclusion
In this work, we implemented a variable permeability Darcy equation in the study of flow through a channel bounded by a porous layer. The form of variable permeability was derived to produce a continuously varying velocity distribution across the channel and layer without resorting to the concept of slip that arises when the Beavers and Joseph condition is used. The main conclusion arrived at in this work is that when the porous layer is of infinite depth then the permeability must essentially be constant. This implies that the current model formulation should mainly be used with finite depth porous layers.
Cite this paper
M. S. AbuZaytoon,T. L.Alderson,M. H.Hamdan, (2016) Flow over a Darcy Porous Layer of Variable Permeability. Journal of Applied Mathematics and Physics,04,86-99. doi: 10.4236/jamp.2016.41013
References
- 1. Nield, D.A. and Kuznetsov, A.V. (2009) The Effect of a Transition Layer between a Fluid and a Porous Medium: Shear Flow in a Channel. Transport in Porous Media, 78, 477-487.
http://dx.doi.org/10.1007/s11242-009-9342-0 - 2. Parvazinia, M., Nassehi, V., Wakeman, R.J. and Ghoreishy, M.H.R. (2006) Finite Element Modeling of Flow through a Porous Medium between Two Parallel Plates Using the Brinkman Equation. Transport in Porous Media, 63, 71-90.
http://dx.doi.org/10.1007/s11242-005-2721-2 - 3. Rudraiah, N. (1986) Flow past Porous Layers and Their Stability. In: Cheremisinoff, N.P., Ed., Encyclopedia of Fluid Mechanics: Slurry Flow Technology, Gulf Publishing, Houston, 567-647.
- 4. Vafai, K. and Thiyagaraja, R. (1987) Analysis of Flow and Heat Transfer at the Interface Region of a Porous Medium. International Journal of Heat and Mass Transfer, 30, 1391-1405.
http://dx.doi.org/10.1016/0017-9310(87)90171-2 - 5. Alazmi, B. and Vafai, K. (2000) Analysis of Variants within the Porous Media Transport Models. Journal of Heat Transfer, 122, 303-326.
http://dx.doi.org/10.1115/1.521468 - 6. Beavers, G.S. and Joseph, D.D. (1967) Boundary Conditions at a Naturally Permeable Wall. Journal of Fluid Mechanics, 30, 197-207.
http://dx.doi.org/10.1017/S0022112067001375 - 7. Ochoa-Tapia, J.A. and Whitaker, S. (1981) Momentum Jump Condition at the Boundary between a Porous Medium and a Homogeneous Fluid: Inertial Effects. Journal of Porous Media, 1, 201-217.
- 8. Neale, G. and Nader, W. (1974) Practical Significance of Brinkman’s Extension of Darcy’s Law: Coupled Parallel Flows within a Channel and a Bounding Porous Medium. The Canadian Journal of Chemical Engineering, 52, 475-478.
http://dx.doi.org/10.1002/cjce.5450520407 - 9. Ehrhardt, M. (2010) An Introduction to Fluid-Porous Interface Coupling. Weierstrass Institute for Applied Analysis and Stochastics, Berlin.
- 10. Tao, L.N. and Joseph, D.D. (1962) Fluid Flow between Porous Rollers. Journal of Applied Mechanics, 29, 429-423.
http://dx.doi.org/10.1115/1.3640566 - 11. Saffman, P.G. (1971) On the Boundary Condition at the Surface of a Porous Medium. Studies in Applied Mathematics, 50, 93-101.
http://dx.doi.org/10.1002/sapm197150293 - 12. Chandesris, M. and Jamet, D. (2007) Boundary Conditions at a Fluid-Porous Interface: An a priori Estimation of the Stress Jump Coefficients. International Journal of Heat and Mass Transfer, 50, 3422-3436.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2007.01.053 - 13. Kaviany, M. (1985) Laminar Flow through a Porous Channel Bounded by Isothermal Parallel Plates. International Journal of Heat and Mass Transfer, 28, 851-858.
http://dx.doi.org/10.1016/0017-9310(85)90234-0 - 14. Chandrasekhara, B.C., Rajani, K. and Rudraiah, N. (1978) Effect of Slip on Porous-Walled Squeeze Films in the Presence of a Transverse Magnetic Field. Applied Scientific Research, 34, 393-411.
http://dx.doi.org/10.1007/BF00383973 - 15. Sahraoui, M. and Kaviany, M. (1992) Slip and No-Slip Velocity Boundary Conditions at Interface of Porous, Plain Media. International Journal of Heat and Mass Transfer, 35, 927-943.
http://dx.doi.org/10.1016/0017-9310(92)90258-T - 16. Cheng, A.H.-D. (1984) Darcy’s Flow with Variable Permeability: A Boundary Integral Solution. Water Resources Research, 20, 980-984.
http://dx.doi.org/10.1029/WR020i007p00980 - 17. Mahmoud, M.S. and Deresiewicz, H. (1980) Settlement of Inhomogeneous Consolidating Soils—I: The Single-Drained Layer under Confined Compression. International Journal for Numerical and Analytical Methods in Geomechanics, 4, 57-72.
http://dx.doi.org/10.1002/nag.1610040105 - 18. Hamdan, M.H. and Kamel, M.T. (2011) Flow through Variable Permeability Porous Layers. Advances in Theoretical and Applied Mechanics, 4, 135-145.









