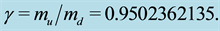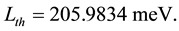Journal of Applied Mathematics and Physics
Vol.03 No.11(2015), Article ID:61351,10 pages
10.4236/jamp.2015.311169
Structure of Schrödinger’s Nucleon. Density Distributions and Zemach Momenta
Gintautas P. Kamuntavičius
Vytautas Magnus University, Kaunas, Lithuania

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 10 October 2015; accepted 20 November 2015; published 23 November 2015

ABSTRACT
The recently introduced Galilei invariant model of the nucleon as a system of three point particles, whose dynamics is governed by Schrödinger equation, is applied for nucleon structure investigation. The obtained charge, magnetism, mass and point particles density distributions of the proton and neutron are in satisfactory agreement with known information about nucleon structure. The model predicts the third Zemach momentum of proton larger than the one obtained in dipole approximation and larger than following from electron-proton data analysis.
Keywords:
Solutions of Wave Equations (Bound States), Potential Models, Proton and Neutron

1. Introduction
The only source of experimental information about nucleon’s charge and magnetism distributions are corresponding elastic form factors. However, the step from known at some set of values of momentum transfer form factor to corresponding density is not easy. The density distribution is completely determined if form factor is known for all values of momentum transfer q2. At large values of q2 it is extremely difficult to obtain form factor, hence phenomenological approach for density distribution with a number of free parameters, reproducing measured values of form factors, is a common praxis. However, even more or less precisely defined density distribution is not the best tool for nucleon structure investigation. Obviously, it is enough for simple multiplicative operators expectation values calculation, but in more complex cases, when for observables description operators are needed, whose place is between bra and ket functions, the density distribution carries crude information about nucleon. The first among these are currents operators, like magnetic momenta. Microscopic model of the nucleon is necessary for calculation of expectation values of these operators.
One of the alternatives for solution of this problem is simple, it is based on Hamiltonian dynamics, model [1] , considering the proton and neutron as different systems of three point particles (PP) in correspondence with the Standard Model recommendations―proton as the system of two up (uPP) and one down (dPP) particle, while neutron―as a system of one uPP and two dPP particles. These particles should not be identified with the quarks of the Standard Model because only their spins (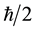 ), charges (
), charges (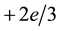 and
and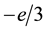 ) and baryon numbers (1/3) match the respective quarks quantum numbers. Both PP of our model are different, thus isospin quantum number is not necessary. Therefore, the color quantum number, which is used in the Standard Model to antisymmetrize the wave function, is also unnecessary. In our model antisymmetry is ensured with a smaller number of wave-function’s degrees of freedom. As usual, the baryon number is necessary to prevent the possibility of system excitation when one or two PP escape to continuous spectrum. The character of PPs, composing the nucleon, allows to define the magnetic momenta of structureless particles in Dirac’s way. The interactions of different pairs of PP (uu, ud and dd) contain the Coulomb and spring (three-dimensional harmonic oscillator) potentials, having four free parameters. Thus, together with PP masses the model Hamiltonian has six parameters. It is shown that these parameters can be chosen so that the masses, magnetic momenta and charge distribution radii of the proton and neutron could be predicted with experimental, present in Particle Data Group 2014 report [2] , precision. The model application for form factors and radii calculation gives results satisfactory agreeing with experimental information [3] . This paper is devoted for developed model application for nucleon’s charge, magnetism, mass and point particles densities distributions and for Zemach momenta of proton investigation.
) and baryon numbers (1/3) match the respective quarks quantum numbers. Both PP of our model are different, thus isospin quantum number is not necessary. Therefore, the color quantum number, which is used in the Standard Model to antisymmetrize the wave function, is also unnecessary. In our model antisymmetry is ensured with a smaller number of wave-function’s degrees of freedom. As usual, the baryon number is necessary to prevent the possibility of system excitation when one or two PP escape to continuous spectrum. The character of PPs, composing the nucleon, allows to define the magnetic momenta of structureless particles in Dirac’s way. The interactions of different pairs of PP (uu, ud and dd) contain the Coulomb and spring (three-dimensional harmonic oscillator) potentials, having four free parameters. Thus, together with PP masses the model Hamiltonian has six parameters. It is shown that these parameters can be chosen so that the masses, magnetic momenta and charge distribution radii of the proton and neutron could be predicted with experimental, present in Particle Data Group 2014 report [2] , precision. The model application for form factors and radii calculation gives results satisfactory agreeing with experimental information [3] . This paper is devoted for developed model application for nucleon’s charge, magnetism, mass and point particles densities distributions and for Zemach momenta of proton investigation.
The value of the third Zemach momentum of the proton is key figure for current puzzle regarding the proton radius, determined from the muon and electron Lamb shifts in hydrogen, resolution [4] -[7] . The proton charge radius, recommended by CODATA compilation [2] , is
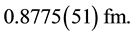 (1)
(1)
However, a very precise measurement of the Lamb-shift in muonic hydrogen [8] has shown that proton charge radius equals (see Ref. [9] ):
 (2)
(2)
Therefore, the remarkable difference between proton charge radii of electronic and muonic hydrogen exists. The origin of this result is unknown yet. As pointed out in [5] , the discrepancy between these results can be explained if the third Zemach momentum of the proton equals
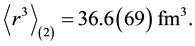 (3)
(3)
This value is more than 13 times larger than the result, obtained applying electron-proton scattering data [6] :
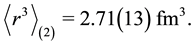 (4)
(4)
Similar value has been obtained in recent paper, Ref. [7] :
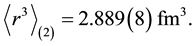 (5)
(5)
Thus, the results of our model, giving possibility for Zemach momenta calculation applying original definition with charge and magnetic form factors convolution can provide some new information about this problem.
2. The Galilei Invariant Density Operator
By definition, the elastic form factor of nucleon is density operator’s Fourier image:
 (6)
(6)
Here  denotes the proton,
denotes the proton,  stands for the neutron, while
stands for the neutron, while
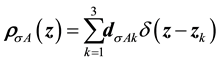 (7)
(7)
is density operator in the nucleon’s center-of-mass reference frame. The  where
where
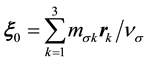 (8)
(8)
is center-of-mass radius vector.  due to
due to
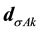




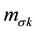

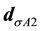
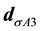
The inverse of (6) defines the density operator in terms of form factor operator:
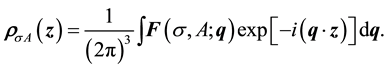
A few modifications of present definitions are useful. The electric and magnetic form factors of nucleon are defined as functions, independent of angles of momentum transfer q, hence in last equation integration by angles 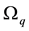
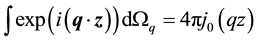
gives the following result:

Therefore, the form factor, independent of angles produces the spherically symmetrical charge and magnetism of nucleon distributions.
The next is introduction of dimensionless form factors defined as

so that 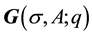
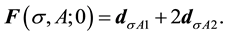
The only problem of this definition is the electric form factor of the neutron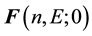
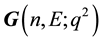
Introduction of dimensionless operators
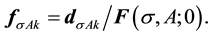
in density definition is also useful. This modifies final expression of form factor operator, applied in a given below text, to the following form:
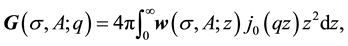
where
The density presentation in terms of dimensionless form factor
can be obtained applying spherical Bessel functions orthogonality relation

The well-known for different evaluations the so called dipole form factor is

where 
is
This density distribution produces following momenta:
hence root mean square radius of nucleon in this approximation equals 0.811 fm.
3. Density Distributions
The density at given z equals the expectation value of operator (16). However, this operator is overcrowded by variables because the coordinates of point particles in reference system which origin is situated in center of mass of nucleon satisfies condition
hence only two of them are independent. These two linear combinations have to be chosen equal to the intrinsic Jacobi variables, present in wave function expression. The operator (16) written in these variables is:
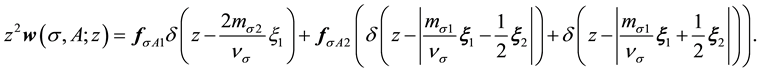
The integration gives
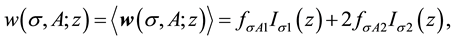
where mean values of operators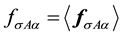
The calculation of expectation value of the first part of this operator is straightforward and can be performed without any problems.

Here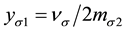
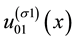

Table 1. Expectation values of operators, present in density definition, Equation (25). The parameter of model
tinguishability of the second and the third PP. The wave function of nucleon is antisymmetric in respect of these particles permutation, sum of the second and the third delta functions of (24) is symmetrical, hence mean values of both deltas coincide, i.e.,
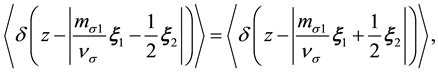
thus
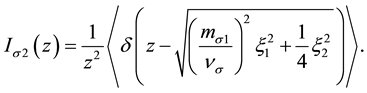
The expectation value of this delta-function calculation requires Dirac delta argument modification, applying the following expression:

where 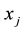
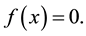
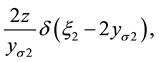
where
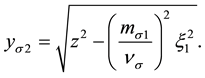
Thus, the second integral takes the form:

By definition, both integrals are normalized
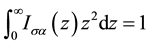
and due to the obvious condition
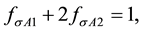
the normalization is valid also for charge and magnetism densities of the proton and magnetism density of neutron. As mentioned above, the only exception is charge density of neutron. In this case
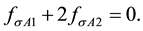
The radial density distributions, defined as
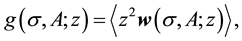
hence normalized in following way:
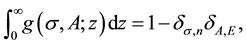
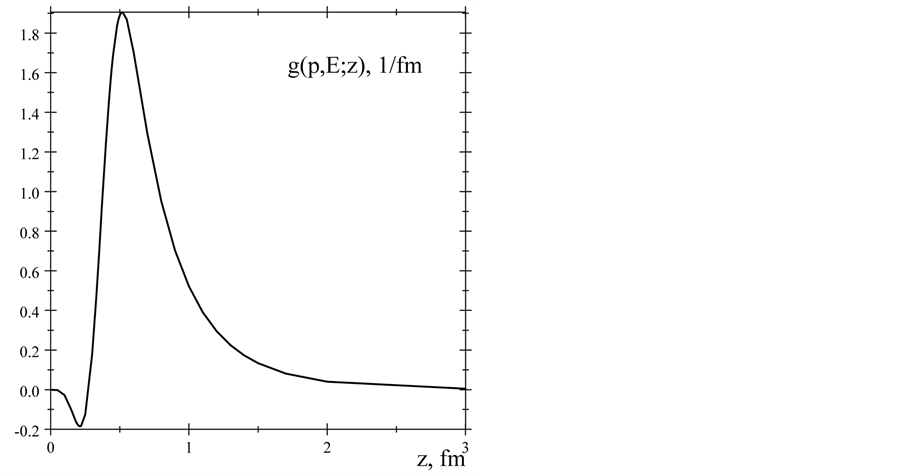
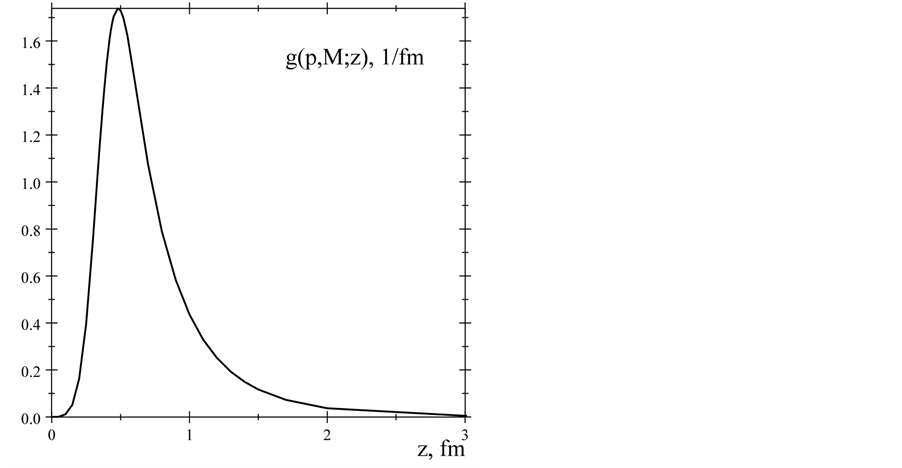
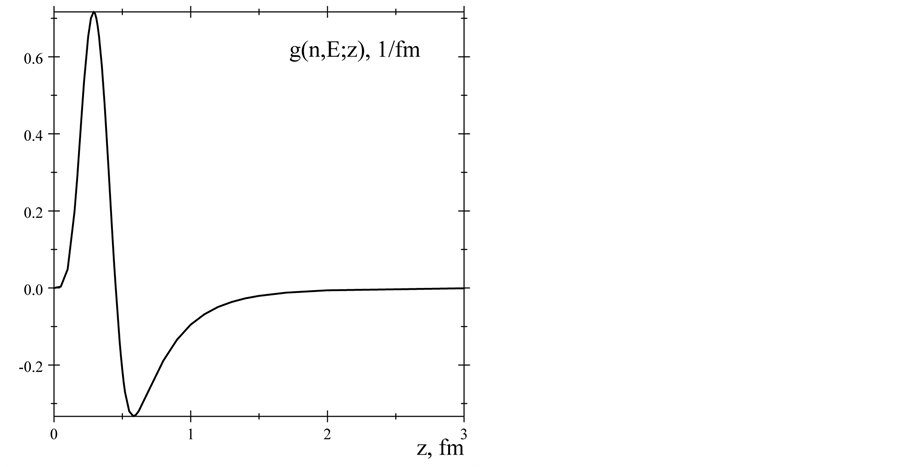
are present in Figures 1-4.
4. Zemach Momenta
The Zemach momenta [10] are defined as:
Figure 1. The proton’s radial charge density distribution.
Figure 2. The proton’s radial magnetism density distribution.

Here 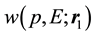
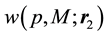

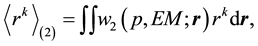
where
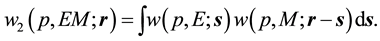
Figure 3. The neutron’s radial charge density distribution.
Figure 4. The neutron’s radial magnetism density distribution.
There is an interesting possibility to express these densities in terms of corresponding elastic form factors, and obtain the following convoluted density presentation
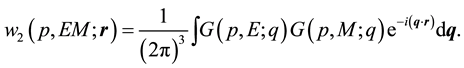
Zemach momenta evaluations with coinciding both density distributions, equal the dipole or charge density distribution are the best known. In dipole approximation the convoluted density can be present as
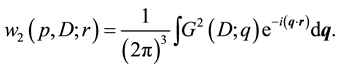
This density again is spherically symmetrical, i.e. independent of angles of r, hence normalized in following way:
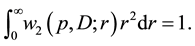
It equals
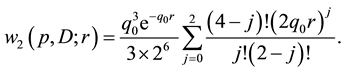
Therefore, the Zemach momenta in dipole approximation are defined by the following expression:
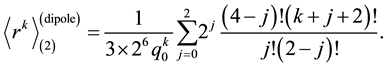
The numerical values of first three Zemach momenta 
5. Conclusions
The obtained density distributions demonstrate good enough comparison with known information about nucleon structure. The proton has a negatively charged dPP situated near the center of mass and cloud of positive charge, created by uPPs, and neutron shows an opposite picture. As mentioned in [1] and follows from the present consideration, the distributions of electric and magnetic charges within the nucleon are significantly different and neutron appears as a more compact structure than the proton. Obtained mass and point particles distribution densities 

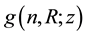
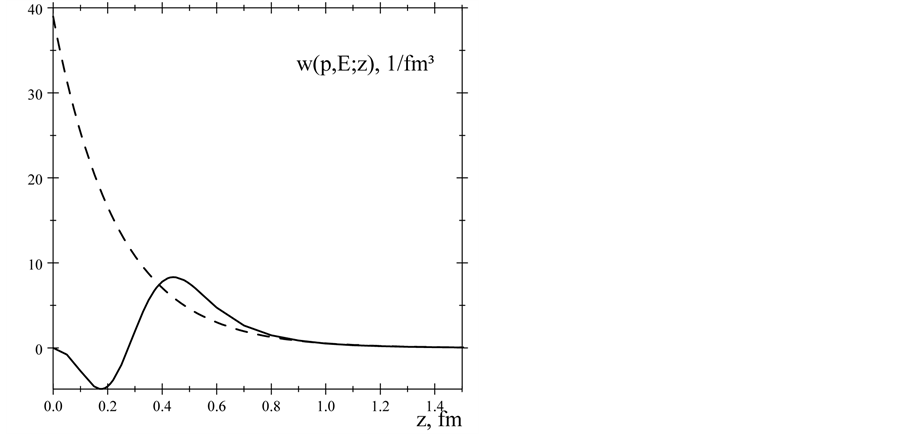
As mentioned earlier, the form factors are the source of information about nucleon density distributions. Different parametrizations of form factors produce different density distributions and radii of nucleon. However, the basic for these modifications is dipole form factor, predicting exponential density dependence, Equation (21). This prediction and our result for proton charge density are presented in Figure 5.
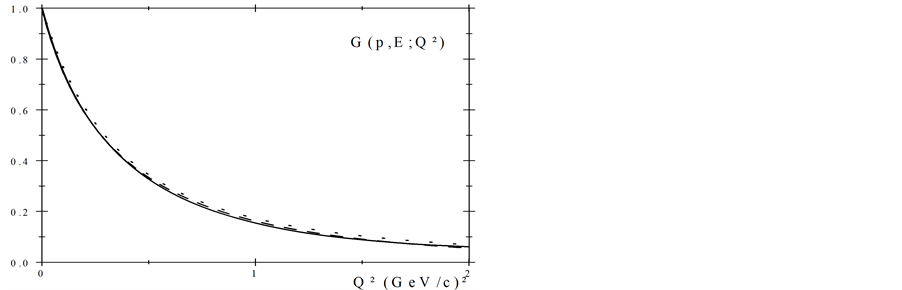
The difference is obvious. However, the charge form factors of proton, obtained in dipole approximation, Equation (19); the charge form factor, given by the best fit to experimental data [11] ; and corresponding form factor, obtained applying our model, are not so different in region of small momentum transfer values, as it follows from Figure 6.
Obviously, the reason of significant difference of proton’s charge distributions is caused by elastic form factor dependence at larger values of momentum transfer. The dipole form factor is smooth function of momentum transfer, taking positive values at any momentum transfer. The model form factor dependence is significantly different. Our form factor possesses the nodes, producing diffraction minima of cross section at larger values of momentum transfer, characteristic for form factor of quantum system with complex intrinsic structure.
The theoretical value of the Lamb shift in the 
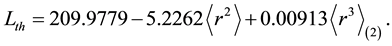
Table 2. Zemach momenta of the proton in dipole approximation 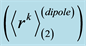
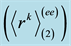

Figure 5. The proton’s charge density distribution w(p, E; z) (solid line) and density distribution corresponding the dipole form factor, Equation (21) (dashed line).
Figure 6. The electric form factor for the proton (solid line). The best fit of corresponding form factor from Ref. [11] (dashed line) and the standard dipole form factor, Equation (19) (dotted line) are shown for comparison.
The experimental value equals [9] :
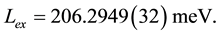
At proton charge radius, equal (2) the Zemach radius, necessary for 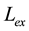
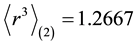
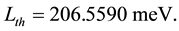
Therefore, the obtained precision of nucleon description allows to conclude that the calculations of other characteristics of the proton and neutron with model wave function may give some interesting and rather reliable results investigating the modifications of nucleon structure when it is present in an atomic nucleus.
Cite this paper
Gintautas P.Kamuntavičius, (2015) Structure of Schrödinger’s Nucleon. Density Distributions and Zemach Momenta. Journal of Applied Mathematics and Physics,03,1412-1421. doi: 10.4236/jamp.2015.311169
References
- 1. Kamuntavicius, G.P. (2014) Nucleon as a Nonrelativistic Three Point Particles System. SOP Transactions on Theoretical Physics, 1, 44-56.
http://dx.doi.org/10.15764/TPHY.2014.04004 - 2. Olive, K.A., et al. (Particle Data Group) (2014) Review of Particle Physics. Chinese Physics C, 38, 090001.
http://dx.doi.org/10.1088/1674-1137/38/9/090001 - 3. Kamuntavicius, G.P. (2015) Structure of Schrödinger’s Nucleon: Elastic Form-Factors and Radii. Journal of Applied Mathematics and Physics, 3, 1352-1360.
http://dx.doi.org/10.4236/jamp.2015.310162 - 4. Cloët, I.C. and Miller, G.A. (2011) Third Zemach Moment of the Proton. Physical Review C, 83, 012201(R).
http://dx.doi.org/10.1103/PhysRevC.83.012201 - 5. De Rújula, A. (2010) QED Is Not Endangered by the Proton’s Size. Physics Letters B, 693, 555-558.
http://dx.doi.org/10.1016/j.physletb.2010.08.074 - 6. Friar, J.L. and Sick, I. (2005) Muonic Hydrogen and the Third Zemach Moment. Physical Review A, 72, 040502(R).
http://dx.doi.org/10.1103/PhysRevA.72.040502 - 7. Graczyk, K.M. and Juszczak, C. (2015) Zemach Moments of the Proton from Bayesian Inference. Physical Review C, 91, 045205.
http://dx.doi.org/10.1103/physrevc.91.045205 - 8. Pohl, R., et al. (2010) The Size of the Proton. Nature (London), 466, 213-216. http://dx.doi.org/10.1038/nature09250
- 9. Antognini, A., et al. (2013) Proton Structure from the Measurement of 2s-2p Transition Frequencies of Muonic Hydrogen. Science, 339, 417-420.
http://dx.doi.org/10.1126/science.1230016 - 10. Zemach, A.C. (1956) Proton Structure and the Hyperfine Shift in Hydrogen. Physical Review, 104, 1771-1781.
http://dx.doi.org/10.1103/PhysRev.104.1771 - 11. Venkat, S., Arrington, J., Miller, G.A. and Zhan, X. (2011) Realistic Transverse Images of the Proton Charge and Magnetization Densities. Physical Review C, 83, 015203.
http://dx.doi.org/10.1103/PhysRevC.83.015203